On the Total Positivity and Accurate Computations of r-Bell Polynomial Bases

Abstract

A new class of matrices defined in terms of r-Stirling numbers is introduced. These r-Stirling matrices are totally positive and determine the linear transformation between monomial and r-Bell polynomial bases. An efficient algorithm for the computation to high relative accuracy of the bidiagonal factorization of r-Stirling matrices is provided and used to achieve computations to high relative accuracy for the resolution of relevant algebraic problems with collocation, Wronskian, and Gramian matrices of r-Bell bases. The numerical experimentation confirms the accuracy of the proposed procedure.

1. Introduction

The Stirling numbers form combinatorial sequences with remarkable properties and many applications in Combinatorics, Number Theory, or Special Functions, among others. The Stirling numbers were so named by Nielsen (cf. [1]) in honor of James Stirling, who computed them in 1730 (cf. [2]). Interested readers are referred to [3,4,5] to find a nice introduction and many nice properties of Stirling numbers. In the literature, many kinds of generalizations of Stirling numbers have been introduced and studied ([3,6]). In this paper, we shall focus on the r-Stirling numbers whose combinatorial and algebraic properties, in most cases, generalize those of the regular Stirling numbers.

The r-Bell polynomials (see [7]) are considered as an efficient mathematical tool for combinatorial analysis (cf. [5]) and can be applied in many different contexts: in the evaluation of some integrals and alternating sums [8,9], for  the analysis of the internal relations for the orthogonal invariants of a positive compact operator [10], in the Blissard problem [5], for the Newton sum rules for the zeros of polynomials [11], in the recurrence relations for a class of Freud-type polynomials [12] and in many other subjects.

In this paper, a class of r-Stirling matrices will be introduced. It will be shown that these matrices determine the linear transformations between monomial and r-Bell polynomial bases and have the property of being totally positive and, therefore, having all of their minors as non-negative. Several applications of the class of totally positive matrices can be found in [13,14,15]. Totally positive matrices can be expressed as a particular product of bidiagonal matrices (see [16,17]). This bidiagonal decomposition provides a representation of the totally positive matrices that exploits their total positivity property and allows us to derive algorithms to high relative accuracy for the resolution of relevant algebraic problems, such as, the computation of their inverses, eigenvalues, singular values, or the solution of some systems of linear equations.

A major issue in Numerical Linear Algebra is to obtain algorithms to high relative accuracy, because the relative errors in their computations will have the order of the machine precision and will not be drastically affected by the dimension or conditioning of the considered matrices. Consequently, the design of algorithms adapted to the structure of totally positive matrices and achieving computations to high relative accuracy has attracted the interest of many researchers (see [18,19,20,21,22,23,24]).

Let us recall that many interpolation, numerical quadrature, and approximation problems require algebra computations with collocation matrices of the considered bases. When solving Taylor interpolation problems, Wronskian matrices have to be considered. On the other hand, Gramian matrices define linear transformations to obtain orthogonal from nonorthogonal bases. Moreover, the inversion of Gramian matrices is also required when approximating, in the least-squares sense, curves by linear combinations of control points and the basis functions. The large range of applications of r-Bell polynomials has motivated us to exploit the total positivity property of r-Stirling matrices to design fast and accurate algorithms for the resolution of algebraic problems with collocation, Wronskian, and Gramian matrices of r-Bell polynomial bases.

The layout of this paper is as follows. Section 2 summarizes some notations and auxiliary results. Section 3 focuses on the class of r-Stirling matrices. Their bidiagonal decomposition is provided and their total positivity property is deduced. In Section 4, r-Bell polynomials are considered. Collocation, Wronskian, and Gramian matrices of r-Bell polynomial bases are shown to be totally positive. Then, using the proposed factorization for r-Stirling matrices, the resolution of the above mentioned algebraic problems can be achieved to high relative accuracy. Finally, Section 5 presents numerical experiments confirming the accuracy of the proposed methods for the computation of eigenvalues, singular values, inverses, or the solution of some linear systems related to collocation, Wronskian, and Gramian matrices of r-Bell polynomial bases.

2. Notations and Auxiliary Results

Let us recall that a matrix is totally positive (respectively, strictly totally positive) if all its minors are nonnegative (respectively, positive).

The Neville elimination is an alternative procedure to Gaussian elimination (see [16,17,25]). Given a nonsingular matrix $A={\left(a_{i,j}\right)}_{1\le i,j\le n+1}$, its Neville elimination calculates a sequence of $(n+1)\times (n+1)$ matrices $A^{\left(k\right)}$, $k=1,\dots ,n+1$, so that their elements below the main diagonal of the $k-1$ first columns are zeros and then $A^{(n+1)}$ is upper triangular.

From $A^{\left(k\right)}={\left(a_{i,j}^{\left(k\right)}\right)}_{1\le i,j\le n+1}$, the Neville elimination computes $A^{(k+1)}={\left(a_{i,j}^{(k+1)}\right)}_{1\le i,j\le n+1}$ as follows,

$$a_{i,j}^{(k+1)}:=\left\{\begin{array}{cc}{a}_{i,j}^{\left(k\right)},\hfill & \mathrm{if}1\le i\le k,\hfill \\ a_{i,j}^{\left(k\right)}-\frac{a_{i,k}^{\left(k\right)}}{a_{i-1,k}^{\left(k\right)}}{a}_{i-1,j}^{\left(k\right)},\hfill & \mathrm{if}k+1\le i,j\le n+1,\mathrm{and}{a}_{i-1,k}^{\left(k\right)}\ne 0,\hfill \\ a_{i,j}^{\left(k\right)},\hfill & \mathrm{if}k+1\le i\le n+1,\mathrm{and}{a}_{i-1,k}^{\left(k\right)}=0,\hfill \end{array}\right.$$

(1)

with $A^{\left(1\right)}:=A$. The element

$$p_{i,j}:=a_{i,j}^{\left(j\right)},1\le j\le i\le n+1,$$

(2)

is called the $(i,j)$ pivot and we say that $p_{i,i}$ is the i-th diagonal pivot of the Neville elimination of A. Whenever all pivots are nonzero, no row exchanges are needed in the Neville elimination procedure. The value

$$m_{i,j}:=\left\{\begin{array}{cc}{a}_{i,j}^{\left(j\right)}/a_{i-1,j}^{\left(j\right)}=p_{i,j}/p_{i-1,j},\hfill & \mathrm{if}{a}_{i-1,j}^{\left(j\right)}\ne 0,\hfill \\ \phantom{(}0,\hfill & \mathrm{if}{a}_{i-1,j}^{\left(j\right)}=0,\hfill \end{array}\right.$$

(3)

for $1\le j<i\le n+1$, is the $(i,j)$ multiplier of the Neville elimination of A.

The Neville elimination procedure of a nonsingular matrix is illustrated with the following example:

$$A=A^{\left(1\right)}=\left(\begin{array}{ccc}2& 4& 12\\ 8& 26& 138\\ 56& 262& 1704\end{array}\right)\to A^{\left(2\right)}=\left(\begin{array}{ccc}2& 4& 12\\ 0& 10& 90\\ 0& 80& 738\end{array}\right)\to A^{\left(3\right)}=\left(\begin{array}{ccc}2& 4& 12\\ 0& 10& 90\\ 0& 0& 18\end{array}\right).$$

(4)

The multipliers and the diagonal pivots are $m_{2,1}=4$, $m_{3,1}=7$, $m_{3,2}=8$, $p_{1,1}=2$, $p_{2,2}=10$, and $p_{3,3}=18$.

By Theorem 4.2 and the arguments of p. 116 of [17], a nonsingular totally positive $A\in {\mathbb{R}}^{(n+1)\times (n+1)}$ can be written as follows,

$$A=F_n{F}_{n-1}\dots F_{1}D{G}_1{G}_2\dots G_n,$$

(5)

where $F_i\in {\mathbb{R}}^{(n+1)\times (n+1)}$ and $G_i\in {\mathbb{R}}^{(n+1)\times (n+1)}$, $i=1,\dots ,n$, are the totally positive, lower and upper triangular bidiagonal matrices with the unit diagonal described by

$$\begin{array}{ccc}\hfill F_i& =& \left(\begin{array}{c}1\\ 0& 1\\ & \ddots & \ddots \\ & & 0& 1\\ & & & m_{i+1,1}& 1\\ & & & & m_{i+2,2}& 1\\ & & & & & \ddots & \ddots \\ & & & & & & m_{n+1,n+1-i}& 1\end{array}\right),\hfill \\ \hfill G_i^T& =& \left(\begin{array}{c}1\\ 0& 1\\ & \ddots & \ddots \\ & & 0& 1\\ & & & {\tilde{m}}_{i+1,1}& 1\\ & & & & {\tilde{m}}_{i+2,2}& 1\\ & & & & & \ddots & \ddots \\ & & & & & & {\tilde{m}}_{n+1,n+1-i}& 1\end{array}\right),\hfill \end{array}$$

(6)

and $D\in {\mathbb{R}}^{(n+1)\times (n+1)}$ is a diagonal matrix with positive diagonal entries. In fact, the elements in the diagonal of D are the diagonal pivots of the Neville elimination of A. On the other hand, the off-diagonal elements $m_{i,j}$ and ${\tilde{m}}_{i,j}$ are the multipliers of the Neville elimination of A and $A^T$, respectively.

Using the results in [16,17,25] and Theorem 2.2 of [22], the Neville elimination of A can be used to derive the following bidiagonal factorization (5) of its inverse matrix,

$$A^{-1}={\widehat{G}}_1{\widehat{G}}_2\dots {\widehat{G}}_n{D}^{-1}{\widehat{F}}_n{\widehat{F}}_{n-1}\dots {\widehat{F}}_1,$$

(7)

where ${\widehat{F}}_i\in {\mathbb{R}}^{(n+1)\times (n+1)}$ and ${\widehat{G}}_i\in {\mathbb{R}}^{(n+1)\times (n+1)}$ are the lower and upper triangular bidiagonal matrices with the form described in (6), which are obtained by replacing the off-diagonal entries $\{m_{i+1,1},\dots ,m_{n+1,n+1-i}\}$ and $\{{\tilde{m}}_{i+1,1},\dots ,{\tilde{m}}_{n+1,n+1-i}\}$ by $\{-m_{i+1,i},\dots ,-m_{n+1,i}\}$ and $\{-{\tilde{m}}_{i+1,i},\dots ,-{\tilde{m}}_{n+1,i}\}$, respectively. The structure of the bidiagonal matrix factors in (7) is described as follows,

$$\begin{array}{c}\hfill {\widehat{F}}_i=\left(\begin{array}{c}1\\ 0& 1\\ & \ddots & \ddots \\ & & 0& 1\\ & & & -m_{i+1,i}& 1\\ & & & & -m_{i+2,i}& 1\\ & & & & & \ddots & \ddots \\ & & & & & & m_{n+1,i}& 1\end{array}\right),\end{array}$$

(8)

$$\begin{array}{c}\hfill {\widehat{G}}_i^T=\left(\begin{array}{c}1\\ 0& 1\\ & \ddots & \ddots \\ & & 0& 1\\ & & & -{\tilde{m}}_{i+1,i}& 1\\ & & & & -{\tilde{m}}_{i+2,i}& 1\\ & & & & & \ddots & \ddots \\ & & & & & & {\tilde{m}}_{n+1,i}& 1\end{array}\right).\end{array}$$

(9)

Let us also observe that, if a matrix $A\in {\mathbb{R}}^{(n+1)\times (n+1)}$ is nonsingular and totally positive, its transpose $A^T$ is also nonsingular and totally positive, and

$$A^T={\tilde{F}}_n{\tilde{F}}_{n-1}\dots {\tilde{F}}_{1}D{\tilde{G}}_1{\tilde{G}}_2\dots {\tilde{G}}_n,$$

(10)

where ${\tilde{F}}_i=G_i^T$, $\widetilde{G_i}=F_i^T$ and $F_i$, $G_i$$i=1,\dots ,n$, are the lower and upper triangular bidiagonal matrices in (5).

The total positivity property of a given matrix can be characterized by analyzing the sign of the diagonal pivots and multipliers of its Neville elimination, as shown in Theorem 4.1, Corollary 5.5 of [25] and the arguments of p. 116 of [17].

Theorem 1. 

A nonsingular matrix A is totally positive (respectively, strictly totally positive) if and only if the Neville elimination of A and $A^T$ can be performed without row exchanges, all the multipliers of the Neville elimination of A and $A^T$ are nonnegative (respectively, positive) and the diagonal pivots of the Neville elimination of A are all positive.

In [19], the bidiagonal factorization (5) of a nonsingular and totally positive $A\in {\mathbb{R}}^{(n+1)\times (n+1)}$ is represented by defining a matrix $BD\left(A\right)={\left(BD{\left(A\right)}_{i,j}\right)}_{1\le i,j\le n+1}$ such that

$$BD{\left(A\right)}_{i,j}:=\left\{\begin{array}{cc}{m}_{i,j},\hfill & \mathrm{if}i>j,\hfill \\ p_{i,i},\hfill & \mathrm{if}i=j,\hfill \\ {\tilde{m}}_{j,i},\hfill & \mathrm{if}i<j.\hfill \end{array}\right.$$

(11)

This representation will allow us to define algorithms adapted to the totally positive structure and provide accurate computations with the matrix.

Let us observe that, for the matrix A in (4), the bidiagonal decomposition (5) can be written as follows:

$$\left(\begin{array}{ccc}2& 4& 12\\ 8& 26& 138\\ 56& 262& 1704\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 7& 1\end{array}\right)\left(\begin{array}{ccc}1& 0& 0\\ 4& 1& 0\\ 0& 8& 1\end{array}\right)\left(\begin{array}{ccc}2& 0& 0\\ 0& 10& 0\\ 0& 0& 18\end{array}\right)\left(\begin{array}{ccc}1& 2& 0\\ 0& 1& 6\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 3\\ 0& 0& 1\end{array}\right).$$

Moreover, since the diagonal pivots and multipliers of the Neville elimination of A and $A^T$ are all positive, we conclude that A is strictly totally positive. The above factorization can be represented in the following matrix form:

$$BD\left(A\right)=\left(\begin{array}{ccc}2& 2& 3\\ 4& 10& 6\\ 7& 8& 18\end{array}\right).$$

Let us also recall that a real value x is computed to high relative accuracy whenever the computed value $\tilde{x}$ satisfies

$$\left|\frac{x-\tilde{x}}{x}\right|<Ku,$$

where u is the unit round-off and $K>0$ is a constant, which is independent of the arithmetic precision. High relative accuracy implies a great accuracy in the computations, since the relative errors have the same order of the machine precision and the accuracy is not affected by the dimension or the conditioning of the problem we are solving.

A sufficient condition to assure that an algorithm can be computed to high relative accuracy is the non-inaccurate cancellation condition, sometimes denoted as the NIC condition, which is satisfied if the algorithm does not require inaccurate subtractions and only evaluates products, quotients, sums of numbers of the same sign, subtractions of numbers of the opposite sign, or subtraction of initial data (cf. [18,19]).

If the bidiagonal factorization (5) of a nonsingular and totally positive matrix A can be computed to high relative accuracy, the computation of its eigenvalues and singular values, the computation of $A^{-1}$, and even the resolution of systems of linear equations $Ax=b$, for vectors b with alternating signs, can be also computed to high relative accuracy, using the algorithms provided in [26].

Let $(u_0,\dots ,u_n)$ be a basis of a space U of functions defined on $I\subseteq R$. Given a sequence of parameters $x_1<\dots <x_{n+1}$ on I, the corresponding collocation matrix is defined by

$$M(x_1,\dots ,x_{n+1}):={\left(u_{j-1}\left(x_i\right)\right)}_{1\le i,j\le n+1}.$$

(12)

The system $(u_0,\dots ,u_n)$ of functions defined on $I\subseteq \mathbb{R}$ is totally positive if all of its collocation matrices $M(x_1,\dots ,x_{n+1})$ are totally positive.

If the space U is formed by n-times continuously differentiable functions and $x\in I$, the Wronskian matrix at x is defined by:

$$W(u_0,\dots ,u_n)\left(x\right):={\left(u_{j-1}^{(i-1)}\left(x\right)\right)}_{1\le i,j\le n+1},$$

(13)

where $u^{\left(i\right)}\left(x\right)$, $i\le n$, denotes the i-th derivative of u at x.

Now, let us suppose that U is a Hilbert space of functions under a given inner product $\langle u,v\rangle$ defined for any $u,v\in U$. Then, given linearly independent functions $u_0,\dots ,u_n$ in U, the corresponding Gram matrix is the symmetric matrix defined by:

$$G(u_0,\dots ,u_n):={\left(\langle u_{i-1},u_{j-1}\rangle \right)}_{1\le i,j\le n+1}.$$

3. Bidiagonal Factorization of $\mathit{r}$-Stirling Matrices

Let us recall that given $n,m\in \mathbb{N}$ with $m<n$, the (signless) Stirling number of the first kind, usually denoted by $\left[\genfrac{}{}{0pt}{}{n}{m}\right]$, can be defined combinatorially as the number of permutations of the set $\{1,\dots ,n\}$ having m cycles.

On the other hand, the Stirling number of the second kind, usually denoted by $\left\{\genfrac{}{}{0pt}{}{n}{m}\right\}$, coincides with the number of partitions of the set $\{1,\dots ,n\}$ into m non-empty disjoint blocks (cf. [3]). Moreover, the Bell number $B_n$ gives the total number of partitions of the set $\{1,\dots ,n\}$; that is,

$$B_n:=\sum _{m=0}^n\left\{\genfrac{}{}{0pt}{}{n}{m}\right\}.$$

The first and second kinds of Stirling numbers can be recursively computed as follows,

$$\left[\genfrac{}{}{0pt}{}{n}{k}\right]=(n-1)\left[\genfrac{}{}{0pt}{}{n-1}{k}\right]+\left[\genfrac{}{}{0pt}{}{n-1}{k-1}\right],\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}=k\left\{\genfrac{}{}{0pt}{}{n-1}{k}\right\}+\left\{\genfrac{}{}{0pt}{}{n-1}{k-1}\right\},$$

(14)

with the initial conditions

$$\left[\genfrac{}{}{0pt}{}{0}{0}\right]:=1,\left[\genfrac{}{}{0pt}{}{n}{0}\right]=\left[\genfrac{}{}{0pt}{}{0}{n}\right]:=0,\left\{\genfrac{}{}{0pt}{}{n}{n}\right\}:=1,\left\{\genfrac{}{}{0pt}{}{n}{0}\right\}=\left\{\genfrac{}{}{0pt}{}{0}{n}\right\}:=0,n\in \mathbb{N}.$$

(15)

The r-Stirling numbers are polynomials in r generalizing the regular Stirling numbers and they count some restricted permutations and partitions of sets with a given number of elements.

For $r\in \mathbb{N}$, the first kind r-Stirling number, denoted by ${\left[\genfrac{}{}{0pt}{}{n}{m}\right]}_r$, counts the number of permutations of the elements $\{1,\dots ,n\}$ having m cycles, such that $1,2,\dots ,r$ are in distinct cycles. In addition, the second kind r-Stirling number, denoted by ${\left\{\genfrac{}{}{0pt}{}{n}{m}\right\}}_r$, is defined as the number of set partitions of $\{1,\dots ,n+r\}$ into $m+r$ blocks such that the first r elements are in distinct blocks. Thus the r-Bell number $B_n^r$ gives the total number of partitions of the set $\{1,\dots ,n+r\}$, such that the first r elements are in distinct blocks; that is,

$$B_n^r:=\sum _{m=0}^n{\left\{\genfrac{}{}{0pt}{}{n}{m}\right\}}_r.$$

Clearly, for $r=0$, the r-Stirling numbers coincide with the corresponding regular Stirling numbers.

Theorems 1 and 2 of [3] prove that the r-Stirling numbers satisfy the recurrence relations verified by the regular Stirling numbers (see (14)); that is,

$${\left[\genfrac{}{}{0pt}{}{n}{k}\right]}_r=(n-1){\left[\genfrac{}{}{0pt}{}{n-1}{k}\right]}_r+{\left[\genfrac{}{}{0pt}{}{n-1}{k-1}\right]}_r,{\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}}_r=k{\left\{\genfrac{}{}{0pt}{}{n-1}{k}\right\}}_r+{\left\{\genfrac{}{}{0pt}{}{n-1}{k-1}\right\}}_r,$$

(16)

but with different initial conditions,

$${\left[\genfrac{}{}{0pt}{}{n}{k}\right]}_r=0,n<r,{\left[\genfrac{}{}{0pt}{}{n}{k}\right]}_r={\delta }_{k,r},n=r,$$

and

$${\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}}_r=0,n<r,{\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}}_r={\delta }_{k,r},n=r.$$

Moreover, for some particular values, the corresponding r-Stirling numbers can be easily obtained:

$$\begin{array}{ccc}& & {\left[\genfrac{}{}{0pt}{}{n}{n}\right]}_r={\left\{\genfrac{}{}{0pt}{}{n}{n}\right\}}_r=1,n\ge r.\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & {\left[\genfrac{}{}{0pt}{}{n}{k}\right]}_r={\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}}_r=0,k>n,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & {\left[\genfrac{}{}{0pt}{}{n}{r}\right]}_r=r^{\overline{n-r}}:=(n-1)(n-2)\dots r,k>n,\hfill \end{array}$$

(19)

$$\begin{array}{ccc}& & {\left\{\genfrac{}{}{0pt}{}{n}{r}\right\}}_r=r^{n-r}.\hfill \end{array}$$

(20)

Finally, let us recall a “cross” recurrence relating r-Stirling numbers of the second kind with a different r that is going to be used in this paper (see Theorem 4 of [3]). The r-Stirling numbers of the second kind satisfy

$$\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}={\left\{\genfrac{}{}{0pt}{}{n}{k}\right\}}_{r-1}-(r-1){\left\{\genfrac{}{}{0pt}{}{n-1}{k}\right\}}_{r-1},1\le r\le n.$$

(21)

Now, we are going to define triangular matrices whose entries are given in terms of r-Stirling numbers. We shall analyze their Neville elimination and derive their bidiagonal factorization (5).

Definition 1.

For $r,n\in \mathbb{N}$ with $0\le r\le n$, the $(n+1)\times (n+1)$ the first kind of r-Stirling matrix is the lower triangular matrix $L_n^r={\left(l_{i,j}^r\right)}_{1\le i,j\le n+1}$ with

$$l_{i,j}^r:={\left[\genfrac{}{}{0pt}{}{i+r-1}{j+r-1}\right]}_r,1\le i,j\le n+1.$$

(22)

On the other hand, the  $(n+1)\times (n+1)$ second kind of r-Stirling matrix, is the lower triangular matrix ${\overline{L}}_n^r={\left({\overline{l}}_{i,j}^r\right)}_{1\le i,j\le n+1}$ with

$${\overline{l}}_{i,j}^r:={\left\{\genfrac{}{}{0pt}{}{i+r-1}{j+r-1}\right\}}_r,1\le i,j\le n+1.$$

(23)

The following results provide the expression of the pivots and multipliers of the Neville elimination of r-Stirling matrices and their inverses. Then, their bidiagonal factorization (5) will be deduced and their total positivity property analyzed.

Theorem 2. 

For $r,n\in \mathbb{N}$ with $r\le n$, the first kind of r-Stirling matrix $L_n^r\in {\mathbb{R}}^{(n+1)\times (n+1)}$ is totally positive and admits the following factorization

$$L_n^r=F_n\dots F_1,$$

(24)

where $F_i$, $i=1,\dots ,n$, are the lower triangular bidiagonal matrices of the form (6), whose off-diagonal entries are given by

$$m_{i,j}=i+r-j-1,1\le j<i\le n+1.$$

(25)

Moreover,

$${\left(L_n^r\right)}^{-1}={\widehat{F}}_n\dots {\widehat{F}}_1,$$

(26)

where ${\widehat{F}}_i$, $i=1,\dots ,n$, are the lower triangular bidiagonal matrices of the form (6), whose off-diagonal entries are given by

$$m_{i,j}=-(r+j-1),1\le j<i\le n+1.$$

(27)

Proof. 

Let us define $L^{\left(1\right)}:=L_n^r$ and $L^{\left(k\right)}={\left(l_{ij}^{\left(k\right)}\right)}_{1\le i,j\le n+1}$, $k=2,\dots ,n$, the matrix obtained after $k-1$ steps of the Neville elimination of $L_n^r$. We shall deduce by induction on $k\in \{1,\dots ,n+1\}$ that

$$l_{i,j}^{\left(k\right)}={\left[\genfrac{}{}{0pt}{}{i+r-k}{j+r-k}\right]}_r.$$

(28)

For $k=1$, identities (28) follow from (22). Now, suppose that (28) is verified for some $k\in \{1,\dots ,n\}$. Then, taking into account (19), we can write

$$l_{i,k}^{\left(k\right)}/l_{i-1,k}^{\left(k\right)}={\left[\genfrac{}{}{0pt}{}{i+r-k}{r}\right]}_r/{\left[\genfrac{}{}{0pt}{}{i+r-k-1}{r}\right]}_r=r^{\overline{i-k}}/r^{\overline{i-k-1}}=i+r-k-1.$$

(29)

By (1), we have $l_{i,j}^{(k+1)}=l_{i,j}^{\left(k\right)}-\left(l_{i,k}^{\left(k\right)}/l_{i-1,k}^{\left(k\right)}\right)l_{l-1,j}^{\left(k\right)}$ and, using (16), (28), and (29), we derive

$$\begin{array}{c}\hfill l_{i,j}^{(k+1)}={\left[\genfrac{}{}{0pt}{}{i+r-k}{j+r-k}\right]}_r-(i+r-k-1){\left[\genfrac{}{}{0pt}{}{i+r-k-1}{j+r-k}\right]}_r={\left[\genfrac{}{}{0pt}{}{i+r-k-1}{j+r-k-1}\right]}_r,\end{array}$$

corresponding to the identity (35) for $k+1$.

By (2), (19), and (28), we deduce that the pivots of the Neville elimination of $L_n^r$ satisfy

$$p_{i,j}=l_{i,j}^{\left(j\right)}={\left[\genfrac{}{}{0pt}{}{i+r-j}{r}\right]}_r,$$

and so the diagonal pivots are $p_{i,i}={\left[\genfrac{}{}{0pt}{}{r}{r}\right]}_r=1$ for $i=1,\dots ,n+1$ (see (17)). Moreover, the following expression for the multipliers can be deduced

$$m_{i,j}=p_{i,j}/p_{i-1,j}={\left[\genfrac{}{}{0pt}{}{i+r-j}{r}\right]}_r/{\left[\genfrac{}{}{0pt}{}{i+r-j-1}{r}\right]}_r=i+r-j-1,1\le j<i\le n+1.$$

Clearly, $p_{i,i}>0$, for  $i=1,\dots ,n+1$, and  $m_{i,j}>0$, for $1\le j<i\le n+1$. Then, using Theorem 1, we deduce that $L_n^r$ is totally positive.

Finally, taking into account the bidiagonal factorization (7) for the inverse of a nonsingular totally positive matrix, the factorization (26) for ${\left(L_n^r\right)}^{-1}$ can be deduced easily.    □

The provided bidiagonal decomposition (5) of the first kind of r-Stirling matrix $L_n^r$ can be stored in a compact form through $BD\left(L_n^r\right)={\left(BD{\left(L_n^r\right)}_{i,j}\right)}_{1\le i,j\le n+1}$ with

$$BD{\left(L_n^r\right)}_{i,j}=\left\{\begin{array}{cc}i+r-j-1,\hfill & 2\le j<i\le n+1,\hfill \\ 1,\hfill & 1\le i=j\le n+1,\hfill \\ 0,\hfill & \mathrm{elsewhere}.\hfill \end{array}\right.$$

(30)

Now, the following result deduces the pivots and multipliers of the Neville elimination of r-Stirling matrices of the second kind and their inverses.

Theorem 3. 

For $r,n\in \mathbb{N}$ with $r\le n$, the $(n+1)\times (n+1)$ second kind r-Stirling matrix ${\overline{L}}_n^r$ admits a bidiagonal factorization

$${\overline{L}}_n^r=F_n\dots F_1,$$

(31)

where $F_i$, $i=1,\dots ,n$, are lower triangular bidiagonal matrices of the form (6), whose off-diagonal entries $m_{i,j}$, $1\le j<i\le n+1$, are given by

$$m_{i,j}=r+j-1,1\le j<i\le n+1.$$

(32)

Moreover,

$${\left({\overline{L}}_n^r\right)}^{-1}={\widehat{F}}_n\dots {\widehat{F}}_1,$$

(33)

where ${\widehat{F}}_i$, $i=1,\dots ,n$, are lower triangular bidiagonal matrices of the form (6), whose off-diagonal entries $m_{i,j}$, $1\le j<i\le n+1$, are given by

$$m_{i,j}=-(r+i-j-1).1\le j<i\le n+1.$$

(34)

Proof. 

Let us define $L^{\left(1\right)}:={\overline{L}}_n^r$ and $L^{\left(k\right)}={\left(l_{ij}^{\left(k\right)}\right)}_{1\le i,j\le n+1}$, $r=2,\dots ,n$, the matrix obtained after $k-1$ steps of the Neville elimination of ${\overline{L}}_n^r$. By induction on $k\in \{1,\dots ,n+1\}$, we shall deduce that

$$l_{i,j}^{\left(k\right)}={\left\{\genfrac{}{}{0pt}{}{i+r-1}{j+r-1}\right\}}_{r+k-1}.$$

(35)

Taking into account (23), identities (35) clearly hold for $k=1$. If (35) holds for some $k\in \{1,\dots ,n\}$, using (20), we have

$$l_{i,k}^{\left(k\right)}/l_{i-1,k}^{\left(k\right)}={\left\{\genfrac{}{}{0pt}{}{i+r-1}{k+r-1}\right\}}_{r+k-1}/{\left\{\genfrac{}{}{0pt}{}{i+r-2}{k+r-1}\right\}}_{r+k-1}=\frac{{(k+r-1)}^{i-k}}{{(k+r-1)}^{i-k-1}}=k+r-1.$$

(36)

Since $l_{i,j}^{(k+1)}=l_{i,j}^{\left(k\right)}-\left(l_{i,k}^{\left(k\right)}/l_{i-1,k}^{\left(k\right)}\right)l_{l-1,j}^{\left(k\right)}$ (see (1)), and taking into account (21), (35), and (36), we derive

$$\begin{array}{c}\hfill l_{i,j}^{(k+1)}={\left\{\genfrac{}{}{0pt}{}{i+r-1}{j+r-1}\right\}}_{r+k-1}-(r+k-1){\left\{\genfrac{}{}{0pt}{}{i+r-2}{j+r-1}\right\}}_{r+k-1}={\left\{\genfrac{}{}{0pt}{}{i+r-1}{j+r-1}\right\}}_{r+k},\end{array}$$

corresponding to the identity (35) for $k+1$.

Now, by considering (2), (20), and (35), we can easily deduce that

$$p_{i,j}=l_{i,j}^{\left(j\right)}={\left\{\genfrac{}{}{0pt}{}{i+r-1}{j+r-1}\right\}}_{r+j-1}={(r+j-1)}^{i-j},$$

and $p_{i,i}=1$, for $i=1,\dots ,n+1$. For the multipliers we have

$$m_{i,j}=p_{i,j}/p_{i-1,j}={(r+j-1)}^{i-j}/{(r+j-1)}^{i-j-1}.=r+j-1,1\le j<i\le n+1.$$

Clearly, $p_{i,i}>0$, for $i=1,\dots ,n+1$, $m_{i,j}>0$, for $1\le j<i\le n+1$ and, using Theorem 1, we conclude that ${\overline{L}}_n^r$ is strictly totally positive.

Finally, taking into account the bidiagonal factorization (7) for the inverse of a nonsingular totally positive matrix, the factorization (33) for ${\left({\overline{L}}_n^r\right)}^{-1}$ can be deduced.    □

The provided bidiagonal factorization (5) of the matrix ${\overline{L}}_n^r$ can be stored in a compact form through $BD\left({\overline{L}}_n^r\right)={\left(BD{\left({\overline{L}}_n^r\right)}_{i,j}\right)}_{1\le i,j\le n+1}$ with

$$BD{\left({\overline{L}}_n^r\right)}_{i,j}=\left\{\begin{array}{cc}r+j-1,\hfill & 2\le j<i\le n+1,\hfill \\ 1,\hfill & 1\le i=j\le n+1,\hfill \\ 0,\hfill & \mathrm{elsewhere}.\hfill \end{array}\right.$$

(37)

Remark 1.

Given a lower triangular $(n+1)\times (n+1)$ matrix, for any $k\le n+1$, the determinants of the submatrices using row $i_1,\dots ,i_k$ and columns $j_1,\dots ,j_k$ with $i_h\ge j_h$ for all $h\le k$ are called nontrivial minors because all other minors are zero. A lower triangular matrix is called ΔSTP if all its nontrivial minors are positive. Since Theorem 2 (respectively, Theorem 3) proves that the lower triangular matrix with unit diagonal $L_n^r$ (respectively, ${\overline{L}}_n^r$) has all multipliers of its Neville elimination positive, by Theorem 4.3 of [16], we conclude that $L_n^r$ (respectiveley, ${\overline{L}}_n^r$) is in fact ΔSTP.

Now, taking into account Theorems 2 and 3, we provide the pseudocode of Algorithms 1 and 2, respectively. Specifically, Algorithm 1 computes the matrix form $BD\left(L_n^r\right)$ in (30), for the bidiagonal decomposition of the first kind r-Stirling matrix $L_n^r$ in (24). Moreover, Algorithm 2 computes the matrix form $BD\left({\overline{L}}_n^r\right)$ in (37) for the bidiagonal decomposition of the r-Stirling matrix of the second kind ${\overline{L}}_n^r$ in (31). The computational cost of both algorithms is $O\left(n^2\right)$. Let us observe that none of the algorithms requires inaccurate subtractions, and so the provided matrices are computed to high relative accuracy. In fact, all of their entries are natural numbers.

Algorithm 1: Computation to high relative accuracy of $BD\left(L_n^r\right)$ (see (30))

Require: n, r Ensure: $BD{L}_n^r$ bidiagonal decomposition of $L_n^r$ to high relative accuracy $BD{L}_n^r=eye(n+1)$    for $i=2:n+1$      for $j=1:i-1$       $BD{L}_n^r(i,j)=i+r-j-1$       end     end

Algorithm 2: Computation to high relative accuracy of $BD\left({\overline{L}}_n^r\right)$ (see (37))

Require: n, r Ensure: $BD{\overline{L}}_n^r$ bidiagonal decomposition of ${\overline{L}}_n^r$ to high relative accuracy $BD{\overline{L}}_n^r=eye(n+1)$    for $i=2:n+1$      for $j=1:i-1$       $BD{\overline{L}}_n^r(i,j)=r+j-1$      end    end

4. Accurate Computations with r-Bell Bases

Let ${\mathbf{P}}^n\left(I\right)$ be the (n+1)-dimensional linear space formed by all polynomials in the variable x defined on a real interval I and whose degree is not greater than n; that is,

$${\mathbf{P}}^n\left(I\right):=\mathrm{span}\{1,x,\dots ,x^n\},x\in I.$$

For $n\in \mathbb{N}$, the  n degree r-Bell polynomial of the first kind is defined as

$$B_n^r\left(x\right):=\sum _{k=0}^n{\left[\genfrac{}{}{0pt}{}{n+r}{k+r}\right]}_r{x}^k.$$

(38)

Then we can define a system $(B_0^r,\dots ,B_n^r)$ of r-Bell polynomials of the first kind that satisfy

$${(B_0^r,\dots ,B_n^r)}^T=L_n^r{(m_0,\dots ,m_n)}^T,$$

(39)

where $m_i\left(x\right):=x^i$, $i=0,\dots ,n$ and $L_n^r$ is the $(n+1)\times (n+1)$ first kind of r-Stirling matrix defined by (22). By (24), $det{L}_n^r=1$ and we can guarantee that ${(B_0^r,\dots ,B_n^r)}^T$ is a basis of ${\mathbf{P}}^n\left(\mathbb{R}\right)$.

Definition 2.

We say that $(B_0^r,\dots ,B_n^r)$ is the r-Bell basis of the first kind of the polynomial space ${\mathbf{P}}^n\left(\mathbb{R}\right)$.

On the other hand, the r-Bell polynomials of the second kind ${\left\{{\overline{B}}_n^r\right\}}_{n\ge 0}$ in [3,27] are called r-Bell polynomials, which are defined by their generating function

$$\sum _{n\ge 0}{\overline{B}}_n^r\left(x\right)\frac{t^n}{n!}=\exp \left(x(e^t-1)+rt\right).$$

They can also be written in terms of the monomial basis as follows,

$${\overline{B}}_n^r\left(x\right)=\sum _{k=0}^n{\left\{\genfrac{}{}{0pt}{}{n+r}{k+r}\right\}}_r{x}^k,n\in \mathbb{N}.$$

(40)

and then

$${({\overline{B}}_0^r,\dots ,{\overline{B}}_n^r)}^T={\overline{L}}_n^r{(m_0,\dots ,m_n)}^T,$$

(41)

where ${\overline{L}}_n^r$ is the $(n+1)\times (n+1)$ second kind of r-Stirling matrix defined by (23). By  (31), $det{\overline{L}}_n^r=1$ and we can guarantee that ${({\overline{B}}_0^r,\dots ,{\overline{B}}_n^r)}^T$ is a basis of ${\mathbf{P}}^n\left(\mathbb{R}\right)$.

Definition 3.

We say that $({\overline{B}}_0^r,\dots ,{\overline{B}}_n^r)$ is the r-Bell basis of the second kind of ${\mathbf{P}}^n\left(\mathbb{R}\right)$.

Let us recall that the monomial basis $(m_0,\dots ,m_n)$, with $m_i\left(x\right)=x^i$ for $i=0,\dots ,n$, is a strictly totally positive basis of ${\mathbf{P}}^n(0,+\infty )$, and so the  collocation matrix

$$V:={\left(x_i^{j-1}\right)}_{1\le i,j\le n+1},$$

(42)

is strictly totally positive for any increasing sequence of positive values $0<x_1<\dots <x_{n+1}$ (see Section 3 of [19]). In fact, V is the Vandermonde matrix at the considered nodes. Let us recall that Vandermonde matrices have relevant applications in linear interpolation and numerical quadrature (see for example [28,29]). As for $BD\left(V\right)$, we have

$$BD{\left(V\right)}_{i,j}:=\left\{\begin{array}{cc}\prod _{k=1}^{j-1}\frac{x_i-x_{i-k}}{x_{i-1}-x_{i-k-1}},\hfill & \mathrm{if}i>j,\hfill \\ \prod _{k=1}^{i-1}(x_i-x_k),\hfill & \mathrm{if}i=j,\hfill \\ x_i,\hfill & \mathrm{if}i<j,\hfill \end{array}\right.$$

(43)

and it can be easily checked that the computation of $BD\left(V\right)$ does not require inaccurate cancellations and can be performed to high relative accuracy.

Taking into account the total positivity of the Vandermonde matrices and the total positivity of r-Stirling matrices of the first and second kinds, we shall derive the total positivity of r-Bell bases, as well as factorizations providing computations to high relative accuracy when considering their collocation matrices.

Theorem 4. 

The r-Bell basis of first and second kind are totally positive bases of ${\mathbf{P}}^n(0,+\infty )$. Moreover, given $0<x_1<\dots <x_{n+1}$, the collocation matrices

$$B:={\left(B_{j-1}^r\left(x_i\right)\right)}_{1\le i,j\le n+1},\overline{B}:={\left({\overline{B}}_{j-1}^r\left(x_i\right)\right)}_{1\le i,j\le n+1},$$

(44)

and their bidiagonal factorization (5) can be computed to high relative accuracy.

Proof. 

Given $0<x_1<\dots <x_{n+1}$, by formulae (39) and (41), the collocation matrices in (44) satisfy

$$B=V{\left(L_n^r\right)}^T,\overline{B}=V{\left({\overline{L}}_n^r\right)}^T,$$

(45)

where V is the Vandermonde matrix (42), and $L_n^r$ and ${\overline{L}}_n^r$ are r-Stirling matrices of the first and second kind, respectively.

It is well known that V is strictly totally positive at $0<x_1<\dots <x_{n+1}$ and its decomposition (5) can be computed to high relative accuracy (see [19]). By Theorem 2 (respectively, Theorem 3), $L_n^r$ (respectively, ${\overline{L}}_n^r$) is a nonsingular totally positive matrix and its decomposition (5) can be computed to high relative accuracy. Taking into account these facts, ${\left(L_n^r\right)}^T$ (respectively, ${\left({\overline{L}}_n^r\right)}^T$) is a nonsingular totally positive matrix and its bidiagonal decomposition can be also computed to high relative accuracy (see (10)). Therefore, we can deduce that B (respectively, $\overline{B}$) is a totally positive matrix since it is the product of totally positive matrices (see Theorem 3.1 of [13]). Moreover, using Algorithm 5.1 of [26], if the decomposition (5) of two nonsingular totally positive matrices is provided to high relative accuracy, then the decomposition of the product can be obtained to high relative accuracy. Consequently, B (respectively, $\overline{B}$) and its decomposition (5) can be obtained to high relative accuracy.    □

Corollary 1 of [20] provides the factorization (5) of $W:=W(m_0,\dots ,m_n)\left(x\right)$, the Wronskian matrix of the monomial basis $(m_0,\dots ,m_n)$ at $x\in \mathbb{R}$. For the matrix representation $BD\left(W\right)$, we have

$$BD{\left(W\right)}_{i,j}:=\left\{\begin{array}{cc}x,\hfill & \mathrm{if}i<j,\hfill \\ (i-1)!,\hfill & \mathrm{if}i=j,\hfill \\ 0,\hfill & \mathrm{if}i>j.\hfill \end{array}\right.$$

(46)

Taking into account the sign of the entries of $BD\left(W\right)$ and Theorem 1, one can derive that the Wronskian matrix of the monomial basis is totally positive for any $x>0$. Moreover, the computation of (46) satisfies the NIC condition and W can be computed to high relative accuracy. Using (46), computations to high relative accuracy when solving algebraic problems related to W have been achieved in [20] for $x>0$.

Using formula (39), it can be checked that

$$W(B_0^r,\dots ,B_n^r)\left(x\right)=W(m_0,\dots ,m_n)\left(x\right){\left(L_n^r\right)}^T,W({\overline{B}}_0^r,\dots ,{\overline{B}}_n^r)\left(x\right)=W(m_0,\dots ,m_n)\left(x\right){\left({\overline{L}}_n^r\right)}^T.$$

So, with the reasoning of the proof of Theorem 4, the next result follows and we can also guarantee computations to high relative accuracy when solving algebraic problems related to Wronkian matrices of r-Bell polynomial bases at positive values.

Theorem 5. 

Let $(B_0^r,\dots ,B_n^r)$ and $({\overline{B}}_0^r,\dots ,{\overline{B}}_n^r)$ be the r-Bell bases of the first and second kind, respectively. For any $x>0$, the Wronskian matrices $W_n^r:=W(B_0^r,\dots ,B_n^r)\left(x\right)$ and ${\overline{W}}_n^r:=W({\overline{B}}_0^r,\dots ,{\overline{B}}_n^r)\left(x\right)$ are nonsingular totally positive and their bidiagonal decomposition (5) can be computed to high relative accuracy.

It is well known that the polynomial space ${\mathbf{P}}^n\left([0,1]\right)$ is a Hilbert space under the inner product

$$〈p,q〉:={\int }_0^{1}p\left(x\right)q\left(x\right)dx,$$

(47)

and the Gramian matrix of the monomial basis $(m_0,\dots ,m_n)$ with respect to (47) is:

$$H_n:={\left({\int }_0^1{x}^{i+j-2}dx\right)}_{1\le i,j\le n+1}={\left(\frac{1}{i+j-1}\right)}_{1\le i,j\le n+1}.$$

(48)

The matrix $H_n$ is the $(n+1)\times (n+1)$ Hilbert matrix. In Numerical Linear Algebra, Hilbert matrices are well-known Hankel matrices. Their inverses and determinants have explicit formulas; however, they are very ill-conditioned for moderate values of their dimension. Then, they can be used to test numerical algorithms and see how they perform on ill-conditioned or nearly singular matrices. It is well known that Hilbert matrices are strictly totally positive. In [19], the pivots and the multipliers of the Neville elimination of H are explicitly derived. It can be checked that $BD\left(H_n\right)={\left(BD{\left(H_n\right)}_{i,j}\right)}_{1\le i,j\le n+1}$ is given by

$$BD{\left(H_n\right)}_{i,j}:=\left\{\begin{array}{cc}\frac{{(i-1)}^2}{(i+j-1)(i+j-2)},\hfill & \mathrm{if}i>j,\hfill \\ \frac{(i-1){!}^4}{(2i-1)!(2i-2)!},\hfill & \mathrm{if}i=j,\hfill \\ \frac{{(j-1)}^2}{(i+j-1)(i+j-2)},\hfill & \mathrm{if}i<j.\hfill \end{array}\right.$$

(49)

Clearly, the computation of the factorization (5) of $H_n$ does not require inaccurate cancellations, and so it can be computed to high relative accuracy.

Using formula (39), it can be checked that the Gramian matrices $G_n^r$ and ${\overline{G}}_n^r$ of the r-Bell bases of the first and second kind, respectively, with respect to the inner product (47), can be written as follows,

$$G_n^r=L_n^r{H}_n{\left(L_n^r\right)}^T,{\overline{G}}_n^r={\overline{L}}_n^r{H}_n{\left({\overline{L}}_n^r\right)}^T,$$

(50)

where $L_n^r$ (respectively, ${\overline{L}}_n^r$) is the $(n+1)\times (n+1)$r-Stirling matrix of the first (respectively, second) kind. According to the reasoning in the proof of Theorem 4, the following result can be deduced.

Theorem 6. 

The Gramian matrices $G_n^r$ and ${\overline{G}}_n^r$ of the r-Bell bases of the first and second kind, respectively, with respect to the inner product (47), are nonsingular and totally positive. Furthermore, $G_n^r$, ${\overline{G}}_n^r$ and their bidiagonal decompositions (5) can be computed to high relative accuracy.

Now, taking into account Algorithms 1 and 2, as well as Theorems 4–6, we provide the pseudocode of Algorithms 3–5 for computing, to high relative accuracy, the matrix form (11) of the bidiagonal decomposition of the collocation matrices $B_n^r$, ${\overline{B}}_n^r$, Wronskian matrices $W_n^r$, ${\overline{W}}_n^r$, and Gramian matrices $G_n^r$, ${\overline{G}}_n^r$ of r-Bell bases of the first and second kind. Algorithm 3 requires $BD\left(L_n^r\right)$, $BD\left({\overline{L}}_n^r\right)$, and the bidiagonal decomposition of the Vandermonde matrix implemented in the MATLAB function $\mathtt{T}\mathtt{N}\mathtt{V}\mathtt{a}\mathtt{n}\mathtt{d}\mathtt{B}\mathtt{D}$ available in [30]. In addition, Algorithm 4 requires $BD\left(L_n^r\right)$, $BD\left({\overline{L}}_n^r\right)$, and the bidiagonal decomposition $BD\left(W\right)$ (46) of the Wronskian matrix W of the monomial basis at x. Moreover, Algorithm 5 requires $BD\left(L_n^r\right)$, $BD\left({\overline{L}}_n^r\right)$, and the bidiagonal decomposition $BD\left(H\right)$ of the Hilbert matrix H implemented in the MATLAB function $\mathtt{T}\mathtt{N}\mathtt{C}\mathtt{a}\mathtt{u}\mathtt{c}\mathtt{h}\mathtt{y}\mathtt{B}\mathtt{D}$ available in [30]. Finally, let us observe that these three algorithms call the MATLAB function $\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}$ available in [30]. Let us recall that, given $A=BD\left(F\right)$ and $B=BD\left(G\right)$ to high relative accuracy, $\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(A,B)$ computes $BD(F·G)$ to high relative accuracy. The computational cost of the mentioned function and mentioned algorithms is $O\left(n^3\right)$ arithmetic operations.

Algorithm 3: Computation to high relative accuracy of the bidiagonal decomposition of collocation matrices $B_n^r$, ${\overline{B}}_n^r$ of r-Bell bases of the first and second kind

Require: n, r, $\mathbf{x}:={\left\{x_i\right\}}_{i=1}^{n+1}$ such that $0<x_1<\dots <x_{n+1}$    Ensure: $BD{B}_n^r$ bidiagonal decomposition of $B_n^r$ to high relative accuracy           $BD{\overline{B}}_n^r$ bidiagonal decomposition of ${\overline{B}}_n^r$ to high relative accuracy $BD{L}_n^r=\mathtt{B}\mathtt{D}{L}_n^r(n,r)$ (see Algorithm 1) $BD{\overline{L}}_n^r=\mathtt{B}\mathtt{D}{\overline{L}}_n^r(n,r)$ (see Algorithm 2) $BDV=\mathtt{T}\mathtt{N}\mathtt{V}\mathtt{a}\mathtt{n}\mathtt{d}\mathtt{B}\mathtt{D}\left(\mathbf{x}\right)$ $BD{B}_n^r=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(BDV,{\left(BD{L}_n^r\right)}^T)$ $BD{\overline{B}}_n^r=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(BDV,{\left(BD{\overline{L}}_n^r\right)}^T)$

Algorithm 4:Computation to high relative accuracy of the bidiagonal decomposition of Wronskian matrices $W_n^r$, ${\overline{W}}_n^r$ of r-Bell bases of the first and second kind

Require: n, r, $x\in (0,\infty )$    Ensure: $BD{W}_n^r$ bidiagonal decomposition of $W_n^r$ to high relative accuracy           $BD{\overline{W}}_n^r$ bidiagonal decomposition of ${\overline{W}}_n^r$ to high relative accuracy $BD{L}_n^r=\mathtt{B}\mathtt{D}{L}_n^r(n,r)$ (see Algorithm 1) $BD{\overline{L}}_n^r=\mathtt{B}\mathtt{D}{\overline{L}}_n^r(n,r)$ (see Algorithm 2) $BDW=\mathtt{B}\mathtt{D}\mathtt{W}\left(x\right)$ $BD{W}_n^r=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(BDW,{\left(BD{L}_n^r\right)}^T)$ $BD{\overline{W}}_n^r=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(BDW,{\left(BD{\overline{L}}_n^r\right)}^T)$

Algorithm 5: Computation to high relative accuracy of the bidiagonal decomposition of Gramian matrices $G_n^r$, ${\overline{G}}_n^r$ of r-Bell bases of the first and second kind

Require: n, r    Ensure: $BD{G}_n^r$ bidiagonal decomposition of $G_n^r$ to high relative accuracy           $BD{\overline{G}}_n^r$ bidiagonal decomposition of ${\overline{G}}_n^r$ to high relative accuracy $BD{L}_n^r=\mathtt{B}\mathtt{D}{L}_n^r(n,r)$ (see Algorithm 1) $BD{\overline{L}}_n^r=B{D}^{\prime \prime }{\overline{L}}_n^r(n,r)$ (see Algorithm 2) $BDH=\mathtt{T}\mathtt{N}\mathtt{C}\mathtt{a}\mathtt{u}\mathtt{c}\mathtt{h}\mathtt{y}\mathtt{B}\mathtt{D}(1:n,0:n-1)$ $B1=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}\left(BD{L}_n^r\right),BDH)$ $BD\tilde{G}=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(B1,{\left(BD{L}_n^r\right)}^T))$ $B2=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(BDL,BDH)$ $BDG=\mathtt{T}\mathtt{N}\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{d}\mathtt{u}\mathtt{c}\mathtt{t}(B2,{\left(BD{\overline{L}}_n^r\right)}^T)$

5. Numerical Experiments

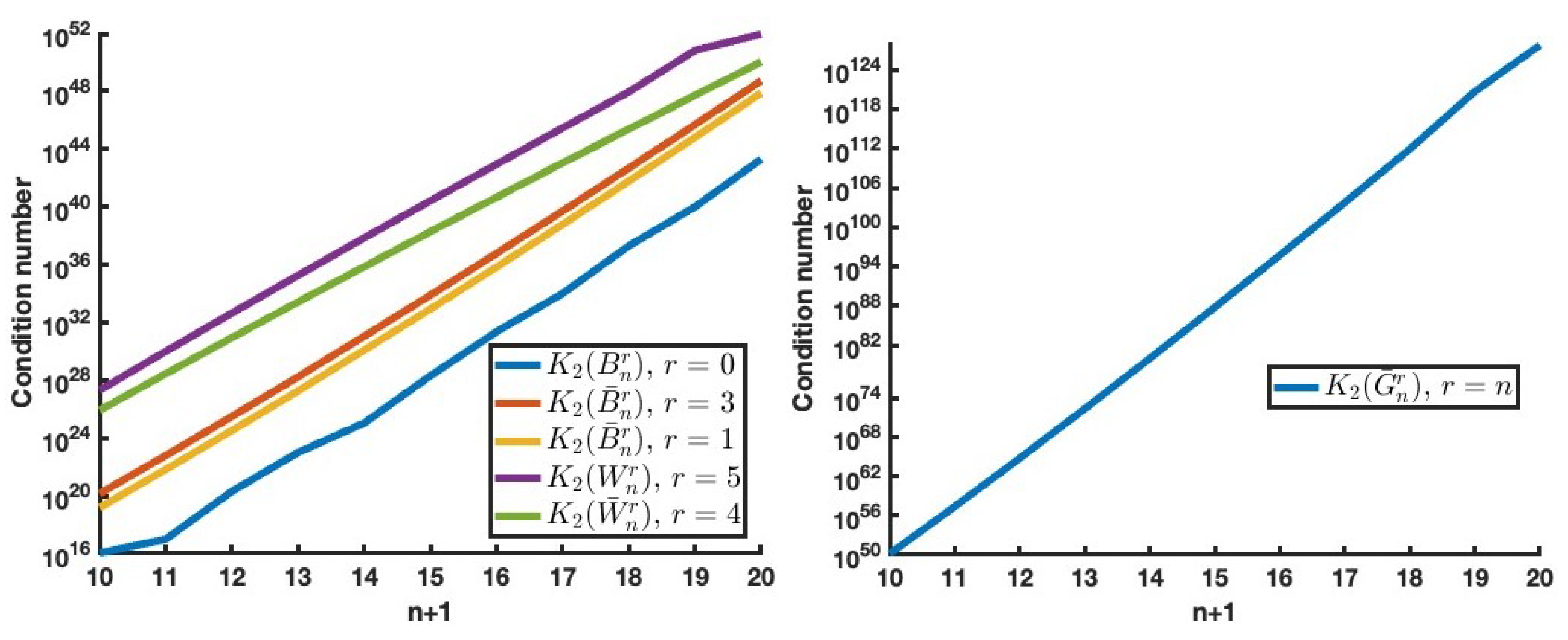
Some numerical tests are presented in this section, supporting the obtained theoretical results. We have considered different nonsingular strictly totally positive collocation matrices $B_n^r$, ${\overline{B}}_n^r$, Wronskian matrices $W_n^r$, ${\overline{W}}_n^r$, and Gramian matrices $G_n^r$, ${\overline{G}}_n^r$ of r-Bell bases of the first and second kind. Specifically, $B_n$ with $r=0$ and $t=(i-1)/(n+1)$, $i=1,\dots ,n+1$, and ${\overline{B}}_n^r$, with $r=1$ and $t=1+(i-1)/(n+1)$, $i=1,\dots ,n+1$, and with $r=3$ and $t=(i-1)/(n+1)$, $i=1,\dots ,n+1$. In addition, $W_n^r$ with $r=5$ and $t=60$ and, ${\overline{W}}_n^r$ with $r=4$ and $t=50$. Finally, ${\overline{G}}_n^r$ with $r=n$, $n=10,11,\dots ,20$.

We have computed, with Mathematica, the 2-norm condition number, which is the ratio of the largest singular value to the smallest, of all considered matrices. This conditioning is depicted in Figure 1. It can be easily observed that the conditioning drastically increases with the size of the matrices. Due to the ill-conditioning of these matrices, standard routines do not obtain accurate solutions because they can suffer from inaccurate cancellations.

Let us recall that if $BD\left(A\right)$ can be obtained to high relative accuracy, then the MATLAB functions TNEigenValues, TNSingularValues, TNInverseExpand and TNSolve available in the software library TNTools in [30], take as input argument $BD\left(A\right)$, and compute to high relative accuracy the eigenvalues and singular values of A, the inverse matrix $A^{-1}$ (using the algorithm presented in [22]) and even the solution of linear systems $Ax=b$, for vectors b with alternating signs.

In order to check the accuracy of our algorithms, we have performed several matrix computations using the mentioned routines available in [30], with the matrix form (11) of the bidiagonal factorization (5) as an input argument. The obtained approximations have been compared with the respective approximations obtained by traditional methods provided in Matlab $R2022b$. In this context, the values provided by Wolfram Mathematica $13.1$ with 100-digit arithmetic have been taken as the exact solution of the considered algebraic problem. For the sake of brevity, only a few of these experiments will be shown.

The relative error of each approximation has also been computed in Mathematica with 100-digit arithmetic as $e:=|y-\tilde{y}|/|y|$, where y denotes the exact solution and $\tilde{y}$ the computed approximation.

Computation of eigenvalues and singular values. For all considered matrices, we have compared the smallest eigenvalue and singular value obtained using the proposed bidiagonal decompositions provided by Algorithms 3–5 with the functions TNEigenvalues and TNSingularvalues, and the smallest eigenvalue and singular value computed with the Matlab commands eig and svd, respectively. Note that the eigenvalues of the Wronskian matrices are exact. Furthermore, the singular values of the Gramian matrices considered coincide with their eigenvalues (since Gramian matrices are symmetric).

The relative errors are shown in Figure 2. Note that our approach accurately computes the smallest eigenvalue and singular value regardless of the 2-norm condition number of the considered matrices. In contrast, the Matlab commands eig and svd return results that are not accurate at all.

Computation of inverses. Further to this, for all considered matrices, we have compared the inverse obtained using the proposed bidiagonal decompositions provided by Algorithms 3–5 with the function TNInverseExpand and the inverse computed with the Matlab command inv. As shown in Figure 3, our procedure provides very accurate results. On the contrary, the results obtained with Matlab reflect poor accuracy.

Resolution of linear systems. Finally, for all considered matrices, we have compared the solution of the linear systems $B_n^{r}c=d$, ${\overline{B}}_n^{r}c=d$, $W_n^{r}c=d$, ${\overline{W}}_n^{r}c=d$, $G_n^{r}c=d$ and ${\overline{G}}_n^{r}c=d$ where $d={\left({(-1)}^{i+1}{d}_i\right)}_{1\le i\le n+1}$ and $d_i$, $i=1,\dots ,n+1$, are random nonnegative integer values, obtained using the proposals for bidiagonal decompositions provided by Algorithms 3–5 with the function TNSolve and the solutions obtained within the Matlab command ∖. As opposed to the results obtained with the command ∖, the proposed procedure preserves the accuracy for all of the dimensions which have been taken into account. Figure 4 illustrates the relative errors.

6. Conclusions

We have introduced a new class of matrices called r-Stirling matrices. These matrices are defined in terms of r-Stirling numbers and have interesting properties, such as being totally positive. They also play a significant role in determining the linear transformation between monomial and r-Bell polynomial bases.

The paper further discusses an efficient algorithm for computing the bidiagonal factorization of r-Stirling matrices to high relative accuracy. This factorization is used for solving relevant algebraic problems involving collocation, Wronskian, and Gramian matrices associated with r-Bell polynomial bases. To validate the proposed procedure and its usefulness, the paper presents numerical experiments that confirm its accuracy.