Reliability Estimation of Inverse Weibull Distribution Based on Intuitionistic Fuzzy Lifetime Data
Abstract
:1. Introduction
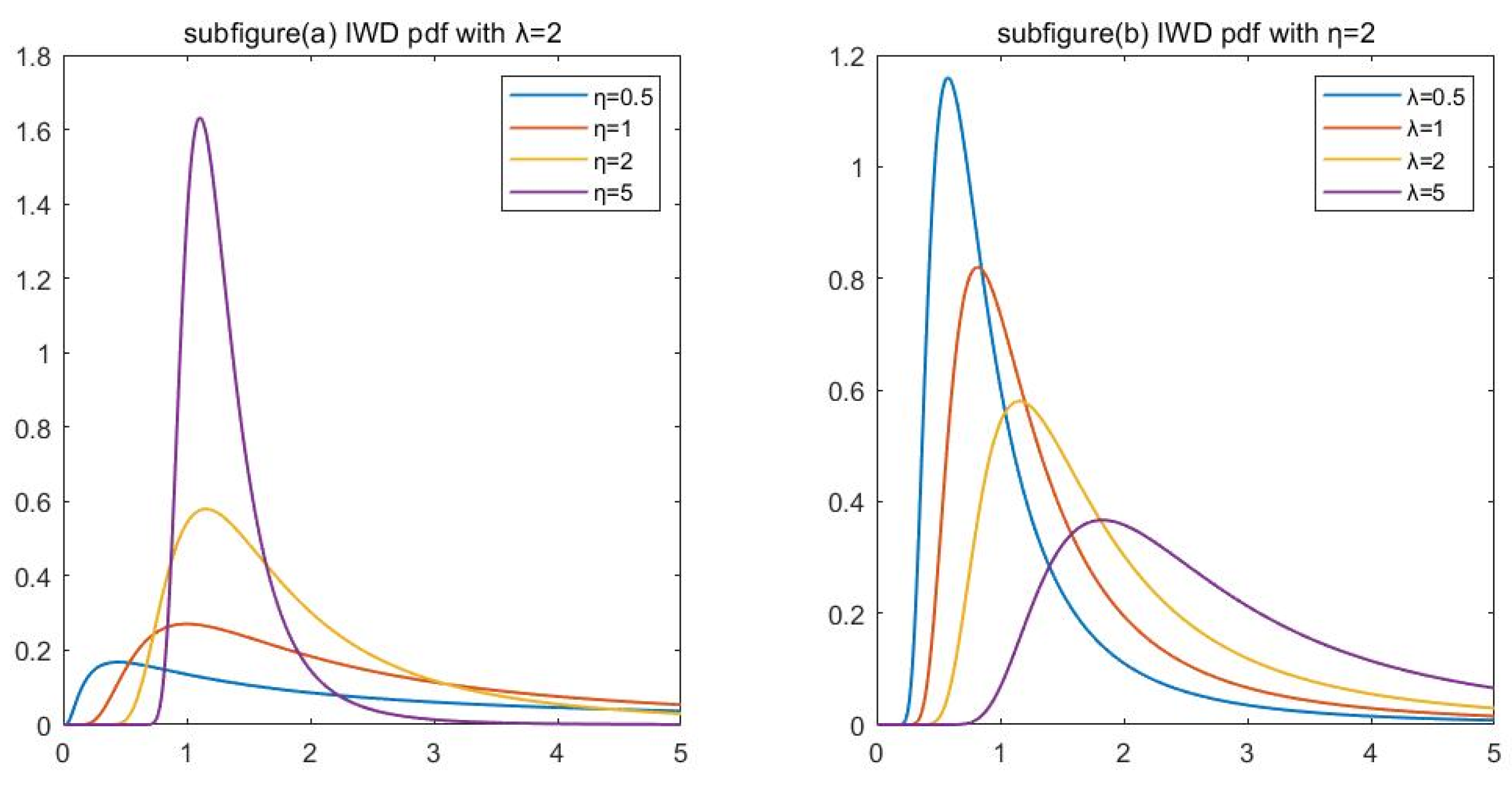
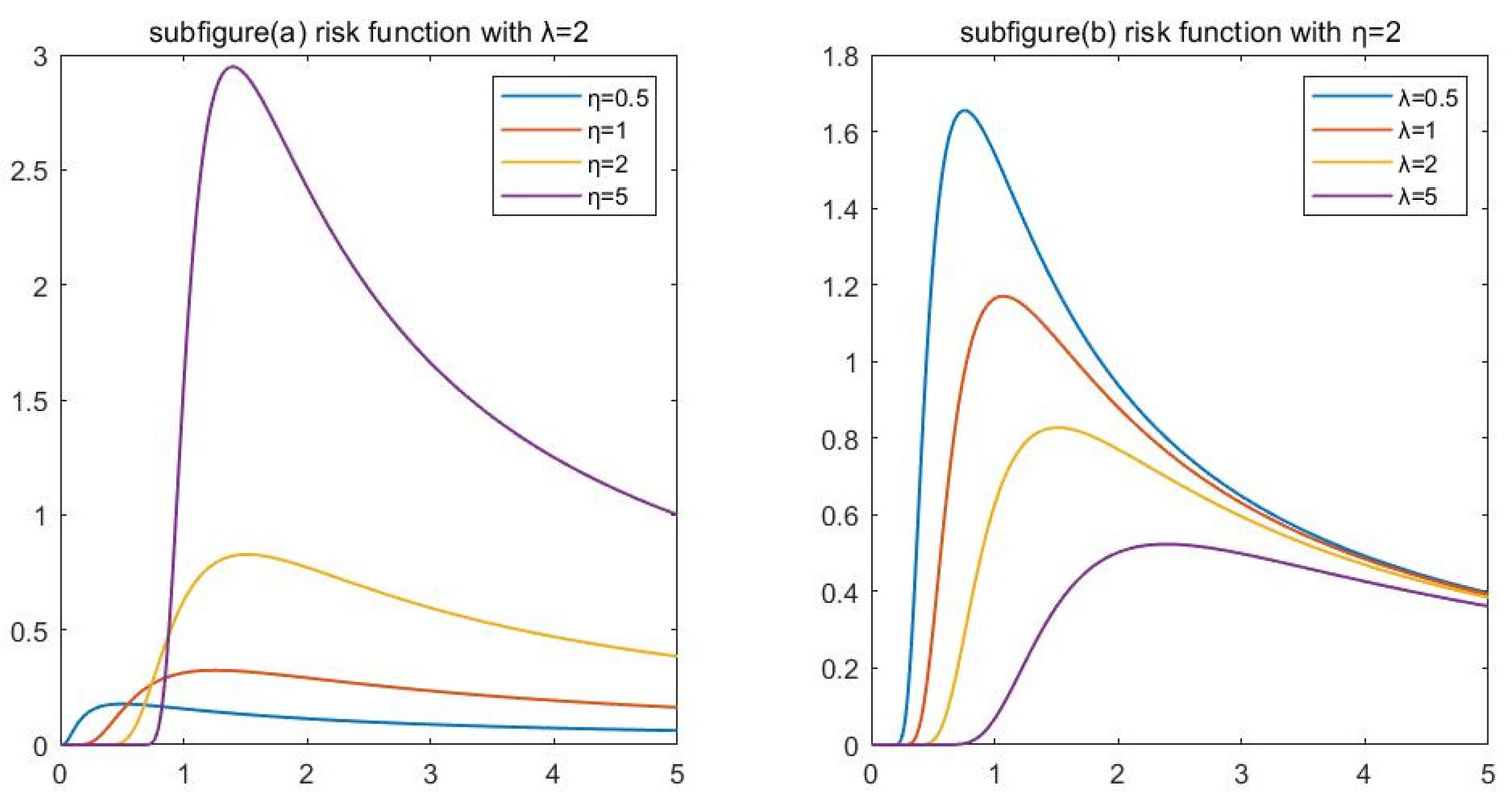
2. Preliminary Knowledge
3. Maximum Likelihood Estimation
- Step 1. Let the initial value be , and set . Give the accuracy .
- Step 2. At the iteration, compute the intuitionistic fuzzy conditional expectations below:
- Step 3. Substitute Equation (18) into (15):
- Step 4. If , the MLEs are obtained by and . If not, then set and return to step 2.
4. Bayesian Estimation
4.1. Bayesian Estimation under the SE Loss Function
4.2. Bayesian Estimation under the SSE Loss Function
5. Monte Carlo Simulation
- (C1) are random samples of observations that are exact and independently and identically distributed and obey .
- (C2) For any , and are chosen randomly with satisfying
- (C3) For any , the and are chosen randomly with satisfying , , and .
- (C4) , .
- (i)
- Generate a set of data from with and . Calculate the real reliability with .
- (ii)
- For convenience, let . The data are transformed into TraIFNs according to Equations (60) and (61).
- (iii)
- Calculate the MLEs by the EM algorithm and calculate the BEs by the Lindley approximation.
- (iv)
- Repeat steps (i) to (iii) 1000 times and obtain 1000 estimates, respectively, and the MSE is calculated according to Equation (59).
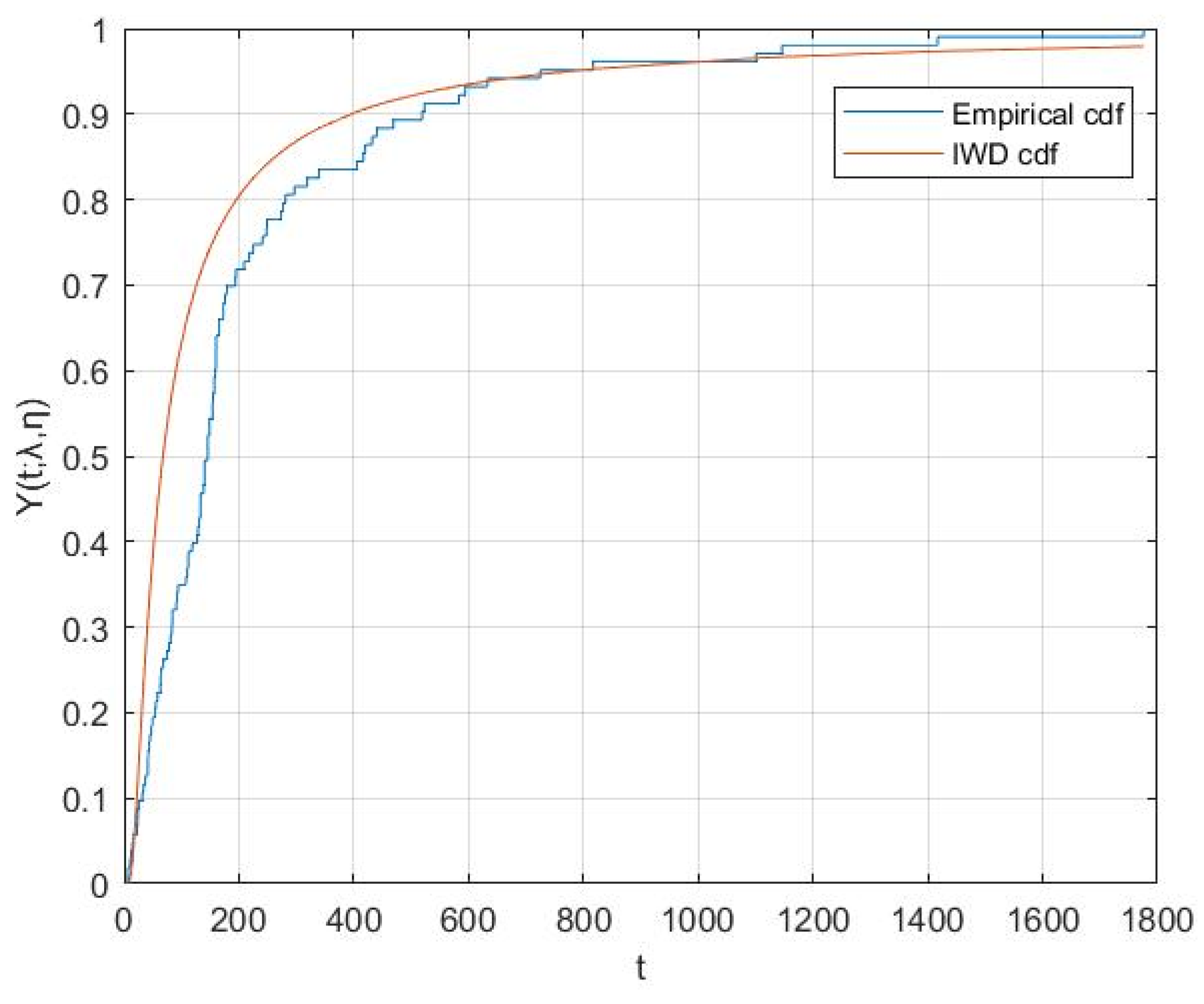
6. Real Dataset Analysis
7. Conclusions, Limitations, and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yilmaz, A.; Kara, M. Reliability estimation and parameter estimation for inverse Weibull distribution under different loss functions. Kuwait J. Sci. 2022, 49, 1–24. [Google Scholar] [CrossRef]
- Chakrabarty, J.B.; Chowdhury, S. Compounded inverse Weibull distributions: Properties, inference and applications. Commun. Stat.-Simul. Comput. 2019, 48, 2012–2033. [Google Scholar] [CrossRef]
- Cai, J.; Shi, Y.M.; Zhang, Y.G. Robust Bayesian analysis for parallel system with masked data under inverse Weibull lifetime distribution. Commun. Stat.-Theor. Methods 2020, 49, 1422–1434. [Google Scholar] [CrossRef]
- Bi, Q.X.; Gui, W.H. Bayesian and classical estimation of stress-strength reliability for inverse Weibull lifetime models. Algorithms 2017, 10, 71. [Google Scholar] [CrossRef]
- Maurya, R.K.; Tripathi, Y.M.; Kayal, T. Reliability Estimation in a Multicomponent Stress-Strength Model Based on Inverse Weibull Distribution. Sankhya B 2022, 84, 364–401. [Google Scholar] [CrossRef]
- Majd, A.; Amal, H. Estimation of the stress-strength reliability for the inverse Weibull distribution under adaptive type-II progressive hybrid censoring. PLoS ONE 2022, 17, 0277514–0277536. [Google Scholar]
- Krishna, H.; Dube, M.; Garg, R. Estimation of stress strength reliability of inverse Weibull distribution under progressive first failure censoring. Aust. J. Stat. 2019, 48, 14–37. [Google Scholar] [CrossRef]
- Yadav, A.S.; Singh, S.K.; Singh, U. Estimation of stress-strength reliability for inverse Weibull distribution under progressive type-II censoring scheme. J. Ind. Prod. Eng. 2018, 35, 48–55. [Google Scholar] [CrossRef]
- Yusra, A.T.; Ehab, M.A.; Randa, R.; Ahmed, M.G.; El-Raouf, M.M.A.; Saima, K.K.; Eslam, H.; Bakr, M.E. Statistical inferences for the extended inverse Weibull distribution under progressive type-II censored sample with applications. Alex. Eng. J. 2022, 65, 493–502. [Google Scholar]
- Zadeh, L.A. Probability measures of Fuzzy events. J. Math. Anal. Appl. 1968, 23, 421–427. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Song, Y.; Wen, C.F. Information structures in a fuzzy set-valued information system based on granular computing. Int. J. Approx. Reason. 2021, 134, 72–94. [Google Scholar] [CrossRef]
- Dang, E.K.F.; Luk, R.; Allan, J. A principled approach using fuzzy set theory for passage-based document retrieval. IEEE Trans. Fuzzy Syst. 2021, 29, 1967–1977. [Google Scholar] [CrossRef]
- Jiang, J.W.; Hu, Y.H.; Fang, Y.H.; Zhang, C.; Rui, X.S.; Wang, M. Fault diagnosis method of marine fans based on MTAD and fuzzy entropy. China Mech. Eng. 2022, 33, 1178–1188. [Google Scholar]
- Pan, J.S. Research progress on deep learning-based image deblurring. Comput. Sci. 2021, 48, 9–13. [Google Scholar]
- Xia, J.N.; Wang, D.J.; Wang, Y.Z.; Jin, Y.C.; Jiang, B. Prostate cancer diagnosis method based on structure adaptive fuzzy neural network. Syst. Eng.-Theor. Pract. 2018, 38, 1331–1342. [Google Scholar]
- Taha, T.A.; Salman, A.N. Comparison Different Estimation Method for Reliability Function of Rayleigh Distribution Based on Fuzzy Lifetime Data. Iraqi J. Sci. 2022, 63, 1707–1719. [Google Scholar] [CrossRef]
- Rudnei, D.D.C.; Elismar, R.O.; Filip, S. Fuzzy-set approach to invariant idempotent measures. Fuzzy Sets Syst. 2023, 457, 46–65. [Google Scholar]
- Hashim, A.N. On the fuzzy reliability estimation for Lomax distribution. AIP Conf. Proc. 2019, 2183, 110002–110011. [Google Scholar]
- Neamah, M.W.; Ali, B.K. Fuzzy reliability estimation for frechet distribution by using simulation. Period. Eng. Nat. Sci. 2020, 8, 632–646. [Google Scholar]
- Abbas, P.; Gholam, A.P.; Mansour, S. Reliability estimation in Rayleigh distribution based on fuzzy lifetime data. Int. J. Syst. Assur. Eng. 2014, 5, 487–494. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yazdi, M. Risk assessment based on novel intuitionistic fuzzy-hybrid-modified TOPSIS approach. Saf. Sci. 2018, 110, 438–448. [Google Scholar] [CrossRef]
- Otay, R.; Ztayi, B.; Onar, S.E.; Kahraman, C. Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology. Knowl.-Based Syst. 2018, 133, 90–106. [Google Scholar]
- Xu, W.; Yu, Y.Y.; Zhang, Q.S. An evaluation method of comprehensive product quality for customer satisfaction based on intuitionistic fuzzy number. Discret. Dyn. Nat. Soc. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Gohain, B.; Chutia, R.; Dutta, P. Distance measure on intuitionistic fuzzy sets and its application in decision-making, pattern recognition, and clustering problems. Int. J. Intell. Syst. 2022, 37, 2458–2501. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Xu, Z. Novel intuitionistic fuzzy weighted geometric operators for intuitionistic fuzzy multi-attribute decision making. J. Ind. Manag. Optim. 2023, 19, 7196–7220. [Google Scholar] [CrossRef]
- Zahra, R.; Ezzatallah, B.J.; Einolah, D. The reliability analysis based on the generalized intuitionistic fuzzy two-parameter Pareto distribution. Soft Comput. 2022, 21, 3095–3113. [Google Scholar]
- Ebrahimnejad, A.; Jamkhaneh, E.B. System reliability using generalized intuitionistic fuzzy Rayleigh lifetime distribution. Appl. Appl. Math. 2018, 13, 97–113. [Google Scholar]
- Huibert, K. Fuzzy random variables—I. definitions and theorems. Inform. Sci. 1978, 15, 1–29. [Google Scholar]
- Zahra, R.; Ezzatallah, B.J.; Einolah, D. Parameters and reliability estimation for the Weibull distribution based on intuitionistic fuzzy lifetime data. Complex Intell. Syst. 2022, 8, 4881–4896. [Google Scholar]
- Shu, M.H.; Cheng, C.H.; Chang, J.R. Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly. Microelectron. Reliab. 2006, 46, 2139–2148. [Google Scholar] [CrossRef]
- Wang, J.Q.; Zhang, Z. Programming method of multi-criteria decision-making based on intuitionistic fuzzy number with incomplete certain information. Control Decis. 2008, 23, 1145–1148. [Google Scholar]
- Dempster, A.P. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Singh, S.; Tripathi, Y.M. Estimating the parameters of an inverse Weibull distribution under progressive type-I interval censoring. Stat. Pap. 2018, 59, 21–56. [Google Scholar] [CrossRef]
- Kurniawan, A.; Avicena, N.; Ana, E. Estimation of the shape parameter of Weibull distribution based on type II censored data using EM algorithm. AIP Conf. Proc. 2020, 2264, 030011–030020. [Google Scholar]
- Barde, S.; Ko, Y.M.; Shin, H. General EM algorithm for fitting non-monotone hazard functions from truncated and censored observations. Oper. Res. Lett. 2022, 50, 476–483. [Google Scholar] [CrossRef]
- Pal, S. A simplified stochastic EM algorithm for cure rate model with negative binomial competing risks: An application to breast cancer data. Stat. Med. 2021, 40, 6387–6409. [Google Scholar] [CrossRef]
- Fu, E.; Heckman, N. Model-based curve registration via stochastic approximation EM algorithm. Comput. Stat. Data An. 2019, 131, 159–175. [Google Scholar] [CrossRef]
- Wang, Z.G.; Liu, W.C. Stochastic reserving using policyholder information via EM algorithm. Appl. Math. Model. 2022, 112, 199–214. [Google Scholar] [CrossRef]
- Lachos, V.H.; Prates, M.O.; Dey, D.K. Heckman selection-t model: Parameter estimation via the EM-algorithm. J. Multivar. Anal. 2021, 184, 104737–104755. [Google Scholar] [CrossRef]
- Jia, X.; Cheng, Z.J.; Guo, B. Reliability evaluation for products based on entropy and Bayes theory. Syst. Eng. Theory Pract. 2020, 40, 1918–1926. [Google Scholar]
- Li, D.W.; Wang, G.D.; Li, Y.Z. Qualification test risk analysis of binomial equipment based on Bayes theory. J. Aerosp. Power 2021, 36, 157–166. [Google Scholar]
- Wang, C.Y.; Huang, X.J. Comparison of Bayesian estimation of the scale parameter for Log gamma distribution under Linex loss function and compound Linex loss function. Math. Appl. 2018, 31, 384–391. [Google Scholar]
- Kundu, D.; Mitra, D. Bayesian inference of Weibull distribution based on left truncated and right censored data. Comput. Stat. Data An. 2016, 99, 38–50. [Google Scholar] [CrossRef]
- Xu, B.; Wang, D.H.; Wang, R.T. Estimator of scale parameter in a subclass of the exponential family under symmetric entropy loss. Northeast Math. J. 2008, 24, 447–457. [Google Scholar]
- Song, L.X.; Chen, Y.S.; Xu, J.M. Bayesian estimation of Poisson distribution parameter under scale squared error loss function. J. Lanzhou Univ. Tech. 2008, 34, 152–154. [Google Scholar]
- Usta, I. Bayesian estimation for geometric process with the Weibull distribution. Commun. Stat.-Simul. Comput. 2022, 1–27. [Google Scholar] [CrossRef]
- González, R.G.; Colubi, A.; Ángeles, G.M. A fuzzy representation of random variables: An operational tool in exploratory analysis and hypothesis testing. Comput. Stat. Data Anal. 2006, 51, 163–176. [Google Scholar] [CrossRef]
- Efron, B. Logistic regression, survival analysis, and the Kaplan-Meier curve. J. Am. Stat. Assoc. 1988, 83, 414–425. [Google Scholar] [CrossRef]
| MSE | ||||||||
|---|---|---|---|---|---|---|---|---|
| 20 | 5 | 1 | 0.6252 | 0.5126 | 0.2208 | 0.1247 | 0.0171 | 0.0056 |
| 8 | 4 | 0.8302 | 0.7005 | 0.4867 | 0.6479 | 0.2369 | 0.1875 | |
| 2 | 3 | 0.8011 | 0.6801 | 0.1644 | 0.8141 | 0.4975 | 0.1810 | |
| 50 | 5 | 1 | 0.4900 | 0.0584 | 0.0543 | 0.0458 | 0.0009 | 9.94 × 10−4 |
| 8 | 4 | 0.6842 | 0.5550 | 0.4786 | 0.3718 | 0.0762 | 0.0530 | |
| 2 | 3 | 0.6195 | 0.0048 | 0.0053 | 0.5094 | 0.1396 | 0.0638 | |
| 100 | 5 | 1 | 0.1330 | 0.0143 | 0.0165 | 0.0358 | 0.0002 | 0.0003 |
| 8 | 4 | 0.2717 | 0.1148 | 0.1819 | 0.1138 | 0.0150 | 0.0154 | |
| 2 | 3 | 0.3339 | 0.0003 | 0.0013 | 0.1838 | 0.0218 | 0.0213 | |
| 200 | 5 | 1 | 0.0525 | 0.0034 | 0.0044 | 0.0217 | 4.64 × 10−5 | 6.51 × 10−5 |
| 8 | 4 | 0.0914 | 0.0562 | 0.0602 | 0.0454 | 0.0033 | 0.0040 | |
| 2 | 3 | 0.1020 | 0.0001 | 0.0004 | 0.0840 | 0.0039 | 0.0052 | |
| 300 | 5 | 1 | 0.0240 | 0.0016 | 0.0021 | 0.0214 | 2.12 × 10−5 | 2.96 × 10−5 |
| 8 | 4 | 0.0840 | 0.0253 | 0.0295 | 0.0096 | 0.0015 | 0.0019 | |
| 2 | 3 | 0.0863 | 5.31 × 10−5 | 0.0002 | 0.0472 | 0.0017 | 0.0024 | |
| 400 | 5 | 1 | 0.0093 | 0.0009 | 0.0012 | 0.0184 | 1.24 × 10−5 | 1.72 × 10−5 |
| 8 | 4 | 0.0692 | 0.0142 | 0.0174 | 0.0016 | 8.25 × 10−4 | 0.0011 | |
| 2 | 3 | 0.0691 | 2.21 × 10−5 | 9.63 × 10−5 | 0.0112 | 9.55 × 10−4 | 0.0014 | |
| 500 | 5 | 1 | 0.0087 | 0.0006 | 0.0008 | 0.0168 | 7.89 × 10−6 | 1.11 × 10−5 |
| 8 | 4 | 0.0590 | 0.0092 | 0.0115 | 0.0008 | 5.50 × 10−4 | 7.24 × 10−4 | |
| 2 | 3 | 0.0489 | 1.27 × 10−5 | 5.98 × 10−5 | 0.0093 | 6.39 × 10−4 | 9.28 × 10−4 | |
| Estimates | MSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 | 5 | 1 | 0.9179 | 0.9500 | 0.8984 | 0.9286 | 0.0024 | 8.98 × 10−4 | 3.21 × 10−3 |
| 8 | 4 | 0.3935 | 0.4089 | 0.3973 | 0.3465 | 0.0185 | 8.60 × 10−3 | 2.80 × 10−3 | |
| 2 | 3 | 0.2212 | 0.2826 | 0.3003 | 0.2798 | 0.0083 | 8.23 × 10−3 | 1.82 × 10−2 | |
| 50 | 5 | 1 | 0.9179 | 0.9483 | 0.9122 | 0.9621 | 0.0011 | 6.48 × 10−5 | 8.72 × 10−5 |
| 8 | 4 | 0.3935 | 0.3872 | 0.4086 | 0.3825 | 0.0048 | 8.11 × 10−4 | 5.79 × 10−4 | |
| 2 | 3 | 0.2212 | 0.1744 | 0.2604 | 0.2373 | 0.0044 | 5.80 × 10−3 | 7.91 × 10−2 | |
| 100 | 5 | 1 | 0.9179 | 0.9262 | 0.9146 | 0.9143 | 0.0006 | 1.32 × 10−5 | 2.04 × 10−5 |
| 8 | 4 | 0.3935 | 0.3891 | 0.4035 | 0.3885 | 0.0029 | 5.51 × 10−5 | 2.55 × 10−5 | |
| 2 | 3 | 0.2212 | 0.2819 | 0.2455 | 0.2312 | 0.0020 | 4.32 × 10−4 | 3.43 × 10−4 | |
| 200 | 5 | 1 | 0.9179 | 0.9213 | 0.9164 | 0.9163 | 0.0002 | 2.69 × 10−6 | 4.52 × 10−6 |
| 8 | 4 | 0.3935 | 0.3351 | 0.3933 | 0.3878 | 0.0012 | 8.66 × 10−6 | 5.45 × 10−6 | |
| 2 | 3 | 0.2212 | 0.1783 | 0.2331 | 0.2251 | 0.0013 | 5.95 × 10−5 | 8.19 × 10−6 | |
| 300 | 5 | 1 | 0.9179 | 0.9399 | 0.9169 | 0.9168 | 0.0002 | 1.46 × 10−6 | 2.23 × 10−6 |
| 8 | 4 | 0.3935 | 0.4096 | 0.3931 | 0.3901 | 0.0008 | 3.82 × 10−6 | 2.18 × 10−6 | |
| 2 | 3 | 0.2212 | 0.2580 | 0.2260 | 0.2235 | 0.0009 | 2.54 × 10−5 | 3.78 × 10−6 | |
| 400 | 5 | 1 | 0.9179 | 0.9230 | 0.9172 | 0.9171 | 0.0001 | 1.25 × 10−6 | 1.63 × 10−6 |
| 8 | 4 | 0.3935 | 0.3826 | 0. 3945 | 0.3917 | 0.0008 | 2.05 × 10−6 | 1.05 × 10−6 | |
| 2 | 3 | 0.2212 | 0.1664 | 0.2252 | 0.2228 | 0.0007 | 1.38 × 10−5 | 1.95 × 10−6 | |
| 500 | 5 | 1 | 0.9179 | 0.9393 | 0.9172 | 0.9171 | 0.0001 | 5.02 × 10−7 | 7.84 × 10−7 |
| 8 | 4 | 0.3935 | 0.3737 | 0.3947 | 0.3921 | 0.0006 | 1.40 × 10−6 | 6.87 × 10−7 | |
| 2 | 3 | 0.2212 | 0.2048 | 0.2236 | 0.2217 | 0.0007 | 9.22 × 10−6 | 1.38 × 10−6 | |
| 6.53 | 7 | 10.42 | 12.2 | 14.48 | 16.1 | 22.7 | 23.56 | 23.74 | 25.87 |
| 31.98 | 34 | 37 | 41.35 | 41.55 | 42 | 43 | 45.28 | 47.38 | 49.4 |
| 53.62 | 55.46 | 58.36 | 63 | 63.47 | 64 | 68.46 | 74.47 | 78.26 | 81 |
| 83 | 84 | 84 | 91 | 92 | 94 | 108 | 110 | 112 | 112 |
| 119 | 127 | 129 | 130 | 133 | 133 | 133 | 139 | 140 | 140 |
| 140 | 146 | 146 | 146 | 149 | 149 | 154 | 154 | 155 | 157 |
| 157 | 159 | 160 | 160 | 160 | 160 | 165 | 165 | 173 | 173 |
| 176 | 179 | 194 | 195 | 209 | 218 | 225 | 241 | 248 | 249 |
| 273 | 277 | 281 | 297 | 319 | 339 | 405 | 417 | 420 | 432 |
| 440 | 469 | 519 | 523 | 583 | 594 | 633 | 725 | 817 | 1101 |
| 1146 | 1417 | 1776 |
| MLE | SE | SSE | MLE | SE | SSE | MLE | SE | SSE |
|---|---|---|---|---|---|---|---|---|
| 64.6171 | 67.7140 | 67.7630 | 0.8000 | 1.0886 | 1.0885 | 0.9423 | 0.6205 | 0.6170 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Ren, H. Reliability Estimation of Inverse Weibull Distribution Based on Intuitionistic Fuzzy Lifetime Data. Axioms 2023, 12, 838. https://doi.org/10.3390/axioms12090838
Hu X, Ren H. Reliability Estimation of Inverse Weibull Distribution Based on Intuitionistic Fuzzy Lifetime Data. Axioms. 2023; 12(9):838. https://doi.org/10.3390/axioms12090838
Chicago/Turabian StyleHu, Xue, and Haiping Ren. 2023. "Reliability Estimation of Inverse Weibull Distribution Based on Intuitionistic Fuzzy Lifetime Data" Axioms 12, no. 9: 838. https://doi.org/10.3390/axioms12090838
APA StyleHu, X., & Ren, H. (2023). Reliability Estimation of Inverse Weibull Distribution Based on Intuitionistic Fuzzy Lifetime Data. Axioms, 12(9), 838. https://doi.org/10.3390/axioms12090838






