The Laplace Transform Shortcut Solution to a One-Dimensional Heat Conduction Model with Dirichlet Boundary Conditions
Abstract
1. Introduction
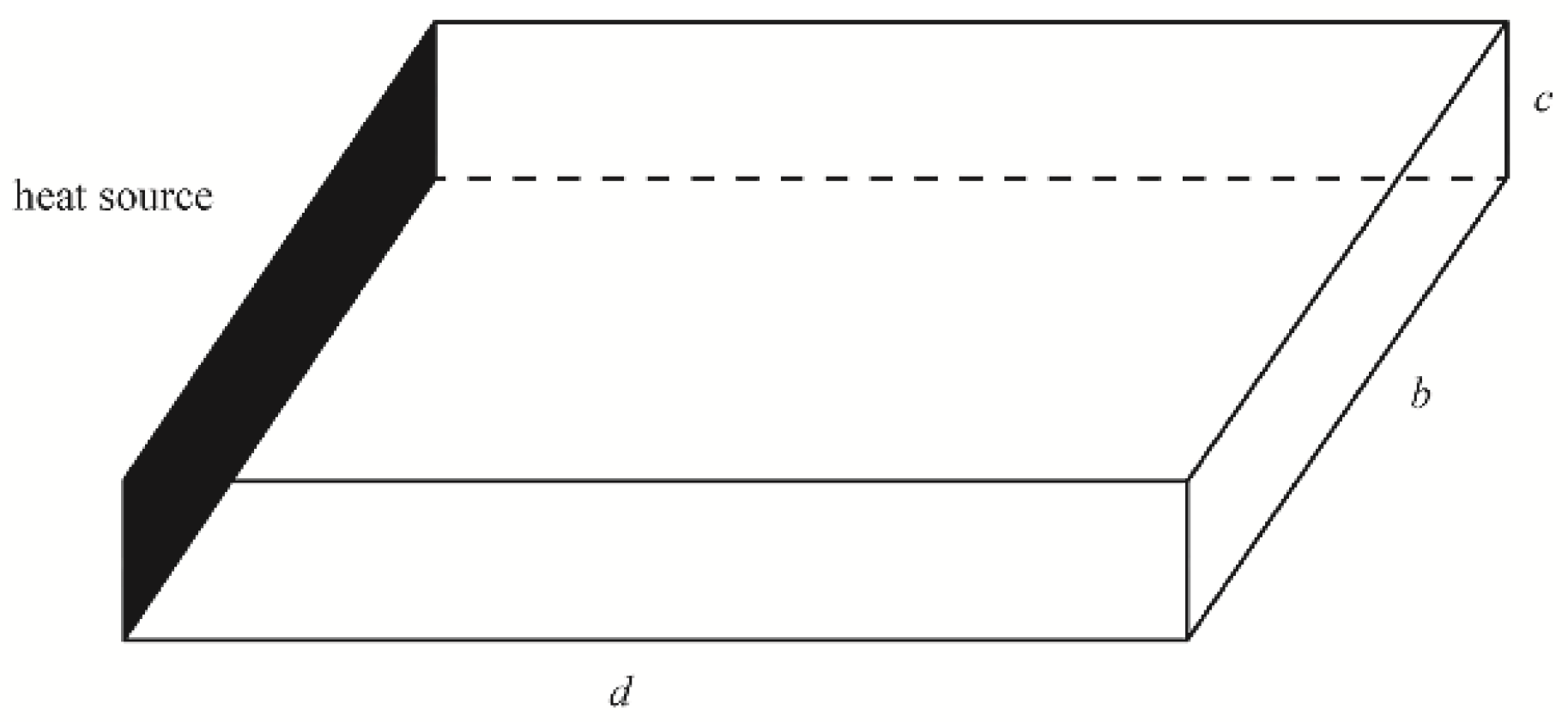
2. Basic Model
- (1)
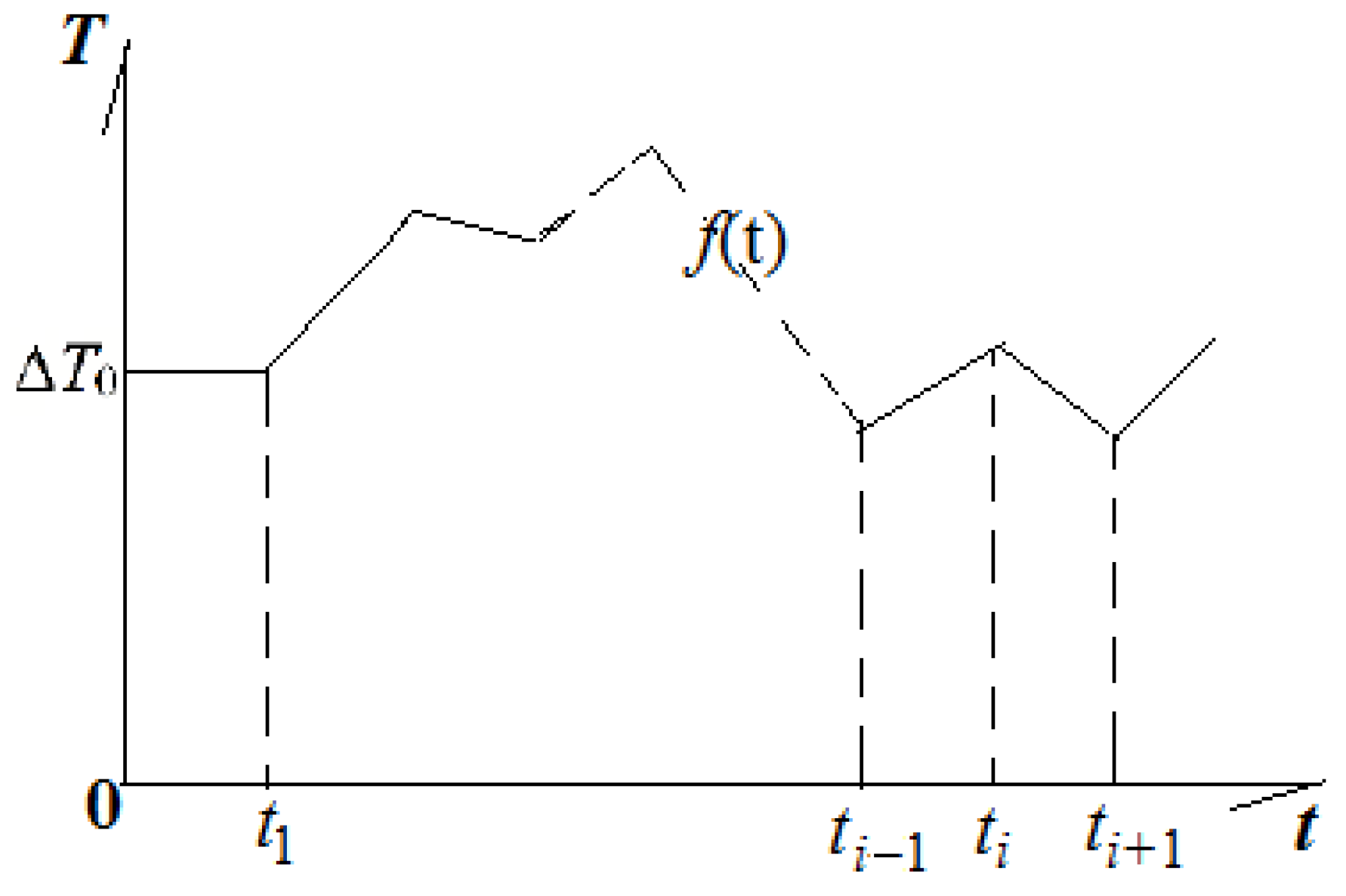
- A homogeneous thin plate extending infinitely in the x-direction, with a heat source at the boundary (x = 0) that varies with time as f(t). f(t) must meet the basic requirements of the Laplace transform.
- (2)
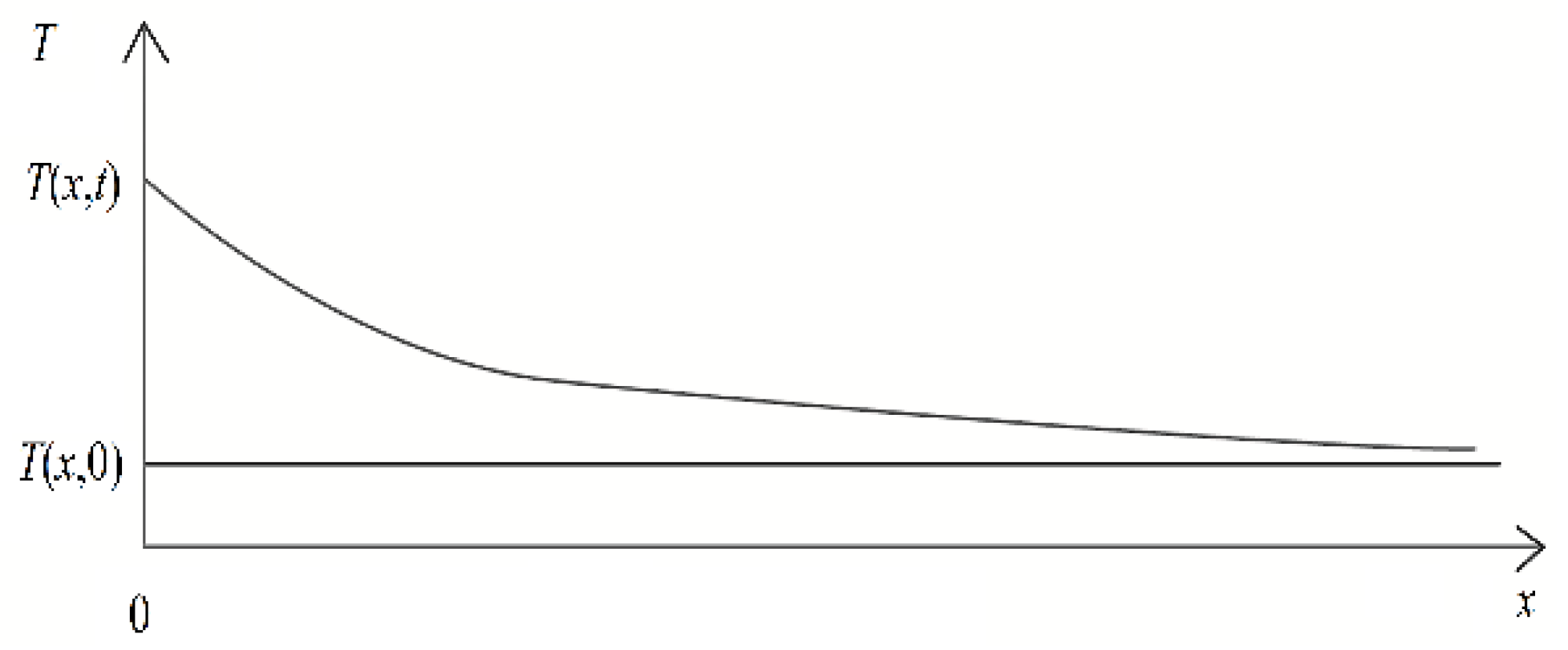
- The temperature at any point within the thin plate can be represented as T(x, t), and the initial temperature is uniformly zero: T(x, 0) = 0.
- (3)
- The outer surface of the thin plate is insulated, indicating that there is no heat exchange between the thin plate and the external environment, and the one-dimensional heat conduction only occurs within the thin plate due to the boundary heat source.
3. General Theoretical Solution
4. Solution for Boundary Functions of Commonly Used Function Types
4.1. Constant Function
4.2. Linear Interpolation Function
4.3. Step Function
4.4. Exponential Function
4.5. Trigonometric Function
5. Application of the Solution
5.1. Specific Solutions and Their Mathematical Significance
5.1.1. When λ = 0
5.1.2. When ∆T0 = 0
5.1.3. When x→∞
5.2. Methods for Calculating Model Parameters
5.2.1. The Inflection Point Method
5.2.2. The Curve Fitting Method
5.3. The Case Study
5.3.1. Calculation Example of the Variable-Temperature-Boundary Inflection Point Method
5.3.2. Calculation Example of Constant Temperature Boundary
5.3.3. Application in Engineering
6. Conclusions
- (1)
- For the one-dimensional heat conduction model with the Dirichlet boundary function f(t), according to the differential properties of the Laplace transform and the convolution theorem, a general theoretical solution can be obtained as a product of erfc(t) and f(0), as well as erfc(t) and f(t). The general theoretical solution is derived for this type of model.
- (2)
- By substituting the boundary function f(t) into the general theoretical solution, the solution to practical problems can be obtained quickly. This shortcut solution method does not directly involve the transformation of f(t) and does not require a complex and cumbersome Laplace transform process.
- (3)
- With the temperature-based dynamic monitoring data and the time variation curve of the temperature change rate φ(x, t) − t, the model parameter “a” can be determined based on the fitting between the measured curve and the theoretical curve.
- (4)
- When calculating the temperature change rate φ(x, t) based on the measured temperature, using forward or backward interpolation has a certain influence on the results; when determining the time of the inflection point based on the self-recorded data, it is advisable to appropriately encrypt the data extraction time near the inflection point to avoid this influence.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | thermal diffusivity, m2/s |
| f | boundary temperature, °C |
| L | Laplace transform operator |
| L−1 | inverse Laplace transform operator |
| image function for Laplace transform | |
| s | Laplace operator |
| erfc(u) | the complementary error function |
| δ(t − ti−1) | Heaviside function |
| t | time, d |
| φ | temperature variation rate of the calculation point, °C/h |
| λ | boundary temperature variation rate, °C/d |
| tg | appearance of inflection point, h |
| T | temperature of calculation point, °C |
| ΔT0 | instantaneous change in boundary temperature, °C |
| x | distance of the calculation point from the boundary, m |
| convolution operator |
References
- Tao, W.Q. Heat Transfer Theory, 5th ed.; Higher Education Press: Beijing, China, 2019; pp. 75–77. [Google Scholar]
- Gu, C.H.; Li, D.Q.; Chen, S.X. Mathematical Physical Equation, 3rd ed.; Higher Education Press: Beijing, China, 2012; pp. 148–150. [Google Scholar]
- Zhang, Y.L. Integral Transformation, 4th ed.; Higher Education Press: Beijing, China, 2012; pp. 96–97. [Google Scholar]
- Hu, X.; Deng, S.; Wang, Y.; Chen, J.; Zhang, L.; Guo, W.; Han, Y. Study progress on analytical solution of static temperature field with artificial ground freezing. Mine Constr. Technol. 2015, 36, 1–9. [Google Scholar]
- Fabrea, A.; Hristov, J. On the integral-balance approach to the transient heat conduction with linearly temperature-dependent thermal diffusivity. Heat Mass Transf. 2016, 53, 177–204. [Google Scholar] [CrossRef]
- Falta, R.W.; Wang, W.W. A semi-analytical method for simulating matrix diffusion in numerical transport models. J. Contam. Hydrol. 2017, 197, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Oldenburg, C.M.; Rutqvist, J. Revisiting the analytical solutions of heat transport in fractured reservoirs using a generalized multirate memory function. Water Resour. Res. 2019, 55, 1405–1428. [Google Scholar] [CrossRef]
- BniLam, N.; Al-Khoury, R.; Shiri, A.; Sluys, L.J. A semi-analytical model for detailed 3D heat flow in shallow geothermal systems. Int. J. Heat Mass Transf. 2018, 123, 911–927. [Google Scholar] [CrossRef]
- Li, Y.; Shu, L.; Xiao, R.; Tao, Y.; Niu, S.; Wang, Z. Effect of pumping-recharge well structures on heat transfer characteristics of double-well groundwater heat pump systems considering hydrothermal coupling. Energy Convers. Manag. 2021, 249, 114871. [Google Scholar] [CrossRef]
- Povstenko, Y.; Klekot, J. Fractional heat conduction with heat absorption in a sphere under Dirichlet boundary condition. Comput. Appl. Math. 2018, 37, 4475–4483. [Google Scholar] [CrossRef]
- Hua, Y.C.; Zhao, T.; Guo, Z.Y. Optimization of the one-dimensional transient heat conduction problems using extended entransy analyses. Int. J. Heat Mass Transf. 2018, 116, 166–172. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y.; Pei, D. Identification of a time-dependent coefficient in heat conduction problem by new iteration method. Adv. Math. Phys. 2018, 2018, 4918256. [Google Scholar] [CrossRef]
- Kot, V.A. Integral method of boundary characteristics: The Dirichlet condition. Principles. Heat Transf.Res. 2016, 47, 1035–1055. [Google Scholar] [CrossRef]
- Chen, H.L.; Liu, Z.L. Solving the inverse heat conduction problem based on data driven model. Chin. J. Comput. Mech. 2021, 38, 272–279. [Google Scholar]
- Sa, M.; Rw, Z. Laplace transform inversion for late-time behavior of groundwater flow problems. Water Resour. Res. 2003, 39, 1283. [Google Scholar]
- Sedghi, M.M.; Zhan, H. Groundwater dynamics due to general stream fluctuations in an unconfined single or dual-porosity aquifer subjected to general areal recharge. J. Hydrol. 2019, 574, 436–449. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.K.; Liang, X. Analytical solutions of three-dimensional groundwater flow to a well in a leaky sloping fault-zone aquifer. J. Hydrol. 2016, 539, 204–213. [Google Scholar] [CrossRef]
- Bansal, R.K. Groundwater flow in floping aquifer under localized transient recharge: Analytical study. J. Hydraul. Eng. 2013, 139, 1165–1174. [Google Scholar] [CrossRef]
- Saeedpanah, I.; Azar, R.G. Solution of unsteady flow in a confined aquifer interacting with a stream with exponentially decreasing stream stage. J. Hydrol. Eng. 2019, 24, 1–11. [Google Scholar] [CrossRef]
- Saeedpanah, I.; Azar, R.G. Modeling the river-aquifer via a new exact model under a more general function of river water level variation. Appl. Water Sci. 2023, 13, 95. [Google Scholar] [CrossRef]
- Wu, D.; Tao, Y.Z.; Lin, F. Application of unsteady phreatic flow model and its solution under the boundary control of complicated function. J. Hydraul. Eng. 2018, 49, 725–731. [Google Scholar]
- Wei, T.; Tao, Y.Z.; Ren, H.L.; Wu, D. The solution to one- dimensional heat conduction problem bounded by the exponential decay condition and its application. Chin. J. Appl. Mech. 2022, 39, 1135–1139,1202. [Google Scholar]
- Ren, H.L.; Tao, Y.Z.; Lin, F.; Wei, T. Analytical Solution to the One-Dimensional Unsteady Temperature Field near the Newtonian Cooling Boundary. Axioms 2023, 12, 61. [Google Scholar] [CrossRef]
- Zhang, J.P. Principles and methods of expressing segmented functions as a single equation using unit step functions. Teach. Res. 1994, 1, 24–26. [Google Scholar]
- Tang, Z.H.; Wang, R.Q. On Definitions and Natures of Dirac Function. J. Liuzhou Voc. Tech. Coll. 2009, 9, 76–78. [Google Scholar]
- Hu, C.J.; Wang, Y.Z. The Laplace transform problem related to series of functions. Eng. Math. 1991, 3, 165–717. [Google Scholar]
- Silva, S. Newton’s cooling law in generalised statistical mechanics. Phys. A Stat. Mech. Appl. 2021, 565, 125539. [Google Scholar] [CrossRef]
- Zhang, S.C. The available range of Newton’s law of cooling. Coll. Phys. 2000, 19, 36–37. [Google Scholar]
- Zhang, W.Z. Calculation of Unsteady Flow of Groundwater and Evaluation of Groundwater Resources; Science Press: Beijing, China, 1983; pp. 69–75. [Google Scholar]
- Alim, T.; Zhou, Z.F.; Mutalip, I. A universal solution to unstable groundwater movement in vicinity of canals. J. Hohai Univ. 2003, 31, 649–651. [Google Scholar]
- Yang, H.P.; Xie, X.Y.; Zhang, J.F. Analytical solution of one-dimensional transient phreatic flow and its application. Adv. Water Sci. 2004, 24, 82–86. [Google Scholar]
- Tang, Z.H.; Qian, G.H.; Qian, W.Q. Estimation of temperature-dependent function of thermal conductivity for a material. Chin. J. Comput. Mech. 2011, 28, 377–382. [Google Scholar]
- Li, Z.J.; Fu, X.; Shi, L.Q. Inversely identified natural ice thermal diffusivity by using measured vertical ice temperature profiles: Recent advancement and considerations. J. Glaciol. Geocryolo. 2023, 45, 599–611. [Google Scholar]
- Dominic, G. Analytical solution to the unsteady one-dimensional conduction problem with two time-varying boundary conditions: Duhamel’s theorem and separation of variables. Heat Mass Transf. 2010, 46, 707–716. [Google Scholar]
- Tadue, A.; Chen, C.S.; Antonio, J. A boundary meshless method for solving heat transfer problems using the Fourier transform. Adv. Appl. Math. Mech. 2011, 3, 572–585. [Google Scholar] [CrossRef]
- He, L.X.; Li, B.J.; Long, Y.; Zhang, Z. Intelligent Optimization Curve Fitting of the Newman Model for the Unsteady Flow of Submerged Aquifer. Haihe Water Resour. 2023, 5, 60–65. [Google Scholar]
- Akbıyık, M.; Yamaç Akbıyık, S.; Karaca, E.; Yılmaz, F. De Moivre’s and Euler Formulas for Matrices of Hybrid Numbers. Axioms 2021, 10, 213. [Google Scholar] [CrossRef]
- Nichita, F.F. Unifification Theories: Rings, Boolean Algebras and Yang–Baxter Systems. Axioms 2023, 12, 341. [Google Scholar] [CrossRef]
- Batiha, I.M.; Abubaker, A.A.; Jebril, I.H.; Al-Shaikh, S.B.; Matarneh, K. A Numerical Approach of Handling Fractional Stochastic Differential Equations. Axioms 2023, 12, 388. [Google Scholar] [CrossRef]
- Ma, S.H. Laplace transformation the uniqueness of primitive function and inverse image function. J. Xi’an Aero. Tech. Coll. 2002, 2, 47–48. [Google Scholar]
- Teng, Y.M. Some problems in integeral transform. Coll. Math. 2015, 31, 105–109. [Google Scholar]
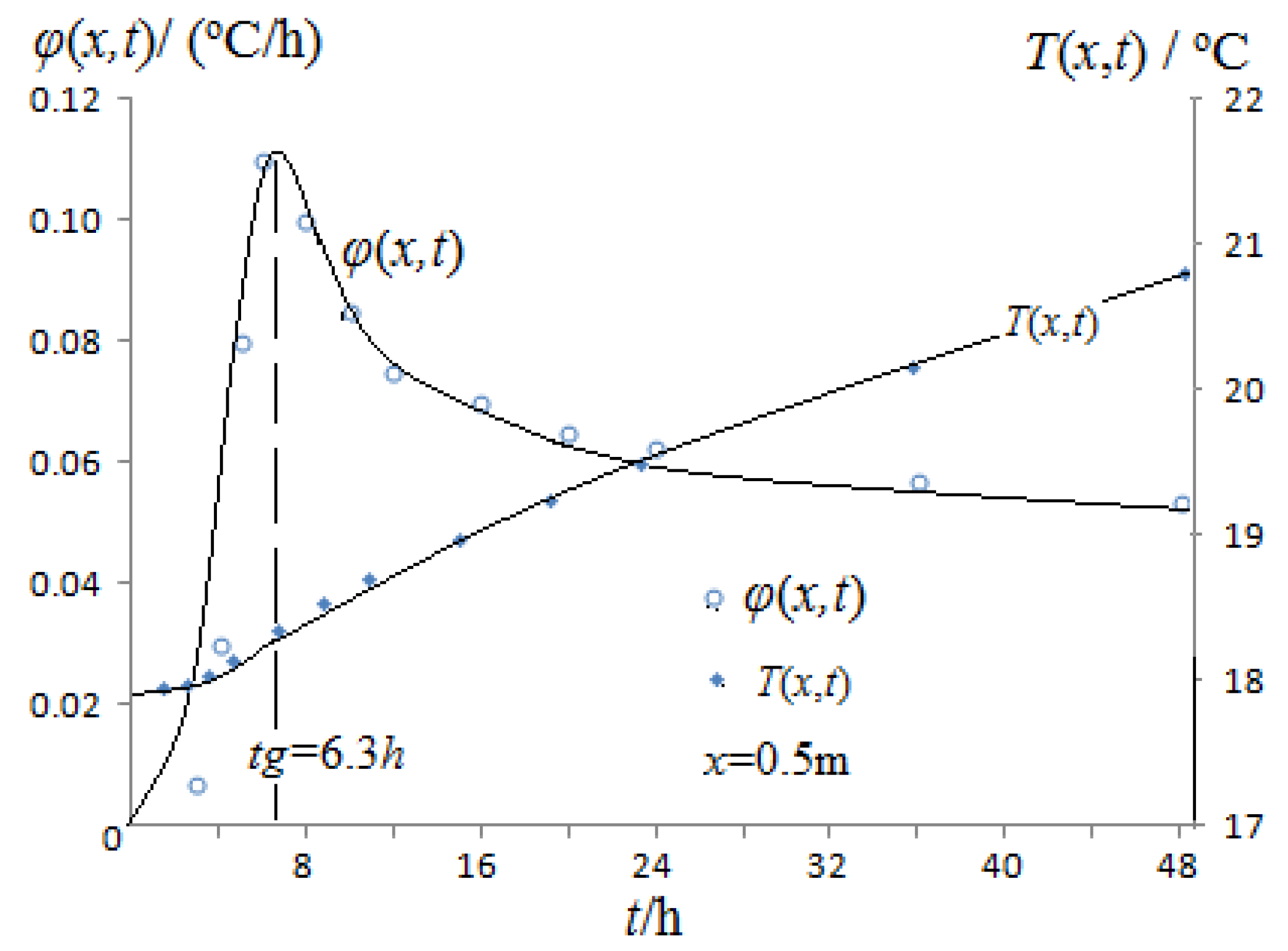

| t/h | 3 | 4 | 5 | 6 | 8 | 10 | 12 | 16 | 20 | 24 | 36 | 48 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T(x,t)/°C | 17.96 | 17.97 | 18.03 | 18.14 | 18.35 | 18.53 | 18.7 | 18.98 | 19.24 | 19.49 | 20.17 | 20.81 |
| φ(x,t)/(°C/h) | 0.007 | 0.010 | 0.060 | 0.110 | 0.105 | 0.090 | 0.085 | 0.070 | 0.065 | 0.063 | 0.057 | 0.053 |
| t/h | 2 | 3 | 4 | 6 | 8 | 10 | 12 | 16 | 20 | 24 | 36 | 48 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T(x,t)/°C | 22.1 | 23.85 | 25.09 | 26.83 | 27.94 | 28.69 | 29.23 | 30.16 | 30.75 | 31.16 | 32 | 32.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Tao, Y.; Ren, H. The Laplace Transform Shortcut Solution to a One-Dimensional Heat Conduction Model with Dirichlet Boundary Conditions. Axioms 2023, 12, 770. https://doi.org/10.3390/axioms12080770
Wu D, Tao Y, Ren H. The Laplace Transform Shortcut Solution to a One-Dimensional Heat Conduction Model with Dirichlet Boundary Conditions. Axioms. 2023; 12(8):770. https://doi.org/10.3390/axioms12080770
Chicago/Turabian StyleWu, Dan, Yuezan Tao, and Honglei Ren. 2023. "The Laplace Transform Shortcut Solution to a One-Dimensional Heat Conduction Model with Dirichlet Boundary Conditions" Axioms 12, no. 8: 770. https://doi.org/10.3390/axioms12080770
APA StyleWu, D., Tao, Y., & Ren, H. (2023). The Laplace Transform Shortcut Solution to a One-Dimensional Heat Conduction Model with Dirichlet Boundary Conditions. Axioms, 12(8), 770. https://doi.org/10.3390/axioms12080770









