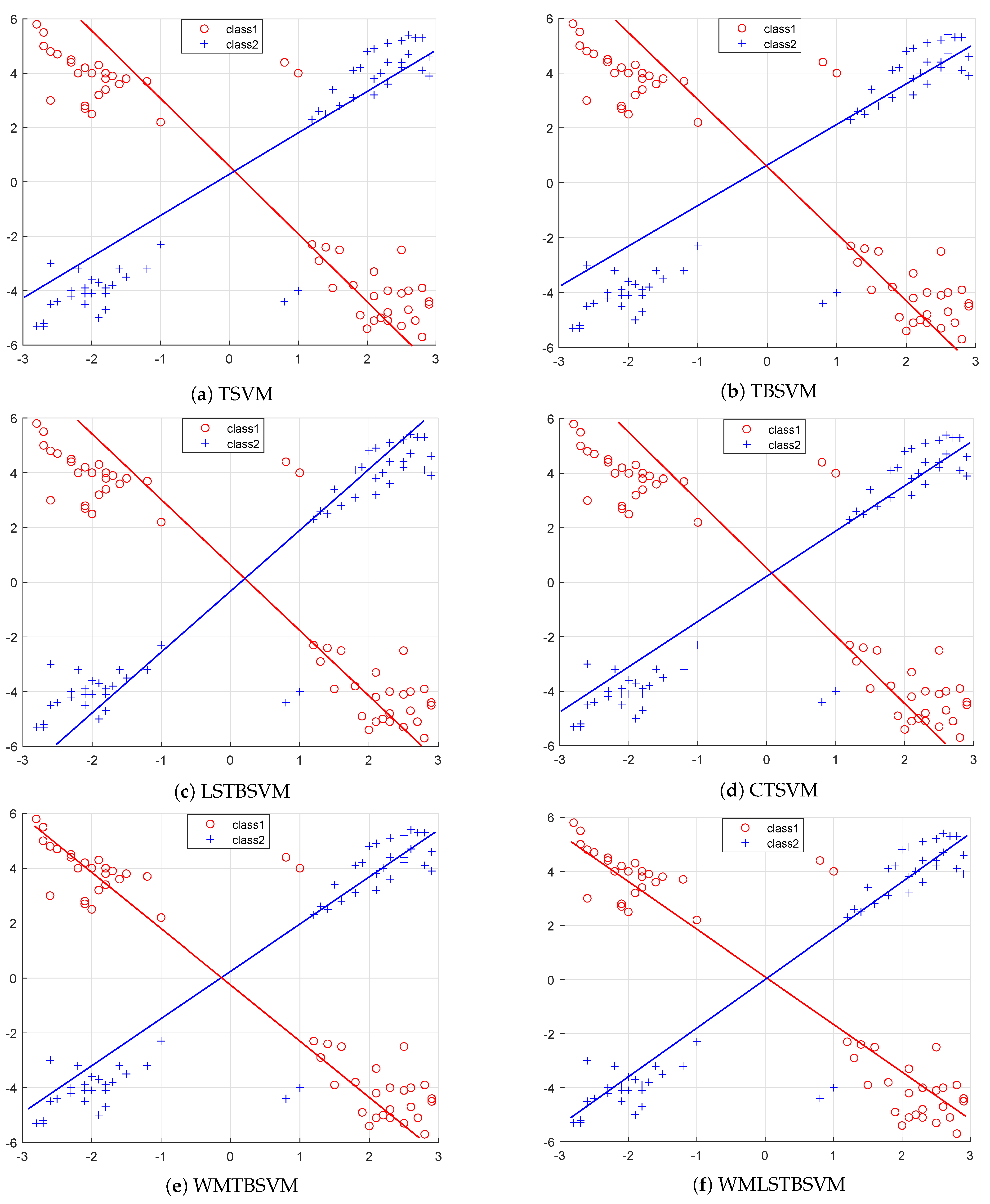
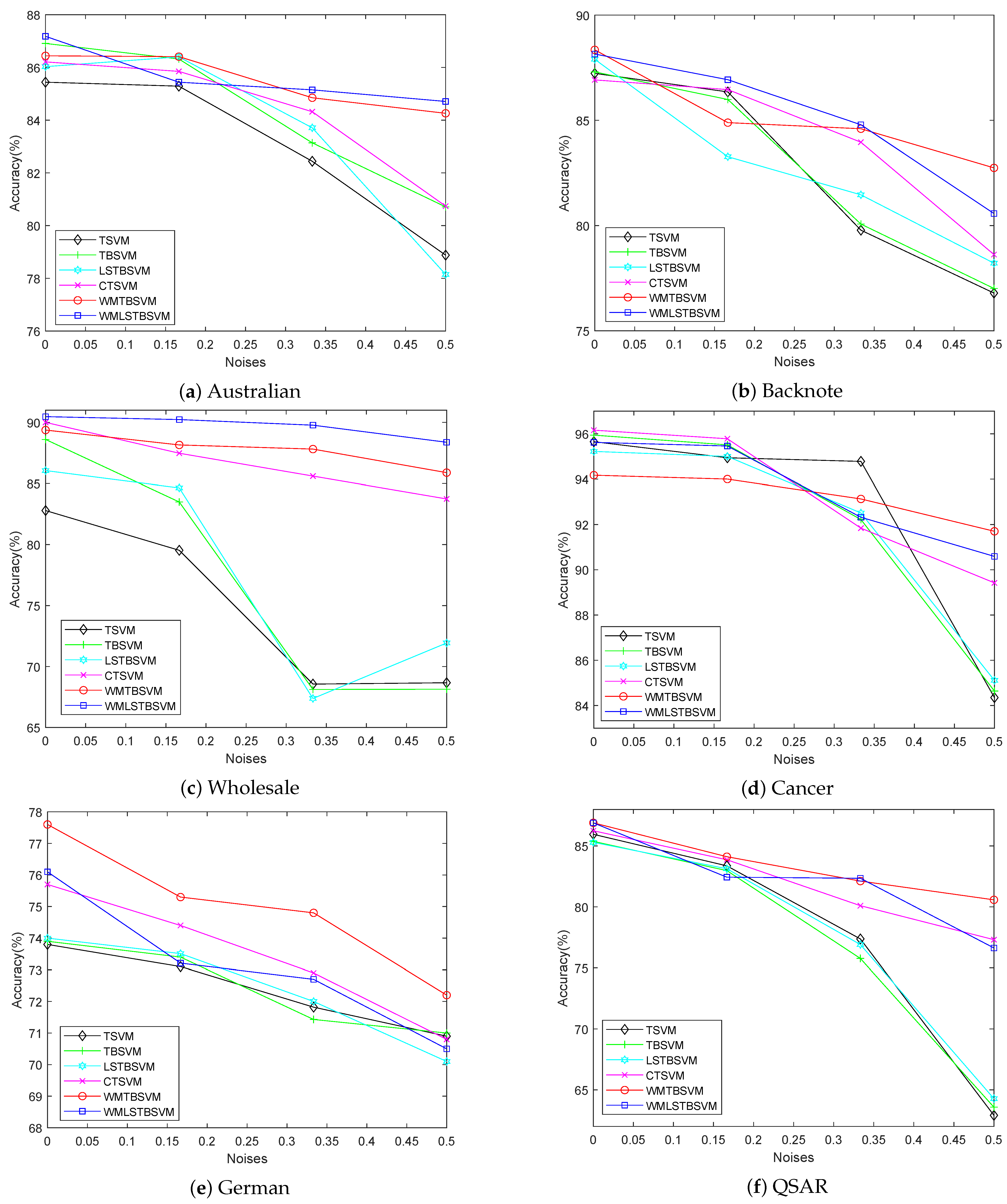
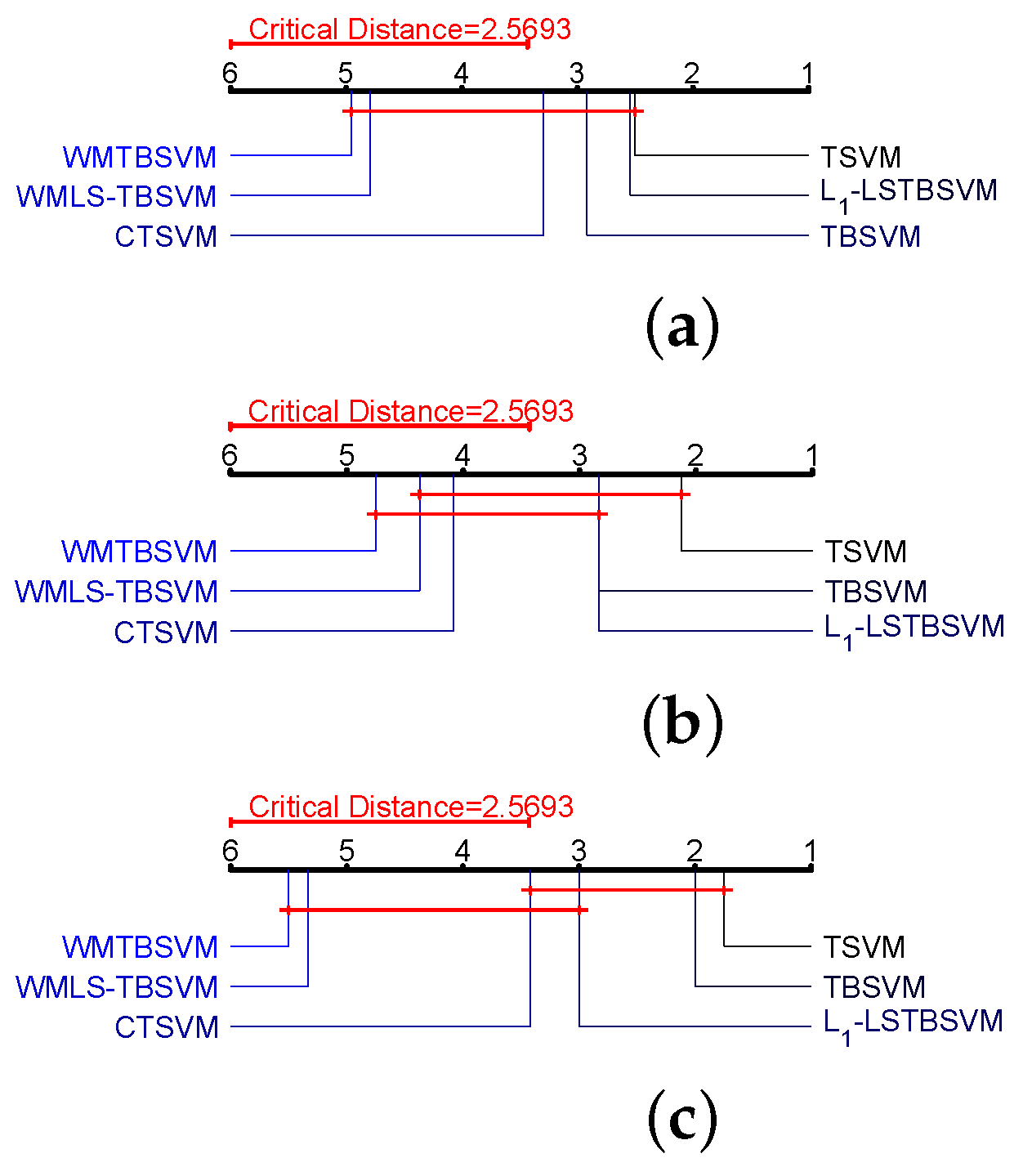
1. Introduction
Data collecting and reasonable processing are becoming increasingly crucial as modern computer technology advances. As an excellent machine learning tool, support vector machine (SVM) [
1,
2,
3] has been widely used in bioinformatics, computer vision, data mining, robotics, and other fields in recent years. The main idea behind SVM classification based on statistical learning theory and optimization theory is to construct a pair of parallel hyperplanes to maximize the minimum distance between two classes of samples. SVMs implement the structural risk minimization (SRM) principle in addition to empirical risk minimization. Although SVM can achieve good classification performance, it needs to solve a large-scale quadratic programming problem (QPP), and learning it takes a lot of time, which seriously hinders the application of SVM in large-scale classification tasks [
4]. Furthermore, when dealing with complicated data, the simple SVM model would run into various issues, which will stymie its development and practical implementation, such as the “XOR” problem.
To overcome the difficulties brought by SVM to solve a QP problem, Jayadeva et al. [
5] proposed a twin support vector machine (TSVM) for pattern classification based on generalized eigenvalue approximation support vector machine (GEPSVM). Since TSVM solves two smaller QPP problems instead of a single large QPP problem, it can theoretically learn four times faster than a standard SVM. The main goal of TSVM is to find two parallel hyperplanes, each of which is as close as possible to the corresponding class in the sample data, while being as far away from the other classes as possible. Further, to overcome the problem that TSVM only considers empirical risk minimization without considering the principle of structural risk minimization, Shao et al. [
6] proposed a twin bounded support vector machine (TBSVM) by introducing two regularization terms. Compared with TSVM, a significant advantage of TBSVM is the principle of structural risk minimization, which embodies the essence of statistical learning theory, so this improvement can improve the classification performance of TSVM. In recent years, some TSVM-based variant algorithms have been proposed for pattern classification tasks, such as least squares twin support vector machine (LSTSVM) [
4], recursive projection twin support vector machine (RPTSVM) [
7], pinball twin support vector machine (Pin-TSVM) [
8], sparse pinball twin support vector machine (SPTWSVM) [
9], least squares recursive projection twin support vector machine (LSRPTSVM) [
10], fuzzy twin support vector machine (FBTSVM) [
11], and so on, which greatly promoted the development of TSVM.
It is well known that distance metrics play a crucial role in many machine learning algorithms [
12]. Although the above algorithms show good performance in pattern classification, it is worth noting that most of them adopt the
-norm distance metric, whose squaring operation will exaggerate the impact of outliers on model performance. To effectively alleviate the impact of the
-norm distance metric on the robustness of the algorithm, the
-norm distance metric c with bounded derivative has received extensive attention and research in many fields of machine learning in recent years [
13,
14,
15,
16,
17,
18]. For example, Zhu et al. [
13] proposed 1-norm SVM (1-SVM) based on an SVM learning framework. Mangasarian [
14] proposed an exact
-norm support vector machine based on unconstrained convex differentiable minimization. Gao [
15] developed a new 1-norm least squares TSVM (NELSTSVM). Ye et al. [
16] proposed a
-norm distance minimization-based robust TSVM. Yan et al. [
17] proposed 1-norm projection TSVM (1-PTSVM), and so on. As mentioned earlier, the
-norm is a better alternative to the squared
-norm in terms of enhancing the robustness of the algorithm. However, when the outliers are large, the existing classification methods based on
-norm distance often cannot achieve satisfactory classification results.
Recently, more and more researchers have paid attention to the capped
-norm and achieved some excellent research results [
19,
20,
21,
22,
23,
24]. Research shows that capped
-norm is considered to be a better approximation of
-norm and more robust than
-norm. In general, the capped
-norm is considered to be a better approximation of the
-norm, with stronger robustness than the
-norm. Some excellent algorithms based on capped
-norm have been proposed for robust classification tasks. For example, Wang et al. [
25] proposed a new robust TSVM (CTSVM) by applying capped
-norm. CTSVM retains the advantages of TSVM and improves the robustness of classification. The experimental results on multiple datasets show that the CTSVM algorithm has good robustness and effectiveness to outliers. The capped
-norm metrics are neither convex nor smooth, which makes them difficult to optimize. There are two general strategies for solving nonconvex optimization problems. The first strategy is to design efficient algorithms, such as the bump process algorithm and the abnormal path algorithm. The second strategy is to smooth the metric function to reduce the complexity of the algorithm. To overcome the shortcomings of capped
-norm, many scholars proposed capped
-norm for robust learning [
26,
27]. Zhang et al. [
28] proposed a new large-scale semi-supervised classification algorithm based on ridge regression and capped
-norm loss function. It is worth noting that by setting the appropriate
p-value, the capped
-norm and capped
-norm are special forms of capped
-norm: when
or
, the capped
-norm corresponds to the capped
-norm or capped
-norm. These algorithms show that the capped distance metric is robust against outliers. However, there are few extensions and related applications of the capped
-norm for twin support vector machine.
In the current scenario, although data collection is easy, obtaining labeled data is difficult [
29]. To address this issue, researchers have proposed semi-supervised learning (SSL) [
29], which uses less labeled data and more unlabeled data to build more reliable classifiers. Graph-based SSL algorithms are a significant branch of SSL. The learning strategy involves first forming edges by connecting points between labeled and unlabeled data points and then creating a graph from these edges that represents the similarity between samples. Manifold regularization-based SSL [
30] is one of the graph-based SSL methods that preserve the manifold structure to improve the discriminative property of the data [
31]. The learning strategy involves mining the geometric distribution information of the data and representing it in the form of regularization terms. The reference [
31] first introduced MR to SSL by proposing the Laplace support vector machine (Lap-SVM) and Laplace regularized least squares (Lap-RLS). Qi et al. [
32] developed a Laplace TSVM (LapTSVM) based on a pair of non-parallel hyperplanes of TSVM. Although the classifier’s generalization performance is improved, the method’s parameter adjustment may be impacted by different datasets, and it may not be able to handle large-scale problems effectively due to high computational complexity. Xie et al. [
33] propose a novel Laplacian
-norm least squares twin support vector machine (Lap-
LSTSVM). The experimental results on both synthetic and real-world datasets show that Lap-
LSTSVM outperforms other state-of-the-art methods and can also deal with noisy datasets [
34,
35].
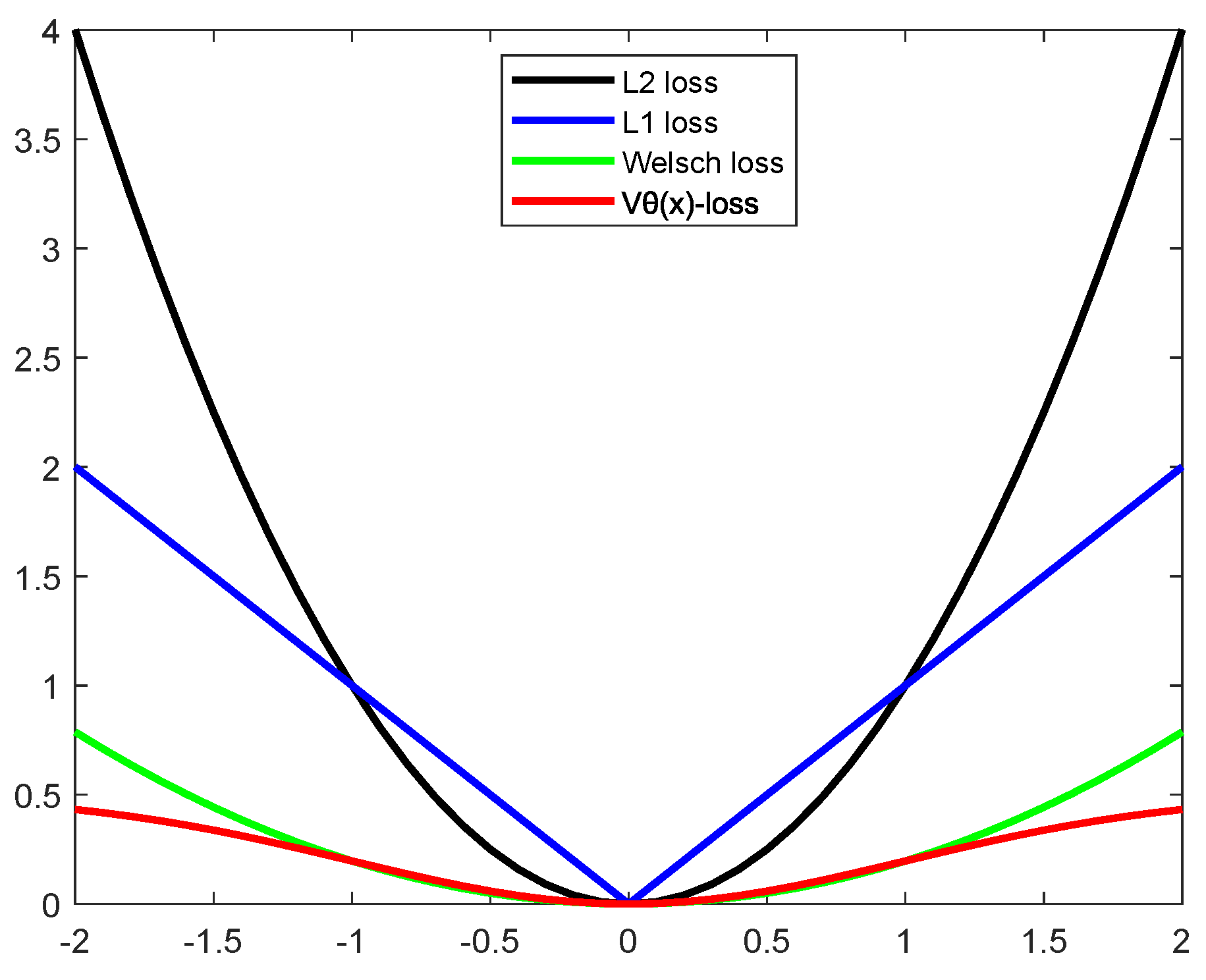
To summarize, prior research on improving the TBSVM classification performance while considering robustness and discriminability is limited. In response, we introduce the WMRTBSVM and WMLSRTBSVM models. Specifically, we replace the hinge loss term in TBSVM with the -norm, and we replace the second term in TBSVM with the Welsch Loss with p-power. This improves the model’s classification performance and robustness. Furthermore, we incorporate a manifold structure into the model to further enhance its classification performance and discriminability. The main contributions of this paper are summarized as follows:
- (1)
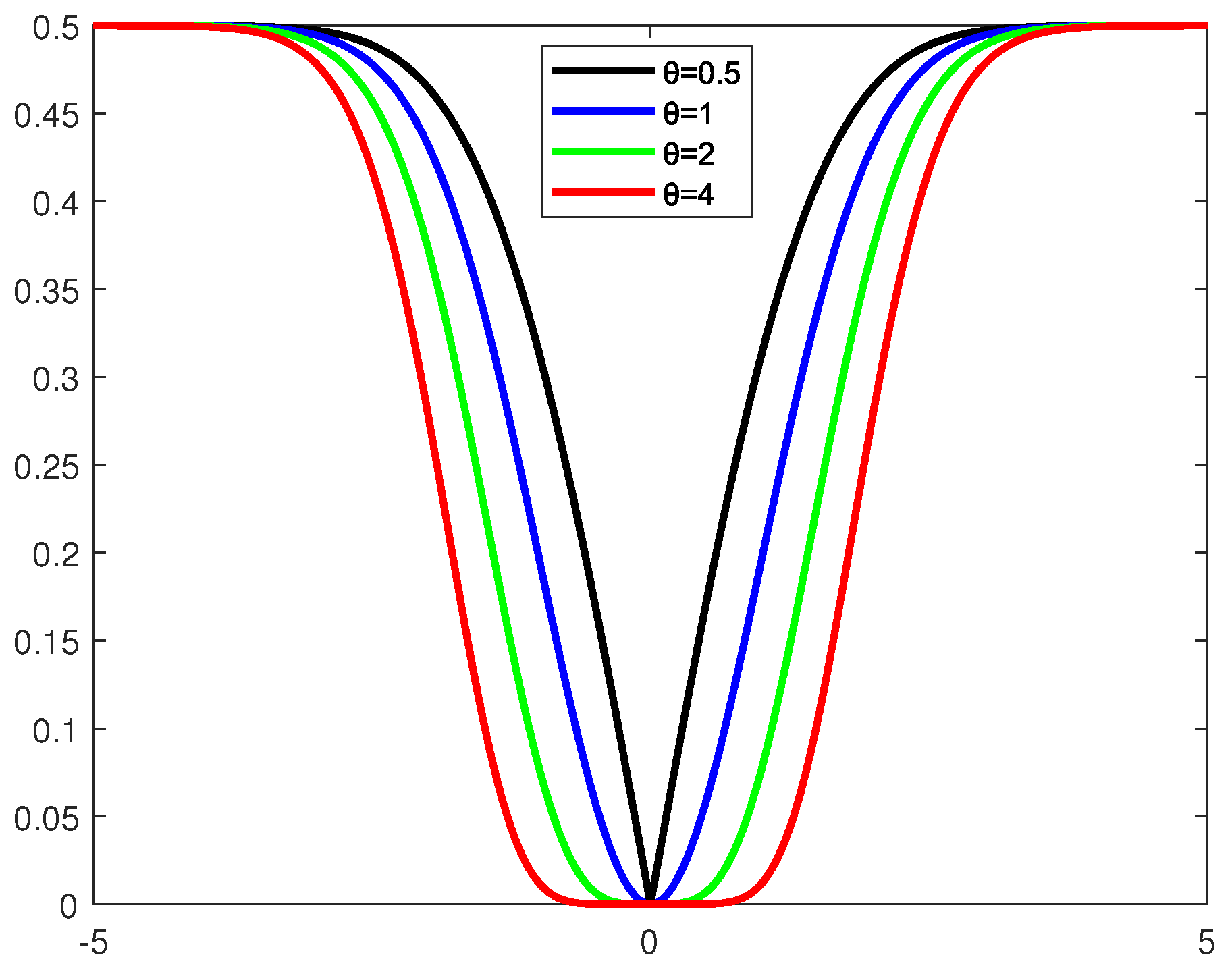
A generalized adaptive robust loss function called is innovatively designed. Intuitively, can improve the robustness of the model by selecting different robust loss functions for different learning tasks during the learning process via the adaptive parameter . Compared with other robust loss functions, has some desirable salient properties, such as symmetry, boundedness, robustness, nonconvexity, and adaptivity.
- (2)
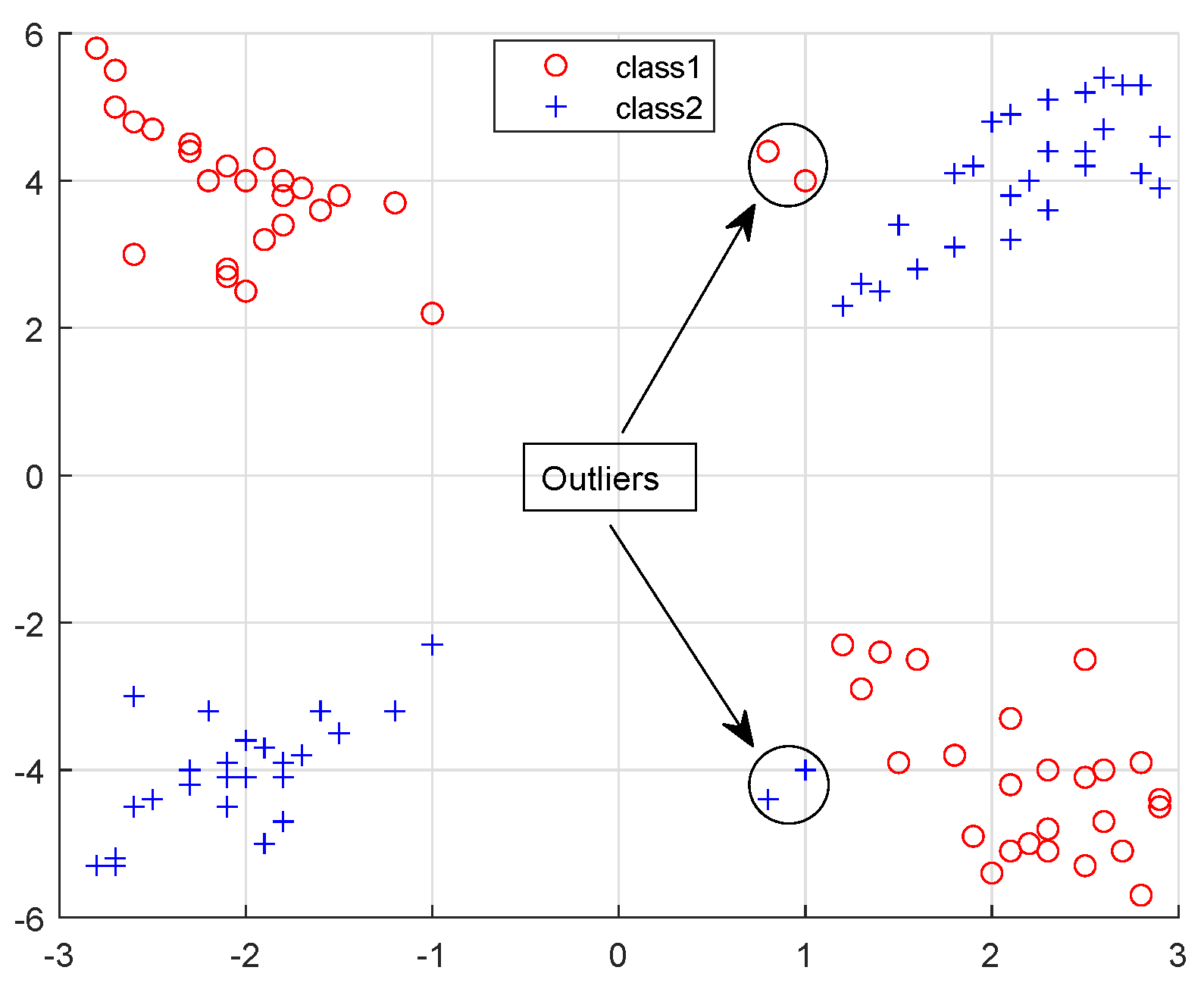
A novel robust manifold learning framework for semi-supervised pattern classification is proposed. In this learning framework, the proposed robust loss function and capped -norm robust distance metric are introduced to improve the robustness and generalization performance of the model, especially when the outliers are far from the normal data distributions.
- (3)
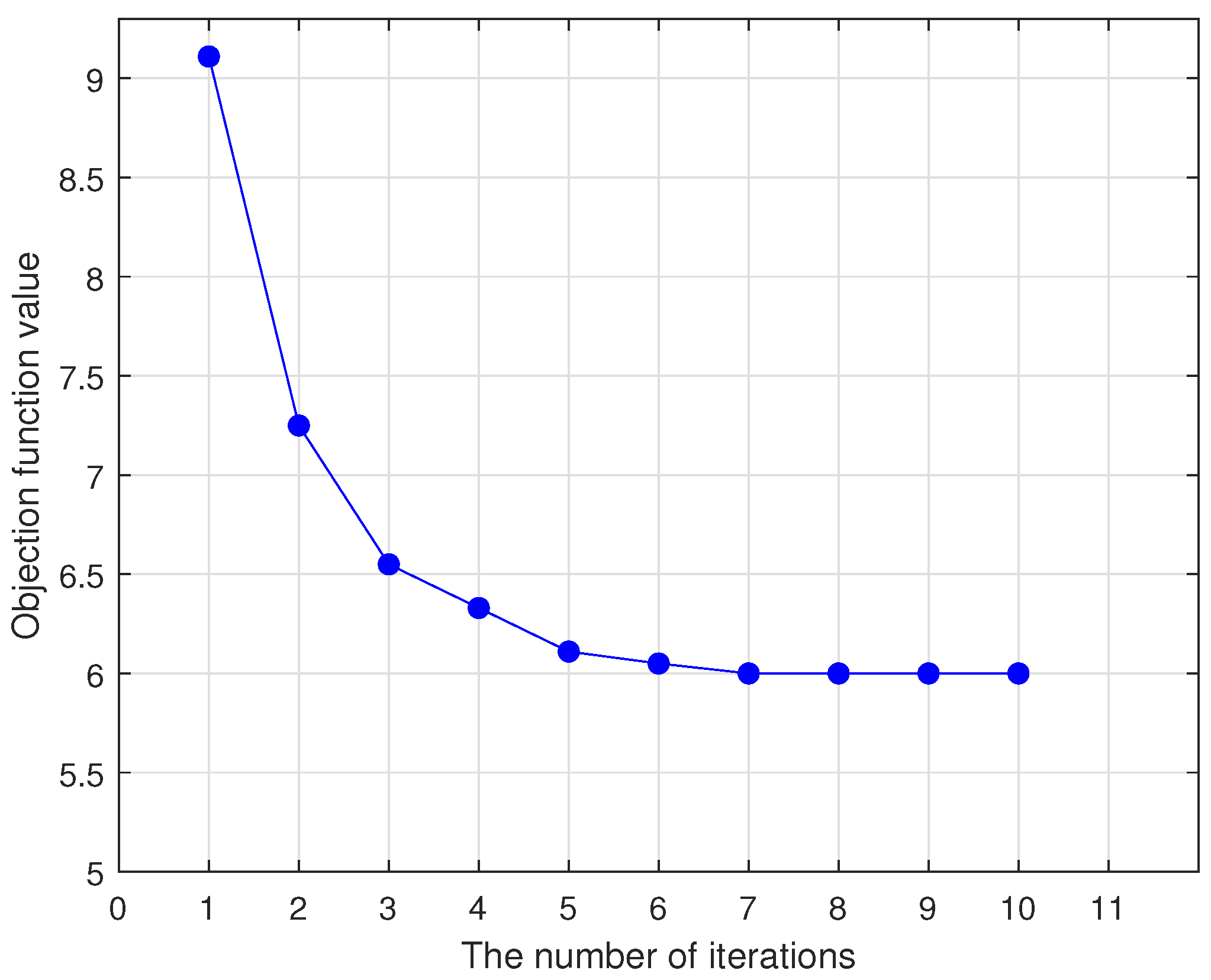
Two effective iterative optimization algorithms are designed for solving our methods by the half-quadratic (HQ) optimization algorithm, and the convergence of the algorithms is demonstrated.
- (4)
Experimental results on artificial and benchmark datasets with different noise settings and different evaluation criteria show that our methods have better classification performance and robustness.
In
Section 2, we introduce the formulas involved in TBSVM and manifold regularization since our model is based on these two approaches. In
Section 3, we present a novel robust manifold learning framework for semi-supervised pattern classification. Finally, we discuss experiments and conclusions in
Section 4 and
Section 5, respectively.
The structure of the rest of this paper is as follows: In
Section 2, as our model is based on TBSVM and manifold regularization, in order to improve our formulas and their derivation, we will introduce the formulas involved in TBSVM and manifold regularization, respectively. In
Section 3, we present a novel robust manifold learning framework for semi-supervised pattern classification. Finally, in
Section 4 and
Section 5, we discuss experiments and conclusions.