Information Processing with Stability Point Modeling in Cohen–Grossberg Neural Networks
Abstract
1. Introduction
2. Cohen–Grossberg Network Training for Different Modalities
3. H-Stability Results
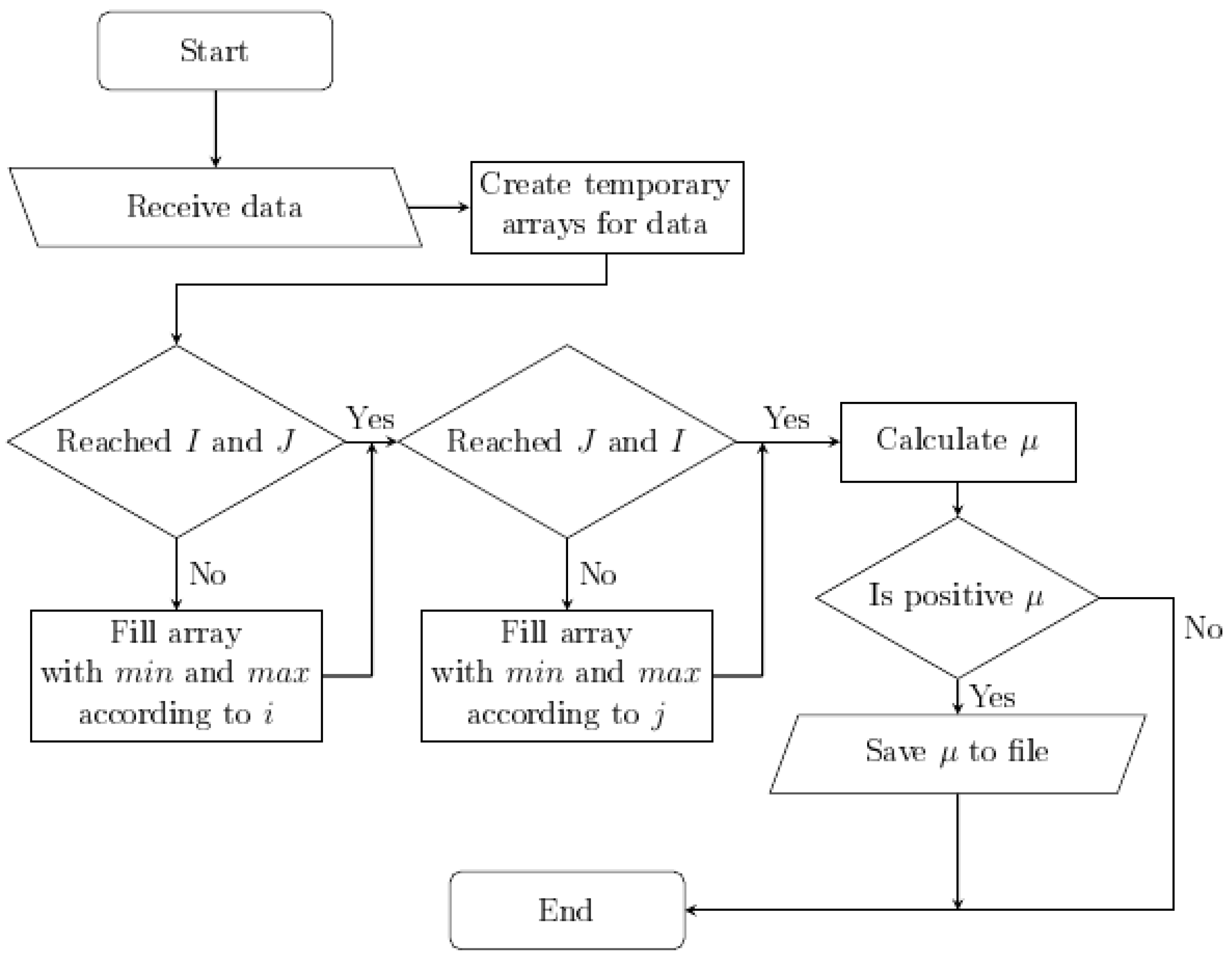
4. Algorithms of a Stability Model in Cohen–Grossberg-Type Neural Networks
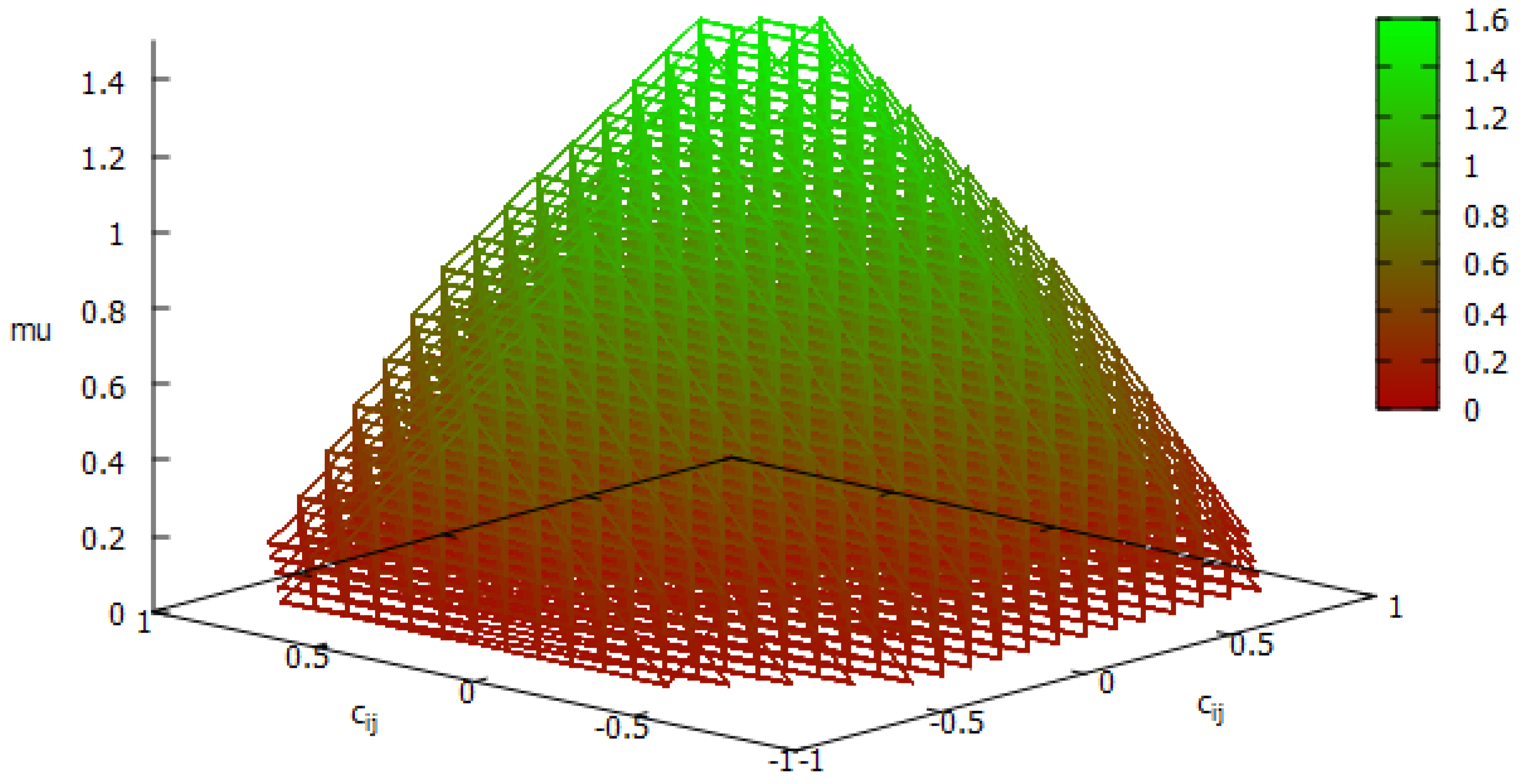
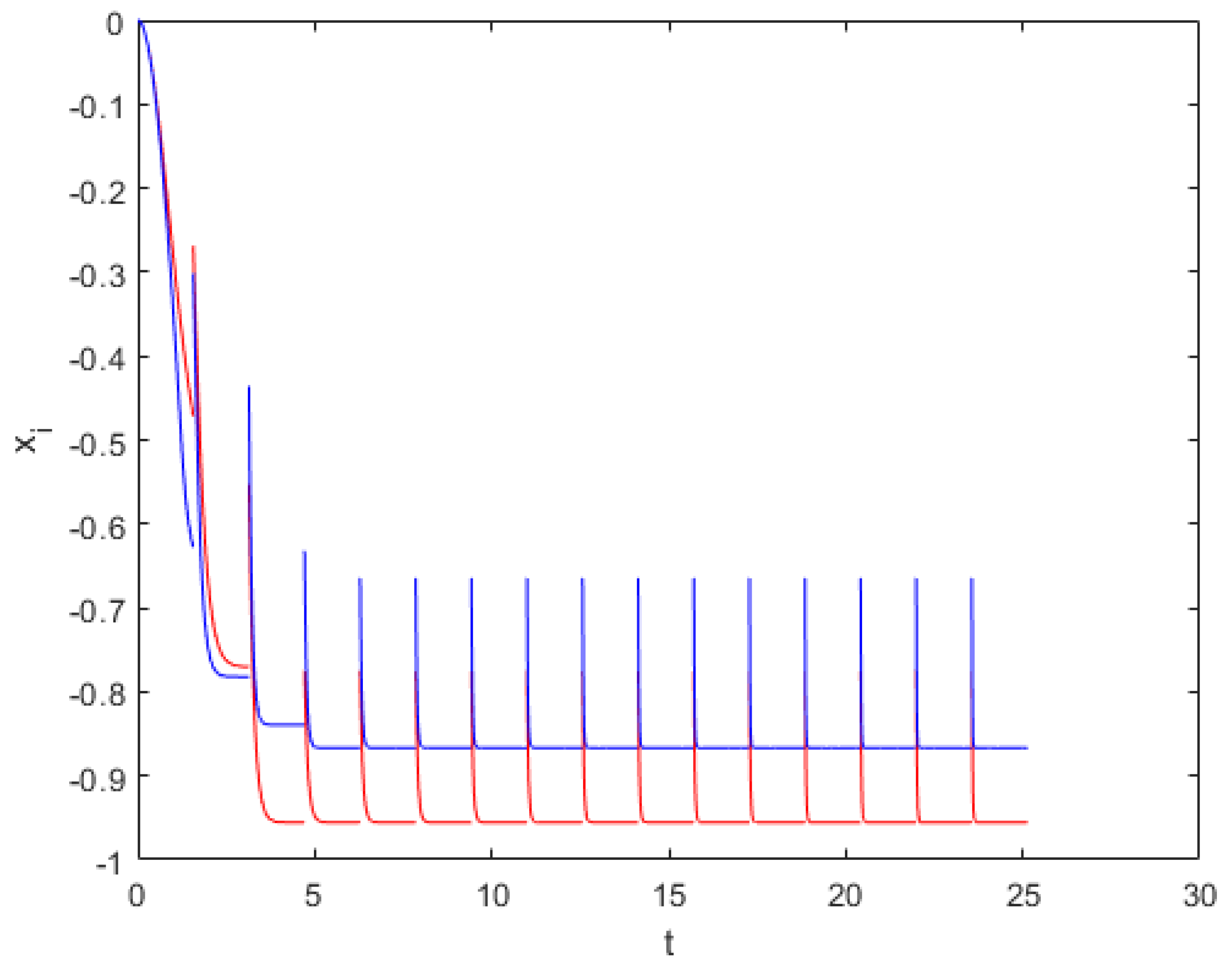
5. Implementation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| CGNN | Cohen–Grossberg neural network |
| IS | Intelligent system |
| LTM | Long-term memory |
| STM | Short-term memory |
| OpenMPI | Open message-passing interface |
References
- Ravindran, K.; Rabby, M. Software cybernetics to infuse adaptation intelligence in networked systems. In Proceedings of the 2013 Fourth International Conference on the Network of the Future (NoF), Pohang, Republic of Korea, 23–25 October 2013; pp. 1–6. [Google Scholar]
- Alkon, D.L.; Amaral, D.G.; Bear, M.F.; Black, J.; Carew, T.J.; Cohen, N.J.; Disterhoft, J.F.; Eichenbaum, H.; Golski, S.; Gorman, L.K.; et al. Learning and memory. Brain Res. Rev. 1991, 16, 193–220. [Google Scholar] [CrossRef] [PubMed]
- PCMagStaff. Better (However, Still Not Perfect) Speech Recognition. 2002. Available online: https://www.pcmag.com/archive/better-but-still-not-perfect-speech-recognition-33255 (accessed on 13 January 2023).
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Kharlamov, A. Attention Mechanism Usage to form Framework-Structures on a Semantic Net. Neurocomput. Atten. Connect. Neurocomput. 1991, 2, 747–756. [Google Scholar]
- Kohonen, T. Self-Organization and Associative Memory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 8. [Google Scholar]
- Lienhart, R.; Pfeiffer, S.; Effelsberg, W. Video abstracting. Commun. ACM 1997, 40, 54–62. [Google Scholar] [CrossRef]
- Ducrot, O. Structuralisme, énonciation et Sémantique. Poétique. Revue de Théorie et d’Analyse Littéraires Paris 1978; 107–128, 1er tr. ISBN 2.02.004801.9—Numéro de la Comission Paritaira, 57274. Available online: https://semanticar.hypotheses.org/files/2023/06/ducrot-structuralisme-enonciation.pdf (accessed on 13 January 2023).
- Rumelhart, D.; Zipser, D. Parallel distributed processing: Explorations in the microstructure of cognition. In Chapter Feature Discovery by Competitive Learning; The MIT Press: Cambridge, MA, USA, 1986; Volume 1. [Google Scholar]
- Schwenk, H. Efficient training of large neural networks for language modeling. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 4, pp. 3059–3064. [Google Scholar]
- Grossberg, S. Adaptive pattern classification and universal recoding: I. Parallel development and coding of neural feature detectors. Biol. Cybern. 1976, 23, 121–134. [Google Scholar] [CrossRef] [PubMed]
- Grossberg, S. Studies of Mind and Brain: Neural Principles of Learning, Perception, Development, Cognition, and Motor Control; Boston Studies in the Philosophy and History of Science; Springer: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Grossberg, S. Stephen Grossberg—Boston University. 2022. Available online: https://sites.bu.edu/steveg/ (accessed on 19 December 2022).
- Anderson, J.A. A simple neural network generating an interactive memory. Math. Biosci. 1972, 14, 197–220. [Google Scholar] [CrossRef]
- Grossberg, S.; Mingolla, E.; Todorovic, D. A neural network architecture for preattentive vision. IEEE Trans. Biomed. Eng. 1989, 36, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Stamov, G.; Simeonov, S.; Torlakov, I. Visualization on Stability of Impulsive Cohen-Grossberg Neural Networks with Time-Varying Delays. In Contemporary Methods in Bioinformatics and Biomedicine and Their Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 195–201. [Google Scholar] [CrossRef]
- Stamov, G.; Stamova, I.; Simeonov, S.; Torlakov, I. On the Stability with Respect to H-Manifolds for Cohen–Grossberg-Type Bidirectional Associative Memory Neural Networks with Variable Impulsive Perturbations and Time-Varying Delays. Mathematics 2020, 8, 335. [Google Scholar] [CrossRef]
- Stamov, G.T.; Stamova, I.M. Integral manifolds for uncertain impulsive differential–difference equations with variable impulsive perturbations. Chaos Solitons Fractals 2014, 65, 90–96. [Google Scholar] [CrossRef]
- Stamova, I.; Sotirov, S.; Sotirova, E.; Stamov, G. Impulsive Fractional Cohen-Grossberg Neural Networks: Almost Periodicity Analysis. Fractal Fract. 2021, 5, 78. [Google Scholar] [CrossRef]
- Stamova, I.M. Impulsive control for stability of n-species Lotka–Volterra cooperation models with finite delays. Appl. Math. Lett. 2010, 23, 1003–1007. [Google Scholar] [CrossRef]
- Stamova, I.M.; Stamov, G.T. Impulsive control on global asymptotic stability for a class of impulsive bidirectional associative memory neural networks with distributed delays. Math. Comput. Model. 2011, 53, 824–831. [Google Scholar] [CrossRef]
- Stamova, I.M.; Stamov, T.; Simeonova, N. Impulsive control on global exponential stability for cellular neural networks with supremums. J. Vib. Control 2013, 19, 483–490. [Google Scholar] [CrossRef]
- Wang, L.; Zou, X. Exponential stability of Cohen–Grossberg neural networks. Neural Netw. 2002, 15, 415–422. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Feng, B.; Ding, Y. QGTC. In Proceedings of the 27th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Seoul, Republic of Korea, 2–6 April 2022. [Google Scholar] [CrossRef]
- Song, Q.; Yang, X.; Li, C.; Huang, T.; Chen, X. Stability analysis of nonlinear fractional-order systems with variable-time impulses. J. Frankl. Inst. 2017, 354, 2959–2978. [Google Scholar] [CrossRef]
- Open MPI, Software in the Public Interest, Open MPI: Open Source High Performance Computing. Available online: https://www.open-mpi.org/ (accessed on 17 November 2022).
- Corporation, I. Intel Xeon Gold 5218R Processor 27.5M Cache 2.10 GHz Product Specifications. Available online: https://ark.intel.com/content/www/us/en/ark/products/199342/intel-xeon-gold-5218r-processor-27-5m-cache-2-10-ghz.html (accessed on 1 August 2022).
- Cohen, M.A.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 815–826. [Google Scholar] [CrossRef]
- Open MPI, Software in the Public Interest, Open MPI v4.1.4 Documentation. 2022. Available online: https://www.open-mpi.org/doc/current/ (accessed on 1 August 2022).
- Stamova, I.; Stamov, G. Applied Impulsive Mathematical Models; CMS Books in Mathematics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gospodinova, E.; Torlakov, I. Information Processing with Stability Point Modeling in Cohen–Grossberg Neural Networks. Axioms 2023, 12, 612. https://doi.org/10.3390/axioms12070612
Gospodinova E, Torlakov I. Information Processing with Stability Point Modeling in Cohen–Grossberg Neural Networks. Axioms. 2023; 12(7):612. https://doi.org/10.3390/axioms12070612
Chicago/Turabian StyleGospodinova, Ekaterina, and Ivan Torlakov. 2023. "Information Processing with Stability Point Modeling in Cohen–Grossberg Neural Networks" Axioms 12, no. 7: 612. https://doi.org/10.3390/axioms12070612
APA StyleGospodinova, E., & Torlakov, I. (2023). Information Processing with Stability Point Modeling in Cohen–Grossberg Neural Networks. Axioms, 12(7), 612. https://doi.org/10.3390/axioms12070612







