Bayesian and Non-Bayesian Estimation for a New Extension of Power Topp–Leone Distribution under Ranked Set Sampling with Applications
Abstract
1. Introduction
- The KMPTL distribution is very simple and it has more flexibility than the PTL distribution, and both distributions have two parameters.
- We demonstrate that the KMPTL distribution may provide desirable features in both practical and theoretical terms.
- Numerous broad statistical and mathematical aspects of the PTL distribution were studied.
- Four different measures of entropy are calculated.
- The cumulative residual Rényi entropy (CRRE) is calculated.
- Classical and Bayesian approaches of estimation were utilized to compute the estimate of parameters for the KMPTL distribution, under SRS and RSS.
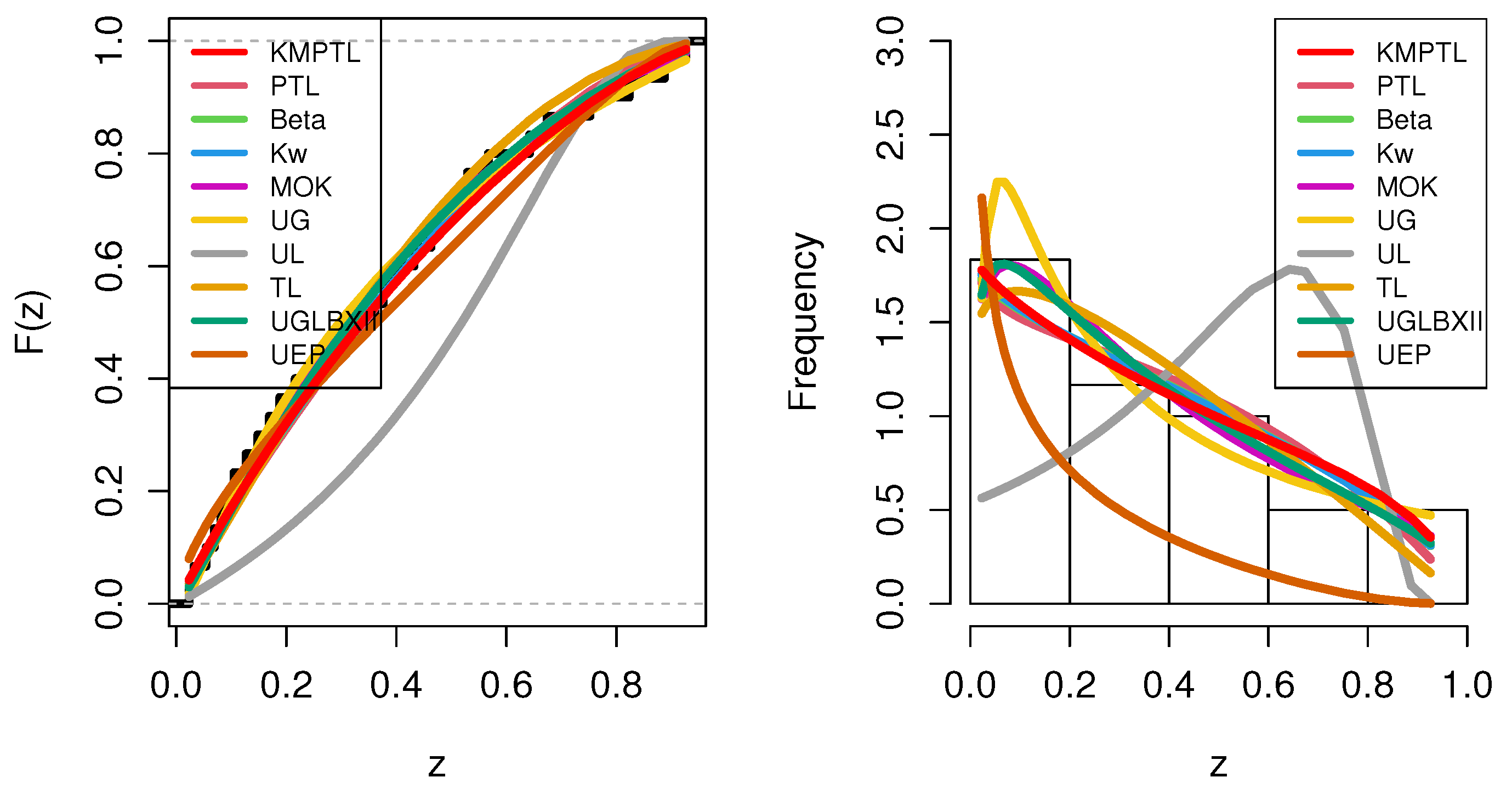
- For modeling, we used two genuine datasets from economics and physics; the KMPTL distribution provides a better fit than the PTL distribution and the other nine competitive statistical distributions, the PTL, unit-Gompertz (UG), unit-Lindley (UL), TL, unit generalized log Burr XII (UGLBXII), unit exponential Pareto distribution (UEPD), Kumaraswamy (Kw), beta, and Marshall-Olkin Kumaraswamy (MOK) distributions, and we suggested this in the application section.
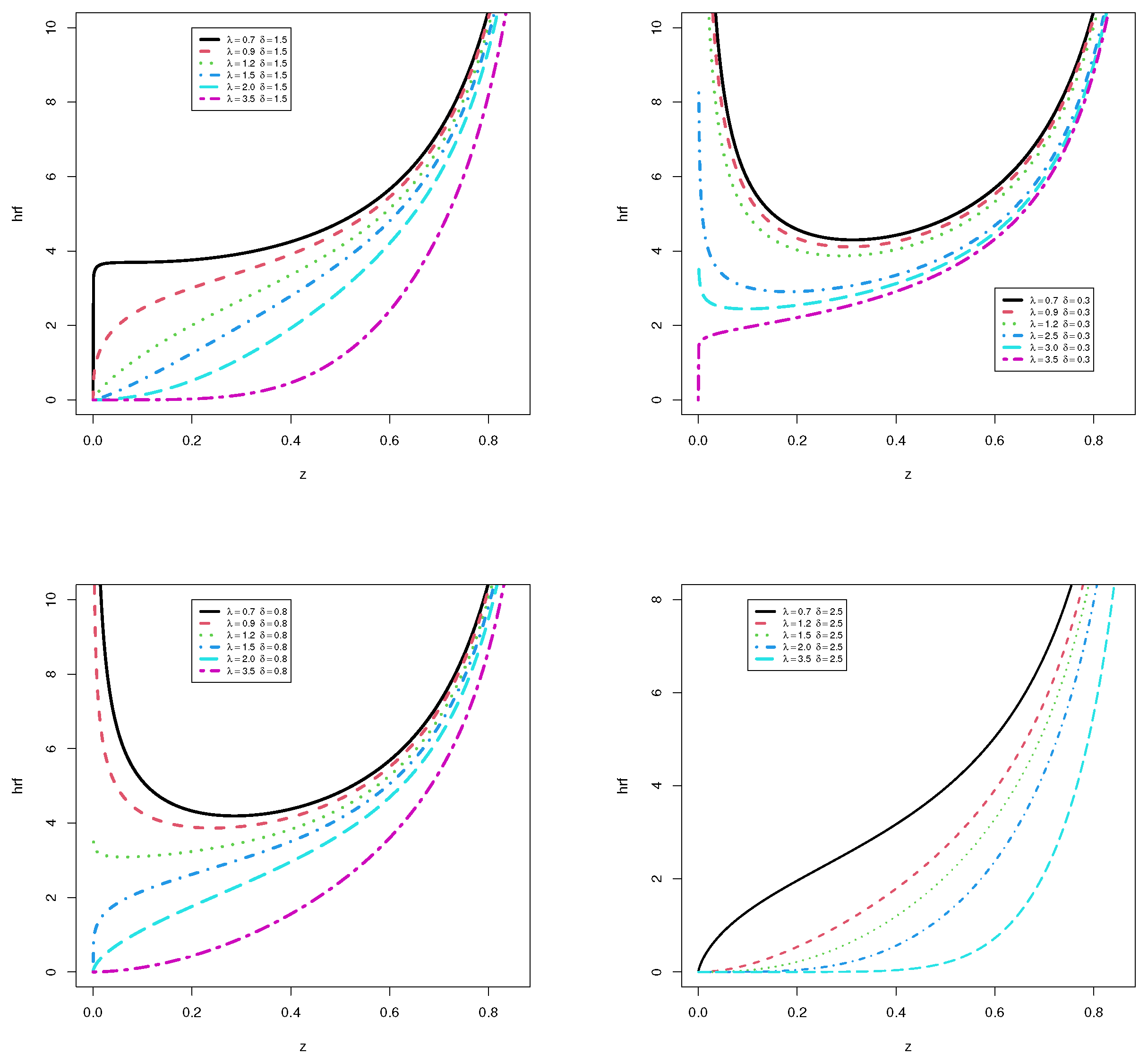
2. The Kavya–Manoharan Power Topp–Leone Distribution
3. Some Basic Statistical Properties
3.1. Quantile Function
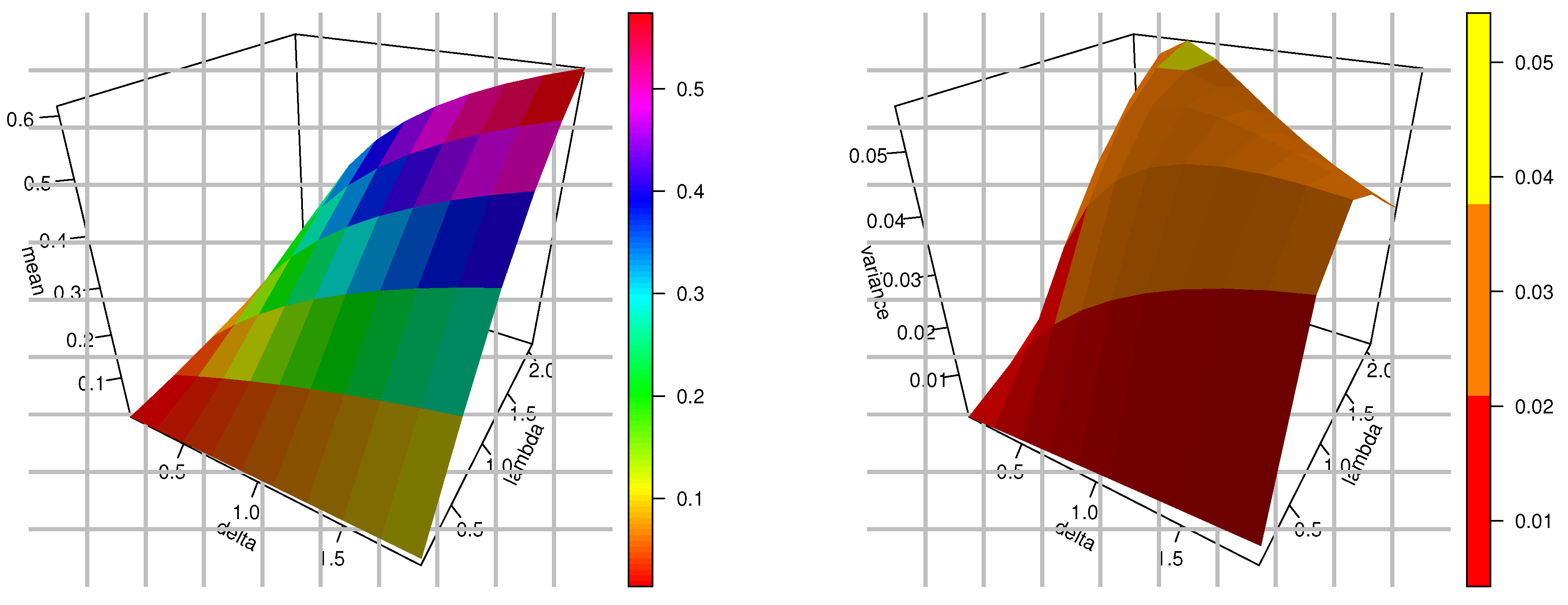
3.2. Moments
3.3. Incomplete Moments
4. Entropy
4.1. Rényi Measure of Entropy
4.2. Arimoto Measure of Entropy
4.3. Tsallis Measure of Entropy
4.4. Havrda and Charvat Measure of Entropy
5. Cumulative Residual Rényi Entropy
6. Estimation Methods Based on Sampling Approach
- Choose observations from an r-set, each of which contains r randomly chosen units.
- Using an accessible auxiliary variable or individual assessment, the units are rated.
- The lowest unit in the first set should be chosen, followed by the second-lowest unit in the second set, and so on until the fourth unit in the fourth set is chosen.where as a cycle iteration.
- The process returns ranked set samples with an r. The operation will therefore be carried out m times in order to obtain the necessary sample n, where , , and samples. According to the foundation of flawless judgement ranking, has the same distribution; see citation [63].
6.1. Maximum Likelihood Estimation under SRS
6.2. Maximum Likelihood Estimation under RSS
6.3. Bayesian Estimation
- Begin with initial values , ;
- Put t = 1;
- Utilize the MHA to create ;
- Utilize the MHA to create ;
- Set t = t + 1;
- Repeat the procedures items I times.
7. Simulation
- Select the replication number M & I, the sample size n, and the parameter values;
- Select the replication number cycle m, and the sample size of each cycle r;
- Generate SRS and RSS from LMPTL by using the “rss” package in the R-4.3.0 program and qf (11) of the KMPTL distribution.
- Using the simulated data, determine the MLEs and BEs of the KMPTL distribution’s parameters;
- Repeat the above steps, M times;
- Determine the mean of bias, average MSE, RE, LCI, and CP for each parameter.
- In every calculation, the bias, MSE and LCI become smaller as n is increased.
- The relevance of the Bias, MSE, and LCI for KMPL distribution parameters decreases as the number of cycles (r) in the RSS sampling rises, but the RE rises.
- As the sample size for each cycle (m) rises in the RSS sampling, the significance of the Bias, MSE, and LCI for KMPTL distribution parameters declines, while the RE increases.
- Comparatively speaking, Bayesian estimates are substantially more efficient than MLE for the majority of KMPTL distribution parameters.
- Comparatively speaking, RSS techniques are substantially more efficient than SRS for the majority of KMPTL distribution parameters.
- The CP rises when the sample size increases.
- Comparatively speaking, credible CI of HPD is substantially more efficient than asymptotic CI for the majority of the KMPTL distribution parameters.
- MSE increases when parameter increased
8. Applications
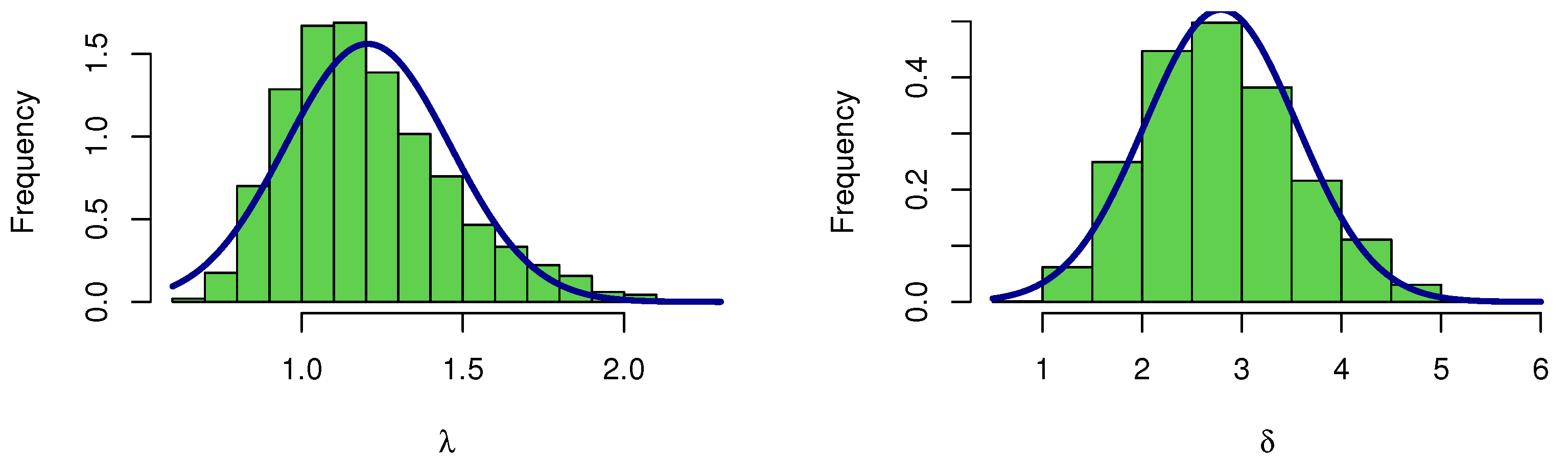
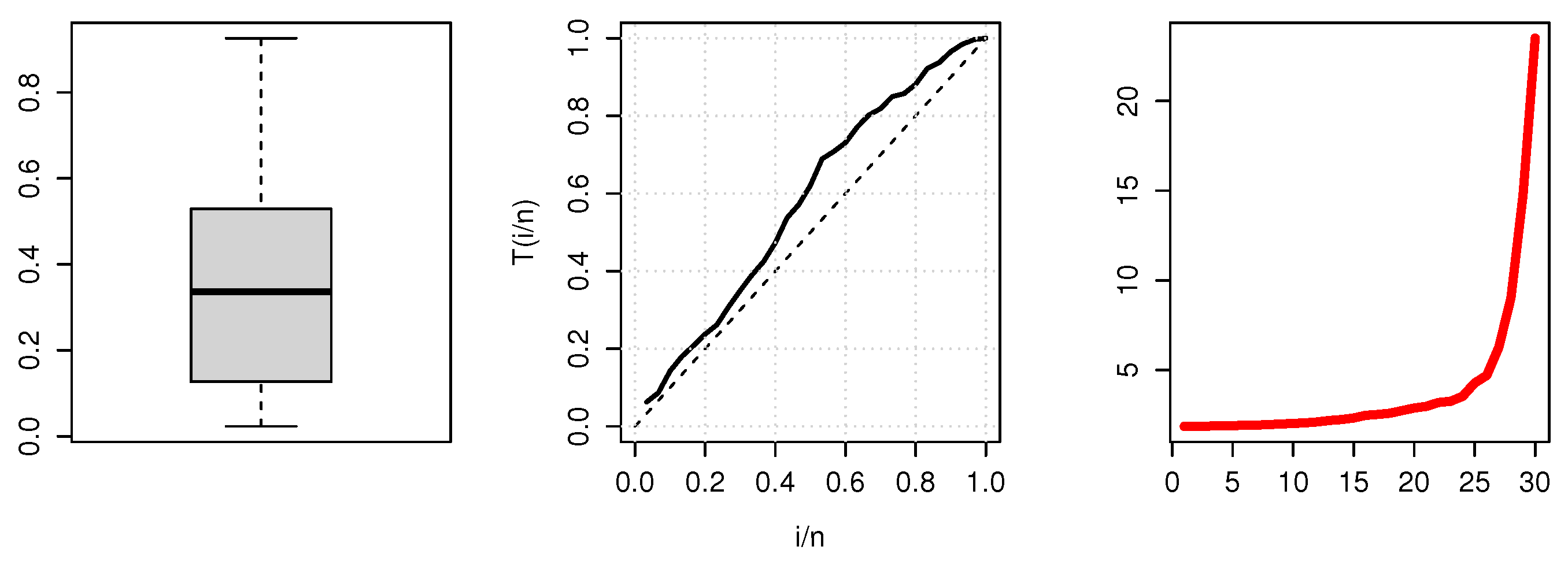
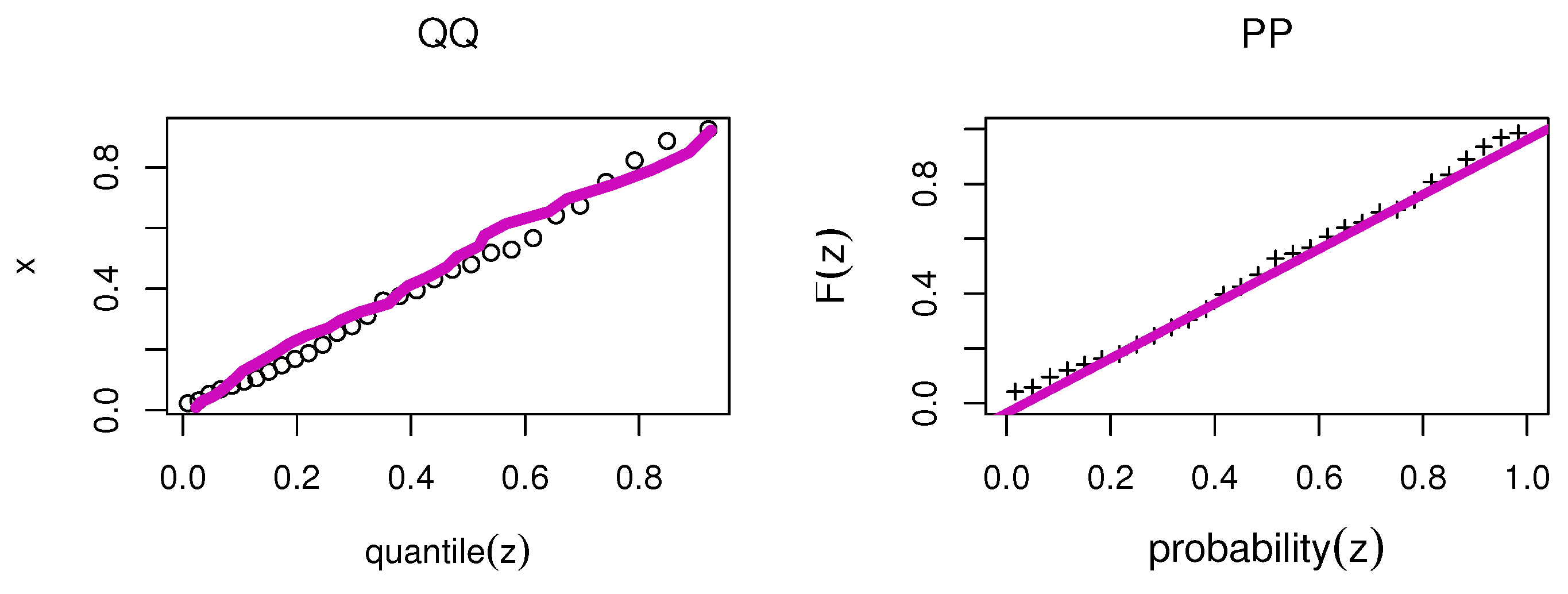
8.1. Economic Growth Data
8.2. Physics Data
9. Conclusions and Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Topp, C.W.; Leone, F.C. A Family of J-Shaped Frequency Functions. J. Am. Stat. Assoc. 1955, 50, 209–219. [Google Scholar] [CrossRef]
- Abbas, S.; Taqi, S.A.; Mustafa, F.; Murtaza, M.; Shahbaz, M.Q. Topp-Leone inverse Weibull distribution: Theory and application. Eur. J. Pure App. Math. 2017, 10, 1005–1022. [Google Scholar]
- ZeinEldin, R.A.; Chesneau, C.; Jamal, F.; Elgarhy, M. Different Estimation Methods for Type I Half-Logistic Topp-Leone Distribution. Mathematics 2019, 7, 985. [Google Scholar] [CrossRef]
- Sudsuk, A.; Bodhisuwan, W. The Topp-Leone geometric distribution. In Proceedings of the 12th International Conference on Mathematics, Statistics, and Their Applications (ICMSA), Banda Aceh, Indonesia, 4–6 October 2016; pp. 108–112. [Google Scholar]
- Mohamed, R.A.H.; Elgarhy, M.; Alabdulhadi, M.H.; Almetwally, E.M.; Radwan, T. Statistical Inference of Truncated Cauchy Power-Inverted Topp-Leone Distribution under Hybrid Censored Scheme with Applications. Axioms 2023, 12, 148. [Google Scholar] [CrossRef]
- Yousof, H.M.; Korkmaz, M.Ç. Topp-Leone Nadarajah-Haghighi distribution. İstatistikçiler Dergisi İstatistik ve Aktüerya 2017, 10, 119–127. [Google Scholar]
- Abushal, T.A.; Hassan, A.S.; El-Saeed, A.R.; Nassr, S.G. Power inverted Topp-Leone distribution in acceptance sampling plans. Comput. Mater. Contin. 2021, 67, 991–1011. [Google Scholar] [CrossRef]
- Atem, B.A.; Nasiru, S.; Nantomah, K. Topp–Leone linear exponential distribution. Stoch. Qual. Cont. 2018, 33, 31–43. [Google Scholar] [CrossRef]
- Hassan, A.S.; Almetwally, E.M.; Ibrahim, G.M. Kumaraswamy inverted Topp-Leone distribution with applications to COVID-19 data. Comput. Mater. Contin. 2021, 68, 337–356. [Google Scholar] [CrossRef]
- Bantan, R.A.; Jamal, F.; Chesneau, C.; Elgarhy, M. A new power Topp-Leone generated family of distributions with applications. Entropy 2019, 21, 1177. [Google Scholar] [CrossRef]
- Ibrahim, G.M.; Hassan, A.S.; Almetwally, E.M.; Almongy, H.M. Parameter estimation of alpha power inverted Topp-Leone distribution with applications. Intell. Autom. Soft Comput. 2021, 29, 353–371. [Google Scholar] [CrossRef]
- Bantan, R.; Elsehetry, M.; Hassan, A.S.; Elgarhy, M.; Sharma, D.; Chesneau, C.; Jamal, F. A Two-Parameter Model: Properties and Estimation under Ranked Sampling. Mathematics 2021, 9, 1214. [Google Scholar] [CrossRef]
- Bantan, R.A.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II power Topp-Leone generated family of distributions with statistical inference and applications. Symmetry 2020, 12, 75. [Google Scholar] [CrossRef]
- Alizadeh, M.; Lak, F.; Rasekhi, M.; Ramires, T.G.; Yousof, H.M.; Altun, E. The odd log-logistic Topp-Leone G family of distributions: Heteroscedastic regression models and applications. Comput. Stat. 2018, 33, 1217–1244. [Google Scholar] [CrossRef]
- Al-Marzouki, S.; Jamal, F.; Chesneau, C.; Elgarhy, M. Topp-Leone odd Fréchet generated family of distributions with applications to Covid-19 datasets. Comput. Model. Eng. Sci. 2020, 125, 437–458. [Google Scholar]
- Chipepa, F.; Oluyede, B.; Peter, O.P. The Burr III-Topp-Leone-G family of distributions with applications. Heliyon 2021, 7, e06534. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elgarhy, M.; Ragab, R. Statistical properties and estimation of inverted Topp-Leone Distribution. J. Stat. Appl. Probab. 2020, 9, 319–331. [Google Scholar]
- Reyad, H.M.; Alizadeh, M.; Jamal, F.; Othman, S.; Hamedani, G.G. The Exponentiated Generalized Topp Leone-G Family of Distributions: Properties and Applications. Pak. J. Stat. Oper. Res. 2019, 15, 1–24. [Google Scholar] [CrossRef]
- Hassan, A.S.; Khaleel, M.A.; Nassr, S.G. Transmuted Topp-Leone power function distribution: Theory and application. J. Stat. Appl. Probab. 2021, 10, 215–227. [Google Scholar]
- Yousof, H.M.; Alizadeh, M.; Jahanshahi, S.M.A.; Ramires, T.G.; Ghosh, I.; Hamedani, G.G. The transmuted Topp-Leone G family of distributions: Theory, characterizations and applications. J. Data Sci. 2017, 15, 723–740. [Google Scholar] [CrossRef]
- Al-Babtain, A.; Elbatal, I.; Chesneau, C.; Elgarhy, M. Sine Topp-Leone-G family of distributions: Theory and applications. Open Phys. 2020, 18, 574–593. [Google Scholar] [CrossRef]
- Hashempour, M. A weighted Topp-Leone G family of distributions: Properties, applications for modelling reliability data and different method of estimation. Stat. Hacett. J. Math. Stat. 2022, 51, 1420–1441. [Google Scholar] [CrossRef]
- Hassan, A.S.; Ismail, D.M. Estimation of parameters of Topp-Leone inverse Lomax distribution in presence of right-censored samples. Gazi Uni. J. Sci. 2021, 34, 1193–1208. [Google Scholar]
- Shaheed, G. A new Weighted Topp-Leone Family of Distributions. Stat. Optim. Inf. Comput. 2023, 11, 615–628. [Google Scholar] [CrossRef]
- Elgarhy, M.; Hassan, A.S.; Nagy, H. Parameter Estimation Methods and Applications of the Power Topp-Leone Distribution. Gazi Uni. J. Sci. 2022, 35, 731–746. [Google Scholar] [CrossRef]
- Aidi, K.; Al-Omari, A.I.; Alsultan, R. The Power Zeghdoudi Distribution: Properties, Estimation, and Applications to Real Right-Censored Data. Appl. Sci. 2022, 12, 12081. [Google Scholar] [CrossRef]
- Afify, A.Z.; Gemeay, A.M.; Alfaer, N.M.; Cordeiro, G.M.; Hafez, E.H. Power-Modified Kies-Exponential Distribution: Properties, Classical and Bayesian Inference with an Application to Engineering Data. Entropy 2022, 24, 883. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Aidi, K.; Alsultan, R. Power Darna distribution with right censoring: Estimation, testing, and applications. Appl. Sci. 2022, 12, 8272. [Google Scholar] [CrossRef]
- Usman, R.M.; Ilyas, M. The power Burr Type X distribution: Properties, regression modeling and applications. Punjab Univ. J. Math. 2020, 52, 27–44. [Google Scholar]
- Hassan, A.S.; Assar, S.M.; Abd Elghaffar, A.M. Statistical properties and estimation of power-transmuted inverse Rayleigh distribution. Stat. Trans. New Ser. 2020, 21, 1–20. [Google Scholar] [CrossRef]
- Abebe, B.; Tesfay, M.; Eyob, T.; Shanker, R. A two-parameter power Rama distribution with properties and applications. Biom. Biostat. Int. J. 2019, 8, 6–11. [Google Scholar]
- Habibi, M.; Asgharzadeh, A. Power binomial exponential distribution: Modeling, simulation and application. Commun. Stat.-Simul. Comput. 2018, 47, 3042–3061. [Google Scholar] [CrossRef]
- Shanker, R.; Shukla, K.K. A two-parameter power Aradhana distribution with properties and application. Indian Soc. Ind. Appl. Math. 2018, 9, 210–220. [Google Scholar] [CrossRef]
- Rady, E.A.; Hassanein, W.A.; Elhaddad, T.A. The power Lomax distribution with an application to bladder cancer data. SpringerPlus 2016, 5, 1838. [Google Scholar] [CrossRef]
- Krishnarani, S. On a power transformation of half-logistic distribution. J. Probab. Stat. 2016, 2016, 2084236. [Google Scholar] [CrossRef]
- Shanker, R.; Shukla, K.K. Power Shanker distribution and its application. Turk. Klin. Biyoistatistik 2017, 9, 175–187. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Mutairi, D.K.; Balakrishnan, N.; Al-Enezi, L.J. Power Lindley distribution and associated inference. Comput. Stat. Data. Anal. 2013, 64, 20–33. [Google Scholar] [CrossRef]
- Rooks, B.; Schumacher, A.; Cooray, K. The Power Cauchy Distribution: Derivation, Description, and Composite Models; NSF-REU Program Reports. 2010. Available online: http://www.cst.cmich.edu/mathematics/research/REU_and_LURE.shtml (accessed on 25 May 2023).
- Kavya, P.; Manoharan, M. Some parsimonious models for lifetimes and applications. J. Statist. Comput. Simul. 2021, 91, 3693–3708. [Google Scholar] [CrossRef]
- Zamanzade, E.; Al-Omari, A.I. New ranked set sampling for estimating the population mean and variance. Hacet. J. Math. Stat. 2016, 45, 1891–1905. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Haq, A. A new sampling method for estimating the population mean. J. Stat. Comput. Simul. 2019, 89, 1973–1985. [Google Scholar] [CrossRef]
- Nagy, H.F.; Al-Omari, A.I.; Hassan, A.S.; Alomani, G.A. Improved Estimation of the Inverted Kumaraswamy Distribution Parameters Based on Ranked Set Sampling with an Application to Real Data. Mathematics 2022, 10, 4102. [Google Scholar] [CrossRef]
- Alghamdi, S.M.; Bantan, R.A.R.; Hassan, A.S.; Nagy, H.F.; Elbatal, I.; Elgarhy, M. Improved EDF-Based Tests for Weibull Distribution Using Ranked Set Sampling. Mathematics 2022, 10, 4700. [Google Scholar] [CrossRef]
- Hassan, A.S.; Almanjahie, I.M.; Al-Omari, A.I.; Alzoubi, L.; Nagy, H.F. Stress-Strength Modeling Using Median-Ranked Set Sampling: Estimation, Simulation, and Application. Mathematics 2023, 11, 318. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elshaarawy, R.S.; Nagy, H.F. Parameter estimation of exponentiated exponential distribution under selective ranked set sampling. Stat. Transit. 2022, 23, 37–58. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Benchiha, S.; Almanjahie, I.M. Efficient estimation of two-parameter Xgamma distribution parameters using ranked set sampling design. Mathematics 2022, 10, 3170. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Almanjahie, I.M.; Hassan, A.S.; Nagy, H.F. Estimation of the stress-strength reliability for exponentiated Pareto distribution using median and ranked set sampling methods. Comput. Mater. Contin. 2020, 64, 835–857. [Google Scholar]
- Khamnei, H.J.; Meidute-Kavaliauskiene, I.; Fathi, M.; Valackienė, A.; Ghorbani, S. Parameter estimation of the exponentiated Pareto distribution using ranked set sampling and simple random sampling. Axioms 2022, 11, 293. [Google Scholar] [CrossRef]
- Jiang, H.; Gui, W. Bayesian inference for the parameters of Kumaraswamy distribution via ranked set sampling. Symmetry 2021, 13, 1170. [Google Scholar] [CrossRef]
- Alduais, F.S.; Yassen, M.F.; Almazah, M.M.A.; Khan, Z. Estimation of the Kumaraswamy distribution parameters using the E-Bayesian method. Alex. Eng. J. 2022, 61, 11099–11110. [Google Scholar] [CrossRef]
- Joukar, A.; Ramezani, M.; MirMostafaee, S.M.T.K. Parameter estimation for the exponential-Poisson distribution based on ranked set samples. Commun. Stat.-Theory Methods 2021, 50, 560–581. [Google Scholar] [CrossRef]
- Akgul, F.G.; Yu, K.; Senoglu, B. Estimation of the system reliability for generalized inverse Lindley distribution based on different sampling designs. Commun. Stat.-Theory Methods 2020, 50, 1532–1546. [Google Scholar] [CrossRef]
- Pedroso, V.C.; Taconeli, C.A.; Giolo, S.R. Estimation based on ranked set sampling for the two-parameter Birnbaum-Saunders distribution. J. Stat. Comput. Simul. 2021, 91, 316–333. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Benchiha, S.; Almanjahie, I.M. Efficient estimation of the generalized Quasi-Lindley distribution parameters under ranked set sampling and applications. Math. Probl. Eng. 2021, 2021, 9982397. [Google Scholar] [CrossRef]
- Helu, A.; Abu-Salih, M.; Alkam, O. Bayes Estimation of Weibull Distribution Parameters Using Ranked Set Sampling. Commun. Stat.-Theory Methods 2010, 39, 2533–2551. [Google Scholar] [CrossRef]
- Bantan, R.; Hassan, A.S.; Elsehetry, M. Zubair Lomax distribution: Properties and estimation based on ranked set sampling. CMC-Comput. Mater. Contin. 2020, 65, 2169–2187. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 30 June–30 July 1960; pp. 547–561. [Google Scholar]
- Arimoto, S. Information-theoretical considerations on estimation problems. Inf. Control 1971, 19, 181–194. [Google Scholar] [CrossRef]
- Tsallis, C. The role of constraints within generalized non-extensive statistics. Physica 1998, 261, 547–561. [Google Scholar]
- Havrda, J.; Charvat, F. Quantification method of classification processes, Concept of Structural Entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- McIntyre, G.A. A method for unbiased selective sampling, using ranked sets. Aust. J. Agric. Res. 1952, 3, 385–390. [Google Scholar] [CrossRef]
- Takahasi, K.; Wakimoto, K. On unbiased estimates of the population mean based on the sample stratified by means of ordering. Ann. Inst. Stat. Math. 1968, 20, 1–31. [Google Scholar] [CrossRef]
- Alotaibi, N.; Al-Moisheer, A.S.; Elbatal, I.; Shrahili, M.; Elgarhy, M.; Almetwally, E.M. Half Logistic Inverted Nadarajah–Haghighi Distribution under Ranked Set Sampling with Applications. Mathematics 2023, 11, 1693. [Google Scholar] [CrossRef]
- Alotaibi, N.; Elbatal, I.; Shrahili, M.; Al-Moisheer, A.S.; Elgarhy, M.; Almetwally, E.M. Statistical inference for the Kavya-Manoharan Kumaraswamy model under ranked set sampling with applications. Symmetry 2023, 15, 587. [Google Scholar] [CrossRef]
- Sabry, M.; Almetwally, E.M.; Almongy, H.M.; Ibrahim, G.M. Assessing the Performance of Some Ranked Set Sampling Designs Using Hybrid Approach. Comput. Mater. Conti. 2021, 68, 3737–3753. [Google Scholar]
- Luo, C.; Shen, L.; Xu, A. Modelling and estimation of system reliability under dynamic operating environments and lifetime ordering constraints. Reliab. Eng. Syst. Saf. 2022, 218 Pt A, 108136. [Google Scholar] [CrossRef]
- Von Toussaint, U. Bayesian inference in physics. Rev. Mod. Phys. 2011, 83, 943. [Google Scholar] [CrossRef]
- Eldessouky, E.A.; Hassan, O.H.M.; Elgarhy, M.; Hassan, E.A.; Elbatal, I.; Almetwally, E.M. A New Extension of the Kumaraswamy Exponential Model with Modeling of Food Chain Data. Axioms 2023, 12, 379. [Google Scholar] [CrossRef]
- Greenland, S. Bayesian perspectives for epidemiological research. II. Regression analysis. Int. J. Epidem. 2007, 36, 195–202. [Google Scholar] [CrossRef]
- Aguilera, P.A.; Fernández, A.; Fernández, R.; Rumí, R.; Salmerón, A. Bayesian networks in environmental modelling. Environ. Model. Softw. 2011, 26, 1376–1388. [Google Scholar] [CrossRef]
- Domínguez-Rodríguez, S.; Villaverde, S.; Sanz-Santaeufemia, F.J.; Grasa, C.; Soriano-Arandes, A.; Saavedra-Lozano, J.; Fumadó, V.; Epalza, C.; Serna-Pascual, M.; Alonso-Cadenas, J.A.; et al. A Bayesian model to predict COVID-19 severity in children. Pediatr. Infect. Dis. J. 2021, 40, e287–e293. [Google Scholar] [CrossRef]
- Chan, J.; Tobias, J.L. Bayesian Econometrics Methods. In Handbook of Labor, Human Resources and Population Economics; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–22. [Google Scholar]
- Zhou, S.; Xu, A.; Tang, Y.; Shen, L. Fast Bayesian Inference of Reparameterized Gamma Process With Random Effects. IEEE Trans. Reliab. 2023. [Google Scholar] [CrossRef]
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. CODA: Convergence diagnosis and output analysis for MCMC. R News 2006, 6, 7–11. [Google Scholar]
- Meredith, M.; Kruschke, J. HDInterval: Highest (Posterior) Density Intervals. R Package Version 0.1. 2016. Available online: https://cran.r-project.org/web/packages/HDInterval/index.html (accessed on 20 March 2023).
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Smith, A.F. Sampling-based approaches to calculating marginal densities. J. Amer. Stat. Assoc. 1990, 85, 398–409. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar]
- Morris, T.P.; White, I.R.; Crowther, M.J. Using simulation studies to evaluate statistical methods. Stat. Med. 2019, 38, 2074–2102. [Google Scholar] [CrossRef] [PubMed]
- Stock, J.H.; Watson, M.W. Introduction to Econometrics, 2nd ed.; Addison Wesley: Boston, MA, USA, 2007; Available online: Https://rdrr.io/cran/AER/man/GrowthSW.html (accessed on 20 June 2020).
- Mazucheli, J.; Menezes, A.F.; Dey, S. Unit-Gompertz distribution with applications. Statistica 2019, 79, 25–43. [Google Scholar]
- Quesenberry, C.P.; Hales, C. Concentration bands for uniformity plots. J. Stat. Comput. Simul. 1980, 11, 41–53. [Google Scholar] [CrossRef]
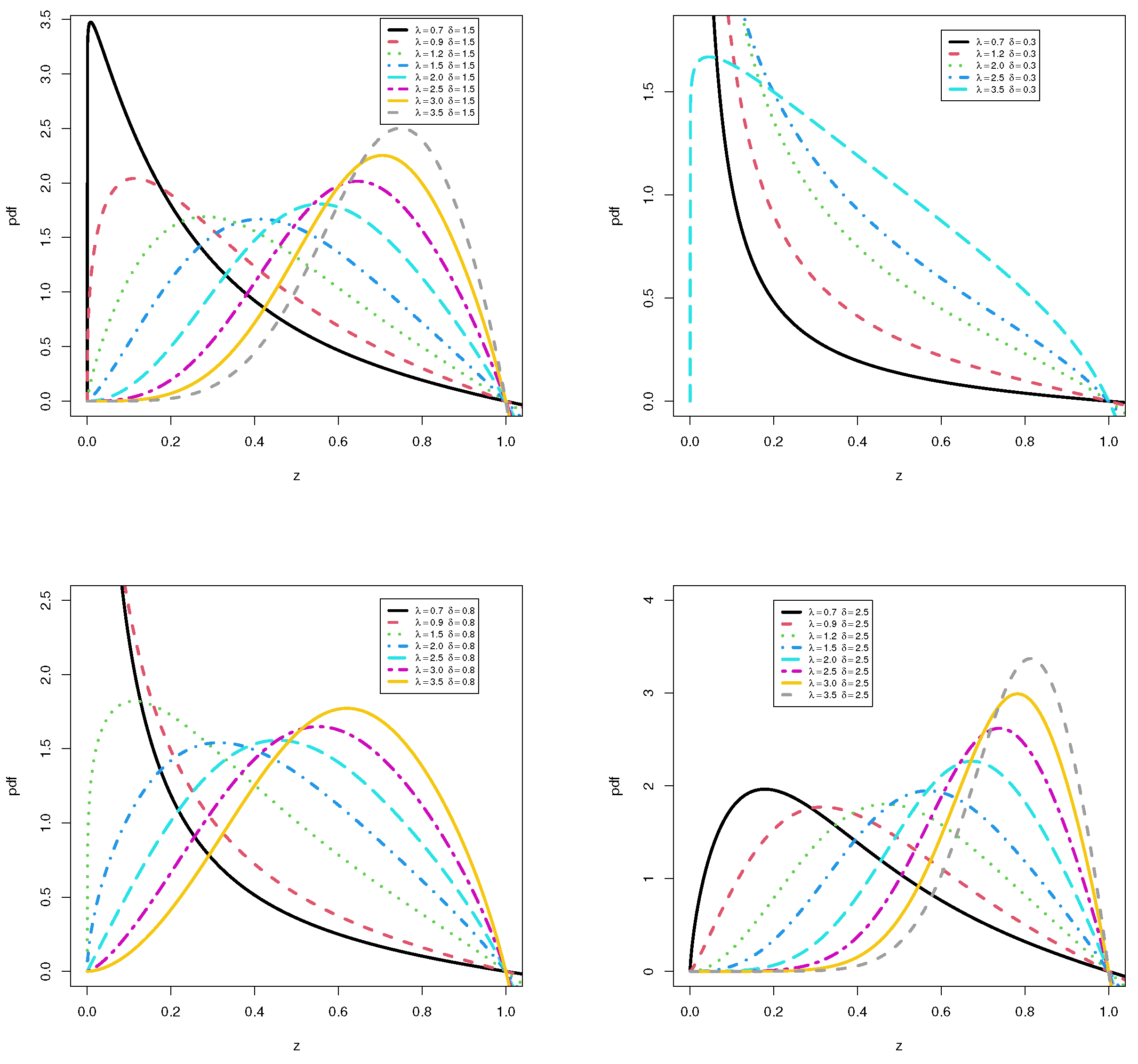

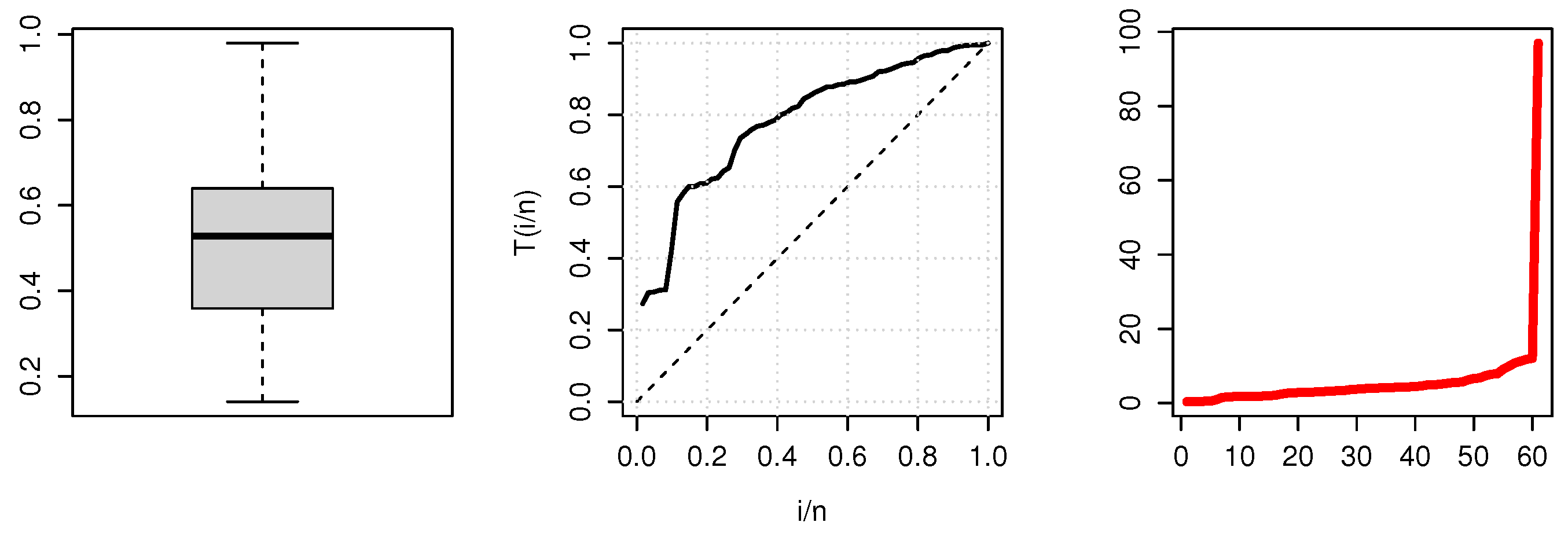
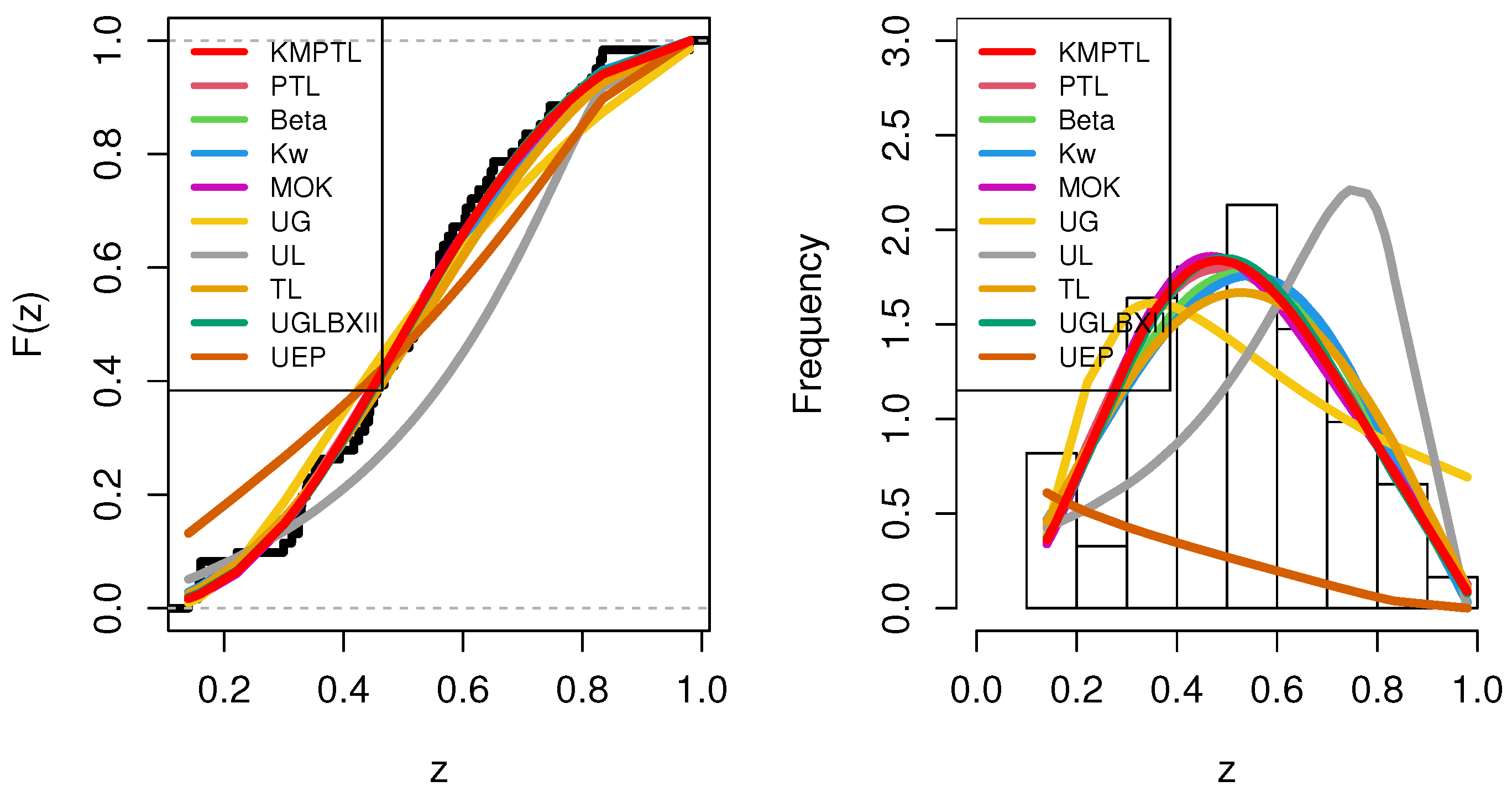
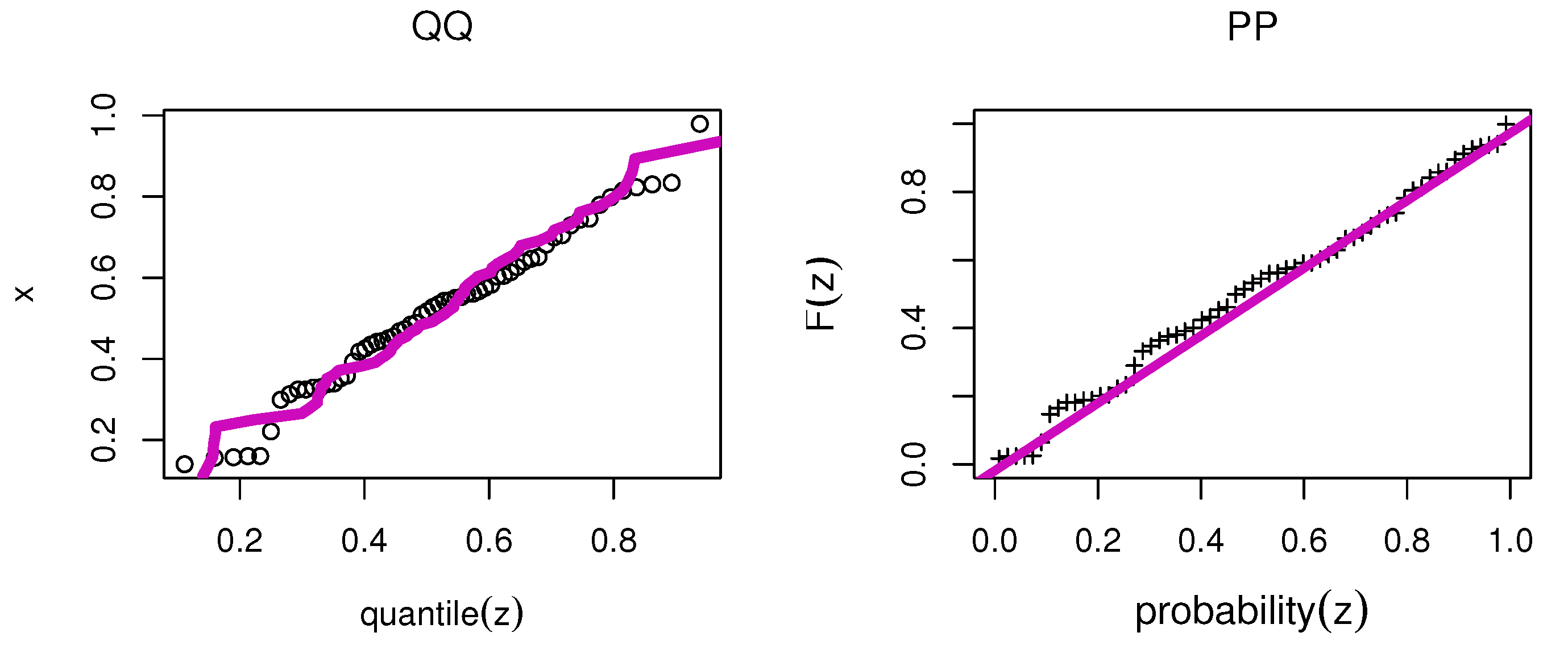
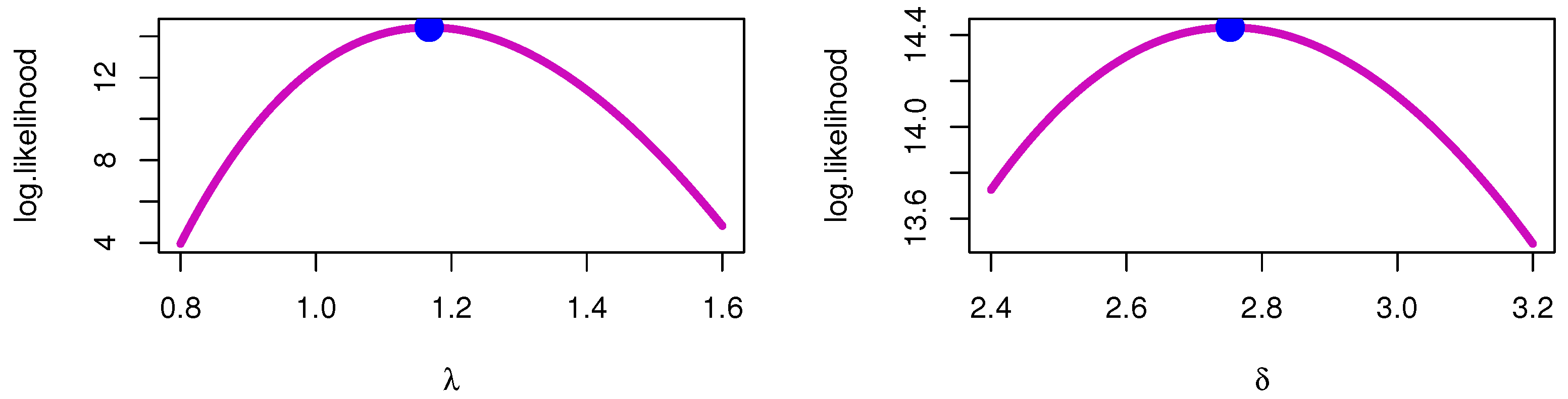

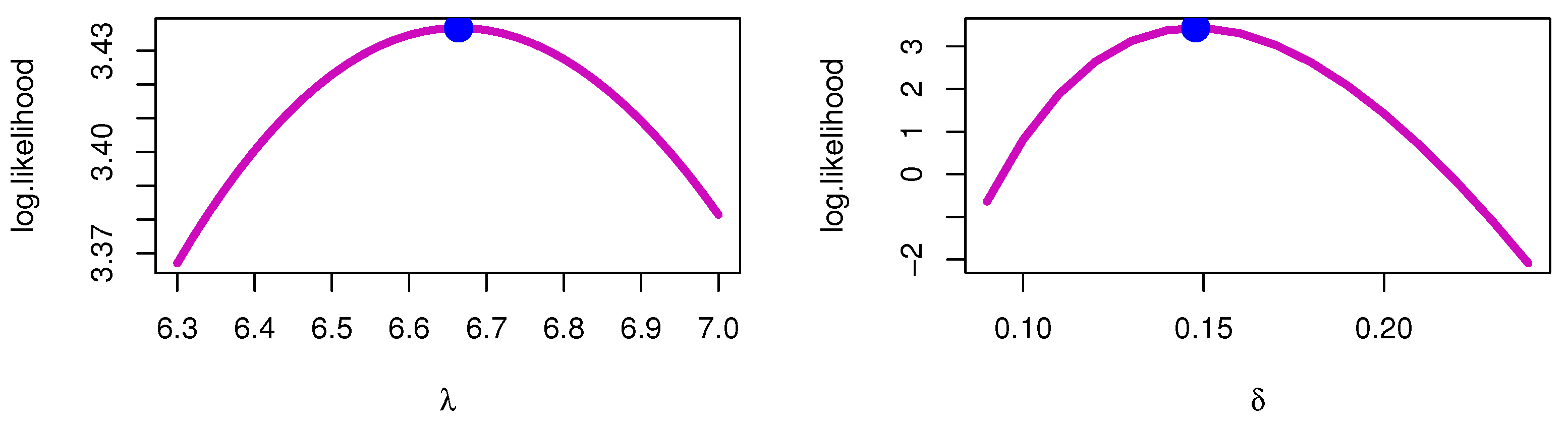

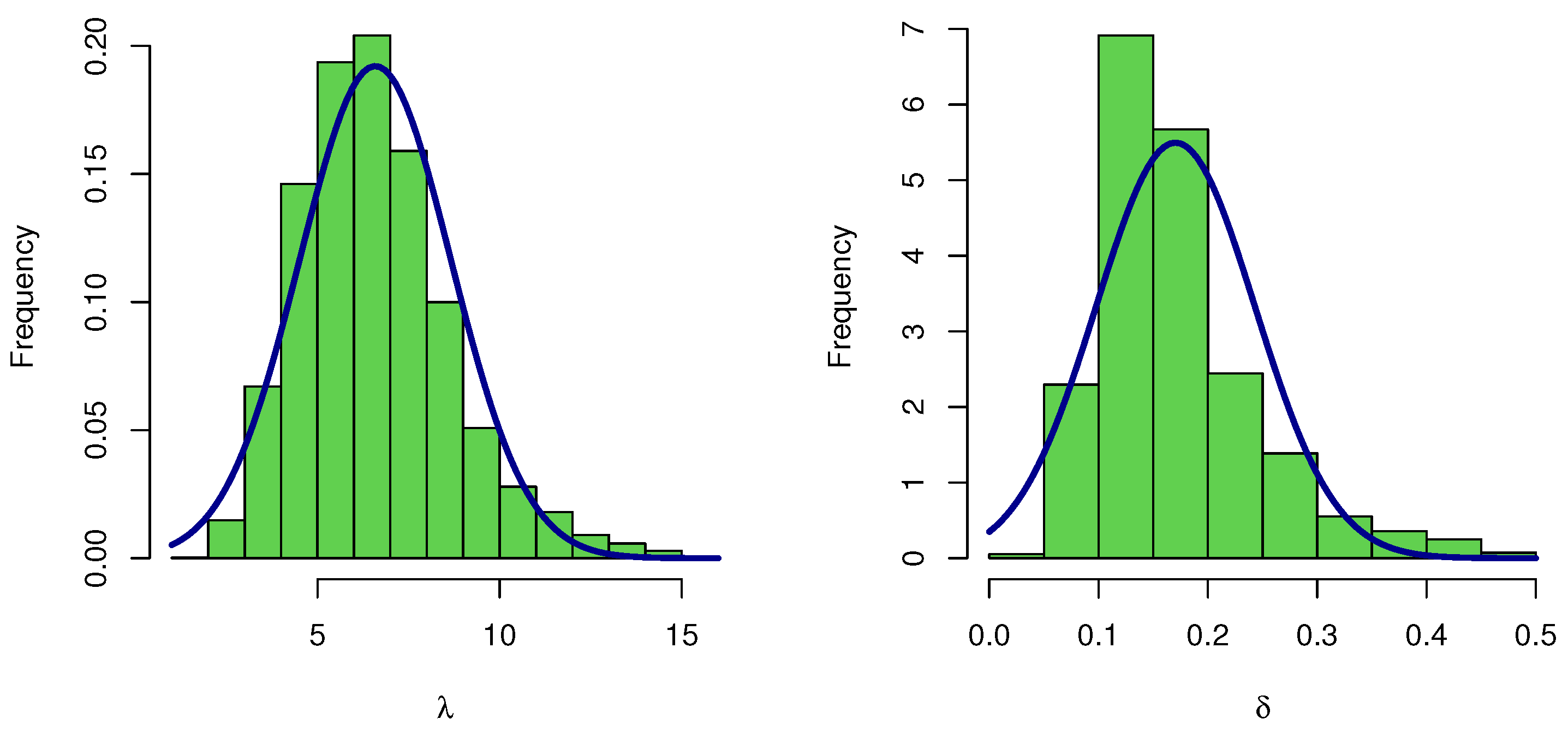
| 1.5 | 1.8 | 0.372 | 0.522 | 0.676 | 0.015 | 1.159 |
| 2.3 | 0.462 | 0.601 | 0.736 | −0.017 | 1.17 | |
| 2.8 | 0.53 | 0.659 | 0.778 | −0.038 | 1.18 | |
| 3.3 | 0.583 | 0.702 | 0.808 | −0.052 | 1.187 | |
| 3.8 | 0.626 | 0.735 | 0.831 | −0.063 | 1.194 | |
| 4.3 | 0.661 | 0.762 | 0.849 | −0.071 | 1.199 | |
| 4.8 | 0.69 | 0.784 | 0.864 | −0.078 | 1.204 | |
| 5.3 | 0.715 | 0.802 | 0.876 | −0.083 | 1.208 | |
| 5.8 | 0.736 | 0.817 | 0.886 | −0.087 | 1.211 | |
| 6.3 | 0.754 | 0.831 | 0.894 | −0.091 | 1.214 | |
| 2 | 1.8 | 0.447 | 0.585 | 0.721 | −0.005 | 1.172 |
| 2.3 | 0.533 | 0.657 | 0.774 | −0.031 | 1.182 | |
| 2.8 | 0.596 | 0.708 | 0.81 | −0.047 | 1.19 | |
| 3.3 | 0.645 | 0.746 | 0.836 | −0.059 | 1.197 | |
| 3.8 | 0.683 | 0.776 | 0.856 | −0.067 | 1.202 | |
| 4.3 | 0.714 | 0.799 | 0.872 | −0.074 | 1.206 | |
| 4.8 | 0.74 | 0.818 | 0.884 | −0.079 | 1.21 | |
| 5.3 | 0.761 | 0.833 | 0.895 | −0.083 | 1.213 | |
| 5.8 | 0.779 | 0.847 | 0.903 | −0.087 | 1.215 | |
| 6.3 | 0.795 | 0.858 | 0.911 | −0.089 | 1.218 | |
| 3.5 | 1.8 | 0.577 | 0.687 | 0.791 | −0.028 | 1.19 |
| 2.3 | 0.65 | 0.745 | 0.832 | −0.045 | 1.198 | |
| 2.8 | 0.702 | 0.785 | 0.86 | −0.056 | 1.204 | |
| 3.3 | 0.741 | 0.815 | 0.88 | −0.064 | 1.208 | |
| 3.8 | 0.771 | 0.837 | 0.895 | −0.069 | 1.211 | |
| 4.3 | 0.794 | 0.854 | 0.906 | −0.074 | 1.214 | |
| 4.8 | 0.814 | 0.869 | 0.916 | −0.077 | 1.216 | |
| 5.3 | 0.83 | 0.88 | 0.923 | −0.08 | 1.218 | |
| 5.8 | 0.843 | 0.89 | 0.93 | −0.082 | 1.22 | |
| 6.3 | 0.854 | 0.898 | 0.935 | −0.084 | 1.221 | |
| 5 | 1.8 | 0.646 | 0.739 | 0.826 | −0.036 | 1.198 |
| 2.3 | 0.71 | 0.789 | 0.861 | −0.049 | 1.204 | |
| 2.8 | 0.755 | 0.823 | 0.884 | −0.058 | 1.208 | |
| 3.3 | 0.788 | 0.848 | 0.901 | −0.064 | 1.212 | |
| 3.8 | 0.813 | 0.867 | 0.913 | −0.068 | 1.214 | |
| 4.3 | 0.833 | 0.881 | 0.923 | −0.071 | 1.216 | |
| 4.8 | 0.849 | 0.893 | 0.931 | −0.074 | 1.218 | |
| 5.3 | 0.862 | 0.902 | 0.937 | −0.076 | 1.219 | |
| 5.8 | 0.873 | 0.91 | 0.942 | −0.078 | 1.22 | |
| 6.3 | 0.883 | 0.917 | 0.947 | −0.079 | 1.221 |
| 1.5 | 1.8 | 0.524 | 0.316 | 0.209 | 0.148 | 0.041 | −0.012 | 2.283 | 0.387 |
| 2.3 | 0.595 | 0.389 | 0.271 | 0.199 | 0.035 | −0.182 | 2.407 | 0.313 | |
| 2.8 | 0.648 | 0.448 | 0.327 | 0.247 | 0.029 | −0.322 | 2.569 | 0.264 | |
| 3.3 | 0.688 | 0.498 | 0.375 | 0.291 | 0.025 | −0.427 | 2.736 | 0.228 | |
| 3.8 | 0.721 | 0.54 | 0.418 | 0.332 | 0.021 | −0.511 | 2.894 | 0.201 | |
| 4.3 | 0.747 | 0.576 | 0.456 | 0.368 | 0.018 | −0.578 | 3.04 | 0.179 | |
| 4.8 | 0.769 | 0.607 | 0.489 | 0.401 | 0.016 | −0.634 | 3.175 | 0.162 | |
| 5.3 | 0.787 | 0.633 | 0.519 | 0.432 | 0.014 | −0.682 | 3.297 | 0.148 | |
| 5.8 | 0.803 | 0.657 | 0.545 | 0.459 | 0.012 | −0.722 | 3.409 | 0.136 | |
| 6.3 | 0.816 | 0.677 | 0.569 | 0.484 | 0.011 | −0.757 | 3.51 | 0.126 | |
| 2 | 1.8 | 0.581 | 0.372 | 0.256 | 0.185 | 0.034 | −0.118 | 2.388 | 0.319 |
| 2.3 | 0.648 | 0.447 | 0.324 | 0.244 | 0.028 | −0.289 | 2.565 | 0.257 | |
| 2.8 | 0.696 | 0.507 | 0.383 | 0.298 | 0.022 | −0.411 | 2.748 | 0.215 | |
| 3.3 | 0.733 | 0.556 | 0.434 | 0.346 | 0.018 | −0.502 | 2.92 | 0.185 | |
| 3.8 | 0.762 | 0.596 | 0.477 | 0.389 | 0.015 | −0.573 | 3.075 | 0.163 | |
| 4.3 | 0.786 | 0.63 | 0.515 | 0.427 | 0.013 | −0.63 | 3.213 | 0.145 | |
| 4.8 | 0.805 | 0.659 | 0.547 | 0.461 | 0.011 | −0.677 | 3.335 | 0.131 | |
| 5.3 | 0.821 | 0.683 | 0.576 | 0.491 | 0.0096 | −0.717 | 3.445 | 0.119 | |
| 5.8 | 0.834 | 0.705 | 0.601 | 0.518 | 0.0084 | −0.75 | 3.543 | 0.11 | |
| 6.3 | 0.846 | 0.723 | 0.624 | 0.543 | 0.0074 | −0.779 | 3.631 | 0.101 | |
| 3.5 | 1.8 | 0.679 | 0.483 | 0.357 | 0.273 | 0.022 | −0.299 | 2.64 | 0.22 |
| 2.3 | 0.735 | 0.557 | 0.433 | 0.344 | 0.017 | −0.429 | 2.847 | 0.175 | |
| 2.8 | 0.775 | 0.613 | 0.494 | 0.405 | 0.013 | −0.518 | 3.024 | 0.146 | |
| 3.3 | 0.804 | 0.657 | 0.544 | 0.456 | 0.01 | −0.584 | 3.173 | 0.125 | |
| 3.8 | 0.827 | 0.692 | 0.585 | 0.5 | 0.0082 | −0.634 | 3.298 | 0.109 | |
| 4.3 | 0.845 | 0.721 | 0.62 | 0.537 | 0.0068 | −0.674 | 3.404 | 0.097 | |
| 4.8 | 0.859 | 0.744 | 0.649 | 0.57 | 0.0057 | −0.706 | 3.495 | 0.087 | |
| 5.3 | 0.872 | 0.764 | 0.674 | 0.598 | 0.0048 | −0.733 | 3.574 | 0.08 | |
| 5.8 | 0.882 | 0.781 | 0.696 | 0.623 | 0.0041 | −0.756 | 3.642 | 0.073 | |
| 6.3 | 0.89 | 0.796 | 0.715 | 0.645 | 0.0036 | −0.775 | 3.702 | 0.067 | |
| 5 | 1.8 | 0.731 | 0.55 | 0.425 | 0.336 | 0.016 | −0.373 | 2.784 | 0.174 |
| 2.3 | 0.78 | 0.621 | 0.502 | 0.412 | 0.012 | −0.479 | 2.978 | 0.138 | |
| 2.8 | 0.815 | 0.672 | 0.561 | 0.474 | 0.0087 | −0.551 | 3.134 | 0.115 | |
| 3.3 | 0.839 | 0.712 | 0.608 | 0.524 | 0.0068 | −0.604 | 3.259 | 0.098 | |
| 3.8 | 0.859 | 0.743 | 0.647 | 0.566 | 0.0054 | −0.644 | 3.361 | 0.086 | |
| 4.3 | 0.874 | 0.768 | 0.678 | 0.602 | 0.0044 | −0.675 | 3.446 | 0.076 | |
| 4.8 | 0.886 | 0.788 | 0.704 | 0.632 | 0.0037 | −0.7 | 3.517 | 0.068 | |
| 5.3 | 0.896 | 0.805 | 0.727 | 0.658 | 0.0031 | −0.721 | 3.577 | 0.062 | |
| 5.8 | 0.904 | 0.82 | 0.746 | 0.681 | 0.0026 | −0.739 | 3.629 | 0.057 | |
| 6.3 | 0.911 | 0.833 | 0.763 | 0.701 | 0.0023 | −0.753 | 3.675 | 0.052 |
| = 0.5 | = 0.8 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.5 | 1.8 | −0.133 | −0.155 | −0.125 | −0.129 | −0.18 | −0.237 | −0.176 | −0.177 |
| 2.3 | −0.2 | −0.23 | −0.182 | −0.191 | −0.259 | −0.34 | −0.251 | −0.252 | |
| 2.8 | −0.277 | −0.313 | −0.242 | −0.259 | −0.348 | −0.452 | −0.333 | −0.336 | |
| 3.3 | −0.356 | −0.394 | −0.299 | −0.326 | −0.436 | −0.562 | −0.413 | −0.418 | |
| 3.8 | −0.432 | −0.469 | −0.351 | −0.389 | −0.521 | −0.665 | −0.488 | −0.495 | |
| 4.3 | −0.505 | −0.539 | −0.397 | −0.446 | −0.601 | −0.762 | −0.558 | −0.566 | |
| 4.8 | −0.575 | −0.603 | −0.437 | −0.499 | −0.677 | −0.851 | −0.623 | −0.633 | |
| 5.3 | −0.64 | −0.662 | −0.473 | −0.548 | −0.748 | −0.934 | −0.682 | −0.694 | |
| 5.8 | −0.703 | −0.715 | −0.505 | −0.593 | −0.815 | −1.011 | −0.737 | −0.752 | |
| 6.3 | −0.762 | −0.765 | −0.533 | −0.634 | −0.878 | −1.083 | −0.788 | −0.805 | |
| 2 | 1.8 | −0.201 | −0.231 | −0.182 | −0.191 | −0.26 | −0.34 | −0.251 | −0.253 |
| 2.3 | −0.297 | −0.333 | −0.257 | −0.276 | −0.368 | −0.478 | −0.352 | −0.355 | |
| 2.8 | −0.394 | −0.431 | −0.325 | −0.357 | −0.477 | −0.611 | −0.449 | −0.455 | |
| 3.3 | −0.487 | −0.522 | −0.386 | −0.432 | −0.579 | −0.735 | −0.539 | −0.547 | |
| 3.8 | −0.575 | −0.603 | −0.437 | −0.5 | −0.674 | −0.848 | −0.62 | −0.63 | |
| 4.3 | −0.657 | −0.676 | −0.482 | −0.56 | −0.762 | −0.951 | −0.694 | −0.707 | |
| 4.8 | −0.734 | −0.741 | −0.52 | −0.614 | −0.844 | −1.045 | −0.761 | −0.777 | |
| 5.3 | −0.806 | −0.801 | −0.553 | −0.663 | −0.92 | −1.13 | −0.822 | −0.84 | |
| 5.8 | −0.873 | −0.854 | −0.582 | −0.708 | −0.991 | −1.21 | −0.878 | −0.899 | |
| 6.3 | −0.937 | −0.903 | −0.608 | −0.748 | −1.058 | −1.283 | −0.93 | −0.954 | |
| 3.5 | 1.8 | −0.392 | −0.429 | −0.324 | −0.356 | −0.471 | −0.605 | −0.445 | −0.45 |
| 2.3 | −0.531 | −0.563 | −0.412 | −0.466 | −0.622 | −0.787 | −0.576 | −0.585 | |
| 2.8 | −0.658 | −0.677 | −0.482 | −0.561 | −0.758 | −0.946 | −0.69 | −0.703 | |
| 3.3 | −0.774 | −0.774 | −0.539 | −0.642 | −0.88 | −1.085 | −0.79 | −0.807 | |
| 3.8 | −0.878 | −0.858 | −0.584 | −0.711 | −0.989 | −1.207 | −0.876 | −0.897 | |
| 4.3 | −0.973 | −0.93 | −0.622 | −0.771 | −1.089 | −1.316 | −0.953 | −0.978 | |
| 4.8 | −1.061 | −0.994 | −0.654 | −0.823 | −1.179 | −1.413 | −1.021 | −1.051 | |
| 5.3 | −1.142 | −1.05 | −0.681 | −0.87 | −1.263 | −1.501 | −1.083 | −1.116 | |
| 5.8 | −1.216 | −1.1 | −0.704 | −0.911 | −1.34 | −1.581 | −1.139 | −1.175 | |
| 6.3 | −1.286 | −1.145 | −0.724 | −0.949 | −1.412 | −1.654 | −1.19 | −1.23 | |
| 5 | 1.8 | −0.541 | −0.572 | −0.418 | −0.474 | −0.63 | −0.797 | −0.583 | −0.592 |
| 2.3 | −0.702 | −0.714 | −0.504 | −0.592 | −0.801 | −0.995 | −0.726 | −0.74 | |
| 2.8 | −0.843 | −0.831 | −0.57 | −0.688 | −0.949 | −1.162 | −0.845 | −0.864 | |
| 3.3 | −0.969 | −0.927 | −0.62 | −0.768 | −1.079 | −1.306 | −0.946 | −0.971 | |
| 3.8 | −1.081 | −1.008 | −0.661 | −0.835 | −1.195 | −1.43 | −1.033 | −1.063 | |
| 4.3 | −1.182 | −1.077 | −0.693 | −0.892 | −1.3 | −1.539 | −1.11 | −1.145 | |
| 4.8 | −1.274 | −1.137 | −0.72 | −0.942 | −1.394 | −1.637 | −1.177 | −1.217 | |
| 5.3 | −1.359 | −1.19 | −0.743 | −0.986 | −1.481 | −1.724 | −1.238 | −1.282 | |
| 5.8 | −1.437 | −1.237 | −0.762 | −1.025 | −1.561 | −1.803 | −1.292 | −1.341 | |
| 6.3 | −1.509 | −1.279 | −0.779 | −1.06 | −1.635 | −1.876 | −1.342 | −1.395 | |
| = 1.2 | = 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.5 | 1.8 | −0.225 | −0.355 | −0.229 | −0.23 | −0.284 | −0.656 | −0.305 | −0.328 |
| 2.3 | −0.312 | −0.498 | −0.321 | −0.322 | −0.378 | −0.92 | −0.417 | −0.46 | |
| 2.8 | −0.409 | −0.658 | −0.423 | −0.426 | −0.481 | −1.237 | −0.544 | −0.618 | |
| 3.3 | −0.503 | −0.818 | −0.525 | −0.53 | −0.582 | −1.578 | −0.675 | −0.789 | |
| 3.8 | −0.593 | −0.974 | −0.624 | −0.63 | −0.676 | −1.932 | −0.804 | −0.966 | |
| 4.3 | −0.678 | −1.122 | −0.718 | −0.726 | −0.764 | −2.295 | −0.931 | −1.148 | |
| 4.8 | −0.757 | −1.263 | −0.807 | −0.818 | −0.847 | −2.663 | −1.054 | −1.332 | |
| 5.3 | −0.831 | −1.397 | −0.892 | −0.905 | −0.923 | −3.035 | −1.173 | −1.518 | |
| 5.8 | −0.901 | −1.525 | −0.972 | −0.987 | −0.995 | −3.41 | −1.289 | −1.705 | |
| 6.3 | −0.966 | −1.647 | −1.048 | −1.066 | −1.062 | −3.786 | −1.402 | −1.893 | |
| 2 | 1.8 | −0.313 | −0.499 | −0.321 | −0.323 | −0.38 | −0.924 | −0.418 | −0.462 |
| 2.3 | −0.43 | −0.694 | −0.446 | −0.449 | −0.504 | −1.31 | −0.573 | −0.655 | |
| 2.8 | −0.545 | −0.89 | −0.571 | −0.576 | −0.625 | −1.735 | −0.733 | −0.868 | |
| 3.3 | −0.653 | −1.078 | −0.69 | −0.697 | −0.737 | −2.179 | −0.891 | −1.089 | |
| 3.8 | −0.752 | −1.254 | −0.802 | −0.812 | −0.84 | −2.632 | −1.044 | −1.316 | |
| 4.3 | −0.844 | −1.421 | −0.906 | −0.92 | −0.935 | −3.092 | −1.191 | −1.546 | |
| 4.8 | −0.929 | −1.577 | −1.005 | −1.021 | −1.022 | −3.556 | −1.334 | −1.778 | |
| 5.3 | −1.008 | −1.725 | −1.097 | −1.116 | −1.103 | −4.023 | −1.471 | −2.012 | |
| 5.8 | −1.081 | −1.865 | −1.185 | −1.207 | −1.178 | −4.493 | −1.603 | −2.246 | |
| 6.3 | −1.15 | −1.997 | −1.267 | −1.292 | −1.247 | −4.963 | −1.732 | −2.482 | |
| 3.5 | 1.8 | −0.538 | −0.877 | −0.563 | −0.568 | −0.616 | −1.702 | −0.721 | −0.851 |
| 2.3 | −0.695 | −1.153 | −0.737 | −0.746 | −0.779 | −2.358 | −0.952 | −1.179 | |
| 2.8 | −0.836 | −1.406 | −0.897 | −0.91 | −0.924 | −3.036 | −1.174 | −1.518 | |
| 3.3 | −0.962 | −1.638 | −1.043 | −1.06 | −1.052 | −3.726 | −1.384 | −1.863 | |
| 3.8 | −1.074 | −1.851 | −1.176 | −1.198 | −1.167 | −4.422 | −1.584 | −2.211 | |
| 4.3 | −1.176 | −2.048 | −1.299 | −1.326 | −1.27 | −5.123 | −1.774 | −2.561 | |
| 4.8 | −1.268 | −2.231 | −1.413 | −1.444 | −1.364 | −5.826 | −1.956 | −2.913 | |
| 5.3 | −1.354 | −2.402 | −1.518 | −1.554 | −1.451 | −6.531 | −2.131 | −3.266 | |
| 5.8 | −1.432 | −2.562 | −1.617 | −1.658 | −1.53 | −7.238 | −2.298 | −3.619 | |
| 6.3 | −1.505 | −2.713 | −1.711 | −1.756 | −1.604 | −7.945 | −2.46 | −3.973 | |
| 5 | 1.8 | −0.703 | −1.166 | −0.746 | −0.755 | −0.785 | −2.387 | −0.962 | −1.193 |
| 2.3 | −0.878 | −1.483 | −0.946 | −0.96 | −0.965 | −3.251 | −1.241 | −1.625 | |
| 2.8 | −1.03 | −1.768 | −1.124 | −1.144 | −1.12 | −4.132 | −1.502 | −2.066 | |
| 3.3 | −1.164 | −2.024 | −1.284 | −1.31 | −1.256 | −5.022 | −1.747 | −2.511 | |
| 3.8 | −1.282 | −2.258 | −1.429 | −1.461 | −1.376 | −5.917 | −1.979 | −2.959 | |
| 4.3 | −1.388 | −2.472 | −1.562 | −1.6 | −1.483 | −6.815 | −2.199 | −3.408 | |
| 4.8 | −1.484 | −2.67 | −1.684 | −1.728 | −1.581 | −7.716 | −2.408 | −3.858 | |
| 5.3 | −1.572 | −2.854 | −1.797 | −1.847 | −1.669 | −8.618 | −2.608 | −4.309 | |
| 5.8 | −1.653 | −3.027 | −1.903 | −1.959 | −1.751 | −9.521 | −2.8 | −4.761 | |
| 6.3 | −1.728 | −3.189 | −2.002 | −2.064 | −1.827 | −10.425 | −2.985 | −5.213 | |
| Point | Confidance | RE | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRS | RSS c = 1 | RSS c = 3 | SRS | RSS c = 1 | RSS c = 3 | |||||||||||||
| n | Bias | MSE | Bias | MSE | Bias | MSE | LCI | CP | LCI | CP | LCI | CP | RE1 | RE2 | RE3 | |||
| MLE | 0.5 | 8 | 0.0855 | 0.2443 | 0.0281 | 0.0898 | 0.0241 | 0.0674 | 1.9103 | 94.00% | 1.1708 | 95.20% | 1.0055 | 95.40% | 272% | 363% | 133% | |
| 0.3527 | 0.4438 | 0.1523 | 0.1346 | 0.0859 | 0.0985 | 2.2175 | 97.20% | 1.3099 | 98.20% | 1.1848 | 97.40% | 330% | 450% | 137% | ||||
| 12 | 0.0420 | 0.1752 | 0.0241 | 0.0889 | 0.0201 | 0.0280 | 1.6342 | 93.80% | 1.1904 | 97.00% | 0.6514 | 97.60% | 197% | 627% | 318% | |||
| 0.3056 | 0.3524 | 0.0975 | 0.0885 | 0.0471 | 0.0506 | 2.4720 | 97.40% | 1.1029 | 98.00% | 0.8634 | 97.60% | 398% | 696% | 175% | ||||
| 17 | 0.0251 | 0.1286 | 0.0324 | 0.0514 | −0.0095 | 0.0187 | 1.4040 | 93.80% | 0.8808 | 96.00% | 0.5355 | 98.00% | 250% | 687% | 275% | |||
| 0.2812 | 0.3066 | 0.0671 | 0.0718 | 0.0529 | 0.0313 | 1.8718 | 97.40% | 1.0178 | 98.00% | 0.6623 | 97.40% | 427% | 980% | 229% | ||||
| 2 | 8 | 0.1813 | 0.3690 | 0.0221 | 0.0468 | 0.0119 | 0.0116 | 2.2748 | 92.80% | 0.8443 | 96.80% | 0.4196 | 97.80% | 789% | 3188% | 404% | ||
| 0.1794 | 1.0304 | 0.0647 | 0.2270 | −0.0054 | 0.0592 | 3.9204 | 96.40% | 1.8523 | 93.20% | 0.9547 | 96.80% | 454% | 1740% | 383% | ||||
| 12 | 0.1628 | 0.2873 | 0.0242 | 0.0456 | −0.0082 | 0.0016 | 2.0040 | 92.00% | 0.9133 | 95.40% | 0.1586 | 95.80% | 630% | 17,571% | 2788% | |||
| 0.0885 | 0.7759 | −0.0063 | 0.2198 | 0.0243 | 0.0418 | 3.4388 | 91.40% | 2.1409 | 94.40% | 0.7969 | 95.40% | 353% | 1855% | 525% | ||||
| 17 | 0.1030 | 0.1748 | 0.0214 | 0.0411 | 0.0072 | 0.0016 | 1.5898 | 93.00% | 0.7911 | 98.60% | 0.5394 | 99.40% | 425% | 10,996% | 2586% | |||
| 0.0675 | 0.5526 | 0.0061 | 0.0859 | 0.0100 | 0.0336 | 2.9049 | 91.00% | 1.1496 | 96.80% | 0.7184 | 96.60% | 644% | 1644% | 255% | ||||
| 3 | 8 | 0.1337 | 0.3223 | 0.0029 | 0.0209 | 0.0045 | 0.0055 | 2.1651 | 94.80% | 0.5676 | 99.00% | 0.2901 | 99.00% | 1540% | 5874% | 381% | ||
| 0.0877 | 0.8553 | 0.0494 | 0.1465 | −0.0041 | 0.0330 | 3.6126 | 92.20% | 1.4892 | 95.00% | 0.7131 | 97.20% | 584% | 2589% | 443% | ||||
| 12 | 0.0793 | 0.1269 | 0.0142 | 0.0127 | −0.0016 | 0.0007 | 1.3628 | 95.40% | 0.4392 | 96.80% | 0.1033 | 96.40% | 997% | 18,240% | 1829% | |||
| 0.0412 | 0.9558 | −0.0008 | 0.1281 | 0.0167 | 0.0311 | 3.8329 | 92.80% | 2.0797 | 95.20% | 0.6886 | 98.20% | 746% | 3076% | 412% | ||||
| 17 | 0.0564 | 0.0992 | 0.0024 | 0.0026 | −0.0010 | 0.0005 | 1.2157 | 95.80% | 0.2007 | 99.40% | 0.0907 | 97.40% | 3783% | 18,510% | 489% | |||
| 0.0230 | 0.4447 | 0.0039 | 0.0472 | 0.0062 | 0.0157 | 2.6153 | 93.20% | 0.8528 | 95.60% | 0.4906 | 96.40% | 941% | 2838% | 302% | ||||
| Bayesian | 0.5 | 8 | 0.1083 | 0.0841 | 0.0517 | 0.0159 | 0.0517 | 0.0015 | 0.9130 | 93.86% | 0.6465 | 98.57% | 0.2523 | 89.00% | 528% | 5498% | 1041% | |
| 0.1445 | 0.1479 | 0.0276 | 0.0114 | 0.0276 | 0.0001 | 1.0408 | 92.29% | 0.6781 | 99.43% | 0.2042 | 82.57% | 1303% | 224,969% | 17272% | ||||
| 12 | 0.0832 | 0.0456 | 0.0297 | 0.0043 | 0.0297 | 0.0007 | 0.8189 | 95.71% | 0.4811 | 100.00% | 0.1731 | 90.29% | 1054% | 6853% | 650% | |||
| 0.1139 | 0.0902 | 0.0114 | 0.0032 | 0.0114 | 0.0000 | 0.9614 | 95.00% | 0.5228 | 100.00% | 0.1451 | 86.71% | 2793% | 334,035% | 11959% | ||||
| 17 | 0.0655 | 0.0296 | 0.0186 | 0.0022 | 0.0186 | 0.0003 | 0.7501 | 98.29% | 0.3906 | 100.00% | 0.1314 | 91.80% | 1352% | 9137% | 676% | |||
| 0.0854 | 0.0577 | 0.0099 | 0.0016 | 0.0099 | 0.0000 | 0.8768 | 94.71% | 0.4388 | 100.00% | 0.1172 | 86.00% | 3585% | 356,028% | 9930% | ||||
| 2 | 8 | 0.0733 | 0.0292 | 0.0116 | 0.0031 | 0.0116 | 0.0011 | 0.7491 | 98.14% | 0.3264 | 99.29% | 0.1657 | 90.57% | 956% | 2773% | 290% | ||
| 0.0728 | 0.1486 | 0.0046 | 0.0010 | 0.0046 | 0.0000 | 2.8695 | 99.57% | 0.9168 | 100.00% | 0.2086 | 99.71% | 14,194% | 632,266% | 4454% | ||||
| 12 | 0.0458 | 0.0115 | 0.0027 | 0.0012 | 0.0027 | 0.0005 | 0.6043 | 99.57% | 0.2217 | 100.00% | 0.1119 | 89.71% | 959% | 2347% | 245% | |||
| 0.0452 | 0.0440 | 0.0028 | 0.0004 | 0.0028 | 0.0000 | 2.2306 | 100.00% | 0.6511 | 100.00% | 0.1449 | 100.00% | 10,682% | 276,372% | 2587% | ||||
| 17 | 0.0292 | 0.0065 | 0.0034 | 0.0007 | 0.0034 | 0.0003 | 0.4974 | 99.71% | 0.1648 | 99.71% | 0.0788 | 89.00% | 992% | 2525% | 255% | |||
| 0.0329 | 0.0202 | 0.0012 | 0.0002 | 0.0012 | 0.0000 | 1.8829 | 100.00% | 0.5275 | 100.00% | 0.1164 | 100.00% | 8281% | 141,788% | 1712% | ||||
| 3 | 8 | 0.0569 | 0.0185 | 0.0122 | 0.0026 | 0.0122 | 0.0010 | 0.6567 | 98.71% | 0.2932 | 99.57% | 0.1538 | 87.71% | 704% | 1800% | 256% | ||
| 0.0599 | 0.0772 | 0.0035 | 0.0006 | 0.0035 | 0.0000 | 3.2656 | 100.00% | 0.9224 | 100.00% | 0.2064 | 100.00% | 12,553% | 275,087% | 2191% | ||||
| 12 | 0.0353 | 0.0103 | 0.0049 | 0.0013 | 0.0049 | 0.0004 | 0.5152 | 99.29% | 0.1994 | 99.86% | 0.1041 | 84.43% | 816% | 2291% | 281% | |||
| 0.0326 | 0.0190 | 0.0022 | 0.0002 | 0.0022 | 0.0000 | 2.4116 | 100.00% | 0.6532 | 100.00% | 0.1430 | 100.00% | 8331% | 79,911% | 959% | ||||
| 17 | 0.0227 | 0.0056 | 0.0012 | 0.0006 | 0.0012 | 0.0003 | 0.4300 | 99.43% | 0.1442 | 100.00% | 0.0731 | 85.00% | 885% | 2252% | 255% | |||
| 0.0148 | 0.0098 | 0.0010 | 0.0002 | 0.0010 | 0.0000 | 1.9831 | 100.00% | 0.5311 | 100.00% | 0.1137 | 100.00% | 5910% | 42,117% | 713% | ||||
| Point | Confidance | RE | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRS | RSS c = 1 | RSS c = 3 | SRS | RSS c = 1 | RSS c = 3 | |||||||||||||
| n | Bias | MSE | Bias | MSE | Bias | MSE | LCI | CP | LCI | CP | LCI | CP | RE1 | RE2 | RE3 | |||
| MLE | 0.5 | 8 | −0.3228 | 1.3168 | −0.2769 | 0.5790 | −0.1696 | 0.4183 | 4.3211 | 96.20% | 2.7810 | 97.40% | 2.4492 | 97.20% | 227% | 315% | 138% | |
| 0.7846 | 1.6061 | 0.3501 | 0.4504 | 0.2261 | 0.2800 | 3.9052 | 97.20% | 2.2466 | 95.20% | 1.8773 | 93.80% | 357% | 574% | 161% | ||||
| 12 | −0.3533 | 1.1530 | −0.1201 | 0.4148 | −0.0659 | 0.1485 | 3.9788 | 96.80% | 2.4830 | 96.20% | 1.4901 | 94.00% | 278% | 776% | 279% | |||
| 0.6764 | 1.2864 | 0.1790 | 0.1909 | 0.0978 | 0.1891 | 3.5723 | 95.20% | 1.5640 | 95.40% | 1.6626 | 96.20% | 674% | 680% | 101% | ||||
| 17 | −0.3775 | 0.9961 | −0.1037 | 0.2216 | −0.0593 | 0.1354 | 3.6253 | 97.00% | 1.8019 | 94.60% | 1.4932 | 94.40% | 449% | 736% | 164% | |||
| 0.6290 | 1.0958 | 0.1070 | 0.0943 | 0.0812 | 0.1325 | 3.2834 | 96.00% | 1.1294 | 94.40% | 2.1871 | 97.80% | 1162% | 827% | 71% | ||||
| 2 | 8 | 0.2120 | 2.3271 | 0.1444 | 0.9670 | 0.1247 | 0.5275 | 5.9261 | 94.86% | 3.8158 | 92.71% | 2.8068 | 95.71% | 241% | 441% | 183% | ||
| 1.1741 | 4.6654 | 0.3296 | 1.1130 | 0.2055 | 0.8799 | 7.1119 | 98.86% | 3.9314 | 98.86% | 3.5904 | 98.29% | 419% | 530% | 126% | ||||
| 12 | 0.1358 | 1.8338 | 0.0884 | 0.6992 | 0.0429 | 0.2391 | 5.2854 | 93.43% | 3.2618 | 93.43% | 1.9107 | 94.14% | 262% | 767% | 292% | |||
| 0.9946 | 3.5393 | 0.3076 | 1.0125 | 0.0967 | 0.3363 | 6.2644 | 98.29% | 4.1378 | 98.14% | 2.2432 | 96.43% | 350% | 1052% | 301% | ||||
| 17 | 0.1497 | 1.3820 | 0.0407 | 0.4263 | 0.0093 | 0.1806 | 4.5740 | 94.71% | 2.5562 | 95.00% | 1.6665 | 95.00% | 324% | 765% | 236% | |||
| 0.6744 | 2.4489 | 0.2204 | 0.6674 | 0.0913 | 0.3156 | 5.5394 | 98.43% | 3.0859 | 97.00% | 2.2826 | 95.86% | 367% | 776% | 212% | ||||
| 3 | 8 | 0.3585 | 2.4085 | 0.2925 | 1.2106 | 0.1777 | 0.6230 | 5.9233 | 93.00% | 4.1608 | 92.43% | 3.0167 | 92.71% | 199% | 387% | 194% | ||
| 0.8685 | 4.3651 | 0.1212 | 1.7243 | 0.1372 | 1.3896 | 7.4541 | 99.43% | 5.1292 | 99.00% | 4.5929 | 97.86% | 253% | 314% | 124% | ||||
| 12 | 0.2974 | 2.2241 | 0.0936 | 0.5135 | 0.0478 | 0.1616 | 5.7327 | 91.57% | 2.7870 | 93.14% | 1.5660 | 95.71% | 433% | 1376% | 318% | |||
| 0.8093 | 4.0765 | 0.2741 | 1.3776 | 0.0374 | 0.4212 | 7.7461 | 98.43% | 4.4769 | 95.57% | 2.5418 | 95.00% | 296% | 968% | 327% | ||||
| 17 | 0.2908 | 1.6559 | 0.1129 | 0.3877 | 0.0281 | 0.1114 | 4.9173 | 93.14% | 2.4022 | 92.29% | 1.3047 | 95.71% | 427% | 1486% | 348% | |||
| 0.5567 | 3.2766 | 0.1160 | 1.0142 | 0.0475 | 0.3522 | 6.7566 | 98.86% | 3.9243 | 96.00% | 2.3204 | 94.43% | 323% | 930% | 288% | ||||
| Bayesian | 0.5 | 8 | 0.0245 | 0.0399 | 0.0178 | 0.0106 | 0.0178 | 0.0057 | 1.9912 | 100.00% | 1.3898 | 100.00% | 0.7058 | 99.71% | 375% | 703% | 187% | |
| 0.1144 | 0.0697 | 0.0262 | 0.0049 | 0.0262 | 0.0002 | 0.9157 | 96.71% | 0.5223 | 100.00% | 0.1831 | 84.71% | 1422% | 44,461% | 3126% | ||||
| 12 | 0.0137 | 0.0120 | 0.0072 | 0.0038 | 0.0072 | 0.0030 | 1.4957 | 100.00% | 0.9943 | 100.00% | 0.4938 | 100.00% | 316% | 398% | 126% | |||
| 0.0737 | 0.0319 | 0.0131 | 0.0019 | 0.0131 | 0.0001 | 0.7516 | 97.86% | 0.3680 | 100.00% | 0.1291 | 87.86% | 1716% | 43,486% | 2534% | ||||
| 17 | 0.0060 | 0.0054 | 0.0011 | 0.0021 | 0.0011 | 0.0015 | 1.2491 | 100.00% | 0.8081 | 100.00% | 0.3874 | 100.00% | 260% | 359% | 138% | |||
| 0.0505 | 0.0166 | 0.0090 | 0.0010 | 0.0090 | 0.0000 | 0.6474 | 98.86% | 0.2921 | 100.00% | 0.1034 | 90.29% | 1657% | 39,855% | 2405% | ||||
| 2 | 8 | 0.0525 | 0.0335 | 0.0216 | 0.0194 | 0.0216 | 0.0082 | 1.8112 | 100.00% | 1.0216 | 99.86% | 0.5501 | 95.29% | 172% | 410% | 238% | ||
| 0.1625 | 0.1404 | 0.0102 | 0.0019 | 0.0102 | 0.0000 | 2.6626 | 99.86% | 0.8821 | 100.00% | 0.2076 | 98.14% | 7545% | 439,806% | 5829% | ||||
| 12 | 0.0341 | 0.0139 | 0.0059 | 0.0083 | 0.0059 | 0.0038 | 1.3486 | 100.00% | 0.7071 | 100.00% | 0.3718 | 96.14% | 166% | 363% | 218% | |||
| 0.0961 | 0.0615 | 0.0036 | 0.0007 | 0.0036 | 0.0000 | 2.0205 | 100.00% | 0.6228 | 100.00% | 0.1433 | 99.43% | 8775% | 280,496% | 3196% | ||||
| 17 | 0.0235 | 0.0083 | 0.0064 | 0.0048 | 0.0064 | 0.0023 | 1.1121 | 100.00% | 0.5422 | 100.00% | 0.2719 | 94.43% | 174% | 357% | 206% | |||
| 0.0677 | 0.0329 | 0.0036 | 0.0004 | 0.0036 | 0.0000 | 1.6737 | 100.00% | 0.5035 | 100.00% | 0.1144 | 99.86% | 8102% | 188,280% | 2324% | ||||
| 3 | 8 | 0.0525 | 0.0335 | 0.0216 | 0.0194 | 0.0216 | 0.0082 | 1.8112 | 100.00% | 1.0216 | 99.86% | 0.5501 | 95.29% | 172% | 410% | 238% | ||
| 0.1625 | 0.1404 | 0.0102 | 0.0019 | 0.0102 | 0.0000 | 2.6626 | 99.86% | 0.8821 | 100.00% | 0.2076 | 98.14% | 7545% | 439,806% | 5829% | ||||
| 12 | 0.0341 | 0.0139 | 0.0059 | 0.0083 | 0.0059 | 0.0038 | 1.3486 | 100.00% | 0.7071 | 100.00% | 0.3718 | 96.14% | 166% | 363% | 218% | |||
| 0.0961 | 0.0615 | 0.0036 | 0.0007 | 0.0036 | 0.0000 | 2.0205 | 100.00% | 0.6228 | 100.00% | 0.1433 | 99.43% | 8775% | 280,496% | 3196% | ||||
| 17 | 0.0235 | 0.0083 | 0.0064 | 0.0048 | 0.0064 | 0.0023 | 1.1121 | 100.00% | 0.5422 | 100.00% | 0.2719 | 94.43% | 174% | 357% | 206% | |||
| 0.0677 | 0.0329 | 0.0036 | 0.0004 | 0.0036 | 0.0000 | 1.6737 | 100.00% | 0.5035 | 100.00% | 0.1144 | 99.86% | 8102% | 188,280% | 2324% | ||||
| Point | Confidance | RE | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRS | RSS c = 1 | RSS c = 3 | SRS | RSS c = 1 | RSS c = 3 | |||||||||||||
| Methods | n | Bias | MSE | Bias | MSE | Bias | MSE | LCI | CP | LCI | CP | LCI | CP | RE1 | RE2 | RE3 | ||
| MLE | 0.3 | 8 | −0.5190 | 1.6445 | −0.0926 | 0.2282 | −0.0331 | 0.0546 | 4.6001 | 98.43% | 1.8386 | 95.14% | 0.9072 | 96.00% | 720% | 3013% | 418% | |
| 0.4907 | 0.9970 | 0.0389 | 0.0346 | 0.0100 | 0.0041 | 3.4111 | 92.29% | 0.7140 | 98.00% | 0.2494 | 98.86% | 2878% | 24,059% | 836% | ||||
| 12 | −0.3785 | 0.9832 | −0.0357 | 0.0950 | −0.0308 | 0.0479 | 3.5952 | 91.43% | 1.2010 | 94.29% | 1.0956 | 94.86% | 1035% | 2053% | 198% | |||
| 0.2685 | 0.4480 | 0.0165 | 0.0101 | 0.0063 | 0.0014 | 2.4050 | 92.14% | 0.3898 | 97.43% | 0.1470 | 95.43% | 4415% | 31,043% | 703% | ||||
| 17 | −0.1941 | 0.5198 | −0.0280 | 0.0331 | −0.0090 | 0.0048 | 2.7238 | 91.86% | 0.7051 | 94.57% | 0.2681 | 97.71% | 1571% | 10939% | 696% | |||
| 0.1332 | 0.2135 | 0.0056 | 0.0011 | 0.0004 | 0.0003 | 1.7356 | 94.43% | 0.1297 | 95.71% | 0.0685 | 95.43% | 18,971% | 69,994% | 369% | ||||
| 0.5 | 8 | −0.6023 | 2.7349 | −0.3043 | 0.8875 | −0.1534 | 0.5473 | 6.0419 | 98.14% | 3.4976 | 95.43% | 2.8390 | 94.14% | 308% | 500% | 162% | ||
| 0.9270 | 2.3289 | 0.2789 | 0.4770 | 0.1122 | 0.1048 | 4.7555 | 96.57% | 2.4786 | 92.00% | 1.1914 | 93.86% | 488% | 2221% | 455% | ||||
| 12 | −0.5364 | 1.8947 | −0.1263 | 0.3544 | −0.0401 | 0.0747 | 4.9727 | 97.43% | 2.2821 | 94.71% | 1.0606 | 96.29% | 535% | 2536% | 474% | |||
| 0.6496 | 1.4060 | 0.0806 | 0.0695 | 0.0155 | 0.0087 | 3.8912 | 94.43% | 0.9846 | 97.00% | 0.3603 | 98.14% | 2023% | 16,212% | 801% | ||||
| 17 | −0.4418 | 1.5273 | −0.1640 | 0.3172 | −0.0329 | 0.0672 | 4.5275 | 98.14% | 2.1134 | 92.14% | 1.0084 | 96.29% | 482% | 2274% | 472% | |||
| 0.4718 | 0.8682 | 0.0757 | 0.0602 | 0.0155 | 0.0073 | 3.1519 | 93.14% | 1.0660 | 95.86% | 0.6308 | 99.57% | 1443% | 11,957% | 829% | ||||
| 2 | 8 | 0.0259 | 3.4728 | −0.0331 | 1.7028 | 0.0438 | 1.1119 | 7.3096 | 94.29% | 5.1173 | 95.29% | 4.1330 | 96.14% | 204% | 312% | 153% | ||
| 1.4484 | 6.0130 | 0.7250 | 2.3908 | 0.4386 | 1.5867 | 7.7619 | 99.43% | 5.3574 | 98.43% | 4.6320 | 96.43% | 252% | 379% | 151% | ||||
| 12 | −0.0296 | 3.1821 | −0.0065 | 1.0169 | −0.0295 | 0.6357 | 6.9967 | 93.86% | 3.9558 | 94.29% | 3.1255 | 94.86% | 313% | 501% | 160% | |||
| 1.3666 | 5.5362 | 0.4086 | 1.1014 | 0.3101 | 0.9477 | 7.5135 | 98.71% | 3.7919 | 98.43% | 3.6200 | 96.43% | 503% | 584% | 116% | ||||
| 17 | −0.0406 | 2.3864 | −0.1251 | 0.7429 | −0.0254 | 0.2637 | 6.0578 | 95.00% | 3.3453 | 96.14% | 2.0118 | 95.43% | 321% | 905% | 282% | |||
| 1.1429 | 4.7424 | 0.3826 | 0.9196 | 0.1264 | 0.2775 | 7.2717 | 97.86% | 3.8494 | 98.00% | 2.0061 | 96.00% | 516% | 1709% | 331% | ||||
| Bayesian | 0.3 | 8 | 0.0081 | 0.0231 | −0.0001 | 0.0062 | −0.0001 | 0.0025 | 2.1588 | 100.00% | 1.5521 | 100.00% | 0.8862 | 100.00% | 375% | 936% | 249% | |
| 0.0612 | 0.0201 | 0.0218 | 0.0030 | 0.0218 | 0.0003 | 0.5223 | 96.43% | 0.3032 | 99.57% | 0.1383 | 84.57% | 675% | 6813% | 1009% | ||||
| 12 | 0.0031 | 0.0054 | −0.0013 | 0.0019 | −0.0013 | 0.0012 | 1.5645 | 100.00% | 1.1041 | 100.00% | 0.6220 | 100.00% | 289% | 462% | 160% | |||
| 0.0372 | 0.0096 | 0.0056 | 0.0010 | 0.0056 | 0.0001 | 0.4228 | 97.14% | 0.2055 | 99.71% | 0.0956 | 87.29% | 924% | 7430% | 804% | ||||
| 17 | 0.0017 | 0.0024 | −0.0020 | 0.0011 | −0.0020 | 0.0007 | 1.2878 | 100.00% | 0.9026 | 100.00% | 0.5028 | 100.00% | 220% | 347% | 158% | |||
| 0.0294 | 0.0066 | 0.0053 | 0.0005 | 0.0053 | 0.0001 | 0.3623 | 98.43% | 0.1577 | 100.00% | 0.0746 | 91.71% | 1379% | 7877% | 571% | ||||
| 0.5 | 8 | −0.0011 | 0.0202 | 0.0054 | 0.0069 | 0.0054 | 0.0048 | 2.1389 | 100.00% | 1.5040 | 100.00% | 0.8219 | 100.00% | 294% | 420% | 143% | ||
| 0.1123 | 0.0569 | 0.0227 | 0.0048 | 0.0227 | 0.0003 | 0.8692 | 97.00% | 0.4606 | 100.00% | 0.1746 | 83.57% | 1194% | 22,408% | 1877% | ||||
| 12 | 0.0015 | 0.0062 | −0.0002 | 0.0023 | −0.0002 | 0.0022 | 1.5528 | 100.00% | 1.0743 | 100.00% | 0.5750 | 100.00% | 266% | 287% | 108% | |||
| 0.0638 | 0.0259 | 0.0099 | 0.0020 | 0.0099 | 0.0001 | 0.6957 | 97.29% | 0.3243 | 100.00% | 0.1217 | 84.57% | 1322% | 23,434% | 1772% | ||||
| 17 | 0.0034 | 0.0027 | 0.0019 | 0.0014 | 0.0019 | 0.0014 | 1.2806 | 100.00% | 0.8677 | 100.00% | 0.4551 | 100.00% | 193% | 187% | 97% | |||
| 0.0384 | 0.0141 | 0.0077 | 0.0012 | 0.0077 | 0.0001 | 0.5817 | 98.43% | 0.2480 | 100.00% | 0.0965 | 84.14% | 1132% | 20,160% | 1782% | ||||
| 2 | 8 | 0.0414 | 0.0249 | 0.0285 | 0.0186 | 0.0285 | 0.0098 | 2.0417 | 100.00% | 1.2539 | 100.00% | 0.6903 | 99.57% | 133% | 253% | 190% | ||
| 0.1342 | 0.1354 | 0.0144 | 0.0027 | 0.0144 | 0.0000 | 2.5164 | 99.86% | 0.8586 | 100.00% | 0.2054 | 96.29% | 5066% | 314,626% | 6211% | ||||
| 12 | 0.0224 | 0.0094 | 0.0123 | 0.0087 | 0.0123 | 0.0044 | 1.4773 | 100.00% | 0.8766 | 100.00% | 0.4703 | 98.86% | 109% | 215% | 197% | |||
| 0.0891 | 0.0633 | 0.0067 | 0.0013 | 0.0067 | 0.0000 | 1.9433 | 100.00% | 0.6057 | 100.00% | 0.1420 | 95.71% | 4939% | 227,059% | 4597% | ||||
| 17 | 0.0109 | 0.0053 | 0.0028 | 0.0052 | 0.0028 | 0.0025 | 1.2093 | 100.00% | 0.6824 | 100.00% | 0.3538 | 99.14% | 102% | 212% | 209% | |||
| 0.0523 | 0.0341 | 0.0025 | 0.0008 | 0.0025 | 0.0000 | 1.5961 | 100.00% | 0.4880 | 100.00% | 0.1130 | 96.57% | 4428% | 147,107% | 3322% | ||||
| Estimates | SE | KSD | SM1 | SM2 | SM3 | SM4 | CVM | AD | ||
|---|---|---|---|---|---|---|---|---|---|---|
| KMPTL | 1.1672 | 0.7731 | 0.0568 | −24.8680 | −20.6462 | −24.6611 | −23.2135 | 0.0456 | 0.3864 | |
| 2.7532 | 2.6813 | |||||||||
| PTL | 0.4601 | 0.4046 | 0.0569 | −24.8276 | −20.6059 | −24.6207 | −23.1731 | 0.0493 | 0.4091 | |
| 9.4177 | 3.8950 | |||||||||
| Beta | a | 2.7940 | 0.4880 | 0.0618 | −23.9056 | −19.6838 | −23.6987 | −22.2510 | 0.0491 | 0.3867 |
| b | 2.6037 | 0.4519 | ||||||||
| Kw | a | 2.3289 | 0.3055 | 0.0689 | −23.2431 | −19.0213 | −23.0362 | −21.5886 | 0.0528 | 0.4009 |
| b | 2.7624 | 0.5550 | ||||||||
| MOK | 0.2984 | 0.2974 | 0.0583 | −22.6334 | −16.3007 | −22.2123 | −20.1516 | 0.0492 | 0.4149 | |
| 3.0632 | 0.6398 | |||||||||
| 1.9447 | 0.9469 | |||||||||
| UG | 0.6157 | 0.2660 | 0.1098 | −17.7512 | −13.5295 | −17.5443 | −16.0967 | 0.1586 | 1.1548 | |
| 1.0927 | 0.2473 | |||||||||
| UL | 0.7248 | 0.0687 | 0.2487 | 33.1918 | 35.3027 | 33.2596 | 34.0191 | 0.6153 | 3.7898 | |
| TL | 2.7394 | 0.3507 | 0.0860 | −23.8362 | −20.2725 | −23.7684 | −23.0090 | 0.0459 | 0.3974 | |
| UGLBXII | 4.8911 | 7.0971 | 0.0569 | −22.9393 | −16.6067 | −22.5183 | −20.4575 | 0.0460 | 0.3947 | |
| 0.9787 | 0.1834 | |||||||||
| 1.7529 | 1.7128 | |||||||||
| UEPD | 0.8117 | 0.0647 | 0.1670 | 214.7548 | 221.0874 | 215.1758 | 217.2366 | 0.3447 | 2.2041 | |
| 1.3071 | 0.6696 | |||||||||
| 0.7641 | 41.1245 |
| Estimates | SE | KSD | SM1 | SM2 | SM3 | SM4 | CVM | AD | ||
|---|---|---|---|---|---|---|---|---|---|---|
| KMPTL | 6.6639 | 1.5843 | 0.0624 | −2.8736 | −0.0712 | −2.4291 | −1.9771 | 0.0169 | 0.1450 | |
| 0.1478 | 0.2745 | |||||||||
| PTL | 1.8949 | 2.3814 | 0.0718 | −2.0977 | 0.7047 | −1.6533 | −1.2012 | 0.0233 | 0.1955 | |
| 0.4895 | 0.7559 | |||||||||
| Beta | a | 0.9666 | 0.2238 | 0.0669 | −2.6101 | 0.1923 | −2.1657 | −1.7136 | 0.0184 | 0.1559 |
| b | 1.6205 | 0.4107 | ||||||||
| Kw | a | 0.9622 | 0.2016 | 0.0649 | −2.6221 | 0.1803 | −2.1776 | −1.7256 | 0.0183 | 0.1550 |
| b | 1.6077 | 0.4135 | ||||||||
| MOK | 0.4363 | 0.4707 | 0.0630 | −1.2087 | 2.9949 | −0.2856 | 0.1361 | 0.0171 | 0.1456 | |
| 1.1869 | 0.3460 | |||||||||
| 1.2584 | 0.6442 | |||||||||
| UG | 1.0380 | 0.7702 | 0.0734 | −2.8098 | −0.0695 | −2.4053 | −1.9001 | 0.0184 | 0.1461 | |
| 0.4212 | 0.1917 | |||||||||
| UL | 1.0505 | 0.1455 | 0.2721 | 20.1704 | 21.5716 | 20.3133 | 20.6187 | 0.1656 | 1.0870 | |
| TL | 1.1090 | 0.2025 | 0.0665 | −3.8078 | −2.4066 | −3.6649 | −3.3595 | 0.0189 | 0.1600 | |
| UGLBXII | 1167.4551 | 810.1270 | 0.0658 | −1.4306 | 2.7730 | −0.5076 | −0.0859 | 0.0173 | 0.1457 | |
| 0.6846 | 0.1003 | |||||||||
| 261.5642 | 1342.7096 | |||||||||
| UEPD | 0.6630 | 0.0882 | 0.1052 | 74.7790 | 78.9826 | 75.7021 | 76.1238 | 0.0637 | 0.4734 | |
| 0.9585 | 106.1478 | |||||||||
| 0.9751 | 71.5895 |
| Mean | SE | Lower | Upper | ||
|---|---|---|---|---|---|
| Economic Growth | 1.2055 | 0.2554 | 0.7643 | 1.7374 | |
| 2.7903 | 0.7658 | 1.3756 | 4.2750 | ||
| polyester fibers | 6.5853 | 2.0764 | 2.7525 | 10.6469 | |
| 0.1703 | 0.0726 | 0.0524 | 0.3178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, N.; Al-Moisheer, A.S.; Elbatal, I.; Shrahili, M.; Elgarhy, M.; Almetwally, E.M. Bayesian and Non-Bayesian Estimation for a New Extension of Power Topp–Leone Distribution under Ranked Set Sampling with Applications. Axioms 2023, 12, 722. https://doi.org/10.3390/axioms12080722
Alotaibi N, Al-Moisheer AS, Elbatal I, Shrahili M, Elgarhy M, Almetwally EM. Bayesian and Non-Bayesian Estimation for a New Extension of Power Topp–Leone Distribution under Ranked Set Sampling with Applications. Axioms. 2023; 12(8):722. https://doi.org/10.3390/axioms12080722
Chicago/Turabian StyleAlotaibi, Naif, A. S. Al-Moisheer, Ibrahim Elbatal, Mansour Shrahili, Mohammed Elgarhy, and Ehab M. Almetwally. 2023. "Bayesian and Non-Bayesian Estimation for a New Extension of Power Topp–Leone Distribution under Ranked Set Sampling with Applications" Axioms 12, no. 8: 722. https://doi.org/10.3390/axioms12080722
APA StyleAlotaibi, N., Al-Moisheer, A. S., Elbatal, I., Shrahili, M., Elgarhy, M., & Almetwally, E. M. (2023). Bayesian and Non-Bayesian Estimation for a New Extension of Power Topp–Leone Distribution under Ranked Set Sampling with Applications. Axioms, 12(8), 722. https://doi.org/10.3390/axioms12080722








