Model-Free Sliding Mode Enhanced Proportional, Integral, and Derivative (SMPID) Control
Abstract
1. Introduction
- (a)
- Take to form a new SMPID to satisfy the Lyapunov asymptotic stability condition rather than (conventionally used for solving nominal models to determine the equivalent control). Note that the condition is one of the causes of the chattering effect (because chattering is subject to such stability).
- (b)
- Significantly reduce the difficulty in tuning PID gains due to the high demands on the PID control roles; that is, a well-designed PID control has been widely demanded for both dynamic and static response. A properly designed PID could just be used for the plant’s dynamic inversion and then leave the dynamic specifications (e.g., damping ratio and undamped natural frequency) to the other controller within a generalised U-control system framework. Consequently, the PID gain tuning is significantly relaxed to achieve the pre-specified dynamic/static performance.
- (1)
- Propose a sliding mode function as the PID controller input, The replacement of conventional PID input makes the input take in comprehensive state error to form a sliding model function in terms of the Hurwitz polynomial and the derivative of the sliding mode is assigned with another polynomial to determine the PID controller output satisfying the asymptotic stability condition rather than the conventional stability condition (NB, this is not asymptotic stability and one of the courses of chattering). The new SMPID effectively drives the system states to achieve and keep on reaching them. The plant is treated as a whole uncertainty.
- (2)
- The new SMPID is different from the other types of SMPID . In terms of practical applications, the new controller can be more easily implemented with commercial PID instruments.
- (3)
- Generalisation of SMC formation: A section is contributed to propose a generalised SMC design prototype to cover both asymptotic time stabilisation and finite-time stabilisation for both model-based and model-free designs. The SMPID is one of the implementations.
- (4)
- Significantly reduce the PID tuning effort in practise: Multiple choices of PID parameters (gains) Distinctively, this new method only needs the PID gains satisfying Lyapunov asymptotic stability conditions to achieve dynamic inversion in the inner loop; the exact linear dynamic and static responses (for example ) are specified/achieved in the outer loop within the U-control framework. In other words, the new PID parameter tuning is largely relaxed, as it is only for stability. However, almost all the other tuning methods (Ziegler-Nichols trial and error methods, model-free online optimisations, etc.) are not only demanding for stability but more demanding for dynamic (transient) responses, which cannot be uniquely specified with a group of PID gains.
- (5)
- Significantly reduce the chattering effect: It is noted that is used for determining the equivalent control in conventional model-based SMC. This is one of the roots of chattering because gives (stable but not asymptotically stable, and chattering is subject to such stability). The new approach determines the equivalent control with (asymptotic stability), this also gives a relaxed sliding band thickness setup without losing accuracy, which relieves the struggling trade-off between accuracy and chattering. This has very practical significance for saving operational energy costs and reducing hardware wear and tear. The simulated case studies well demonstrate the claims.
- (6)
- As the independent/separate design of dynamic inversion and whole control system performance controller within the U-control system framework, this study provides a potential for co-design for practical applications, such as Unmanned Aerial Vehicles (UAV), separating the airframe design and its control system design, then seamlessly integrating them to simplify/speed up the whole system setup and maintenance. The principle/technique should be applicable to most motion and processing systems.
- (7)
- Provide a set of transparent, user-friendly simulation demonstrations for guiding applications and expansions.
2. Preliminary
2.1. Problem Formulation—Control of Model Unknown Nonlinear Dynamic Plants
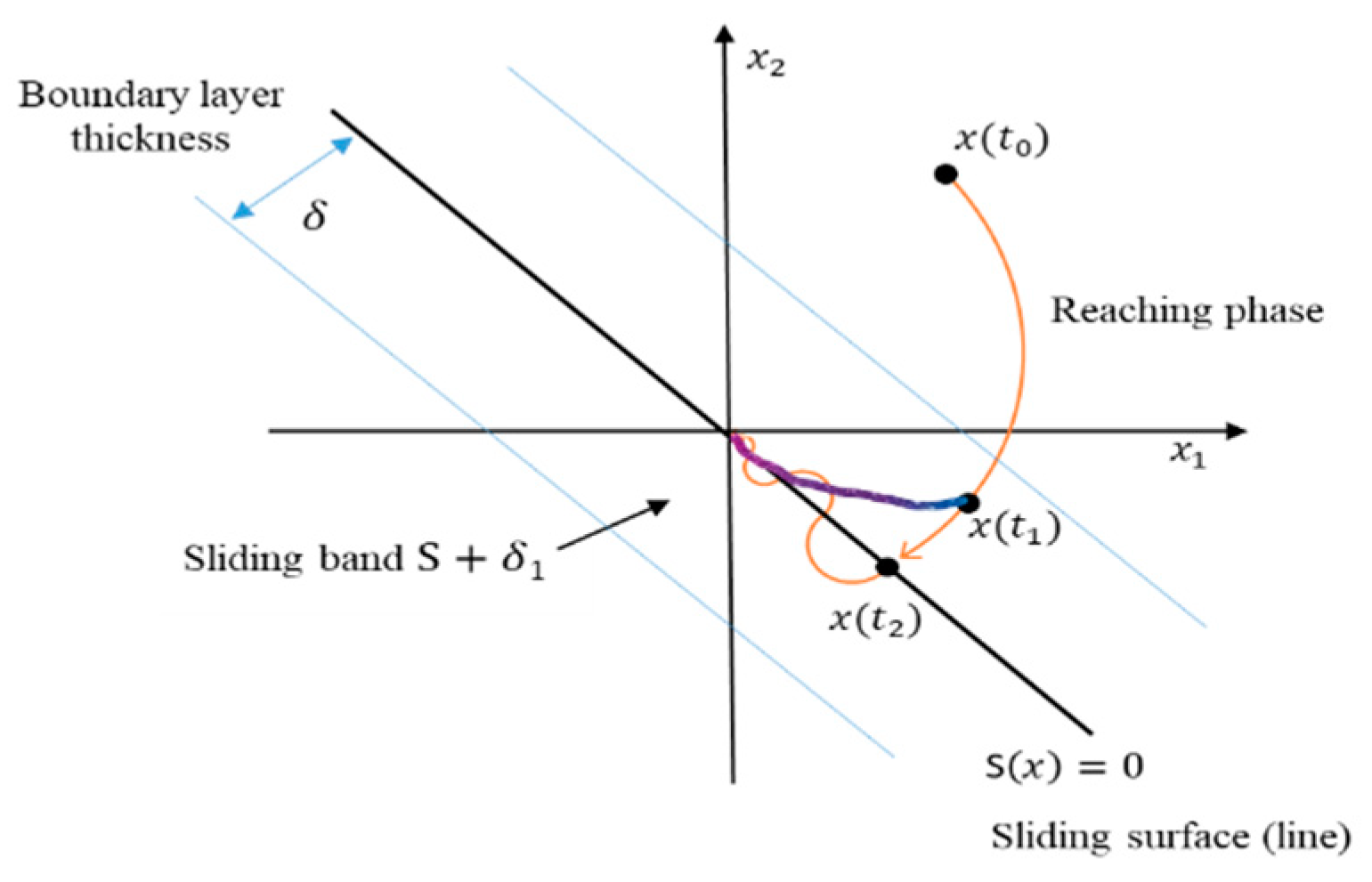
2.2. SMC
2.3. Model-Free Observer
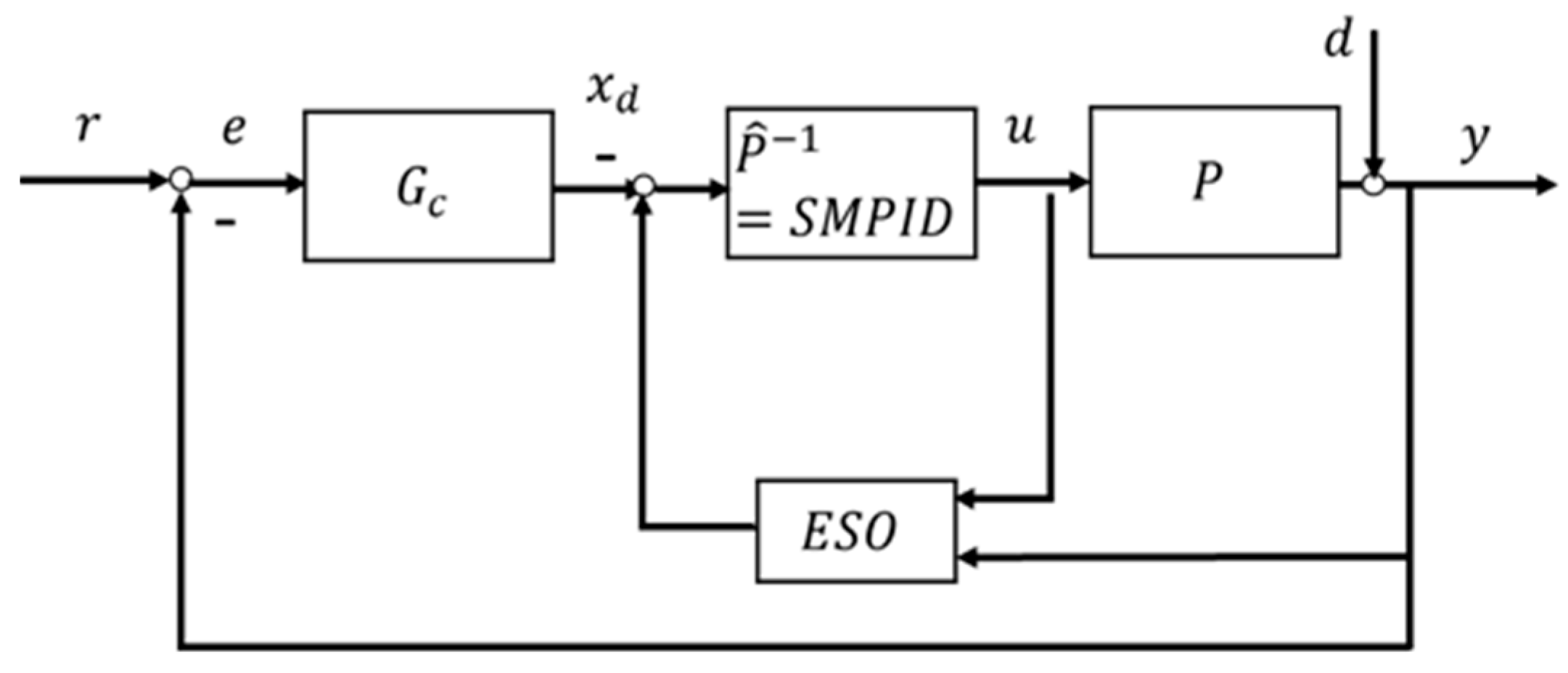
3. Sliding Mode Function-Based PID and Model-Free Control System Design
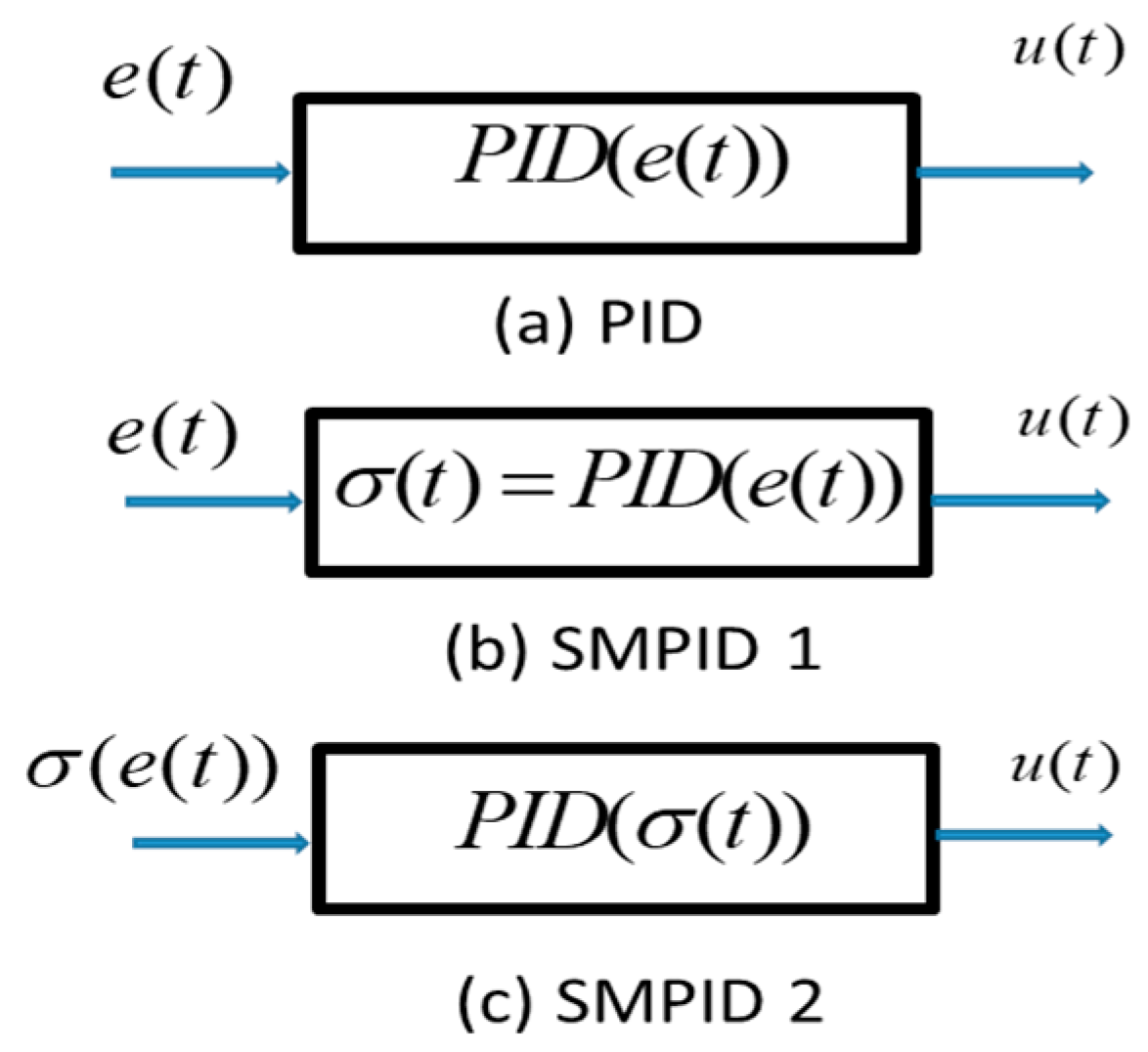
3.1. SMPID
3.2. SMPID Design
- Proportional (P) function
- Proportional and Integral (PI) functions
- Proportional, Integral, and Derivative (PID) functions
- Nonlinear function
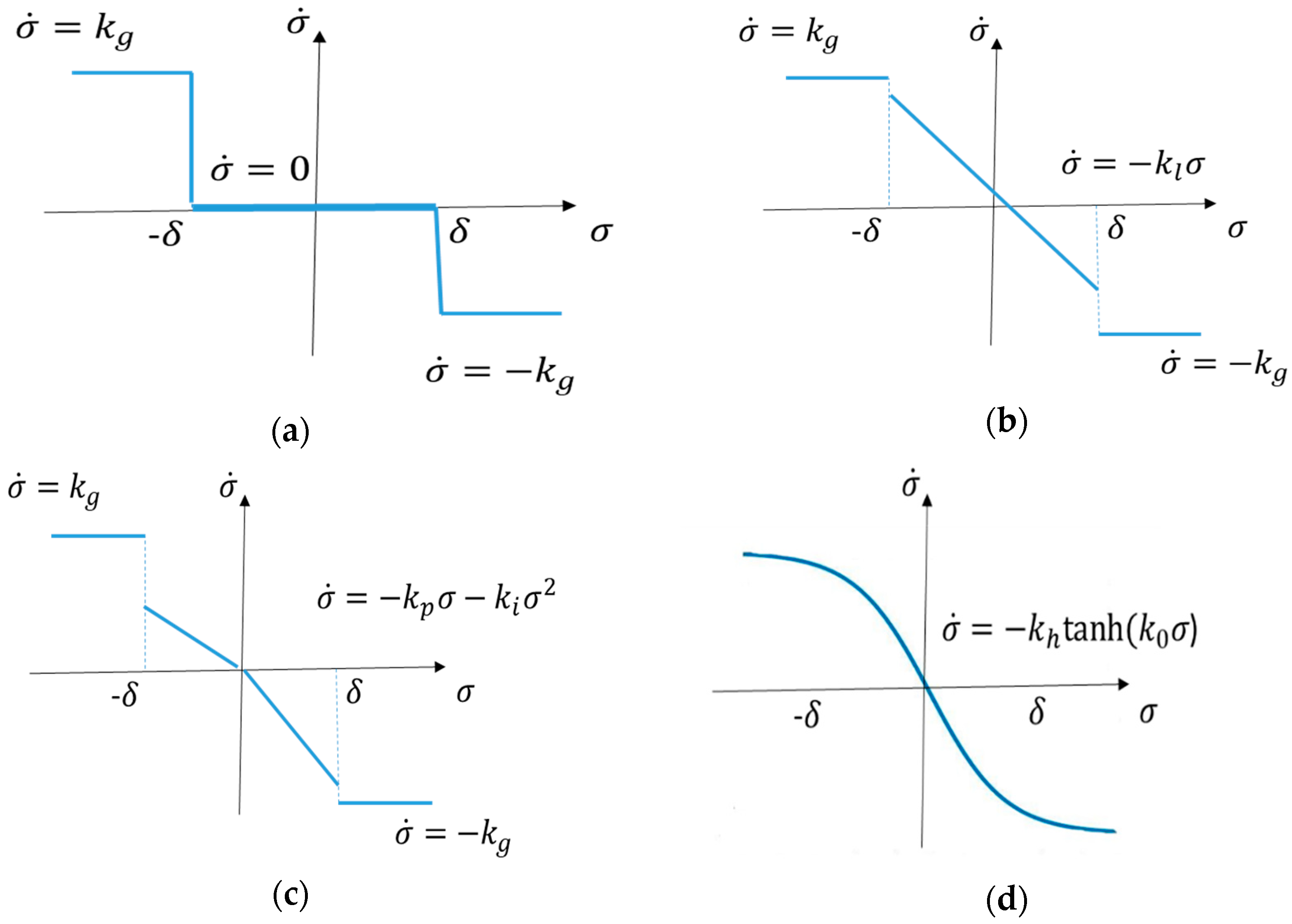
3.3. Analysis of Convergence
- (1)
- For the SMP controller, within the sliding bands, locally, its sliding mode function monotonically exponentially converges with or .
- (2)
- For the SMPI controller, within the sliding bands, locally, its sliding mode function monotonically exponentially converges with .
- (3)
- For the nonlinear (with tanh) control, globally its sliding mode function monotonically converges with .
- (1)
- For SMP, it has been proven [27].
- (2)
- For SMPI, take the Laplace transform of to yield , where poles are negative (stable) and real (monotonic) conditioned with and . The corresponding step response is . Therefore, the sliding mode function is monotonically exponentially converged with . This can be proved by taking up the Laplace transform final value theorem as well.
- (3)
- For nonlinear systems (with tanh), it is difficult to obtain the global differential equation solutions. Heuristically, from the properties of the tanh function, it is monotonic and .
3.4. Analysis of Robustness and Chattering
- (1)
- As the MFSMC ( in terms of asymptotic stability) is smoothly converged within the sliding model band, the sliding mode band can be relaxed to a reasonably larger thickness without losing performance against conventional SMC ( in terms of stability). Accordingly, reduce the chattering effects and relax the sliding band thickness setup without losing accuracy.
- (2)
- If the chattering effects come from unmodeled plant dynamics in equivalent controller design with the conventional SMC, then the MFSMC takes the whole plant as uncertainty in designing the equivalent controller. This could reduce the chattering effects, obviously.
3.5. Generalisation of SMC
4. Case Studies
4.1. Pre-Setups
- (1)
- the SMPID developed in dynamic inversion and facilitation of U-control configuration,
- (2)
- robustness of the SMPID against uncertainty and disturbance,
- (3)
- dealing with chattering effects,
- (4)
- the new PID tuning and the whole U-control system’s performance.
- (1)
- A sequence of levelled references is assigned with
- (2)
- The external disturbance is assigned as a constant added at the output.
- (3)
- Select the sliding function with , in which the estimate vector from the LESO is used to replace the plant states in the simulation processes. Setup the sliding mode boundary thickness .
- (4)
- The control system output is specified in the outer loop via a standard linear second-order dynamic in terms of the Laplace transform.
- (5)
- For state feedback control, it is requested to obtain the estimated state vector from plant (17) input/output measurements. Select a LESO below,
4.2. SMPI Control—Model-Free Variable Structure SMC
4.3. SM Nonlinear P Control—Model-Free Non-Variable Structure (Non-Switching) SMC
4.4. Discussions on the Computational Demonstrations
- (1)
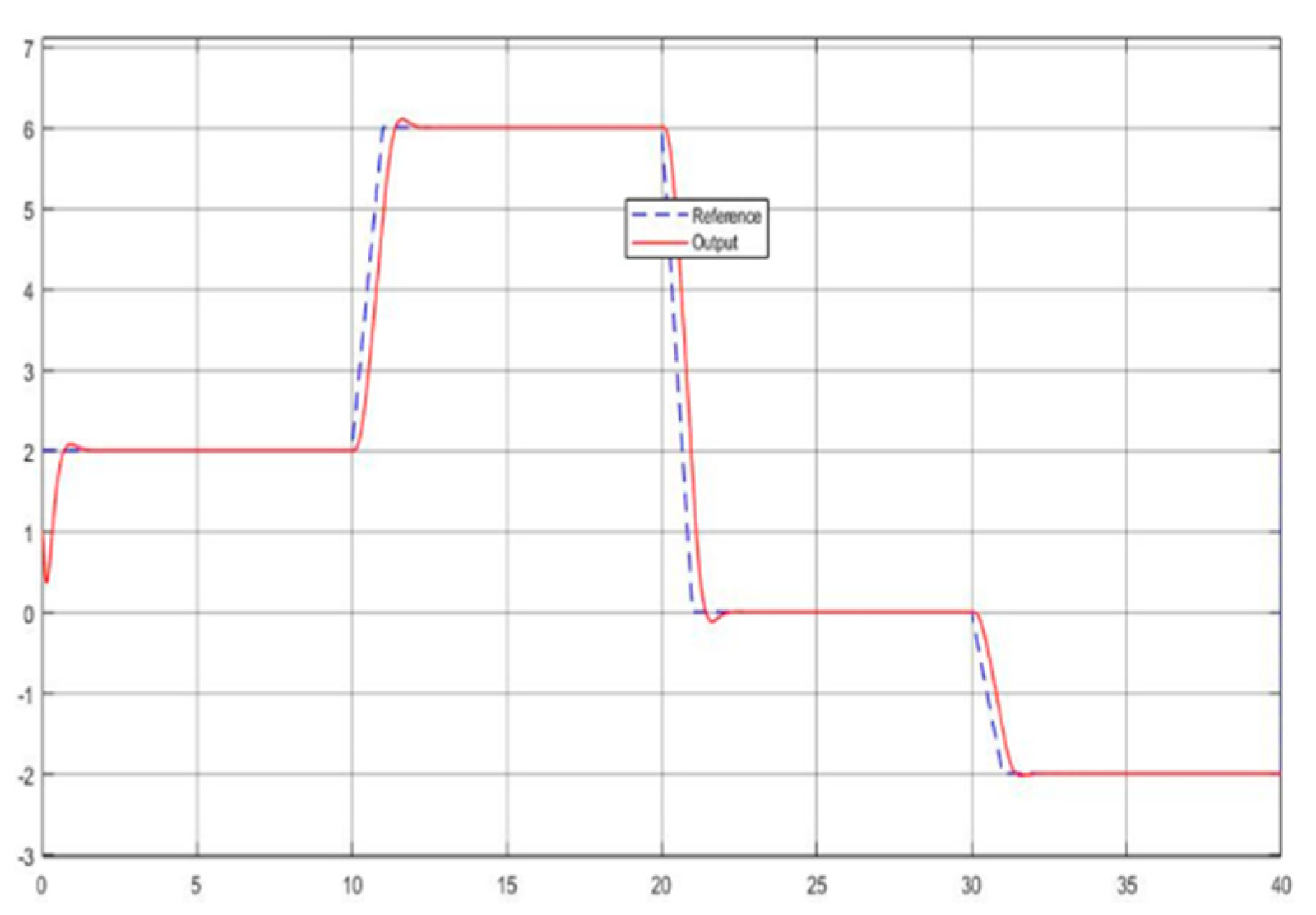
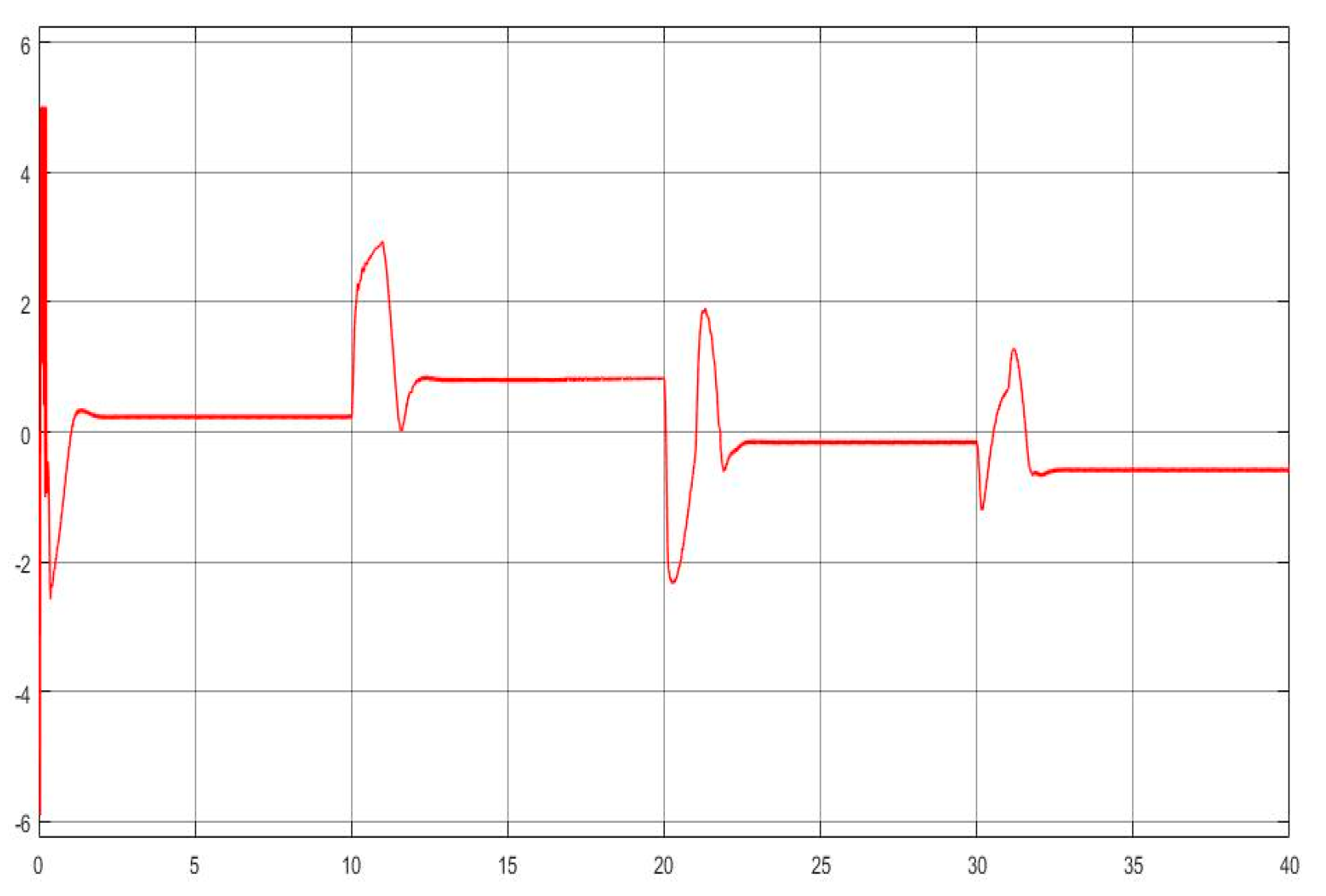
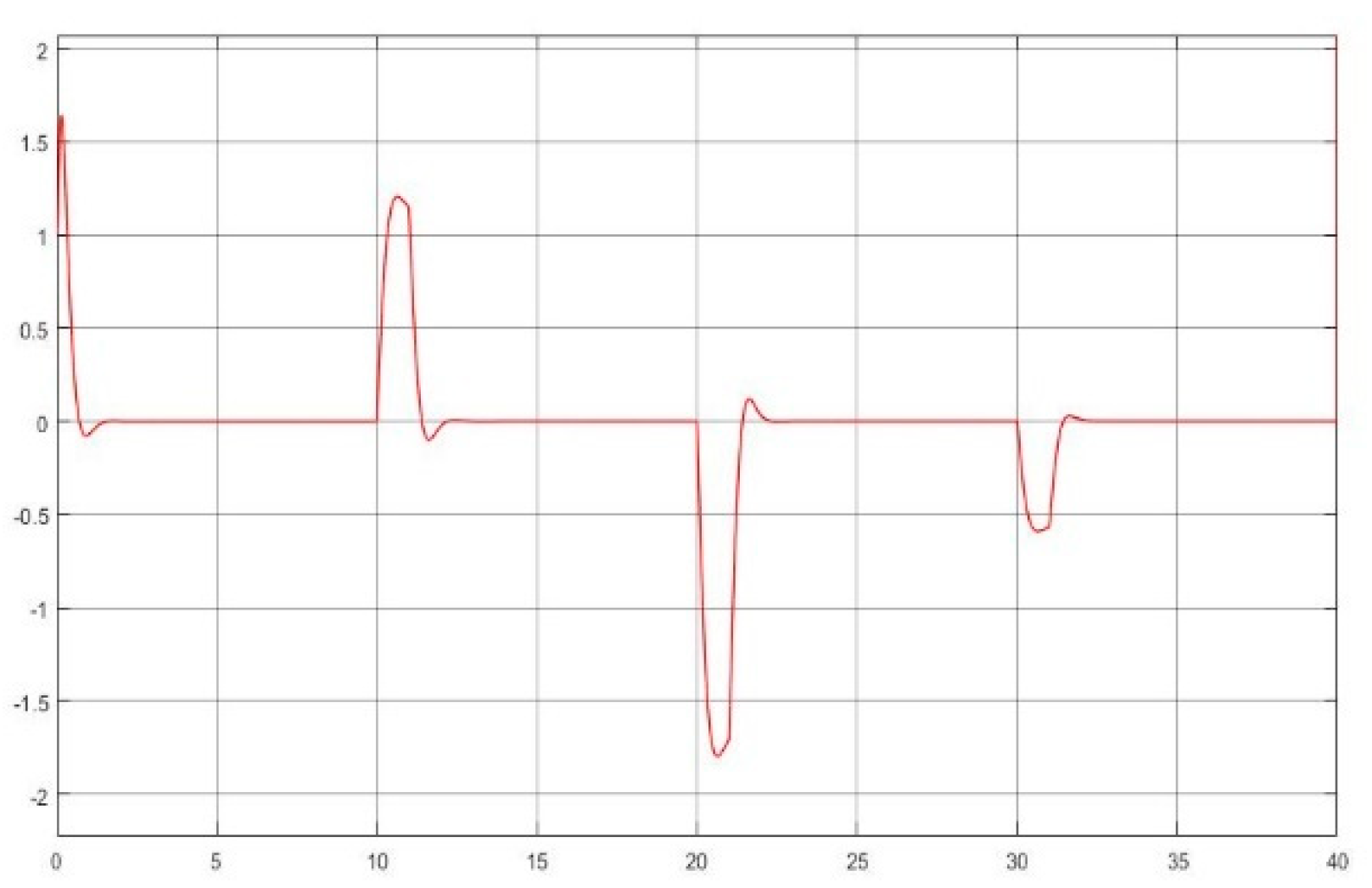
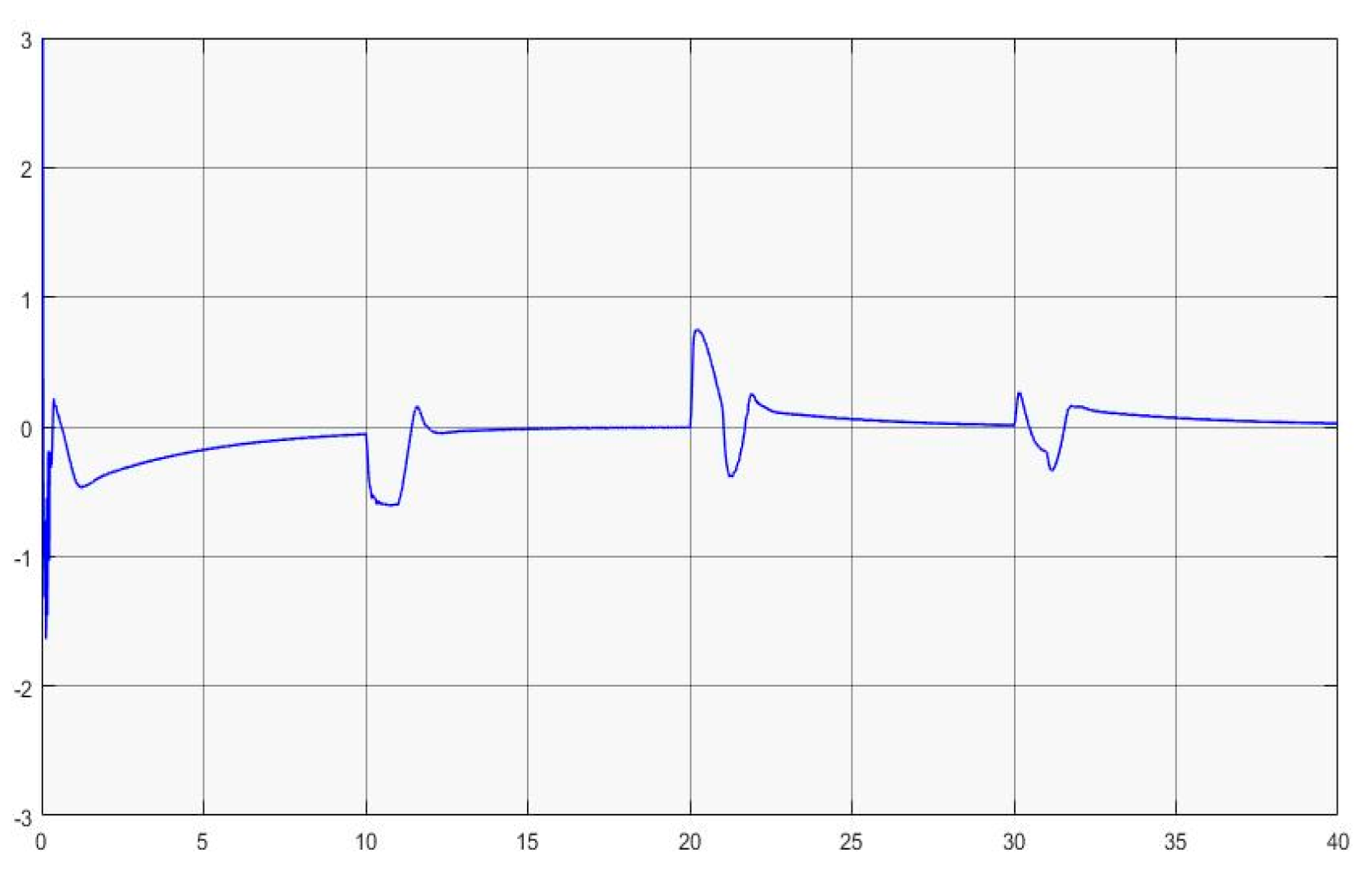
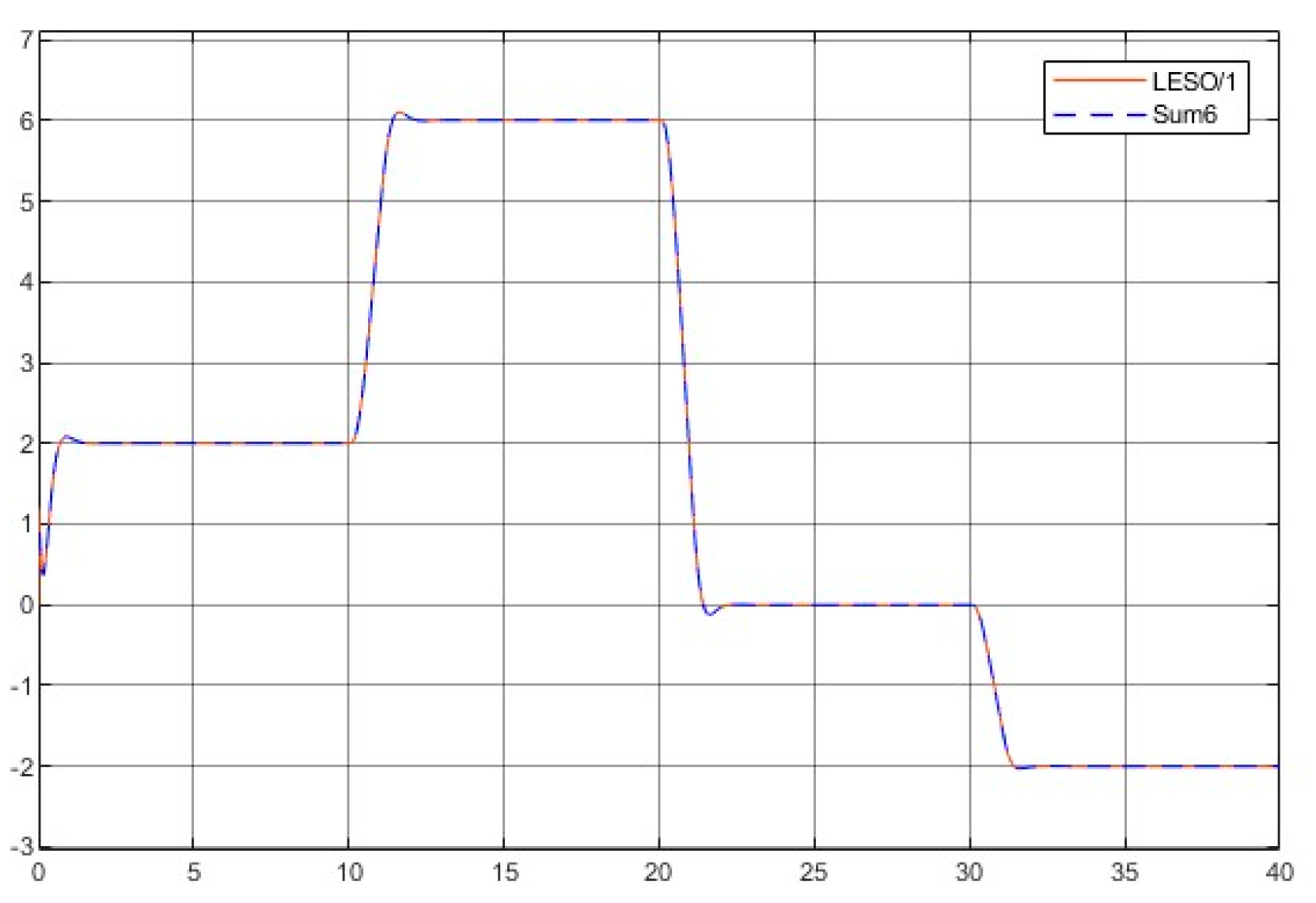
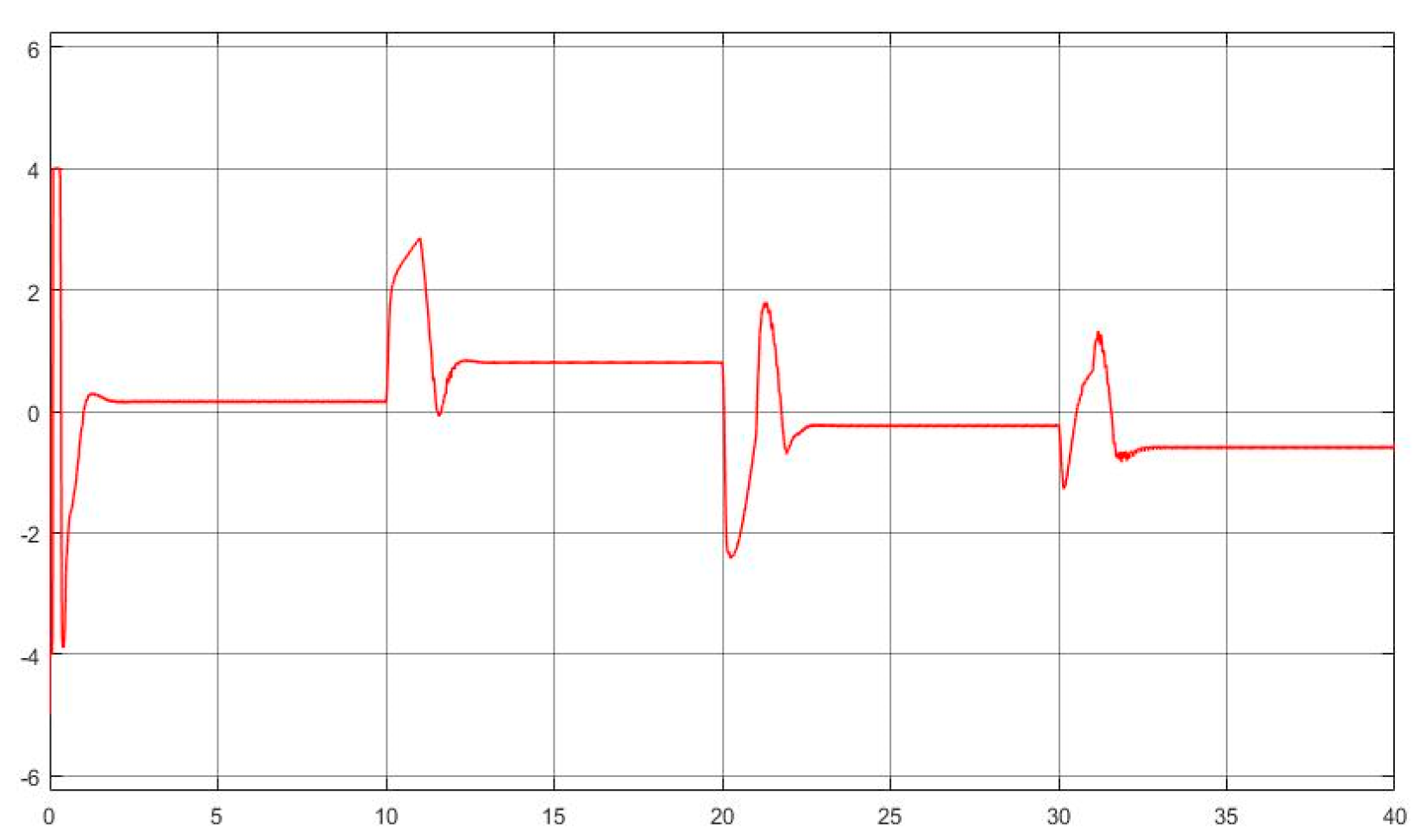
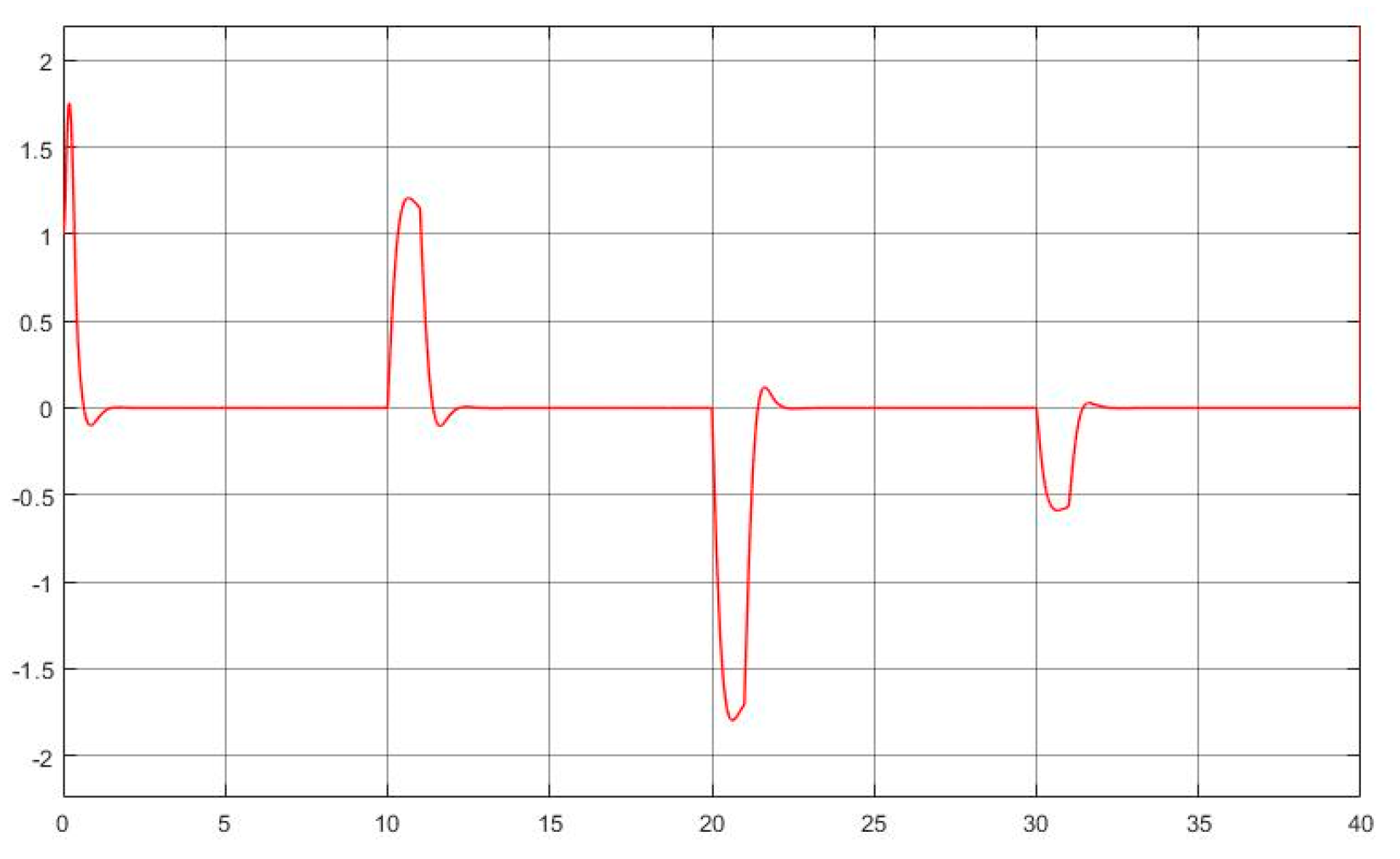
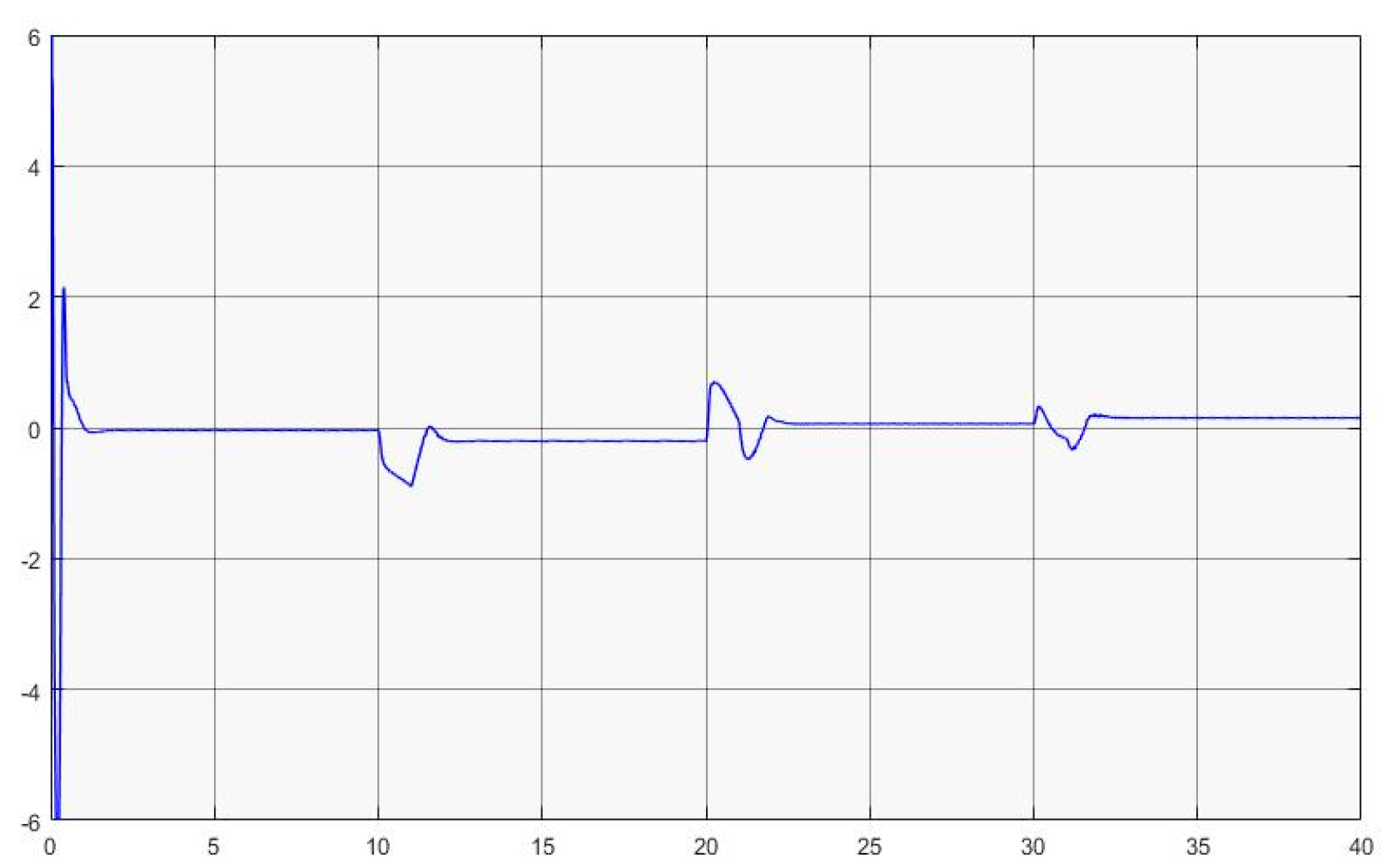
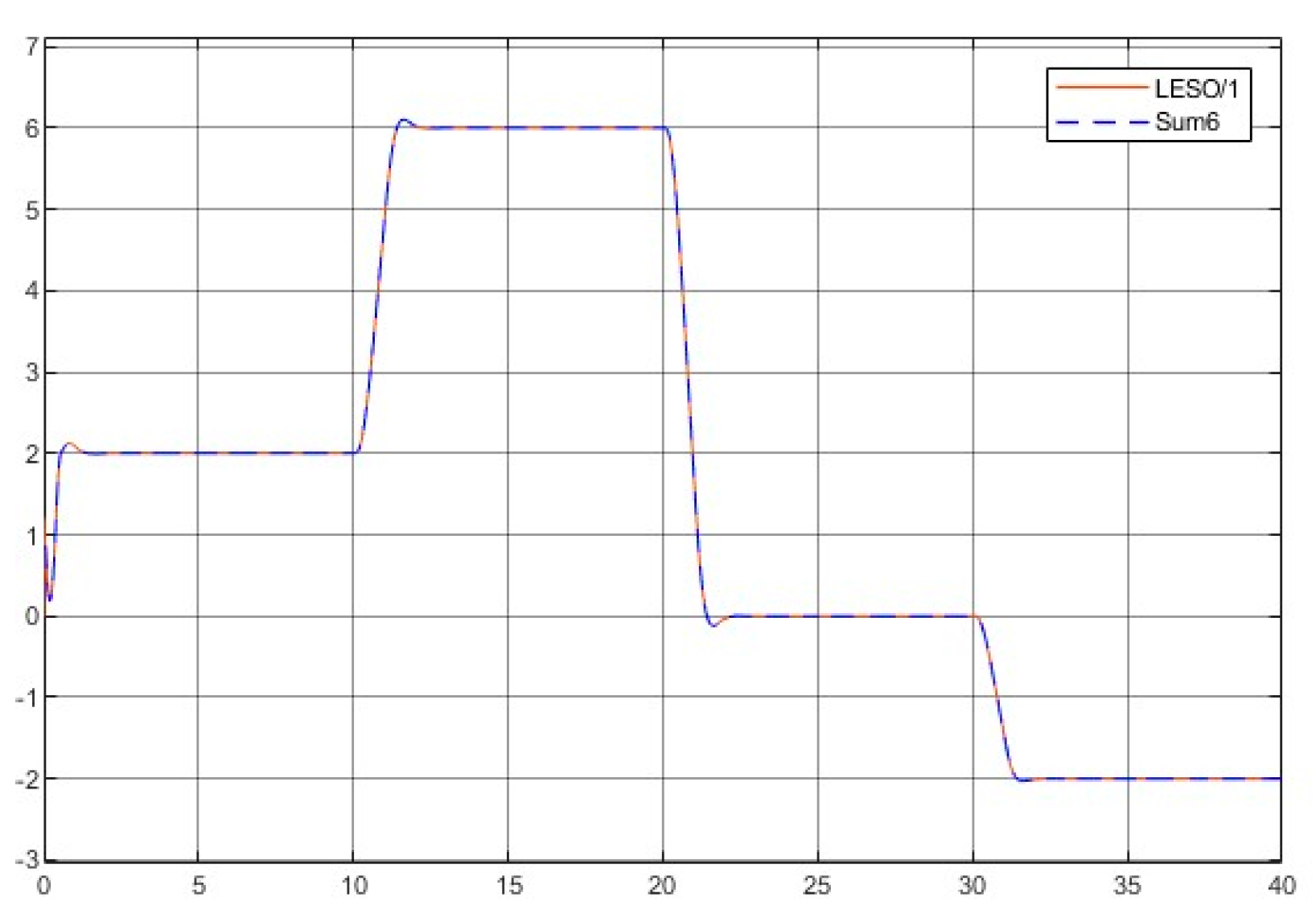
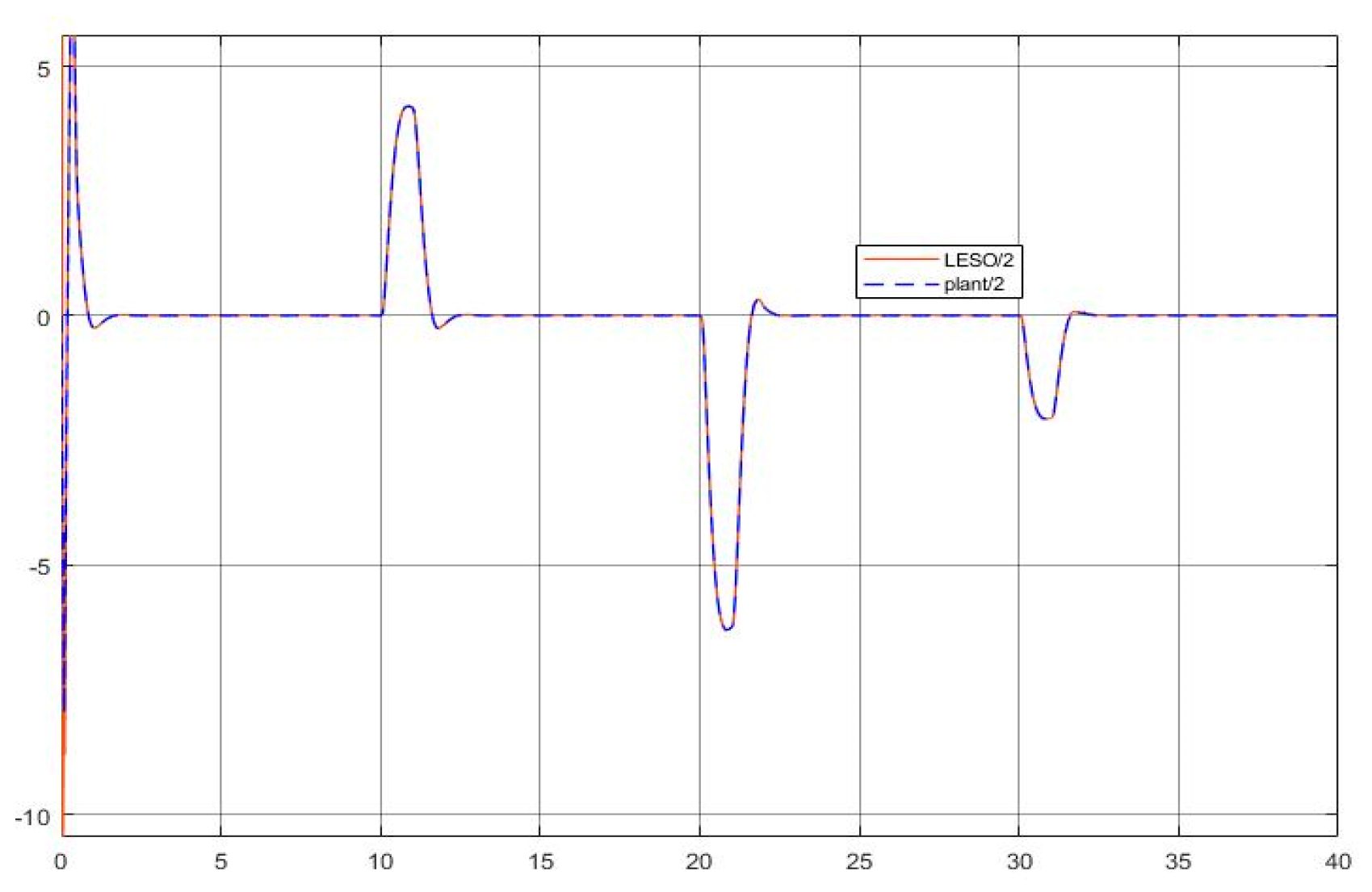
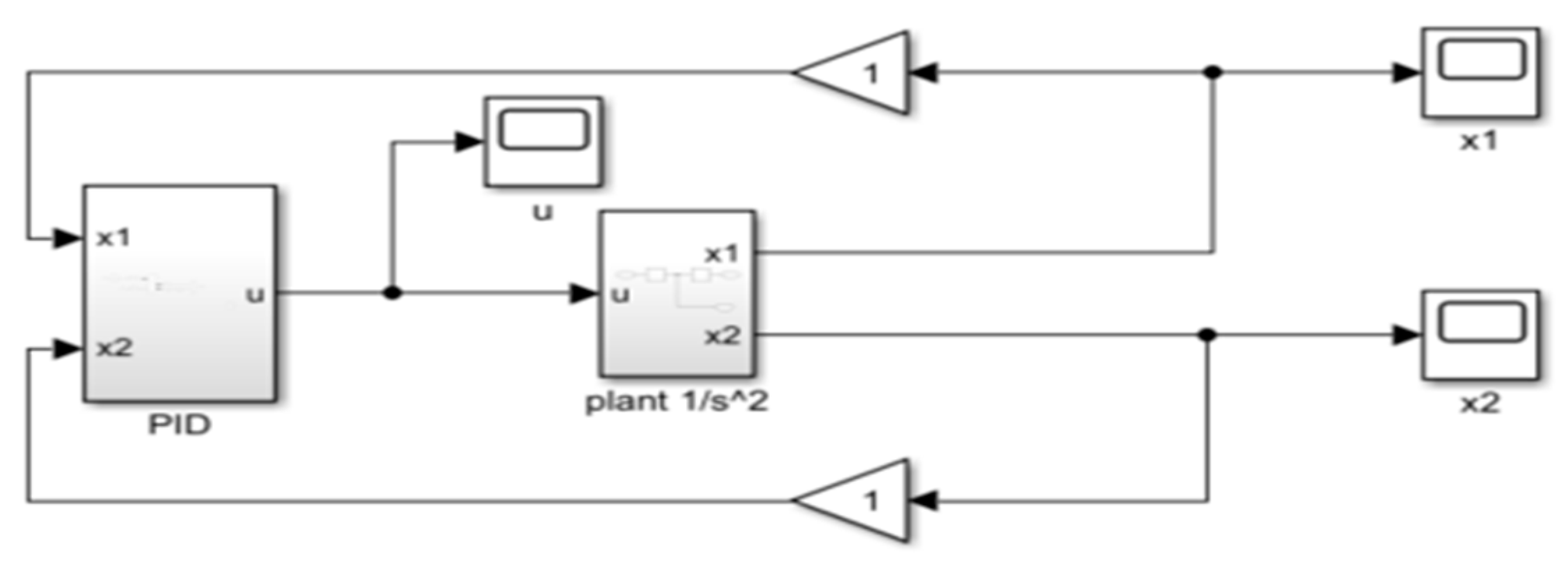
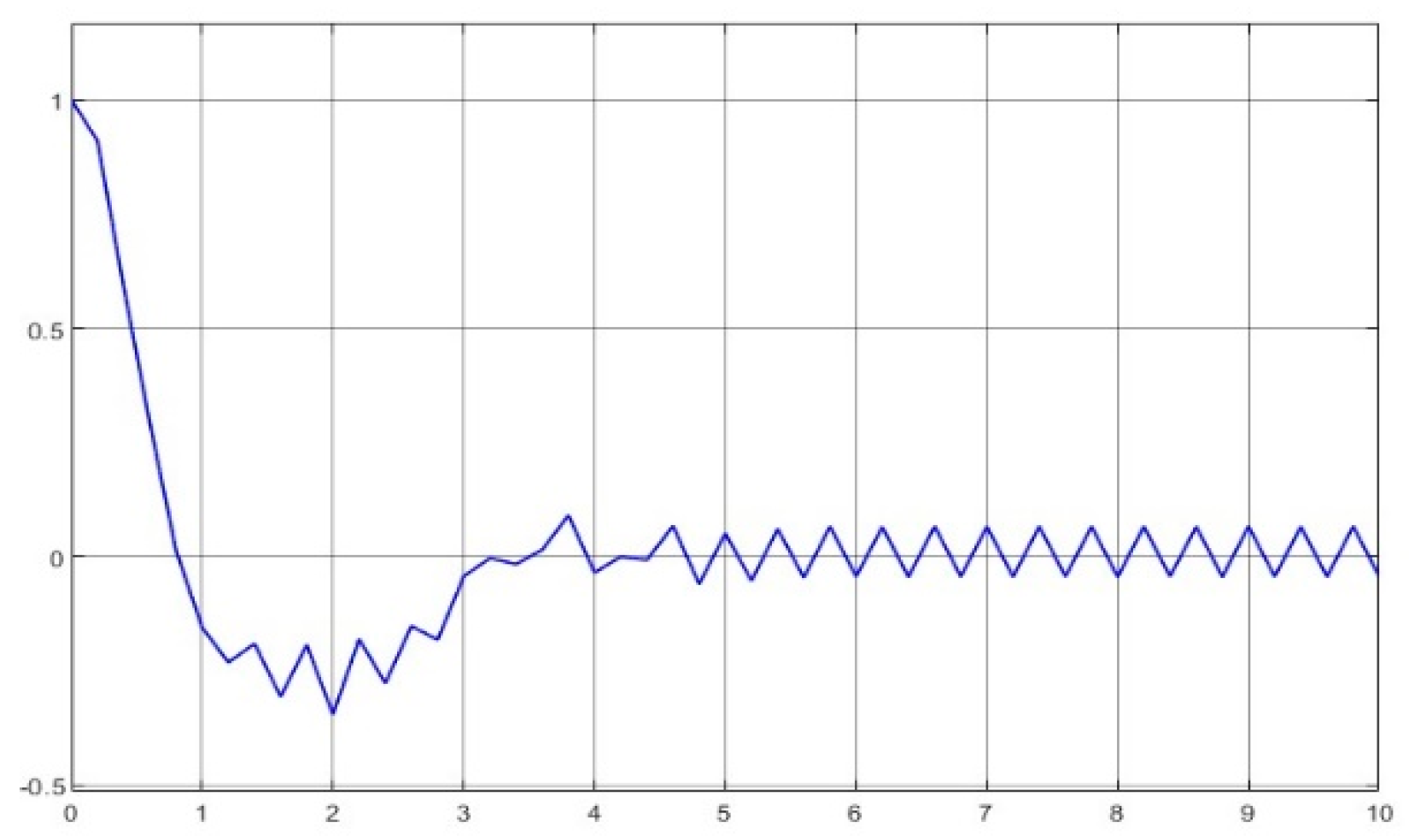
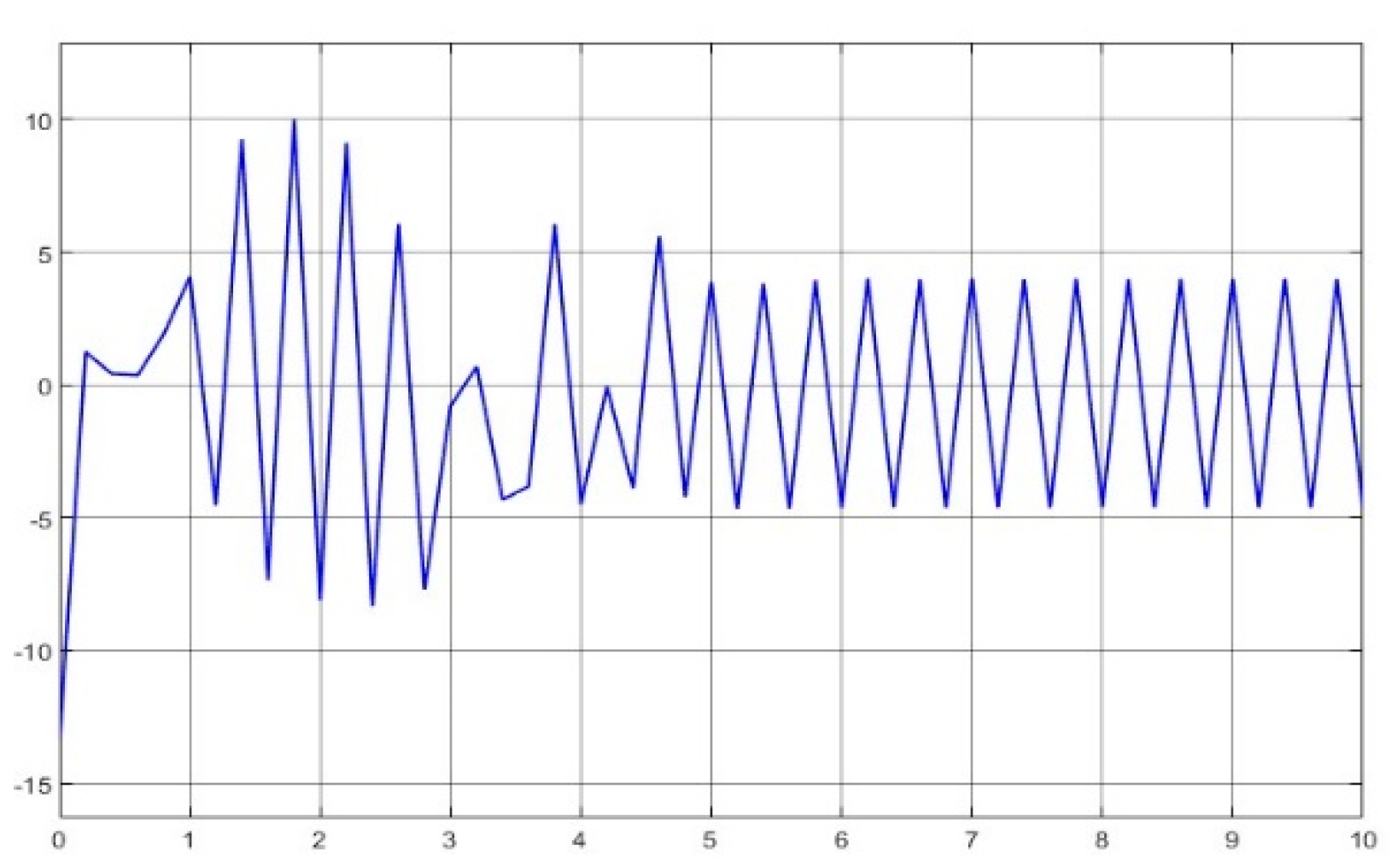
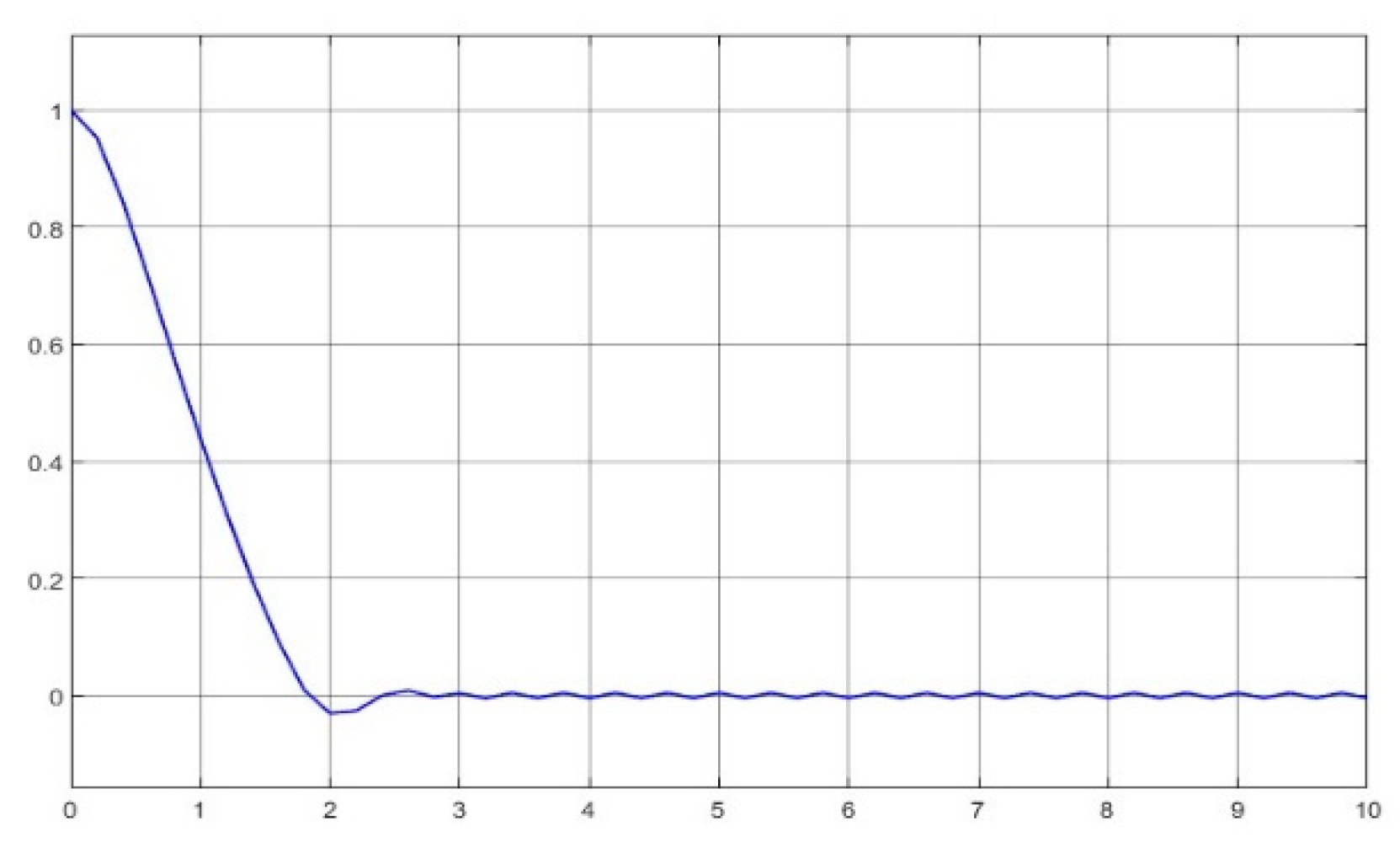
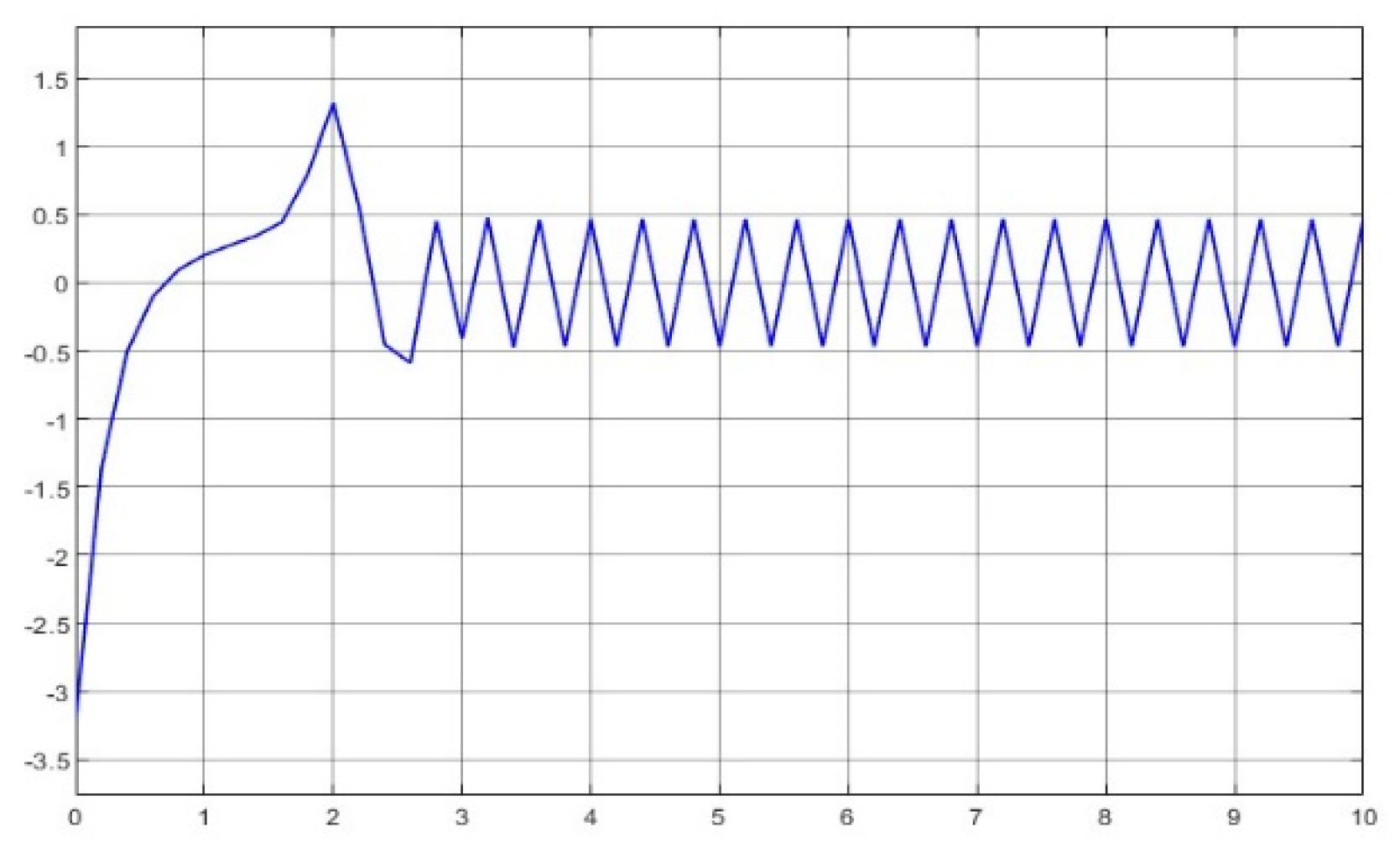
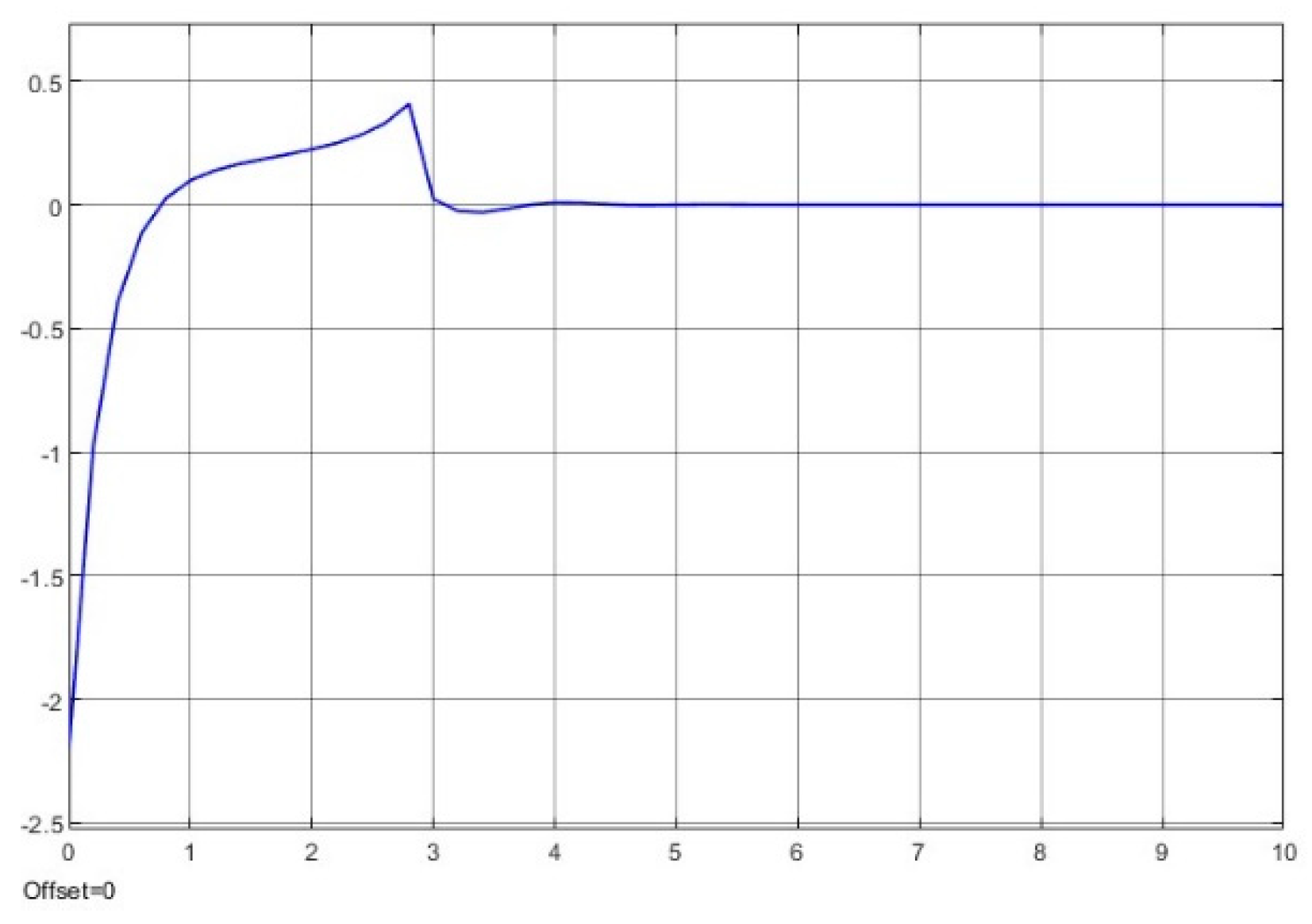
- The kernel idea (in terms of two dynamic inversions, MFSMC, SMPID, LESO, and the integration of the functionalities) of the U-control is demonstrated with the first two case study plots in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, which is consistent with the analytical results presented in the study.
- (2)
- The simulated plots in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 have shown that the designed control systems can effectively drive the system states asymptotically to achieve and keep in once driven in with the given simulation conditions.
- (3)
- Total robustness against model internal uncertainty: The control system is designed to take the plant model as a whole uncertainty. Let NM be the nominal model and UC for uncertainty. The two-pack plots confirm the analysis in Section 3 that the U-control deals with (total) uncertainty in design, compared with those nominal model-based designs dealing with uncertainty of .
- (4)
- External disturbance rejection: Inspection of Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, the constant disturbance () has been well suppressed, particularly in the plots show and in Figure 9, Figure 10, Figure 15, and Figure 16. It is noted that the estimated states from LESO have been used for the state feedback control design to deal with both uncertainty and disturbance, and jointly the inner loop (state feedback) and the external loop (output feedback) cope with the disturbance effectively. Accordingly, these efforts have achieved the desired responses.
- (5)
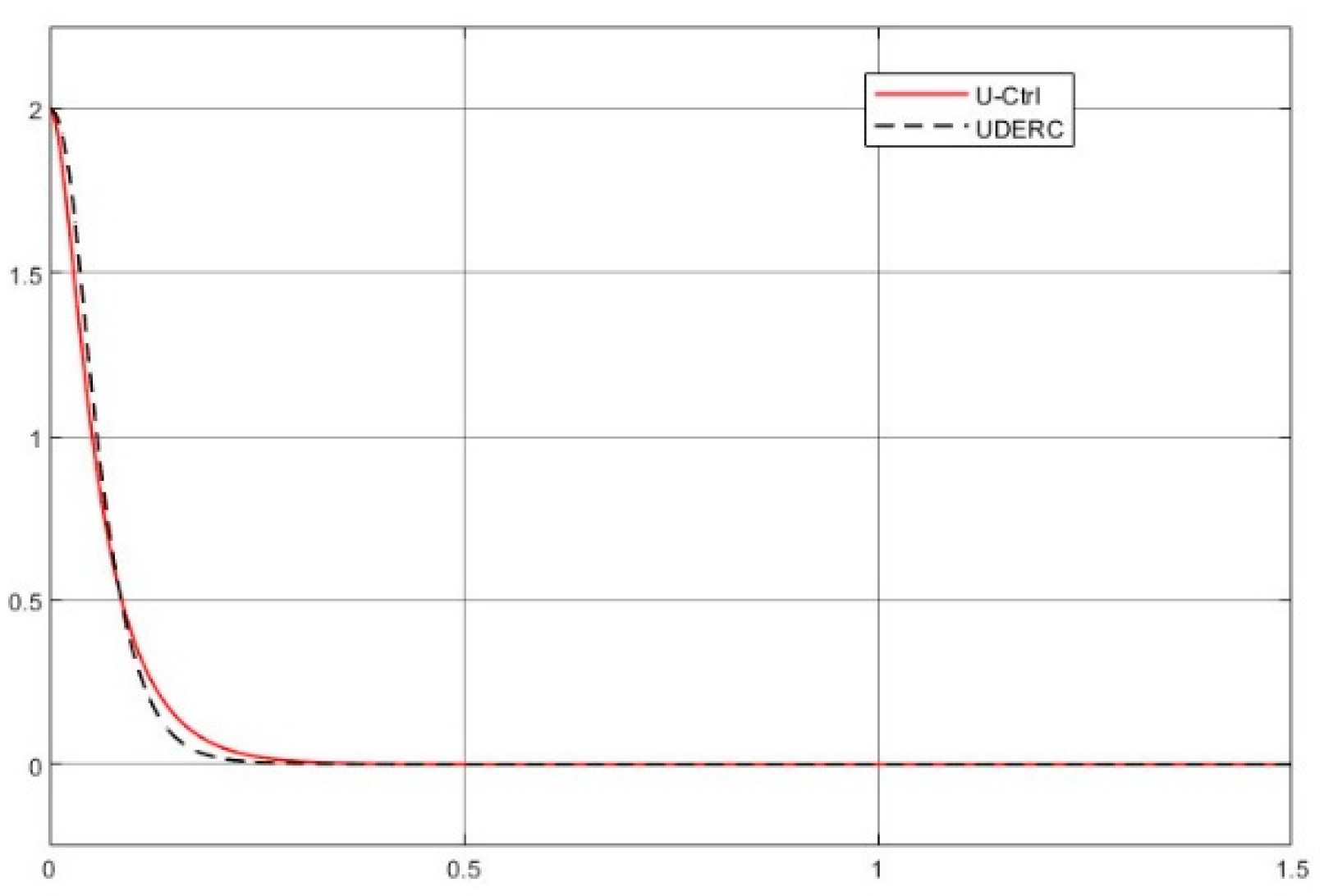
- Dealing with chattering effects at the controller output: As predicted, this performance in removing the chattering effect is mainly achieved by using asymptotically stable functions to drive the derivative of the sliding mode function once the sliding mode function enters the sliding mode band. Accordingly, the sliding mode boundary thickness can be assigned relatively wider without inducing steady state errors for levelled references. These are shown in Figure 6 and Figure 12. For model-based SMC, predominantly, it has been forced to determine the equivalent control while sliding mode functions enter the sliding mode band, where the jump/switching is the main cause of chattering with the conjunction of a narrow sliding mode band for accuracy.
- (6)
- (7)
- Tuning of the SMPID controller gains: The simulations have tested various selections of the gains to achieve similar performance, which indicate a large range of options, under the guarantee of Lyapunov stability, feasible to make the gain tuning procedure relaxed and robustness. This is because there are many solutions for the inequality .
- (8)
- Non-switching SMC alike: The plots, in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, generated from the second case study illustrate similar performance as those obtained from the first case studies. The nonlinear function achieves good performance in the regions outside/inside of the sliding mode band. The roles of the parameters with the nonlinear function have been tested in the simulation studies, the sign of the gain for convergent direction and the value for convergent speed. Similarly, the width can be used to adjust the sliding mode band thickness.
- (9)
- The contents presented analytically and validated computationally in the study have followed a route from complexity (problems) to simplicity (analysis and solutions). The derived and simulated results are consistent and basically feasible for those with reasonably good control system knowledge to use/expand for their ad hoc research and development. In some sense, this simulation study could be treated as a user manual.
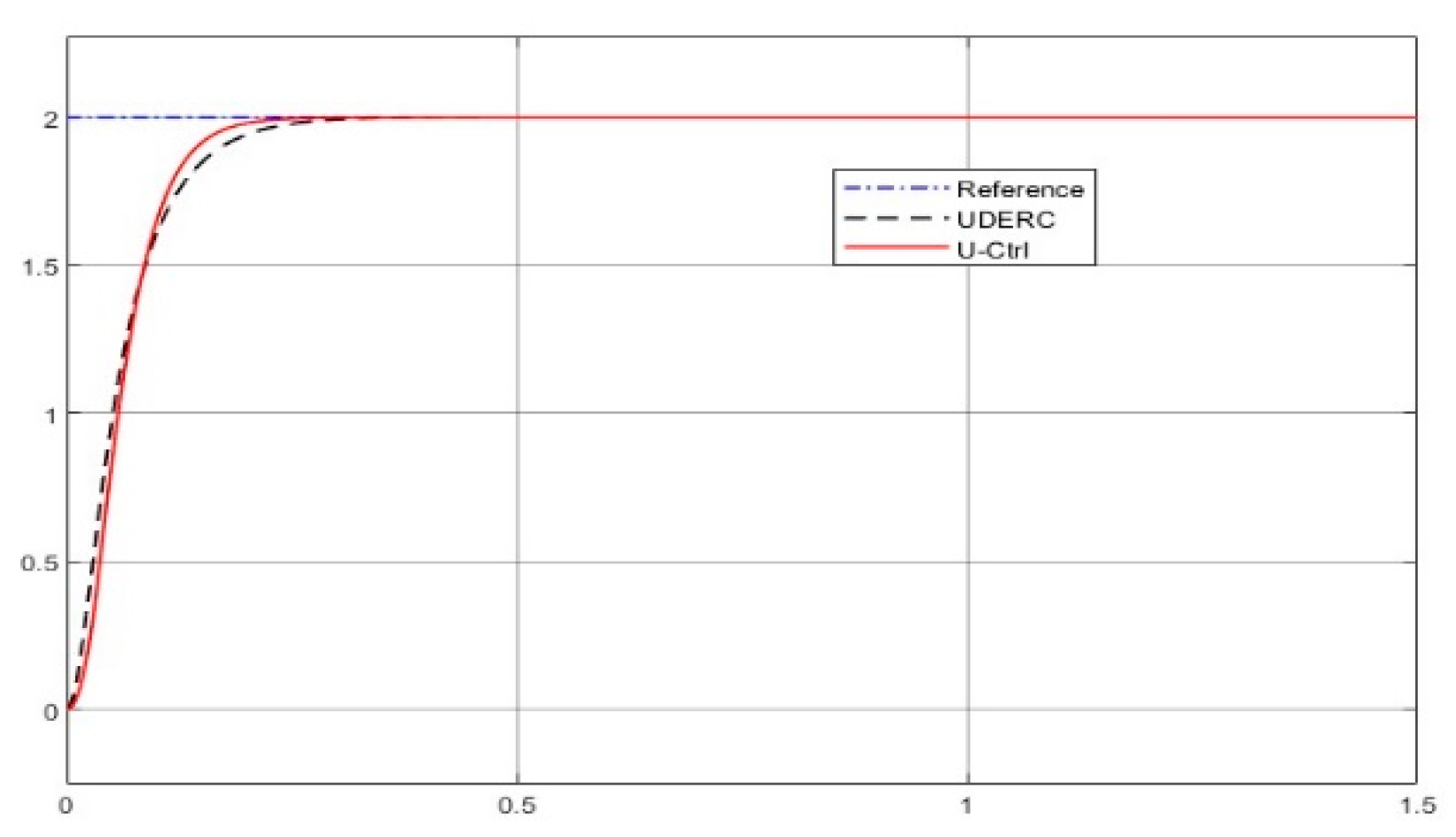
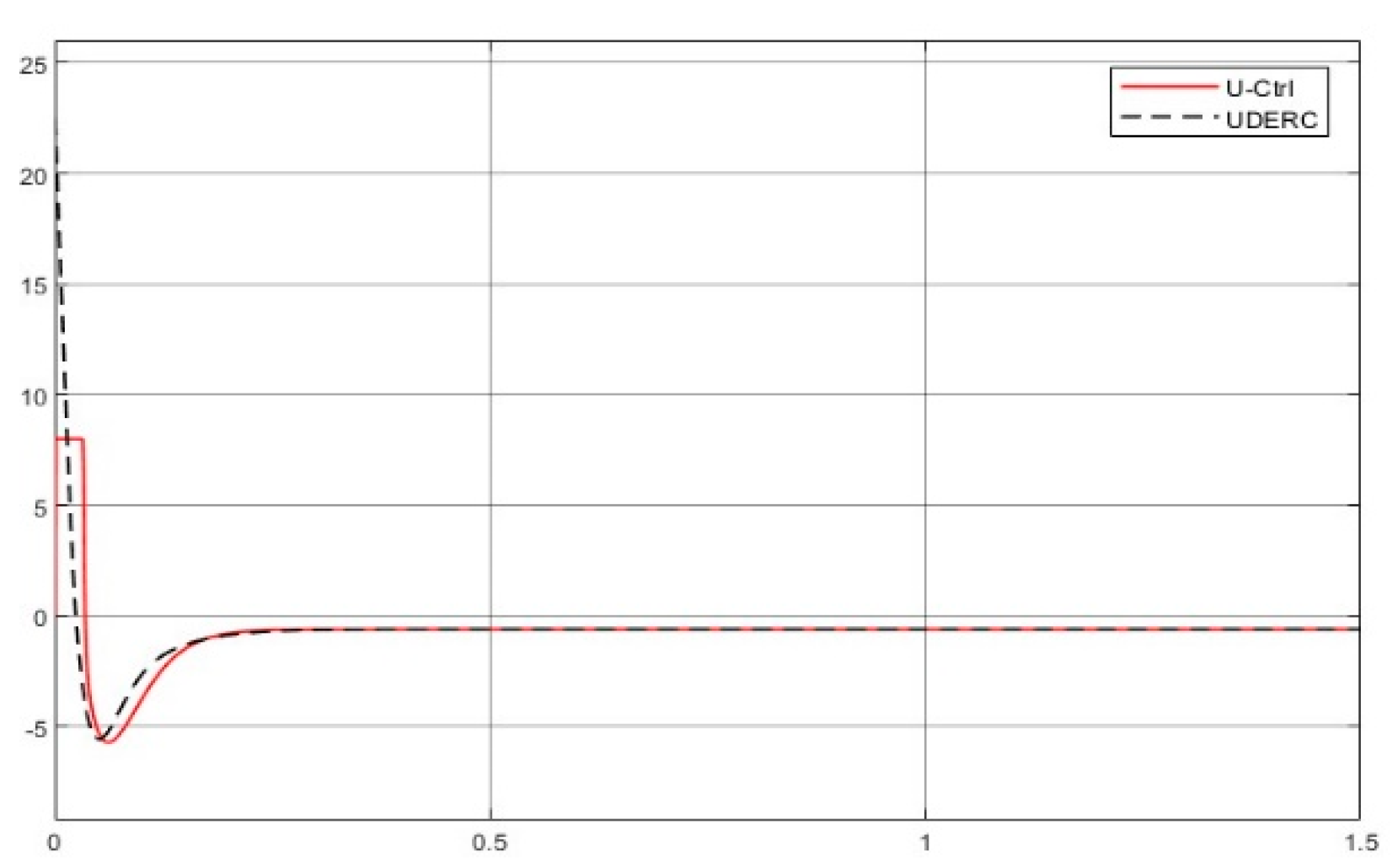
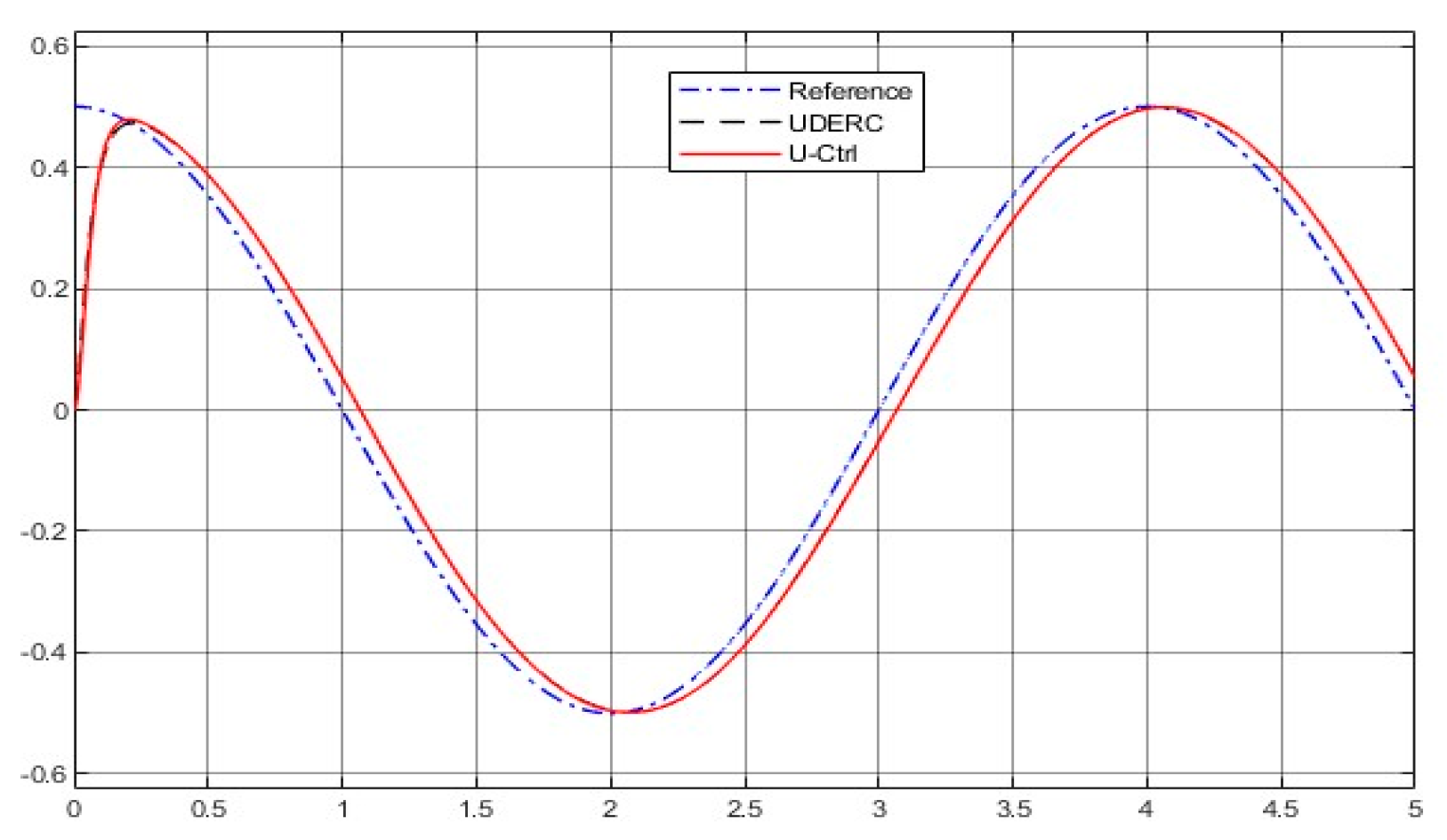
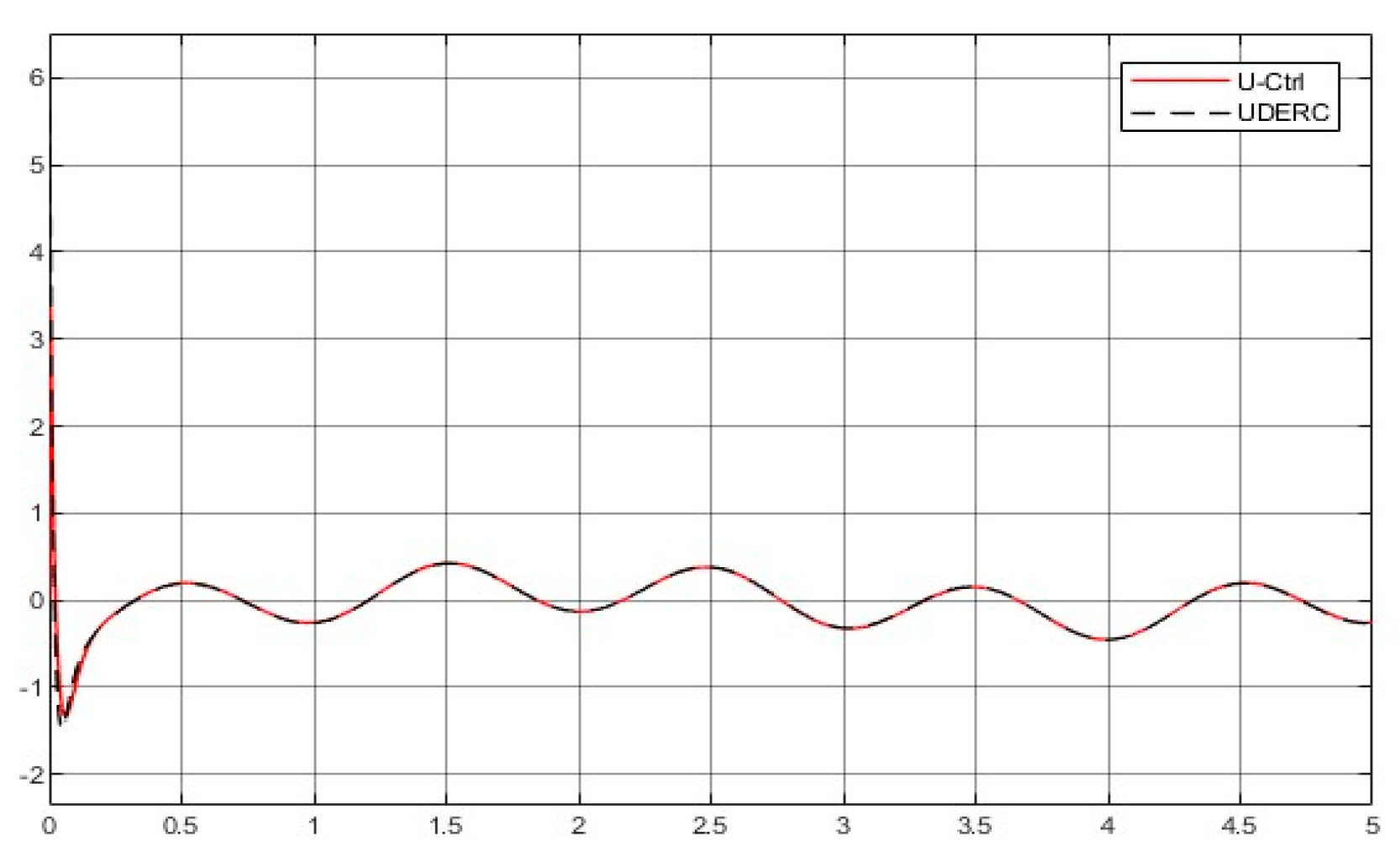
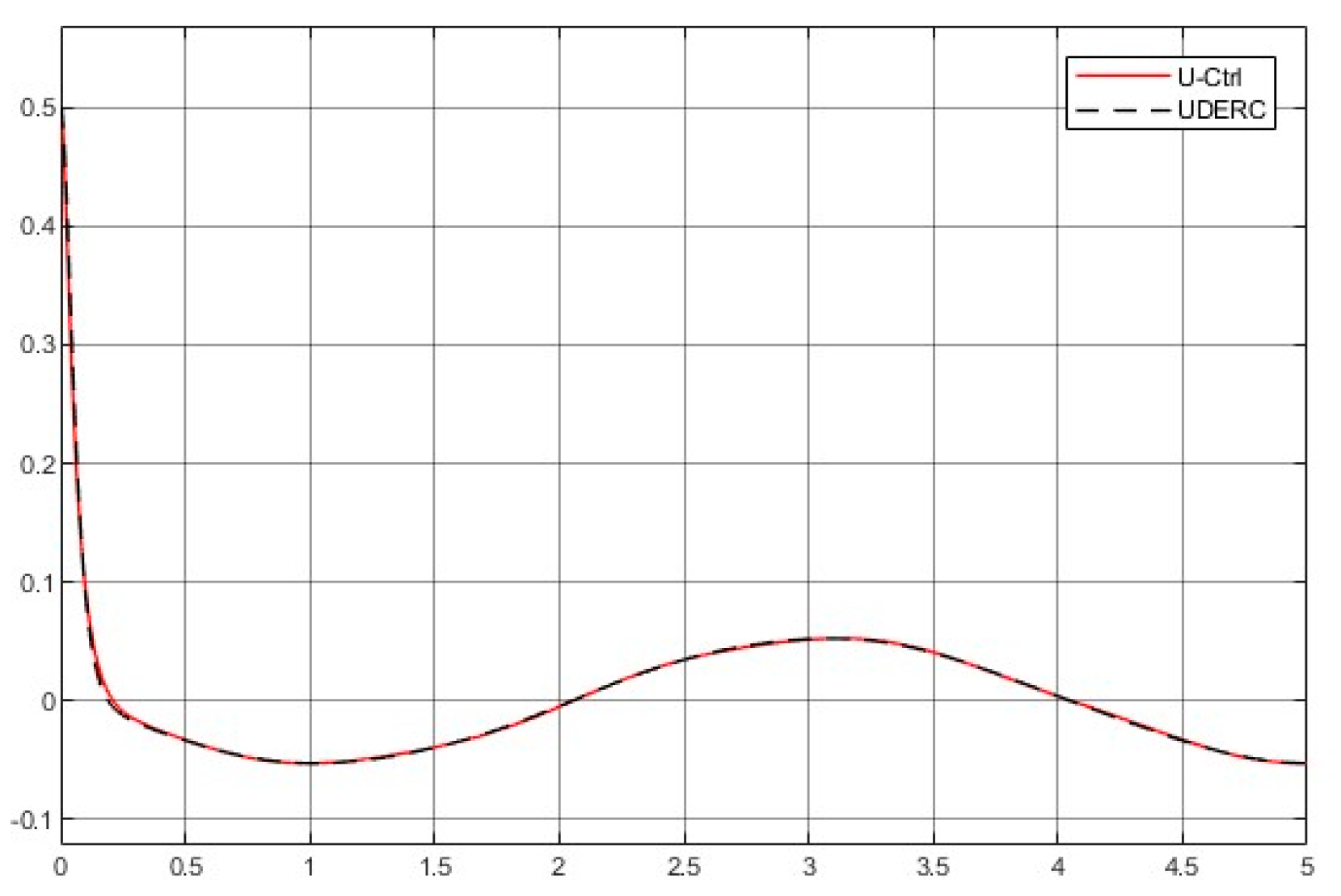
4.4.1. Comparative Demonstration (1)—Control of a Rotary Servo System
- Comparison of the simulated plots
- (1)
- (2)
- Regarding design procedure, the UDERC requests three designs: plant dynamic inversion, desired performance implementation, and uncertainty estimation/rejection. The U-control takes two dynamic inversions and is repetitively used for both case studies. Basically, the UDERC is model-based design, and the U-control is model-free design without traditional iterative learning routines.
- (3)
- Knowledge request of uncertainties and disturbances, the UDERC needs a filter to estimate the uncertainty, and the U-control only needs the assumption that the unknown bound exists.
4.4.2. Comparative Demonstration (2)—Two Types of SMPIDs for Finite Time Control
- (1)
- PID-CSMC [25]
- (2)
- SMP and SMPI presented in this study in terms of
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Ang, K.H.; Chong, G.C.Y. Patents, software, and hardware for PID control: An overview and analysis of the current art. IEEE Control Syst. Mag. 2006, 26, 42–54. [Google Scholar]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Powar, S.N. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2020. [Google Scholar]
- Zhao, C.; Guo, L. Towards a theoretical foundation of PID control for uncertain nonlinear systems. Automatica 2022, 142, 110360. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control and intelligent PID controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. 2009, 42, 1531–1550. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Atherton, D.P.; Benouartes, M.; Nanka-Bruce, O. Design of nonlinear PID controllers for nonlinear plants. IFAC Proc. 1993, 26, 125–128. [Google Scholar] [CrossRef]
- Tian, Y.C.; Tadé, M.O.; Tang, J.Y. A nonlinear PID controller with applications. IFAC Proc. 1999, 32, 2657–2661. [Google Scholar] [CrossRef]
- Astrom, K.J.; Wittenmark, B. Adaptive Control, 2nd ed.; Addison Wesley: Reading, PA, USA, 1995. [Google Scholar]
- Sifuentes-Mijares, J.; Santibáñez, V.; Meza-Medina, J.L. Nonlinear PID global regulators with selftuned PD gains for robot manipulators: Theory and experimentation. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 223. [Google Scholar] [CrossRef]
- Shu, H.; Pi, Y.G. PID neural networks for time-delay systems. Comput. Chem. Eng. 2000, 24, 859–862. [Google Scholar] [CrossRef]
- Yesil, E.; Guzelkaya, M.; Eksin, I. Fuzzy PID controllers: An overview. In Proceedings of the 3rd Triennial ETAI International Conference on Applied Automatic Systems, Ohrid, Macedonia, September 2003. [Google Scholar]
- Carvajal, J.; Chen, G.R.; Ogmen, H. Fuzzy PID controller: Design, performance evaluation, and stability analysis. Inf. Sci. 2000, 123, 249–270. [Google Scholar] [CrossRef]
- Gani, M.M.; Islam, M.S.; Ullah, M.A. Optimal PID tuning for controlling the temperature of electric furnace by genetic algorithm. SN Appl. Sci. 2019, 1, 880. [Google Scholar] [CrossRef]
- Kristiansson, B.; Lennartson, B. Robust and optimal tuning of PI and PID controllers. IEEE Proc. Contr. Theory Appl. 2002, 149, 17–25. [Google Scholar] [CrossRef]
- Killingsworth, N.; Krstic, M. PID tuning using extremum seeking - Online, model-free performance optimization. IEEE Control Syst. Mag. 2006, 26, 70–79. [Google Scholar] [CrossRef]
- Khan, A.T.; Li, S.A.; Stanimirovic, P.S.; Zhang, Y.Y. Model-free optimization using eagle perching optimizer. arXiv 2018, arXiv:1807.02754. [Google Scholar] [CrossRef]
- Marino, A.; Neri, F. PID Tuning with Neural Networks. In Intelligent Information and Database Systems; ACIIDS: Phuket, Thailand, 2019; pp. 476–487. [Google Scholar] [CrossRef]
- MathWorks. How PID Autotuning Works. Available online: https://uk.mathworks.com/help/slcontrol/ug/how-pid-autotuning-works.html (accessed on 2 October 2022).
- Li, R.H.; Li, T.S.; Bu, R.X.; Zheng, Q.L.; Chen, C.L.P. Active disturbance rejection with sliding mode control based course and path following for underactuated ships. Math. Probl. Eng. 2013, 2013, 743716. [Google Scholar] [CrossRef]
- Eker, I. Sliding mode control with PID sliding surface and experimental application to an electromechanical plant. ISA Trans. 2006, 45, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.M.; Xu, Q.S. Adaptive sliding mode control with perturbation estimation and pid sliding surface for motion tracking of a piezo-driven micromanipulator. IEEE Trans. Control Syst. Technol. 2010, 18, 798–810. [Google Scholar] [CrossRef]
- Moreno-Gonzalez, M.; Artuñedo, A.; Villagra, J.; Join, C.; Fliess, M. Speed-Adaptive Model-Free Lateral Control for Automated Cars. IFAC-PapersOnLine 2022, 55, 84–89. [Google Scholar] [CrossRef]
- Khan, A.H.; Li, S. Sliding mode control with PID sliding surface for active vibration damping of pneumatically actuated soft robots. IEEE Access 2020, 8, 88793–88800. [Google Scholar] [CrossRef]
- Pérez-Ventura, U.; Mendoza-Avila, J.; Fridman, L. Design of a proportional integral derivative-like continuous sliding mode controller. Int. J. Robust Nonlinear Control 2021, 31, 3439–3454. [Google Scholar] [CrossRef]
- Mendoza-Avila, J.; Moreno, J.A.; Fridman, L. Continuous twisting algorithm for third order systems. IEEE Trans. Autom. Control 2020, 65, 2814–2825. [Google Scholar] [CrossRef]
- Zhu, Q.M. Complete model-free sliding mode control (CMFSMC). Sci. Rep. 2021, 11, 22565. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.M.; Mobayen, S.; Nemati, H.; Zhang, J.H.; Wei, W. A new configuration of composite nonlinear feedback control for nonlinear systems with input saturation. J. Vib. Control 2023, 29, 1143–1417. [Google Scholar] [CrossRef]
- Zhu, Q.M.; Guo, L. A pole placement controller for non-linear dynamic plants. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2002, 216, 467–476. [Google Scholar] [CrossRef]
- Zhang, W.C.; Zhu, Q.M.; Mobayen, S.; Yan, H.; Qiu, J.; Narayan, P. U-Model and U-control methodology for nonlinear dynamic systems. Complexity 2020, 2020, 1050254. [Google Scholar] [CrossRef]
- Li, R.; Zhu, Q.M.; Kiely, J.; Zhang, W.C. Algorithms for U-model-based dynamic inversion (UM-dynamic inversion) for continuous time control systems. Complexity 2020, 2020, 3640210. [Google Scholar] [CrossRef]
- Hussain, N.A.A.; Ali, S.S.A.; Ovinis, M.; Arshad, M.; Al-saggaf, U.M. Underactuated coupled nonlinear adaptive control synthesis using U-model for multivariable unmanned marine robotics. IEEE Access 2020, 8, 1851–1965. [Google Scholar] [CrossRef]
- Wei, W.; Duan, B.W.; Zuo, M.; Zhu, Q.M. An extended state observer based U-model control of the COVID-19. ISA Trans. 2021, 124, 115–123. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Huang, H.-P.; Roan, M.-L.; Jeng, J.-C. On-line adaptive tuning for PID controllers. IEE Proc. Contr. Theory Appl. 2002, 149, 60–67. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W.P. Applied Nonlinear Control; Prentice Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Yang, I.; Lee, D.; Han, D.S. Designing a robust nonlinear dynamic inversion controller for spacecraft formation flying. Math. Probl. Eng. 2014, 2014, 471352. [Google Scholar] [CrossRef]
- Yan, X.G.; Spurgeon, S.K.; Edwards, C. Variable structure control of complex systems. In Communications and Control Engineering; Springer: London, UK, 2017. [Google Scholar]
- Kang, W.; Krener, A.J.; Xiao, M.Q.; Xu, L. A Survey of Observers for Nonlinear Dynamical Systems. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S., Xu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume II. [Google Scholar] [CrossRef]
- Radke, A.; Gao, Z.Q. A survey of state and disturbance observers for practitioners. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar] [CrossRef]
- Wikipedia. Sigmoid Function. Available online: https://en.wikipedia.org/wiki/Sigmoid_function (accessed on 19 September 2022).
- Ren, B.; Zhong, Q.C.; Chen, J. Robust control for a class of nonaffine nonlinear systems based on the uncertainty and disturbance estimator. IEEE Trans. Ind. Electron. 2015, 62, 5881–5888. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q. Model-Free Sliding Mode Enhanced Proportional, Integral, and Derivative (SMPID) Control. Axioms 2023, 12, 721. https://doi.org/10.3390/axioms12080721
Zhu Q. Model-Free Sliding Mode Enhanced Proportional, Integral, and Derivative (SMPID) Control. Axioms. 2023; 12(8):721. https://doi.org/10.3390/axioms12080721
Chicago/Turabian StyleZhu, Quanmin. 2023. "Model-Free Sliding Mode Enhanced Proportional, Integral, and Derivative (SMPID) Control" Axioms 12, no. 8: 721. https://doi.org/10.3390/axioms12080721
APA StyleZhu, Q. (2023). Model-Free Sliding Mode Enhanced Proportional, Integral, and Derivative (SMPID) Control. Axioms, 12(8), 721. https://doi.org/10.3390/axioms12080721





