The Investigation of Dynamical Behavior of Benjamin–Bona–Mahony–Burger Equation with Different Differential Operators Using Two Analytical Approaches
Abstract
1. Introduction
2. Preliminaries
2.1. -Derivative and Its Properties
- The -derivative is a linear operator; , .
- It satisfies the product rule; .
- It satisfies the quotient rule; .
- The -derivative of a constant is zero; ,for any constant c.
2.2. M-Truncated Derivative and Its Properties
- The M-TD is a linear operator; ,.
- It satisfies the product rule; .
- It satisfies the quotient rule; .
- The M-TD for a differentiable function is defined, as:
2.3. Conformable Derivative
3. Mathematical Interpretation of the Proposed Model
4. Application of RB Sub-ODE Method
5. Utilizing the MAEM
- If , then, or
- If , then, or
- If , then, .
- For , the trigonometric solutions are found.or
- For , the hyperbolic solutions are obtained.or
- For , the following trigonometric solutions resulted.or
- For , the following hyperbolic solutions are found.or
- For , the trigonometric solutions are found.or
- For , the following hyperbolic solutions are obtained.or
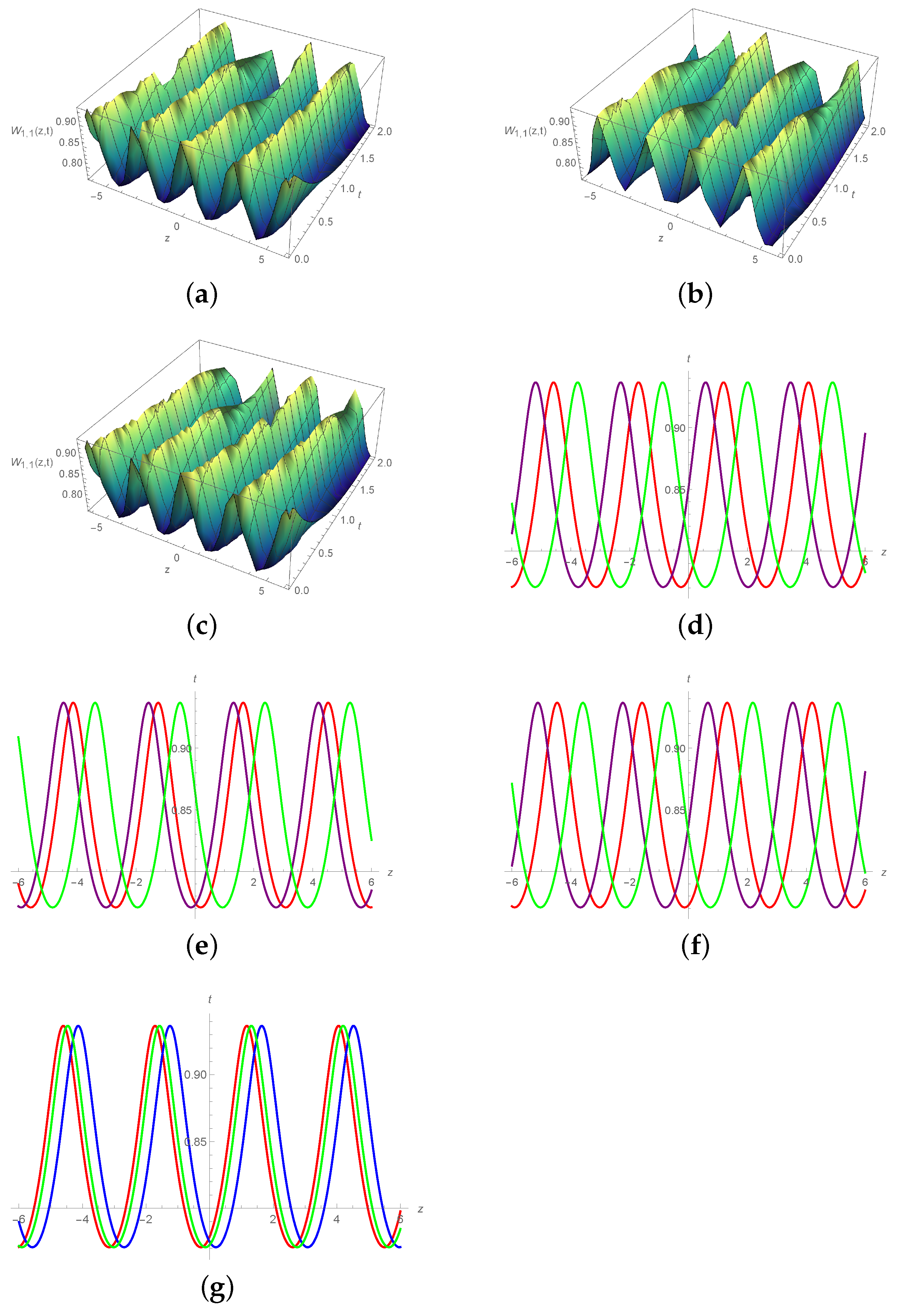
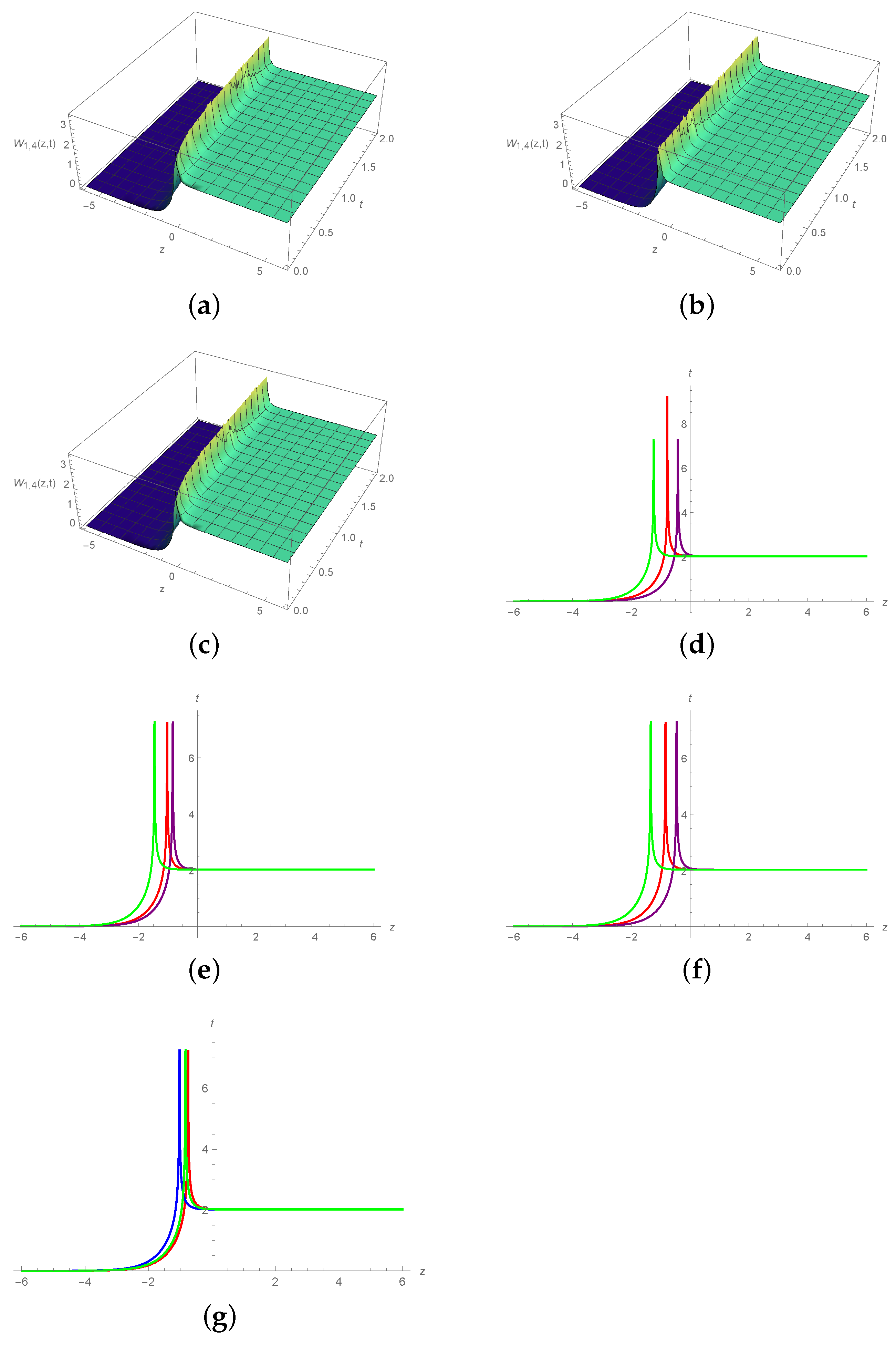
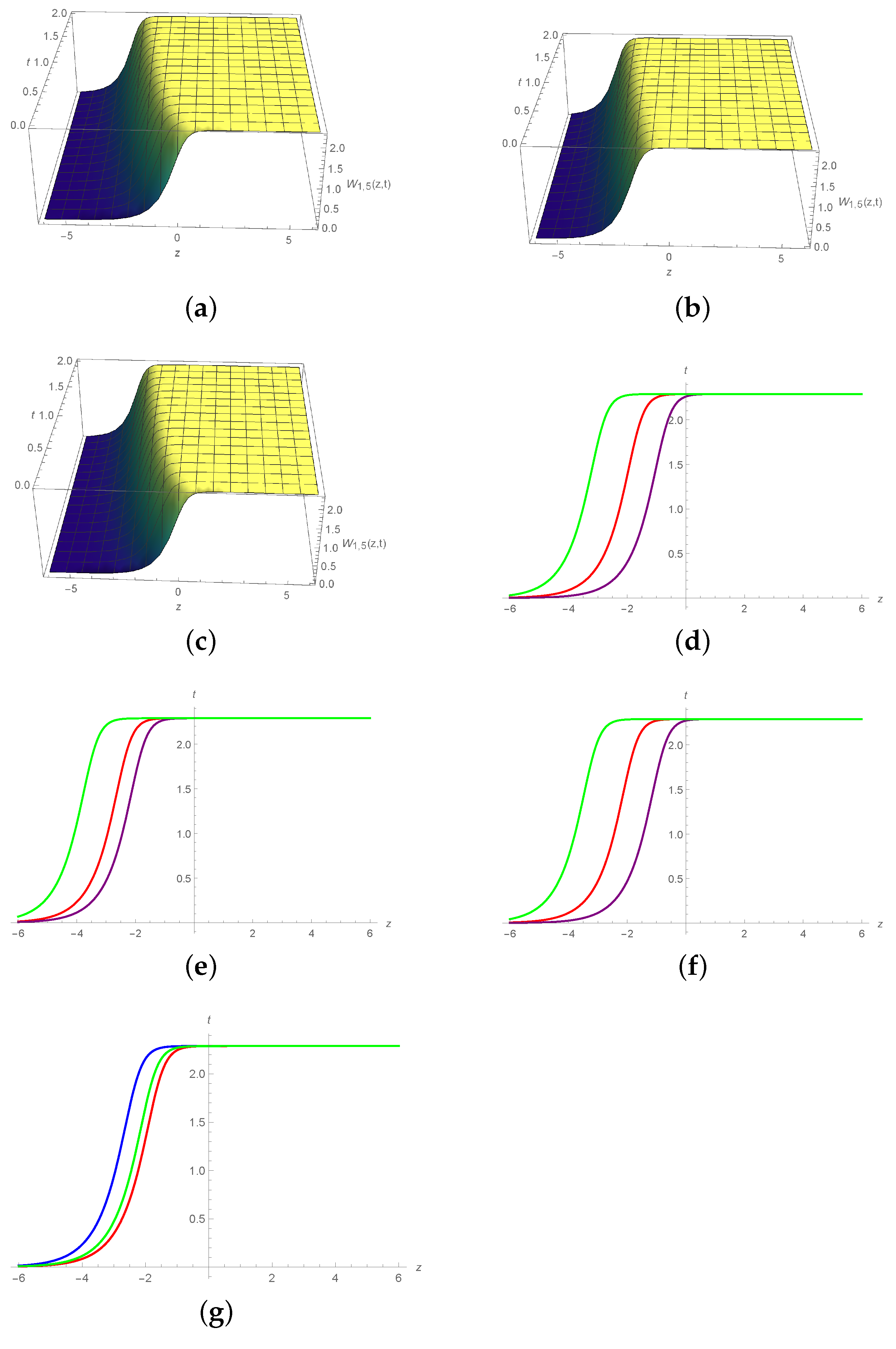
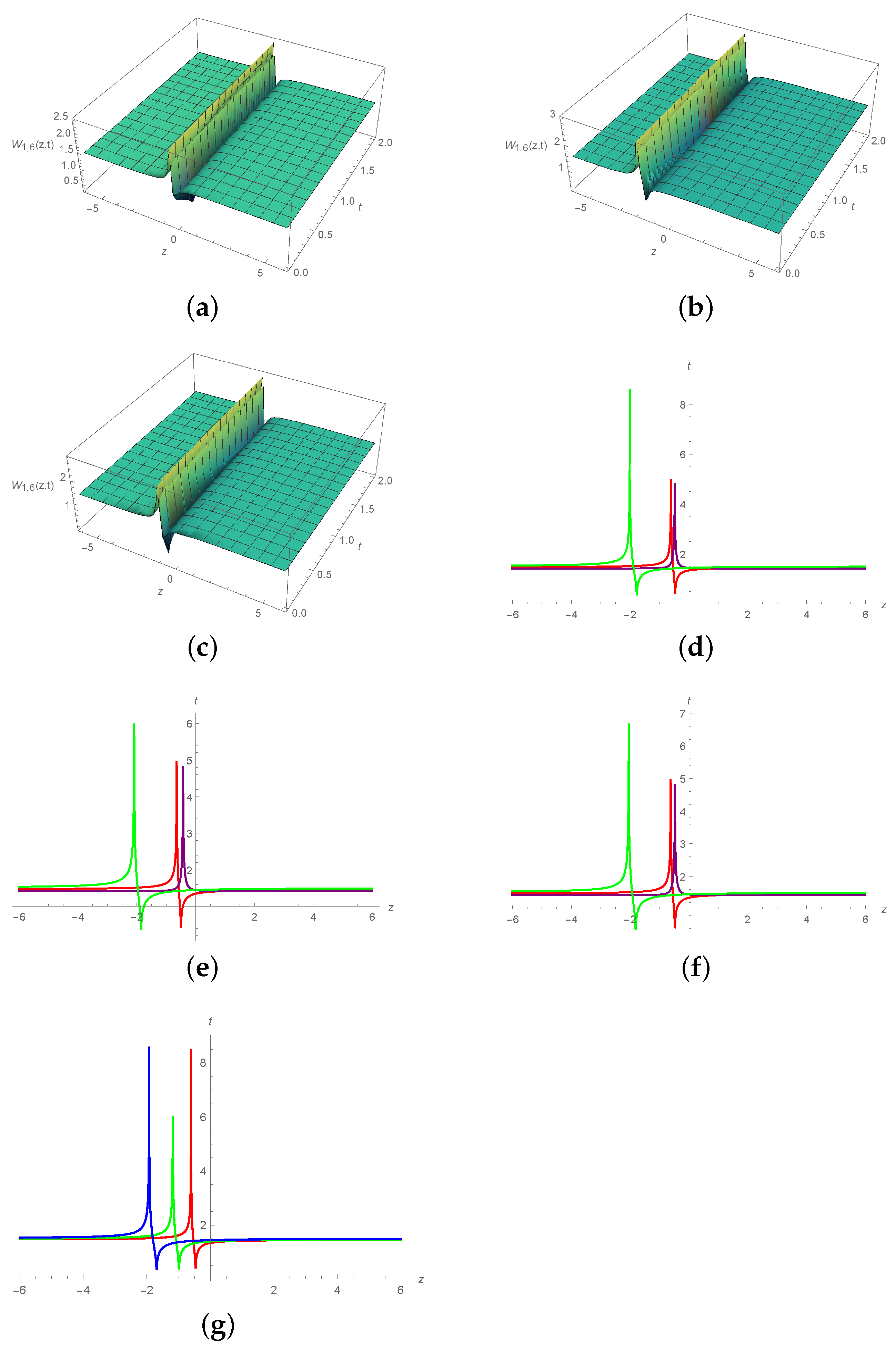
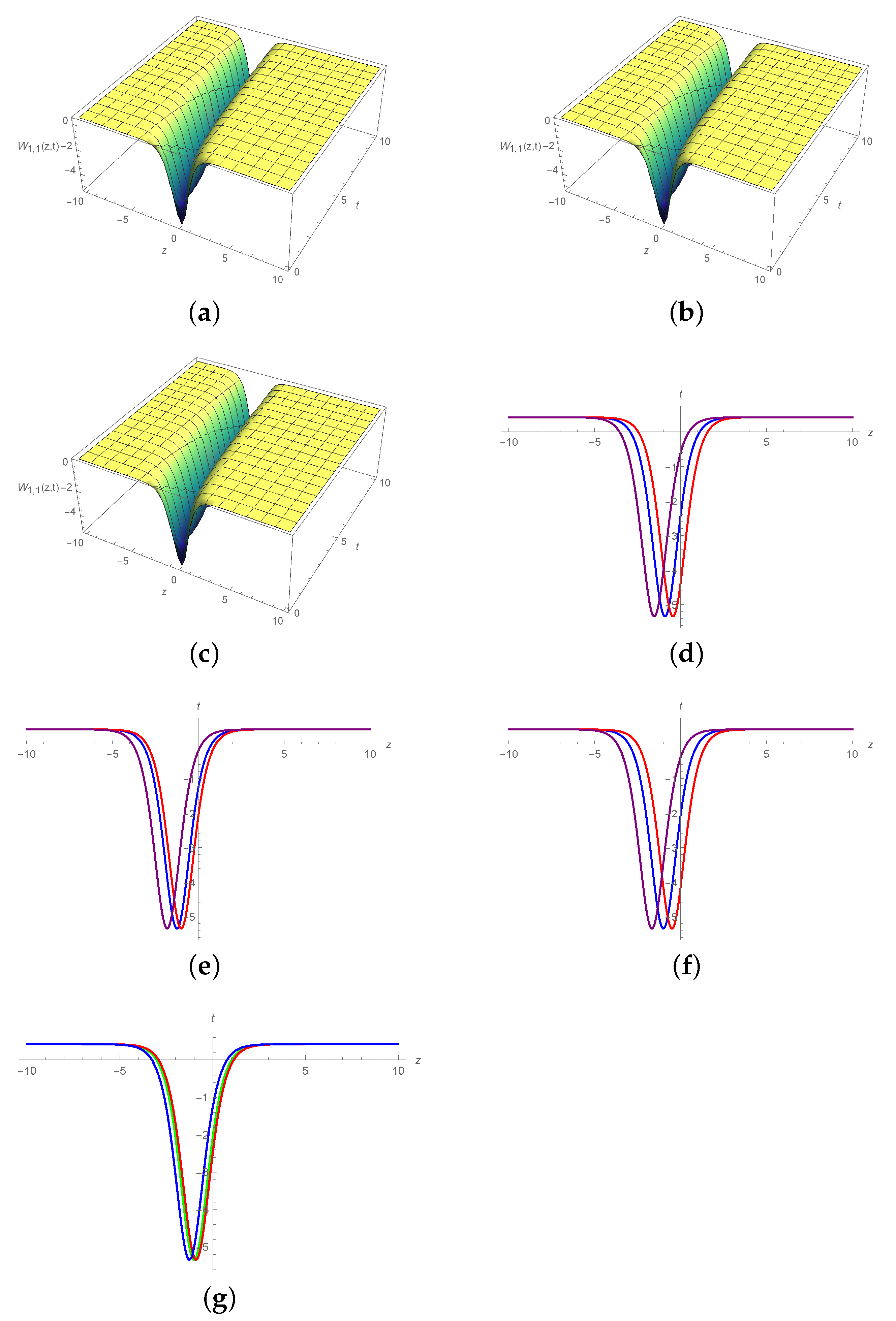
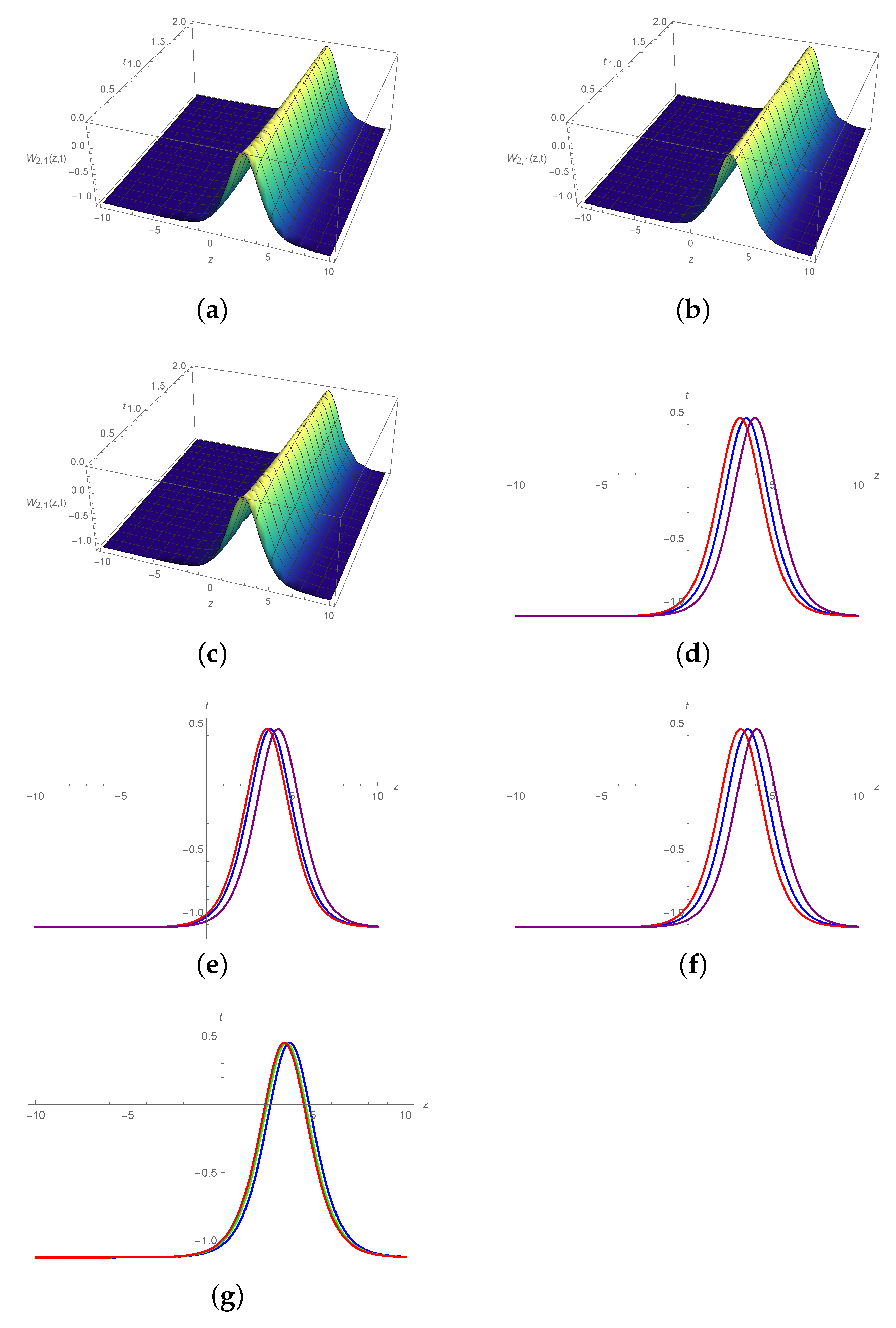
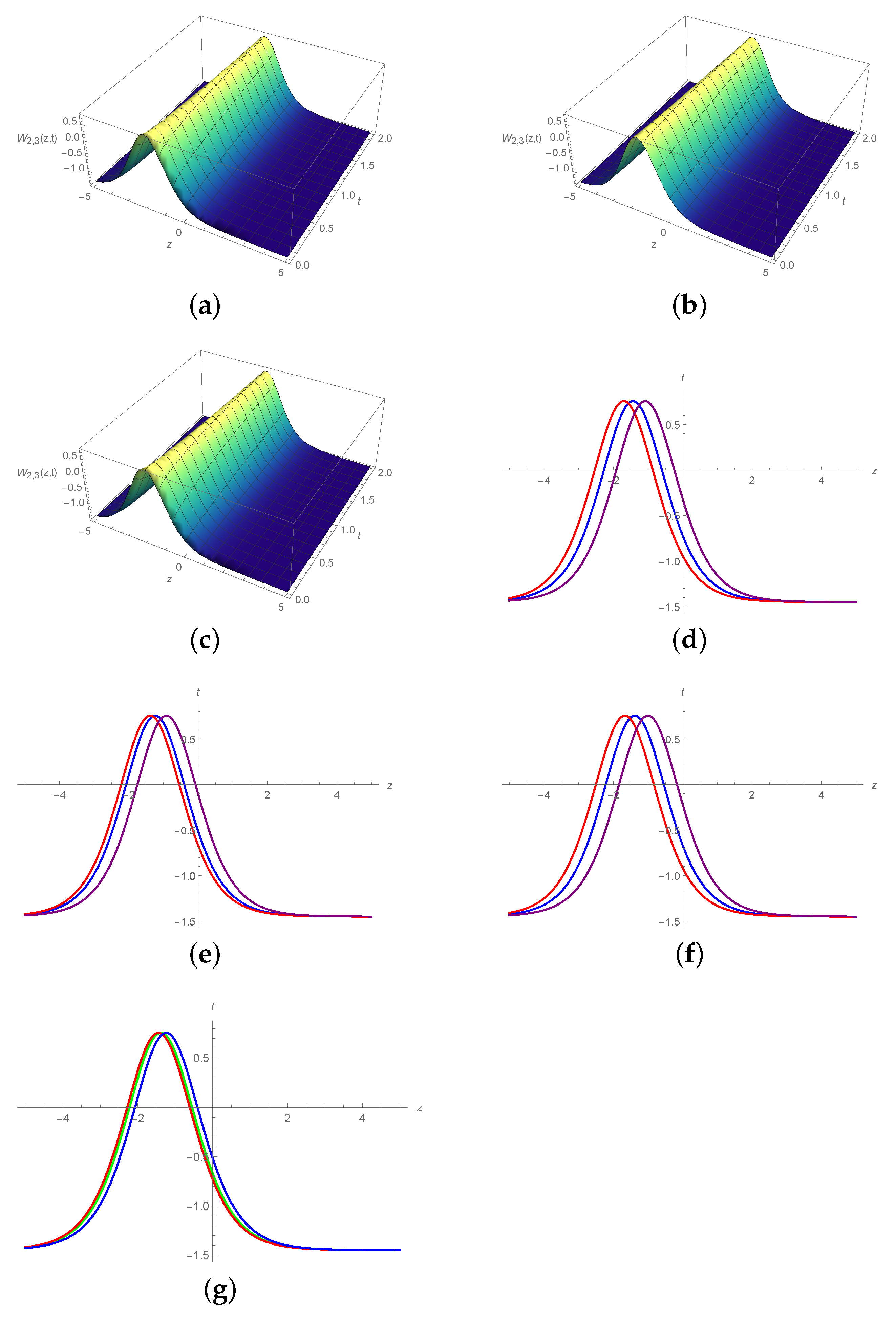
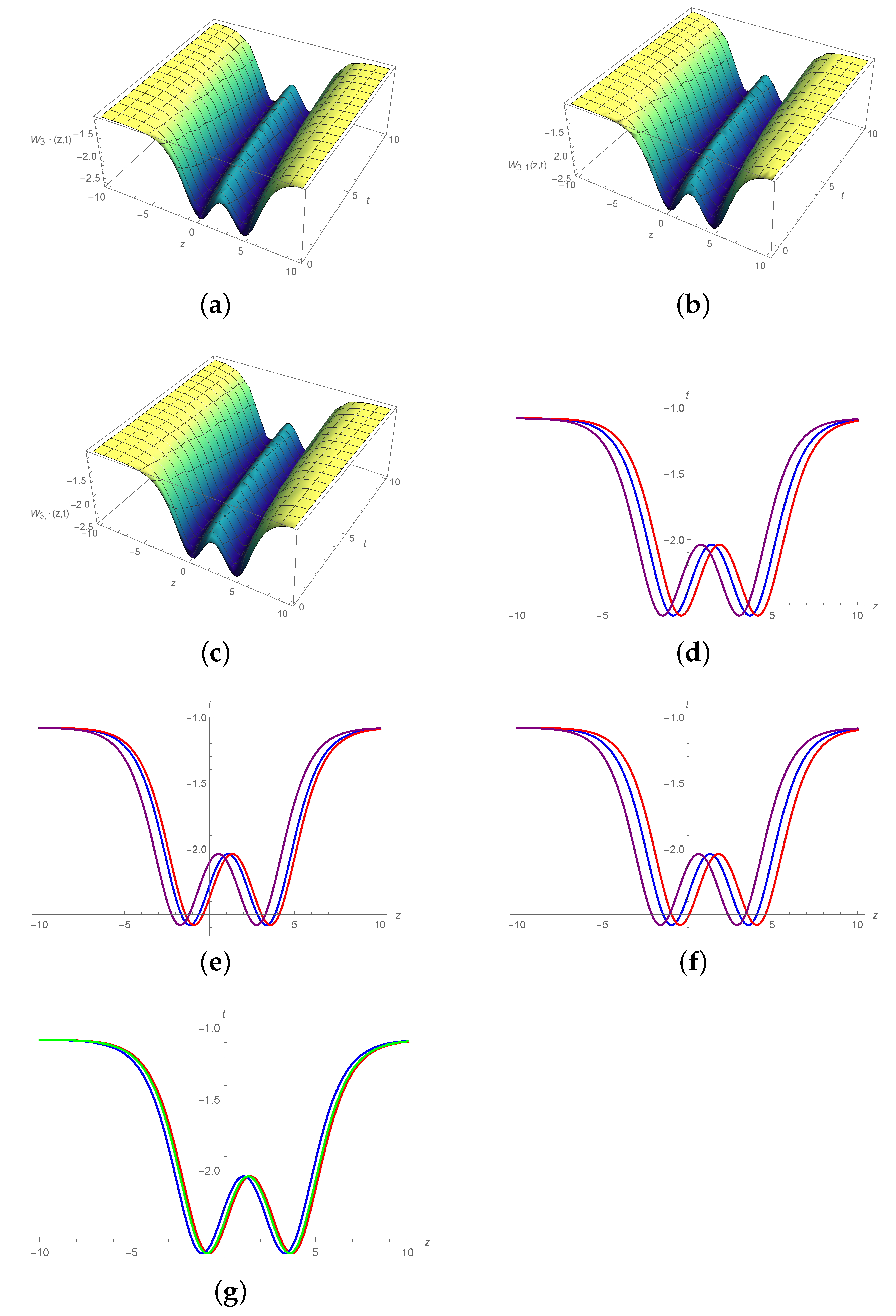
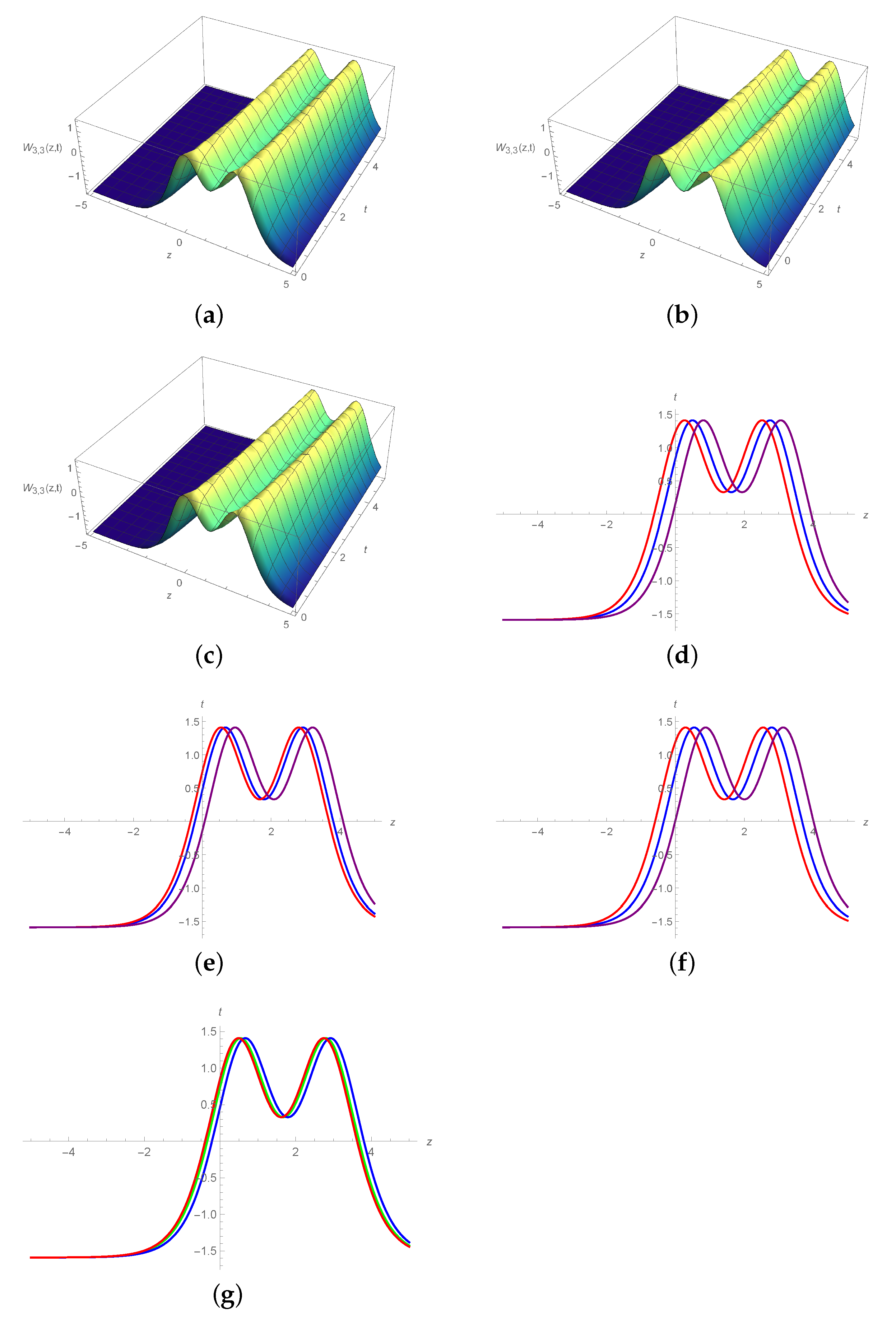
6. Graphical Illustration
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BBM-Burger | Benjamin–Bona–Mahony–Burger |
| MAEM | Modified auxiliary equation method |
| RB | Ricatti–Bernoulli |
| CD | Conformable derivative |
| M-TD | M-truncated derivatives |
| DEs | Differential equations |
| NLPDEs | Nonlinear partial differential equations |
| FDEs | Fractional differential equations |
| FC | Fractional calculus |
| FDs | Fractional derivatives |
| -derivative | Beta-derivative |
| JEFM | Jacobi elliptic function method |
References
- Ablowitz, M.J.; Ramani, A.; Segur, H. Nonlinear evolution equations and ordinary differential equations of Painleve’type. Lett. Nuovo Cim. 1978, 23, 333–338. [Google Scholar] [CrossRef]
- Renardy, M.; Rogers, R.C. An Introduction to Partial Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 13. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1998; p. 198. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Singh, J.; Kumar, D.; Al Qurashi, M.; Baleanu, D. A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017, 2017, 88. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Caputo, M.; Fabricio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2019, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel. Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Almeida, R. Caputo–Hadamard fractional derivatives of variable order. Numer. Funct. Anal. Optim. 2017, 38, 1–19. [Google Scholar] [CrossRef]
- Anderson, D.R.; Ulness, D.J. Properties of the Katugampola fractional derivative with potential application in quantum mechanics. J. Math. Phys. 2015, 56, 063502. [Google Scholar] [CrossRef]
- Amado Mendez Cruz, G.; Torres Ledesma, C.E. Multiplicity of solutions for fractional Hamiltonian systems with Liouville-Weyl fractional derivatives. Fract. Calc. Appl. Anal. 2015, 18, 875–890. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Hanna, L.M.; Luchko, Y.F. Operational calculus for the Caputo-type fractional Erdélyi–Kober derivative and its applications. Integral Transform. Spec. Funct. 2014, 25, 359–373. [Google Scholar] [CrossRef]
- Huang, F.; Liu, F. The space-time fractional diffusion equation with Caputo derivatives. J. Appl. Math. Comput. 2005, 19, 179–190. [Google Scholar] [CrossRef]
- Kumar, V.; Gupta, R.K.; Jiwari, R. Painlevé analysis, Lie symmetries and exact solutions for variable coefficients Benjamin-Bona-Mahony-Burger (BBMB) equation. Commun. Theor. Phys. 2013, 60, 175. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg—de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192. [Google Scholar] [CrossRef]
- Jena, S.R.; Senapati, A. On numerical soliton and convergence analysis of Benjamin-Bona-Mahony-Burger equation via octic B-spline collocation. Arab. J. Basic Appl. Sci. 2023, 30, 146–163. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Baleanu, D.; Ebaid, A. Physical properties of the projectile motion using the conformable derivative. Chin. J. Phys. 2019, 58, 18–28. [Google Scholar] [CrossRef]
- Wang, X.; Ehsan, H.; Abbas, M.; Akram, G.; Sadaf, M.; Abdeljawad, T. Analytical solitary wave solutions of a time-fractional thin-film ferroelectric material equation involving beta-derivative using modified auxiliary equation method. Results Phys. 2023, 48, 106411. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; Aly, E.S. The Soliton Solutions of the Stochastic Shallow Water Wave Equations in the Sense of Beta-Derivative. Mathematics 2023, 11, 1338. [Google Scholar] [CrossRef]
- Martínez, F.; Martínez, I.; Kaabar, M.K.; Paredes, S. Generalized conformable mean value theorems with applications to multivariable calculus. J. Math. 2021, 2021, 5528537. [Google Scholar] [CrossRef]
- Hussain, A.; Jhangeer, A.; Abbas, N.; Khan, I.; Sherif, E.S.M. Optical solitons of fractional complex Ginzburg-Landau equation with conformable, beta, and M-truncated derivatives: A comparative study. Adv. Differ. Equ. 2020, 2020, 612. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M. Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics 2022, 11, 194. [Google Scholar] [CrossRef]
- Akram, G.; Gillani, S.R. Sub pico-second Soliton with Triki–Biswas equation by the extended ()-expansion method and the modified auxiliary equation method. Optik 2021, 229, 166227. [Google Scholar] [CrossRef]
- Wan, P.; Manafian, J.; Ismael, H.F.; Mohammed, S.A. Investigating one-, two-, and triple-wave solutions via multiple exp-function method arising in engineering sciences. Adv. Math. Phys. 2020, 2020, 8018064. [Google Scholar] [CrossRef]
- He, X.J.; Lü, X. M-lump solution, soliton solution and rational solution to a (3+1)-dimensional nonlinear model. Math. Comput. Simul. 2022, 197, 327–340. [Google Scholar] [CrossRef]
- Rehman, H.U.; Iqbal, I.; Subhi Aiadi, S.; Mlaiki, N.; Saleem, M.S. Soliton solutions of Klein–Fock–Gordon equation using Sardar subequation method. Mathematics 2022, 10, 3377. [Google Scholar] [CrossRef]
- Parkes, E.J.; Duffy, B.R.; Abbott, P.C. The Jacobi elliptic-function method for finding periodic-wave solutions to nonlinear evolution equations. Phys. Lett. A 2002, 295, 280–286. [Google Scholar] [CrossRef]
- Yusuf, A.; Inc, M.; Aliyu, A.I.; Baleanu, D. Optical solitons possessing beta derivative of the Chen-Lee-Liu equation in optical fibers. Front. Phys. 2019, 7, 34. [Google Scholar] [CrossRef]
- Hassan, S.Z.; Abdelrahman, M.A. A Riccati–Bernoulli sub-ODE method for some nonlinear evolution equations. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 303–313. [Google Scholar] [CrossRef]
- Arife, A.S. The modified variational iteration transform method (MVITM) for solve non linear partial differential equation (NLPDE). World Appl. Sci. J. 2011, 12, 2274–2278. [Google Scholar]
- Jiong, S. Auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2003, 309, 387–396. [Google Scholar]
- Akram, G.; Sadaf, M.; Abbas, M.; Zainab, I.; Gillani, S.R. Efficient techniques for traveling wave solutions of time-fractional Zakharov–Kuznetsov equation. Math. Comput. Simul. 2022, 193, 607–622. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Abundant Solitary Wave Solutions for the Boiti–Leon–Manna–Pempinelli Equation with M-Truncated Derivative. Axioms 2023, 12, 466. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The Influence of White Noise and the Beta Derivative on the Solutions of the BBM Equation. Axioms 2023, 12, 447. [Google Scholar] [CrossRef]
- Ghanbari, B.; Baleanu, D. New optical solutions of the fractional Gerdjikov-Ivanov equation with conformable derivative. Front. Phys. 2020, 8, 167. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. Solitary Wave Solutions of the Fractional-Stochastic Quantum Zakharov–Kuznetsov Equation Arises in Quantum Magneto Plasma. Mathematics 2023, 11, 488. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. Optical solitons and other solutions to the Hirota–Maccari system with conformable, M-truncated and beta derivatives. Mod. Phys. Lett. B 2022, 36, 2150625. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ansar, R.; Abbas, M.; Abdullah, F.A.; Abualnaja, K.M. The Investigation of Dynamical Behavior of Benjamin–Bona–Mahony–Burger Equation with Different Differential Operators Using Two Analytical Approaches. Axioms 2023, 12, 599. https://doi.org/10.3390/axioms12060599
Wang X, Ansar R, Abbas M, Abdullah FA, Abualnaja KM. The Investigation of Dynamical Behavior of Benjamin–Bona–Mahony–Burger Equation with Different Differential Operators Using Two Analytical Approaches. Axioms. 2023; 12(6):599. https://doi.org/10.3390/axioms12060599
Chicago/Turabian StyleWang, Xiaoming, Rimsha Ansar, Muhammad Abbas, Farah Aini Abdullah, and Khadijah M. Abualnaja. 2023. "The Investigation of Dynamical Behavior of Benjamin–Bona–Mahony–Burger Equation with Different Differential Operators Using Two Analytical Approaches" Axioms 12, no. 6: 599. https://doi.org/10.3390/axioms12060599
APA StyleWang, X., Ansar, R., Abbas, M., Abdullah, F. A., & Abualnaja, K. M. (2023). The Investigation of Dynamical Behavior of Benjamin–Bona–Mahony–Burger Equation with Different Differential Operators Using Two Analytical Approaches. Axioms, 12(6), 599. https://doi.org/10.3390/axioms12060599






