New Wave Solutions for the Two-Mode Caudrey–Dodd–Gibbon Equation
Abstract
:1. Introduction
2. Two-Mode Equations
2.1. Generic Two-Mode Equations
2.2. Two-Mode Caudrey–Dodd–Gibbon (TMCDG) Equation
3. Brief Overview of The Applied Methods
3.1. The Kudryashov Method (KM)
3.2. The Exponential Expansion Method (EEM)
4. Dual Wave Solutions of the TMCDG Equation
4.1. Application of the Kudryashov Method
4.2. Application of the Exponential Expansion Method (EEM)
5. Discussions on the Dual-Wave Solutions
6. Conclusions
- -
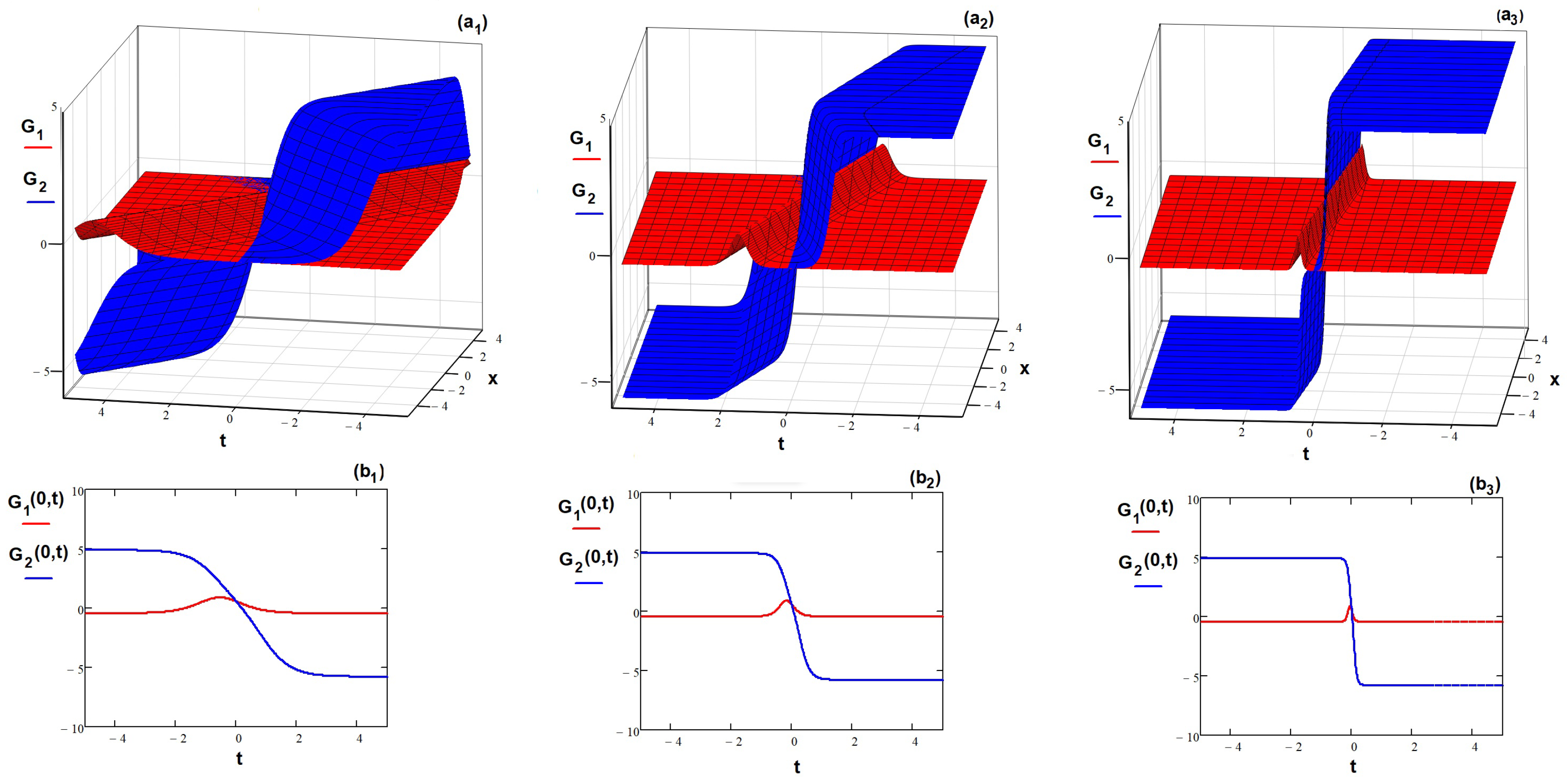
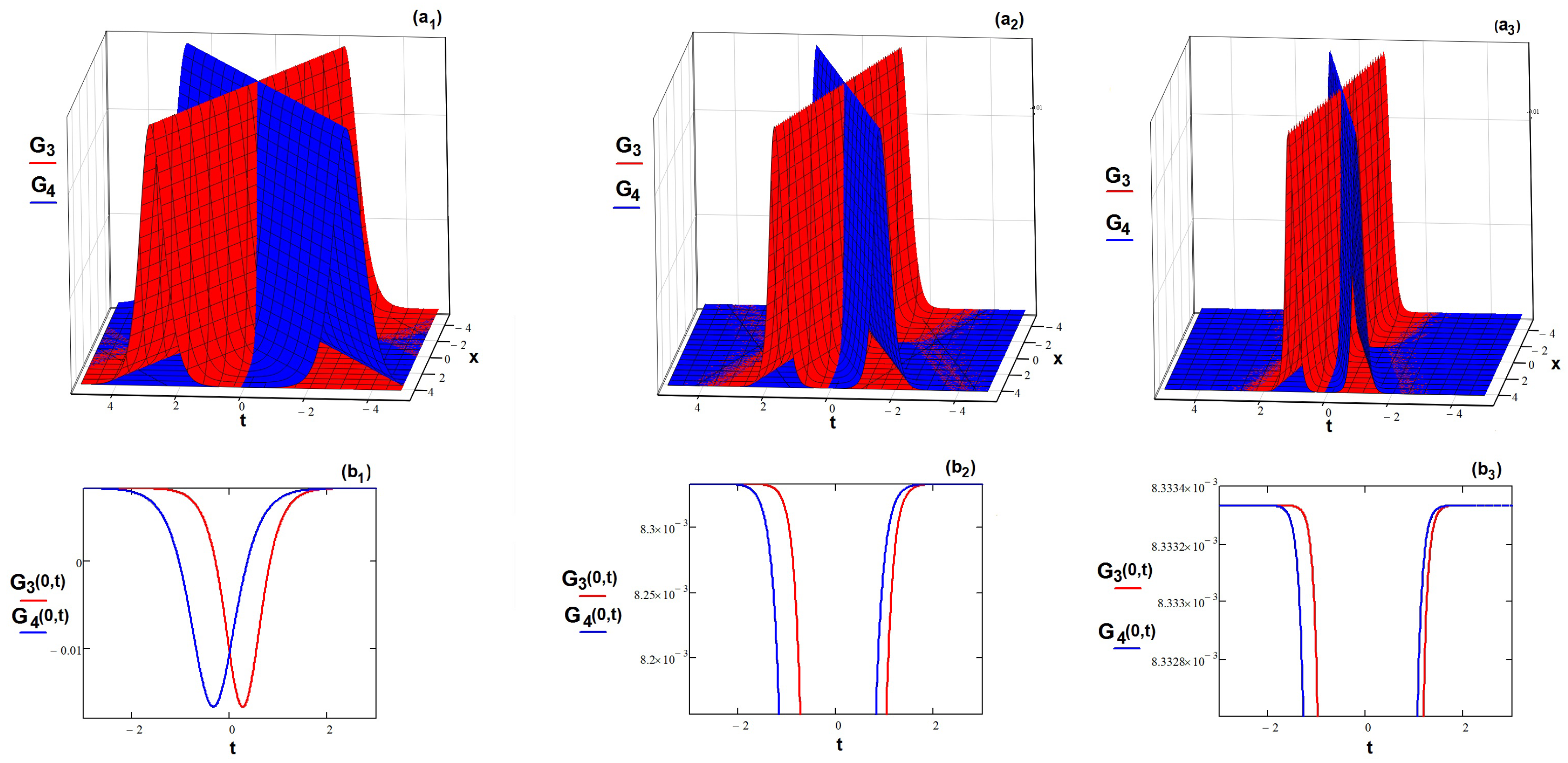
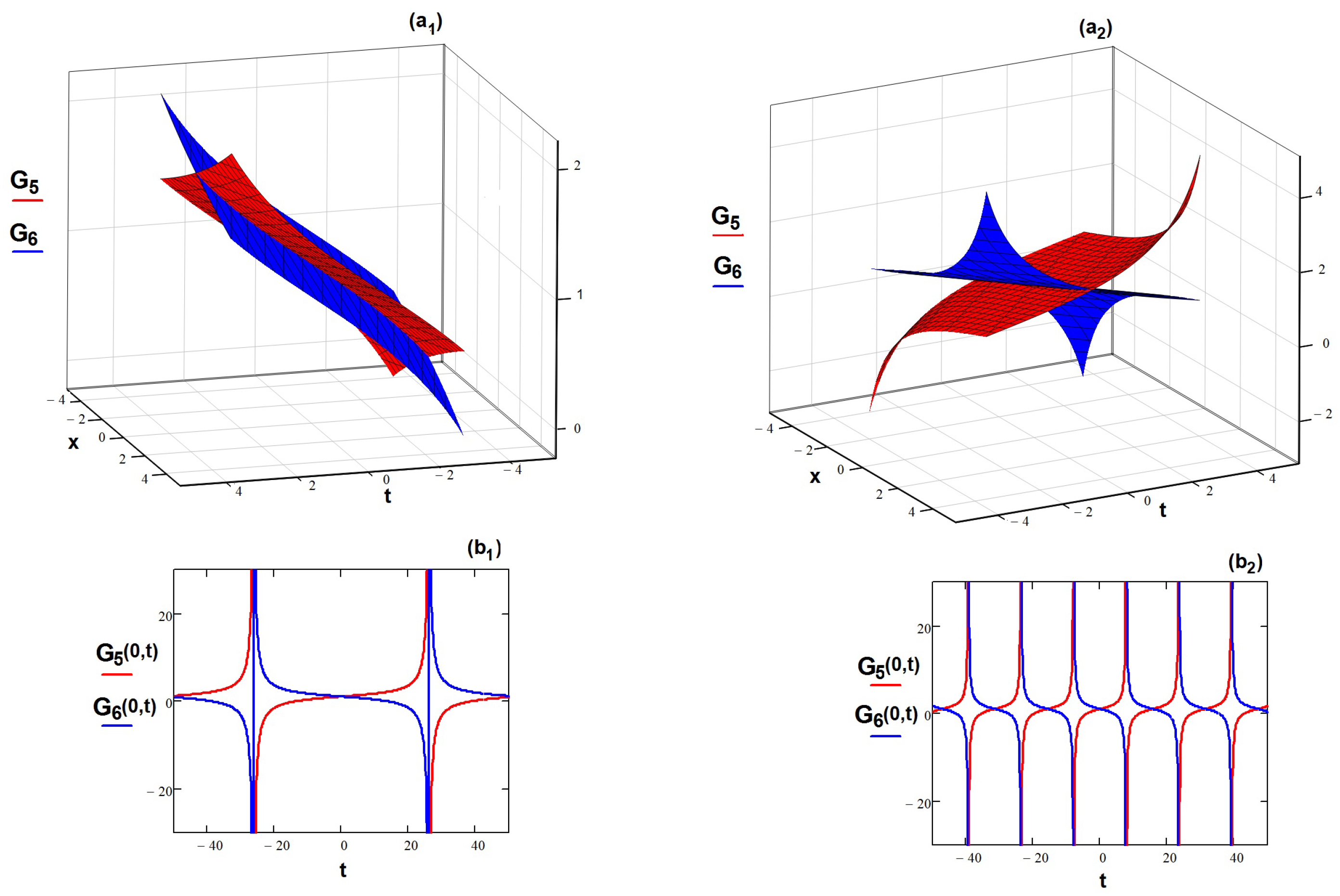
- The TMCDG equation admits all of the same classes of solutions—hyperbolic, harmonic, and rational—as the unimodal Equation (3). As examples, we show that, using the Kudryashov expansion method, the TMCDG waves move in dual-mode, bright, and kink-wave shapes, while using the exponential expansion method, the motion could appear as having a dual -periodic pattern. Of course, these are not the only solutions that can be generated; other solutions appear for different values of p and r.
- -
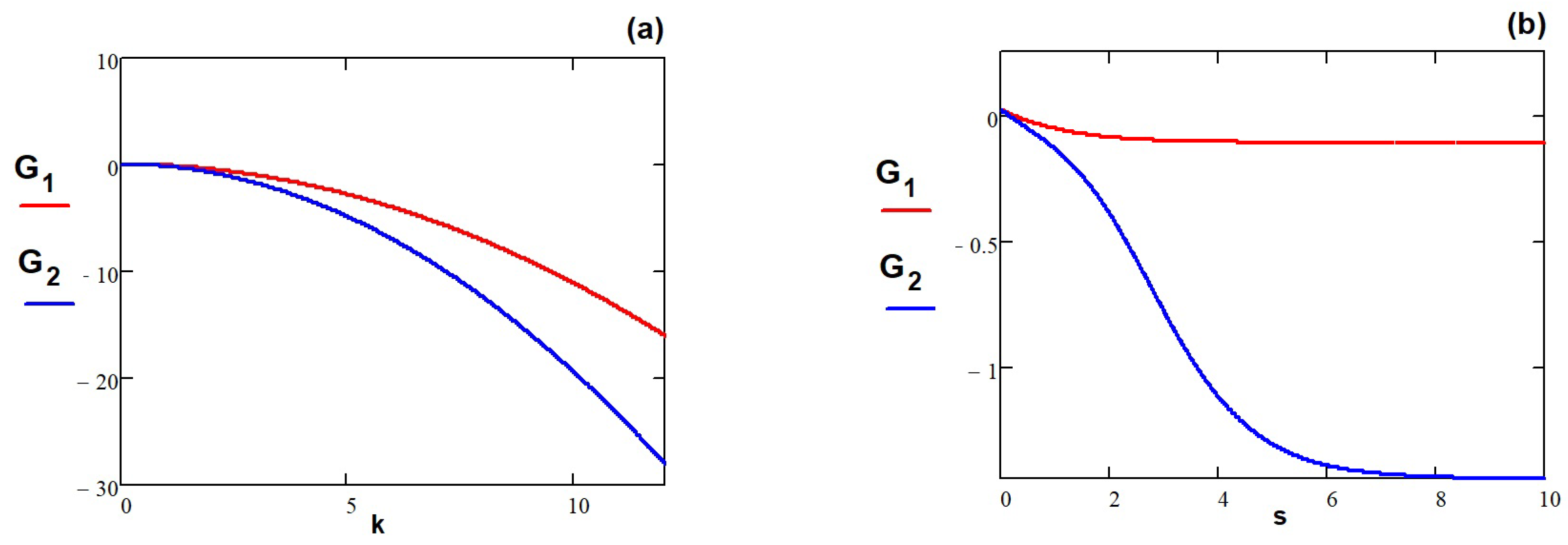
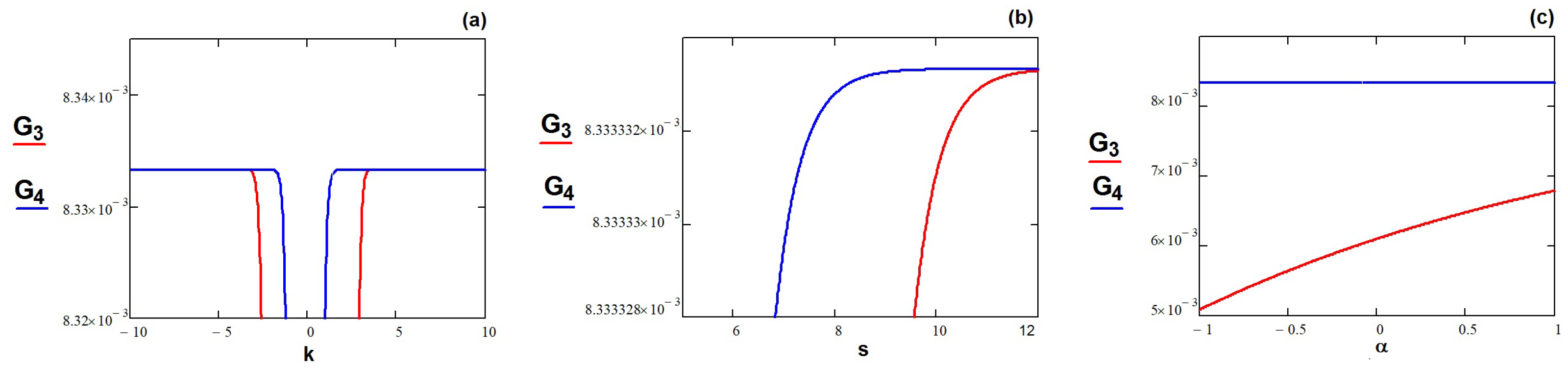
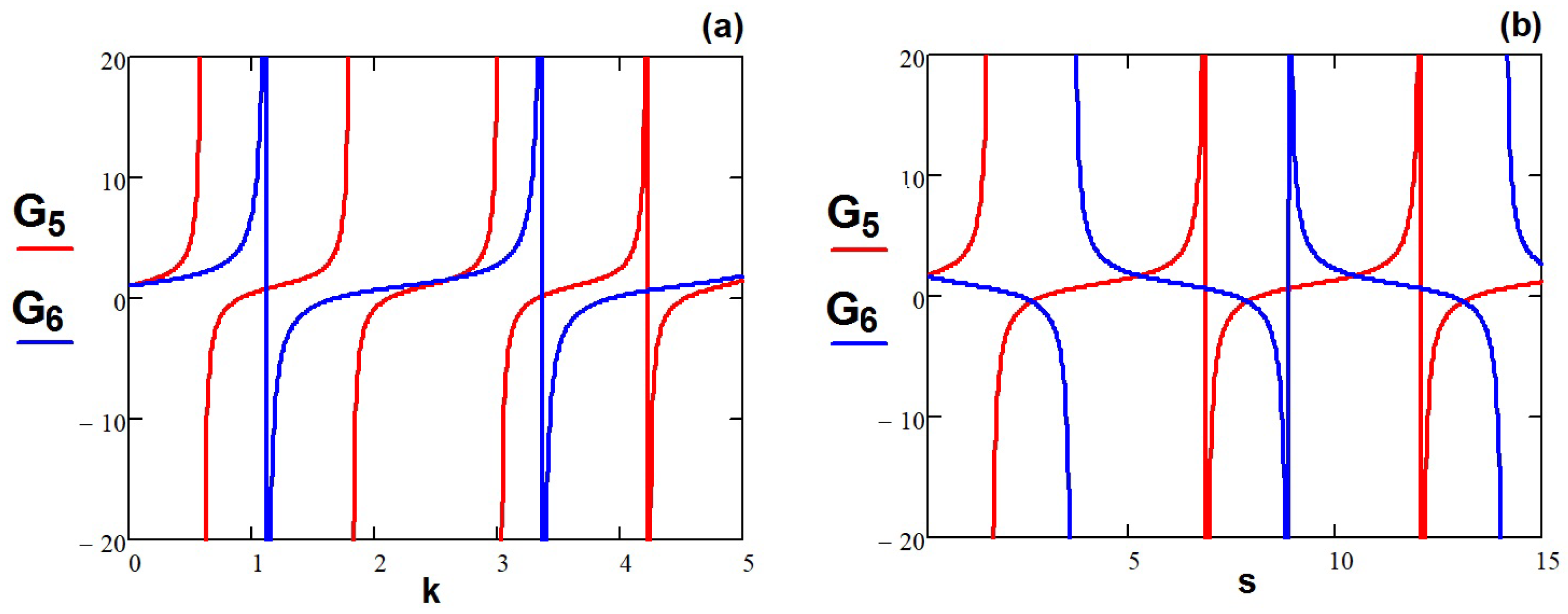
- All solutions depend on the involved parameters, but the dependence is different. We note, for example, that the nonlinearity parameter cannot take any value, but one depending on . For , the dependence is linear, while for , a more complicated relation (17) appears. The periodic solution asks for unitary values of the two parameters and , as the relation (22) shows.
- -
- The influence of the main parameters (phase velocity s, wave number k and nonlinearity ) is explained using the graphic representation of the solutions. Depending on their values, the parameters can increase or decrease the velocity of the dual waves.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zwillinger, D. Handbook of Differential Equations; Academic Press: New York, NY, USA, 1992. [Google Scholar]
- Korsunsky, S.V. Soliton solutions for a second order KdV equation. Phys. Lett. A 1994, 185, 174–176. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A study on a two-wave mode Kadomtsev–Petviashvili equation: Conditions for multiple soliton solutions to exist. Math. Method Appl. Sci. 2017, 40, 4128–4133. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two wave mode higher-order modified KdV equations: Essential conditions for multiple soliton solutions to exist. Int. J. Numer. Method H. 2017, 27, 2223–2230. [Google Scholar] [CrossRef]
- Alquran, M.; Sulaiman, T.A.; Yusuf, A. Kink-soliton, singular-kink-soliton and singular-periodic solutions for a new two-mode version of the Burger-Huxley model: Applications in nerve fibers and liquid crystals. Opt. Quant. Electron. 2021, 53, 227. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M. Geometric perspectives of the two-mode upgrade of a generalized Fisher–Burgers equation that governs the propagation of two simultaneously moving waves. J. Comput. Appl. Math. 2022, 404, 113908. [Google Scholar] [CrossRef]
- Lee, C.T.; Liu, J.L. A Hamiltonian model and soliton phenomenon for a two-mode KdV equation. Rocky Mt. J. Math. 2011, 41, 1273–1289. [Google Scholar] [CrossRef]
- Lee, C.T.; Lee, C.C. On wave solutions of a weakly nonlinear and weakly dispersive two-mode wave system. Wave Random Complex 2013, 23, 56–76. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple soliton solutions and other exact solutions for a two-mode KdV equation. Math. Method Appl. Sci. 2017, 40, 2277–2283. [Google Scholar] [CrossRef]
- Xiao, Z.J.; Tian, B.; Zhen, H.L.; Chai, J.; Wu, X.Y. Multi-soliton solutions and Bcklund transformation for a two-mode KdV equation in a fluid. Wave Random Complex 2017, 27, 1–14. [Google Scholar] [CrossRef]
- Kumar, D.; Park, C.; Tamanna, N.; Paul, G.C.; Osman, M.S. Dynamics of two-mode Sawada-Kotera equation: Mathematical and graphical analysis of its dual-wave solutions. Results Phys. 2020, 19, 103581. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Momani, S.; Biswas, A. Dark and singular optical solutions with dual-mode nonlinear Schrödinger’s equation and Kerr-law nonlinearity. Optik 2018, 172, 822–825. [Google Scholar] [CrossRef]
- Abu Irwaq, I.; Alquran, M.; Jaradat, I.; Baleanu, D. New dual-mode Kadomtsev–Petviashvili model with strong–weak surface tension: Analysis and application. Adv. Differ. Equ. 2018, 2018, 433. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two-mode Sharma-Tasso-Olver equation and two-mode fourth-order Burgers equation: Multiple kink solutions. Alex. Eng. J. 2018, 57, 1971–1976. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, I.; Baleanu, D. Shapes and dynamics of dual-mode Hirota–Satsuma coupled KdV equations: Exact traveling wave solutions and analysis. Chin. J. Phys. 2019, 58, 49–56. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two-mode fifth-order KdV equations: Necessary conditions for multiple-soliton solutions to exist. Nonlinear Dynam. 2017, 87, 1685–1691. [Google Scholar] [CrossRef]
- Kumar, S.; Mohan, B.; Kumar, R. Lump, soliton, and interaction solutions to a generalized two-mode higher-order nonlinear evolution equation in plasma physics. Nonlinear Dyn. 2022, 110, 693–704. [Google Scholar] [CrossRef]
- Alquran, M.; Alhami, R. Convex-periodic, kink-periodic, peakon-soliton and kink bidirectional wave-solutions to new established two-mode generalization of cahn-allen equation. Results Phys. 2022, 34, 105257. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Pauna, A.S. Complementary wave solutions for the long-short wave resonance model via the extended trial equation method and the generalized Kudryashov method. Open Phys. 2018, 16, 419–426. [Google Scholar] [CrossRef]
- Ferdous, F.; Hafez, M.G.; Akther, S. Oblique traveling wave closed-form solutions to space-time fractional coupled dispersive long wave equation through the generalized exponential expansion method. Int. J. Comput. Math. 2022, 8, 142. [Google Scholar] [CrossRef]
- Babalic, C.N. Complete integrability and complex solitons for generalized Volterra system with branched dispersion. Int. J. Mod. Phys. B 2020, 34, 2050274. [Google Scholar] [CrossRef]
- Babalic, C.N. Integrable discretization of coupled Ablowitz-Ladik equations with branched dispersion. Rom. J. Phys. 2018, 63, 114. [Google Scholar]
- Cimpoiasu, R.; Constantinescu, R. Invariant solutions of the Eckhaus-Kundu model with nonlinear dispersion and non-Kerr nonlinearities. Wave Random Complex 2021, 31, 331–341. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Rezazadeh, H.; Florian, D.A.; Ahmad, H.; Nonlaopon, K.; Altanji, M. Symmetry reductions and invariant-group solutions for a two-dimensional Kundu-Mukherjee-Naskar model. Results Phys. 2021, 28, 104583. [Google Scholar] [CrossRef]
- Khater, M.M. Computational and numerical wave solutions of the Caudrey–Dodd–Gibbon equation. Heliyon 2023, 9, e13511. [Google Scholar] [CrossRef]
- Polat, M.; Oruç, Ö. A combination of Lie group-based high order geometric integrator and delta-shaped basis functions for solving Korteweg-de Vries (KdV) equation. Int. J. Geom. M. 2021, 18, 2150216. [Google Scholar] [CrossRef]
- Hu, X.B.; Li, Y. Some results on the Caudrey-Dodd-Gibbon-Kotera-Sawada equation. J. Phys. A-Math. Gen. 1991, 24, 3205. [Google Scholar] [CrossRef]
- Majeed, A.M.; Rafiq, V.; Kamran, M.; Abbas, M.; Inc, M. Analytical solutions of the fifth-order time fractional nonlinear evolution equations by the unified method. Mod. Phys. Lett. B 2022, 36, 2150546. [Google Scholar] [CrossRef]
- Ionescu, C. The sp(3) BRST Hamiltonian formalism for the Yang-Mills fields. Mod. Phys. Lett. A 2008, 23, 737–775. [Google Scholar] [CrossRef]
- Adeyemo, O.D.; Khalique, C.M. Lie group theory, stability analysis with dispersion property, new soliton solutions and conserved quantities of 3D generalized nonlinear wave equation in liquid containing gas bubbles with applications in mechanics of fluids, biomedical sciences and cell biology. Commun. Nonlinear Sci. 2023, 123, 107261. [Google Scholar]
- Márquez, A.P.; Bruzón, M.S. Lie point symmetries, traveling wave solutions and conservation laws of a non-linear viscoelastic wave equation. Mathematics 2021, 9, 2131. [Google Scholar] [CrossRef]
- Cimpoiasu, R. Conservation Laws and associated Lie symmetries for 2D Ricci flow model. Rom. J. Phys. 2013, 58, 519–528. [Google Scholar]
- Cimpoiasu, R. Multiple invariant solutions of the 3 D potential Yu–Toda–Fukuyama equation via symmetry technique. Int. J. Mod. Phys. B 2020, 34, 2050188. [Google Scholar] [CrossRef]
- Ionescu, C.; Constantinescu, R. Solving Nonlinear Second-Order Differential Equations through the Attached Flow Method. Mathematics 2022, 10, 2811. [Google Scholar] [CrossRef]
- Henneaux, M.; Teitelboim, C. Quantization of Gauge Systems; Princeton University Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Alquran, M. Optical bidirectional wave-solutions to new two-mode extension of the coupled KdV–Schrodinger equations. Opt. Quant. Electron. 2021, 53, 588. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M. Construction of solitary two-wave solutions for a new two-mode version of the Zakharov-Kuznetsov equation. Mathematics 2020, 8, 1127. [Google Scholar] [CrossRef]
- Akbar, M.A.; Akinyemi, L.; Yao, S.W.; Jhangeer, A.; Rezazadeh, H.; Khater, M.M.; Ahmad, H.; Inc, M. Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results Phys. 2021, 25, 104228. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Tanjim, T. Outset of multiple soliton solutions to the nonlinear Schrodinger equation and the coupled Burgers equation. J. Phys. Commun. 2019, 3, 095013. [Google Scholar] [CrossRef]
- Vijayakumar, V.; Nisar, K.S.; Chalishajar, D.; Shukla, A.; Malik, M.; Alsaadi, A.; Aldosary, S.F. A note on approximate controllability of fractional semilinear integrodifferential control systems via resolvent operators. Fractal Fract 2022, 6, 73. [Google Scholar] [CrossRef]
- Xu, G.Q.; Wazwaz, A.M. Bidirectional solitons and interaction solutions for a new integrable fifth-order nonlinear equation with temporal and spatial dispersion. Nonlinear Dyn. 2020, 101, 581–595. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Cimpoiasu, V.; Constantinescu, R. Nonlinear dynamical systems in various space-time dimensions. Rom. J. Phys. 2010, 55, 25–35. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cimpoiasu, R.; Constantinescu, R. New Wave Solutions for the Two-Mode Caudrey–Dodd–Gibbon Equation. Axioms 2023, 12, 619. https://doi.org/10.3390/axioms12070619
Cimpoiasu R, Constantinescu R. New Wave Solutions for the Two-Mode Caudrey–Dodd–Gibbon Equation. Axioms. 2023; 12(7):619. https://doi.org/10.3390/axioms12070619
Chicago/Turabian StyleCimpoiasu, Rodica, and Radu Constantinescu. 2023. "New Wave Solutions for the Two-Mode Caudrey–Dodd–Gibbon Equation" Axioms 12, no. 7: 619. https://doi.org/10.3390/axioms12070619
APA StyleCimpoiasu, R., & Constantinescu, R. (2023). New Wave Solutions for the Two-Mode Caudrey–Dodd–Gibbon Equation. Axioms, 12(7), 619. https://doi.org/10.3390/axioms12070619







