An Intelligent Fuzzy MCDM Model Based on D and Z Numbers for Paver Selection: IMF D-SWARA—Fuzzy ARAS-Z Model
Abstract
1. Introduction
2. Literature Review
3. Methods
3.1. Z Numbers
3.2. IMF D-SWARA Algorithm
3.3. Fuzzy Bonferroni Mean (BM) Operator
3.4. Fuzzy ARAS Method Based on Z Numbers
- Define the required number of criteria and alternatives, followed by the formation of an MCDM model based on the performance of m alternatives evaluated on the basis of n criteria.
- 2.
- Performing the normalization procedure depending on a type of criteria.
- 3.
- Multiplication of the normalized fuzzy Z matrix with previously calculated criterion weights wj.
- 4.
- Determining the optimality function:
- 5.
- The utility degree of alternatives is calculated by comparing the analyzed alternatives with the optimal one, which is denoted Oo.
4. Formulation of the MCDM Model
- Category 1—asphalting width is up to 5 m.
- Category 2—asphalting width is from 5 m to 10 m.
- Category 3—asphalting width is over 10 m.
4.1. Description of the Problem
4.2. Definition of Alternatives
4.3. Definition of Criteria
5. Intelligent MCDM Model Based on D and Z Numbers for Paver Selection
6. Tests of Verification
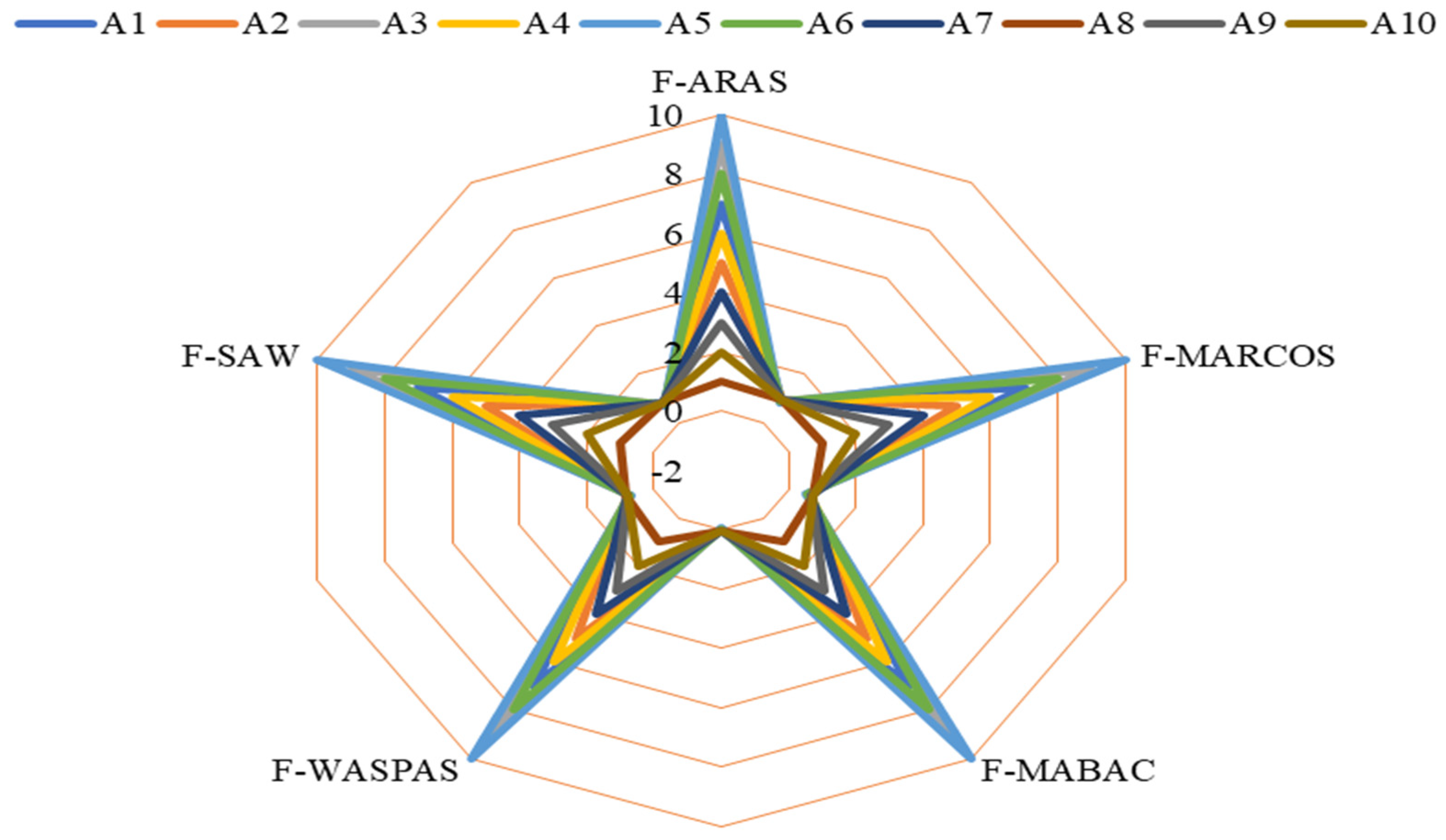
6.1. Comparative Analysis
6.2. The Influence of Changing the Size of the Initial Fuzzy Decision Matrix
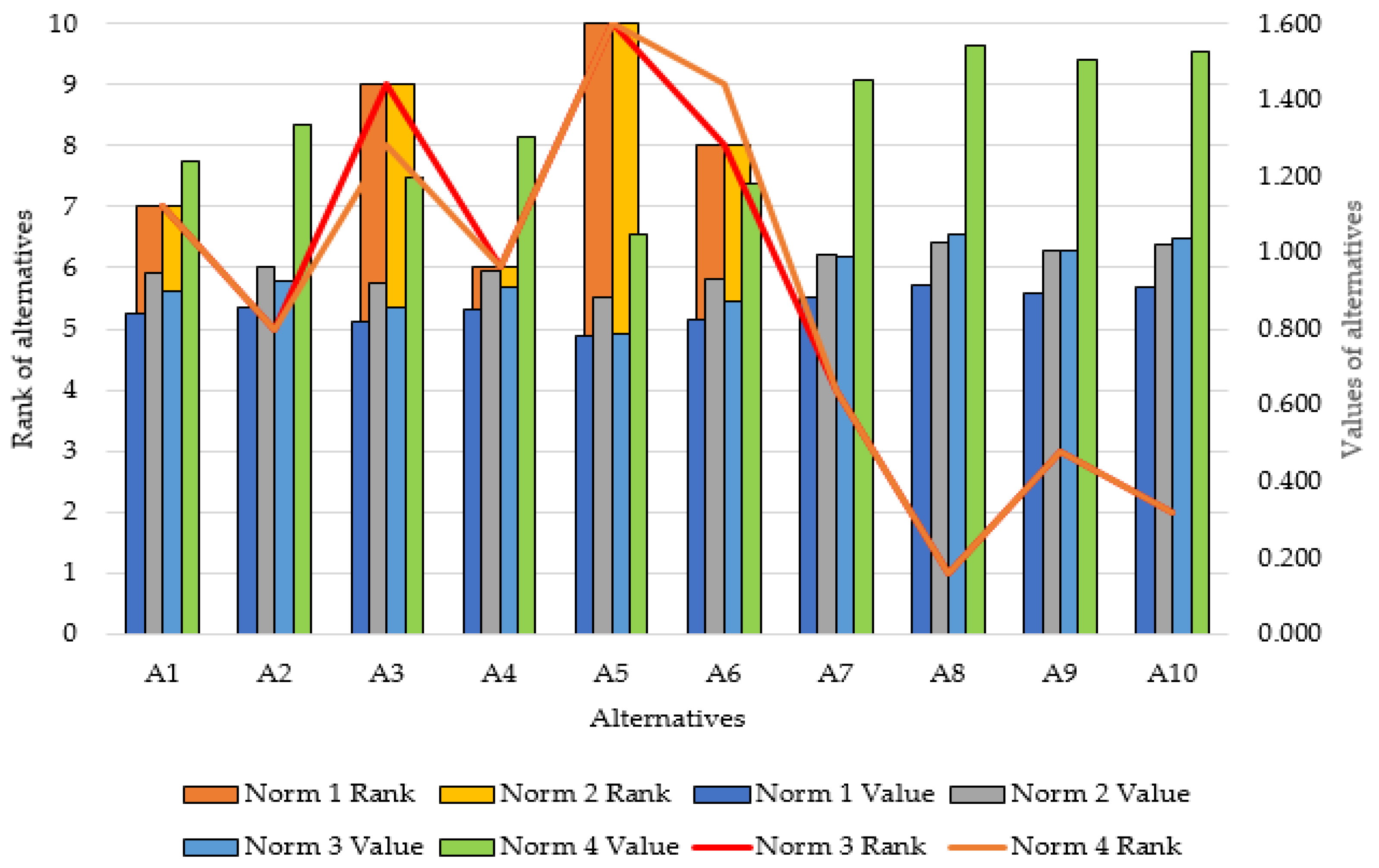
6.3. Impact of Changing the Normalization Procedure
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gerland, P.; Raftery, A.E.; Ševčíková, H.; Li, N.; Gu, D.; Spoorenberg, T.; Alkema, L.; Fosdick, B.K.; Chunn, J.; Lalic, N.; et al. World population stabilization unlikely this century. Science 2014, 346, 234–237. [Google Scholar] [CrossRef] [PubMed]
- Afanasyev, A.S.; Egoshin, A.M.; Alekseev, S.V. The choice substantiation method of road construction equipment for mining enterprises. J. Phys. Conf. Ser. 2019, 1399, 033021. [Google Scholar] [CrossRef]
- Atnaw, S.M.; Singh, L.; Hagos, F.Y.; Yousuf, A. Road Construction Equipment Management: A Case Study on Selected Industry. Int. J. Eng. Technol. Sci. 2016, 3, 91–97. [Google Scholar] [CrossRef]
- Bryan, J.; Hill, S.; Munday, M.; Roberts, A. Road infrastructure and economic development in the periphery: The case of A55 improvements in North Wales. J. Transp. Geogr. 1997, 5, 227–237. [Google Scholar] [CrossRef]
- Elmansouri, O.; Alossta, A.; Badi, I. Pavement Condition Assessment Using Pavement Condition Index and Multi-Criteria Decision-Making Model. Mechatron. Intell. Transp. Syst. 2022, 1, 57–68. [Google Scholar] [CrossRef]
- Gibbons, S.; Lyytikäinen, T.; Overman, H.G.; Sanchis-Guarner, R. New road infrastructure: The effects on firms. J. Urban Econ. 2019, 110, 35–50. [Google Scholar] [CrossRef]
- Tihonov, A.; Velichkin, V. Paver automation for road surfacing. IOP Conf. Ser. Earth Environ. Sci. 2017, 90, 012148. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Sadeghi, H.; Mahdiyar, A.; Durdyev, S.; Banaitis, A.; Yahya, K.; Ismail, S. Assessing construction labours’ safety level: A fuzzy mcdm approach. J. Civ. Eng. Manag. 2020, 26, 175–188. [Google Scholar] [CrossRef]
- Duckstein, L.; Ashkar, F. A multiple criteria decision modelling approach to selection of estimation techniques for fitting extreme floods. Stoch. Hydrol. Hydraul. 1991, 5, 227–238. [Google Scholar] [CrossRef]
- Temiz, I.; Calis, G. Selection of Construction Equipment by Using Multi-Criteria Decision Making Methods. In Proceedings of the Creative Construction Conference 2017, CCC 2017, Primosten, Croatia, 19–22 June 2017. [Google Scholar]
- Ivanović, B.; Saha, A.; Stević, Ž.; Puška, A.; Zavadskas, E.K. Selection of truck mixer concrete pump using novel MEREC DNMARCOS model. Arch. Civ. Mech. Eng. 2022, 22, 173. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. A new hybrid fuzzy MCDM approach for evaluation of construction equipment with sustainability considerations. Arch. Civ. Mech. Eng. 2018, 18, 32–49. [Google Scholar] [CrossRef]
- Phogat, M.V.S.; Singh, A.P. Selection of Equipment for Construction of a Hilly Road Using Multi Criteria Approach. Procedia-Soc. Behav. Sci. 2013, 104, 282–291. [Google Scholar] [CrossRef]
- Karleuša, B.; Dragičević, N.; Deluka-Tibljaš, A. Review of multicriteria-analysis methods application in decision making about transport infrastructure. J. Croat. Assoc. Civ. Eng. 2013, 65, 619–631. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Castillo-Lopez, E.; Rodriguez-Hernandez, J.; Canteras-Jordana, J.C. A review of application of multi-criteria decision making methods in construction. Autom. Constr. 2014, 45, 151–162. [Google Scholar] [CrossRef]
- Çalişkan, E.; Bediroglu, Ş.; Yildirim, V. Determination Forest Road Routes via Gis-based Spatial Multi-Criterion Decision Methods. Appl. Ecol. Environ. Res. 2019, 17, 759–779. [Google Scholar] [CrossRef]
- Vilke, S.; Krpan, L.; Milković, M. Application of the Multi-Criteria Analysis in the Process of Road Route Evaluation. Teh. Vjesn. 2018, 25, 1851–1859. [Google Scholar] [CrossRef]
- Sekulić, M.; Marinković, M.; Ivković, I. Spatial Multi-Criteria Evaluation Method for Planning of Optimal Roads Alignments, with Emphasize on Robustness Analysis. Int. J. Traffic Transp. Eng. 2021, 11, 424–441. [Google Scholar] [CrossRef]
- Straka, M.; Balog, M.; Trebuna, P. Multi-Criteria Decision Marking for the Needs of Layout of Haulage Parks. Asian J. Eng. Technol. 2015, 3, 55–64. [Google Scholar]
- Marzouk, M.; Abdelakder, E.M. On the use of multi-criteria decision making methods for minimizing environmental emissions in construction projects. Decis. Sci. Lett. 2019, 8, 373–392. [Google Scholar] [CrossRef]
- Marcelino, P.; de Lurdes Antunes, M.; Fortunato, E.; Gomes, M.C. Development of a Multi Criteria Decision Analysis Model for Pavement Maintenance at the Network Level: Application of the MACBETH Approach. Front. Built Environ. 2019, 5, 6. [Google Scholar] [CrossRef]
- Matić, B.; Marinković, M.; Jovanović, S.; Sremac, S.; Stević, Ž. Intelligent Novel IMF D-SWARA—Rough MARCOS Algorithm for Selection Construction Machinery for Sustainable Construction of Road Infrastructure. Buildings 2022, 12, 1059. [Google Scholar] [CrossRef]
- Zadeh, L.A. A note on Z-number. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Kang, B.; Wei, D.; Li, Y.; Deng, Y. Decision Making Using Z-numbers under Uncertain Environment. J. Comput. Inf. Syst. 2012, 8, 2807–2814. [Google Scholar]
- Božanić, D.; Jurišić, D.; Erkić, D. LBWA–Z-MAIRCA model supporting decision making in the army. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 87–110. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Görçün, Ö.F.; Küçükönder, H. Evaluating logistics villages in Turkey using hybrid improved fuzzy SWARA (IMF SWARA) and fuzzy MABAC techniques. Technol. Econ. Dev. Econ. 2021, 27, 1582–1612. [Google Scholar] [CrossRef]
- Vojinović, N.; Sremac, S.; Zlatanović, D. A Novel Integrated Fuzzy-Rough MCDM Model for Evaluation of Companies for Transport of Dangerous Goods. Complexity 2021, 2021, 5141611. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Görener, A.; Toker, K. A hybrid fuzzy MCDM approach for prioritizing the solutions of resource re-covery business model adoption to overcome its barriers in emerging economies. J. Clean. Prod. 2023, 413, 137362. [Google Scholar] [CrossRef]
- Sivageerthi, T.; Bathrinath, S.; Uthayakumar, M.; Bhalaji, R. A SWARA method to analyze the risks in coal supply chain management. Mater. Today Proc. 2021, 50, 935–940. [Google Scholar] [CrossRef]
- Xiong, L.; Su, X.; Qian, H. Supplier Selection Model Based on D Numbers and Transformation Function. Int. J. Comput. Commun. Control 2022, 17, 1–20. [Google Scholar] [CrossRef]
- Ashraf, A.; Ullah, K.; Hussain, A.; Bari, M. Interval-Valued Picture Fuzzy Maclaurin Symmetric Mean Operator with Application in Multiple Attribute Decision-Making. Rep. Mech. Eng. 2022, 3, 301–317. [Google Scholar] [CrossRef]
- Pamučar, D.; Deveci, M.; Canıtez, F.; Bozanic, D. A fuzzy Full Consistency Method-Dombi-Bonferroni Model for Prioritizing Transportation Demand Management Measures. Appl. Soft Comput. 2020, 87, 105952. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Karagöz, S.; Deveci, M.; Simic, V.; Aydin, N. Interval type-2 Fuzzy ARAS method for recycling facility location problems. Appl. Soft Comput. 2021, 102, 107107. [Google Scholar] [CrossRef]
- Jovčić, S.; Simić, V.; Průša, P.; Dobrodolac, M. Picture Fuzzy ARAS Method for Freight Distribution Concept Selection. Symmetry 2020, 12, 1062. [Google Scholar] [CrossRef]
- Fischer, A.; Schug, R. Vögele Booklet on Paving; Joseph Vögele AG: Ludwigshafen, Germany, 2012. [Google Scholar]
- Arbeider, C.G.; Miller, S.R.; Doree, A.G.; Oosterveld, M. Planning the asphalt construction process—Towards more consistent paving and compaction operations. In Proceedings of the 17th AAPA International Flexible Pavements Conference 2017, Melbourne, Australia, 13–16 August 2017. [Google Scholar]
- Ma, F.; Sha, A.; Lin, R.; Huang, Y.; Wang, C. Greenhouse Gas Emissions from Asphalt Pavement Construction: A Case Study in China. Int. J. Environ. Res. Public Health 2016, 13, 351. [Google Scholar] [CrossRef]
- Filip, F.G. Collaborative Decision-Making: Concepts and Supporting Information and Communication Technology Tools and Systems. Int. J. Comput. Commun. Control 2022, 17, 4732. [Google Scholar] [CrossRef]
- Petrovas, A.; Baušys, R.; Zavadskas, E.K.; Smarandache, F. Generation of creative game scene patterns by the neu-trosophic genetic CoCoSo method. Stud. Inform. Control 2022, 31, 5–11. [Google Scholar] [CrossRef]
- Tešić, D.; Božanić, D.; Puška, A.; Milić, A.; Marinković, D. Development of the MCDM fuzzy LMAW-grey MARCOS model for selection of a dump truck. Rep. Mech. Eng. 2023, 4, 1–17. [Google Scholar] [CrossRef]
- Božanić, D.; Tešić, D.; Milić, A. Multicriteria Decision Making Model with Z-Numbers Based on FUCOM and MABAC Model. Decis. Mak. Appl. Manag. Eng. 2020, 3, 19–36. [Google Scholar] [CrossRef]
- Puška, A.; Stojanović, I. Fuzzy Multi-Criteria Analyses on Green Supplier Selection in an Agri-Food Company. J. Intell. Manag. Decis. 2022, 1, 2–16. [Google Scholar] [CrossRef]
- Akbari, R.; Dabbagh, R.; Ghoushchi, S.J. HSE risk prioritization of molybdenum operation process using extended FMEA approach based on Fuzzy BWM and Z-WASPAS. J. Intell. Fuzzy Syst. 2020, 38, 5157–5173. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Havle, C.A.; Feyzioğlu, O. An integrated SWOT based fuzzy AHP and fuzzy MARCOS methodology for digital transformation strategy analysis in airline industry. J. Air Transp. Manag. 2021, 97, 102142. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, P.; Zavadskas, E.K.; Stević, Ž.; Vujović, V. A New Joint Strategy for Multi-Criteria Decision-Making: A Case Study for Prioritizing Solid-State Drive. Int. J. Comput. Commun. Control 2022, 17, 5010. [Google Scholar] [CrossRef]
- Aytekin, A. Comparative Analysis of the Normalization Techniques in the Context of MCDM Problems. Decis. Mak. Appl. Manag. Eng. 2021, 4, 1–25. [Google Scholar] [CrossRef]
- Bakır, M.; Akan, Ş.; Özdemir, E. Regional aircraft selection with fuzzy piprecia and fuzzy marcos: A case study of the Turkish airline industry. Facta Univ. Ser. Mech. Eng. 2021, 19, 423–445. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L. A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Mater. Des. 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Mukhametzyanov, I. On the conformity of scales of multidimensional normalization: An application for the problems of decision making. Decis. Mak. Appl. Manag. Eng. 2023, 6, 399–431. [Google Scholar] [CrossRef]
- Subotić, M.; Softić, E.; Radičević, V.; Bonić, A. Modeling of Operating Speeds as a Function of Longitudinal Gradient in Local Conditions on Two-Lane Roads. Mechatron. Intell. Transp. Syst. 2022, 1, 24–34. [Google Scholar] [CrossRef]


| Linguistic Variable | TFN A | Linguistic Variable | TFN B |
|---|---|---|---|
| Extremely poor—EP | (1, 1, 1) | Very small (VS) | (0, 0, 0.2) |
| Very poor—VP | (1, 1, 3) | Small (S) | (0.1, 0.25, 0.4) |
| Poor—P | (1, 3, 3) | Medium (M) | (0.3, 0.5, 0.7) |
| Medium poor—MP | (3, 3, 5) | High (H) | (0.55, 0.75, 0.95) |
| Medium—M | (3, 5, 5) | Very high (VH) | (0.8, 1, 1) |
| Medium good—MG | (5, 5, 7) | ||
| Good—G | (5, 7, 7) | ||
| Very good—VG | (7, 7, 9) | ||
| Extremely good—EG | (7, 9, 9) |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
| A1—Volvo P2820D ABG | 20 | 4.5 | 17.9 | 72 | 9 | 55.4 | caterpillars | 300 |
| A2—P2870D ABG | 20 | 16 | 17.9 | 72 | 9 | 55.4 | wheels | 300 |
| A3—AP355F | 25 | 11 | 20 | 80 | 9 | 55 | caterpillars | 260 |
| A4—AP300F | 30 | 16 | 20 | 80 | 9 | 55 | wheels | 260 |
| A5—SUPER 1000 | 18 | 4.5 | 21 | 85 | 10 | 55 | caterpillars | 300 |
| A6—SUPER 1003 | 18 | 20 | 22 | 85 | 10 | 55 | wheels | 300 |
| A7—SUPER 1300 | 30 | 4.5 | 25 | 80 | 10 | 74.4 | caterpillars | 300 |
| A8—SUPER 1300-3 | 30 | 4.5 | 29 | 85 | 10 | 74.4 | caterpillars | 300 |
| A9—SUPER 1303 | 30 | 20 | 25 | 80 | 10 | 74.4 | wheels | 300 |
| A10—SUPER 1303-3 | 30 | 20 | 29.4 | 85 | 10 | 74.4 | wheels | 300 |
| C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | |
| A1—Volvo P2820D ABG | 4.5 | Up to 20 | 5300/3240/3995 | 8155 | 250 | 330 with one conveyor; 230- with two conveyors | EU Stage V | 148,000 |
| A2—P2870D ABG | 4.5 | to 25 | 5320/3240/3995 | 7635 | 110 | 330 with one conveyor; 230- with two conveyors | EU Stage V | 152,000 |
| A3—AP355F | 4.6 | to 20 | 5047/3180/3415 | 7300 | 110 | 406 | EU Stage IIIB, U.S. EPA Tier 4 Final, | 255,000 |
| A4—AP300F | 4 | to 30 | 4870/3180/3340 | 6600 | 110 | 406 | EU Stage IIIB, US EPA Tier 4 Final | 230,000 |
| A5—SUPER 1000 | 3.9 | to 15 | 4950/3350/3515 | 10,250 | 110 | 270 | EU Stage IIIa, US EPA Tier 3 | 165,000 |
| A6—SUPER 1003 | 3.9 | to 15 | 4950/3265/3515 | 10,000 | 105 | 230 | EU Stage IIIa, US EPA Tier 3 | 165,000 |
| A7—SUPER 1300 | 5 | to 25 | 4950/3350/3500 | 10,600 | 105 | 350 | EU Stage IIIa, US EPA Tier 3 | 180,000 |
| A8—SUPER 1300-3 | 5 | to 25 | 4950/3350/3500 | 11,400 | 110 | 350 | EU Stage IIIa, US EPA Tier 3 | 180,000 |
| A9—SUPER 1303 | 4.5 | to 25 | 4950/3265/3500 | 10,200 | 110 | 250 | EU Stage IIIa, US EPA Tier 3 | 185,000 |
| A10 -SUPER 1303-3 | 4.5 | to 25 | 4950/3265/3500 | 11,100 | 100 | 250 | EU Stage IIIa, US EPA Tier 3 | 185,000 |
| E1 | ||||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |||||||||
| A1 | G | VH | M | VH | MG | H | G | VH | VG | H | G | H | G | VH | VG | H |
| A2 | G | VH | VG | H | MG | H | G | VH | VG | H | G | H | VG | VH | VG | H |
| A3 | VG | H | G | VH | MG | VH | VG | VH | VG | H | G | H | G | VH | G | H |
| A4 | EG | H | VG | H | MG | VH | VG | VH | VG | H | G | H | VG | VH | G | H |
| A5 | G | H | M | VH | G | H | EG | VH | VG | VH | G | H | G | VH | VG | H |
| A6 | G | H | EG | H | G | VH | EG | VH | VG | VH | VG | VH | VG | VH | VG | H |
| A7 | EG | H | M | VH | VG | H | VG | VH | VG | VH | VG | VH | G | VH | VG | H |
| A8 | EG | H | M | VH | EG | H | EG | VH | VG | VH | VG | VH | G | VH | VG | H |
| A9 | EG | H | EG | H | VG | H | VG | VH | VG | VH | VG | VH | VG | VH | VG | H |
| A10 | EG | H | EG | H | EG | VH | EG | VH | VG | VH | VG | VH | VG | VH | VG | H |
| E1 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | ||||||||
| A1 | VG | H | VG | H | VG | VH | G | VH | EG | VH | VG | H | EG | VH | EG | VH |
| A2 | VG | H | VG | VH | VG | VH | G | H | G | VH | VG | H | EG | VH | EG | H |
| A3 | VG | VH | VG | H | VG | H | G | H | G | VH | EG | VH | VG | VH | MP | H |
| A4 | G | VH | EG | VH | G | H | M | VH | G | VH | EG | VH | VG | VH | M | H |
| A5 | G | H | G | VH | G | VH | VG | H | G | VH | G | VH | VG | H | G | VH |
| A6 | G | H | G | VH | G | VH | VG | M | G | H | G | M | VG | H | G | VH |
| A7 | EG | VH | VG | VH | G | VH | VG | VH | G | H | VG | VH | VG | H | G | H |
| A8 | EG | VH | VG | VH | G | VH | EG | VH | G | VH | VG | VH | VG | H | G | H |
| A9 | VG | H | VG | VH | G | VH | VG | H | G | VH | G | H | VG | H | G | M |
| A10 | VG | H | VG | VH | G | VH | EG | H | G | M | G | H | VG | H | G | M |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
| A1 | (4.83, 5.77, 6.76) | (4.83, 5.77, 6.76) | (4.45, 4.87, 6.23) | (4.73, 6.12, 6.49) | (5.17, 6.06, 6.91) | (4.9, 5.78, 6.56) | (4.7, 6.09, 6.59) | (5.75, 6.23, 7.53) |
| A2 | (4.83, 5.77, 6.76) | (4.83, 5.77, 6.76) | (4.45, 4.87, 6.23) | (4.73, 6.12, 6.49) | (5.17, 6.06, 6.91) | (4.9, 5.78, 6.56) | (6.09, 6.59, 7.97) | (5.75, 6.23, 7.53) |
| A3 | (5.78, 6.14, 7.43) | (5.78, 6.14, 7.43) | (4.83, 5.77, 6.76) | (6.76, 6.76, 8.69) | (5.17, 6.06, 6.91) | (4.9, 5.78, 6.56) | (4.7, 6.09, 6.59) | (4.45, 5.3, 6.23) |
| A4 | (6.23, 7.53, 8.02) | (6.23, 7.53, 8.02) | (4.83, 5.77, 6.76) | (6.76, 6.76, 8.69) | (5.17, 6.06, 6.91) | (4.9, 5.78, 6.56) | (6.09, 6.59, 7.97) | (4.45, 5.3, 6.23) |
| A5 | (4.33, 5.17, 6.06) | (4.33, 5.17, 6.06) | (5.17, 6.06, 6.91) | (6.59, 7.97, 8.47) | (5.77, 6.76, 7.71) | (4.9, 5.78, 6.56) | (4.7, 6.09, 6.59) | (5.75, 6.23, 7.53) |
| A6 | (4.33, 5.17, 6.06) | (4.33, 5.17, 6.06) | (5.77, 6.76, 7.71) | (6.41, 8.24, 8.24) | (5.77, 6.76, 7.71) | (6.59, 7.49, 8.47) | (6.09, 6.59, 7.97) | (5.75, 6.23, 7.53) |
| A7 | (6.06, 7.79, 7.79) | (6.06, 7.79, 7.79) | (6.06, 6.91, 7.79) | (6.41, 6.41, 8.24) | (5.77, 6.76, 7.71) | (6.59, 7.49, 8.47) | (4.7, 6.09, 6.59) | (5.75, 6.23, 7.53) |
| A8 | (6.41, 8.24, 8.24) | (6.41, 8.24, 8.24) | (6.41, 8.24, 8.24) | (6.41, 8.24, 8.24) | (5.77, 6.76, 7.71) | (6.59, 7.49, 8.47) | (4.7, 6.09, 6.59) | (5.75, 6.23, 7.53) |
| A9 | (6.41, 8.24, 8.24) | (6.41, 8.24, 8.24) | (6.06, 6.91, 7.79) | (6.76, 6.76, 8.69) | (5.77, 6.76, 7.71) | (6.59, 7.49, 8.47) | (6.09, 6.59, 7.97) | (5.75, 6.23, 7.53) |
| A10 | (6.41, 8.24, 8.24) | (6.41, 8.24, 8.24) | (6.76, 8.69, 8.69) | (6.41, 8.24, 8.24) | (5.77, 6.76, 7.71) | (6.59, 7.49, 8.47) | (6.09, 6.59, 7.97) | (5.75, 6.23, 7.53) |
| Ao | (6.41, 8.24, 8.24) | (6.06, 7.35, 7.79) | (6.76, 8.69, 8.69) | (6.76, 8.24, 8.69) | (5.77, 6.76, 7.71) | (6.59, 7.49, 8.47) | (6.09, 6.59, 7.97) | (5.75, 6.23, 7.53) |
| C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | |
| A1 | (5.12, 5.5, 6.69) | (6.23, 7.12, 8.02) | (6.12, 6.49, 7.87) | (4.83, 6.76, 6.76) | (6.76, 7.71, 8.69) | (5.33, 5.78, 6.99) | (6.76, 8.69, 8.69) | (6.76, 8.69, 8.69) |
| A2 | (5.12, 5.5, 6.69) | (6.59, 7.49, 8.47) | (6.12, 6.49, 7.87) | (4.45, 5.75, 6.23) | (4.7, 6.09, 6.59) | (5.33, 5.78, 6.99) | (6.76, 8.69, 8.69) | (6.76, 8.69, 8.69) |
| A3 | (5.95, 6.41, 7.79) | (6.23, 7.12, 8.02) | (5.5, 5.5, 7.07) | (4.45, 5.75, 6.23) | (4.83, 5.77, 6.76) | (6.41, 8.24, 8.24) | (6.59, 7.02, 8.47) | (2.9, 2.9, 4.83) |
| A4 | (4.58, 5.95, 6.41) | (6.59, 8.47, 8.47) | (4.13, 5.33, 5.78) | (3.82, 4.83, 5.77) | (4.7, 6.09, 6.59) | (6.41, 6.84, 8.24) | (6.59, 7.02, 8.47) | (2.9, 4.83, 4.83) |
| A5 | (3.93, 5.12, 5.5) | (4.7, 6.59, 6.59) | (4.58, 6.41, 6.41) | (6.06, 6.06, 7.79) | (4.83, 5.77, 6.76) | (4.7, 6.09, 6.59) | (6.06, 6.06, 7.79) | (4.33, 5.17, 6.06) |
| A6 | (3.93, 5.12, 5.5) | (4.7, 6.59, 6.59) | (4.58, 6.41, 6.41) | (4.95, 4.95, 6.36) | (4.13, 5.33, 5.78) | (3.27, 4.57, 4.57) | (6.06, 6.06, 7.79) | (4.33, 5.17, 6.06) |
| A7 | (6.41, 7.79, 8.24) | (6.59, 7.49, 8.47) | (4.58, 6.41, 6.41) | (6.76, 6.76, 8.69) | (4.33, 5.17, 6.06) | (6.09, 6.59, 7.97) | (6.06, 6.06, 7.79) | (4.33, 5.17, 6.06) |
| A8 | (6.41, 7.79, 8.24) | (6.59, 7.49, 8.47) | (4.58, 6.41, 6.41) | (6.76, 8.69, 8.69) | (4.7, 6.09, 6.59) | (6.09, 6.59, 7.97) | (6.06, 6.06, 7.79) | (4.33, 5.17, 6.06) |
| A9 | (5.12, 5.5, 6.69) | (6.59, 7.49, 8.47) | (4.58, 6.41, 6.41) | (5.78, 6.14, 7.43) | (4.83, 5.77, 6.76) | (3.93, 5.5, 5.5) | (6.06, 6.06, 7.79) | (4.33, 5.17, 6.06) |
| A10 | (5.12, 5.5, 6.69) | (6.59, 7.49, 8.47) | (4.58, 6.41, 6.41) | (6.06, 7.79, 7.79) | (3.93, 4.64, 5.5) | (3.93, 5.5, 5.5) | (6.06, 6.06, 7.79) | (4.33, 5.17, 6.06) |
| Ao | (6.41, 7.79, 8.24) | (6.59, 8.47, 8.47) | (6.12, 6.49, 7.87) | (6.76, 8.69, 8.69) | (6.76, 7.71, 8.69) | (6.41, 8.24, 8.24) | (6.76, 8.69, 8.69) | (6.76, 8.69, 8.69) |
| C1 | C2 | C3 | C4 | |
| A1 | (0.06, 0.08, 0.11) | (0.04, 0.06, 0.1) | (0.05, 0.07, 0.1) | (0.05, 0.08, 0.09) |
| A2 | (0.06, 0.08, 0.11) | (0.07, 0.09, 0.14) | (0.05, 0.07, 0.1) | (0.05, 0.08, 0.09) |
| A3 | (0.07, 0.08, 0.12) | (0.05, 0.08, 0.11) | (0.06, 0.08, 0.11) | (0.08, 0.08, 0.13) |
| A4 | (0.08, 0.1, 0.13) | (0.08, 0.1, 0.15) | (0.06, 0.08, 0.11) | (0.08, 0.08, 0.13) |
| A5 | (0.05, 0.07, 0.1) | (0.04, 0.06, 0.1) | (0.06, 0.08, 0.11) | (0.07, 0.1, 0.12) |
| A6 | (0.05, 0.07, 0.1) | (0.09, 0.12, 0.15) | (0.07, 0.09, 0.13) | (0.07, 0.1, 0.12) |
| A7 | (0.07, 0.1, 0.13) | (0.04, 0.06, 0.1) | (0.07, 0.09, 0.13) | (0.07, 0.08, 0.12) |
| A8 | (0.08, 0.11, 0.13) | (0.04, 0.06, 0.1) | (0.08, 0.11, 0.13) | (0.07, 0.1, 0.12) |
| A9 | (0.08, 0.11, 0.13) | (0.09, 0.12, 0.15) | (0.07, 0.09, 0.13) | (0.08, 0.08, 0.13) |
| A10 | (0.08, 0.11, 0.13) | (0.09, 0.12, 0.15) | (0.08, 0.12, 0.14) | (0.07, 0.1, 0.12) |
| Ao | (0.08, 0.11, 0.13) | (0.09, 0.12, 0.15) | (0.08, 0.12, 0.14) | (0.08, 0.1, 0.13) |
| C5 | C6 | C7 | C8 | |
| A1 | (0.06, 0.08, 0.11) | (0.06, 0.08, 0.1) | (0.06, 0.09, 0.11) | (0.07, 0.09, 0.12) |
| A2 | (0.06, 0.08, 0.11) | (0.06, 0.08, 0.1) | (0.08, 0.09, 0.13) | (0.07, 0.09, 0.12) |
| A3 | (0.06, 0.08, 0.11) | (0.06, 0.08, 0.1) | (0.06, 0.09, 0.11) | (0.06, 0.08, 0.1) |
| A4 | (0.06, 0.08, 0.11) | (0.06, 0.08, 0.1) | (0.08, 0.09, 0.13) | (0.06, 0.08, 0.1) |
| A5 | (0.07, 0.09, 0.13) | (0.06, 0.08, 0.1) | (0.06, 0.09, 0.11) | (0.07, 0.09, 0.12) |
| A6 | (0.07, 0.09, 0.13) | (0.08, 0.1, 0.13) | (0.08, 0.09, 0.13) | (0.07, 0.09, 0.12) |
| A7 | (0.07, 0.09, 0.13) | (0.08, 0.1, 0.13) | (0.06, 0.09, 0.11) | (0.07, 0.09, 0.12) |
| A8 | (0.07, 0.09, 0.13) | (0.08, 0.1, 0.13) | (0.06, 0.09, 0.11) | (0.07, 0.09, 0.12) |
| A9 | (0.07, 0.09, 0.13) | (0.08, 0.1, 0.13) | (0.08, 0.09, 0.13) | (0.07, 0.09, 0.12) |
| A10 | (0.07, 0.09, 0.13) | (0.08, 0.1, 0.13) | (0.08, 0.09, 0.13) | (0.07, 0.09, 0.12) |
| Ao | (0.07, 0.09, 0.13) | (0.08, 0.1, 0.13) | (0.08, 0.09, 0.13) | (0.07, 0.09, 0.12) |
| C9 | C10 | C11 | C12 | |
| A1 | (0.07, 0.08, 0.12) | (0.07, 0.09, 0.12) | (0.08, 0.09, 0.14) | (0.06, 0.09, 0.11) |
| A2 | (0.07, 0.08, 0.12) | (0.07, 0.09, 0.12) | (0.08, 0.09, 0.14) | (0.06, 0.08, 0.1) |
| A3 | (0.08, 0.09, 0.13) | (0.07, 0.09, 0.12) | (0.07, 0.08, 0.13) | (0.06, 0.08, 0.1) |
| A4 | (0.06, 0.09, 0.11) | (0.07, 0.1, 0.12) | (0.06, 0.08, 0.1) | (0.05, 0.07, 0.1) |
| A5 | (0.05, 0.08, 0.09) | (0.05, 0.08, 0.1) | (0.06, 0.09, 0.12) | (0.08, 0.08, 0.13) |
| A6 | (0.05, 0.08, 0.09) | (0.05, 0.08, 0.1) | (0.06, 0.09, 0.12) | (0.06, 0.07, 0.1) |
| A7 | (0.08, 0.11, 0.14) | (0.07, 0.09, 0.12) | (0.06, 0.09, 0.12) | (0.08, 0.09, 0.14) |
| A8 | (0.08, 0.11, 0.14) | (0.07, 0.09, 0.12) | (0.06, 0.09, 0.12) | (0.08, 0.12, 0.14) |
| A9 | (0.07, 0.08, 0.12) | (0.07, 0.09, 0.12) | (0.06, 0.09, 0.12) | (0.07, 0.09, 0.12) |
| A10 | (0.07, 0.08, 0.12) | (0.07, 0.09, 0.12) | (0.06, 0.09, 0.12) | (0.08, 0.11, 0.13) |
| Ao | (0.08, 0.11, 0.14) | (0.07, 0.1, 0.12) | (0.08, 0.09, 0.14) | (0.08, 0.12, 0.14) |
| C13 | C14 | C15 | C16 | |
| A1 | (0.09, 0.12, 0.16) | (0.07, 0.08, 0.12) | (0.08, 0.11, 0.12) | (0.09, 0.13, 0.17) |
| A2 | (0.06, 0.09, 0.12) | (0.07, 0.08, 0.12) | (0.08, 0.11, 0.12) | (0.09, 0.13, 0.17) |
| A3 | (0.06, 0.09, 0.12) | (0.08, 0.12, 0.14) | (0.07, 0.09, 0.12) | (0.04, 0.04, 0.09) |
| A4 | (0.06, 0.09, 0.12) | (0.08, 0.1, 0.14) | (0.07, 0.09, 0.12) | (0.04, 0.07, 0.09) |
| A5 | (0.06, 0.09, 0.12) | (0.06, 0.09, 0.11) | (0.07, 0.08, 0.11) | (0.06, 0.08, 0.12) |
| A6 | (0.06, 0.08, 0.11) | (0.04, 0.07, 0.08) | (0.07, 0.08, 0.11) | (0.06, 0.08, 0.12) |
| A7 | (0.06, 0.08, 0.11) | (0.08, 0.09, 0.14) | (0.07, 0.08, 0.11) | (0.06, 0.08, 0.12) |
| A8 | (0.06, 0.09, 0.12) | (0.08, 0.09, 0.14) | (0.07, 0.08, 0.11) | (0.06, 0.08, 0.12) |
| A9 | (0.06, 0.09, 0.12) | (0.05, 0.08, 0.09) | (0.07, 0.08, 0.11) | (0.06, 0.08, 0.12) |
| A10 | (0.05, 0.07, 0.1) | (0.05, 0.08, 0.09) | (0.07, 0.08, 0.11) | (0.06, 0.08, 0.12) |
| Ao | (0.09, 0.12, 0.16) | (0.08, 0.12, 0.14) | (0.08, 0.11, 0.12) | (0.09, 0.13, 0.17) |
| Oi | Ai | Crisp Ai | Rank | |
|---|---|---|---|---|
| A1 | (0.06, 0.09, 0.13) | (0.38, 0.80, 1.80) | 0.895 | 7 |
| A2 | (0.06, 0.09, 0.13) | (0.40, 0.81, 1.84) | 0.911 | 5 |
| A3 | (0.06, 0.08, 0.13) | (0.38, 0.76, 1.78) | 0.864 | 9 |
| A4 | (0.06, 0.09, 0.13) | (0.38, 0.80, 1.79) | 0.895 | 6 |
| A5 | (0.05, 0.08, 0.12) | (0.34, 0.74, 1.67) | 0.829 | 10 |
| A6 | (0.06, 0.09, 0.13) | (0.37, 0.78, 1.73) | 0.872 | 8 |
| A7 | (0.06, 0.09, 0.14) | (0.40, 0.83, 1.87) | 0.932 | 4 |
| A8 | (0.06, 0.10, 0.14) | (0.41, 0.87, 1.89) | 0.965 | 1 |
| A9 | (0.06, 0.09, 0.14) | (0.41, 0.84, 1.89) | 0.945 | 3 |
| A10 | (0.06, 0.10, 0.14) | (0.41, 0.87, 1.89) | 0.960 | 2 |
| So | (0.07, 0.11, 0.15) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jovanović, S.; Zavadskas, E.K.; Stević, Ž.; Marinković, M.; Alrasheedi, A.F.; Badi, I. An Intelligent Fuzzy MCDM Model Based on D and Z Numbers for Paver Selection: IMF D-SWARA—Fuzzy ARAS-Z Model. Axioms 2023, 12, 573. https://doi.org/10.3390/axioms12060573
Jovanović S, Zavadskas EK, Stević Ž, Marinković M, Alrasheedi AF, Badi I. An Intelligent Fuzzy MCDM Model Based on D and Z Numbers for Paver Selection: IMF D-SWARA—Fuzzy ARAS-Z Model. Axioms. 2023; 12(6):573. https://doi.org/10.3390/axioms12060573
Chicago/Turabian StyleJovanović, Stanislav, Edmundas Kazimieras Zavadskas, Željko Stević, Milan Marinković, Adel F. Alrasheedi, and Ibrahim Badi. 2023. "An Intelligent Fuzzy MCDM Model Based on D and Z Numbers for Paver Selection: IMF D-SWARA—Fuzzy ARAS-Z Model" Axioms 12, no. 6: 573. https://doi.org/10.3390/axioms12060573
APA StyleJovanović, S., Zavadskas, E. K., Stević, Ž., Marinković, M., Alrasheedi, A. F., & Badi, I. (2023). An Intelligent Fuzzy MCDM Model Based on D and Z Numbers for Paver Selection: IMF D-SWARA—Fuzzy ARAS-Z Model. Axioms, 12(6), 573. https://doi.org/10.3390/axioms12060573









