Periodic and Almost Periodic Solutions of Stochastic Inertial Bidirectional Associative Memory Neural Networks on Time Scales

Abstract

The stochastic inertial bidirectional associative memory neural networks (SIBAMNNs) on time scales are considered in this paper, which can unify and generalize both continuous and discrete systems. It is of primary importance to derive the criteria for the existence and uniqueness of both periodic and almost periodic solutions of SIBAMNNs on time scales. Based on that, the criteria for their exponential stability on time scales are studied. Meanwhile, the effectiveness of all proposed criteria is demonstrated by numerical simulation. The above study proposes a new way to unify and generalize both continuous and discrete SIBAMNNs systems, and is applicable to some other practical neural network systems on time scales.

1. Introduction

Bidirectional associative memory neural networks (BAMNNs) are a special class of recurrent neural networks that can store bipolar vector pairs, which were originally introduced and investigated by Kosko in 1988 [1]. BAMNNs have been widely studied due to their important applications in many fields [2,3,4,5,6,7], such as signal processing, image processing, associative memories and pattern recognition. It is well known that BAMNNs can be construed as a super damping (i.e., the damping tends to infinity) system physically, but the ones with weak damping play more important roles in actual applications. Therefore, the weak damping BAMNNs are proposed, which are also named inertial BAMNNs [8].

Artificial intelligence meets the requirements of being more intelligent and suitable for complex cases. As the most important branch of modern artificial intelligence, neural networks possess the advantages of massive parallel processing, self-learning abilities and nonlinear mapping, which motivated the development of intelligent control systems [9,10,11]. It is widely known that neural networks can be divided into continuous [12,13] and discrete cases [14,15], which have been thoroughly studied and widely applied. However, many complex systems include both continuous and discrete cases, and previous research on these two cases was carried out separately [16]. Therefore, it is challenging to consider neural networks under the unified framework, which can unify and generalize both continuous and discrete systems.

Fortunately, the calculus of time scales initiated by Hilger [17] can perfectly solve the problem of unifying and generalizing continuous and discrete cases. Many related works have sprung up that generalized classical methods under the time-scale framework, including the Darboux transformation method [18], the Hirota bilinear method [19], the Lie symmetry method [20] and the Lyapunov function method [21]. Recently, the research on neural networks on time scales has aroused wide attention, especially on the solutions of neural networks on time scales involving equilibrium [22], periodic [23], almost periodic [24], pseudo-almost periodic [25], almost automorphic solutions [26], etc. Moreover, some results on the dynamical properties of solutions have been achieved, such as their existence, stability and synchronization and periodic and almost periodic oscillatory behaviors. For instance, Yang et al. [23] studied the existence and exponential stability of periodic solutions of stochastic high-order Hopfield neural networks on time scales. Zhou et al. [24] investigated the existence and exponential stability of almost periodic solutions of neutral-type BAM neural networks on time scales.

The study of stochastic inertial BAM neural networks (SIBAMNNs) on time scales is still new, although there have been some studies on continuous or discrete cases. Considering the importance of SIBAMNNs and the significance of studying the system under a unified framework, we explore the existence, uniqueness and stability of both periodic and almost periodic solutions of the SIBAMNNs on time scales with discrete and distributed delays, which can unify and generalize the continuous and discrete cases. The analysis of SIBAMNNs on time scales built a bridge between continuous and discrete analyses. This provides an effective way of studying complex models that include both continuous and discrete factors, such as hybrid systems. The remaining paper is organized as follows: In Section 2, we give some Definitions and Lemmas for time scales. In Section 3, the criteria for the existence and uniqueness of periodic and almost periodic solutions of SIBAMNNs on time scales are explored. The exponential stability of SIBAMNNs on time scales is discussed in Section 4. The effectiveness of the proposed criteria for SIBAMNNs is demonstrated by considering numerical simulation in Section 5.

2. Preliminaries

Definition 1

([27] (periodic time scale)). A time scale $\mathbb{T}$ is called a periodic time scale if there exists $p>0$ such that

$$\mathrm{\Pi }:=\left\{p\in \mathbb{R}:t\pm p\in \mathbb{T},\forall t\in \mathbb{T}\right\}\ne \left\{0\right\}.$$

(1)

Definition 2

([27] (periodic function)). Let $\mathbb{T}$ be a periodic time scale with period p. The function $f:\mathbb{T}\to \mathbb{R}$ is called a periodic function with period $\omega >0$ if there exists $n\in {\mathbb{N}}^{*}$ such that $\omega =np$, $f(t+\omega )=f\left(t\right)$ for all $t\in \mathbb{T}$, where ω is the smallest number satisfying $f(t+\omega )=f\left(t\right)$.

Definition 3

([28] (almost periodic function)). Let $\mathbb{T}$ be a periodic time scale. The function $x:\mathbb{T}\to \mathbb{R}$ can be called almost periodic if the ε-translation set of x

$$\mathbb{E}\{\epsilon ,x\}=\left\{{\tau \in \mathrm{\Pi }:E|x(t+\tau )-x\left(t\right)|}^2<\epsilon ,\forall t\in \mathbb{T}\right\}$$

is relatively dense for all $\epsilon >0$. I.e., for any $\epsilon >0$, there exists a constant $l\left(\epsilon \right)>0$ such that each interval of length $l\left(\epsilon \right)$ contains a $\tau \left(\epsilon \right)\in \mathbb{E}\{\epsilon ,x\}$ such that

$${E|x(t+\tau )-x\left(t\right)|}^2<\epsilon ,\forall t\in \mathbb{T}.$$

τ is called the ε-translation number of x and $l\left(\epsilon \right)$ is the inclusion length of $E\{\epsilon ,x\}$.

Definition 4

([29,30] (jump operator)). Let $\mathbb{T}$ be a time scale.

1. 

The forward jump operator $\sigma :\mathbb{T}\to \mathbb{T}$ is defined by

$$\sigma \left(t\right):=inf\left\{s\in \mathbb{T}:s>t\right\}.$$

2. 

The graininess function $\mu :\mathbb{T}\to [0,\infty )$ is defined by

$$\mu \left(t\right):=\sigma \left(t\right)-t.$$

Definition 5

([29,30] (rd-continuous and regressive)).

1. 

$f:\mathbb{T}\to \mathbb{R}$ is called rd-continuous provided it is continuous at right-dense points in T and its left-sided limits exist (finite) at left-dense points in $\mathbb{T}$. The set of rd-continuous functions $f:\mathbb{T}\to \mathbb{R}$ is denoted by ${\mathrm{C}}_{rd}^{}$.

2. 

A function $p:\mathbb{T}\to \mathbb{R}$ is regressive provided

$$1+\mu \left(t\right)p\left(t\right)\ne 0$$

for all $t\in {\mathbb{T}}^{\kappa }$, where ${\mathbb{T}}^{\kappa }=\mathbb{T}-\left\{m\right\}$ if the maximum m of $\mathbb{T}$ is left-scattered. Otherwise, ${\mathbb{T}}^{\kappa }=\mathbb{T}$. A function $p:\mathbb{T}\to \mathbb{R}$ is positively regressive provided

$$1+\mu \left(t\right)p\left(t\right)>0$$

for all $t\in {\mathbb{T}}^{\kappa }$.

3. 

The set of all regressive and rd-continuous functions $f:\mathbb{T}\to \mathbb{R}$ is denoted by

$$\mathcal{R}=\mathcal{R}(\mathbb{T},\mathbb{R}).$$

The set of all positively regressive and rd-continuous functions $f:\mathbb{T}\to \mathbb{R}$ is denoted by

$${\mathcal{R}}^{+}={\mathcal{R}}^{+}(\mathbb{T},\mathbb{R}).$$

Definition 6

([29]). A function $f:\mathbb{T}\to \mathbb{R}$ is delta-differential at $t\in {\mathbb{T}}^{\kappa }$ if there is a number $f^{\mathrm{\Delta }}\left(t\right)$ such that, for all $\epsilon >0$, there exists a neighborhood U of t (i.e., $U=(t-\delta ,t+\delta )\bigcap \mathbb{T}$ for some $\delta >0$) such that

$$\left|f\left(\sigma \left(t\right)\right)-f\left(s\right)-f^{\mathrm{\Delta }}\left(t\right)(\sigma \left(t\right)-s)\right|\le \epsilon \left|\sigma \left(t\right)-s\right|,\mathit{for}\mathit{all}s\in U.$$

$f^{\mathrm{\Delta }}\left(t\right)$ is called the delta derivative of f at t. f is delta-differentiable on ${\mathbb{T}}^{\kappa }$ provided $f^{\mathrm{\Delta }}\left(t\right)$ exists for all $t\in {\mathbb{T}}^{\kappa }$.

Lemma 1

([28]). Let $\mathbb{T}$ satisfy (1), then

$$\sigma (t+\tau )=\sigma \left(t\right)+\tau ,\mu (t+\tau )=\mu \left(t\right).$$

(2)

Lemma 2

([29]). If $p\in \mathcal{R}$, then

$${\left(e_p(t,s)\right)}^{\mathrm{\Delta }}=p\left(t\right)e_p(t,s).$$

(3)

Proof. 

Using Theorem 2.62 in [29], (3) can be easily derived. □

Lemma 3

([29]). If $p\in \mathcal{R}$ and $a,b,c\in \mathbb{T}$, then

1. 

${\left(e_p(c,t)\right)}^{\mathrm{\Delta }}=-p\left(t\right)\left(e_p(c,\sigma \left(t\right))\right).$

2. 

${\int }_a^{b}p\left(t\right)e_p(c,\sigma \left(t\right))\mathrm{\Delta }t=e_p(c,a)-e_p(c,b).$

3. 

The function $\ominus p$ defined by $(\ominus p)\left(t\right)=-\frac{p\left(t\right)}{1+\mu \left(t\right)p\left(t\right)}$ for all $t\in {\mathbb{T}}^{\kappa }$ is also an element of $\mathcal{R}$.

4. 

$e_p(\sigma \left(t\right),s)=(1+\mu \left(t\right)p\left(t\right))e_p(t,s)$.

 For more properties of exponential functions on time scales, please refer to Section 2.2 in [29].

Lemma 4

([31]). For any $F\in {\mathbb{R}}_{+}^N$ and $p>0$,

$${\left|F\right|}^p\le N^{(\frac{p}{2}-1)\vee 0}\sum _{l=1}^N{F}_l^p,{\left(\sum _{l=1}^N{F}_l\right)}^p\le N^{(p-1)\vee 0}\sum _{l=1}^N{F}_l^p.$$

(4)

Lemma 5

([32]). For the $\mathrm{\Delta }$-stochastic integral, if $E\left({\int }_a^b{x}^2\left(t\right)\mathrm{\Delta }t\right)<\infty$, then $E\left({\int }_a^{b}x\left(t\right)\mathrm{\Delta }w\left(t\right)\right)=0$ and the $It\widehat{o}$-isometry

$$E\left({\left({\int }_a^{b}x\left(t\right)\mathrm{\Delta }w\left(t\right)\right)}^2\right)=E\left({\int }_a^b{x}^2\left(t\right)\mathrm{\Delta }t\right)$$

(5)

holds.

3. Existence and Uniqueness of Solution for SIBAMNNs on Time Scales

 Consider the SIBAMNNs [33] on time scales

$$\begin{array}{cc}\hfill x_i^{{\mathrm{\Delta }}^2}\left(t\right)& =-{\beta }_i\left(t\right)x_i^{{\mathrm{\Delta }}^{}}\left(t\right)-a_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^m{c}_{ij}\left(t\right)f_j\left(y_j\left(t\right)\right)+\sum _{j=1}^m{d}_{ij}\left(t\right)f_j\left(y_j(t-{\tau }_{ij}^{\left(1\right)}\left(t\right))\right)\hfill \\ \hfill & +\sum _{j=1}^m{h}_{ij}\left(t\right){\int }_{t-{\tau }_{ij}^{\left(2\right)}\left(t\right)}^t{f}_j\left(y_j\left(s\right)\right)\mathrm{\Delta }s+I_i\left(t\right)+\sum _{j=1}^m{\delta }_{ij}\left(y_j\left(t\right)\right)w_{1j}^{\mathrm{\Delta }}\left(t\right),\hfill \\ \hfill y_j^{{\mathrm{\Delta }}^2}\left(t\right)& =-{\gamma }_j\left(t\right)y_j^{{\mathrm{\Delta }}^{}}\left(t\right)-b_j\left(t\right)y_j\left(t\right)+\sum _{i=1}^n{l}_{ji}\left(t\right)g_i\left(x_i\left(t\right)\right)+\sum _{i=1}^n{p}_{ji}\left(t\right)g_i\left(x_i(t-{\zeta }_{ji}^{\left(1\right)}\left(t\right))\right)\hfill \\ \hfill & +\sum _{i=1}^n{q}_{ji}\left(t\right){\int }_{t-{\zeta }_{ji}^{\left(2\right)}\left(t\right)}^t{g}_i\left(x_i\left(s\right)\right)\mathrm{\Delta }s+J_j\left(t\right)+\sum _{i=1}^n{\phi }_{ji}\left(x_i\left(t\right)\right)w_{2i}^{\mathrm{\Delta }}\left(t\right),\hfill \end{array}$$

(6)

with initial data

$$x_i\left(t\right)={\theta }_i^{\left(1\right)}\left(t\right),y_j\left(t\right)={\theta }_j^{\left(2\right)}\left(t\right),t\in {[t_0-\vartheta ,t_0]}_{\mathbb{T}},$$

(7)

where $\vartheta =max\left\{\underset{i,j}{max}\{{\tau }_{ij}^{\left(\rho \right)}\left(t\right),{\zeta }_{ji}^{\left(\rho \right)}\left(t\right)\}\right\}$, $\rho =1,2$, $i=1,2,...,n,j=1,2,...,m$. $m,n$ are the numbers of neurons in layers. $x_i,y_j$ denote the state of the i-th and j-th neurons, respectively. $a_i,b_j$ denote the rate with which the i-th and j-th neurons will reset their potential to the resting state in isolation when disconnected from the networks and external inputs $f_j,g_i$ are activation functions. $c_{ij},l_{ji}$ are the connection weight parameters, $d_{ij},h_{ij},p_{ji}$ and $q_{ji}$ are delayed connection weight parameters. ${\tau }_{ij}^{\left(1\right)}\left(t\right),{\zeta }_{ji}^{\left(1\right)}\left(t\right)$, ${\tau }_{ij}^{\left(2\right)}\left(t\right)$ and ${\zeta }_{ji}^{\left(2\right)}\left(t\right)$ correspond to the discrete and distributed time-varying delays along the axon of the i-th and j-th units satisfying for $t\in \mathbb{T}$, $t-{\tau }_{ij}^{\left(\rho \right)}\left(t\right),t-{\zeta }_{ji}^{\left(\rho \right)}\left(t\right)\in \mathbb{T}$. $I_i$, $J_j$ are the external biases on the i-th and j-th units at time t. $w_{1j},w_{2i}$ are Brownian motions defined on complete probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$, where $\mathrm{\Omega }$ is a nonempty set, $\mathcal{F}$ is the associated $\sigma$-algebra on $\mathrm{\Omega }$ with the probability measure $\mathbb{P}$ on $(\mathrm{\Omega },\mathcal{F})$. ${\delta }_{ij}$, ${\phi }_{ji}$ denote the noise intensity.

Using variable substitution

$$x_i^{\mathrm{\Delta }}\left(t\right)+{\xi }_i{x}_i\left(t\right)=u_i\left(t\right),y_j^{\mathrm{\Delta }}\left(t\right)+{\kappa }_j{y}_j\left(t\right)=v_j\left(t\right),$$

(6) and (7) are equivalent to

$$\begin{array}{ccc}\hfill x_i^{\mathrm{\Delta }}\left(t\right)& =& -{\xi }_i{x}_i\left(t\right)+u_i\left(t\right), \hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill u_i^{\mathrm{\Delta }}\left(t\right)& =& -(a_i\left(t\right)-{\beta }_i\left(t\right){\xi }_i+{\xi }_i^2)x_i\left(t\right)-({\beta }_i\left(t\right)-{\xi }_i)u_i\left(t\right)\hfill \\ & +& \sum _{j=1}^m{c}_{ij}\left(t\right)f_j\left(y_j\left(t\right)\right)+\sum _{j=1}^m{d}_{ij}\left(t\right)f_j\left(y_j(t-{\tau }_{ij}^{\left(1\right)}\left(t\right))\right)\hfill \\ & +& \sum _{j=1}^m{h}_{ij}\left(t\right){\int }_{t-{\tau }_{ij}^{\left(2\right)}\left(t\right)}^t{f}_j\left(y_j\left(s\right)\right)\mathrm{\Delta }s+I_i\left(t\right)+\sum _{j=1}^n{\delta }_{ij}\left(y_j\left(t\right)\right)w_{1j}^{\mathrm{\Delta }}\left(t\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill y_j^{\mathrm{\Delta }}\left(t\right)& =& -{\kappa }_j{y}_j\left(t\right)+v_j\left(t\right), \hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill v_j^{\mathrm{\Delta }}\left(t\right)& =& -(b_j\left(t\right)-{\gamma }_j\left(t\right){\kappa }_j+{\kappa }_j^2)y_j\left(t\right)-({\gamma }_j\left(t\right)-{\kappa }_j)v_j\left(t\right)\hfill \\ & +& \sum _{i=1}^n{l}_{ji}\left(t\right)g_i\left(x_i\left(t\right)\right)+\sum _{i=1}^n{p}_{ji}\left(t\right)g_i\left(x_i(t-{\zeta }_{ji}^{\left(1\right)}\left(t\right))\right)\hfill \\ & +& \hfill \sum _{i=1}^n{q}_{ji}\left(t\right){\int }_{t-{\zeta }_{ji}^{\left(2\right)}\left(t\right)}^t{g}_i\left(x_i\left(s\right)\right)\mathrm{\Delta }s+J_j\left(t\right)+\sum _{i=1}^n{\phi }_{ji}\left(x_i\left(t\right)\right)w_{2i}^{\mathrm{\Delta }}\left(t\right).\end{array}$$

(11)

with initial data

$$x_i\left(t\right)={\theta }_i^{\left(1\right)}\left(t\right),y_j\left(t\right)={\theta }_j^{\left(2\right)}\left(t\right),t\in {[t_0-\vartheta ,t_0]}_{\mathbb{T}}.$$

(12)

Denote

$${\underline{\mathcal{X}}}_i=\underset{t\in \mathbb{T}}{inf}|{\mathcal{X}}_i\left(t\right)|,{\overline{\mathcal{X}}}_i=\underset{t\in \mathbb{T}}{sup}\left|{\mathcal{X}}_i\left(t\right)\right|,{\mathrm{\Psi }}_i=\underset{t\in \mathbb{T}}{sup}{\left|{\beta }_i{\xi }_i-a_i-{\xi }_i^2\right|}^2,{\mathrm{\Gamma }}_j=\underset{t\in \mathbb{T}}{sup}{\left|{\gamma }_j{\kappa }_j-b_j-{\kappa }_j^2\right|}^2$$

for $i=1,2,...,n,j=1,2,...,m.$

3.1. Periodic Solution

Assumption 1.

$f_j$, ${\delta }_{ij}$, $g_i$ and ${\phi }_{ji}$ are Lipschitz-continuous with positive constants $L_j^f$, $L_{ij}^{\delta }$, $L_i^g$ and $L_{ji}^{\phi }$, respectively, and $f_j\left(0\right)=g_i\left(0\right)={\delta }_{ij}\left(0\right)={\phi }_{ji}\left(0\right)=0$ for $i=1,2,...,n,j=1,2,...,m$.

Assumption 2.

${\xi }_i,{\kappa }_j,{\beta }_i\left(t\right)-{\xi }_i,{\gamma }_j\left(t\right)-{\kappa }_j>0$ with $-{\xi }_i,-{\kappa }_j,-({\beta }_i\left(t\right)-{\xi }_i),-({\gamma }_j\left(t\right)-{\kappa }_j)\in \mathcal{R}$. $a_i\left(t\right)$, $b_j\left(t\right)$, ${\beta }_i\left(t\right)$, ${\gamma }_j\left(t\right)$, $c_{ij}\left(t\right)$, $l_{ji}\left(t\right)$, $d_{ij}\left(t\right)$, $p_{ji}\left(t\right)$, $h_{ij}\left(t\right)$, $q_{ji}\left(t\right)$, $I_i\left(t\right)$, $J_j\left(t\right)$$(i=1,2,...,n,j=1,2,...,m)$ are periodic functions with period $\omega >0$.

Lemma 6.

Suppose Assumptions 1 and 2 hold, for $i=1,2,...,n,j=1,2,...,m$, $(x_i\left(t\right),y_j\left(t\right))$ is an ω-periodic solution of (6) if and only if it is the solution of

$$\begin{array}{ccc}\hfill x_i\left(t\right)& =& {\int }_t^{t+\omega }{A}_i(t,s)u_i\left(s\right)\mathrm{\Delta }s, \hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill u_i\left(t\right)& =& {\int }_t^{t+\omega }{B}_i(t,s)[-(a_i\left(s\right)-{\beta }_i\left(s\right){\xi }_i+{\xi }_i^2)x_i\left(s\right)+\sum _{j=1}^m{c}_{ij}\left(s\right)f_j\left(y_j\left(s\right)\right)\hfill \\ & +& \sum _{j=1}^m{d}_{ij}\left(s\right)f_j\left(y_j(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right)+\sum _{j=1}^m{h}_{ij}\left(s\right){\int }_{s-{\tau }_{ij}^{\left(2\right)}\left(s\right)}^s{f}_j\left(y_j\left(r\right)\right)\mathrm{\Delta }r\hfill \\ & +& I_i\left(s\right)]\mathrm{\Delta }s+{\int }_t^{t+\omega }{B}_i(t,s)\sum _{j=1}^m{\delta }_{ij}\left(y_j\left(s\right)\right)\mathrm{\Delta }{w}_{1j}\left(s\right),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill y_j\left(t\right)& =& {\int }_t^{t+\omega }{F}_j(t,s)v_j\left(s\right)\mathrm{\Delta }s, \hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill v_j\left(t\right)& =& {\int }_t^{t+\omega }{G}_j(t,s)[-(b_j\left(s\right)-{\gamma }_j\left(s\right){\kappa }_j+{\kappa }_j^2)y_j\left(s\right)+\sum _{i=1}^n{l}_{ji}\left(s\right)g_i\left(x_i\left(s\right)\right)\hfill \\ & +& \sum _{i=1}^n{p}_{ji}\left(s\right)g_i\left(x_i(s-{\zeta }_{ji}^{\left(1\right)}\left(s\right))\right)+\sum _{i=1}^n{q}_{ji}\left(s\right){\int }_{s-{\zeta }_{ji}^{\left(2\right)}\left(s\right)}^s{g}_i\left(x_i\left(r\right)\right)\mathrm{\Delta }r\hfill \\ & +& J_j\left(s\right)]\mathrm{\Delta }s+{\int }_t^{t+\omega }{G}_j(t,s)\sum _{i=1}^n{\phi }_{ji}\left(x_i\left(s\right)\right)\mathrm{\Delta }{w}_{2i}\left(s\right),\hfill \end{array}$$

(16)

where

$$A_i(t,s)=\frac{e_{-{\xi }_i}(t+\omega ,\sigma \left(s\right))}{1-e_{-{\xi }_i}(t+\omega ,t)},B_i(t,s)=\frac{e_{-({\beta }_i-{\xi }_i)}(t+\omega ,\sigma \left(s\right))}{1-e_{-({\beta }_i-{\xi }_i)}(t+\omega ,t)},$$

$$F_j(t,s)=\frac{e_{-{\kappa }_j}(t+\omega ,\sigma \left(s\right))}{1-e_{-{\kappa }_j}(t+\omega ,t)},G_j(t,s)=\frac{e_{-({\gamma }_j-{\kappa }_j)}(t+\omega ,\sigma \left(s\right))}{1-e_{-({\gamma }_j-{\kappa }_j)}(t+\omega ,t)}.$$

Proof. 

Multiplying both sides of (8) by $e_{-{\xi }_i}(\theta ,\sigma \left(t\right))$, using Lemma 2, we have

$${\left[e_{-{\xi }_i}(\theta ,t)x_i\left(t\right)\right]}^{\mathrm{\Delta }}=e_{-{\xi }_i}(\theta ,\sigma \left(t\right))u_i\left(t\right).$$

(17)

Integrating both sides of (17) from t to $t+\omega$ and choosing $\theta =t+\omega$, we obtain

$$x_i(t+\omega )=e_{-{\xi }_i}(t+\omega ,t)x_i\left(t\right)+{\int }_t^{t+\omega }{e}_{-{\xi }_i}(t+\omega ,\sigma \left(s\right))u_i\left(s\right)\mathrm{\Delta }s.$$

(18)

Since $x_i(t+\omega )=x_i\left(t\right)$, then $x_i\left(t\right)$ satisfies (13). Similarly, we can obtain that $u_i\left(t\right)$, $y_i\left(t\right)$, $v_i\left(t\right)$ satisfy (14)–(16). Vice versa, (18) can be derived from (13) and derivative on both sides of (18), we can obtain that $x_i\left(t\right)$ satisfies (8). Similarly, $u_i\left(t\right)$, $y_i\left(t\right)$, $v_i\left(t\right)$ satisfy (9)–(11). □

 Let $\mathbb{X}=\{\left.z\in B{C}_{{\mathcal{F}}_0}^b(\mathbb{T},{\mathbb{R}}^{2n+2m})\right|z_k\left(t\right)=z_k(t+\omega ),{∥z∥}_{\mathbb{X}}\le R,k=1,2,...,2n+2m\}$ with norm

$${∥z∥}_{\mathbb{X}}=\underset{1\le k\le 2n+2m}{max}\underset{t\in {[t_0,t_0+\omega ]}_{\mathbb{T}}}{sup}E\left({\left|z_k\left(t\right)\right|}^2\right),k=1,2,...,2n+2m,$$

where $z={(z_1,...,z_n,z_{n+1},...,z_{2n},z_{2n+1},...,z_{2n+m},...,z_{2n+2m})}^T=(x_1,...,x_n,u_1,...,u_n,y_1,...,$$y_m,v_1,...,v_m{)}^T$. $B{C}_{{\mathcal{F}}_0}^b(\mathbb{T},{\mathbb{R}}^{2n+2m})$ is the family of bounded ${\mathcal{F}}_0$-measurables. $E(·)$ is the correspondent expectation operator and R is finite, which will be determined later, then $\mathbb{X}$ is a Banach space [34].

Theorem 1

(periodic solution). Let Assumptions 1 and 2 hold. If

$$\mathrm{\Lambda }=\underset{1\le i\le n,1\le j\le m}{max}\{{\mathrm{\Lambda }}_{1i},{\mathrm{\Lambda }}_{2i},{\mathrm{\Lambda }}_{3j},{\mathrm{\Lambda }}_{4j}\}<1,$$

(19)

where

$$\begin{array}{ccc}{\mathrm{\Lambda }}_{1i}\hfill & =& {\omega }^2\underset{t,s}{sup}\left\{A_i(t,s)\right\}, \hfill \end{array}$$

(20)

$$\begin{array}{lll}{\mathrm{\Lambda }}_{2i}\hfill & =& 5{\omega }^2\underset{t,s}{sup}\left\{B_i(t,s)\right\}[{\mathrm{\Psi }}_i+\sum _{j=1}^m{\left(L_j^f\right)}^2({\overline{c}}_{ij}^2+{\overline{d}}_{ij}^2+{\left({\overline{\tau }}_{ij}^{\left(2\right)}{\overline{h}}_{ij}^{}\right)}^2)+\frac{1}{\omega }{\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2],\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill {\mathrm{\Lambda }}_{3j}& =& {\omega }^2\underset{t,s}{sup}\left\{F_j(t,s)\right\}, \hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\mathrm{\Lambda }}_{4j}& =& 5{\omega }^2\underset{t,s}{sup}\left\{G_j(t,s)\right\}[{\mathrm{\Gamma }}_i+\sum _{i=1}^n{\left(L_i^g\right)}^2({\overline{l}}_{ji}^2+{\overline{p}}_{ji}^2+{\left({\overline{q}}_{ji}^2{\overline{\zeta }}_{ji}^{\left(2\right)}\right)}^2)+\frac{1}{\omega }{\left(\sum _{i=1}^n{L}_{ji}^{\phi }\right)}^2],\hfill \end{array}$$

(23)

where $t,s\in {[t_0,t_0+\omega ]}_{\mathbb{T}},t\le s$, then (6) and (7) have a unique ω-periodic solution in $\mathbb{X}$.

Proof. 

Define an operator $\Phi$ on $\mathbb{X}$ by

$$\Phi z={({\left(\Phi z\right)}_1,...,{\left(\Phi z\right)}_n,{\left(\Phi z\right)}_{n+1},...,{\left(\Phi z\right)}_{2n},{\left(\Phi z\right)}_{2n+1},...,{\left(\Phi z\right)}_{2n+m},...,{\left(\Phi z\right)}_{2n+2m})}^T,$$

in which

$$\begin{array}{ccc}\hfill {\left(\Phi z\right)}_i\left(t\right)& =& {\int }_t^{t+\omega }{A}_i(t,s)z_{n+i}\left(s\right)\mathrm{\Delta }s,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\left(\Phi z\right)}_{n+i}\left(t\right)& =& {\int }_t^{t+\omega }{B}_i(t,s)[-(a_i\left(s\right)-{\beta }_i\left(s\right){\xi }_i+{\xi }_i^2)z_i\left(s\right)+\sum _{j=1}^m{c}_{ij}\left(s\right)f_j\left(z_{2n+j}\left(s\right)\right)\hfill \\ & +& \sum _{j=1}^m{d}_{ij}\left(s\right)f_j\left(z_{2n+j}(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right)+\sum _{j=1}^m{h}_{ij}\left(s\right){\int }_{s-{\tau }_{ij}^{\left(2\right)}\left(s\right)}^s{f}_j\left(z_{2n+j}\left(r\right)\right)\mathrm{\Delta }r\hfill \\ & +& I_i\left(s\right)+\sum _{j=1}^m{\delta }_{ij}\left(z_{2n+j}\left(s\right)\right)\mathrm{\Delta }{w}_{1j}\left(s\right)]\mathrm{\Delta }s,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\left(\Phi z\right)}_{2n+j}\left(t\right)& =& {\int }_t^{t+\omega }{F}_j(t,s)z_{2n+m+j}\left(s\right)\mathrm{\Delta }s,\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\left(\Phi z\right)}_{2n+m+j}\left(t\right)& =& {\int }_t^{t+\omega }{G}_j(t,s)[-(b_j\left(s\right)-{\gamma }_j\left(s\right){\kappa }_j+{\kappa }_j^2)z_{2n+j}\left(s\right)+\sum _{i=1}^n{l}_{ji}\left(s\right)g_i\left(z_i\left(s\right)\right)\hfill \\ & +& \sum _{i=1}^n{p}_{ji}\left(s\right)g_i\left(z_i(s-{\zeta }_{ji}^{\left(1\right)}\left(s\right))\right)+\sum _{i=1}^n{q}_{ji}\left(s\right){\int }_{s-{\zeta }_{ji}^{\left(2\right)}\left(s\right)}^s{g}_i\left(z_i\left(r\right)\right)\mathrm{\Delta }r\hfill \\ & +& J_j\left(s\right)+\sum _{i=1}^n{\phi }_{ji}\left(z_i\left(s\right)\right)\mathrm{\Delta }{w}_{2i}\left(s\right)]\mathrm{\Delta }s.\hfill \end{array}$$

(27)

Using Assumption 2, it follows from (24)–(27) that ${\left(\Phi z\right)}_k\left(t\right)={\left(\Phi z\right)}_k(t+\omega )$ for $k=1,2,...,2n+2m$.

 Next, we prove ${∥\Phi z∥}_{\mathbb{X}}\le R$. It follows from (24)–(27) that

$$\begin{array}{ccc}& & E{\left|{\left(\Phi z\right)}_i\left(t\right)\right|}^2=E{\left|\underset{t,s}{sup}\left\{A_i(t,s)\right\}{\int }_t^{t+\omega }{z}_{n+i}\left(s\right)\mathrm{\Delta }s\right|}^2\le {\mathrm{\Lambda }}_{1i}{∥z∥}_{\mathbb{X}},\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & E{\left|{\left(\Phi z\right)}_{n+i}\left(t\right)\right|}^2\le \frac{6}{5}{\mathrm{\Lambda }}_{2i}{∥z∥}_{\mathbb{X}}+6E{\left|{\int }_t^{t+\omega }{B}_i(t,s)I_i\left(s\right)\mathrm{\Delta }s\right|}^2,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}& & E{\left|{\left(\Phi z\right)}_{2n+j}\left(t\right)\right|}^2={\mathrm{\Lambda }}_{3j}{∥z∥}_{\mathbb{X}},\hfill \end{array}$$

(30)

$$\begin{array}{ccc}& & E{\left|{\left(\Phi z\right)}_{2n+m+j}\left(t\right)\right|}^2\le \frac{6}{5}{\mathrm{\Lambda }}_{4j}{∥z∥}_{\mathbb{X}}+6E{\left|{\int }_t^{t+\omega }{G}_j(t,s)J_j\left(s\right)\mathrm{\Delta }s\right|}^2,\hfill \end{array}$$

(31)

Let

$$\begin{array}{ccc}\hfill {\mathrm{\Lambda }}_5& =& \underset{1\le i\le n,1\le j\le m}{max}\{{\mathrm{\Lambda }}_{1i},\frac{6}{5}{\mathrm{\Lambda }}_{2i},{\mathrm{\Lambda }}_{3j},\frac{6}{5}{\mathrm{\Lambda }}_{4j}\},\hfill \\ \hfill {\mathrm{\Lambda }}_6& =& \underset{1\le i\le n,1\le j\le m}{max}\left\{6E{\left|{\int }_t^{t+\omega }{B}_i(t,s)I_i\left(s\right)\mathrm{\Delta }s\right|}^2,6E{\left|{\int }_t^{t+\omega }{G}_j(t,s)J_j\left(s\right)\mathrm{\Delta }s\right|}^2\right\},\hfill \end{array}$$

then

$${∥\Phi z∥}_{\mathbb{X}}\le {\mathrm{\Lambda }}_5{∥z∥}_{\mathbb{X}}+{\mathrm{\Lambda }}_6.$$

(32)

Choosing $R\ge {\mathrm{\Lambda }}_6/\left(1-{\mathrm{\Lambda }}_5\right)$, we have ${∥\Phi z∥}_{\mathbb{X}}\le R$, which means $\Phi \mathbb{X}\subset \mathbb{X}$.

Then, we prove $\mathrm{\Phi }$ is a contraction mapping. For any $z,z^{*}\in \mathbb{X}$, it follows from (28)–(31) that

$$\begin{array}{ccc}\hfill E{\left|{(\mathrm{\Phi }z-\mathrm{\Phi }{z}^{*})}_i\left(t\right)\right|}^2& =& E{\left|{\int }_t^{t+\omega }\underset{t,s}{sup}\left\{A_i(t,s)\right\}(z_{n+i}\left(s\right)-z_{n+i}^{*}\left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & \le & {\mathrm{\Lambda }}_{1i}E\left({\left|{\int }_t^{t+\omega }(z_{n+i}\left(s\right)-z_{n+i}^{*}\left(s\right))\mathrm{\Delta }s\right|}^2\right)\le {\mathrm{\Lambda }}_{1i}{∥z-z^{*}∥}_{\mathbb{X}}.\hfill \end{array}$$

(33)

Similarly,

$$\begin{array}{ccc}\hfill E{\left|{(\mathrm{\Phi }z-\mathrm{\Phi }{z}^{*})}_{n+i}\left(t\right)\right|}^2& \le & {\mathrm{\Lambda }}_{2i}{∥z-z^{*}∥}_{\mathbb{X}}.\hfill \\ \hfill E{\left|{(\mathrm{\Phi }z-\mathrm{\Phi }{z}^{*})}_{2n+j}\left(t\right)\right|}^2& \le & {\mathrm{\Lambda }}_{3j}{∥z-z^{*}∥}_{\mathbb{X}}.\hfill \\ \hfill E{\left|{(\mathrm{\Phi }z-\mathrm{\Phi }{z}^{*})}_{2n+m+j}\left(t\right)\right|}^2& \le & {\mathrm{\Lambda }}_{4j}{∥z-z^{*}∥}_{\mathbb{X}}.\hfill \end{array}$$

We obtain

$${∥\mathrm{\Phi }z-\mathrm{\Phi }{z}^{*}∥}_{\mathbb{X}}\le \mathrm{\Lambda }{∥z-z^{*}∥}_{\mathbb{X}}<{∥z-z^{*}∥}_{\mathbb{X}}$$

for $\mathrm{\Lambda }={\displaystyle \underset{1\le i\le n,1\le j\le m}{max}}\{{\mathrm{\Lambda }}_{1i},{\mathrm{\Lambda }}_{2i},{\mathrm{\Lambda }}_{3j},{\mathrm{\Lambda }}_{4j}\}<1$, which means $\mathrm{\Phi }$ is a contraction mapping in $\mathbb{X}$. Thus, $\mathrm{\Phi }$ possesses a unique fixed point and there exists a unique periodic solution for systems (6) and (7) in $\mathbb{X}$. □

3.2. Almost Periodic Solution

Assumption 3.

${\xi }_i,{\kappa }_j,{\beta }_i\left(t\right)-{\xi }_i,{\gamma }_j\left(t\right)-{\kappa }_j>0$ with $-{\xi }_i,-{\kappa }_j,-({\beta }_i\left(t\right)-{\xi }_i),-({\gamma }_j\left(t\right)-{\kappa }_j)\in {\mathcal{R}}^{+}$. $a_i\left(t\right)$, $b_j\left(t\right)$, ${\beta }_i\left(t\right)$, ${\gamma }_j\left(t\right)$, $c_{ij}\left(t\right)$, $l_{ji}\left(t\right)$, $d_{ij}\left(t\right)$, $p_{ji}\left(t\right)$, $h_{ij}\left(t\right)$, $q_{ji}\left(t\right)$, $I_i\left(t\right)$, $J_j\left(t\right)$$(i=1,2,...,n,$$j=1,2,...,m)$ are almost periodic with period $\tau >0$.

Lemma 7

([35]). If $p\in {\mathcal{R}}^{+}$ and $p\left(t\right)<0$ for $t\in \mathbb{T}$, then for $\forall s\le t$ and $s\in \mathbb{T}$,

$$0<e_p(t,s)\le exp\left({\int }_s^{t}p\left(r\right)\mathrm{\Delta }r\right)<1.$$

(34)

Lemma 8

([36]). If $\alpha \in {\mathbb{R}}^{+}$, then

$$e^{-\alpha (t-s)}\le e_{\ominus \alpha }(t,s),s\le t,s,t\in \mathbb{T}.$$

We give an important Proposition to be used in the study of the existence of an almost periodic solution for (6) and (7).

Lemma 9.

If ${\xi }_i,{\kappa }_j,{\beta }_i\left(t\right)-{\xi }_i,{\gamma }_j\left(t\right)-{\kappa }_j>0$ with $-{\xi }_i,-{\kappa }_j,-({\beta }_i\left(t\right)-{\xi }_i),-({\gamma }_j\left(t\right)-{\kappa }_j)\in {\mathcal{R}}^{+}$, ${\beta }_i\left(t\right)$, ${\gamma }_j\left(t\right)$ are almost periodic, then

$$e_{-{\xi }_i}(t+\tau ,\sigma \left(s\right)+\tau )-e_{-{\xi }_i}(t,\sigma \left(s\right))=0,e_{-{\kappa }_j}(t+\tau ,\sigma \left(s\right)+\tau )-e_{-{\kappa }_j}(t,\sigma \left(s\right))=0.$$

(35)

$$\begin{array}{ccc}& & E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & \le & \widehat{\epsilon }{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}.\hfill \end{array}$$

(36)

$$\begin{array}{ccc}& & E{\left|{\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t+\tau ,\sigma (s+\tau ))-e_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & \le & \widehat{\epsilon }{(\frac{2}{{({\underline{\gamma }}_j-{\kappa }_j)}^2}+\frac{\overline{\mu }}{{\underline{\gamma }}_j-{\kappa }_j})}^2{e}^{2({\underline{\gamma }}_j-{\kappa }_j)\overline{\mu }}.\hfill \end{array}$$

(37)

$$\begin{array}{ccc}& & E{\int }_{-\infty }^t{(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))}^2\mathrm{\Delta }s\hfill \\ & \le & \widehat{\epsilon }(\frac{4}{{({\underline{\beta }}_i-{\xi }_i)}^3}+\frac{4\overline{\mu }}{{\left({\underline{\beta }}_i-{\xi }_i\right)}^2})e^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}.\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& & E{\int }_{-\infty }^t{(e_{-({\gamma }_j-{\kappa }_j)}(t+\tau ,\sigma (s+\tau ))-e_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right)))}^2\mathrm{\Delta }s\hfill \\ & \le & \widehat{\epsilon }(\frac{4}{{({\underline{\gamma }}_j-{\kappa }_j)}^3}+\frac{4\overline{\mu }}{{\left({\underline{\gamma }}_j-{\kappa }_j\right)}^2})e^{2({\underline{\gamma }}_j-{\kappa }_j)\overline{\mu }}.\hfill \end{array}$$

(39)

Proof. 

Using Lemmas 2 and 3, we obtain

$${\left(e_{-{\xi }_i}(r+\tau ,\sigma \left(s\right)+\tau )\right)}^{{\mathrm{\Delta }}_r}=-{\xi }_i{e}_{-{\xi }_i}(r+\tau ,\sigma \left(s\right)+\tau ),$$

(40)

and

$${\left(e_{-{\xi }_i}(t,r)\right)}^{{\mathrm{\Delta }}_r}={\xi }_i{e}_{-{\xi }_i}(t,\sigma \left(r\right)).$$

(41)

Multiplying both sides of (40) by $e_{-{\xi }_i}(t,\sigma \left(r\right))$ and using (41),

$${\left(e_{-{\xi }_i}(r+\tau ,\sigma \left(s\right)+\tau )e_{-{\xi }_i}(t,r)\right)}^{\mathrm{\Delta }r}=0.$$

(42)

Integrating (42) from $\sigma \left(s\right)$ to t, we have

$${\left.e_{-{\xi }_i}(r+\tau ,\sigma \left(s\right)+\tau )e_{-{\xi }_i}(t,r)\right|}_{r=\sigma \left(s\right)}^{r=t}=0.$$

Similarly, we can obtain

$${\left.e_{-{\kappa }_j}(r+\tau ,\sigma \left(s\right)+\tau )e_{-{\kappa }_j}(t,r)\right|}_{r=\sigma \left(s\right)}^{r=t}=0,$$

which means (35) holds.

For (36), it follows from Lemma 2 that

$$\begin{array}{cc}\hfill & {\left(e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )\right)}^{{\mathrm{\Delta }}_r}\hfill \\ \hfill =& -({\beta }_i(r+\tau )-{\xi }_i)e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )\hfill \\ \hfill =& -({\beta }_i\left(r\right)-{\xi }_i)e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )\hfill \\ \hfill +& ({\beta }_i\left(r\right)-{\beta }_i(r+\tau ))e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau ).\hfill \end{array}$$

(43)

Multiplying both sides of (43) by $e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(r\right))$ and integrating it from $\sigma \left(s\right)$ to t, using Lemma 3,

$${\left(e_{-({\beta }_i-{\xi }_i)}(t,r)\right)}^{{\mathrm{\Delta }}_r}=({\beta }_i\left(r\right)-{\xi }_i)e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(r\right)),$$

we have

$$\begin{array}{cc}\hfill & E{\left|{\int }_{-\infty }^t{\left.e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )e_{-({\beta }_i-{\xi }_i)}(t,r)\right|}_{r=\sigma \left(s\right)}^{r=t}\mathrm{\Delta }s\right|}^2\hfill \\ \hfill =& E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma \left(s\right)+\tau )-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ \hfill \le & E{\left|{\int }_{-\infty }^t{\int }_{\sigma \left(s\right)}^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(r\right))e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )({\beta }_i\left(r\right)-{\beta }_i(r+\tau ))\mathrm{\Delta }r\mathrm{\Delta }s\right|}^2\hfill \\ \hfill \le & \widehat{\epsilon }E{\left|{\int }_{-\infty }^t{\int }_{\sigma \left(s\right)}^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(r\right))e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )\mathrm{\Delta }r\mathrm{\Delta }s\right|}^2,\hfill \end{array}$$

(44)

where

$$\begin{array}{cc}& e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(r\right))e_{-({\beta }_i-{\xi }_i)}(r+\tau ,\sigma \left(s\right)+\tau )\le e^{-({\underline{\beta }}_i-{\xi }_i)(t-\sigma \left(r\right))}{e}^{-({\underline{\beta }}_i-{\xi }_i)(r-\sigma \left(s\right))}\hfill \\ \hfill =& e^{-({\underline{\beta }}_i-{\xi }_i)(t-r)}{e}^{({\underline{\beta }}_i-{\xi }_i)(\sigma \left(r\right)-r)}{e}^{-({\underline{\beta }}_i-{\xi }_i)(r-\sigma \left(s\right))}\le e^{-({\underline{\beta }}_i-{\xi }_i)(t-\sigma \left(s\right))}{e}^{({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}\hfill \end{array}$$

by using Lemma 7. With $\sigma (s+\tau )=\sigma \left(s\right)+\tau$ derived from Lemma 1, it follows from (44) that

$$\begin{array}{ccc}\hfill & & E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & =& E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma \left(s\right)+\tau )-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & \le & \widehat{\epsilon }E{\left|{\int }_{-\infty }^t{e}^{({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}{e}^{-({\underline{\beta }}_i-{\xi }_i)(t-\sigma \left(s\right))}(t-\sigma \left(s\right))\mathrm{\Delta }s\right|}^2.\hfill \end{array}$$

(45)

Using $\frac{(t-\sigma (s\left)\right)}{2}({\underline{\beta }}_i-{\xi }_i)\le e^{\frac{{\underline{\beta }}_i-{\xi }_i}{2}(t-\sigma \left(s\right))}$, and Lemmas 3 and 8, it follows from (45) that

$$\begin{array}{cc}\hfill & E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ \hfill \le & \frac{4\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}E{\left|{\int }_{-\infty }^t{e}^{-\frac{1}{2}({\underline{\beta }}_i-{\xi }_i)(t-\sigma \left(s\right))}\mathrm{\Delta }s\right|}^2\hfill \\ \hfill \le & \frac{4\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}E{\left|{\int }_{-\infty }^t{e}_{\ominus \left(\frac{1}{2}({\underline{\beta }}_i-{\xi }_i)\right)}(t,\sigma \left(s\right))\mathrm{\Delta }s\right|}^2\le \widehat{\epsilon }{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}.\hfill \end{array}$$

(46)

Thus (36) holds. Similarly, (37) can be derived.

For (38), using $\frac{(t-\sigma (s\left)\right)}{2}({\underline{\beta }}_i-{\xi }_i)\le e^{\frac{{\underline{\beta }}_i-{\xi }_i}{2}(t-\sigma \left(s\right))}$, and Lemmas 3 and 8,

$$\begin{array}{cc}\hfill & E{\int }_{-\infty }^t{(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))}^2\mathrm{\Delta }s\hfill \\ \hfill \le & \widehat{\epsilon }E{\int }_{-\infty }^t{\left[e^{({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}{e}^{-({\underline{\beta }}_i-{\xi }_i)(t-\sigma \left(s\right))}(t-\sigma \left(s\right))\right]}^2\mathrm{\Delta }s\hfill \\ \hfill \le & \widehat{\epsilon }\frac{4}{{({\underline{\beta }}_i-{\xi }_i)}^2}{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}E{\int }_{-\infty }^t{e}^{-({\underline{\beta }}_i-{\xi }_i)(t-\sigma \left(s\right))}\mathrm{\Delta }s\hfill \\ \hfill \le & \widehat{\epsilon }\frac{4}{{({\underline{\beta }}_i-{\xi }_i)}^2}{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}E{\int }_{-\infty }^t{e}_{\ominus ({\underline{\beta }}_i-{\xi }_i)}(t,\sigma \left(s\right))\mathrm{\Delta }s\le \widehat{\epsilon }(\frac{4}{{({\underline{\beta }}_i-{\xi }_i)}^3}+\frac{4\mu }{{({\underline{\beta }}_i-{\xi }_i)}^2})e^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}.\hfill \end{array}$$

(47)

Similarly, (39) can be derived. □

Let $\mathbb{Y}=\{\left.z\in B{C}_{{\mathcal{F}}_0}^b(\mathbb{T},{\mathbb{R}}^{2n+2m})\right|z_k\left(t\right)\mathrm{be}\mathrm{almost}\mathrm{periodic},{∥z∥}_{\mathbb{Y}}\le \tilde{R},k=1,2,...,2n+2m\}$ with norm

$${∥z∥}_{\mathbb{Y}}=\underset{1\le k\le 2n+2m}{max}\underset{t\in \mathbb{T}}{sup}E\left({\left|z_k\left(t\right)\right|}^2\right),k=1,2,...,2n+2m,$$

where $\tilde{R}$ is finite, which will be determined later, then $\mathbb{Y}$ is a Banach space [37].

Theorem 2

(almost periodic solution). Let Assumptions 1 and 3 hold. If

$$M=\underset{1\le i\le n,1\le j\le m}{max}\{M_{1i},M_{2j},M_{3i},M_{4j}\}<1,$$

(48)

where

$$\begin{array}{ccc}\hfill M_{1i}& =& \frac{1}{{\left({\xi }_i\right)}^2},M_{2j}=\frac{1}{{\left({\kappa }_j\right)}^2},\hfill \\ \hfill M_{3i}& =& \frac{5}{{({\underline{\beta }}_i-{\xi }_i)}^2}[{\mathrm{\Psi }}_i+{\left(\sum _{j=1}^m{\overline{c}}_{ij}{L}_j^f\right)}^2+{\left(\sum _{j=1}^m{\overline{d}}_{ij}{L}_j^f\right)}^2+{\left(\sum _{j=1}^m{\overline{h}}_{ij}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2+({\underline{\beta }}_i-{\xi }_i){\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2],\hfill \\ \hfill M_{4j}& =& \frac{5}{{({\underline{\gamma }}_j-{\kappa }_j)}^2}[{\mathrm{\Gamma }}_j+{\left(\sum _{i=1}^n{\overline{l}}_{ji}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{p}}_{ji}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{q}}_{ji}{\overline{\zeta }}_{ji}^{\left(2\right)}{L}_i^g\right)}^2+({\underline{\gamma }}_j-{\kappa }_j){\left(\sum _{i=1}^n{L}_{ji}^{\phi }\right)}^2],\hfill \end{array}$$

(49)

then (6) and (7) have a unique almost periodic solution in $\mathbb{Y}$.

Proof. 

From (8), we have

$$x_i\left(t\right)=e_{-{\xi }_i}(t,t_0)x_i\left(t_0\right)+{\int }_{t_0}^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))u_i\left(s\right)\mathrm{\Delta }s,$$

(50)

where $t_0,t\in \mathbb{T}$, $t\ge t_0$. As $t_0\to -\infty$ in (50), we have

$$x_i\left(t\right)={\int }_{-\infty }^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))u_i\left(s\right)\mathrm{\Delta }s.$$

(51)

Similarly, it follows from (9)–(11) that

$$\begin{array}{ccc}\hfill u_i\left(t\right)& =& -{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))(a_i\left(s\right)-{\beta }_i\left(s\right){\xi }_i+{\xi }_i^2)x_i\left(s\right)\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m(c_{ij}\left(s\right)f_j\left(y_j\left(s\right)\right)+d_{ij}\left(s\right)f_j\left(y_j(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right))\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{h}_{ij}\left(s\right){\int }_{s-{\tau }_{ij}^{\left(2\right)}\left(s\right)}^s{f}_j\left(y_j\left(r\right)\right)\mathrm{\Delta }r\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))I_i\left(s\right)\mathrm{\Delta }s+{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{\delta }_{ij}\left(y_j\left(s\right)\right)\mathrm{\Delta }{w}_{1j}\left(s\right),\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill y_j\left(t\right)& =& {\int }_{-\infty }^t{e}_{-{\kappa }_j}(t,\sigma \left(s\right))v_j\left(s\right)\mathrm{\Delta }s,\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill v_j\left(t\right)& =& -{\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))(b_j\left(s\right)-{\gamma }_j\left(s\right){\kappa }_j+{\kappa }_j^2)y_j\left(s\right)\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\sum _{i=1}^n(l_{ji}\left(s\right)g_i\left(x_i\left(s\right)\right)+p_{ji}\left(s\right)g_i\left(x_i(s-{\zeta }_{ji}^{\left(1\right)}\left(s\right))\right))\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\sum _{i=1}^n{q}_{ji}\left(s\right){\int }_{s-{\zeta }_{ji}^{\left(2\right)}\left(s\right)}^s{g}_i\left(x_i\left(r\right)\right)\mathrm{\Delta }r\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))J_j\left(s\right)\mathrm{\Delta }s+{\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\sum _{i=1}^n{\phi }_{ji}\left(x_i\left(s\right)\right)\mathrm{\Delta }{w}_{2i}\left(s\right).\hfill \end{array}$$

(54)

Define an operator $\mathrm{\Theta }$ on $\mathbb{Y}$ with

$$\mathrm{\Theta }z={({\left(\mathrm{\Theta }z\right)}_1,...,{\left(\mathrm{\Theta }z\right)}_n,{\left(\mathrm{\Theta }z\right)}_{n+1},...,{\left(\mathrm{\Theta }z\right)}_{2n},{\left(\mathrm{\Theta }z\right)}_{2n+1},...,{\left(\mathrm{\Theta }z\right)}_{2n+m},...,{\left(\mathrm{\Theta }z\right)}_{2n+2m})}^T,$$

in which

$$\begin{array}{ccc}\hfill {\left(\mathrm{\Theta }z\right)}_i\left(t\right)& =& {\int }_{-\infty }^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))u_i\left(s\right)\mathrm{\Delta }s,\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill {\left(\mathrm{\Theta }z\right)}_{n+i}\left(t\right)& =& -{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))(a_i\left(s\right)-{\beta }_i\left(s\right){\xi }_i+{\xi }_i^2)x_i\left(s\right)\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m(c_{ij}\left(s\right)f_j\left(y_j\left(s\right)\right)+d_{ij}\left(s\right)f_j\left(y_j(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right))\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{h}_{ij}\left(s\right){\int }_{s-{\tau }_{ij}^{\left(2\right)}\left(s\right)}^s{f}_j\left(y_j\left(r\right)\right)\mathrm{\Delta }r\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))I_i\left(s\right)\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{\delta }_{ij}\left(y_j\left(s\right)\right)\mathrm{\Delta }{w}_{1j}\left(s\right),\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill {\left(\mathrm{\Theta }z\right)}_{2n+j}\left(t\right)& =& {\int }_{-\infty }^t{e}_{-{\kappa }_j}(t,\sigma \left(s\right))v_j\left(s\right)\mathrm{\Delta }s,\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill {\left(\mathrm{\Theta }z\right)}_{2n+m+j}\left(t\right)& =& -{\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))(b_j\left(s\right)-{\gamma }_j\left(s\right){\kappa }_j+{\kappa }_j^2)y_j\left(s\right)\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\sum _{i=1}^n(l_{ji}\left(s\right)g_i\left(x_i\left(s\right)\right)+p_{ji}\left(s\right)g_i\left(x_i(s-{\zeta }_{ji}^{\left(1\right)}\left(s\right))\right))\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\sum _{i=1}^n{q}_{ji}\left(s\right){\int }_{s-{\zeta }_{ji}^{\left(2\right)}\left(s\right)}^s{g}_i\left(x_i\left(r\right)\right)\mathrm{\Delta }r\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))J_j\left(s\right)\mathrm{\Delta }s\hfill \\ & +& {\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))\sum _{i=1}^n{\phi }_{ji}\left(x_i\left(s\right)\right)\mathrm{\Delta }{w}_{2i}\left(s\right).\hfill \end{array}$$

(58)

First, we prove $\mathrm{\Psi }z\in \mathbb{Y}$. Using Proposition 9, we obtain

$$e_{-{\xi }_i}(t+\tau ,\sigma \left(s\right)+\tau )-e_{-{\xi }_i}(t,\sigma \left(s\right))=0.$$

(59)

Using Lemma 4, it follows from (59) that

$$\begin{array}{cc}\hfill & E{\left|{\left(\mathrm{\Theta }z\right)}_i(t+\tau )-{\left(\mathrm{\Theta }z\right)}_i\left(t\right)\right|}^2\le 2E{\left|{\int }_{-\infty }^t(e_{-{\xi }_i}(t+\tau ,\sigma (s+\tau ))-e_{-{\xi }_i}(t,\sigma \left(s\right)))u_i(s+\tau )\mathrm{\Delta }s\right|}^2\hfill \\ \hfill & +2E{\left|{\int }_{-\infty }^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))(u_i(s+\tau )-u_i\left(s\right))\mathrm{\Delta }s\right|}^2\le \frac{2}{{\xi }_i^2}\widehat{\epsilon }.\hfill \end{array}$$

(60)

Since

$$\begin{array}{ccc}\hfill & & E{\left|{\left(\mathrm{\Theta }z\right)}_{n+i}(t+\tau )-{\left(\mathrm{\Theta }z\right)}_{n+i}\left(t\right)\right|}^2\hfill \\ & \le & 12E|{\int }_{-\infty }^t(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))\hfill \\ & \times & ({\beta }_i\left(s\right){\xi }_i-a_i\left(s\right)-{\xi }_i^2)x_i{(s+\tau )\mathrm{\Delta }s|}^2\hfill \\ & +& 12E\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))(({\beta }_i(s+\tau ){\xi }_i-a_i(s+\tau )-{\xi }_i^2)x_i(s+\tau )\right.\hfill \\ & -& {\left.({\beta }_i\left(s\right){\xi }_i-a_i\left(s\right)-{\xi }_i^2)x_i\left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E{\left|{\int }_{-\infty }^t(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))\sum _{j=1}^m{c}_{ij}(s+\tau )f_j\left(y_j(s+\tau )\right)\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))(\sum _{j=1}^m{c}_{ij}(s+\tau )f_j\left(y_j(s+\tau )\right)-\sum _{j=1}^m{c}_{ij}\left(s\right)f_j\left(y_j\left(s\right)\right))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E\left|{\int }_{-\infty }^t(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))\right.\hfill \\ & \times & {\left.\sum _{j=1}^m{d}_{ij}(s+\tau )f_j\left(y_j(s+\tau -{\tau }_{ij}^{\left(1\right)}\left(s\right))\right)\mathrm{\Delta }s\right|}^2+12E\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\right.\hfill \\ & \times & {\left.(\sum _{j=1}^m{d}_{ij}(s+\tau )f_j(y_j(s+\tau -{\tau }_{ij}^{(1)}(s)))-\sum _{j=1}^m{d}_{ij}(s)f_j(y_j(s-{\tau }_{ij}^{(1)}(s))))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E\left|{\int }_{-\infty }^t(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))\right.\hfill \\ & \times & {\left.\sum _{j=1}^m{h}_{ij}(s+\tau ){\int }_{s+\tau -{\tau }_{ij}^{\left(2\right)}\left(s\right)}^{s+\tau }{f}_j\left(y_j\left(r\right)\right)\mathrm{\Delta }r\mathrm{\Delta }s\right|}^2+12E\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\right.\hfill \\ & \times & {\left.(\sum _{j=1}^m{h}_{ij}(s+\tau ){\int }_{s+\tau -{\tau }_{ij}^{(2)}(s)}^{s+\tau }{f}_j(y_j(r))\mathrm{\Delta }r-\sum _{j=1}^m{h}_{ij}(s){\int }_{s-{\tau }_{ij}^{(2)}(s)}^s{f}_j(y_j(r))\mathrm{\Delta }r\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E{\left|{\int }_{-\infty }^t(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))I_i(s+\tau )\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))(I_i(s+\tau )-I_i\left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 12E{\left|{\int }_{-\infty }^t(e_{-({\beta }_i-{\xi }_i)}(t+\tau ,\sigma (s+\tau ))-e_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right)))\sum _{j=1}^m{\delta }_{ij}\left(y_j(s+\tau )\right)\mathrm{\Delta }{w}_{1j}\left(s\right)\right|}^2\hfill \\ & +& 12E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))(\sum _{j=1}^m{\delta }_{ij}\left(y_j(s+\tau )\right)-\sum _{j=1}^m{\delta }_{ij}\left(y_j\left(s\right)\right))\mathrm{\Delta }{w}_{1j}\left(s\right)\right|}^2\hfill \\ & =& \sum _{\upsilon =1}^{12}{\mathrm{\Omega }}_{\upsilon },\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_1& \le & 12\widehat{\epsilon }\tilde{R}{\mathrm{\Psi }}_i{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }},\hfill \\ \hfill {\mathrm{\Omega }}_2& \le & \frac{12\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}(2{\mathrm{\Psi }}_i+2{({\xi }_i-1)}^2\tilde{R}),\hfill \\ \hfill {\mathrm{\Omega }}_3& \le & 12\widehat{\epsilon }\tilde{R}{\left(\sum _{j=1}^m{\overline{c}}_{ij}{L}_j^f\right)}^2{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }},\hfill \\ \hfill {\mathrm{\Omega }}_4& \le & \frac{12\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}[2{\left(\sum _{j=1}^m{\overline{c}}_{ij}{L}_j^f\right)}^2+2{\left(\sum _{j=1}^m{L}_j^f\right)}^2\tilde{R}],\hfill \\ \hfill {\mathrm{\Omega }}_5& \le & 12\widehat{\epsilon }\tilde{R}{\left(\sum _{j=1}^m{\overline{d}}_{ij}{L}_j^f\right)}^2{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }},\hfill \\ \hfill {\mathrm{\Omega }}_6& \le & \frac{12\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}[2{\left(\sum _{j=1}^m{\overline{d}}_{ij}{L}_j^f\right)}^2+2{\left(\sum _{j=1}^m{L}_j^f\right)}^2\tilde{R}],\hfill \\ \hfill {\mathrm{\Omega }}_7& \le & 12\widehat{\epsilon }\tilde{R}{\left(\sum _{j=1}^m{\overline{h}}_{ij}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }},\hfill \\ \hfill {\mathrm{\Omega }}_8& \le & \frac{12\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}[2{\left(\sum _{j=1}^m{\overline{h}}_{ij}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2+2{\left(\sum _{j=1}^m{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2\tilde{R}],\hfill \\ \hfill {\mathrm{\Omega }}_9& \le & 12\widehat{\epsilon }{\overline{I}}_i^2{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }},{\mathrm{\Omega }}_{10}\le \frac{12\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}.\hfill \end{array}$$

(61)

Using Lemma 5 and (38),

$${\mathrm{\Omega }}_{11}\le 12\widehat{\epsilon }\tilde{R}{\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2(\frac{4}{{({\underline{\beta }}_i-{\xi }_i)}^3}+\frac{4\overline{\mu }}{{({\underline{\beta }}_i-{\xi }_i)}^2})e^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }},$$

(62)

Using Lemmas 5 and 7,

$${\mathrm{\Omega }}_{12}\le \frac{12\widehat{\epsilon }}{{\underline{\beta }}_i-{\xi }_i}{\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2.$$

(63)

It follows from (61)–(63) that

$$\begin{array}{ccc}\hfill & & E{\left|{\left(\mathrm{\Theta }z\right)}_{n+i}(t+\tau )-{\left(\mathrm{\Theta }z\right)}_{n+i}\left(t\right)\right|}^2\hfill \\ & \le & 12\widehat{\epsilon }\tilde{R}{(\frac{2}{{({\underline{\beta }}_i-{\xi }_i)}^2}+\frac{\overline{\mu }}{{\underline{\beta }}_i-{\xi }_i})}^2{e}^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}[{\mathrm{\Psi }}_i+{\left(\sum _{j=1}^m{\overline{c}}_{ij}{L}_j^f\right)}^2+{\left(\sum _{j=1}^m{\overline{d}}_{ij}{L}_j^f\right)}^2\hfill \\ & +& {\left(\sum _{j=1}^m{\overline{h}}_{ij}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2+\frac{1}{\tilde{R}}{\overline{I}}_i^2]+12\widehat{\epsilon }\tilde{R}{\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2(\frac{4}{{({\underline{\beta }}_i-{\xi }_i)}^3}+\frac{4\overline{\mu }}{{({\underline{\beta }}_i-{\xi }_i)}^2})e^{2({\underline{\beta }}_i-{\xi }_i)\overline{\mu }}\hfill \\ & +& \frac{24\widehat{\epsilon }}{{({\underline{\beta }}_i-{\xi }_i)}^2}[{\mathrm{\Psi }}_i+{({\xi }_i-1)}^2\tilde{R}+{\left(\sum _{j=1}^m{\overline{c}}_{ij}{L}_j^f\right)}^2+{\left(\sum _{j=1}^m{\overline{d}}_{ij}{L}_j^f\right)}^2+2{\left(\sum _{j=1}^m{L}_j^f\right)}^2\tilde{R}\hfill \\ & +& {\left(\sum _{j=1}^m{\overline{h}}_{ij}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2+{\left(\sum _{j=1}^m{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2\tilde{R}+\frac{1}{2}+\frac{1}{2}({\underline{\beta }}_i-{\xi }_i){\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2].\hfill \end{array}$$

(64)

Similarly to (60) and (64),

$$\begin{array}{ccc}& & E{\left|{\left(\mathrm{\Theta }z\right)}_{2n+j}(t+\tau )-{\left(\mathrm{\Theta }z\right)}_{2n+j}\left(t\right)\right|}^2\hfill \\ & \le & 2E{\left|{\int }_{-\infty }^t(e_{-{\kappa }_j}(t+\tau ,\sigma (s+\tau ))-e_{-{\kappa }_j}(t,\sigma \left(s\right)))v_j(s+\tau )\mathrm{\Delta }s\right|}^2\hfill \\ & +& 2E{\left|{\int }_{-\infty }^t{e}_{-{\kappa }_j}(t,\sigma \left(s\right))(v_j(s+\tau )-v_j\left(s\right))\mathrm{\Delta }s\right|}^2\le \frac{2}{{\kappa }_j^2}\widehat{\epsilon },\hfill \end{array}$$

(65)

$$\begin{array}{ccc}& & E{\left|{\left(\mathrm{\Psi }z\right)}_{2n+m+j}(t+\tau )-{\left(\mathrm{\Psi }z\right)}_{2n+m+j}\left(t\right)\right|}^2\hfill \\ & \le & 12\widehat{\epsilon }\tilde{R}{(\frac{2}{{({\underline{\gamma }}_j-{\kappa }_j)}^2}+\frac{\overline{\mu }}{{\underline{\gamma }}_j-{\kappa }_j})}^2{e}^{2({\underline{\gamma }}_j-{\kappa }_j)\overline{\mu }}[{\mathrm{\Gamma }}_j+{\left(\sum _{i=1}^n{\overline{l}}_{ji}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{p}}_{ji}{L}_i^g\right)}^2\hfill \\ & +& {\left(\sum _{i=1}^n{\overline{q}}_{ji}{\overline{\zeta }}_{ji}^{\left(2\right)}{L}_i^g\right)}^2+\frac{1}{\tilde{R}}{\overline{J}}_j^2]+12\widehat{\epsilon }\tilde{R}{\left(\sum _{i=1}^n{L}_{ji}^{\phi }\right)}^2(\frac{4}{{({\underline{\gamma }}_j-{\kappa }_j)}^3}+\frac{4\overline{\mu }}{{({\underline{\gamma }}_j-{\kappa }_j)}^2})e^{2({\underline{\gamma }}_j-{\kappa }_j)\overline{\mu }}\hfill \\ & +& \frac{24\widehat{\epsilon }}{{({\underline{\gamma }}_j-{\kappa }_j)}^2}[{\mathrm{\Gamma }}_j+{({\kappa }_j-1)}^2\tilde{R}+{\left(\sum _{i=1}^n{\overline{l}}_{ji}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{p}}_{ji}{L}_i^g\right)}^2+2{\left(\sum _{i=1}^n{L}_i^g\right)}^2\tilde{R}\hfill \\ & +& {\left(\sum _{i=1}^n{\overline{q}}_{ji}{\overline{\zeta }}_{ji}^{\left(2\right)}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{\zeta }}_{ji}^{\left(2\right)}{L}_i^g\right)}^2\tilde{R}+\frac{1}{2}+\frac{1}{2}({\underline{\gamma }}_j-{\kappa }_j){\left(\sum _{i=1}^n{L}_{ji}^{\phi }\right)}^2].\hfill \end{array}$$

(66)

From (60) and (64)–(66), for any $\epsilon >0$, there exists a corresponding $\widehat{\epsilon }$ which produces

$$E{\left|{\left(\mathrm{\Theta }z\right)}_k(t+\tau )-{\left(\mathrm{\Theta }z\right)}_k\left(t\right)\right|}^2\le \epsilon \mathrm{for}k=1,2,...,2m+2n.$$

Therefore, $\mathrm{\Psi }z$ is almost periodic.

Second, we prove ${∥\mathrm{\Psi }z∥}_{\mathbb{Y}}\le \tilde{R}$. It follows from (55)–(58) that

$$\hfill E{\left|{\left(\mathrm{\Theta }z\right)}_i\left(t\right)\right|}^2& \le & E{\left|{\int }_{-\infty }^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))u_i\left(s\right)\mathrm{\Delta }s\right|}^2\le \frac{1}{{\xi }_i^2}{∥z∥}_{\mathbb{Y}},\hfill$$

(67)

$$\begin{array}{ccc}\hfill E{\left|{\left(\mathrm{\Theta }z\right)}_{n+i}\left(t\right)\right|}^2& \le & 6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))({\beta }_i{\xi }_i-a_i-{\xi }_i^2)x_i\left(s\right)\mathrm{\Delta }s\right|}^2\hfill \\ & +& 6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{c}_{ij}\left(s\right)f_j\left(y_j\left(s\right)\right)\mathrm{\Delta }s\right|}^2\hfill \\ & +& 6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{d}_{ij}\left(s\right)f_j\left(y_j(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right)\mathrm{\Delta }s\right|}^2\hfill \\ & +& 6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{h}_{ij}\left(s\right){\int }_{s-{\tau }_{ij}^{\left(2\right)}\left(s\right)}^s{f}_j\left(y_j\left(r\right)\right)\mathrm{\Delta }r\mathrm{\Delta }s\right|}^2\hfill \\ & +& 6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))I_i\left(s\right)\mathrm{\Delta }s\right|}^2\hfill \\ & +& 6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{\delta }_{ij}\left(y_j\left(s\right)\right)\mathrm{\Delta }{w}_{1j}\left(s\right)\right|}^2\hfill \\ & \le & \frac{6{∥z∥}_{\mathbb{Y}}}{{({\underline{\beta }}_i-{\xi }_i)}^2}[{\mathrm{\Psi }}_i+{\left(\sum _{j=1}^n{\overline{c}}_{ij}^{}{L}_j^f\right)}^2+{\left(\sum _{j=1}^n{\overline{d}}_{ij}^{}{L}_j^f\right)}^2+{\left(\sum _{j=1}^n{\overline{h}}_{ij}^{}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2\hfill \\ & +& ({\underline{\beta }}_i-{\xi }_i){\left(\sum _{j=1}^n{L}_{ij}^{\delta }\right)}^2]+6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))I_i\left(s\right)\mathrm{\Delta }s\right|}^2,\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill E{\left|{\left(\mathrm{\Theta }z\right)}_{2n+j}\left(t\right)\right|}^2& \le & E{\left|{\int }_{-\infty }^t{e}_{-{\kappa }_j}(t,\sigma \left(s\right))v_j\left(s\right)\mathrm{\Delta }s\right|}^2\le \frac{1}{{\kappa }_j^2}{∥z∥}_{\mathbb{Y}},\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill E{\left|{\left(\mathrm{\Theta }z\right)}_{2n+m+j}\left(t\right)\right|}^2& \le & \frac{6{∥z∥}_{\mathbb{Y}}}{{({\underline{\gamma }}_j-{\kappa }_j)}^2}[{\mathrm{\Gamma }}_i+{\left(\sum _{i=1}^n{\overline{l}}_{ji}^{}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{p}}_{ji}^{}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{q}}_{ji}^{}{\overline{\zeta }}_{ji}^{\left(2\right)}{L}_i^g\right)}^2\hfill \\ & +& ({\underline{\gamma }}_j-{\kappa }_j){\left(\sum _{i=1}^n{L}_{ji}^{\phi }\right)}^2]+6E{\left|{\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))J_j\left(s\right)\mathrm{\Delta }s\right|}^2\hfill \end{array}$$

(70)

Let

$$\begin{array}{ccc}\hfill M_5& =& \underset{1\le i\le n,1\le j\le m}{max}\left\{M_{1i},\frac{6}{5}{M}_{3i},M_{2j},\frac{6}{5}{M}_{4j}\right\},\hfill \\ \hfill M_6& =& \underset{1\le i\le n,1\le j\le m}{max}\left\{6E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))I_i\left(s\right)\mathrm{\Delta }s\right|}^2,6E{\left|{\int }_{-\infty }^t{e}_{-({\gamma }_j-{\kappa }_j)}(t,\sigma \left(s\right))J_j\left(s\right)\mathrm{\Delta }s\right|}^2\right\}.\hfill \end{array}$$

From (67)–(70),

$${∥\mathrm{\Theta }z∥}_{\mathbb{Y}}\le M_5\tilde{R}+M_6\le \tilde{R}.$$

(71)

Choosing $\tilde{R}\ge M_6/\left(1-M_5\right)$, we obtain ${∥\mathrm{\Theta }z∥}_{\mathbb{Y}}\le \tilde{R}$, which means $\mathrm{\Theta }\mathbb{Y}\subset \mathbb{Y}$.

Next, we prove $\mathrm{\Theta }$ is a contraction mapping. It follows from (55) that

$$\begin{array}{ccc}\hfill \left|{\left(\mathrm{\Theta }z-\mathrm{\Theta }{z}^{*}\right)}_i\left(t\right)\right|& \le & \left|{\int }_{-\infty }^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))(u_i\left(s\right)-u_i^{*}\left(s\right))\mathrm{\Delta }s\right|.\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill E{\left|{\left(\mathrm{\Theta }z-\mathrm{\Theta }{z}^{*}\right)}_i\left(t\right)\right|}^2& \le & E{\left|{\int }_{-\infty }^t{e}_{-{\xi }_i}(t,\sigma \left(s\right))(u_i\left(s\right)-u_i^{*}\left(s\right))\mathrm{\Delta }s\right|}^2<\frac{1}{{\left({\xi }_i\right)}^2}{∥z∥}_{\mathbb{Y}}.\hfill \end{array}$$

(73)

Similarly, we have

$$\begin{array}{ccc}& & E{\left|{(\mathrm{\Theta }z-\mathrm{\Theta }{z}^{*})}_{n+i}\left(t\right)\right|}^2\hfill \\ & \le & 5E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))({\beta }_i{\xi }_i-a_i-{\xi }_i^2)(x_i\left(s\right)-x_i^{*}\left(s\right))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 5E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{c}_{ij}\left(s\right)(f_j\left(y_j\left(s\right)\right)-f_j\left(y_j^{*}\left(s\right)\right))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 5E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{d}_{ij}\left(s\right)(f_j\left(y_j(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right)-f_j\left(y_j^{*}(s-{\tau }_{ij}^{\left(1\right)}\left(s\right))\right))\mathrm{\Delta }s\right|}^2\hfill \\ & +& 5E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{\int }_{s-{\tau }_{ij}^{\left(2\right)}\left(s\right)}^s{h}_{ij}\left(r\right)(f_j\left(y_j\left(r\right)\right)-f_j\left(y_j^{*}\left(r\right)\right))\mathrm{\Delta }r\mathrm{\Delta }s\right|}^2\hfill \\ & +& 5E{\left|{\int }_{-\infty }^t{e}_{-({\beta }_i-{\xi }_i)}(t,\sigma \left(s\right))\sum _{j=1}^m{\delta }_{ij}(y_j\left(s\right)-y_j^{*}\left(s\right))\mathrm{\Delta }{w}_{1j}\left(s\right)\right|}^2\hfill \\ & <& \frac{5}{{({\underline{\beta }}_i-{\xi }_i)}^2}{[{\mathrm{\Psi }}_i+\sum _{j=1}^m({\overline{c}}_{ij}{L}_j^f)}^2+\sum _{j=1}^m{\left({\overline{d}}_{ij}{L}_j^f\right)}^2\hfill \\ & +& \sum _{j=1}^m{\left({\overline{\tau }}_{ij}^{\left(2\right)}{\overline{h}}_{ij}{L}_j^f\right)}^2+({\underline{\beta }}_i-{\xi }_i){\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2]{∥z∥}_{\mathbb{Y}}.\hfill \end{array}$$

(74)

$$\begin{array}{ccc}& & E{\left|{\left(\mathrm{\Theta }z-\mathrm{\Theta }{z}^{*}\right)}_{2n+j}\left(t\right)\right|}^2\hfill \\ & \le & E{\left|{\int }_{-\infty }^t{e}_{-{\kappa }_j}(t,\sigma \left(s\right))(v_j\left(s\right)-v_j^{*}\left(s\right))\mathrm{\Delta }s\right|}^2<\frac{1}{{\left({\kappa }_j\right)}^2}{∥z∥}_{\mathbb{Y}}.\hfill \end{array}$$

(75)

$$\begin{array}{ccc}& & E{\left|{(\mathrm{\Theta }z-\mathrm{\Theta }{z}^{*})}_{2n+m+j}\left(t\right)\right|}^2\hfill \\ & <& \frac{5}{{({\underline{\gamma }}_j-{\kappa }_j)}^2}[{\mathrm{\Gamma }}_i+\sum _{j=1}^m({\overline{l}}_{ji}{L}_j^f{)}^2+\sum _{j=1}^m({\overline{p}}_{ji}{L}_j^f{)}^2\hfill \\ & +& \sum _{j=1}^m({\overline{\zeta }}_{ji}^{\left(2\right)}{\overline{q}}_{ji}{L}_i^g{)}^2+({\underline{\gamma }}_j-{\kappa }_j)(\sum _{j=1}^m{L}_{ji}^{\phi }{)}^2]{∥z∥}_{\mathbb{Y}}.\hfill \end{array}$$

(76)

Let $M_{1i}$, $M_{2j}$, $M_{3i}$, $M_{4j}$ be (49), if $M={\displaystyle \underset{1\le i\le n,1\le j\le m}{max}}\{M_{1i},M_{2j},M_{3i},M_{4j}\}<1$, then

$${∥\mathrm{\Theta }(z-z^{*})∥}_{\mathbb{Y}}\le M{∥z-z^{*}∥}_{\mathbb{Y}}<{∥z-z^{*}∥}_{\mathbb{Y}}.$$

$\mathrm{\Theta }$ is a contraction mapping in $\mathbb{Y}$. Then, $\mathrm{\Theta }$ possesses a unique fixed point and there exists a unique almost periodic solution for systems (6) and (7) in $\mathbb{Y}$. □

4. Exponential Stability

Theorem 3.

If

$$\underset{1\le i\le n,1\le j\le m}{max}\{2M_{1i},2M_{2j},\frac{6}{5}{M}_{3i},\frac{6}{5}{M}_{4j}\}<1,$$

(77)

then the solution of SIBAMNNs (6) and (7) on time scales is exponentially stable.

Proof. 

Let $z_{k1}\left(t\right)$ and $z_{k2}\left(t\right)$ be two solutions of systems (6) and (7) with initial data $({\theta }_{i1}^{\left(1\right)}\left(s\right)$, $u_{i1}\left(t_0\right),{\theta }_{j1}^{\left(2\right)}\left(s\right),v_{j1}\left(t_0\right))$ and $({\theta }_{i2}^{\left(1\right)}\left(s\right),u_{i2}\left(t_0\right),{\theta }_{j2}^{\left(2\right)}\left(s\right),v_{j2}\left(t_0\right))$, and ${\tilde{z}}_k\left(t\right)=z_{k1}\left(t\right)-z_{k2}\left(t\right)$, ${\tilde{x}}_i\left(t\right)=x_{i1}\left(t\right)-x_{i2}\left(t\right)$, ${\tilde{u}}_i\left(t\right)=u_{i1}\left(t\right)-u_{i2}\left(t\right)$, ${\tilde{y}}_i\left(t\right)=y_{i1}\left(t\right)-y_{i2}\left(t\right)$, ${\tilde{v}}_i\left(t\right)=v_{i1}\left(t\right)-v_{i2}\left(t\right)$. For initial state, set ${\psi }_i\left(s\right)={\theta }_{i1}^{\left(1\right)}\left(s\right)-{\theta }_{i2}^{\left(1\right)}\left(s\right)$, ${\psi }_{n+i}\left(t_0\right)=u_{i1}^{}\left(t_0\right)-u_{i2}^{}\left(t_0\right)$, ${\psi }_{2n+j}\left(s\right)={\theta }_{i1}^{\left(2\right)}\left(s\right)-{\theta }_{i2}^{\left(2\right)}\left(s\right)$, ${\psi }_{2n+m+j}\left(t_0\right)=v_{j1}^{}\left(t_0\right)-v_{j2}^{}\left(t_0\right)$ for $i=1,2,...n,j=1,2,...m,k=1,2,...2m+2n$. From (8), we have

$${\tilde{z}}_i\left(t\right)=e_{-{\xi }_i}(t,t_0){\tilde{x}}_i\left(t_0\right)+{\int }_{t_0}^t{e}_{-{\xi }_i}(t,\sigma \left(s\right)){\tilde{u}}_i\left(s\right)\mathrm{\Delta }s.$$

(78)

Let $0<{\alpha }_1<{\displaystyle \underset{1\le i\le n}{min}}\left\{{\xi }_i\right\}$. It follows from (78) that

$$e_{{\alpha }_1}(t,t_0)E\left({\left|{\tilde{z}}_i\left(t\right)\right|}^2\right)\le 2E\left({\left|{\tilde{x}}_i\left(t_0\right)\right|}^2\right)+2e_{{\alpha }_1}(t,t_0)E\left({\left|{\int }_{t_0}^t{e}_{-{\xi }_i}(t,\sigma \left(s\right)){\tilde{u}}_i\left(s\right)\mathrm{\Delta }s\right|}^2\right),$$

(79)

where

$$E\left({\left|{\int }_{t_0}^t{e}_{-{\xi }_i}(t,\sigma \left(s\right)){\tilde{u}}_i\left(s\right)\mathrm{\Delta }s\right|}^2\right)\le \frac{1}{{\xi }_i^2}E\left({\left|{\tilde{u}}_i\left(s\right)\right|}^2\right).$$

Then, from (79), we have

$$e_{{\alpha }_1}(t,t_0)E\left({\left|{\tilde{z}}_i\left(t\right)\right|}^2\right)\le 2E{\left|{\tilde{z}}_i\left(t_0\right)\right|}^2+2{\xi }_i^{-2}{e}_{{\alpha }_1}(t,t_0)E\left({\left|{\tilde{u}}_i\left(t\right)\right|}^2\right).$$

(80)

Let $0<{\alpha }_2<{\displaystyle \underset{1\le i\le n}{min}}\left\{{\underline{\beta }}_i-{\xi }_i\right\}$, $0<{\alpha }_3<{\displaystyle \underset{1\le j\le m}{min}}\left\{{\kappa }_j\right\}$, $0<{\alpha }_4<{\displaystyle \underset{1\le j\le m}{min}}\left\{{\underline{\gamma }}_j-{\kappa }_j\right\}$. Similarly, we have

$$\begin{array}{ccc}\hfill e_{{\alpha }_2}(t,t_0)E\left({\left|{\tilde{z}}_{n+i}\left(t\right)\right|}^2\right)& \le & 6E{\left|{\tilde{z}}_{n+i}\left(t_0\right)\right|}^2+6{({\underline{\beta }}_i-{\xi }_i)}^{-2}{\mathrm{\Psi }}_i{e}_{{\alpha }_2}(t,t_0)E\left({\left|{\tilde{x}}_i\left(t\right)\right|}^2\right)\hfill \\ & +& 6{({\underline{\beta }}_i-{\xi }_i)}^{-2}{e}_{{\alpha }_2}(t,t_0)[{\left(\sum _{j=1}^m{\overline{c}}_{ij}{L}_j^f\right)}^2+{\left(\sum _{j=1}^m{\overline{d}}_{ij}{L}_j^f\right)}^2\hfill \\ & +& {\left(\sum _{j=1}^m{\overline{h}}_{ij}{\overline{\tau }}_{ij}^{\left(2\right)}{L}_j^f\right)}^2+({\underline{\beta }}_i-{\xi }_i){\left(\sum _{j=1}^m{L}_{ij}^{\delta }\right)}^2]E{\left|{\tilde{y}}_j\left(t\right)\right|}^2,\hfill \end{array}$$

(81)

$$\begin{array}{ccc}\hfill e_{{\alpha }_3}(t,t_0)E\left({\left|{\tilde{z}}_{2n+j}\left(t\right)\right|}^2\right)& \le & 2E{\left|{\tilde{z}}_{2n+j}\left(t_0\right)\right|}^2+2{\kappa }_j^{-2}{e}_{{\alpha }_3}(t,t_0)E\left({\left|{\tilde{v}}_j\left(t\right)\right|}^2\right),\hfill \end{array}$$

(82)

$$\begin{array}{ccc}\hfill e_{{\alpha }_4}(t,t_0)E\left({\left|{\tilde{z}}_{2n+m+j}\left(t\right)\right|}^2\right)& \le & 6E{\left|{\tilde{z}}_{2n+m+j}\left(t_0\right)\right|}^2+6{({\underline{\gamma }}_j-{\kappa }_j)}^{-2}{\mathrm{\Gamma }}_i{e}_{{\alpha }_4}(t,t_0)E\left({\left|{\tilde{y}}_j\left(t\right)\right|}^2\right)\hfill \\ & +& 6{({\underline{\gamma }}_j-{\kappa }_j)}^{-2}{e}_{{\alpha }_4}(t,t_0)[{\left(\sum _{i=1}^n{\overline{l}}_{ji}{L}_i^g\right)}^2+{\left(\sum _{i=1}^n{\overline{p}}_{ji}{L}_i^g\right)}^2\hfill \\ & +& {\left(\sum _{i=1}^n{\overline{q}}_{ji}{\overline{\zeta }}_{ji}^{\left(2\right)}{L}_j^f\right)}^2+({\underline{\gamma }}_j-{\kappa }_j){\left(\sum _{i=1}^n{L}_{ji}^{\phi }\right)}^2]E{\left|{\tilde{x}}_i\left(t\right)\right|}^2.\hfill \end{array}$$

(83)

From (80)–(83), choose

$$C>\underset{1\le i\le n,1\le j\le m}{max}\left\{\frac{2}{1-2M_{1i}},\frac{2}{1-2M_{2j}},\frac{6}{1-\frac{6}{5}{M}_{3i}},\frac{6}{1-\frac{6}{5}{M}_{4j}}\right\},$$

and $0<\alpha <{\displaystyle \underset{1\le l\le 4}{min}}\left\{{\alpha }_l\right\}$. If (80) holds, then $C>1$. Since $e_{\ominus \alpha }(t,t_0)>1$ for $t\le t_0$, then $\forall t\in {[t_0-\vartheta ,t_0]}_{\mathbb{T}}$, and we obtain

$$\underset{k}{max}E\left({\left|{\tilde{z}}_k\left(t\right)\right|}^2\right)\le C{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},k=1,2,...,2m+2n$$

for the periodic solution and

$$\underset{k}{max}E\left({\left|{\tilde{z}}_k\left(t\right)\right|}^2\right)\le C{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{Y}},k=1,2,...,2m+2n$$

for the almost periodic solution. We claim that for $\forall t\in {(t_0,+\infty )}_{\mathbb{T}}$,

$$\underset{k}{max}E\left({\left|{\tilde{z}}_k\left(t\right)\right|}^2\right)\le C{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},\underset{k}{max}E\left({\left|{\tilde{z}}_k\left(t\right)\right|}^2\right)\le C{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{Y}}.$$

i.e., for any $p>1$, the periodic solution satisfies

$$\underset{1\le k\le 2n+2m}{max}E\left({\left|{\tilde{z}}_k\left(t\right)\right|}^2\right)<pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},\forall t\in {(t_0,+\infty )}_{\mathbb{T}},$$

(84)

and the almost periodic solution satisfies

$$\underset{1\le k\le 2n+2m}{max}E\left({\left|{\tilde{z}}_k\left(t\right)\right|}^2\right)<pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{Y}},\forall t\in {(t_0,+\infty )}_{\mathbb{T}}.$$

(85)

We give the proof by contradiction. Without a loss of generality, assume that (84) is not satisfied, then there exist $t_1\in {(t_0,+\infty )}_{\mathbb{T}}$ and $i_0\in \{1,2,...,2m+2n\}$ such that

$$E\left({\left|{\tilde{z}}_{i_0}\left(t_1\right)\right|}^2\right)\ge pC{e}_{\ominus \alpha }(t_1,t_0){∥\psi ∥}_{\mathbb{X}},E\left({\left|{\tilde{z}}_{i_0}\left(t\right)\right|}^2\right)<pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},t\in {(t_0,t_1)}_{\mathbb{T}},$$

$$E\left({\left|{\tilde{z}}_l\left(t\right)\right|}^2\right)<pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},t\in {(t_0,t_1]}_{\mathbb{T}}\mathrm{for}l=1,2,...,2m+2n,l\ne i_0.$$

Hence, there exists a constant $\lambda \ge 1$ such that

$$E\left({\left|{\tilde{z}}_{i_0}\left(t_1\right)\right|}^2\right)=\lambda pC{e}_{\ominus \alpha }(t_1,t_0){∥\psi ∥}_{\mathbb{X}},E\left({\left|{\tilde{z}}_{i_0}\left(t\right)\right|}^2\right)<\lambda pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},t\in {(t_0,t_1)}_{\mathbb{T}},$$

$$E\left({\left|{\tilde{z}}_l\left(t\right)\right|}^2\right)<\lambda pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},t\in {(t_0,t_1]}_{\mathbb{T}},l=1,2,...,2m+2n,l\ne i_0.$$

It follows from (78) that

$$\begin{array}{cc}\hfill E\left({\left|{\tilde{z}}_{i_0}\left(t_1\right)\right|}^2\right)& =E{\left|e_{-{\xi }_{i_0}}(t_1,t_0){\tilde{z}}_{i_0}\left(t_0\right)+{\int }_{t_0}^{t_1}{e}_{-{\xi }_{i_0}}(t_1,\sigma \left(s\right)){\tilde{z}}_{n+i_0}\left(s\right)\mathrm{\Delta }s\right|}^2\hfill \\ \hfill & \le 2E{\left|e_{-{\xi }_{i_0}}(t_1,t_0){\tilde{z}}_{i_0}\left(t_0\right)\right|}^2+2E{\left|{\int }_{t_0}^{t_1}{e}_{-{\xi }_{i_0}}(t_1,\sigma \left(s\right)){\tilde{z}}_{n+i_0}\left(s\right)\mathrm{\Delta }s\right|}^2\hfill \\ \hfill & <2{∥\psi ∥}_{\mathbb{X}}+\frac{2\lambda pC}{{\xi }_i^2}{∥\psi ∥}_{\mathbb{X}}<\lambda pC{∥\psi ∥}_{\mathbb{X}}(\frac{2}{C}+\frac{2}{{\xi }_i^2}).\hfill \end{array}$$

(86)

Since $C>2/\left(1-2M_{1i}\right)$, we obtain $E\left({\left|{\tilde{z}}_{i_0}\left(t_1\right)\right|}^2\right)<\lambda pC{∥\psi ∥}_{\mathbb{X}}$ from (86), which means contradiction. Therefore, (84) holds. Similarly, we can derive that (85) holds. Therefore,

$${∥\tilde{z}∥}_{\mathbb{X}}<pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{X}},{∥\tilde{z}∥}_{\mathbb{Y}}<pC{e}_{\ominus \alpha }(t,t_0){∥\psi ∥}_{\mathbb{Y}},$$

which means the exponential stability of the solutions for systems (6) and (7) is obtained. □

5. Numerical Example

The accuracy and effectiveness of the obtained results are demonstrated by numerical example in this section.

Let $i=j=2$. Consider the SIBAMNNs on time scales

$$\begin{array}{cc}\hfill x_i^{{\mathrm{\Delta }}^2}\left(t\right)& =-{\beta }_i\left(t\right)x_i^{{\mathrm{\Delta }}^{}}\left(t\right)-a_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^2{c}_{ij}\left(t\right)f_j\left(y_j\left(t\right)\right)+\sum _{j=1}^2{d}_{ij}\left(t\right)f_j\left(y_j(t-{\tau }_{ij}^{\left(1\right)}\left(t\right))\right)\hfill \\ \hfill & +\sum _{j=1}^2{h}_{ij}\left(t\right){\int }_{t-{\tau }_{ij}^{\left(2\right)}\left(t\right)}^t{f}_j\left(y_j\left(s\right)\right)\mathrm{\Delta }s+I_i\left(t\right)+\sum _{j=1}^2{\delta }_{ij}\left(y_j\left(t\right)\right)w_{1j}^{\mathrm{\Delta }}\left(t\right),\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill y_j^{{\mathrm{\Delta }}^2}\left(t\right)& =-{\gamma }_j\left(t\right)y_j^{{\mathrm{\Delta }}^{}}\left(t\right)-b_j\left(t\right)y_j\left(t\right)+\sum _{i=1}^2{l}_{ji}\left(t\right)g_j\left(x_i\left(t\right)\right)+\sum _{i=1}^2{p}_{ji}\left(t\right)g_i\left(x_i(t-{\zeta }_{ji}^{\left(1\right)}\left(t\right))\right)\hfill \\ \hfill & +\sum _{i=1}^2{q}_{ji}\left(t\right){\int }_{t-{\zeta }_{ji}^{\left(2\right)}\left(t\right)}^t{g}_i\left(x_i\left(s\right)\right)\mathrm{\Delta }s+J_j\left(t\right)+\sum _{i=1}^2{\phi }_{ji}\left(x_i\left(t\right)\right)w_{2i}^{\mathrm{\Delta }}\left(t\right).\hfill \end{array}$$

(88)

Choose

$$C={\left(c_{ij}\right)}_{2\times 2}=\left(\begin{array}{cc}0.5cost& 0.3cost\\ 0.3sint& 0.5sint\end{array}\right),D={\left(d_{ij}\right)}_{2\times 2}=\left(\begin{array}{cc}0.1cost& 0.08cost\\ 0.08sint& 0.1sint\end{array}\right),$$

$$H={\left(h_{ij}\right)}_{2\times 2}=\left(\begin{array}{cc}0.12sint& 0.1sint\\ 0.1cost& 0.12cost\end{array}\right),P={\left(p_{ji}\right)}_{2\times 2}=\left(\begin{array}{cc}0.1sint& 0.08sint\\ 0.08cost& 0.1cost\end{array}\right),$$

$$L={\left(l_{ji}\right)}_{2\times 2}=\left(\begin{array}{cc}0.5sint& 0.3sint\\ 0.3cost& 0.5cost\end{array}\right),Q={\left(q_{ji}\right)}_{2\times 2}=\left(\begin{array}{cc}0.12cost& 0.1cost\\ 0.1sint& 0.12sint\end{array}\right),$$

${\beta }_1\left(t\right)=6.8+0.3sint$, ${\beta }_2\left(t\right)=7+0.4sint$, ${\gamma }_1\left(t\right)=6.8+0.3cost$, ${\gamma }_2\left(t\right)=7+0.4cost$, $a_1\left(t\right)=6.5+0.3sint$, $a_2\left(t\right)=6.6+0.4sint$, $b_1\left(t\right)=6.5+0.3cost$, $b_2\left(t\right)=6.6+0.4cost$, $f_1\left(y_1\left(t\right)\right)=0.06sin\left(y_1\left(t\right)\right)$, $f_2\left(y_2\left(t\right)\right)=0.04sin\left(y_2\left(t\right)\right)$, $g_1\left(x_1\left(t\right)\right)=0.03sin\left(2x_1\left(t\right)\right)$, $g_2\left(x_2\left(t\right)\right)=0.02sin\left(2x_2\left(t\right)\right)$, ${\xi }_1={\xi }_2=1.5$, ${\kappa }_1={\kappa }_2=1.6$, $I_1=J_2=0.85sint$, $I_2=J_1=0.85cost$, ${\tau }_{ij}^{\left(1\right)}={\zeta }_{ji}^{\left(1\right)}=0.03$, ${\tau }_{ij}^{\left(2\right)}={\zeta }_{ji}^{\left(2\right)}=0$, ${\delta }_{ij}\left(y_j\left(t\right)\right)=0.01sin\left(y_j\left(t\right)\right)$, ${\phi }_{ji}\left(x_i\right))=0.01sin\left(x_i\left(t\right)\right)$.

(1) For $\mathbb{T}=\mathbb{R}$, Assumption 1, Assumption 2, (19) and (77) are satisfied under the above parameters, which means (87) and (88) have a periodic solution which is exponentially stable (Figure 1 and Figure 2).

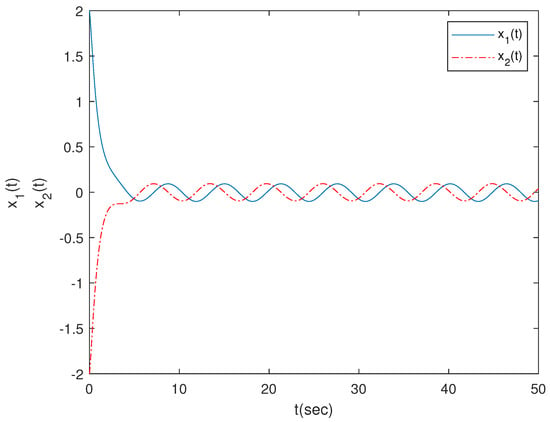
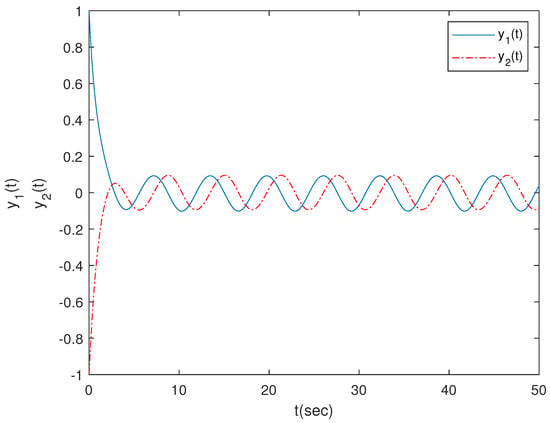
(2) For $\mathbb{T}=\bigcup _l[a_l,b_l]$ and $a_l=2k\pi$, $b_l=(2k+1)\pi$, $k\in \mathbb{Z}$, Assumptions 1 and 2 and (19) and (77) are satisfied under the above parameters, which means (87) and (88) have a periodic solution which is exponentially stable.

(3) For general time scales, Assumption 1, Assumption 3 and (77) are satisfied under the above parameters, which means (87) and (88) have an almost periodic solution which is exponentially stable.

Remark 1.

It follows from the above analysis that changes in the time scale can cause changes in the periodicity and stability of the solutions of SIBAMNNs.

6. Conclusions

We derive the criteria for the existence, uniqueness and exponential stability of both periodic and almost periodic solutions of SIBAMNNs on time scales, which unify and generalize the continuous and discrete cases and provide greater flexibility in handling time scales of practical importance. One can observe that the method for continuous-time inertial BAM neural networks in [38] and discrete-time inertial neural networks in [39] cannot directly be applied to system (6). The exponential stability of the solution on time scales is investigated without constructing a Lyapunov function, which provides a way to study the stability of neural networks that are not easy to construct Lyapunov functions for on time scales. Moreover, the inertial term, stochastic process and distributed time delay on time scales are considered simultaneously, which makes the model more applicable. Furthermore, new estimations for the exponential functions with almost periodic parameters on time scales are derived in Lemma 9. It is meaningful to study the existence and stability of periodic and almost periodic solutions for systems on time scales which can unify the continuous and discrete situations. A possible future direction is how to generalize the technique to deal with the time-scale cases and the methods used in this paper to resolve some other types of neural networks on time scales. Moreover, the study of periodic, almost periodic, pseudo-almost periodic and almost automorphic solutions of neural networks on time scales is also another possible future direction.