An Energy-Efficient Optimal Operation Control Strategy for High-Speed Trains via a Symmetric Alternating Direction Method of Multipliers
Abstract
1. Introduction
2. Problem Statement
2.1. Train Dynamics
2.2. Operation Constraints
2.3. Optimization Objective
3. Discrete-Time Optimal Control Problem
4. Symmetric Alternating Direction Method of Multipliers
4.1. The Algorithm Framework for the Control Problem
4.1.1. -Minimization Step
4.1.2. z-Minimization Step
4.2. Convergence of the SADMM and Stopping Criterion
| Algorithm 1 Proposed SADMM for Problem (44)–(46) |
|
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ichikawa, K. Application of optimization theory for bounded state variable problems to the operation of train. Bull. JSME 1968, 11, 857–865. [Google Scholar] [CrossRef]
- Howlett, P. Optimal strategies for the control of a train. Automatica 1996, 32, 519–532. [Google Scholar] [CrossRef]
- Guerra, T.-M.; Aguiar, B.; Berdjag, D.; Demaya, B. Robust estimation for nonlinear continuous-discrete systems with missing outputs: Application to automatic train control. IEEE Trans. Control. Syst. Technol. 2022, 30, 1304–1310. [Google Scholar] [CrossRef]
- Havaei, P.; Sandidzadeh, M.A. Intelligent-PID controller design for speed track in automatic train operation system with heuristic algorithms. J. Rail Transp. Plan. Manag. 2022, 22, 100321. [Google Scholar] [CrossRef]
- Ichikawa, S.; Miyatake, M. Energy efficient train trajectory in the railway system with moving block signaling scheme. IEEJ J. Ind. Appl. 2019, 8, 586–591. [Google Scholar] [CrossRef]
- Sato, K.; Kato, H.; Fukushima, T. Development of SiC applied traction system for next-generation Shinkansen high-speed trains. IEEJ J. Ind. Appl. 2018, 9, 453–459. [Google Scholar] [CrossRef]
- Nallaperuma, S.; Fletcher, D.; Harrison, R. Optimal control and energy storage for DC electric train systems using evolutionary algorithms. Railw. Eng. Sci. 2021, 29, 327–335. [Google Scholar] [CrossRef]
- Khmelnitsky, E. On an optimal control problem of train operation. IEEE Trans. Autom. Control 2000, 45, 1257–1266. [Google Scholar] [CrossRef]
- Bai, W.; Lin, Z.; Dong, H. Coordinated control in the presence of actuator saturation for multiple high-speed trains in the moving block signaling system mode. IEEE Trans. Veh. Technol. 2020, 69, 8054–8064. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Li, K.; Gao, Z. Robust sampled-data cruise control scheduling of high speed train. Transp. Res. Part C Emerg. Technol. 2014, 46, 274–283. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Coordinated cruise control for high-speed train movements based on a multi-agent model. Transp. Res. Part C Emerg. Technol. 2015, 56, 281–292. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Li, K.; Gao, Z. Adaptive coordinated control of multiple high-speed trains with input saturation. Nonlinear Dyn. 2016, 83, 2157–2169. [Google Scholar] [CrossRef]
- Lin, F.; Fardad, M.; Jovanovic, M.R. Optimal control of vehicular formations with nearest neighbor interactions. IEEE Trans. Autom. Control 2012, 57, 2203–2218. [Google Scholar] [CrossRef]
- Yan, X.; Cai, B.; Ning, B.; ShangGuan, W. Online distributed cooperative model predictive control of energy-saving trajectory planning for multiple high-speed train movements. Transp. Res. Part C Emerg. Technol. 2016, 69, 60–78. [Google Scholar] [CrossRef]
- Wang, Y.; De Schutter, B.; van den Boom, T.J.; Ning, B. Optimal trajectory planning for trains-a pseudospectral method and a mixed integer linear programming approach. Transp. Res. Part C Emerg. Technol. 2013, 29, 97–114. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Eric, C.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Lin, F.; Fardad, M.; Jovanović, M.R. Design of optimal sparse feedback gains via the alternating direction method of multipliers. IEEE Trans. Autom. Control 2013, 58, 2426–2431. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Distributed optimal control for multiple high-speed train movement: An alternating direction method of multipliers. Automatica 2020, 112, 108646–108654. [Google Scholar] [CrossRef]
- He, B.; Liu, H.; Wang, Z.; Yuan, X. A strictly contractive peaceman-rachford splitting method for convex programming. SIAM J. Optim. 2014, 24, 1011–1040. [Google Scholar] [CrossRef]
- He, B.; Ma, F.; Yuan, X. Convergence study on the symmetric version of ADMM with larger step sizes. SIAM J. Imaging Sci. 2016, 9, 1467–1501. [Google Scholar] [CrossRef]
- He, B.; Ma, F.; Yuan, X. Optimally linearizing the alternating direction method of multipliers for convex programming. Comput. Optim. Appl. 2020, 75, 361–388. [Google Scholar] [CrossRef]
- Gao, B.; Ma, F. Symmetric alternating direction method with indefinite proximal regularization for linearly constrained convex optimization. J. Optim. Theory Appl. 2018, 176, 178–204. [Google Scholar] [CrossRef]
- Jiao, Y.; Jin, Q.; Lu, X.; Wang, W. Alternating direction method of multipliers for linear inverse problems. SIAM J. Numer. Anal. 2016, 54, 2114–2137. [Google Scholar] [CrossRef]
- Yang, L.; Luo, J.; Xu, Y.; Zhang, Z.; Dong, Z. A distributed dual consensus ADMM based on partition for dc-dopf with carbon emission trading. IEEE Trans. Ind. Inform. 2019, 16, 1858–1872. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J.; Mikosch, T.V.; Resnick, S.I.; Robinson, S.M. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
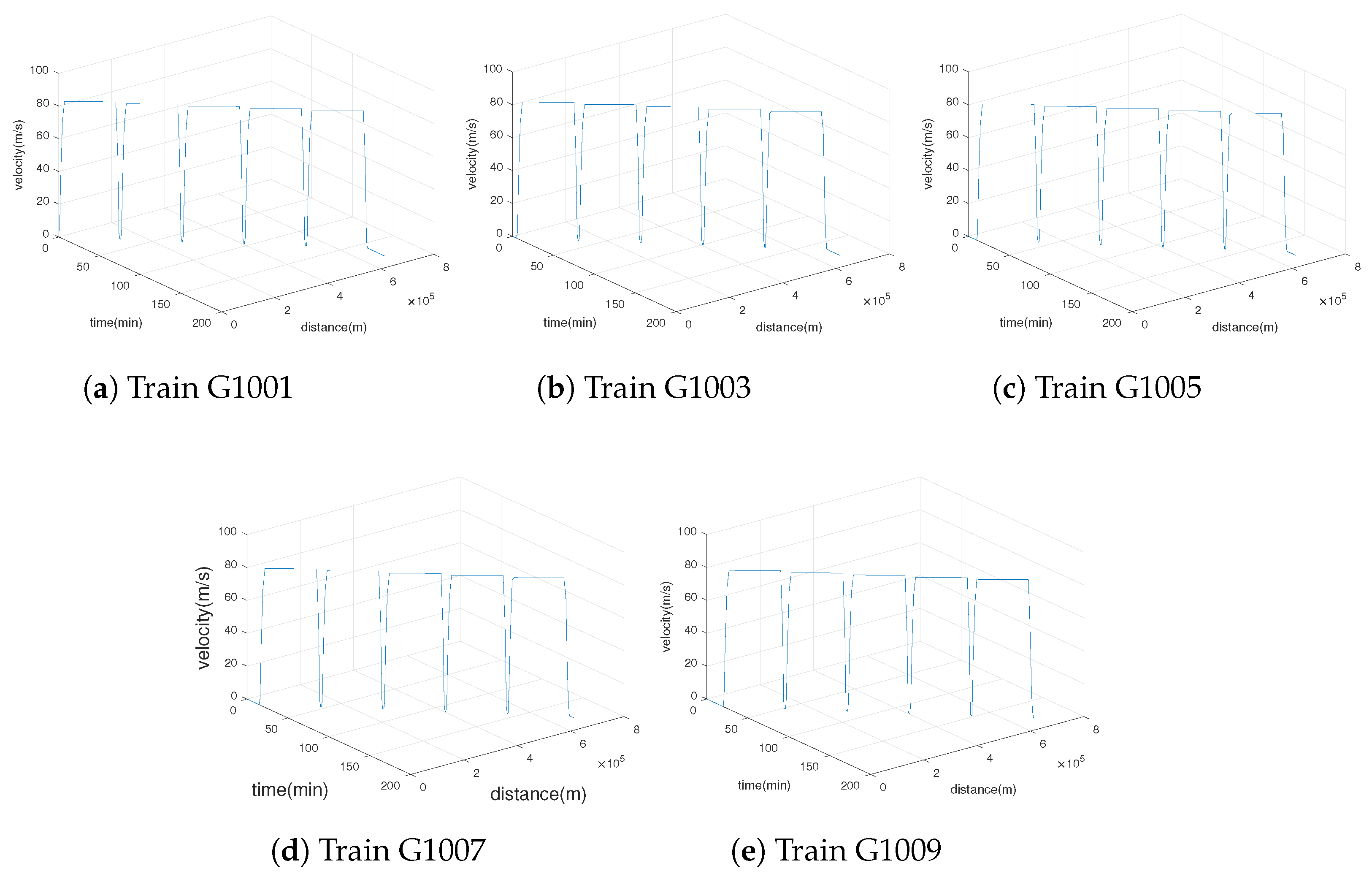
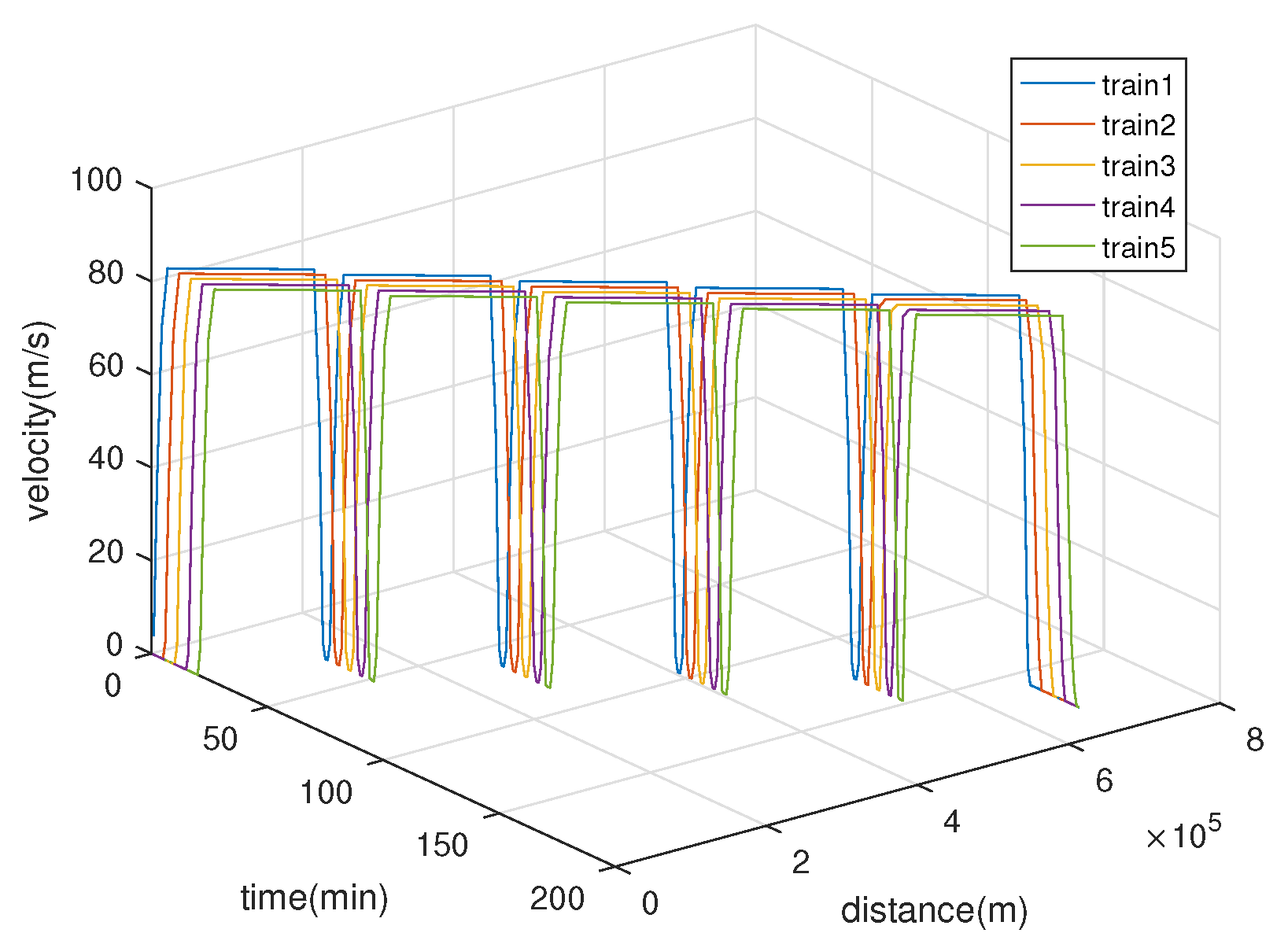


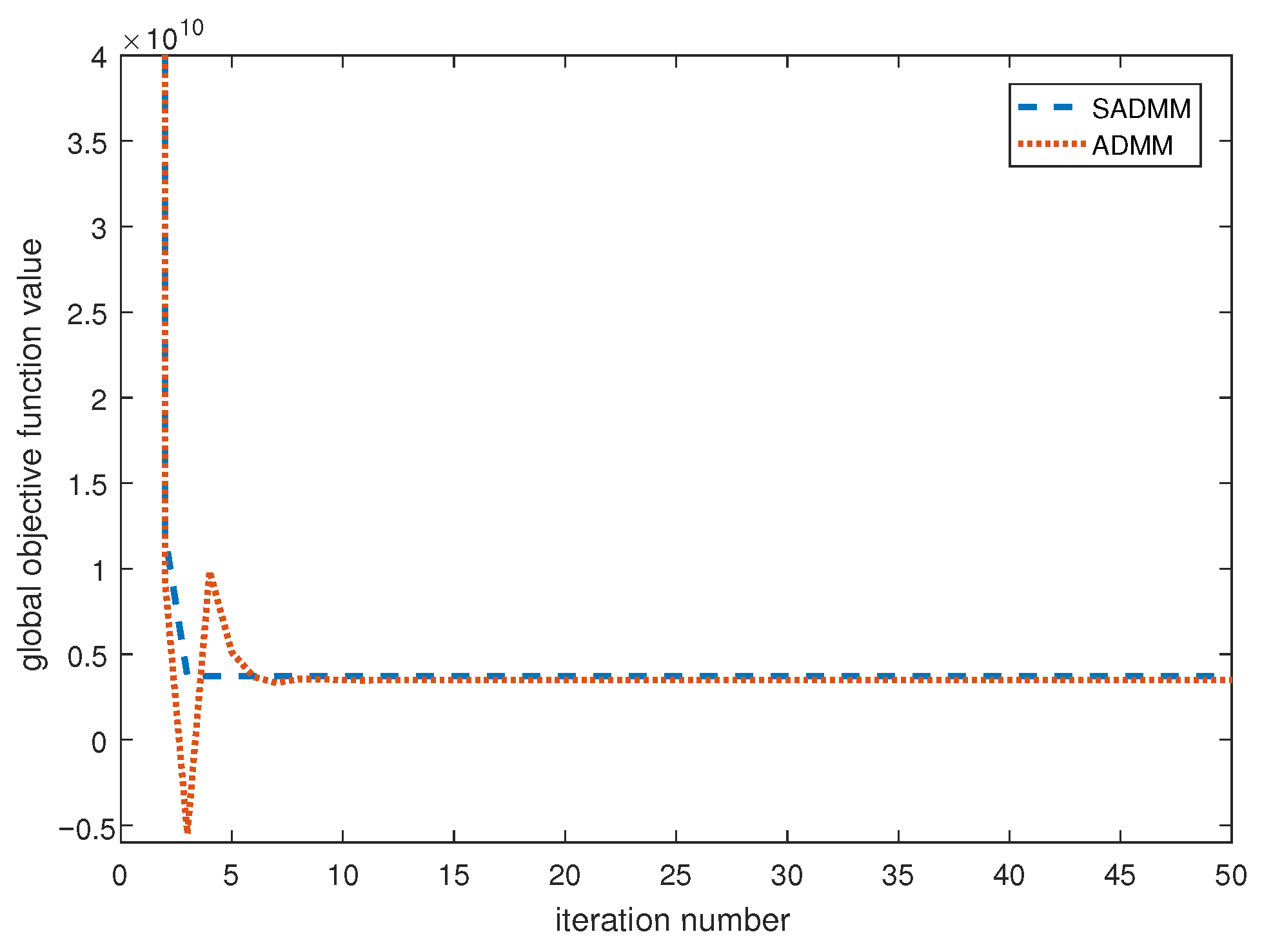
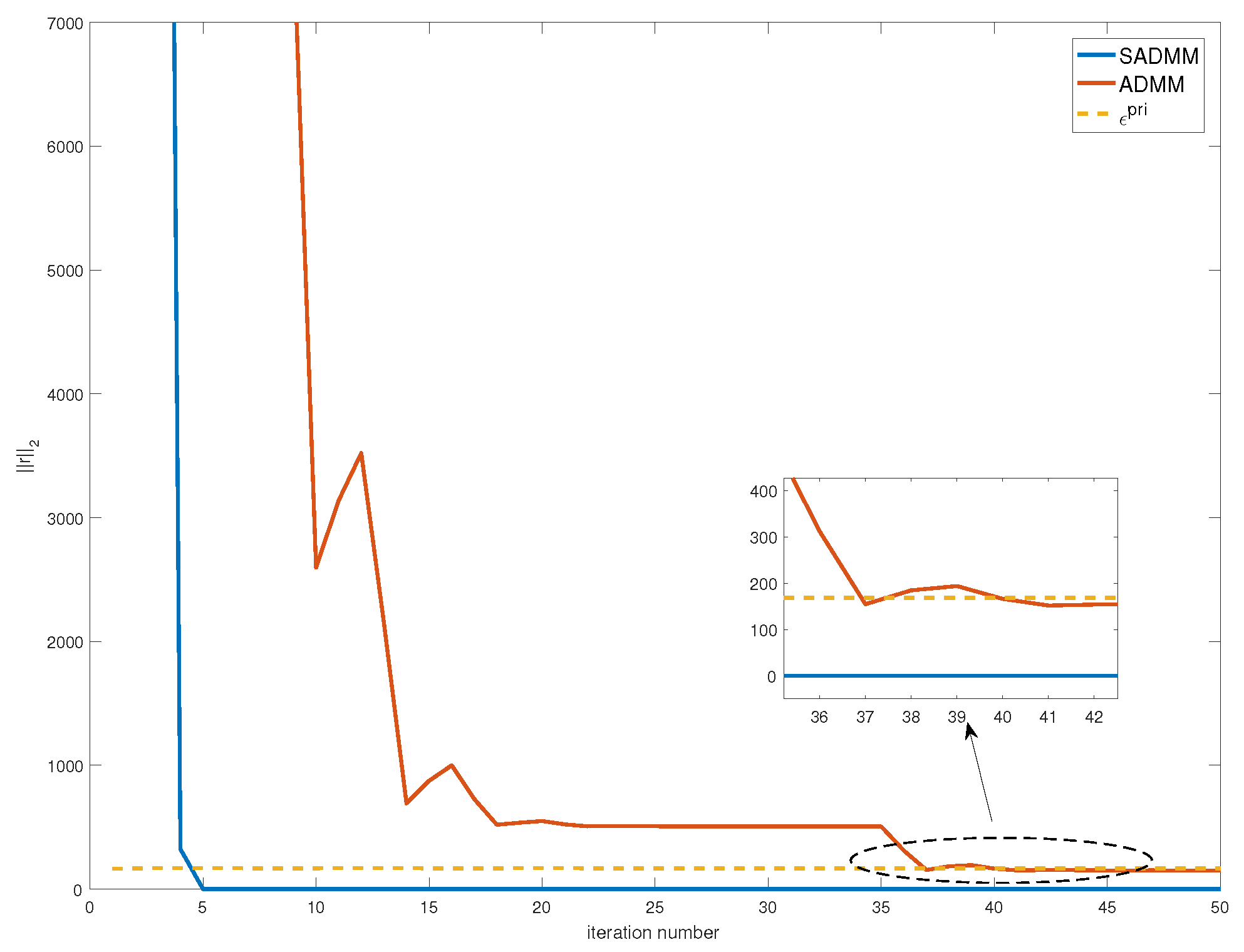
| Station | State | S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|---|---|
| Train | ||||||||
| G1001 | arrive | 8:00 | 8:28 | 8:58 | 9:28 | 9:58 | 10:28 | |
| depart | 8:00 | 8:30 | 9:00 | 9:30 | 10:00 | 10:30 | ||
| G1003 | arrive | - | 8:33 | 9:03 | 9:33 | 10:03 | 10:33 | |
| depart | 8:05 | 8:35 | 9:05 | 9:35 | 10:05 | 10:35 | ||
| G1005 | arrive | - | 8:38 | 9:08 | 9:38 | 10:08 | 10:38 | |
| depart | 8:10 | 8:40 | 9:10 | 9:40 | 10:10 | 10:40 | ||
| G1007 | arrive | - | 8:43 | 9:13 | 9:43 | 9:13 | 10:43 | |
| depart | 8:15 | 8:45 | 9:15 | 9:45 | 10:15 | 10:45 | ||
| G1009 | arrive | - | 8:48 | 9:18 | 9:48 | 10:18 | 10:48 | |
| depart | 8:20 | 8:50 | 9:20 | 9:50 | 10:20 | 10:50 | ||
| Parameters | Value | Unit |
|---|---|---|
| The weight of trains, | 450 | ton |
| Maximum acceleration, | N/kg | |
| Maximum deceleration, | N/kg | |
| Maximum control force, | 500 | kN |
| Minimum control force, | kN | |
| Resistance force, f | kN | |
| Sampled time period, d | 60 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Ma, F.; Tang, C. An Energy-Efficient Optimal Operation Control Strategy for High-Speed Trains via a Symmetric Alternating Direction Method of Multipliers. Axioms 2023, 12, 489. https://doi.org/10.3390/axioms12050489
Ma S, Ma F, Tang C. An Energy-Efficient Optimal Operation Control Strategy for High-Speed Trains via a Symmetric Alternating Direction Method of Multipliers. Axioms. 2023; 12(5):489. https://doi.org/10.3390/axioms12050489
Chicago/Turabian StyleMa, Shan, Feng Ma, and Chaoyu Tang. 2023. "An Energy-Efficient Optimal Operation Control Strategy for High-Speed Trains via a Symmetric Alternating Direction Method of Multipliers" Axioms 12, no. 5: 489. https://doi.org/10.3390/axioms12050489
APA StyleMa, S., Ma, F., & Tang, C. (2023). An Energy-Efficient Optimal Operation Control Strategy for High-Speed Trains via a Symmetric Alternating Direction Method of Multipliers. Axioms, 12(5), 489. https://doi.org/10.3390/axioms12050489






