Abstract
The diagnosis of structural damage usually belongs to a mathematical inverse problem. This work presents a novel frequency-shift flexibility sensitivity algorithm for structural damage assessment using only the first-order vibration mode to achieve the goal of successfully identifying structural damage with fewer modal parameters. The core idea of the proposed method is to make the first-order vibration mode contribute the most to a structural flexibility matrix through the frequency-shift operation. A high-precision flexibility matrix can be obtained after the frequency-shift operation, which only needs the first mode of structural free vibration. Through this special advantage, structural damage coefficients can be accurately calculated by the frequency-shift flexibility sensitivity equation. Thus, a reliable identification result can be obtained according to the values of the calculated damage coefficients. In some engineering applications, another advantage of the proposed method is that it does not require a complete finite element modeling process, as long as a few lower-frequency vibration modes of the intact structure are measured. A truss structure and a beam structure are used as two numerical examples to demonstrate the proposed approach. The results show that the proposed method has higher calculation accuracy than the ordinary flexibility sensitivity method by using only the first-order vibration mode. The proposed method can overcome possible misdiagnosis of the ordinary flexibility sensitivity method. It also has been shown that the proposed method may have the potential to identify minor damage in a structure. Using the experimental data of a steel frame structure, the effectiveness and reliability of the proposed method have been further verified. The proposed method provides a simple way for structural damage identification with only a few vibration modal data.
Keywords:
damage diagnosis; frequency-shift flexibility; sensitivity analysis; vibration mode; damage parameter MSC:
65M32
1. Introduction
During the service period, an engineering structure will inevitably be damaged due to the influence of environmental corrosion or a disaster load. Local damage in a structure may lead to a sudden collapse of the whole structure, thus causing serious loss of life or property. In view of this, it is very necessary to conduct timely damage diagnosis for a structure to avoid catastrophic consequences. Due to the large volume and numerous components of engineering structures, traditional non-destructive testing techniques such as ultrasound, radiographic testing, and penetration testing cannot complete defect diagnosis of large engineering structures. In the past few decades, methods for diagnosing structural damage using the response parameters of structures under static or dynamic loads have been continuously studied in depth. The theoretical basis for this type of method is that faults in structures can cause changes in structural static and vibration response parameters. In practice, the response data of structures can be measured through special testing equipment, and then their changes can be used to diagnose structural fault conditions. In view of this, many methods based on static or dynamic response parameters have been developed for structural damage identification [1,2,3] in recent years. These methods can be mathematically attributed to an inverse problem.
Among these methods, the flexibility-based approach is favored because of its simple operation and wide application [4]. It is known that a structural flexibility matrix can be obtained from both static data and the low-order vibration modes. Pandey and Biswas [5] used the flexibility matrix change to determine the damage location of the beam structure without constructing the finite element model (FEM). It was found that the diagonal element in the flexibility difference matrix can indicate the damage location. Jaishi and Ren [6] employed the flexibility difference as the objective function to modify the structural FEM for detecting structural damage. Catbas et al. [7] found that the dynamic test without a fixed reference measurement position can also be used to generate data for calculating the modal flexibility. Then, the displacement distribution can be obtained by using the modal flexibility for damage detection. Duan et al. [8] extended the damage location method based on flexibility to the case of environmental vibration with incomplete measured degrees of freedom (DOFs). Tomaszewska [9] discussed the damage detection method based on the structural dynamic flexibility of the building structure. In order to distinguish the true and false damage detection results, the absolute damage index was proposed to constrain the influence of the modal identification errors. Yang [10] proposed a new damage identification method based on structural flexible disassembly. The scheme has a unique advantage in that it can accurately calculate the stiffness damage parameters without any high-order sensitivity analysis or iteration. Maghsoodi et al. [11] proposed a simple method based on local flexibility to detect, locate, and quantify multiple cracks in Euler–Bernoulli multi-step beams. The main advantage of their method is that it can detect a number of unknown cracks.
Weng et al. [12] presented a new substructure method for structural damage detection by using the substructure dynamic flexibility matrix. The main advantage of their method is that the substructure characteristic parameters are more sensitive to local damage than the global characteristic parameters. Using Dempster–Shafer evidence theory, Grande and Imbimbo [13] proposed a multi-stage flexibility method for damage detection in the case of multiple damage locations and three-dimensional systems. Hosseinzadeh et al. [14] developed a damage detection method by introducing an effective objective function based on modal assurance criteria and modal flexibility. It was found that the proposed method can only use the data of the first few modes to accurately identify the damage even if the incomplete noise modal data are taken as the input data. Altunisik et al. [15] used modal curvature and modal flexibility methods to locate cracks in steel cantilever beams. The comparison shows that the modal flexibility method is effective in determining the crack location. Wickramasinghe et al. [16] developed the vertical damage index and transverse damage index based on the modal flexibility to detect and locate the damage of the main cable and hanger of a suspension bridge. The results confirm the applicability of the vertical damage index to accurately detect the damage in the actual suspension bridge by using only the first few modes. Sarmadi et al. [17] improved the sensitivity function of modal flexibility and proposed a new iterative regularization method to solve the ill-posed problem to locate and quantify the damage. It was found that their method is robust enough to solve the ill-posed problem of damage location and quantification under noise-free and noisy modal data. Ahmadi-Nedushan and Fathnejat [18] proposed a two-stage structural damage detection method based on modal flexibility and an improved teaching–learning optimization algorithm to reduce the influence of measurement noise.
Feng et al. [19] proposed a Bayesian model updating method with modal flexibility to find the most probable value of the model parameters for damage identification. Bernagozzi et al. [20] proposed a data-driven standard for structural type classification, which can be used in the framework of modal flexibility-based damage identification methods. Yang and Peng [21] developed a highly efficient model reduction method for structural damage identification based on the reduced flexibility matrix. Dinh-Cong et al. [22] used the damage index based on modal flexibility sensitivity to detect damages in functionally graded beams. The results indicate that when the noise level added to the vibration mode data is less than 10%, the provided method can correctly locate the position of damaged components. Darshan et al. [23] developed the damage detection procedure based on strain energy and a flexibility matrix to detect single and multiple damages in plate structures. Quqa and Landi [24] proposed a damage identification method based on bridge flexibility curvature with sparse acceleration measurement. The damage index proposed by them is particularly sensitive to the damage location and can be successfully applied to the steel truss bridge with different damage patterns. Nick et al. [25] proposed a damage index based on modal flexibility and modal strain energy, and a two-stage multi-criteria damage detection method using an artificial neural network (ANN) to locate and quantify the damage of steel frames. The modal flexibility matrix was obtained by the first three bending vibration modes. Cuomo et al. [26] proposed a new baseline free method for real-time structural damage diagnosis during low-speed and high-speed collisions, which is based on the decomposition of propagation patterns caused by collision events. Aulakh et al. [27] developed the curvature and coordinated modal assurance criteria based on strain modal flexibility for structural damage monitoring. They found that strain modal flexibility is more sensitive to structural damage than displacement mode flexibility.
The limitation of the existing flexibility-based method is that several low-order vibration modes are needed to approximately obtain the dynamic flexibility matrix. This leads to a large workload of dynamic analysis and a high requirement for analysis accuracy. To overcome this limitation, this work presents a novel frequency-shift flexibility sensitivity method for structural damage detection by only using the first-order vibration mode. Based on the frequency-shift operation, the first-order vibration mode will account for the majority of the dynamic flexibility of the structure. As a result, the damage coefficients in structural FEM can be solved accurately through the frequency-shift flexibility sensitivity equation, which indicates the damage locations and extents. The innovation of this work mainly lies in two aspects. The first innovation is that the ordinary flexibility sensitivity method has been improved through the frequency-shift operation for achieving the goal of identifying structural damage with fewer modal parameters. The second innovation is that in some engineering applications, the tested modal data can be used to directly compute the frequency-shift flexibility without the need for a complete finite element modeling process. Two numerical examples and one experimental example are used to validate the presented frequency-shift flexibility sensitivity method. It is found that the proportion of the higher-order vibration modes in the frequency-shift flexibility is greatly reduced. For this reason, the damage coefficients of the structure can be calculated accurately by the frequency-shift flexibility sensitivity analysis with only a few modal data. It has been shown that the proposed method requires fewer modal parameters but has higher calculation accuracy than the ordinary flexibility sensitivity method. It may be a valuable new approach to structural damage identification in engineering practice.
2. Theoretical Development
In this section, the ordinary flexibility sensitivity method is first briefly reviewed, and then a new frequency-shift flexibility sensitivity algorithm is developed for structural damage detection.
Based on structural FEM, the free vibration eigen-parameters can be computed by solving the following generalized eigenvalue problem as:
where and are the stiffness and mass matrices of a structure with DOFs, and are the -th eigenvalue and eigenvector ( and , also called the -th eigen-pair), respectively. Similarly, the eigen-solutions of the damaged structure can be also obtained by
where is the damaged stiffness matrix, and are the -th eigenvalue and eigenvector of the damaged structure, is the stiffness reduction due to structural damage, and are the damage coefficient and elementary stiffness matrix of the -th element in FEM, and is the total number of the elements in FEM. It is known that the flexibility matrix is the inverse of the stiffness matrix and can be obtained approximately by several low-order eigen-pairs as:
where and are the flexibility matrices of the undamaged and damaged structures, and is the number of the measured modes in the vibration testing. Subtracting (5) from (6), one obtains:
Equation (8) shows that the flexibility change can be approximately obtained by the measured lower eigen-parameters of the structure before and after damage. Substituting Equation (3) into (7), one obtains:
Using Neumann series expansion, Equation (9) can be further simplified as:
Ignoring the higher-order items in Equation (10) yields:
Substituting Equation (4) into (11), one obtains:
Equation (12) is called the ordinary flexibility sensitivity equation and will be used to compute the unknown damage coefficients () for damage identification. The matrix is called the elementary flexibility sensitivity of the -th element in FEM. The operation steps of the above flexibility sensitivity method are summarized as follows:
- (1)
- Establish the FEM of the intact structure to obtain the stiffness and mass matrices and .
- (2)
- Conduct dynamic analysis on the structure and measure the lower-order eigen-pairs of the intact and damaged structures.
- (3)
- Compute the flexibility change by Equation (8) and compute the elementary flexibility sensitivity matrix by Equation (13).
- (4)
- Compute the damage coefficients () by solving Equation (12). Finally, the damage locations and extents in the structure can be determined according to the values of ().
The advantage of the flexibility sensitivity method is that the calculation formula of elementary flexibility sensitivity (i.e., Equation (13)) is very simple, especially compared with the calculation formula of the eigenvector sensitivity [28]. The limitation of the ordinary flexibility sensitivity method is that several low-order eigen-pairs are still needed when applying Equation (8) to calculate the flexibility change . This leads to a large workload of dynamic analysis and a high requirement for analysis accuracy. However, only the first mode of structural vibration, namely the fundamental frequency and mode shape, is usually measured in practical engineering. This limits the successful application of the traditional flexibility sensitivity method in actual engineering structural damage identification. The method of successfully identifying structural damage using only the fundamental frequency and mode of structural vibration will be very popular in engineering practice.
To overcome this limitation, a novel frequency-shift flexibility sensitivity method is proposed in this work to compute the damage coefficients only using the first-order eigen-pairs. The key idea of the proposed method is to make the first eigenvalue () of the new system very close to zero through the frequency-shift operation. This will cause the reciprocal of the first eigenvalue to be particularly large and far exceed the reciprocals of other eigenvalues. As a result, the flexibility matrix of the new system can be accurately calculated by only the first-order eigen-pairs. The specific formulas of the proposed method are derived as follows. From Equations (1) and (2), the generalized eigenvalue equations of the intact and damaged systems after frequency shift are expressed as:
where denotes the frequency-shift distance, and denote the stiffness matrices of the intact and damaged systems after frequency shift, and and denote the eigenvalues of the intact and damaged systems after frequency shift. The frequency-shift operation shown in Equations (16)–(19) has been shown to be an effective means for quickly calculating the eigenvalues of large structures. The related content can be referred to in [29] and [30]. Similar to Equations (5) and (6), the intact and damaged flexibility matrices of the systems after frequency shift can also be obtained approximately by several low-order eigen-pairs as:
where and are the intact and damaged flexibility matrices of the systems after frequency shift. As can be seen in Equation (20) or (21), the first-order eigen-pairs will contribute most to the flexibility matrix when the frequency-shift distance is close to or . The basis for determining the frequency-shift distance is that the contribution of the first mode to the flexibility matrix after the frequency-shift operation exceeds 95% or more, since the allowable data error level in the engineering field is usually around 5%. The vibration frequencies of actual engineering structures are all greater than zero and sorted in ascending order. In view of this, a simple criterion for determining the value of is that the ratio of the first to second frequency after the frequency-shift operation is less than 5% or more. In most cases, the frequency-shift distance can be taken as a number between 0.90 and 0.99 times the first eigenvalue, which can basically meet the above requirement. Without loss of generality, taking , , and as an example, the reciprocals of these eigenvalues are , , and . The ratio of the reciprocal of the first-order eigenvalue to the sum of all reciprocals is . Letting , the eigenvalues of the system after frequency shift are , , and , and the corresponding reciprocals are , , and . The ratio of the reciprocal of the first-order eigenvalue to the sum of all reciprocals is . It is clear that the contribution of the first-order eigen-pairs to the flexibility matrix increased from 76.92% to 99.64% for the system before and after frequency shift. In other words, the contribution of the higher-order modes to the flexibility matrix can be greatly reduced by the frequency-shift operation. As a result, the frequency-shift flexibility change can be accurately estimated by only the first-order eigen-pairs as:
On the other hand, the frequency-shift flexibility sensitivity equation can also be derived by using the similar process from Equation (9) to (13) as:
Equation (23) is called the frequency-shift flexibility sensitivity equation and will be used to compute the unknown damage coefficients () for damage identification. The matrix is called the elementary frequency-shift flexibility sensitivity of the -th element in FEM.
In the end, the operation steps of the proposed frequency-shift flexibility sensitivity method are summarized as follows:
- (1)
- Establish the FEM of the intact structure to obtain the stiffness and mass matrices and .
- (2)
- Conduct dynamic analysis on the structure and measure the first-order eigen-pairs of the intact and damaged structures.
- (3)
- Compute the frequency-shift flexibility change by Equation (22) and compute the elementary frequency-shift flexibility sensitivity matrix by Equation (24).
- (4)
- Compute the damage coefficients () by solving Equation (23). Finally, the damage locations and extents in the structure can be determined according to the values of (). To resist the adverse effects of data noise due to measurement error, the singular-value truncation algorithm [31,32] is used in the process of solving the linear Equation (23) for achieving stable computational results in engineering applications. The core idea of the singular-value truncation algorithm is to ignore small singular values to partially eliminate the impact of data noise on the calculation results. The main formulas of the singular-value truncation algorithm are briefly illustrated as follows. Firstly, Equation (23) can be rewritten as a system of linear equations as:
Compared with the ordinary flexibility sensitivity method, the frequency-shift flexibility sensitivity approach greatly reduces the adverse effect of the higher-order modal truncation on damage identification. Theoretically, the proposed method can accurately calculate the structural damage parameters only by using the first-order eigen-parameters of structural free vibration. From Equations (24) and (25), one can find that the system matrices and of the undamaged FEM are used in the computation of the frequency-shift flexibility sensitivity. However, Equation (25) can be approximated by using Equation (20) with a few lower-frequency vibration modes.
Combining Equations (20) and (24), it can be found that the frequency-shift flexibility sensitivity equations can also be established by only using the tested vibration modes of the intact structure, rather than the system matrices and obtained from the FEM of the intact structure. This advantage makes it possible to conduct structural damage identification even without finite element modeling. In other words, another advantage of the proposed method is that it does not require a complete finite element modeling process, as long as a few lower-frequency vibration modes of the intact structure are measured. Therefore, the proposed method is simpler in operation compared to other existing sensitivity methods, as these existing sensitivity methods require the use of the system matrices and of the structural FEM. The case verification of this advantage is detailed in the following section of the experimental example.
3. Numerical Example
3.1. A Truss Structure
A 23-bar truss structure as shown in Figure 1 is used as the first numerical example to verify the frequency-shift flexibility sensitivity method. The main parameters of this steel truss structure are as follows: Young’s modulus is 200 GPa, density is 7800 kg/m3, length of each bar is 1 m, and cross-sectional area is 1.759 × 10−4 m2. The vibration test data used were generated through the numerical finite element model of the undamaged and damaged systems. Note that the data noise was not considered in this example in order to purely investigate the improvement effect of the frequency-shift process on the solution accuracy. Three damage scenarios are simulated in this example. The first damage scenario assumes that the elastic modulus of bar elements 10 and 13 are both reduced by 5%. The second damage scenario assumes that the elastic modulus of bar elements 9, 10, and 11 are reduced by 10%, 5%, and 5%, respectively. The third damage scenario assumes that the elastic modulus of bar element 13 is reduced by 2%. Table 1 presents the first natural frequencies of the undamaged and damage scenarios. In engineering practice, fatigue and corrosion of materials will lead to a decrease in the elastic modulus. Note that the proposed method is also applicable to other types of damage such as cracks or notches, as shown in the next experimental example. Figure 2, Figure 3 and Figure 4 present the calculation results of the damage coefficients by the proposed method and the ordinary flexibility sensitivity method, respectively. Only the first-order eigen-parameters are used in the calculation, and the frequency-shift distance is taken as , , and , respectively. Table 2, Table 3 and Table 4 present the comparison between the calculated value and the actual value of the damage extent for these three damage scenarios. The values in brackets in these tables represent the relative error between the calculated values and the true values.
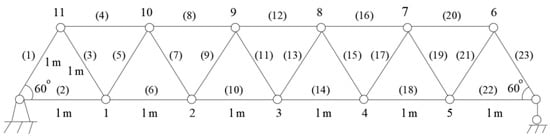
Figure 1.
A 23-bar truss structure.

Table 1.
The first natural frequencies of the undamaged and damage scenarios.
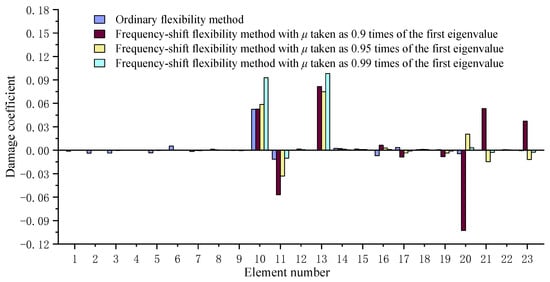
Figure 2.
Calculation result comparison of the proposed method and the ordinary flexibility sensitivity method for the first damage scenario.
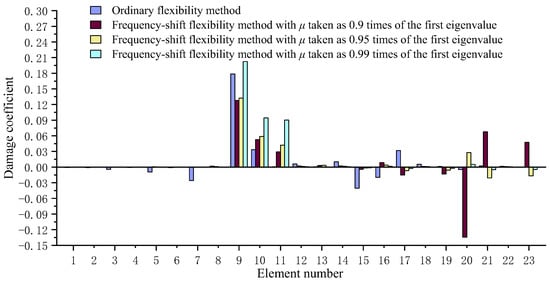
Figure 3.
Calculation result comparison of the proposed method and the ordinary flexibility sensitivity method for the second damage scenario.
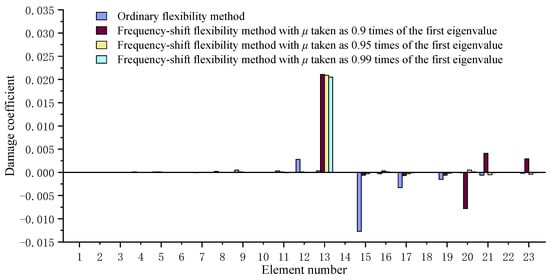
Figure 4.
Calculation result comparison of the proposed method and the ordinary flexibility sensitivity method for the third damage scenario.

Table 2.
Comparison between the calculated value and the actual value of the damage coefficient for the first damage scenario.

Table 3.
Comparison between the calculated value and the actual value of the damage coefficient for the second damage scenario.

Table 4.
Comparison between the calculated value and the actual value of the damage coefficient for the third damage scenario.
For the first damage scenario, one can find from Figure 2 that the proposed method can successfully identify elements 10 and 13 as the damaged bars. However, the ordinary flexibility sensitivity method can only identify element 10 as the damaged bar, while element 13 cannot be identified. This indicates that the traditional flexibility sensitivity method may result in a missed diagnosis, while the proposed frequency-shift flexibility sensitivity method performs well. When the frequency-shift distance changes, Table 2 shows that the calculation error of the damage coefficient is relatively minimal when . However, Figure 2 shows that the accuracy of damage localization is highest when , since there is a misjudgment of damage location when . When , a good balance can be achieved between the damage localization and damage quantification of the frequency-shift flexibility method. For the second damage scenario, it can be seen from Figure 3 that the proposed method can successfully identify elements 9, 10, and 11 as the damaged bars. Again, the ordinary flexibility sensitivity method failed since element 11 cannot be identified by it. This once again demonstrates that the proposed frequency-shift flexibility sensitivity method is more reliable in calculating results than the traditional flexibility sensitivity method. When the frequency-shift distance changes, Table 3 shows that the calculation error of the damage coefficient is relatively minimal when , and Figure 3 shows that the accuracy of damage localization is highest when . For the third damage scenario (minor damage), one can find from Figure 4 that the proposed method more clearly indicates that element 13 is the damaged bar than the ordinary flexibility sensitivity method. It has been shown that the proposed method may have better ability to identify the minor damage than the ordinary flexibility sensitivity method. When the frequency-shift distance changes, Table 4 and Figure 4 show that the frequency-shift flexibility algorithm has the best accuracy in damage localization and quantification when . Based on the above results, it can be concluded that the smaller the degree of damage, the larger the frequency-shift distance should be taken. In summary, the proposed frequency-shift flexibility algorithm is very efficient with only the first-order modal parameters. This new method can achieve the goal of improving the accuracy and reliability of the damage identification results through only the simple frequency-shift operation.
3.2. A Beam Structure
A beam structure with fixed ends (as shown in Figure 5) is used as the second numerical example to further verify the proposed method. The Young’s modulus and density of this beam structure are 193 GPa and 7850 kg/m3, respectively. The vibration test data used were generated through the numerical FEMs of the undamaged and damaged systems. In this example, a 5% random noise level is added to the first mode shape to simulate the measurement error as
where is the contaminated mode shape, is the noise level, and represents a random number located in the interval of [−1,1].

Figure 5.
A beam structure.
Two fault scenarios are simulated in this example. The first fault scenario assumes that the elastic modulus of elements 3 and 10 are reduced by 10% and 15%, respectively. The second fault scenario assumes that the elastic modulus of elements 6, 10, and 14 are all reduced by 10%. As stated before, the singular-value truncation algorithm is used in this example to overcome the adverse effects of data noise. Figure 6 and Figure 7 present the calculation results of the damage coefficients by the proposed method and the ordinary flexibility sensitivity method, respectively. Note that only the first-order eigen-parameters are used in the calculation, and the frequency-shift distance is taken as . Table 5 and Table 6 present the comparison between the calculated value and the actual value of the damage extent for the two damage scenarios. The values in brackets in these tables represent the relative error between the calculated values and the true values.
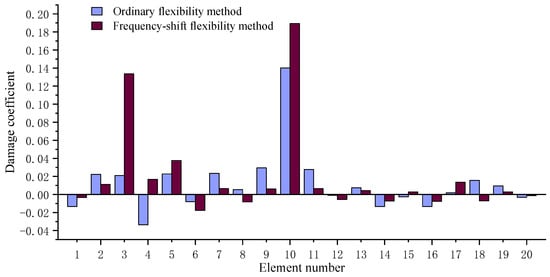
Figure 6.
Calculation result comparison of the proposed method and the ordinary flexibility sensitivity method when elements 3 and 10 are damaged.
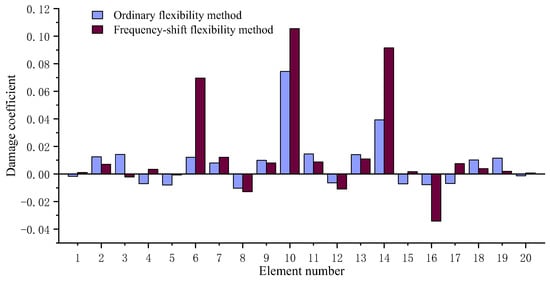
Figure 7.
Calculation result comparison of the proposed method and the ordinary flexibility sensitivity method when elements 6, 10, and 14 are damaged.

Table 5.
Comparison between the calculated value and the actual value of the damage coefficient when elements 3 and 10 are damaged.

Table 6.
Comparison between the calculated value and the actual value of the damage coefficient when elements 6, 10, and 14 are damaged.
For the first fault scenario, one can find from Figure 6 that the proposed method can successfully identify elements 3 and 10 as the fault locations. However, the ordinary flexibility sensitivity method can only identify element 10 as the fault location, while element 3 cannot be identified. This indicates that the traditional flexibility sensitivity method may result in misdiagnosis, while the proposed frequency-shift flexibility sensitivity method performs well. For the second fault scenario, it can be seen from Figure 7 that the proposed method can successfully identify elements 6, 10, and 14 as the damage locations. Again, the ordinary flexibility sensitivity method failed since element 6 cannot be identified by it. From Table 5 and Table 6, one can find that the proposed frequency-shift flexibility method achieves better computational accuracy than the ordinary flexibility method. This once again demonstrates that the proposed method can achieve the goal of improving the accuracy and reliability of fault identification through only the simple frequency-shift operation.
4. Validation by the Experimental Data of a Steel Frame Structure
The presented algorithm is further verified by the experimental data obtained from a three-story steel frame structure from [33]. As shown in Figure 8a, the experimental structure consists of three steel plates and four rectangular columns. These steel plates and columns are welded to form a rigid shear system as shown in Figure 8b. Detailed descriptions of material physical parameters and testing processes are provided in [33]. The fault condition is simulated by cutting from 75 mm to 51.3 mm on the first floor as shown in Figure 9, with a corresponding damage severity of 11.6%. The first frequency and vibration mode of the undamaged system measured are and . The second frequency and vibration mode of the undamaged system are and . The third frequency and vibration mode of the undamaged system are and . For the structure with damage, the measured first frequency and vibration mode are and . As stated before, the frequency-shift flexibility sensitivity equations in this example are established by directly using the tested vibration modes of the intact structure, rather than the system matrices and obtained from the FEM of the intact structure. Therefore, this example does not require a complete finite element modeling process to perform damage identification. Figure 10 presents the calculation results of the damage coefficients by the proposed method with the frequency-shift distance . From Figure 10, one can find that the proposed method can accurately identify the first floor as the damage location, and the calculated value of damage degree is 0.22. It has been shown that the proposed method can also complete the task of damage identification without the need for a complete finite element modeling process.
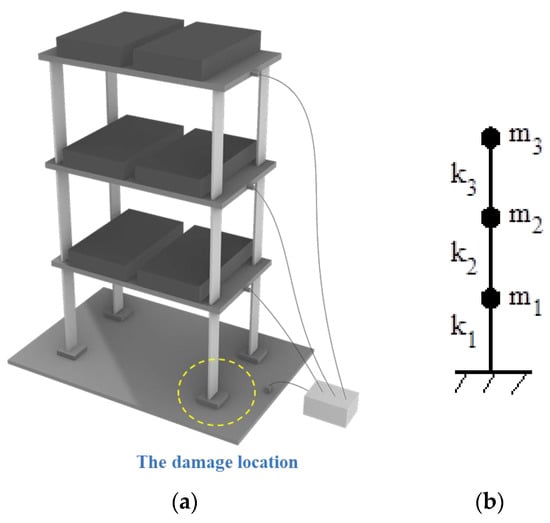
Figure 8.
(a) A three-story experimental steel frame structure; (b) simplified shear system corresponding to the experimental structure.
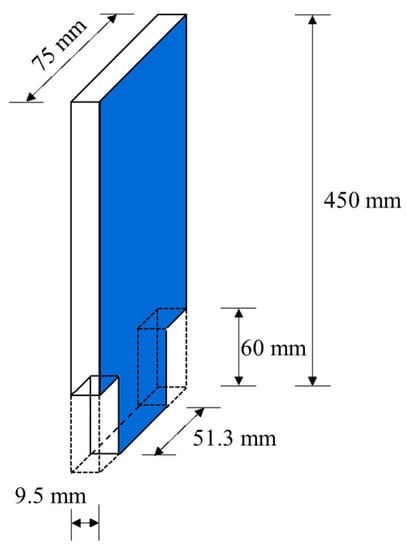
Figure 9.
The column width is cut from 75 mm to 51.3 mm to simulate the damage.
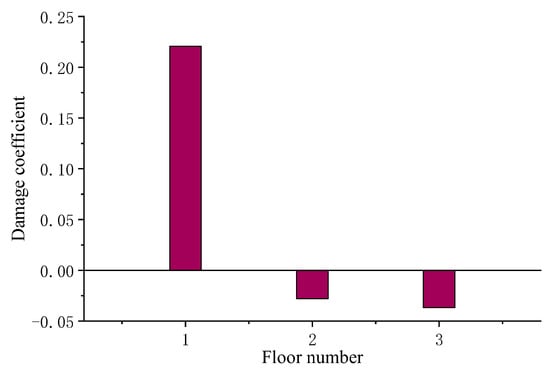
Figure 10.
Calculation result of the proposed method when the first floor is damaged.
5. Conclusions
In this work, a new frequency-shift flexibility sensitivity technique was developed for structural damage evaluation using only the first-order mode of structural free vibration. With the help of the frequency-shift operation, the first-order vibration mode will contribute the most to the structural flexibility matrix. This results in a significant reduction in the adverse effect of the higher-order modal truncation on structural damage identification. Theoretically, the proposed method can accurately calculate the structural damage coefficients by using only the first-order modal parameters. As a result, the reliable identification results can be achieved according to the values of the calculated damage coefficients. Another advantage of the proposed method is that it does not require a complete finite element modeling process, as long as a few lower-frequency vibration modes of the intact structure are measured. Based on the calculation results of the numerical and experimental examples, it can be concluded that the proposed method requires fewer modal parameters but has higher calculation accuracy than the ordinary flexibility sensitivity method. For the multiple damages case, this new approach can overcome the possible missed diagnosis of the ordinary flexibility sensitivity method. For the minor damage case, the numerical results also showed that the proposed algorithm may have the potential to identify the minor damage in the structure. The proposed method provides a new way for structural damage identification with only the first-order modal parameters. Note that the proposed method is only applicable to linear structures, and research on damage identification of nonlinear structures will be conducted in the future.
Author Contributions
Conceptualization, S.C. and Q.Y.; methodology, S.C. and Q.Y.; software, X.P.; validation, S.C., Q.Y. and X.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Zhejiang public welfare technology application research project (LGF22E080021), Ningbo natural science foundation project (202003N4169), Natural Science Foundation of China (11202138, 52008215), the Natural Science Foundation of Zhejiang Province, China (LQ20E080013), and the major special science and technology project (2019B10076) of “Ningbo science and technology innovation 2025”.
Data Availability Statement
The data used to support the findings of this study are included in this study and also available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Torzoni, M.; Manzoni, A.; Mariani, S. A multi-fidelity surrogate model for structural health monitoring exploiting model order reduction and artificial neural networks. Mech. Syst. Signal Process. 2023, 197, 110376. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Q.W. Damage detection in beam-like structures using static shear energy redistribution. Front. Struct. Civ. Eng. 2022, 16, 1552–1564. [Google Scholar] [CrossRef]
- Peng, X.; Tian, C.; Yang, Q. Structural Damage Identification Using the Optimal Achievable Displacement Variation. Materials 2022, 15, 8440. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.W.; Liu, J.K. Structural damage identification with flexibility changed: A review. J. Vib. Shock 2011, 30, 147–153. [Google Scholar]
- Pandey, A.K.; Biswas, M. Damage detection in structures using changes in flexibility. J. Sound Vib. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Jaishi, B.; Ren, W.X. Damage detection by finite element model updating using modal flexibility residual. J. Sound Vib. 2006, 290, 369–387. [Google Scholar] [CrossRef]
- Catbas, F.N.; Brown, D.L.; Aktan, A.E. Use of modal flexibility for damage detection and condition assessment: Case studies and demonstrations on large structures. J. Struct. Eng. 2006, 132, 1699–1712. [Google Scholar] [CrossRef]
- Duan, Z.; Yan, G.; Ou, J.; Spencer, B.F. Damage detection in ambient vibration using proportional flexibility matrix with incomplete measured DOFs. Struct. Control Health Monit. 2007, 14, 186–196. [Google Scholar] [CrossRef]
- Tomaszewska, A. Influence of statistical errors on damage detection based on structural flexibility and mode shape curvature. Comput. Struct. 2010, 88, 154–164. [Google Scholar] [CrossRef]
- Yang, Q.W. A new damage identification method based on structural flexibility disassembly. J. Vib. Control 2011, 17, 1000–1008. [Google Scholar] [CrossRef]
- Maghsoodi, A.; Ghadami, A.; Mirdamadi, H.R. Multiple-crack damage detection in multi-step beams by a novel local flexibility-based damage index. J. Sound Vib. 2013, 332, 294–305. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.P.; Xia, Y.; Mao, L. Damage detection using the eigenparameter decomposition of substructural flexibility matrix. Mech. Syst. Signal Process. 2013, 34, 19–38. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M. A multi-stage approach for damage detection in structural systems based on flexibility. Mech. Syst. Signal Process. 2016, 76, 455–475. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.Z.; Amiri, G.G.; Razzaghi, S.S.; Koo, K.Y.; Sung, S.H. Structural damage detection using sparse sensors installation by optimization procedure based on the modal flexibility matrix. J. Sound Vib. 2016, 381, 65–82. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Okur, F.Y.; Karaca, S.; Kahya, V. Vibration-based damage detection in beam structures with multiple cracks: Modal curvature vs. modal flexibility methods. Nondestruct. Test. Eval. 2019, 34, 33–53. [Google Scholar] [CrossRef]
- Wickramasinghe, W.R.; Thambiratnam, D.P.; Chan, T.H. Damage detection in a suspension bridge using modal flexibility method. Eng. Fail. Anal. 2020, 107, 104194. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Ghalehnovi, M. On model-based damage detection by an enhanced sensitivity function of modal flexibility and LSMR-Tikhonov method under incomplete noisy modal data. Eng. Comput. 2022, 38, 111–127. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B.; Fathnejat, H. A modified teaching–learning optimization algorithm for structural damage detection using a novel damage index based on modal flexibility and strain energy under environmental variations. Eng. Comput. 2022, 38, 847–874. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, W.; Zhang, J. Probabilistic Structural Model Updating with Modal Flexibility Using a Modified Firefly Algorithm. Materials 2022, 15, 8630. [Google Scholar] [CrossRef]
- Bernagozzi, G.; Quqa, S.; Landi, L.; Diotallevi, P. Structure-type classification and flexibility-based detection of earthquake-induced damage in full-scale RC buildings. J. Civ. Struct. Health Monit. 2022, 12, 1443–1468. [Google Scholar] [CrossRef]
- Yang, Q.W.; Peng, X. A highly efficient method for structural model reduction. Int. J. Numer. Methods Eng. 2023, 124, 513–533. [Google Scholar] [CrossRef]
- Dinh-Cong, D.; Nguyen-Huynh, P.; Nguyen, S.; Nguyen-Thoi, T. Damage Identification of Functionally Graded Beams using Modal Flexibility Sensitivity-based Damage Index. Period. Polytech. Civ. Eng. 2023, 67, 272–281. [Google Scholar] [CrossRef]
- Darshan, B.U.; Siddesha, H.; Rajanna, T. Structural Damage Detection for Plates Using Flexibility Based Strain Energy Method. Lect. Notes Civ. Eng. 2023, 256, 285–300. [Google Scholar]
- Quqa, S.; Landi, L. Integrating flexibility-based curvature with quasi-static features induced by traffic loads for high-resolution damage localization in bridges. Mech. Syst. Signal Process. 2023, 186, 109907. [Google Scholar] [CrossRef]
- Nick, H.; Ashrafpoor, A.; Aziminejad, A. Damage identification in steel frames using dual-criteria vibration-based damage detection method and artificial neural network. Structures 2023, 51, 1833–1851. [Google Scholar] [CrossRef]
- Cuomo, S.; Boccaccio, M.; Meo, M. Damage identification during an impact event using the Hilbert-Huang transform of decomposed propagation modes. Mech. Syst. Signal Process. 2023, 191, 110126. [Google Scholar] [CrossRef]
- Aulakh, D.S.; Bhalla, S. Piezo sensor based multiple damage detection under output only structural identification using strain modal flexibility. Mech. Syst. Signal Process. 2023, 194, 110272. [Google Scholar] [CrossRef]
- He, S.; Shi, Y.; Jonsson, E.; Martins, J. Eigenvalue problem derivatives computation for a complex matrix using the adjoint method. Mech. Syst. Signal Process. 2023, 185, 109717. [Google Scholar] [CrossRef]
- Zheng, S.; Ni, W.; Wang, W. Combined method for calculating eigenvector derivatives with repeated eigenvalues. AIAA J. 1998, 36, 428–431. [Google Scholar] [CrossRef]
- Xu, T.; Guo, G.; Zhang, H. Vibration reanalysis using frequency-shift combined approximations. Struct. Multidiscip. Optim. 2011, 44, 235–246. [Google Scholar] [CrossRef]
- Ren, W.X. A singular value decomposition based truncation algorithm in solving the structural damage equations. Acta Mech. Solida Sin. 2005, 18, 181–188. [Google Scholar]
- Yang, B.; Huang, H.; Ma, H.; Zhou, L.; Du, Q. Calculation of microwave heating temperature distribution based on SVD truncation. J. Microw. Power Electromagn. Energy 2022, 56, 238–258. [Google Scholar] [CrossRef]
- Li, L. Numerical and Experimental Studies of Damage Detection for Shear Buildings. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).