Abstract
This work purposes to establish two small numerical modifications for the Fractional Euler method (FEM) and the Modified Fractional Euler Method (MFEM) to deal with fractional initial value problems. Two such modifications, which are named Improved Modified Fractional Euler Method 1 (IMFEM 1) and Improved Modified Fractional Euler Method 2 (IMFEM 2), endeavor to further enhance FEM and MFEM in terms of attaining more accuracy. By utilizing certain theoretical results, the resultant error bounds of the proposed methods are analyzed and estimated. Several numerical comparisons are carried out to validate the efficiency of our proposed methods.
Keywords:
fractional differential equations; fractional Euler method; Caputo fractional derivative operator MSC:
26A33; 65M99
1. Introduction
A differential equation that begins with an initial condition that specifies the value of an unknown function at a particular location in the domain is known as an initial value problem (IVP). Many physical challenges encountered in research and engineering are typically solved using differential equations. Such solutions to differential equations can be allocated using a variety of analytical techniques. Numerical methods are typically used to solve difficult differential equations. Such methods are very helpful for quickly resolving many complex problems during the use of connections in computer programming [1,2,3,4]. Several researchers have tried to solve several IVPs using various techniques including the Euler Method (EM), Modified Euler Method (MEM), Improved Modified Euler Method (IMEM), and Improved Euler’s Method (IEM). Several precise numerical methods have been improved with better precision, dependability, and accuracy. Sometimes, to give better performance according to certain requirements, several numerical methods are improved.
Fractional calculus indicates the integration or the differentiation of a non-integer order. Interestingly enough, this topic has a long history in calculus. The first discussion of fractional calculus was between Leibniz and L’Hopital [5]. The former actually asked the latter about the differentiation of the order half of certain functions. However, there are some mathematicians, like Riemann, Abel, Liouville, and Lacroix, who laid the foundations for fractional calculus and dominated the field. In his famous paper on the even time problem, Abel was the first one who gave a physical description of the integral system of order 1/2. Indeed, this article went further for solving an integral equation. A fractional derivative was originally mentioned by Lacroix in a paper that was published in 1819. He applied fractional calculus to resolve an integral equation arising from the formulation of the tautochrone problem. Applications of the theory of fractional calculus expanded greatly during the nineteenth and twentieth centuries, and many contributors provided definitions of fractional derivatives and integrals.
Over the recent years, the applications of fractional differential equations (FDEs) have been significantly implemented in widely different practical and engineering fields such as viscosity, signal processing, control, and process modeling. For instance, in [6], the authors studied the numerical performances of the fractional-order mathematical model based on the Majnun and Layla romantic story. In [7], the authors combined fixed-point theory with a set of falling fractional functions in a Banach space to prove the existence and uniqueness of solutions of a class of fractional difference equations. In [8], the authors introduced the distributed-order time fractional Klein–Gordon–Zakharov system by substituting the second-order temporal derivative with a distributed-order fractional derivative. In [9], the authors defined the distributed-order time fractional version of the Schrödinger problem by replacing the first-order derivative in the classical problem with the fractional derivative. In this regard, it is interesting to notice that the numerical solutions of the nonlinear FDEs mentioned previously are significantly simpler to acquire, and for this reason, we resort to approximations. Numerical techniques have become a must [10,11,12,13]. In this regard, various numerical methods have been recently established and used to address this gap. Most of these methods have proved their accuracy in obtaining accurate approximate solutions when dealing with many linear and nonlinear problems.
In [14], the authors proposed a numerical generalization to the classical Euler method called the Fractional Euler Method (FEM). This method played and still plays an active role in handling fractional IVPs (FIVPs). In addition, a recently modified fractional Euler method has been proposed in [15]. Such a new modification proved its efficiency over FEM.
The research context presented in this paper tends to develop two numerical modifications for the use of FEM and MFEM; the first one is called the Improved Modified Fractional Euler Method 1 (IMFEM 1), while the second one is the Improved Modified Fractional Euler Method 2 (IMFEM 2). This is, of course, for finding approximate numerical solutions for linear and nonlinear FDEs. These proposed algorithms are characterized by the fact that they can provide more accuracy and efficiency than FEM and MFEM. This will be confirmed by performing several numerical comparisons via several illustrative examples. The error bound generated by the proposed methods will be analyzed and estimated by demonstrating specific theoretical results.
2. Preliminaries
This section aims to recall the most important definitions and concepts that will be useful throughout the paper. To deal with the FIVP formulated in the sense of a Caputo fractional differentiator, we consider the following equation [5,16]:
with the initial condition:
where .
Definition 1
([16]). The Riemann–Liouville integral operator of order α is defined as:
where and .
The Riemann–Liouville integrator satisfies the following properties [16]:
- ;
- ;
Definition 2
([16]). Suppose such that and . The Caputo fractional differentiator is defined by:
Lemma 1
([16]). If , and such that , we have:
and
Lemma 2
([17]). Suppose that t and s are two positive real numbers and is a sequence satisfying and , . Then:
Definition 3
([16]). The Mittag–Leffler function of two parameters α and β is outlined by the following series:
where and .
Theorem 1
(Generalized Taylor’s formula [14]). Suppose that for , where . Then, we can expand the function f about the node as follows:
with , .
For more illustration, we can express the above expression of the function f as follows:
3. Some Existing Numerical Methods
The aim of this section is to recall some existing numerical methods to deal with FIVPs. These methods are FEM and MFEM. Herein, we suppose that are distinct points in the interval such that , where is the step size of the discretization. In particular, the authors in [14] developed a generalization of the classical Euler method by proposing a general formula for solving FIVPs (1) and (2). This formula can be described by:
or approximately by:
for . More recently, the authors in [15] have successfully developed a new further modification for FEM, called MFEM, for solving FIVP (1) and (2). This formula can be expressed by:
or approximately by:
for . Note that denotes the exact solution of problems (1) and (2) at , and denotes the numerical solution of the same problem at .
In the next section, we aim to present two further numerical modifications for the above two formulas: the Improved Modified Fractional Euler Method 1 (IMFEM 1) and Improved Modified Fractional Euler Method 2 (IMFEM 2).
4. Novel Numerical Modifications for FEM and MFEM
With the aim of handling the classical version of problems (1) and (2), two small modifications to the classical Euler Method were proposed in [18]. These methods have confirmed their reliability and validity in dealing with the classical form of problems (1) and (2). In particular, it was declared in [18] that the numerical method that could be used to solve the classical form of problems (1) and (2) applies to the following formulas:
and:
Next, we will utilize the above two approximations for the purpose of establishing IMFEM 1 and IMFEM 2.
4.1. Improved Modified Fractional Euler Method 1
In view of approximation (13), we intend in this subsection to propose a new method called the Improved Modified Fractional Euler Method 1 (IMFEM 1) that would help one to solve the FIVPs (1) and (2). The IMFEM 1 represents an improvement of the well-known FEM and MFEM that is typically applied to deal with problems (1) and (2). For instance, to deal with such a problem, we first suppose that in which the mesh points are , with the step size . Now, by using the first three terms of the generalized Taylor theorem given in Theorem 1, we can expand about as follows:
where . If one substitutes instead of t in the above equality, we obtain:
which immediately implies:
Now, based on approximation (13), we can propose the following formula:
From now on, we shall use to denote the exact solution of problems (1) and (2) at , and to denote the numerical solution of the same problem at the same point, such that:
for (Algorithm 1).
| Algorithm 1 (IMFEM 1) |
|
4.2. Improved Modified Fractional Euler Method 2 (IMFEM 2)
By following the same manner as in Section 4.1 and by using approximation (14) in (17), we can propose the following formula:
Similarly, is used here to denote the exact solution of problems (1) and (2) at , and is used to denote the numerical solution of the same problem, such that:
for (Algorithm 2).
| Algorithm 2 (IMFEM 2) |
|
5. Estimations of Error Bounds
In this section, we aim to estimate the error bounds gained from our proposed schemes established in approximations (19) and (21). Furthermore, we introduce some theoretical results that concern estimations of the upper bounds of the errors generated by the proposed schemes, IMFEM 1 and IMFEM 2.
Theorem 2
(The error bound of IMFEM 1). Suppose that f is a continuous real-valued function satisfying the Lipschitz condition with constant L on , i.e.,
Suppose that a constant M exists with:
Then, we have:
where:
Proof.
In order to prove this result, we first subtract (19) from (18) to obtain:
By using the Lipschitz condition, we obtain:
which implies:
Immediately, we can have:
i.e.,
This means that:
Now, by letting , and , we obtain:
Thus, by Lemma 2, we obtain:
which means that:
However, since , we have:
which gives:
□
Theorem 3
(The error bound of IMFEM 2). Suppose that f is a continuous real-valued function and satisfying Lipschitz condition with constant L on , i.e.,
Suppose that a constant M exists with:
Then, we have:
where:
and:
Proof.
To prove this result, we first subtract (21) from (20) to obtain:
By using the Lipschitz condition, we obtain:
which leads to the following inequality:
Consequently, we have:
This means that:
In other words, we have:
Now, by letting , and , we obtain:
for . Thus, by Lemma 2, we obtain:
which means that:
But since , we have:
which gives:
for , and this completes the proof. □
6. Numerical Simulations
Three numerical examples are provided in this section to demonstrate the efficiency of the suggested methodology. In particular, the solutions generated by FEM, MFEM, IMFEM 1, and IMFEM 2, are displayed for a range of . The solutions’ behaviors produced by the proposed techniques seem to be dependent on the values of , and the approximation’s accuracy seems to be correlated with the step size h.
Example 1.

Consider the following FIVP:
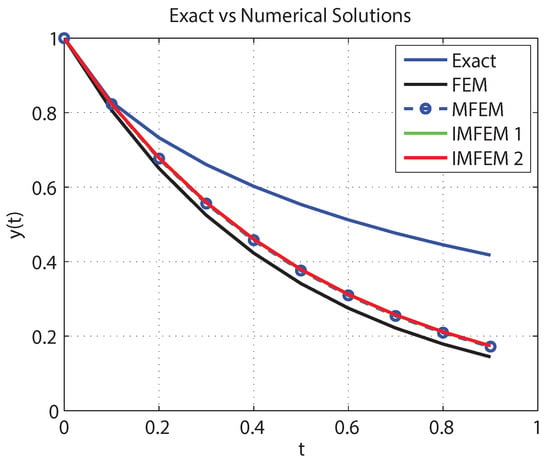
where . Note that the exact solution of the above problem is . However, to deal with such a problem, we apply Formulas (19) and (21). This would produce Figure 1, which includes a numerical comparison between the numerical solutions of problem (22) gained by using FEM, MFEM, IMFEM 1, and IMFEM 2 according to and .

Figure 1.
Numerical solutions of problem (22) using FEM, MFEM, IMFEM 1, and IMFEM 2 when and .
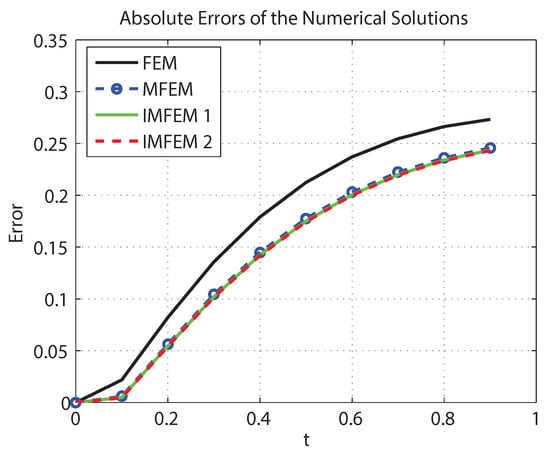
For more illustration, we plotted below Figure 2 and produced Table 1; both show a strong contrast in absolute error values for the numerical solutions between the four schemes in favor of our proposed schemes.

Figure 2.
Absolute errors between the exact and numerical solutions of problem (22).

Table 1.
Absolute error values between the exact and numerical solutions of problem (22).
Based on the previous numerical simulations, it can be noticed that the IMFEM 2 solution is closer to the exact solution than any solution generated by the considered methods.
Example 2.

Consider the following FIVP:
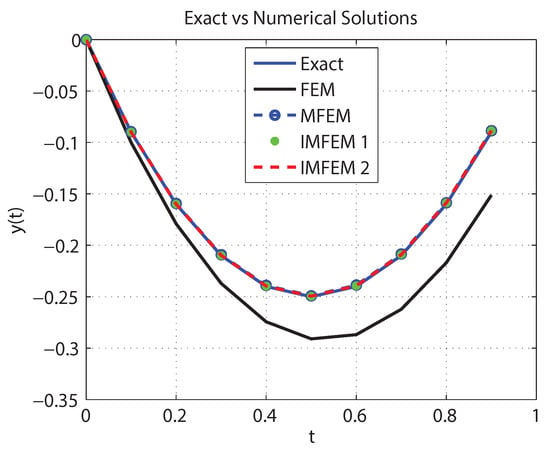
where . The exact solution of the above problem is . Herein, we applied Formulas (19) and (21) to solve problem (23), and hence generated Figure 3. The figure illustrates the numerical solutions of the considered problem generated by using FEM, MFEM, IMFEM 1, and IMFEM 2 according to and .

Figure 3.
Numerical solutions of problem (23) using FEM, MFEM, IMFEM 1, and IMFEM 2 when and .
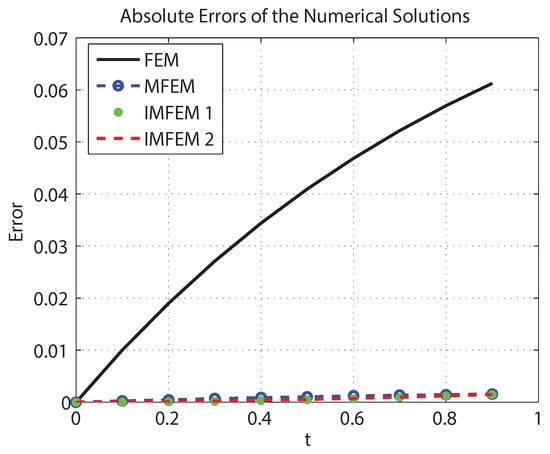
In order to take a look at the absolute error values for the numerical solutions generated by FEM, MFEM, IMFEM 1, and IMFEM 2, we plotted Figure 4 and produced Table 2.

Figure 4.
Absolute error between the exact and numerical solutions of problem (23).

Table 2.
Absolute error values between the exact and numerical solutions of problem (23).
In view of the previous numerical results, one can clearly observe that the accuracies of the proposed two methods, IMFEM 1 and IMFEM 2, are better than those of the solutions obtained by FEM and MFEM.
Example 3.

Consider the following FIVP:
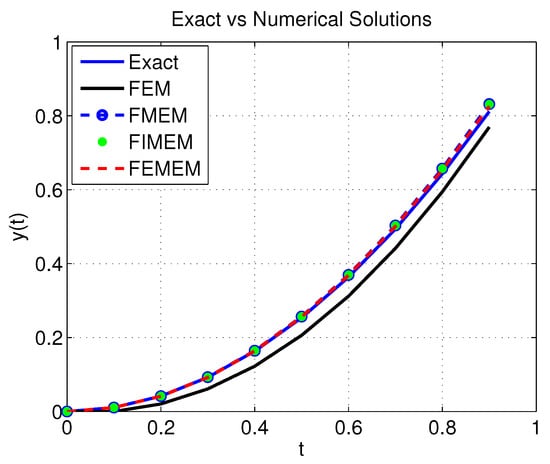
where . The exact solution to the above problem is given by . In a similar manner to the previous two examples, we applied Formulas (19) and (21) to solve this problem. As a result, Figure 5 was then generated, which illustrates the numerical solutions of such a problem using FEM, MFEM, IMFEM 1, and IMFEM 2 with and . In the same regard, we plotted Figure 6 and produced Table 3 for the purpose of highlighting the absolute error values for the numerical solutions generated by all considered methods.

Figure 5.
Numerical solution of problem (3) using FEM, MFEM, IMFEM 1, and IMFEM 2 when and .

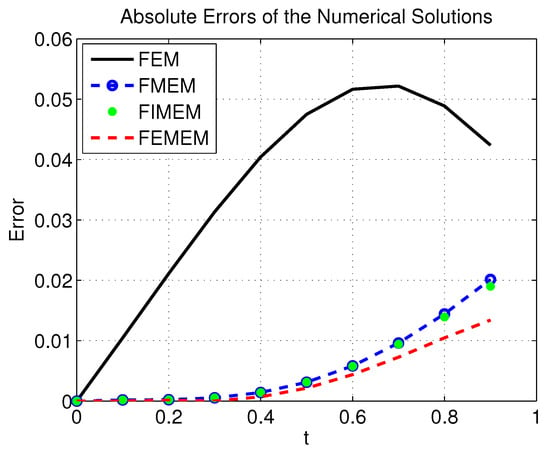
Figure 6.
Absolute error between the exact and numerical solutions of problem (3).

Table 3.
Absolute error values between the exact and numerical solutions of problem (3).
Clearly, one can note that the numerical solutions generated by the presented methods are closer to the exact solution than that of the numerical solutions generated by other considered methods. Thus, we conclude the importance of the presented methods in gaining reasonable accuracy when dealing with FIVPs.
7. Conclusions
In order to address the fractional initial value problems, this study aimed to develop two novel numerical approaches referring to the Fractional Euler Method (FEM) and the Modified Fractional Euler Method (MFEM). These approaches, which are called the Improved Modified Fractional Euler Method 1 (IMFEM 1) and Improved Modified Fractional Euler Method 2 (IMFEM 2), are regarded as two numerical adaptations aimed to increase the accuracy of FEM and MFEM. The resulting error bounds of the suggested strategies have been estimated using specific theoretical results. It should be noted, in this regard, that expressing approximate solutions generated by using our proposed algorithms when we deal with certain nonlinear multi-term complicated initial value problems may be regarded as the most important limitations of these algorithms. In spite of the existence of this notion, the IMFEM 2 has yielded, based on several numerical comparisons, high accuracy solutions to the linear and nonlinear fractional initial value problems in comparison with all other considered methods, followed by IMFEM 1, then MFEM, and finally FEM. This would allow one to apply our proposed methods to several problems such as the problems of solving fractional partial differential equations, systems of fractional differential equations, epidemic models, and many others.
Author Contributions
Conceptualization, I.M.B. and I.H.J.; methodology, A.A.A.; software, S.B.A.-S.; validation, K.M.; formal analysis, I.M.B.; investigation, A.A.A.; resources, S.B.A.-S.; data curation, I.H.J.; writing—original draft preparation, K.M.; writing—review and editing, I.M.B.; visualization, A.A.A.; supervision, I.H.J.; project administration, S.B.A.-S.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Arab Open University for funding this work through AOU research fund No. AOURG-2023-008.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Arab Open University and Al-Zaytoonah University for providing the necessary scientific research supplies to implement the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aho, A.; Hopcroft, J.E.; Ullman, J.D. The Design and Analysis of Algorithms; Addison-Wesley: Reading, MA, USA, 1975. [Google Scholar]
- Aitken, A.C. On interpolation by iteration of proportional parts without the use of differences. Proc. Edinb. Math. Soc. 1932, 3, 56–76. [Google Scholar] [CrossRef]
- Aitken, A.C. On the theory of graduation. Proc. R. Soc. Edinb. 1925, 46, 36–45. [Google Scholar] [CrossRef]
- Allgower, E.L.; Georg, K. Numerical Continuation Methods: An Introduction; Volume 13 of Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Batiha, I.; Shameseddin Alshorm, M.; Jebril, I.; Hammad, M.A. A Brief Review about Fractional Calculus. Int. J. Open Probl. Compt. Math. 2022, 15, 39–56. [Google Scholar]
- Sabir, Z.; Guirao, J.L.G. A Soft Computing Scaled Conjugate Gradient Procedure for the Fractional Order Majnun and Layla Romantic Story. Mathematics 2023, 11, 835. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Srivastava, H.M.; Guirao, J.L.; Hamed, Y.S. Existence of solutions for a class of nonlinear fractional difference equations of the Riemann–Liouville type. Adv. Cont. Discr. Mod. 2022, 2022, 32. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M.; Baleanu, D. Numerical solution of distributed-order time fractional Klein–Gordon–Zakharov system. J. Comput. Sci. 2023, 67, 101961. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M.; Baleanu, D. A numerical method based on the piecewise Jacobi functions for distributed-order fractional Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106873. [Google Scholar] [CrossRef]
- Albadarneh, R.B.; Batiha, I.M.; Adwai, A.; Tahat, N.; Alomari, A.K. Numerical approach of Riemann–Liouville fractional derivative operator. Int. J. Electr. Comput. Eng. 2021, 11, 5367–5378. [Google Scholar] [CrossRef]
- Batiha, I.M.; Alshorm, S.; Ouannas, A.; Momani, S.; Ababneh, O.Y.; Albdareen, M. Modified Three-Point Fractional Formulas with Richardson Extrapolation. Mathematics 2022, 10, 3489. [Google Scholar] [CrossRef]
- Hussain, K.H. Some new existence and uniqueness results of Caputo fractional integro-differential equations. Int. J. Innov. Inf. Control 2021, 17, 2071–2079. [Google Scholar]
- Yasmin, H.; Abu Hammad, M.; Shah, R.; Alotaibi, B.M.; Ismaeel, S.M.E.; El-Tantawy, S.A. On the Solutions of the Fractional-Order Sawada–Kotera–Ito Equation and Modeling Nonlinear Structures in Fluid Mediums. Symmetry 2023, 15, 605. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Momani, S. An algorithm for the numerical solution of differential equations of fractional order. J. Appl. Math. Inform. 2008, 26, 15–27. [Google Scholar]
- Batiha Iqbal, M.; Anwar, B.; Al-Nana Abeer, A.; Shameseddin, A.; Jebril Iqbal, H.; Amjed, Z. A numerical scheme for dealing with fractional initial value problem. Int. J. Innov. Comput. Inf. Control 2023, 19, 763. [Google Scholar]
- Podlubny, I. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA; Boston, MA, USA; New York, NY, USA; London, UK; Tokyo, Japan; Toronto, ON, Canada, 1999; 368p, ISBN 0125588402. [Google Scholar]
- Burden, R.L.; Faires, J.D.; Burden, A.M. Numerical Analysis, 9th ed.; Thomson Brooks/Cole: Boston, MA, USA, 2005. [Google Scholar]
- Workie, A.H. Small Modification on Modified Euler Method for Solving Initial Value Problems. Abstr. Appl. Anal. 2021, 2021, 9951815. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).