Semi-Hyers–Ulam–Rassias Stability of Some Volterra Integro-Differential Equations via Laplace Transform

Abstract

In this paper the semi-Hyers–Ulam–Rassias stability of some Volterra integro-differential equations is investigated, using the Laplace transform. This is a continuation of some previous work on this topic. The equation in the general form contains more terms, where the unknown function appears together with the derivative of order one and with two integral terms. The particular cases that are considered illustrate the main results for some polynomial and exponential functions.

1. Introduction

The study of Ulam stability was initiated due to an interesting problem posed in the year 1940, by Ulam [1], regarding the stability for the equation of group homomorphisms. An answer was given by Hyers [2], in 1941, in the framework of Banach spaces, for the additive Cauchy equation. In the following years, many mathematicians were concerned with this problem, also for the case of differential equations, integral equations, and partial differential equations.

First, results regarding Hyers–Ulam stability of differential equations were provided by Obloza [3] and Alsina and Ger [4]. Further, in the papers [5,6,7,8,9], the stability of first order linear differential equations and linear differential equations of higher order was studied.

Brzdek, Popa, Rasa, and Xu presented in [10] a collection of results related to Hyers–Ulam stability.

The Hyers–Ulam–Rassias stability of a Volterra integral equation was first studied by Jung in [11], using the fixed point method, adopting an idea of Cadariu and Radu from [12]. In [11] the following equation was investigated:

$$x\left(t\right)={\int }_c^{t}f\left(\tau ,x\left(\tau \right)\right)d\tau ,c\in \mathbb{R},t\in [a,b].$$

Next, Castro and Ramos in [13] obtained the stability of the integral equation

$$x\left(t\right)={\int }_c^{t}f\left(t,\tau ,x\left(\tau \right)\right)d\tau ,c\in \mathbb{R},t\in [a,b].$$

A more complicated equation,

$$x\left(t\right)=p\left(t\right)+f(t,x\left(t\right)){\int }_c^{t}g(t,\tau )h\left(\tau ,x\left(\tau \right)\right)d\tau ,c\in \mathbb{R},t\in [a,b],$$

was considered in [14] by Castro and Simões. The same authors studied in the paper [15] two more equations:

$$x\left(t\right)=f\left(t,x\left(t\right),x\left(\alpha \left(t\right)\right),{\int }_a^{b}k\left(t,\tau ,x\left(\tau \right),x\left(\beta \left(\tau \right)\right)\right)d\tau \right),t\in [a,b]$$

and

$$x\left(t\right)=f\left(t,x\left(t\right),x\left(\alpha \left(t\right)\right),{\int }_a^{t}k\left(t,\tau ,x\left(\tau \right),x\left(\beta \left(\tau \right)\right)\right)d\tau \right),t\in [a,b]$$

through the generalized Bielecki metric.

Generalized Bielecki metric was also used by Castro and Simões in [16], where the equation

$$x^{\prime }\left(t\right)=f\left(t,x\left(t\right),{\int }_a^{b}k\left(t,\tau ,x\left(\tau \right),x\left(\alpha \left(\tau \right)\right)\right)d\tau \right),t\in [a,b]$$

was studied, and in [17], by Simoes, Carapau, Correia, where the equation

$$x^{\left(n\right)}\left(t\right)=f\left(t,x\left(t\right),{\int }_a^{b}k\left(t,\tau ,x\left(\tau \right),x^{\prime }\left(\tau \right),\cdots ,x^{(n-1)}\left(\tau \right)\right)d\tau \right),t\in [a,b]$$

was investigated.

In [18], Otrocol and Ilea proved stability results for the equation

$$x\left(t\right)=p\left(t\right)+{\int }_a^{t}f\left(t,\tau ,x\left(\tau \right),\underset{\theta \in [a,\tau ]}{sup}y\left(\theta \right)\right)d\tau ,t\in [a,b].$$

Hyers–Ulam stability of integral equations was also studied, by various methods, in numerous papers among which we mention [19,20,21,22,23,24,25,26,27,28,29].

The Laplace integral transform was employed for the first time to investigate the stability of linear differential equations in the recent work of Rezaei, Jung, and Rassias [30]. The idea was developed and extended subsequently also in several other papers, such as [31,32,33].

Using the previously mentioned method of Rezaei, Jung, and Rassias [30], we have established in [34] the semi-Hyers–Ulam–Rassias stability of the integral-differential equation:

$$x^{\prime }\left(t\right)+{\int }_0^{t}x\left(\tau \right)g\left(t-\tau \right)d\tau -f\left(t\right)=0,t\in \left(0,\infty \right),$$

and in [35] the semi-Hyers–Ulam–Rassias stability of the another integral-differential equation:

$$x^{″}\left(t\right)+{\int }_0^{t}x\left(\tau \right)g\left(t-\tau \right)d\tau -f\left(t\right)=0,t\in \left(0,\infty \right).$$

Other types of convolutional equations have been studied in [36,37].

In this paper, we will study the semi-Hyers–Ulam–Rassias stability of the equation

$$x^{\prime }\left(t\right)+ax\left(t\right)+b{\int }_0^t{x}^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau +c{\int }_0^{t}x\left(\tau \right)d\tau -f\left(t\right)=0,t\in \left(0,\infty \right),$$

(1)

$a,b,c\in \mathbb{F},$ where $\mathbb{F}$ is the real set $\mathbb{R}$ or the complex set $\mathbb{C}$. The functions $f,g:(0,\infty )\to \mathbb{F}$ are given continuous functions and $x:(0,\infty )\to \mathbb{F}$ is continuously differentiable.

The contents of the paper are the following: in Section 2 we recall some properties of the Laplace transform and define the semi-Hyers–Ulam–Rassias stability of the Equation (1). The main results (Theorems 1–5) are presented in the next section. The first theorem is formulated for the general form of the equation, and the estimation of the difference between the exact and the approximate solutions is given in terms of the inverse Laplace transform. Afterwards, several particular cases of the function g are treated. In Theorems 2 and 3 the function $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=t$ is considered, for the cases $b+c=0$ and $b+c\ne 0$ respectively. In Theorem 4 the function $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=t^n,n\in \mathbb{N},n\ge 2$ and in Theorem 5 the function $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=e^{\gamma t}$ with $\gamma \in {\mathbb{R}}^{\ast }$ are taken. It is often difficult to calculate the inverse Laplace transform, however, this could be done in the special cases studied. Two examples illustrate the general theorem. The last section contains stability results for two equations (a general one and a particular one) obtained with the help of the double Laplace transform.

2. Preliminary Notions and Results

In the next sections, if not mentioned otherwise, consider the functions $f,g,x:\left(0,\infty \right)\to \mathbb{F}$, where by $\mathbb{F}$ is denoted the set of real numbers $\mathbb{R}$ or the set of complex numbers $\mathbb{C}$. Suppose that these functions are continuous and of exponential order, such that their Laplace transform is well defined. Suppose also that the function x is continuously differentiable. For the sake of simplicity, instead of the lateral limits $f\left(0^{+}\right),g\left(0^{+}\right),x\left(0^{+}\right)$, we write $f\left(0\right),g\left(0\right),x\left(0\right)$, respectively.

As usual, $\mathcal{L}\left(x\right)$ denotes the Laplace integral transform of the function x, defined by

$$\mathcal{L}\left(x\right)\left(s\right)=X\left(s\right)={\int }_0^{\infty }x\left(t\right)e^{-st}dt,$$

on the open half plane $\{s\in \mathbb{C}|\Re \left(s\right)>{\sigma }_x\}$, where ${\sigma }_x$ is the abscissa of convergence of the function x and $\Re \left(s\right)$ stands for the real part of the complex number s. The inverse Laplace transform of a function X will be denoted by ${\mathcal{L}}^{-1}\left(X\right)$. Some properties used in the paper are

$$\mathcal{L}\left(x^{\prime }\right)\left(s\right)=s\mathcal{L}\left(x\right)\left(s\right)-x\left(0\right),$$

$$\mathcal{L}(f\ast g)\left(s\right)=\mathcal{L}\left(f\right)\left(s\right)·\mathcal{L}\left(g\right)\left(s\right),$$

where by $(f\ast g)\left(t\right)={\int }_0^{t}f(t-\tau )g\left(\tau \right)d\tau$ is denoted the convolution product of the two functions f and g. It is a well known property that the Laplace transform is bijective and linear.

The following lemma will be used in the main results of the paper. It assures the existence of the Laplace inverse for a class of rational functions.

Lemma 1

([30]). Let $P\left(s\right)=a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0$ and $Q\left(s\right)=b_m{s}^m+b_{m-1}{s}^{m-1}+\cdots +b_{1}s+b_0$ where $m,n$ are non-negative integers with $m<n$ and $a_i,b_i$ are scalars, $i\in \left\{0,1,\dots ,n\right\}.$ Then there exists an infinitely differentiable function $g:\left(0,\infty \right)\to \mathbb{F}$, such that

$$\mathcal{L}\left(g\right)=\frac{Q\left(s\right)}{P\left(s\right)},\Re \left(s\right)>{\sigma }_P,$$

and

$$g^{\left(k\right)}\left(0\right)=\left\{\begin{array}{c}0,k\in \left\{0,1,\dots ,n-m-2\right\}\hfill \\ \frac{b_m}{a_n},k=n-m-1\hfill \end{array},\right.$$

where ${\sigma }_P=max\left\{\Re \left(s\right):P\left(s\right)=0\right\}$.

Let $\epsilon >0.$ We associate to the equation in study the inequality

$$\left|x^{\prime }\left(t\right)+ax\left(t\right)+b{\int }_0^t{x}^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau +c{\int }_0^{t}x\left(\tau \right)d\tau -f\left(t\right)\right|\le \epsilon ,t\in \left(0,\infty \right).$$

(2)

According to [16] we formulate the following definition:

Definition 1.

The Equation (1) is said to be semi-Hyers–Ulam–Rassias stable if there exists a function $k:\left(0,\infty \right)\to \left(0,\infty \right)$ such that for each x that verifies the inequality (2), there exists a solution $x_0$ of the Equation (1) with

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le k\left(t\right),\forall t\in \left(0,\infty \right).$$

(3)

Notice that a function $x:\left(0,\infty \right)\to \mathbb{F}$ is a solution of the inequality (2) if, and only if, there exists a function $h:\left(0,\infty \right)\to \mathbb{F}$ such that the following hold:

(1) $\left|h\left(t\right)\right|\le \epsilon ,\forall t\in \left(0,\infty \right)$,

(2) $x^{\prime }\left(t\right)+ax\left(t\right)+b{\int }_0^t{x}^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau +c{\int }_0^{t}x\left(\tau \right)d\tau -f\left(t\right)=h\left(t\right),\forall t\in \left(0,\infty \right)$.

3. Main Results

The main result regarding the stability of Equation (1) is the next Theorem. We will also particularize it to some special cases for the integrand function g.

Theorem 1.

Suppose that the Laplace inverse ${\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t\right)$ is well defined and also that ${\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(0\right)=1$. If a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ satisfies the inequality (2), then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of (1), such that

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t-\tau \right)\right|d\tau ,\forall t\in \left(0,\infty \right),$$

that is the Equation (1) is semi-Hyers–Ulam–Rassias stable.

Proof. 

Let $h:\left(0,\infty \right)\to \mathbb{F}$,

$$h\left(t\right)=x^{\prime }\left(t\right)+ax\left(t\right)+b{\int }_0^t{x}^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau +c{\int }_0^{t}x\left(\tau \right)d\tau -f\left(t\right).$$

(4)

We can write (4) as

$$h\left(t\right)=x^{\prime }\left(t\right)+ax\left(t\right)+bg\left(t\right)\ast x^{\prime }\left(t\right)+c·1\ast x\left(t\right)-f\left(t\right).$$

Applying the Laplace transform to the above equality, we have

$$\mathcal{L}\left(h\right)=s\mathcal{L}\left(x\right)-x\left(0\right)+a\mathcal{L}\left(x\right)+b\mathcal{L}\left(g\right)·\left[s\mathcal{L}\left(x\right)-x\left(0\right)\right]+c·\frac{1}{s}·\mathcal{L}\left(x\right)-\mathcal{L}\left(f\right),$$

hence

$$\begin{array}{cc}\hfill & \mathcal{L}\left(x\right)=\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(h\right)+\frac{bx\left(0\right)s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(g\right)\hfill \\ \hfill & +\frac{x\left(0\right)s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}+\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(f\right).\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill & x_0\left(t\right)={\mathcal{L}}^{-1}\left(\frac{bx\left(0\right)s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(g\right)\right)\left(t\right)+{\mathcal{L}}^{-1}\left(\frac{x\left(0\right)s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t\right)\hfill \\ \hfill & +{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(f\right)\right)\left(t\right),\forall t\in \left(0,\infty \right).\hfill \end{array}$$

We remark that $x_0\left(0\right)=x\left(0\right).$

Hence we obtain

$$\begin{array}{cc}\hfill & \mathcal{L}\left[x_0^{\prime }\left(t\right)+a{x}_0\left(t\right)+b{\int }_0^t{x}_0^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau +c{\int }_0^t{x}_0\left(\tau \right)d\tau -f\left(t\right)\right]\hfill \\ \hfill & =s\mathcal{L}\left(x_0\right)-x_0\left(0\right)+a\mathcal{L}\left(x_0\right)+b\mathcal{L}\left(g\right)·\left[s\mathcal{L}\left(x_0\right)-x_0\left(0\right)\right]+c·\frac{1}{s}·\mathcal{L}\left(x_0\right)-\mathcal{L}\left(f\right)\hfill \\ \hfill & =\mathcal{L}\left(x_0\right)\left[\frac{s^2(1+b\mathcal{L}\left(g\right))+as+c}{s}\right]-x_0\left(0\right)-b{x}_0\left(0\right)\mathcal{L}\left(g\right)-\mathcal{L}\left(f\right)\hfill \\ \hfill & =\left[\frac{bx\left(0\right)s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(g\right)+\frac{x\left(0\right)s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}+\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(f\right)\right]\hfill \\ \hfill & ·\left[\frac{s^2(1+b\mathcal{L}\left(g\right))+as+c}{s}\right]-x_0\left(0\right)-b{x}_0\left(0\right)\mathcal{L}\left(g\right)-\mathcal{L}\left(f\right)=0.\hfill \end{array}$$

Since the transform $\mathcal{L}$ is bijective, it follows that

$$x_0^{\prime }\left(t\right)+a{x}_0\left(t\right)+b{\int }_0^t{x}_0^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau +c{\int }_0^t{x}_0\left(\tau \right)d\tau -f\left(t\right)=0,$$

which means that $x_0$ is indeed a solution of (1).

We can write

$$\mathcal{L}\left(x\right)-\mathcal{L}\left(x_0\right)=\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(h\right),$$

hence

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|=\left|{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(h\right)\right)\right|\hfill \\ \hfill & =\left|{\mathcal{L}}^{-1}\left(\mathcal{L}\left(h\right)\right)\ast {\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\right|=\left|h\ast {\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\right|\hfill \\ \hfill & =\left|{\int }_0^{t}h\left(\tau \right)·{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t-\tau \right)d\tau \right|\hfill \\ \hfill & \le {\int }_0^t\left|h\left(\tau \right)\right|·\left|{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t-\tau \right)\right|d\tau \hfill \\ \hfill & \le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t-\tau \right)\right|d\tau .\hfill \end{array}$$

□

Example 1.

Study the semi-Hyers–Ulam–Rassias stability of the equation

$$x^{\prime }\left(t\right)-x\left(t\right)+{\int }_0^t{x}^{\prime }\left(\tau \right)\left(t-\tau \right)d\tau -{\int }_0^{t}x\left(\tau \right)d\tau -t=0,t\in \left(0,\infty \right),$$

(5)

$x:\left(0,\infty \right)\to \mathbb{R}$ continuously differentiable.

For $\epsilon >0$, we consider the inequality

$$\left|x^{\prime }\left(t\right)-x\left(t\right)+{\int }_0^t{x}^{\prime }\left(\tau \right)\left(t-\tau \right)d\tau -{\int }_0^{t}x\left(\tau \right)d\tau -t\right|\le \epsilon ,t\in \left(0,\infty \right).$$

(6)

In order to apply Theorem 1, we notice that ${\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{1}{s-1}\right)=e^t,$ and ${\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(0\right)=1$. Hence, if a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ satisfies the inequality (6), then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of (5) such that

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t-\tau \right)\right|d\tau \hfill \\ \hfill & =\epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{1}{s-1}\right)\left(t-\tau \right)\right|d\tau =\epsilon {\int }_0^t\left|e^{t-\tau }\right|d\tau =\epsilon e^t{\int }_0^t{e}^{-\tau }d\tau =\epsilon (e^t-1),\forall t\in \left(0,\infty \right),\hfill \end{array}$$

that is the Equation (5) is semi-Hyers–Ulam–Rassias stable.

The exact solution of the Equation (7) is

$$x_0\left(t\right)={\mathcal{L}}^{-1}\left(\frac{s^2+2}{s^2(s-1)}\right)={\mathcal{L}}^{-1}\left(\frac{3}{s-1}-\frac{2}{s^2}-\frac{2}{s}\right)\left(t\right)=3e^t-2t-2.$$

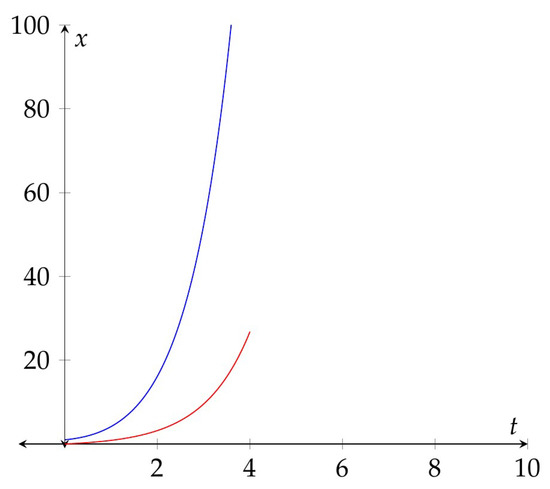
In Figure 1 the exact solution $x_0$ (blue color) of the Equation (5) and the function $p\left(t\right)=\frac{1}{2}(e^t-1)$ (red color), which borders the difference $\left|x\left(t\right)-x_0\left(t\right)\right|$ on $\left[0,4\right]$, for $\epsilon =\frac{1}{2}$, are represented.

Figure 1. Representation of the exact solution $x_0\left(t\right)=3e^t-2t-2$ (blue color), and of the function $p\left(t\right)=\frac{1}{2}(e^t-1)$ (red color), which borders the difference $\left|x\left(t\right)-x_0\left(t\right)\right|$ on $\left[0,4\right]$, for $\epsilon =\frac{1}{2}$, together.

Example 2.

Study the semi-Hyers–Ulam–Rassias stability of the equation

$$x^{\prime }\left(t\right)-{\int }_0^t{x}^{\prime }\left(\tau \right)sin\left(t-\tau \right)d\tau -sint=0,x\left(0\right)=0,t\in \left(0,\infty \right),$$

(7)

$x:\left(0,\infty \right)\to \mathbb{R}$ continuously differentiable.

For $\epsilon >0$, we consider the inequality

$$\left|x^{\prime }\left(t\right)-{\int }_0^t{x}^{\prime }\left(\tau \right)sin\left(t-\tau \right)d\tau -sint\right|\le \epsilon ,t\in \left(0,\infty \right).$$

(8)

We have in this case that ${\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{s^2+1}{s^3}\right)\left(t\right)=1+\frac{t^2}{2},$ and further on ${\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(0\right)=1$. We apply Theorem 1, hence if a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ satisfies the inequality (8), then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of (7), such that

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t-\tau \right)\right|d\tau \hfill \\ \hfill & =\epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{s^2+1}{s^3}\right)\left(t-\tau \right)\right|d\tau =\epsilon {\int }_0^t\left|1+\frac{{(t-\tau )}^2}{2}\right|d\tau =\epsilon (t+\frac{t^3}{6}),\forall t\in \left(0,\infty \right),\hfill \end{array}$$

that is the Equation (5) is semi-Hyers–Ulam–Rassias stable.

Remark that the exact solution of the Equation (7) is

$$x_0\left(t\right)={\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\mathcal{L}\left(f\right)\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{1}{s^3}\right)\left(t\right)=\frac{t^2}{2}.$$

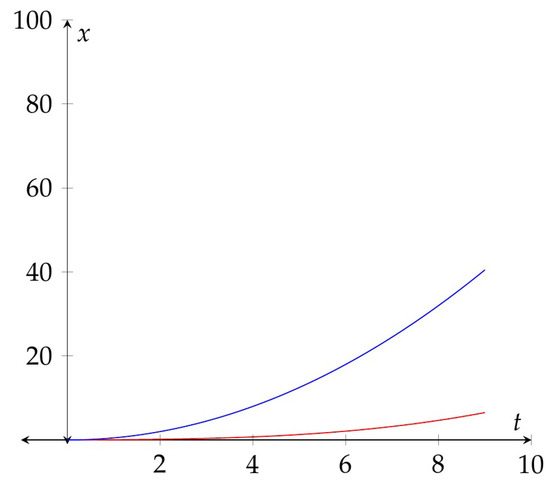
In Figure 2 the exact solution $x_0$ (blue color) of the Equation (7) and the function $p\left(t\right)=\frac{1}{20}(t+\frac{t^3}{6})$ (red color), which borders the difference $\left|x\left(t\right)-x_0\left(t\right)\right|$ on $\left[0,9\right]$, for $\epsilon =\frac{1}{20}$, is represented.

Figure 2. Representation of the exact solution $x_0\left(t\right)=\frac{t^2}{2}$ (blue color), and of the function $p\left(t\right)=\frac{1}{20}(t+\frac{t^3}{6})$ (red color), which borders the difference, $\left|x\left(t\right)-x_0\left(t\right)\right|$ on $\left[0,9\right]$, for $\epsilon =\frac{1}{20}$, together.

Next we will study several particular cases of functions g. The first to be considered is the case where $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=t.$

Theorem 2.

Let $g:\left(0,\infty \right)\to \mathbb{F}$, with $g\left(t\right)=t$ and suppose that $b+c=0$.

If a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ satisfies the inequality (2), then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of the Equation (1), such that

$$\begin{array}{c}\hfill \left|x\left(t\right)-x_0\left(t\right)\right|\le \left\{\begin{array}{c}\epsilon \frac{1-e^{-\Re \left(a\right)t}}{\Re \left(a\right)},\mathit{if} \Re \left(a\right)\ne 0,\hfill \\ \epsilon t,\mathit{if} \Re \left(a\right)=0\hfill \end{array}\right..\end{array}$$

Proof. 

If $a=0$ then $\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}=\frac{1}{s},$ hence

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{1}{s}\right)\left(t-\tau \right)\right|d\tau \le \epsilon {\int }_0^{t}d\tau =\epsilon t.$$

Suppose now that $a\ne 0$. We have

$$\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}=\frac{s}{s^2(1+b\frac{1}{s^2})+as+c}=\frac{s}{s^2+as+b+c}.$$

Since $b+c=0,$ it follows that ${\mathcal{L}}^{-1}\left(\frac{s}{s^2+as+b+c}\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{1}{s+a}\right)\left(t\right)=e^{-at},$ we apply Theorem 1 and we obtain

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{1}{s+a}\right)\left(t-\tau \right)\right|d\tau \le \epsilon {\int }_0^t\left|e^{-a\left(t-\tau \right)}\right|d\tau =\epsilon e^{-\Re \left(a\right)t}{\int }_0^t{e}^{\Re \left(a\right)\tau }d\tau ,\hfill \end{array}$$

which completes the proof. □

Theorem 3.

Let $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=t$ and suppose that $b+c\ne 0$ and $a^2\ne 4b+4c$. Let ${\sigma }_1,{\sigma }_2$ be the zeroes of the equation $s^2+as+b+c=0$. Let $A_1,A_2\in \mathbb{F}$ such that

$$\frac{s}{s^2+as+b+c}=\frac{A_1}{s-{\sigma }_1}+\frac{A_2}{s-{\sigma }_2},$$

that is $A_1=\frac{{\sigma }_1}{{\sigma }_1-{\sigma }_2}$ and $A_2=-\frac{{\sigma }_2}{{\sigma }_1-{\sigma }_2}.$

If a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ satisfies the inequality (2), then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of (1), such that

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\hfill \\ \hfill & \le \left\{\begin{array}{c}\epsilon \left(\frac{\left|A_1\right|}{\Re \left({\sigma }_1\right)}\left(e^{\Re \left({\sigma }_1\right)t}-1\right)+\frac{\left|A_2\right|}{\Re \left({\sigma }_2\right)}\left(e^{\Re \left({\sigma }_2\right)t}-1\right)\right),\mathit{if} \Re \left({\sigma }_k\right)\ne 0,\forall k\in \{1,2\}\hfill \\ \epsilon \left(t\left|A_1\right|+\frac{\left|A_2\right|}{\Re \left({\sigma }_2\right)}\left(e^{\Re \left({\sigma }_2\right)t}-1\right)\right),\mathit{if} \Re \left({\sigma }_1\right)=0,\Re \left({\sigma }_2\right)\ne 0\hfill \\ \epsilon t\left(\left|A_1\right|+\left|A_2\right|\right),\mathit{if} \Re \left({\sigma }_k\right)=0,\forall k\in \{1,2\}\hfill \end{array}\right..\hfill \end{array}$$

Proof. 

We have

$$\begin{array}{cc}\hfill & {\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{s}{s^2+as+b+c}\right)\left(t\right)\hfill \\ \hfill & ={\mathcal{L}}^{-1}\left(\frac{s}{(s-{\sigma }_1)(s-{\sigma }_2)}\right)\left(t\right)=A_1{\mathcal{L}}^{-1}\left(\frac{1}{s-{\sigma }_1}\right)+A_2{\mathcal{L}}^{-1}\left(\frac{1}{s-{\sigma }_2}\right)=A_1{e}^{{\sigma }_{1}t}+A_2{e}^{{\sigma }_{2}t}.\hfill \end{array}$$

We apply Theorem 1 and we obtain

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|A_1{e}^{{\sigma }_1\left(t-\tau \right)}+A_2{e}^{{\sigma }_2\left(t-\tau \right)}\right|d\tau \hfill \\ \hfill & \le \epsilon \left({\int }_0^t\left|A_1{e}^{{\sigma }_1\left(t-\tau \right)}\right|d\tau +{\int }_0^t\left|A_2{e}^{{\sigma }_2\left(t-\tau \right)}\right|d\tau \right)\hfill \\ \hfill & \le \epsilon \left(\left|A_1\right|e^{\Re \left({\sigma }_1\right)t}{\int }_0^t{e}^{-\Re \left({\sigma }_1\right)\tau }d\tau +\left|A_2\right|e^{\Re \left({\sigma }_2\right)t}{\int }_0^t{e}^{-\Re \left({\sigma }_2\right)\tau }d\tau \right),\hfill \end{array}$$

which completes the proof. □

We examine now the case when $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=t^n$, $n\in \mathbb{N},n\ge 2.$

Theorem 4.

Let $g:\left(0,\infty \right)\to \mathbb{F}$, $g\left(t\right)=t^n,n\in \mathbb{N},n\ge 2.$

If a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ satisfies the inequality (2), then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of (1), such that

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{s^n}{s^{n+1}+a{s}^n+c{s}^{n-1}+bn!}\right)\left(t-\tau \right)\right|d\tau ,\forall t\in \left(0,\infty \right).$$

Proof. 

We have

$$\begin{array}{cc}\hfill & {\mathcal{L}}^{-1}\left(\frac{s}{s^2(1+b\mathcal{L}\left(g\right))+as+c}\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{s}{s^2\left(1+b\frac{n!}{s^{n+1}}\right)+as+c}\right)\left(t\right)\hfill \\ \hfill & ={\mathcal{L}}^{-1}\left(\frac{s^n}{s^{n+1}+a{s}^n+c{s}^{n-1}+bn!}\right)\left(t\right)\hfill \end{array}$$

and ${\mathcal{L}}^{-1}\left(\frac{s^n}{s^{n+1}+a{s}^n+c{s}^{n-1}+bn!}\right)\left(0\right)=1,$ using Lemma 1. Hence, we can apply Theorem 1, which completes the proof. □

We consider now another particular case of the equation, namely when $c=0$, $a,b\in \mathbb{R}$, $a\ne 0$, $b\ne 0$ and g is an exponential function.

Theorem 5.

Let $g:\left(0,\infty \right)\to \mathbb{F}$ be defined as $g\left(t\right)=e^{\gamma t}$, with $\gamma \in \mathbb{R}$, $\gamma \ne 0$. Suppose that $a,b\in \mathbb{R}$, $a\ne 0$, $b\ne 0$ and ${(a+b-\gamma )}^2+4\gamma a\ne 0$. Let $\epsilon >0$.

If a continuously differentiable function $x:\left(0,\infty \right)\to \mathbb{F}$ verifies the inequality

$$\left|x^{\prime }\left(t\right)+ax\left(t\right)+b{\int }_0^t{x}^{\prime }\left(\tau \right)g\left(t-\tau \right)d\tau -f\left(t\right)\right|\le \epsilon ,t\in \left(0,\infty \right),$$

then there exists a solution $x_0:\left(0,\infty \right)\to \mathbb{F}$ of (1), such that

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le \left\{\begin{array}{c}\epsilon t\left(\left|A_1\right|+\left|A_2\right|\right),\mathit{if} \gamma =a+b\mathit{and}\gamma a<0,\hfill \\ {\displaystyle \epsilon \sum _{j=1}^2\frac{\left|A_j\right|}{\Re \left({\sigma }_j\right)}\left(e^{\Re \left({\sigma }_j\right)t}-1\right),\mathit{if} \gamma =a+b\mathit{and}\gamma a>0,\mathrm{or}\gamma \ne a+b,}\hfill \end{array}\right.$$

for any $t\ge 0$, where ${\sigma }_1,{\sigma }_2$ are the roots of $s^2+(a+b-\gamma )s-\gamma a=0$ and $A_1,A_2\in \mathbb{C}$, such that $\frac{s-\gamma }{s^2+(a+b-\gamma )s-\gamma a}=\frac{A_1}{s-{\sigma }_1}+\frac{A_2}{s-{\sigma }_2}$.

Proof. 

Theorem 1 provides, for $c=0$, the inequality

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|{\mathcal{L}}^{-1}\left(\frac{1}{s(1+b\mathcal{L}\left(g\right))+a}\right)\left(t-\tau \right)\right|d\tau ,\forall t\in \left(0,\infty \right).$$

When g is the exponential function $g\left(t\right)=e^{\gamma t}$, it follows that

$$\frac{1}{s(1+b\mathcal{L}\left(g\right))+a}=\frac{s-\gamma }{s^2+(a+b-\gamma )s-\gamma a}.$$

Let ${\sigma }_1,{\sigma }_2\in \mathbb{C}$ be the zeroes of the equation $s^2+(a+b-\gamma )s-\gamma a=0$, which are distinct since ${(a+b-\gamma )}^2+4\gamma a\ne 0$. Let $A_1,A_2\in \mathbb{C}$ be such that

$$\frac{s-\gamma }{s^2+(a+b-\gamma )s-\gamma a}=\frac{A_1}{s-{\sigma }_1}+\frac{A_2}{s-{\sigma }_2}.$$

We obtain ${\mathcal{L}}^{-1}\left(\frac{s-\gamma }{s^2+(a+b-\gamma )s-\gamma a}\right)\left(t\right)=A_1{e}^{{\sigma }_{1}t}+A_2{e}^{{\sigma }_{2}t}$ and, in consequence,

$${\mathcal{L}}^{-1}\left(\frac{s-\gamma }{s^2+(a+b-\gamma )s-\gamma a}\right)\left(0\right)=A_1+A_2=1.$$

The evaluation given by Theorem 1 becomes

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|A_1{e}^{{\sigma }_1(t-\tau )}+A_2{e}^{{\sigma }_2(t-\tau )}\right|\mathrm{d}\tau \hfill \\ \hfill & \le \epsilon \left(\left|A_1\right|e^{\Re \left({\sigma }_1\right)t}{\int }_0^t{e}^{-\Re \left({\sigma }_1\right)\tau }\mathrm{d}\tau +\left|A_2\right|e^{\Re \left({\sigma }_2\right)t}{\int }_0^t{e}^{-\Re \left({\sigma }_2\right)\tau }\mathrm{d}\tau \right).\hfill \end{array}$$

Let ${\sigma }_j$ be one of the previously mentioned roots. Suppose that $\Re \left({\sigma }_j\right)=0$, that is ${\sigma }_j=i\beta$, with $\beta \in {\mathbb{R}}^{\ast }$. Then, $-{\beta }^2+i\beta (a+b-\gamma )-\gamma a=0$, so $a+b-\gamma =0$ and $-{\beta }^2-\gamma a=0$. Since $\beta$ is a real number, this implies $\gamma =a+b$ and $\gamma a<0$. By this remark, we can distinguish several situations.

If $\gamma =a+b$ and $\gamma a<0$, then the roots of the equation are ${\sigma }_{1,2}=\pm i\sqrt{-\gamma a}$, so $\Re \left({\sigma }_1\right)=\Re \left({\sigma }_2\right)=0$. We obtain further

$$\left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon \left(\left|A_1\right|{\int }_0^t\mathrm{d}\tau +\left|A_2\right|{\int }_0^t\mathrm{d}\tau \right)=\epsilon t\left(\left|A_1\right|+\left|A_2\right|\right).$$

If $\gamma =a+b$ and $\gamma a>0$, then ${\sigma }_{1,2}$ are real, non-zero numbers, so $\Re \left({\sigma }_1\right)\ne 0$ and $\Re \left({\sigma }_2\right)\ne 0$. We obtain

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon \left(\left|A_1\right|e^{\Re \left({\sigma }_1\right)t}\frac{1-e^{-\Re \left({\sigma }_1\right)t}}{\Re \left({\sigma }_1\right)}+\left|A_2\right|e^{\Re \left({\sigma }_2\right)t}\frac{1-e^{-\Re \left({\sigma }_2\right)t}}{\Re \left({\sigma }_2\right)}\right)\hfill \\ \hfill & =\epsilon \left(\frac{\left|A_1\right|}{\Re \left({\sigma }_1\right)}\left(e^{\Re \left({\sigma }_1\right)t}-1\right)+\frac{\left|A_2\right|}{\Re \left({\sigma }_2\right)}\left(e^{\Re \left({\sigma }_2\right)t}-1\right)\right).\hfill \end{array}$$

If $\gamma \ne a+b$, then also $\Re \left({\sigma }_1\right)\ne 0$ and $\Re \left({\sigma }_2\right)\ne 0$, so the previous estimation holds. □

Remark 1.

If $g\left(t\right)=e^{\gamma t}$, with $a,b,\gamma \in {\mathbb{R}}^{\ast }$ like in the previous Theorem, but ${(a+b-\gamma )}^2+4\gamma a=0$, then the equation $s^2+(a+b-\gamma )s-\gamma a=0$ admits a double root $\sigma =\frac{\gamma -a-b}{2}\in \mathbb{R}$. Since $a\ne 0$, it follows that also $\sigma \ne 0$. We have

$${\mathcal{L}}^{-1}\left(\frac{s-\gamma }{s^2+(a+b-\gamma )s-\gamma a}\right)\left(t\right)={\mathcal{L}}^{-1}\left(\frac{s-\gamma }{{(s-\sigma )}^2}\right)=e^{\sigma t}(1+(\sigma -\gamma )t).$$

The estimation of the difference between the approximate and the exact solution will be in this case

$$\begin{array}{cc}\hfill & \left|x\left(t\right)-x_0\left(t\right)\right|\le \epsilon {\int }_0^t\left|e^{\sigma (t-\tau )}+(\sigma -\gamma )(t-\tau )e^{\sigma (t-\tau )}\right|\mathrm{d}\tau \hfill \\ \hfill & \le \epsilon \frac{1-e^{\sigma t}}{\sigma }\left(\frac{|\sigma -\gamma |}{\sigma }-|\sigma -\gamma |t-1\right)+\epsilon \frac{|\sigma -\gamma |}{\sigma }t.\hfill \end{array}$$

4. Study of Other Equations via Double Laplace Transform

Next we will apply double Laplace transform to study semi-Hyers–Ulam–Rassias stability of convolution type equations, when functions of two variables are involved.

According to [38], the double Laplace transform of a function $f(u,v)$ is

$${\mathcal{L}}_2\left(f(u,v)\right)=F(p,q)=\stackrel{=}{f}\left(p,q\right)={\int }_0^{\infty }{\int }_0^{\infty }f(u,v)e^{-(pu+qv)}dudv,$$

provided that the integral exists.

The corresponding inverse double Laplace transform is

$${\mathcal{L}}_2^{-1}\left(\stackrel{=}{f}\left(p,q\right)\right)=f\left(u,v\right)=\frac{1}{2\pi i}{\int }_{c-i\infty }^{c+i\infty }{e}^{pu}dp\frac{1}{2\pi i}{\int }_{d-i\infty }^{d+i\infty }{e}^{qv}\stackrel{=}{f}\left(p,q\right)dq,$$

where $\stackrel{=}{f}\left(p,q\right)$ must be analytic for all $p,q$ in the region defined by the inequalities $\Re p\ge c$, $\Re q\ge d$, where c, d are real constants, suitably chosen.

$${\mathcal{L}}_2(f\ast \ast g)(u,v)={\mathcal{L}}_2\left(f(u,v)\right)·{\mathcal{L}}_2\left(g(u,v)\right),$$

where by $(f\ast \ast g)(u,v)={\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)g\left(\xi ,\eta \right)d\xi d\eta$ is denoted the convolution product of $f\left(u,v\right)$ and $g\left(u,v\right)$.

Now, we consider the functions $f,g,h:\left(0,\infty \right)\times \left(0,\infty \right)\to \mathbb{F}$ and $\alpha \in \mathbb{R}$. Suppose that these functions are continuous and of exponential order.

We consider $\epsilon >0,$ the equation

$$f\left(u,v\right)-\alpha {\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)g\left(\xi ,\eta \right)d\xi d\eta -h\left(u,v\right)=0,$$

(9)

and the inequality

$$\left|f\left(u,v\right)-\alpha {\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)g\left(\xi ,\eta \right)d\xi d\eta -h\left(u,v\right)\right|\le \epsilon .$$

(10)

Theorem 6.

Suppose that the Laplace inverse ${\mathcal{L}}_2^{-1}\left(\frac{1}{1-\alpha \overline{\overline{g}}\left(p,q\right)}\right)=k(u,v)$ exists. If a function f satisfies the inequality (10), then there exists a solution $f_0$ of (9), such that

$$\left|f\left(u,v\right)-f_0\left(u,v\right)\right|\le \epsilon {\int }_0^u{\int }_0^v\left|k\left(u-\xi ,v-\eta \right)\right|d\xi d\eta ,$$

that is the Equation (9) is semi-Hyers–Ulam–Rassias stable.

Proof. 

Let

$$r\left(u,v\right)=f\left(u,v\right)-\alpha {\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)g\left(\xi ,\eta \right)d\xi d\eta -h\left(u,v\right).$$

We have

$$\overline{\overline{r}}\left(p,q\right)=\stackrel{=}{f}\left(p,q\right)-\alpha \stackrel{=}{f}\left(p,q\right)\overline{\overline{g}}\left(p,q\right)-\overline{\overline{h}}\left(p,q\right),$$

hence

$$\stackrel{=}{f}\left(p,q\right)=\frac{\overline{\overline{r}}\left(p,q\right)}{1-\alpha \overline{\overline{g}}\left(p,q\right)}+\frac{\overline{\overline{h}}\left(p,q\right)}{1-\alpha \overline{\overline{g}}\left(p,q\right)}.$$

Let

$$f_0\left(u,v\right)={\mathcal{L}}_2^{-1}\left(\overline{\overline{h}}\left(p,q\right)·\frac{1}{1-\alpha \overline{\overline{g}}\left(p,q\right)}\right)={\int }_0^u{\int }_0^{v}h\left(u-\xi ,v-\eta \right)k\left(\xi ,\eta \right)d\xi d\eta .$$

We remark that $f_0$ is a solution of the Equation (9). We have

$$\stackrel{=}{f}\left(p,q\right)-{\stackrel{=}{f}}_0\left(p,q\right)=\frac{\overline{\overline{r}}\left(p,q\right)}{1-\alpha \overline{\overline{g}}\left(p,q\right)}.$$

Applying the inverse Laplace transform we obtain

$$\begin{array}{ccc}\hfill \left|f\left(u,v\right)-f_0\left(u,v\right)\right|& =& \left|{\mathcal{L}}_2^{-1}\left(\frac{\overline{\overline{r}}\left(p,q\right)}{1-\alpha \overline{\overline{g}}\left(p,q\right)}\right)\right|=\left|{\int }_0^u{\int }_0^{v}r\left(u,v\right)k\left(u-\xi ,v-\eta \right)d\xi d\eta \right|\hfill \\ & \le & \epsilon {\int }_0^u{\int }_0^v\left|k\left(u-\xi ,v-\eta \right)\right|d\xi d\eta .\hfill \end{array}$$

□

Example 3.

Let $f:\left(0,\infty \right)\times \left(0,\infty \right)\to {\mathbb{R}}_{+},$ $\epsilon >0,$$\lambda \in {\mathbb{R}}_{+}$, the equation

$${\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)f\left(\xi ,\eta \right)d\xi d\eta -{\lambda }^2=0,$$

(11)

and the inequality

$$\left|{\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)f\left(\xi ,\eta \right)d\xi d\eta -{\lambda }^2\right|\le \epsilon .$$

(12)

If a function $f:\left(0,\infty \right)\times \left(0,\infty \right)\to {\mathbb{R}}_{+}$ satisfies the inequality (12), then there exists a solution $f_0$ of (11) such that

$$\left|f\left(u,v\right)-f_0\left(u,v\right)\right|\le \sqrt{\epsilon },$$

that is the Equation (11) is Hyers–Ulam stable.

Let

$$r\left(u,v\right)={\int }_0^u{\int }_0^{v}f\left(u-\xi ,v-\eta \right)f\left(\xi ,\eta \right)d\xi d\eta -{\lambda }^2.$$

We have

$$\overline{\overline{r}}\left(p,q\right)=\stackrel{=}{f}\left(p,q\right)\stackrel{=}{f}\left(p,q\right)-\frac{{\lambda }^2}{pq},$$

hence

$${\stackrel{=}{f}}^2\left(p,q\right)=\overline{\overline{r}}\left(p,q\right)-\frac{{\lambda }^2}{pq}.$$

We remark that

$$f_0\left(u,v\right)=\frac{\lambda }{\pi \sqrt{uv}}$$

is a positive solution of the Equation (11).

We obtain

$$\left|f^2\left(u,v\right)-f_0^2\left(u,v\right)\right|=\left|\overline{\overline{r}}\left(p,q\right)\right|\le \epsilon ,$$

hence, since $f,f_0$ are positive functions, we obtain

$${\left|f\left(u,v\right)-f_0\left(u,v\right)\right|}^2\le \left|f^2\left(u,v\right)-f_0^2\left(u,v\right)\right|\le \epsilon ,$$

and

$$\left|f\left(u,v\right)-f_0\left(u,v\right)\right|\le \sqrt{\epsilon }.$$

5. Conclusions

Hyers–Ulam stability has been extensively studied for various types of equations and by various methods. In this work, we continued the study of semi-Hyers–Ulam–Rassias stability of integral-differential equations, started in the works [34,35], using the Laplace transform. The equations considered in this paper, with two convolutional type integrals, have not been studied yet from this point of view. Equations of this type can appear in image processing. A general theorem, in which the inverse Laplace transform occurs, is established first. Next, various functions are considered, providing cases when the inverse transform can be actually determined. One can also examine some other functions g for which the hypotheses of Theorem 1 are checked.

The results can be extended, in this respect the last section is dedicated to the stability of two equations of convolution type, of two variables. In these cases, the method involves the double Laplace transform, which opens new possibilities for further research.