Abstract
Many isothermal dissipative continuum problems can be formulated in a variational setting using the concept of “standard dissipative continua”. A major advantage of this approach is that complex problems can be cast into a compact, thermodynamically consistent formulation based on a single space–time continuous functional together with a corresponding variational principle. Formulating the problem in terms of a functional provides an immediate avenue for performing spatial and temporal discretization, which are the prerequisites for a numerical solution. Within the present contribution, a novel systematic approach to standard dissipative formulations is proposed, with the main goal being the development and implementation of generic procedures and algorithms for the formulation as well as the computational solution of a subset of isothermal dissipative continuum problems. In order to demonstrate the capabilities of the approach, its application to example problems is discussed.
MSC:
35A15; 49S05; 49-04; 65M60; 74F99; 68V99
1. Introduction
Starting from classical continuum theories, recent decades have seen substantial developments towards the modeling of nonlinear dissipative multi-physics phenomena. Examples include electromechanical coupling in ferroelectric materials [1], magnetoelectromechanical coupling in multiferroic materials [2] as well as electrochemomechanical coupling in batteries [3] and hydrogels [4]. Although most continuum concepts are, in principle, readily extended to account for such multiphysics effects, the formulation of thermodynamically consistent theories and their solution by numerical methods becomes an increasingly tedious task as the number of coupled physics and, therefore, unknown variables increases. This is particularly of concern for:
- 1.
- The model formulation in terms of a number of partial differential (or differential algebraic) equations, which may often be combined in many different ways to form a final set of space–time continuous equations;
- 2.
- The mathematical analysis of the space–time continuous equations, e.g., with regard to the well posedness of the problem and stability properties;
- 3.
- The development of consistent, robust and efficient spatial and temporal discretization schemes;
- 4.
- The numerical solution of the space–time discrete problem.
An established approach to reduce the mentioned difficulties is to formulate continuum models in terms of variational principles based on a single functional of the unknowns instead of partial differential equations, so that the solution of the problem furnishes an extremum or a saddle point of the functional. This approach often provides a compact statement of the problem, which clearly exposes its structure, and thereby facilitates the mathematical analysis as well as the development of robust and efficient discretization and numerical solution procedures. The latter has, e.g., been demonstrated by Simo and Honein [5], Ortiz and Stainier [6], and Hackl and Fischer [7] in the context of plasticity and viscoplasticity, by Yang et al. [8] in the context of thermomechanically coupled problems, and by Carstensen et al. [9] and Ortiz and Repetto [10] in the context of micro-structure formation. Of particular interest in this regard is the concept of “standard dissipative continua” (see, e.g., Halphen and Nguyen [11], Germain et al. [12]), which effectively involves minimum or saddle point formulations, with thermodynamic consistency being ensured by choosing a so-called dissipation functional to satisfy certain conditions. Examples illustrating the wide applicability of this concept are, e.g., the early work of Biot [13] on fluid transport in porous media as well as a multitude of contributions covering the homogenization of inelastic micro-structures [14,15], gradient-enhanced plasticity [16,17,18,19,20], rate-dependent ferroelectricity [21], magnetostriction with hysteresis [22], electro-magneto-mechanics [2], fluid transport in porous media [23], Cahn–Hilliard-type and classical diffusion [24,25], and fracture in lithium-ion batteries [26].
Regardless of whether differential (algebraic) equations or a functional together with a variational principle are chosen as the point of departure, the mere implementation effort required to obtain validated numerical software remains a substantial obstacle, especially in the case of multiphysics problems. Due to this aspect, many sophisticated continuum formulations are often only demonstrated for highly simplified situations (e.g., one-dimensional problems), while their application to real-world examples remains elusive. This aspect provides the main motivation for the present contribution. In particular, a systematic approach to standard dissipative formulations is proposed, which covers the steps from problem formulation in the space–time continuous setting through its discretization to implementation.
The plan of the paper is as follows: Firstly, the standard dissipative space–time continuous problem formulation is formalized without reference to particular physics. Secondly, simple approaches for the spatial and temporal discretization of the space–time continuous problem are described. Thirdly, a preliminary implementation based on the open source finite element library deal.II (Alzetta et al. [27], Bangerth et al. [28]) is briefly discussed. Finally, the usefulness of the approach is shown by the application to two multiphysics examples. The first example addresses the buckling behavior of a viscoelastic dielectric elastomer subjected to an electric voltage, while the second example concerns the swelling/shrinking of a hydrogel upon a change of exterior ion concentrations. Both examples include numerical convergence studies with regard to spatial and temporal discretization in order to show that the expected numerical properties indeed translate to practical computations.
2. Formalization of the Space–Time Continuous Problem
In this section, a generic formulation for standard dissipative continua is proposed, with the scope being limited to isothermal problems with elliptic or parabolic structure. It is emphasized in this context that more general standard dissipative formulations than the one presented below are possible. However, certain simplifications are unavoidable in view of implementation aspects. The proposed formulation essentially represents a trade-off between the generality of the formulation and complexity of the implementation into numerical software. Furthermore, it is remarked that most of the theoretical developments are, at least as far as the general ideas are concerned, in some form already available in the pertinent literature. Here, the intended contribution is to compile the theory in a form suitable for subsequent implementation.
The contents of this section are summarized as follows: Firstly, the computational domain including subdomains, boundaries and interfaces is described together with the notation required for bookkeeping purposes. Secondly, the notions of “generalized fields” and “dependent fields” are introduced, and the form of the functionals considered in this work is specified. Despite the fact that these aspects are of subordinate importance from a physical standpoint, they are indispensable with regard to the desired problem-independent implementation of the approach into computer code. Thirdly, the unknowns involved in the statement of the problem are grouped into several categories based on their role in the variational formulation. Fourthly, the space–time continuous incremental potential is introduced, followed by a statement of the space–time continuous incremental variational principle assumed in the present work. Finally, ways to systematically reduce the number of unknowns involved in the problem formulation are described.
2.1. Computational Domain
The Euclidean d-space with or is considered for a range of time , with and being the initial and the final times, respectively. In what follows, denotes a spatial location and an instant of time. As illustrated in Figure 1, is assumed to be split into (i) the “environment” ; (ii) the bounded domain , which is further subdivided into “domain portions” labeled by ; and (iii) the bounded, sufficiently smooth dimensional interface , which is further subdivided into “interface portions” labeled by . It is generally assumed that the boundary of each domain portion is a part of . This means that . Moreover, it is understood that and have no points in common, i.e., . In the sequel, the union of and will be referred to as the “computational domain”. This computational domain is generally assumed to be kept fixed. This means that it does not change with time. Together with the interface , a piece-wise continuous unit normal field is introduced. Using this unit normal field, the ‘+’ and ‘−’ sides of the interface at a location are defined such that points from the − to the + side.
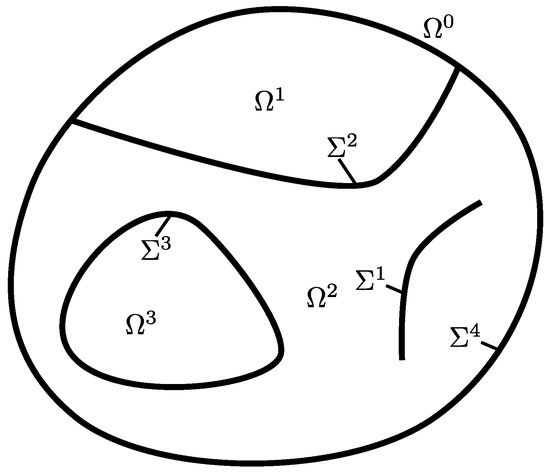
Figure 1.
Domain under consideration.
Remark 1.
- An interface portion need not necessarily be aligned with an interface between different domain portions or an interface between a domain portion and the environment . This means that a “slit” within a domain portion is permissible, as can be seen in the interface portion in Figure 1.
- A more complete description would also involve lower-dimensional entities (lines, line portions, and points in three dimensions; points in two dimensions). However, these are firstly rarely relevant to practical examples, and secondly, these are more difficult to implement. Therefore, they are ignored below.
- The introduction of different domain and interface portions concerns in particular multiphysics phenomena, with different physics being operative in different regions, and, possibly, combined with interfacial effects.
- Keeping the domain of computation fixed does not imply that a Lagrangian or Eulerian viewpoint is adopted. In fact, even arbitrary Lagrangian Eulerian formulations are possible.
2.2. Generalized Fields, Dependent Fields and the Form of Functionals
Before discussing the standard dissipative formulation considered in this work,
- (i)
- the notions of “generalized fields” and “dependent fields” are introduced, and
- (ii)
- the form a functional can take within this work is narrowed down.
2.2.1. Generalized Fields
A generalized field comprises:
- 1.
- A number of time-dependent scalar fields, which are formally defined on the entire computational domain, but which may only be non-zero on . These fields are collected in the vector and will be referred to as “domain-related fields”. The latter may represent, e.g., mechanical displacements, velocities, pressures, electric fields, etc.
- 2.
- A number of time-dependent scalar fields, which are formally defined on the entire computational domain, but which may only be non-zero on . These fields are collected in the vector and will be referred to as “interface-related fields”. The latter may represent, e.g., curvatures, electrical surface charges, interfacial reaction rates, etc.
- 3.
- A number of time-dependent scalars. These scalars are collected in the vector ; and they may represent quantities such as integral electric currents, displacements and rotations of rigid domain portions, etc.
With these definitions,
is as a vector of dimension .
The derivative of with respect to , i.e., the gradient, is introduced according to
with indicating the surface gradient, and if and if . It is noted that may be interpreted as an matrix.
The derivative of with respect to t, i.e., the rate, is denoted by
Two generalized fields and may be concatenated to form a single generalized field . In this case, it is understood that the components are rearranged such that the domain-related fields, the interface-related fields and the scalars are contiguous again. This means that:
This procedure can be applied recursively to concatenate more than two generalized fields.
Remark 2.
Vector/tensor fields are considered to be represented by an appropriate number of scalar fields, with the individual scalar fields typically representing vector/tensor coordinates with regard to a particular basis system.
2.2.2. Dependent Fields
For each generalized field , a number of “domain-related dependent fields” and a number of “interface-related dependent fields” are introduced. These dependent fields are collected in the vectors and , respectively. In this section, the convention will be followed that upper case letters denote generalized fields, while the corresponding lower case letters denote the associated dependent fields.
The purpose of the dependent fields is the introduction of variables, in terms of which the functionals governing the standard dissipative formulation can be conveniently expressed without direct use of spatial derivatives. A typical example for a dependent field is the mechanical strain field, which is used to introduce the strain energy density in continuum mechanics.
The dependent fields and are assumed to be linearly related to the generalized field . In particular,
if and otherwise, with , and being constants, constant vectors of dimension d, and denoting the component of a vector . Similarly,
if and otherwise, with , , , and being constants, and , , constant vectors of dimension d. In the latter equation as well as in the following, the notation indicates that reference is made to the limit value as points are approached from the + and the − side of the interface , respectively.
Remark 3.
- The restriction of and to a dependence on first spatial derivatives of the generalized field may seem rather limiting. However, the formulation to be described does enable the effective incorporation of higher-order derivatives through the introduction of auxiliary quantities. In fact, including higher spatial derivatives would, in a finite element context, require higher-order continuous finite elements; and the latter are rarely used in practice due to the superiority of mixed formulations eliminating the higher spatial derivatives through auxiliary quantities.
- The choice of the dependent fields is usually subject to a substantial degree of freedom and will typically be determined by what is most convenient for the definition of the governing functionals.
- The constants and constant vectors appearing in (5) and (6) may be made dependent upon without affecting the discussion below. Furthermore, nonlinear dependencies of the dependent fields on the generalized fields and derivatives thereof may be allowed for . However, such dependencies are omitted here as they have not yet been implemented (nonetheless, they can be incorporated through constraints, which can be implemented using Lagrangian multipliers).
2.2.3. Form of Functionals
Let be a functional of a number of generalized fields indexed by and a number of generalized fields indexed by , with the semicolon indicating that the quantities to the right are regarded as parameters when the variations of the functional H are computed. In the sequel it is assumed that every such functional is of the specific form
where is the volume element, the interface element, and , and are functions.
Remark 4.
The previous assumption regarding the form of a functional will eventually ensure that the incremental variational principle to be stated below implies a set of partial differential (algebraic) equations and equations without spatial dependency (which may, however, involve integrals).
2.3. Unknown Variables
Conceptually, three different types of unknowns are considered, leading to the definition of the three following generalized fields:
- 1.
- A generalized “state variable” , which is used to describe the state within the computational domain. may, besides classical “thermodynamic state variables”, also comprise a number of “auxiliary state variables”, which will be used in the usual way as Lagrangian multipliers enforcing constraints on the admissible thermodynamic states (incompressibility constraints, electroneutrality constraints, etc.). In particular, is assumed to be of the formatwhere comprises the thermodynamic state variables, while comprises the auxiliary state variables/Lagrangian multipliers. is subject to an initial condition of the formwhere may need to satisfy certain consistency requirements as will be remarked later.
- 2.
- A generalized “process variable” , which may be interpreted as an auxiliary quantity used to constrain the ways the thermodynamic state can change in that only certain combinations of the rates and are admissible. is, without loss of generality, subjected to the initial condition
- 3.
- A generalized Lagrangian multiplier , which will be used to actually incorporate constraints for and .
Remark 5.
- The explicit distinction between state variables and process variables appears to be a feature distinguishing the present standard dissipative formulation from what is available in the literature to date, although it is acknowledged that, e.g., the works of Biot [13] and Miehe et al. [23], Miehe et al. [24], Miehe et al. [25] implicitly contain such a distinction. Physically, the introduction of process variables may, e.g., be motivated by the following two simple examples: (i) diffusion processes, in which molar concentrations are changed by species fluxes; and (ii) chemical reactions, in which the amounts of the substances involved are changed by chemical reaction processes.
- Ultimately, only the rate of the process variable, , will enter the formulation. Hence, it would seem more natural to directly introduce the rate as an unknown. However, the viewpoint adopted here proves beneficial from the implementation point of view.
2.4. Space–Time Continuous Incremental Potential
The space–time continuous problem formulation in terms of an incremental variational principle (herein, the term “incremental” refers to a formulation in terms of rate-type quantities, and does not refer to a time-discrete formulation as it is often the case in the literature) is based on
- 1.
- A Helmholtz free energy functional . Specifically, the Helmholtz free energy functional is assumed to be of the formwith being linear in its first argument. In general, will be assumed to be Fréchet differentiable. It is remarked in this context that the constraints for the thermodynamic states are obtained by requiring the first variation of with respect to to be zero; and represents the physical Helmholtz free energy for all thermodynamic states consistent with these constraints.
- 2.
- A power functional accounting for the influence of the environment on the computational domain under consideration. P is assumed to be linear in the pair .
- 3.
- A dissipation functional , which is related to the description of dissipative effects. It is assumed that is (i) non-negative; (ii) convex in the pair ; and (iii) satisfies the condition . The latter conditions are, within the standard dissipative framework, sufficient for the satisfaction of the second law of thermodynamics as will be remarked later.
- 4.
- A Lagrangian multiplier functional incorporating constraints for and . L is assumed to be of the formwhere is bilinear with regard to and the pair and is linear in .
Finally, the space–time continuous incremental potential
is introduced, where
2.5. Space–Time Continuous Incremental Variational Principle
Using the previously introduced functionals, the space–time continuous incremental variational principle now requires that furnishes a stationary point of at every instant of time. This means that the problem can be formulated as
where the notation is used here and henceforth that the first variation of a functional is .
Find the unknowns such that , and , and
for all and all ,
Remark 6.
- Equation (15) may be seen as an extension of Biot’s equation, cf. Equation (2.14) in Biot [29] and Equation (2.14) in Biot [30].
- For the general case, partial differential algebraic equations are involved and, therefore, (15) cannot generally be used as a “point-wise” equation to determine the rates , based on the current thermodynamic state . Rather, neighboring instants of time need to be taken into consideration by differentiating the equations implied by (15) with respect to time. This aspect becomes particularly evident when considering the example of elasticity (which does not involve dissipative processes). In this case, (15) implies the mechanical equilibrium condition, which only involves the mechanical displacement and not the rate of the mechanical displacement. Therefore, differentiation with respect to time is necessary in order to obtain an equation in the rates.
- In order for the problem to be well posed, further conditions need to be satisfied. Although a general discussion of this aspect without reference to a particular problem appears to be difficult, a few further remarks are made in the following:
- -
- The constraints represented by the functionals and L must be consistent in that they are neither redundant nor contradictory.
- -
- Non-convex and/or domains of admissible thermodynamic states may be a severe issue with regard to unique solvability and stability, as can be seen in the discussion in Abed-Meraim and Nguyen [31].
- -
- The initial conditions need to be consistent in that must be such that a stationary point of Π exists at .
- The problem formulation in terms of the first variation of Π implies the assumption of sufficient regularity of the functionals involved. This becomes a crucial aspect in the case of problems including rate-independent processes. In this case, the dissipation functional contains contributions which are positively homogeneous of degree one in the rates. The associated non-differentiability of invalidates (15), and hence it may appear that the formulation cannot be used for these cases. However, the situation can be remedied by employing the techniques of convex analysis and, in particular, replacing regular differentiation by the use of subdifferentials (as can be seen, e.g., in Rockafellar [32], pp. 213 ff.), thus extending the formulation to rate-independent processes.
- The above formulation in terms of an incremental variational principle is motivated by the description of reversible isothermal processes, in which case the concepts of equilibrium thermodynamics apply and the free energy of the system under consideration is minimized at all times. In order to account for the actual dissipative nature of the problem under consideration, “generalized dissipative forces” are included into the formulation, which are mathematically characterized by the Fréchet derivative of with respect to and . These generalized dissipative forces may be interpreted as those external loads, which would have to be applied by an external agency at a certain instant of time t to bring the system instantaneously into equilibrium. This approach is abstract in that these external loads are fictitious and cannot be applied in reality. However, accepting the approach based on the experience that it has been succesfully applied to a wide range of problems in the past, the situation is formally transformed from a problem of non-equilibrium thermodynamics into one of equilibrium thermodynamics, so that the well-known concepts of equilibrium thermodynamics can be used, and a mathematically sound formulation results, as can also be seen in Germain et al. [12]. Moreover, by ensuring that for any choice of , it is guaranteed that the generalized dissipative forces are always associated with a negative power (i.e., a positive dissipation), such that the second law of thermodynamics is satisfied a priori and need not be discussed further. The assumptions made above ( is non-negative, convex with respect to the pair and satisfies the condition ) indeed imply that .
2.6. Reduced Space–Time Continuous Incremental Variational Principles
In the following, two straightforward possibilities to reduce the set of unknown variables are described. It is emphasized that further possibilities exist, which are not discussed here. Furthermore, it is noted that the space–time discretization methods as well as the implementation discussed in the next sections are equally applicable to both, the original and the reduced formulations.
2.6.1. Reduction of the Set of Process Variables and Lagrangian Multipliers
The introduction of the generalized process variable and the generalized Lagrangian multiplier often leads to an excessive number of unknown fields. However, in many cases, it is possible to systematically eliminate and , or rather subsets thereof, before actually numerically solving the problem. In particular, the space–time continuous incremental functional only depends on , but not on itself. Furthermore, depends on and only through the contribution . Thus, a reduced functional
may be introduced by joint partial minimization and maximization, where
Then, can be replaced by in (15) to obtain an equivalent formulation in the reduced set of variables .
Remark 7.
The selection of the variables and typically depends on the properties of the dissipation functional . However, numerical considerations (e.g., with respect to the choice of finite elements) may also be important in this regard.
2.6.2. Reduction of the Set of State Variables
Another possibility to reduce the set of variables exists if certain state variables factor into , while is independent of these variables. In order to discuss this case, it is assumed that
and that neither depends on nor on , meaning that there exists a functional such that
Then, if is additionally convex in , a reduced thermodynamic potential
may be introduced; and and can be replaced by and in (15) to obtain an equivalent formulation in the reduced set of variables .
Remark 8.
Using this approach, the linearity of Ψ with regard to may be lost, which does, however, not have consequences for the applicability of (15).
3. Space–Time Discrete Formulation
The spatial discretization of the fields involved in , and is assumed to be performed using the finite element method in this work. In this regard, standard methods can be used, which will not be further discussed here. However, it is pointed out that the satisfaction of the condition is typically the most difficult part of spatial discretization if the variational problem to be solved is of saddle point type, see, e.g., Bathe [33] and Auricchio et al. [34].
With regard to temporal discretization, a number of simple and straightforward-to-implement one step schemes have been discussed and analyzed in a somewhat narrower context in a previous work [35]. These methods can be readily extended to the current formulation; and for the self-containedness of the present work, these will be briefly described below, although the reader is referred to [35] for details.
In the following, it is assumed throughout that the time interval is divided by the discrete time points , where and (however, the formulations are not restricted to uniform time increments). The numerically approximated values of , and at time are denoted by , and , respectively; and the initial values at time are given by and .
3.1. Variationally Consistent Method
The “variationally consistent method” is based on a straightforward discretization of the space–time continuous incremental functional . In particular, a time-discrete counterpart of is introduced according to
Then, the stationary point of is searched during each time step to obtain , and based on the solution of the previous time step. The corresponding stationarity condition leads to the time-discrete variational formulation
which is a consistent approximation of (15). According to the analysis in [35], the method represents a first-order accurate time integrator, provided that the the problem is sufficiently regular.
Find the unknowns such that
for all and all ,
Remark 9.
As a result of discretizing Π, the variational structure of the space–time continuous problem is preserved, which makes the method particularly attractive from the mathematical point of view. This concerns, e.g., the fact that the resulting finite element systems are symmetric.
3.2. The -Family
The “-family” is based on the introduction of a real parameter , where corresponds to a forward Euler type scheme, to a Crank–Nicolson type scheme, and to a backward Euler type scheme. Moreover, the following quantities are defined:
Then, the time-discrete version of (15) reads
For a sufficiently regular problem, the method is second-order accurate for or otherwise first-order accurate [35]. However, the method is non-convergent for if the system of equations implied by (15) is of differential algebraic nature. Furthermore, no associated time-discrete incremental potential exists for the method if exhibits a parametric dependence on , so that the finite element systems are unsymmetric in this case.
Find the unknowns such that
for all and all .
3.3. The Modified -Family
The “modified -family” is a “predictor-corrector” method. In particular, the quantities , , are introduced, which are “predictions” of , and . During the predictor step, the problem
is solved. Based on the resulting predicted values, the time-discrete problem is then
For many (but not all) cases, the method provides the same accuracy as the -family, while retaining the symmetric and variational structure, so that corresponding time-discrete incremental potentials exist for both steps.
Find the unknowns such that
for all
Find the unknowns such that
for all and all , where .
4. Implementation
In order to show the feasibility of the approach, the space–time discrete formulation described above has been preliminarily implemented in two and three dimensions for both sequential and distributed memory parallel computations. In particular, the open source C++ libraries GalerkinTools and IncrementalFE have been developed. The library GalerkinTools allows for the definition of weak forms corresponding to functionals of the generic form (7) (in fact, the library covers slightly more general weak forms including those unsymmetric weak forms required for the -family of methods for temporal discretization). Furthermore, GalerkinTools provides methods for the automatic assembly of the corresponding finite element systems based on the functionalities of the open source finite element library deal.II (Alzetta et al. [27], Bangerth et al. [28]). In addition, interfaces for the solution of the resulting linear systems of equations are included. For this purpose, the unsymmetric sparse direct UMFPACK solver (Davis [36]), the symmetric and unsymmetric sparse direct PARDISO solvers (Schenk and Gärtner [37], Schenk and Gärtner [38], Karypis and Kumar [39]), the symmetric and unsymmetric sparse direct MUMPS solvers (Amestoy et al. [40,41]) and the symmetric sparse direct MA57 solver (HSL, a collection of Fortran codes for large-scale scientific computation, see http://www.hsl.rl.ac.uk/ (accessed on 5 January 2023)) can currently be used. Based on the library GalerkinTools, the library IncrementalFE then encapsulates the special functionality required for the solution of problems formulated within the standard dissipative framework. In particular, this involves functionalities for the definition of the functionals and , together with the temporal discretization schemes described in the previous section. Furthermore, IncrementalFE implements a simple Newton–Raphson scheme, optionally combined with a line search, to solve the nonlinear finite element problems arising in each time step. For details regarding the functionalities and implementation of the libraries GalerkinTools and IncrementalFE, the reader is referred to the documentation bundled with these libraries. However, the general sequence of steps needed to define and solve a particular problem is briefly described in the following:
- 1.
- Setup of the finite element mesh, which corresponds to the definition of the computational domain. During this step, the domain is first meshed using either the built-in functionalities of deal.II or by importing a mesh from an external mesh generator. Subsequently, the domain is partitioned into domain portions by assigning “material IDs” to the individual cells of the mesh. This is followed by the definition of the interface based on faces of the previously defined volume-related cells, which also goes along with the definition of the − and + sides of the interface as well as a partitioning of the interface by assigning “material IDs”. As a final step of mesh generation, local mesh refinement may be performed.
- 2.
- Definition of the unknowns , and of the problem and the corresponding finite element spaces. During this step, the domain-related unknown fields, the interface-related unknown fields and the scalars are defined. This includes the definition of the finite elements to be used for the discretization of the domain-related and interface-related unknowns as well as Dirichlet-type constraints. Furthermore, for each unknown field, the domain portions and interface portions, respectively, are defined where the respective field may be non-zero. In order to allow for the use of vector-valued finite elements, several unknown fields of a particular type may be defined at once.
- 3.
- 4.
- Definition of and as functionals of the form (7). It is noted in this context that the definition of the integrals over and , respectively, may be split into several integrals, which are summed up subsequently. This split (i) facilitates the re-usability of the implementation of certain terms (e.g., a Neo-Hookean strain energy density) and thus makes the definition of and “modular”; (ii) allows for using different numerical quadrature schemes for different terms; and (iii) allows for a better structuring of the problem, which can be internally exploited by the library GalerkinTools to determine which entries in the finite element system matrix are non-zero. The actual definition of a single integral typically involves (i) the implementation of the integrand (which is expressed in terms of the dependent fields relevant to the integral) and its first and second derivatives; (ii) the specification of domain and interface portions, respectively, where the integrand is non-zero; (iii) the definition of the quadrature scheme to be used for evaluating the integral; (iv) the definition of the temporal integration scheme to be used (in fact, one may use different schemes for different terms, although this has not been discussed above); and (v) the definition of parameters (particularly constitutive parameters).
- 5.
- Solving the problem. Currently, time-stepping needs to be implemented manually, although single time steps are automatically handled by the library IncrementalFE.
Remark 10.
- The entire problem definition is facilitated by the use of C++ as an object-oriented language. As a result, e.g., each unknown field is a separate object, which leads to a rather natural structuring of the code in that it closely resembles the underlying mathematical statement of the problem under study in terms of formulae.
- Typically, the most time-consuming step of the problem definition is, besides in some cases the mesh generation, the implementation of the integrands for the definition of Ψ and Γ. However, due to the mentioned modular design, the implementation of certain integrands can be re-used. This does, in principle, allow for a library of integrands covering a multitude of situations. Furthermore, automatic differentiation schemes may be used in order to simplify the implementation of the first and second derivatives of the integrands, which are required for the solution of the problem.
- The library GalerkinTools also allows for the definition of “hidden variables” for each integrand, so that, in principle, classical rate-independent plasticity approaches are covered. For example, for the variationally consistent method, the latter may easily be achieved by locally “pre-minimizing” the time-discrete incremental potential with respect to the plastic deformation variables. However, proper testing of classical plasticity approaches is yet to be performed. Therefore, a discussion of these is not included in the present contribution.
- Implementation-wise, the main difficulties are the definition of functionals of the generic form (7) and the assembly procedures for the associated finite-element systems. These functionalities are provided by GalerkinTools; and, on this basis, the implementation of particular temporal discretization schemes and iterative algorithms for the solution of the nonlinear problems arising in each time step is straightforward. Hence, the library IncrementalFE is rather slim; and if temporal discretization schemes and/or iterative algorithms other than those discussed in this work need to be considered, these can be implemented with little effort (provided that the temporally discretized versions are compatible with the assumed form for functionals). The same applies to the use of other linear solvers than those mentioned above, and, in particular, iterative linear solvers.
5. Examples
In this section, (i) the buckling behavior of a viscoelastic dielectric elastomer subjected to an electric voltage, and (ii) the swelling/shrinking of a hydrogel subjected to a change in exterior ion concentrations are discussed as examples. It is emphasized that the main objective is to demonstrate the feasibility and practicability of the approach, and not to give a detailed exposition of particular physical effects. Therefore, the statement of the problems will be kept concise; and a discussion of the differential (algebraic) equations implied by the formulations is omitted.
It is emphasized that the discussion of the example problems mostly follows the sequence of steps described in Section 4, which highlights the systematic approach to standard dissipative problems proposed in this work. The equations are written using the symbolic vector/tensor notation; and it is tacitly assumed that each vector/tensor field is represented by an appropriate number of domain-related/interface-related scalar fields, which embody vector/tensor coordinates with regard to the standard basis of .
Moreover, it is noted that both example problems have been chosen to be axisymmetric in order to reduce the computational cost and, therefore, facilitate numerical convergence studies. Despite this fact, the problems will be described in the fully three-dimensional setting for the sake of simplicity. The steps necessary for reduction to the axisymmetric setting should be sufficiently obvious and are, therefore, not described in detail.
5.1. Example 1: Buckling of a Viscoelastic Dielectric Elastomer
The first example problem is illustrated in Figure 2. A circular disc of incompressible viscoelastic dielectric elastomer with radius L and thickness H is considered. The constitutive behavior is assumed to be described by the relations proposed by Hong [42]. The radial displacement is constrained to zero on the entire lateral surface of the disc. Furthermore, the average axial displacement is constrained to zero on the lateral surface. The latter constraint was chosen instead of a homogeneous constraint on the entire surface in order to avoid stress/strain singularities, which would complicate the convergence studies due to the need for excessive local mesh refinement. The bottom surface and the top surface are assumed to be electrodes, with a transient voltage applied across these electrodes. As a result of Maxwell stress, the disc shrinks in the axial direction; and due to the incompressibility of the material, this leads to buckling and large deformations of the disc in the axial direction. In order to induce the “imperfection” needed for a well-defined buckling behavior, the gravitational acceleration g is taken into account and assumed to point downwards in the figure. Fringing fields at the edges of the electrodes are neglected for simplicity.
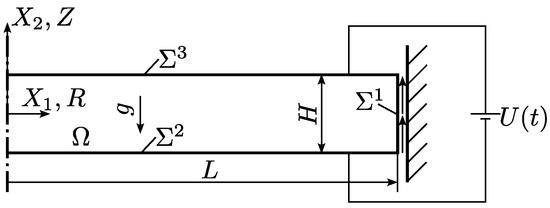
Figure 2.
Illustration of example problem 1.
5.1.1. Computational Domain
The computational domain shown in Figure 2 represents the reference configuration of the disc, which is assumed to be stress-free. It is noted that this reference configuration is not actually assumed at any instant of time due to the action of the gravitational acceleration. The in-plane Cartesian coordinates in Figure 2 are and , while the out-of-plane coordinate is . If a radial coordinate R and an axial coordinate Z of a cylindrical coordinate system are introduced as shown in the figure, the body occupies the region described by and . The lateral surface of this disc is , the bottom surface and the top surface .
5.1.2. Unknown Variables
State Variables
The thermodynamic state variables
are introduced together with the corresponding initial conditions
with being the identity tensor of rank 2. The thermodynamic state variables have the following significance:
- is the mechanical displacement field. It describes how the placements of material points in the reference configuration are mapped onto their placements in the current configuration. In particular, , with being the placement of the material point at time t.
- is the referential electric displacement field.
- is the (symmetric) inelastic stretch tensor.
The thermodynamic state variables are supplemented by the auxiliary state variables
together with the corresponding initial conditions
The auxiliary state variables have the following significance:
- is the electric scalar potential, which acts as a Lagrangian multiplier enforcing the condition that there is no free space charge density in the interior of the domain.
- p is a pressure type variable, which acts as a Lagrangian multiplier enforcing the condition that the elastomer does not exhibit any overall local volume change.
- is a further pressure type variable, which acts as a Lagrangian multiplier enforcing the condition that the elastomer does not exhibit any inelastic local volume change.
- is used to constrain the average axial displacement of the disc on the lateral surface to zero.
The practical determination of the initial values , , , , and will be discussed later.
Process Variables and Lagrangian Multipliers
For this first example, neither process variables nor Lagrangian multipliers are needed.
Dirichlet Constraints
The state variables and are constrained by the Dirichlet conditions
5.1.3. Dependent Fields
Here and in the following, only those dependent fields are listed explicitly, which are “non-trivial” in that they are not equal to an unknown field itself or the gradient/divergence/curl of an unknown field (the divergence actually involves three unknown scalar fields in three dimensions since a vector field is formally represented by an appropriate number of scalar fields; and the curl involves three unknown scalar fields and three dependent fields). In particular, the only non-trivial domain-related dependent fields used below represent the mechanical deformation gradient
where the latter equation must be expanded into coordinate-wise relations in order to be consistent with the generic form of domain-related dependent fields according to Equation (5).
5.1.4. The Functionals
As noted above, the functionals describing the variational problem are chosen such that the constitutive behavior of the viscoelastic dielectric elastomer is described by the constitutive model of Hong [42].
Helmholtz Free-Energy Functional
The Helmholtz free energy functional is composed of the contributions
and
In these equations, , , is the axial displacement, g is the gravitational acceleration, is the mass density of the elastomer in the reference state, is the permittivity of the material and and are elastic constants.
Power Functional P
The power functional takes the form
In the following, the ramp loading
with the maximum voltage will be considered.
Dissipation Functional
For the dissipation functional, the form
is assumed, where is the viscosity and is the inelastic stretching.
5.1.5. Reduced Formulations
Variant 1: Vector Potential Formulation
A first possibility to reduce the set of variables is to express in terms of a vector potential according to
By doing so, becomes a dependent field, while
becomes a state variable. As a consequence of the identity , the Lagrangian multiplier term drops out in (47), such that is no longer required as an unknown variable. Furthermore, the Dirichlet constraint on is transformed to
where is the unit normal vector in the axial direction, and
is another state variable. For details regarding this boundary condition, the reader is referred to [43]. In general, gauging is required for the uniqueness of the vector potential in three dimensions, as can also be seen in [43]. However, for the axisymmetric case considered herein, gauging can be achieved by requiring that only the circumferential component of is non-zero, which is assumed henceforth.
Variant 2: Scalar Potential Formulation
Another possibility is to apply the procedure described in Section 2.6.2 to eliminate . A technical difficulty occurring in this context is that the normal electric displacement on the surfaces and cannot be eliminated. To resolve this issue, the additional state variable
is introduced, which represents . Then,
and
while remains unchanged. In this formulation, acts as a Lagrange multiplier enforcing the boundary conditions
By imposing the latter conditions directly as Dirichlet constraints for , the state variable is eliminated from the set of unknown variables.
5.1.6. Normalization
In order to improve the conditioning of the finite element system matrices and to remove units from the simulations, it is advantageous to normalize the equations. Here, the normalization proposed by Hong [42] is used:
where .
5.1.7. Parameters
The parameters used in the numerical example below are listed in Table 1.

Table 1.
Parameters used for example 1.
5.1.8. Spatial Discretization, Temporal Discretization
The -family with is used for temporal discretization. The spatial discretization is done in the two-dimensional axisymmetric setting, thus reducing the number of scalar fields required for the representation of and to two each, and for to four. In the case of the vector potential , only a single scalar field is required since only the circumferential component is non-zero. The particular quadrilateral finite elements employed for the analysis are compiled in Table 2. In this table, the nomenclature of the deal.II library [44] is used. It is noted that the use of the pair for is empirical since the usual proof of stability cannot be readily extended to the axisymmetric case. In contrast, positive results concerning the stability of the pair for for the axisymmetric Stokes problem are available in the literature [45]. Moreover, it is noted that the support points of the elements used for and have been chosen to coincide with the quadrature points; and, as a consequence, these variables become “local” variables similar to the plastic strain in classical elastoplasticity (in fact, these variables can be eliminated at the quadrature point level, although this was not performed herein).

Table 2.
Finite elements used for example 1.
5.1.9. Initial Values
As mentioned earlier, the initial values for the state variables and auxiliary state variables need to be determined before the calculation. Due to the action of the gravitational acceleration, the initial state is inhomogeneous and must, therefore, be determined numerically. This has for simplicity been achieved by taking a very small time step of with before the actual computation, such that any increments in remain negligibly small. A more rigorous approach would be to explicitly constrain to zero for determining the initial values. This has, however, not been implemented yet.
5.1.10. Example Calculations and Results
The implementation of the constitutive equations and the numerical procedures were first validated against the results obtained by Hong [42], as can be seen in Appendix A. Subsequently, spatial and temporal convergence studies have been performed for the formulations in terms of (“mixed formulation”), (“vector potential formulation”) and (“scalar potential formulation”). The starting point for these simulations is to take equally spaced time increments for the entire simulation together with a coarse finite element mesh consisting of five rectangular cells in the radial direction and a single rectangular cell in the axial direction, see Figure 3 for an illustration of the coarse finite element mesh. Then, the number of time increments is increased to , where is the refinement cycle. Similarly, the finite element mesh is uniformly refined times (in this work, the term “uniform refinement” refers to splitting a rectangular cell into four equally shaped rectangular cells by introducing new vertices at the midpoints of the edges and at the center of the cell). In particular, calculations with () and were performed to study the convergence behavior in time; and calculations with () and were performed to study the spatial convergence behavior. For the finest mesh with , this results in degrees of freedom for the scalar potential formulation, degrees of freedom for the mixed formulation, and degrees of freedom for the vector potential formulation. However, it is emphasized that the computational cost cannot be directly related to the number of unknowns, since the system structure as well as the linear solver employed also play a major role in this regard; and the study of these aspects is beyond the scope of the present contribution.
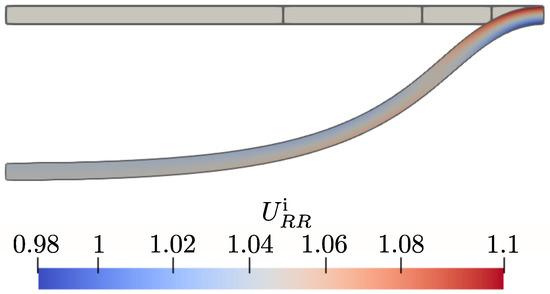
Figure 3.
Coarse finite element mesh in the reference configuration together with radial inelastic stretch in the deformed configuration at (result obtained with and ).
With regard to the convergence behavior in time, the error is, for each , evaluated according to
For simplicity, no other unknowns are included into the error. However, it has also been checked that the other unknowns show the expected convergence behavior.
An analogous approach is utilized to assess the spatial convergence behavior. In particular, the error is, for each , evaluated according to
The deformed shape of the disc is shown in Figure 3 together with the radial inelastic stretch. It can be noticed that substantial inelastic deformation of approximately takes place at the lateral surface of the body. Figure 4 shows the results of the convergence studies. In particular, Figure 4a shows the temporal convergence behavior, while Figure 4b shows the spatial convergence behavior. It is seen that in both cases the expected rates of convergence of and are observed for all three formulations, which confirms the validity of the approach. It is interesting that all three formulations essentially exhibit the same convergence behavior, a fact which is likely to be attributed to the relatively simple electric field distribution in the disc.
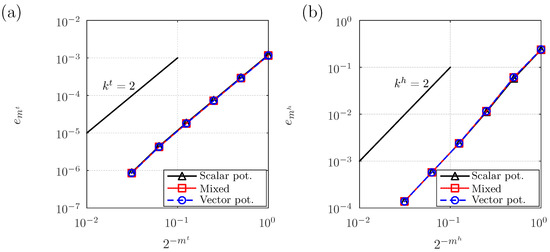
Figure 4.
Convergence results for example 1: (a) temporal convergence; and (b) spatial convergence.
5.2. Example 2: Swelling/Shrinking of a Hydrogel
The second example problem is illustrated in Figure 5. A circular cylinder of hydrogel material with radius H and height H is considered. The hydrogel is assumed to consist of a polymeric backbone material with charged groups attached to it, and an electrolyte composed of water and the ions of a fully dissociated monovalent salt. The polymeric backbone material and water are assumed to be incompressible, and the volume change associated with a change in the concentrations of cations and anions is neglected. It is further assumed that there are no voids in the hydrogel and, hence, the volume fractions of polymeric backbone material and water must locally add up to 1. The constitutive behavior of the hydrogel is assumed to be described by the relations proposed by Acartürk [4], with the simplification of local electroneutrality (i.e., the local net space charge density is assumed to be zero). The displacement is fixed to zero at the center of the bottom surface of the cylinder, while all other surfaces are mechanically free. No matter is allowed to flow across the bottom and lateral surfaces. In contrast, water and ions may be exchanged across the top surface, which is in contact with an external electrolytic solution. The latter is composed of water and a fully dissociated monovalent salt of the same type as in the hydrogel, with a prescribed transient homogeneous molar concentration of both cations and anions, of . Starting from equilibrium, the external ion concentration is changed and the response of the hydrogel in terms of swelling/shrinking deformation and change in local water and ion concentrations is tracked.
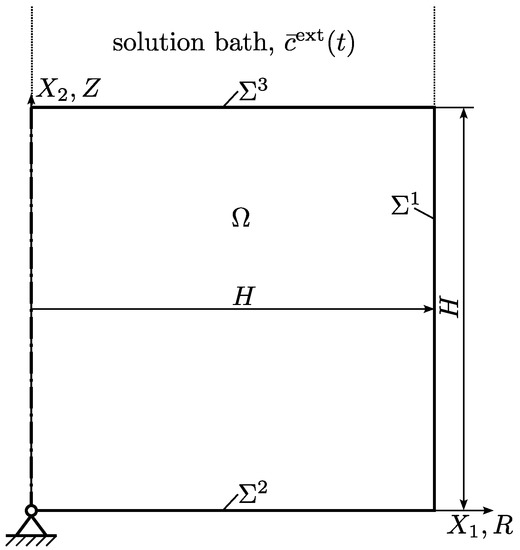
Figure 5.
Illustration of example problem 2.
5.2.1. Computational Domain
The computational domain shown in Figure 5 represents the reference configuration of the cylinder, which coincides with the configuration at the initial time . The in-plane Cartesian coordinates in Figure 2 are again and , while the out-of-plane coordinate is . In terms of the radial coordinate R and the axial coordinate Z of a cylindrical coordinate system, the body occupies the region described by and . The lateral surface of the cylinder is , the bottom surface , and the top surface .
5.2.2. Unknown Variables
State Variables
The thermodynamic state variables
are introduced, where . The corresponding initial conditions read
with and being constants since the initial state is homogeneous. The thermodynamic state variables have the following significance:
- is the mechanical displacement field.
- is the referential molar concentration of water (with regard to the total volume in the reference state).
- are the referential molar concentrations of the and ions (with regard to the total volume in the reference state).
These thermodynamic state variables are supplemented by the auxiliary state variables
together with the corresponding initial conditions
where and are constants. The auxiliary state variables have the following significance:
- p is a pressure type variable, which acts as a Lagrangian multiplier enforcing the condition that the volume fractions of water and polymeric backbone material must add up to 1 everywhere.
- is the electric scalar potential, which enforces the local electroneutrality condition.
It is noted that the constants , , , and cannot be chosen independently. Rather, they are interrelated through the assumption that the initial state at time is equilibrated.
Process Variables
The process variables involved in the problem are
These have the following significance:
- is the time-integrated referential flux of water in the hydrogel.
- are the time-integrated referential fluxes of the ionic species .
Lagrangian Multipliers
The Lagrangian multipliers
are introduced. These have the following significance:
- and are used to incorporate the respective balance equations for water and the ionic species and .
- is used to ensure that no net charge flows locally across . It is noted in this context that the assumption of no local net charge flow implies a certain behavior of the external solution bath. Other assumptions are possible (e.g., no global net charge flow), however, these are in any case only an approximation to the real behavior; and for the proper resolution of the behavior at the boundary, the exterior solution bath needs to be explicitly modeled.
Dirichlet Constraints
The unknowns , , and are subject to the following Dirichlet type constraints
Here, is constrained to the arbitrary constant at the origin in order to ensure the uniqueness of the involved scalar potential type quantities, which are only determined up to a constant by the model.
5.2.3. Dependent Fields
As before, only the “non-trivial”-dependent fields are listed; and the mechanical deformation gradient
is the only field of this type.
5.2.4. The Functionals
Helmholtz Free Energy Functional
The part of the Helmholtz free energy functional is assumed to take the form
with the first integral representing the elastic-free energy contribution of the polymeric backbone and the second integral the free energy contributions of the fluid. In particular,
are assumed. Here, again, and are Lamé’s constants, is the volume fraction of polymeric backbone material in the reference state, where denotes the molar volume of water, R is the gas constant and T is the temperature.
The part of the Helmholtz free energy functional reads
where the first integral enforces the condition that the volume fractions of fluid and polymeric backbone material add up to 1, and the second integral incorporates the electroneutrality condition. In the latter term, F is Faraday’s constant, and z are the respective charges of the ionic species , and the charged groups attached to the backbone polymer in multiples of the elementary charge, and c is the (constant) referential molar concentration of the charged groups.
Power Functional P
For the power functional, the form
is assumed, where
For the purposes of this example, the ramp function
is used for , where is the initial concentration of ions in the external solution at time , and the final concentration at time .
Lagrangian Multiplier Functional L
The Lagrangian multiplier functional is assumed to take the form
where the first two integrals incorporate the respective balance equations for water and the two ion species, and the third integral enforces the condition that the local net charge flow across is zero.
Dissipation Functional
For the dissipation functional, the form
is assumed. In this relation,
is the local dissipation function, where are the respective diffusivities of the ionic species in water, and is a material parameter characterizing the Darcy type “resistance” associated with the motion of water through the polymeric backbone material.
For later use, the dual local dissipation function is introduced according to
5.2.5. Reduced Formulation
By using the procedure described in Section 2.6.1, the variables and can be eliminated on . This leads to the reduced sets of variables
where
represent and , respectively, on . The corresponding reduced functional is obtained from Equation (16) using the dual local dissipation function (95). It reads
Similarly to example 1, and can be eliminated by imposing appropriate Dirichlet conditions for and . However, due to the involvement of in these conditions, the resulting equations are more complicated to implement and hence, and are kept as variables.
5.2.6. Normalization
All quantities are normalized using the reference values , , , , and . In particular, the normalized quantities are
5.2.7. Parameters
The set of parameters used below is listed in Table 3. The constitutive parameters have been taken from Table 5.1 in Acartürk [4] and normalized. It is noted in this context that some of the parameters are defined differently in the latter work than in the present work, so that some conversion between the parameters is involved. This applies in particular to , which is equal to in the work of Acartürk [4] (the quantities and are defined in [4]).

Table 3.
The parameters used for the hydrogel example.
The initial values appearing in Table 3 were computed from the condition that the initial state is an equilibrium state, which leads to the following equations
The corresponding normalized values given in Table 3 are subject to rounding. However, in the simulations, values accurate to within numerical accuracy have been used. This also applies to , and .
5.2.8. Spatial Discretization and Temporal Discretization
Again, the -family with is used for temporal discretization, and the spatial discretization is performed in the two-dimensional axisymmetric setting. The particular quadrilateral finite elements employed for the analysis are compiled in Table 4. No elements are given for and in this table because only the reduced formulation is considered in the numerical example below. It is noted that there are no interface terms coupling the unknowns associated with the discontinuous finite elements of type between neighboring cells. This means that the unknowns associated with these elements are local to the cell and can be eliminated with little cost by the direct linear solver. Another possibility would be to use discontinuous Lagrange elements of type for , and with the support points coinciding with the quadrature points. However, to fully benefit from this approach where the respective unknowns are local to the quadrature points, changes to the implementation would be necessary, which have not been implemented yet.

Table 4.
Finite elements used for example 2.
5.2.9. Example Calculations and Results
The implementation of the constitutive equations and the numerical procedures was first validated against a result obtained by Acartürk [4], as can be seen in Appendix B. Subsequently, spatial and temporal convergence studies have been performed for the reduced formulation. In the latter case, the starting point is to take equally spaced time increments for the entire simulation together with a coarse finite element mesh consisting of a single cell. With regard to the definition and evaluation of errors, exactly the same approach as in Section 5.1.10 is used. However, for this example, the convergence behavior in time is studied with and , while the spatial convergence study is conducted with and . In the latter case, this results in unknowns for the finest mesh with .
The deformed shape of the hydrogel cylinder is shown in Figure 6 together with the cation concentration and the outline of the undeformed cylinder; whilst Figure 7a,b show the results of the temporal and spatial convergence study, respectively. The expected rates of convergence of and are clearly observed as for the first example.
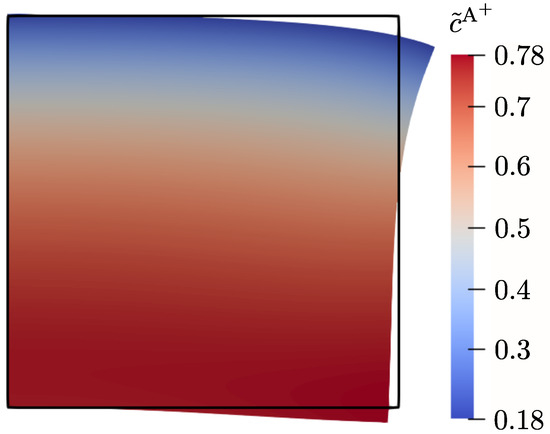
Figure 6.
Deformed shape of the hydrogel cylinder at time together with cation concentration and outline of the undeformed shape (result obtained with and ).
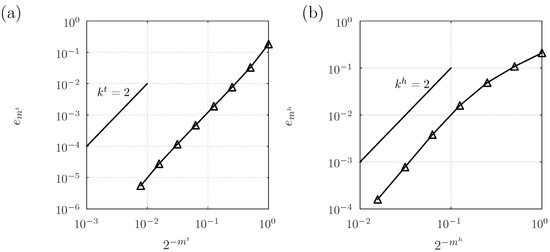
Figure 7.
Convergence results for example 2: (a) temporal convergence, (b) spatial convergence.
6. Concluding Remarks
In the present contribution, a systematic approach to the thermodynamically consistent modeling of isothermal dissipative continuum problems using the concept of standard dissipative continua is proposed and applied to two example problems. The formulation does explicitly allow for different spatial regions, which are associated with different physics, as well as for the description of interfacial processes, which may be coupled to the physics in the volume. An important conceptual feature of the approach is the distinction between state variables, process variables and Lagrangian multipliers. While the state variables have the usual significance in that they describe the thermodynamic state of the system under consideration, the process variables are used to constrain the ways in which the thermodynamic state can change; and the latter constraints are incorporated with the help of the Lagrangian multipliers. Due to the variational structure of the formulation, a systematic elimination of variables is possible under certain circumstances, thus reducing the number of unknown variables, which is an important aspect for numerical solution procedures.
The variational approach is also beneficial in view of the temporal and spatial discretization of the space–time continuous problem. With regard to temporal discretization, it is, at least for a certain class of problems, possible to use generic discretization approaches with known convergence properties. Similarly, when using the finite element method for spatial discretization, much of the classical theory applies.
Albeit a large amount of formalization is clearly involved in the presented formulation, it is expected that the associated systematic approach substantially reduces the time penalty associated with implementing complex multiphysics models. At the same time, it likely reduces the potential for error both, during the formulation of multiphysics models as well as during the implementation into program code. In particular, it appears possible to solve a large class of problems using a single, well-tested implementation.
Some of the above aspects were demonstrated by considering two example problems. In this context, it was empirically shown that optimal rates of convergence in space and time can be achieved. For the purposes of this work, the example problems were kept simple. However, applications to more complex problems will be described in forthcoming contributions.
Funding
Financial support from the Deutsche Forschungsgemeinschaft (DFG) under Grants STA 1593/1-1 and STA 1593/2-1 is gratefully acknowledged.
Data Availability Statement
The source code for the library GalerkinTools and the corresponding documentation are available from the following repository: https://github.com/sebastian-stark/GalerkinTools (accessed on 26 February 2023); The source code for the library IncrementalFE and the corresponding documentation are available from the following repository: https://github.com/sebastian-stark/IncrementalFE (accessed on 26 February 2023); The source code used for the second example is available from the following repository: https://github.com/sebastian-stark/hydrogel_model_concentration_change (accessed on 26 February 2023); The source code used for the first example is in part available from the author upon request (the full source code cannot be made publicly available due to the use of a software library, which cannot be made available for legal reasons).
Acknowledgments
The author wishes to thank B.D. Reddy for an invitation for a research visit at the Centre for Research in Computational and Applied Mechanics at the University of Cape Town, during which part of the work underlying the present contribution was conducted.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Validation of the Implementation for Example 1
In order to verify the correct implementation of the constitutive relations for example 1, some results were compared to those obtained by Hong [42], with Figure A1 showing a representative example. In particular, a laterally free plate of viscoelastic dielectric elastomer is considered, with the fringing fields neglected. An electric voltage is applied across the electrodes on the bottom and top faces of this plate. The resulting nominal electric field in the plate is , with being the normalized thickness of the plate. The nominal electric field is increased at a rate of until instability takes place. The material parameters used by Hong [42] coincide with the parameters given in Table 1 (note that the definition of the viscosity used by Hong [42] differs by a factor of 2 from the one used in the present work). For the comparisons, the total time interval was split into 1024 equally spaced time increments, and the -family with was used for temporal discretization. Since the fields are homogeneous, the use of a single finite element is sufficient. Figure A1 shows the results for the total lateral stretch and the inelastic lateral stretch . It is seen that the results obtained with all three formulations are indistinguishable; and these results are consistent with the results of Hong [42], which confirms the correct implementation for at least the case of homogeneous uniaxial fields.
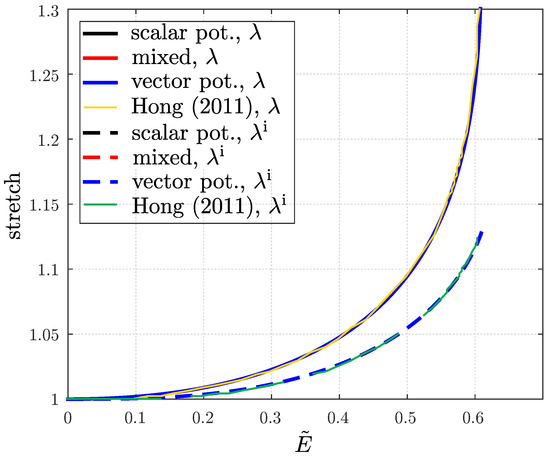
Figure A1.
Comparison between the present formulation and the results obtained by Hong [42].
Appendix B. Validation of the Implementation for Example 2
In order to verify the correct implementation of the constitutive relations for example 2, an example problem described by Acartürk [4] is considered. The problem involves a block of hydrogel material with a width of and a height of in a plane strain setting. The normal mechanical displacement is constrained to zero on the lateral surfaces of the block as well as on its bottom surface, while the top surface is mechanically free. No matter is allowed to flow across the lateral surfaces and the bottom surfaces, while the top surface is in contact with a solution bath in the same way as shown in Figure 5. The ion concentration is linearly ramped from to between time and . Subsequently, the external ion concentration is kept constant until the end of the simulation at time . In the present work, the calculation was performed with 80 finite elements in the axial direction. For the time stepping, an initial grid was created with 8 equally spaced time increments for the linear ramp and another 8 time increments for the subsequent step with constant external concentration. In the case of the latter, no equal time increment spacing was chosen. Rather, the time increment size was increased by a factor of 3 between subsequent time increments. For the actual computation, this initial temporal grid was uniformly refined six times, thus resulting in 1024 time increments in total. The resulting numerical solution is compared to the variant (SIb) discussed in Acartürk [4]. For this variant, the net electric current is constrained to zero; and for the particular one-dimensional problem with a monovalent salt considered herein, this is equivalent to the requirement of local electroneutrality used in this work. It is noted in this context that a number of different formulations were discussed by Acartürk [4], which should theoretically be equivalent. However, different results were obtained by Acartürk [4]; and this suggests that there are either errors in the implementation or other numerical issues for some of the formulations. The choice to consider the variant (SIb) for comparison is motivated by the fact that the results of this variant agree very well with the results of the present formulation. In particular, Figure A2 shows a comparison of the normal displacement of the top surface of the hydrogel block over time. Excellent agreement is evident for this case. Figure A3 shows comparisons for the cation concentrations (with regard to the actual volume of the electrolyte) at different instants of time. Again, good agreement is observed.
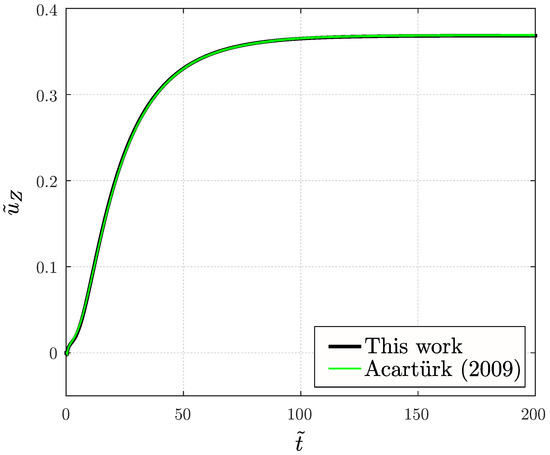
Figure A2.
Comparison of the results for the normal displacement of the top surface of the hydrogel block [4].
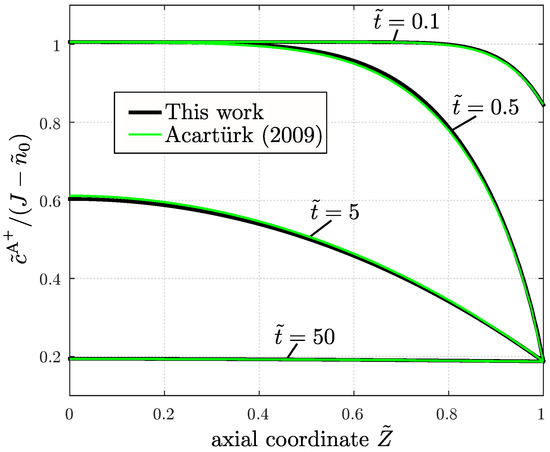
Figure A3.
Comparison of the results for the cation concentration along the axial coordinate at different times [4].
References
- Landis, C. Fully coupled, multi-axial, symmetric constitutive laws for polycrystalline ferroelectric ceramics. J. Mech. Phys. Solids 2002, 50, 127–152. [Google Scholar] [CrossRef]
- Miehe, C.; Rosato, D.; Kiefer, B. Variational principles in dissipative electro-magneto-mechanics: A framework for the macro-modeling of functional materials. Int. J. Numer. Methods Eng. 2011, 86, 1225–1276. [Google Scholar] [CrossRef]
- Bucci, G.; Chiang, Y.M.; Carter, W.C. Formulation of the coupled electrochemical-mechanical boundary-value problem, with applications to transport of multiple charged species. Acta Mater. 2016, 104, 33–51. [Google Scholar] [CrossRef]
- Acartürk, A.Y. Simulation of Charged Hydrated Porous Materials. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2009. [Google Scholar]
- Simo, J.C.; Honein, T. Variational Formulation, Discrete Conservation Laws, and Path-Domain Independent Integrals for Elasto-Viscoplasticity. J. Appl. Mech. 1990, 57, 488–497. [Google Scholar] [CrossRef]
- Ortiz, M.; Stainier, L. The variational formulation of viscoplastic constitutive updates. Comput. Methods Appl. Mech. Eng. 1999, 171, 419–444. [Google Scholar] [CrossRef]
- Hackl, K.; Fischer, F.D. On the relation between the principle of maximum dissipation and inelastic evolution given by dissipation potentials. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2008, 464, 117–132. [Google Scholar] [CrossRef]
- Yang, Q.; Stainier, L.; Ortiz, M. A variational formulation of the coupled thermo-mechanical boundary-value problem for general dissipative solids. J. Mech. Phys. Solids 2006, 54, 401–424. [Google Scholar] [CrossRef]
- Carstensen, C.; Hackl, K.; Mielke, A. Non-convex potentials and microstructures in finite-strain plasticity. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2002, 458, 299–317. [Google Scholar] [CrossRef]
- Ortiz, M.; Repetto, E.A. Nonconvex energy minimization and dislocation structures in ductile single crystals. J. Mech. Phys. Solids 1999, 47, 397–462. [Google Scholar] [CrossRef]
- Halphen, B.; Nguyen, Q.S. Sur les matériaux standard généralisés. J. De Mécanique 1975, 14, 39–63. [Google Scholar]
- Germain, P.; Nguyen, Q.S.; Suquet, P. Continuum Thermodynamics. J. Appl. Mech. 1983, 50, 1010–1020. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Finite Deformations of Porous Solids. Indiana Univ. Math. J. 1972, 21, 597–620. [Google Scholar] [CrossRef]
- Miehe, C. Strain-driven homogenization of inelastic microstructures and composites based on an incremental variational formulation. Int. J. Numer. Methods Eng. 2002, 55, 1285–1322. [Google Scholar] [CrossRef]
- Miehe, C.; Schotte, J.; Lambrecht, M. Homogenization of inelastic solid materials at finite strains based on incremental minimization principles. Application to the texture analysis of polycrystals. J. Mech. Phys. Solids 2002, 50, 2123–2167. [Google Scholar] [CrossRef]
- Miehe, C. A multi-field incremental variational framework for gradient-extended standard dissipative solids. J. Mech. Phys. Solids 2011, 59, 898–923. [Google Scholar] [CrossRef]
- Miehe, C. Variational gradient plasticity at finite strains. Part I: Mixed potentials for the evolution and update problems of gradient-extended dissipative solids. Comput. Methods Appl. Mech. Eng. 2014, 268, 677–703. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Aldakheel, F. Variational gradient plasticity at finite strains. Part II: Local-global updates and mixed finite elements for additive plasticity in the logarithmic strain space. Comput. Methods Appl. Mech. Eng. 2014, 268, 704–734. [Google Scholar] [CrossRef]
- Miehe, C.; Mauthe, S.; Hildebrand, F. Variational gradient plasticity at finite strains. Part III: Local-global updates and regularization techniques in multiplicative plasticity for single crystals. Comput. Methods Appl. Mech. Eng. 2014, 268, 735–762. [Google Scholar] [CrossRef]
- McBride, A.T.; Reddy, B.D.; Steinmann, P. Dissipation-consistent modelling and classification of extended plasticity formulations. J. Mech. Phys. Solids 2018, 119, 118–139. [Google Scholar] [CrossRef]
- Miehe, C.; Rosato, D. A rate-dependent incremental variational formulation of ferroelectricity. Int. J. Eng. Sci. 2011, 49, 466–496. [Google Scholar] [CrossRef]
- Miehe, C.; Kiefer, B.; Rosato, D. An incremental variational formulation of dissipative magnetostriction at the macroscopic continuum level. Int. J. Solids Struct. 2011, 48, 1846–1866. [Google Scholar] [CrossRef]
- Miehe, C.; Mauthe, S.; Teichtmeister, S. Minimization principles for the coupled problem of Darcy-Biot-type fluid transport in porous media linked to phase field modeling of fracture. J. Mech. Phys. Solids 2015, 82, 186–217. [Google Scholar] [CrossRef]
- Miehe, C.; Hildebrand, F.E.; Böger, L. Mixed variational potentials and inherent symmetries of the Cahn-Hilliard theory of diffusive phase separation. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2014, 470, 20130641. [Google Scholar] [CrossRef]
- Miehe, C.; Mauthe, S.; Ulmer, H. Formulation and numerical exploitation of mixed variational principles for coupled problems of Cahn-Hilliard-type and standard diffusion in elastic solids. Int. J. Numer. Methods Eng. 2014, 99, 737–762. [Google Scholar] [CrossRef]
- Miehe, C.; Dal, H.; Schänzel, L.M.; Raina, A. A phase-field model for chemo-mechanical induced fracture in lithium-ion battery electrode particles. Int. J. Numer. Methods Eng. 2016, 106, 683–711. [Google Scholar] [CrossRef]
- Alzetta, G.; Arndt, D.; Bangerth, W.; Boddu, V.; Brands, B.; Davydov, D.; Gassmoeller, R.; Heister, T.; Heltai, L.; Kormann, K.; et al. The deal.II Library, Version 9.0. J. Numer. Math. 2018, 26, 173–183. [Google Scholar] [CrossRef]
- Bangerth, W.; Hartmann, R.; Kanschat, G. deal.II—A General Purpose Object Oriented Finite Element Library. ACM Trans. Math. Softw. 2007, 33, 24/1–24/27. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Stress-Strain Relations in Anisotropic Viscoelasticity and Relaxation Phenomena. J. Appl. Phys. 1954, 25, 1385–1391. [Google Scholar] [CrossRef]
- Biot, M.A. Variational Principles in Irreversible Thermodynamics with Application to Viscoelasticity. Phys. Rev. 1955, 97, 1463–1469. [Google Scholar] [CrossRef]
- Abed-Meraim, F.; Nguyen, Q.S. A quasi-static stability analysis for Biot’s equation and standard dissipative systems. Eur. J. Mech.—A/Solids 2007, 26, 383–393. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Bathe, K.J. The inf−sup condition and its evaluation for mixed finite element methods. Comput. Struct. 2001, 79, 243–252. [Google Scholar] [CrossRef]
- Auricchio, F.; da Veiga, L.B.; Brezzi, F.; Lovadina, C. Mixed Finite Element Methods. In Encyclopedia of Computational Mechanics Second Edition; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 1–53. [Google Scholar] [CrossRef]
- Stark, S. On a certain class of one step temporal integration methods for standard dissipative continua. Comput. Mech. 2021, 67, 265–287. [Google Scholar] [CrossRef]
- Davis, T.A. Algorithm 832: UMFPACK V4.3—An Unsymmetric-pattern Multifrontal Method. ACM Trans. Math. Softw. 2004, 30, 196–199. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. On fast factorization pivoting methods for symmetric indefinite systems. Electron. Trans. Numer. Anal. 2006, 23, 158–179. [Google Scholar]
- Karypis, G.; Kumar, V. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs. SIAM J. Sci. Comput. 1998, 20, 359–392. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Duff, I.S.; Koster, J.; L’Excellent, J.Y. A Fully Asynchronous Multifrontal Solver Using Distributed Dynamic Scheduling. SIAM J. Matrix Anal. Appl. 2001, 23, 15–41. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Guermouche, A.; L’Excellent, J.Y.; Pralet, S. Hybrid scheduling for the parallel solution of linear systems. Parallel Comput. 2006, 32, 136–156. [Google Scholar] [CrossRef]
- Hong, W. Modeling viscoelastic dielectrics. J. Mech. Phys. Solids 2011, 59, 637–650. [Google Scholar] [CrossRef]
- Stark, S.; Semenov, A.; Balke, H. On the boundary conditions for the vector potential formulation in electrostatics. Int. J. Numer. Methods Eng. 2015, 102, 1704–1732. [Google Scholar] [CrossRef]
- deal.II Documentation. Available online: https://www.dealii.org/current/doxygen/deal.II/ (accessed on 28 January 2023).
- Ruas, V. Mixed finite element methods with discontinuous pressures for the axisymmetric Stokes problem. ZAMM—J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2003, 83, 249–264. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).