A Fractional Rheological Model of Viscoanelastic Media
Abstract
1. Introduction
2. The Rheological Equation
3. Mechanical Representation of the Viscoanelastic Media According to the Ciancio–Kluitenberg Model
4. Fractional Rheological Model with Four Parameters of a Viscoanelastic Medium for a Single Relaxation Process
- , depends on the stress time constant , with:
- , depends on the stress relaxation time , with:
- , coincides with the complex module due to the impulsive stress applied at the initial instant.
- , depends on natural angular frequency
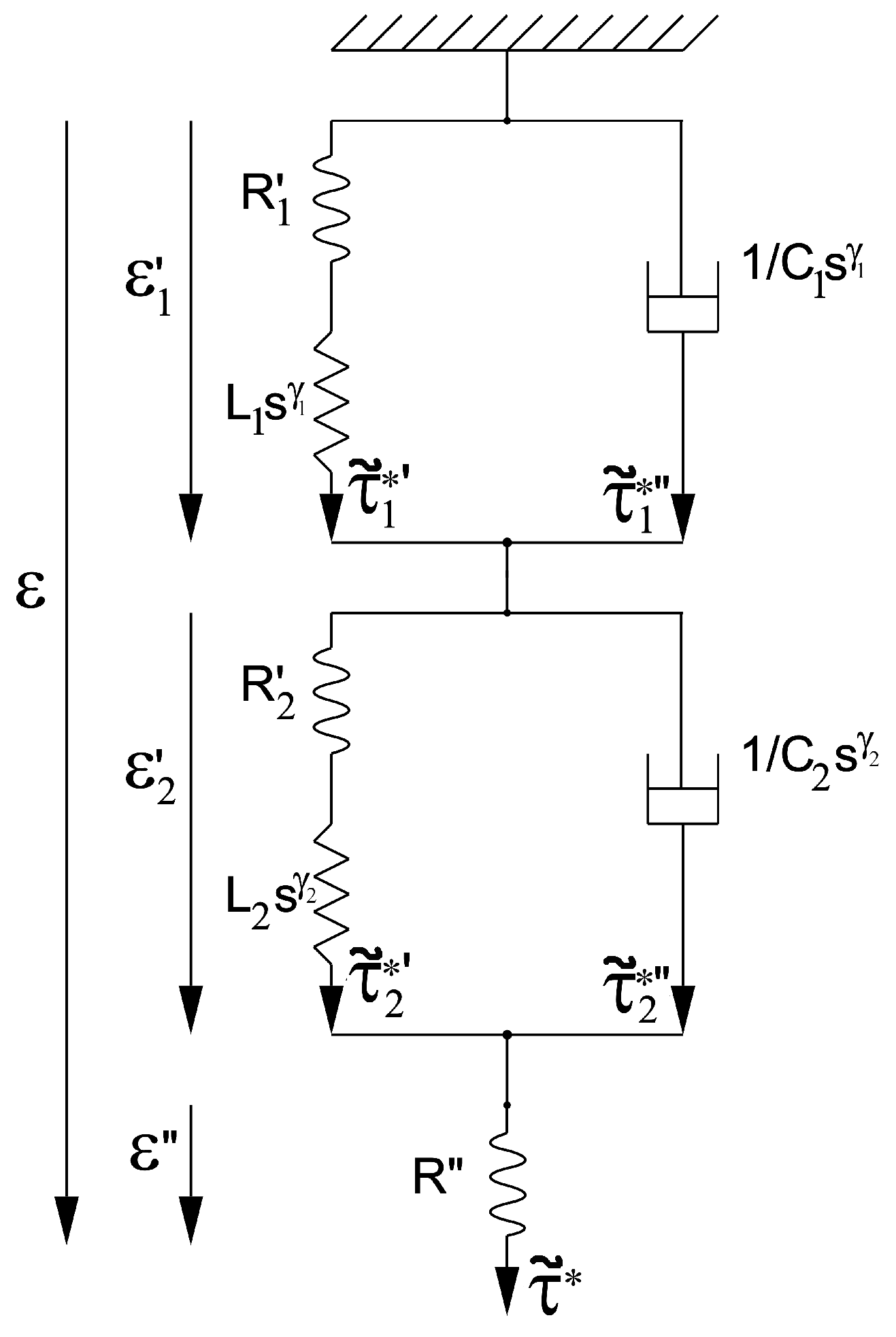
5. Fractional Rheological Model with Eight Parameters of a Viscoanelastic Medium for Two Single Relaxation Processes
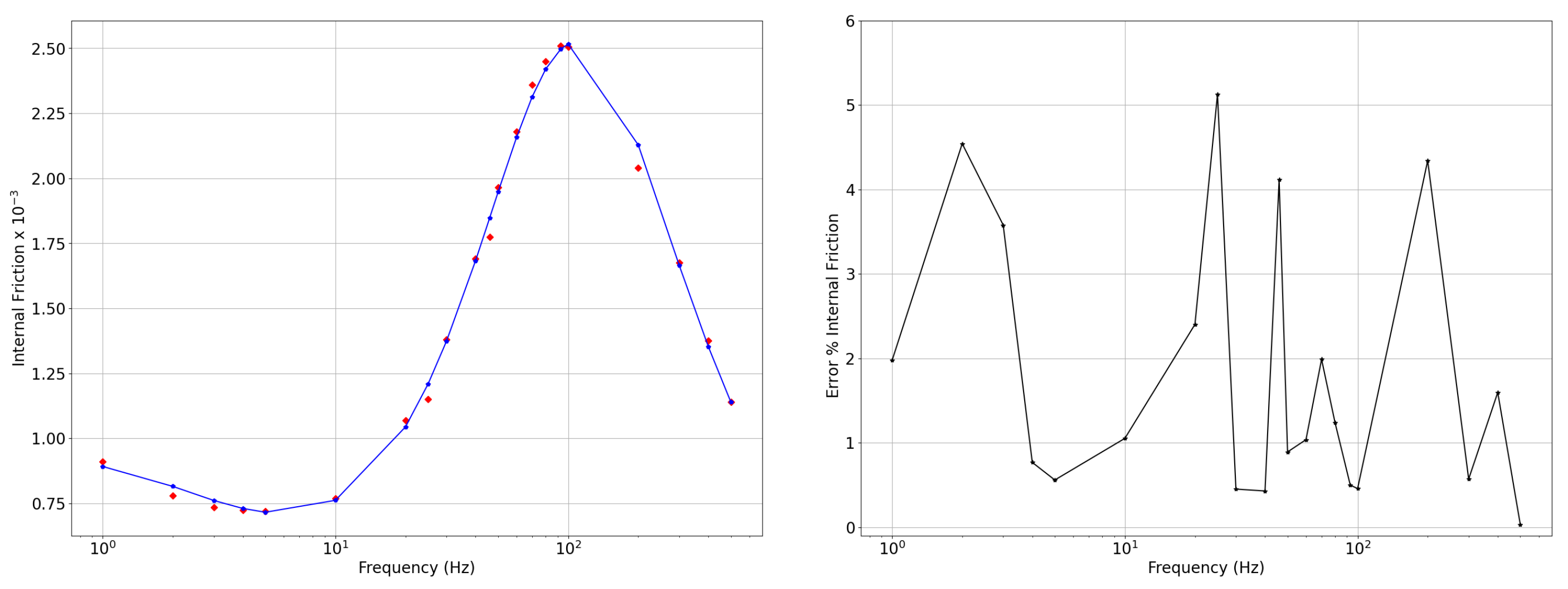
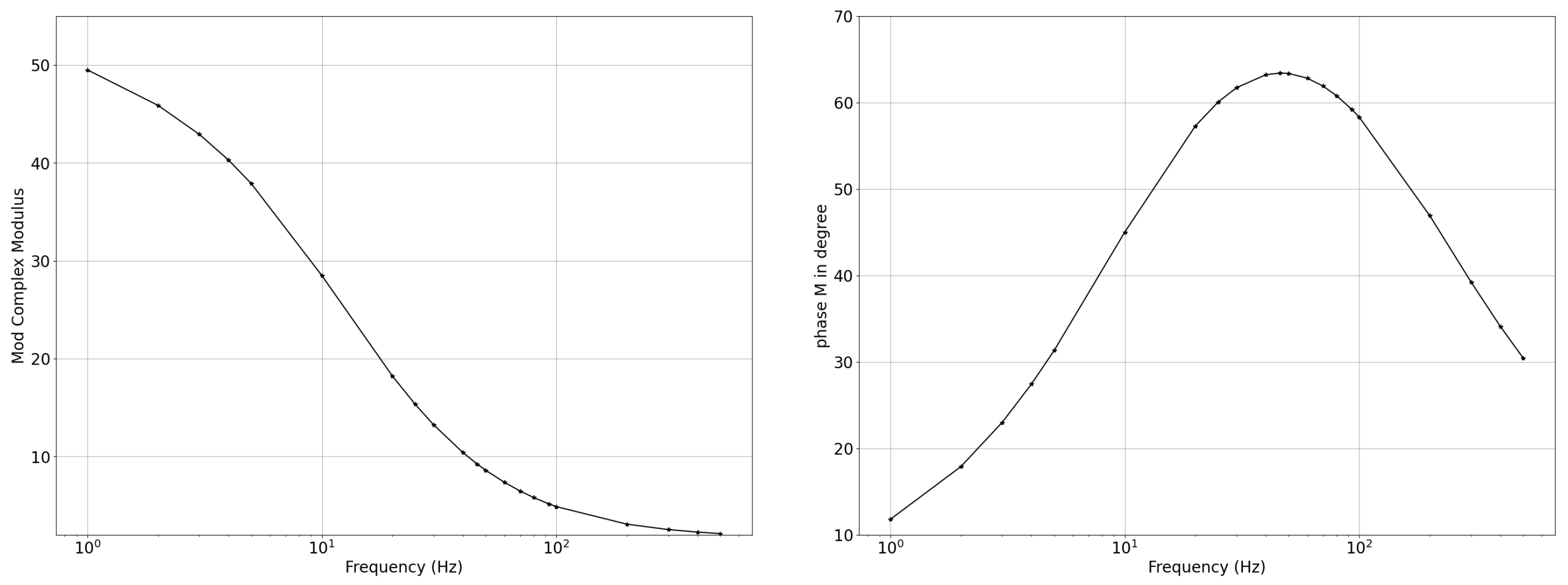
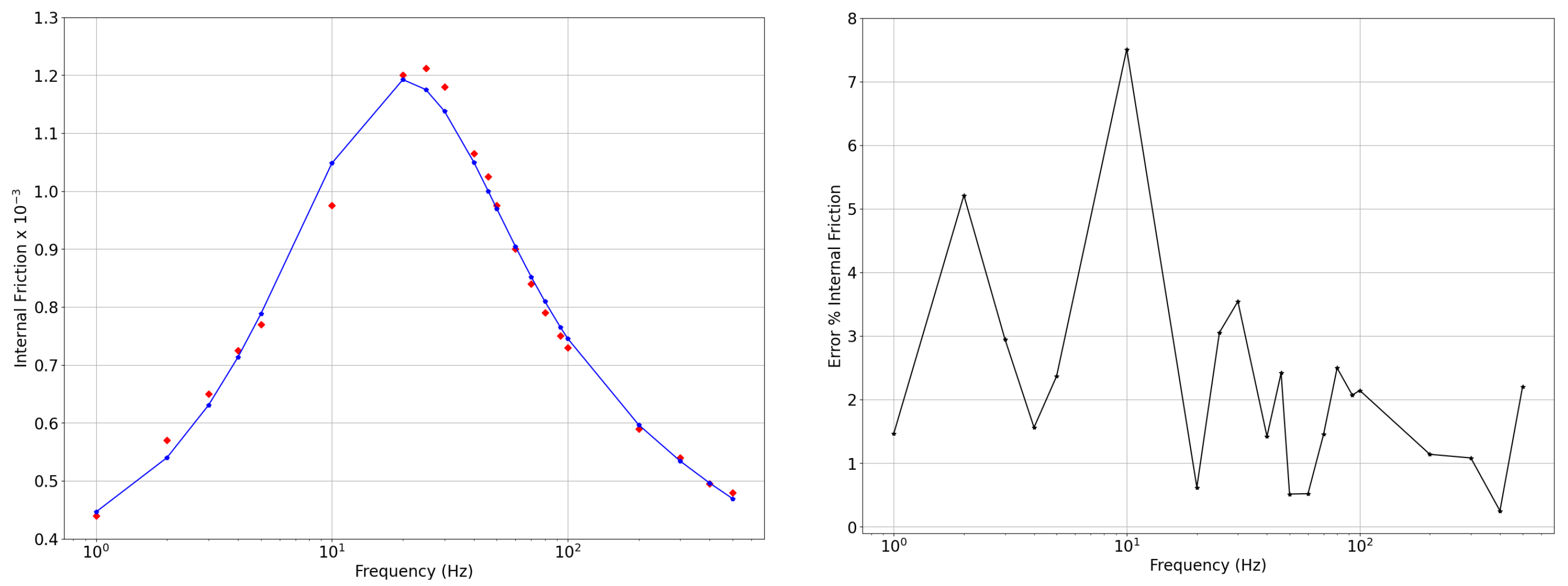
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kluitenberg, G. On rheology and thermodynamics of irreversible processes. Physica 1962, 28, 1173–1183. [Google Scholar] [CrossRef]
- Kluitenberg, G. A note on the thermodynamics of Maxwell bodies, Kelvin bodies (Voigt bodies), and fluids. Physica 1962, 28, 561–568. [Google Scholar] [CrossRef]
- Kluitenberg, G. On the thermodynamics of viscosity and plasticity. Physica 1963, 29, 633–652. [Google Scholar] [CrossRef]
- Kluitenberg, G. On heat dissipation due to irreversible mechanical phenomena in continuous media. Physica 1967, 35, 177–192. [Google Scholar] [CrossRef]
- Kluitenberg, G. A thermodynamic derivation of the stress–strain relations for burgers media and related substances. Physica 1968, 38, 513–548. [Google Scholar] [CrossRef]
- Kluitenberg, G.; Ciancio, V. On linear dynamical equations of state for isotropic media I: General formalism. Phys. Stat. Mech. Appl. 1978, 93, 273–286. [Google Scholar] [CrossRef]
- Cianco, V.; Kluitenberg, G. On linear dynamical equations of state for isotropic media II. Phys. Stat. Mech. Appl. 1979, 99, 592–600. [Google Scholar] [CrossRef]
- Ciancio, V. Propagation and attenuation of singular wave surfaces in linear inelastic media. Phys. Stat. Mech. Appl. 1979, 97, 127–138. [Google Scholar] [CrossRef]
- Turrisi, E.; Ciancio, V.; Kluitenberg, G. On the propagation of linear transverse acoustic waves in isotropic media with mechanical relaxation phenomena due to viscosity and a tensorial internal variable II. Some cases of special interest (Poynting-Thomson, Jeffreys, Maxwell, Kelvin-Voigt, Hooke and Newton media). Phys. Stat. Mech. Appl. 1982, 116, 594–603. [Google Scholar] [CrossRef]
- Ciancio, V.; Bartolotta, A.; Farsaci, F. Experimental confirmations on a thermodynamical theory for viscoanelastic media with memory. Phys. Condens. Matter 2007, 394, 8–13. [Google Scholar] [CrossRef]
- Ciancio, A.; Ciancio, V.; Farsaci, F. Wave propagation in media obeying a thermoviscoanelastic model. UPB Sci. Bull. Ser. A 2007, 69, 69–79. [Google Scholar]
- Ciancio, V.; Ciancio, A.; Farsaci, F. On general properties of phenomenological and state coefficients for isotropic viscoanelastic media. Phys. Condens. Matter 2008, 403, 3221–3227. [Google Scholar] [CrossRef]
- Ciancio, A. An approximate evalutation of the phenomenological and state coefficients for viscoanelastic media with memory. U.P.B. Sci. Bull. 2011, 73, 3–14. [Google Scholar]
- Ciancio, V.; Restuccia, L. On heat equation in the framework of classic irreversible thermodynamics with internal variables. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1640003. [Google Scholar] [CrossRef]
- Ciancio, V.; Palumbo, A. A thermodynamical theory with internal variables describing thermal effects in viscous fluids. J. -Non-Equilib. Thermodyn. 2018, 43, 171–184. [Google Scholar] [CrossRef]
- Ciancio, V. On the temperature equation in classical irreversible thermodinamics. Appl. Sci. 2022, 24, 71–86. [Google Scholar]
- Ciancio, V. On the Generalized Debye Equation for Media with Dielectric Relaxation Phenomena Described by Vectorial Internal Thermodynamic Variables. J. Non-Equilib. Thermodyn. 1989, 14, 239–250. [Google Scholar] [CrossRef]
- Ciancio, V.; Kluitenberg, G. On electromagnetic waves in isotropic media with dielectric relaxation. Acta Phys. Hung. 1989, 66, 251–276. [Google Scholar] [CrossRef]
- Ciancio, V.; Restuccia, L.; Kluitenberg, G. A Thermodynamic Derivation of Equations for Dielectric Relaxation Phenomena in Anisotropic Polarizable Media. J. Non.-Equil. Thermodyn. 1990, 15, 157–172. [Google Scholar] [CrossRef]
- Ciancio, V.; Farsaci, F.; Di Marco, G. A method for experimental evaluation of phenomenological coefficients in media with dielectric relaxation. Phys. Condens. Matter 2007, 387, 130–135. [Google Scholar] [CrossRef]
- Ciancio, V.; Verhás, J. A Thermodynamic Theory for Heat Radiation Through the Atmosphere. J. Non.-Equil. Thermodyn. 1991, 16, 57–66. [Google Scholar] [CrossRef]
- Zener, C. Internal friction in solids. Proc. Phys. Soc. 1940, 52, 152. [Google Scholar] [CrossRef]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Coleman, B.D.; Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. Arch. Ration. Mech. Anal. 1963, 13, 167–178. [Google Scholar] [CrossRef]
- Coleman, B.D.; Noll, W. Foundations of linear viscoelasticity. Rev. Mod. Phys. 1961, 33, 239. [Google Scholar] [CrossRef]
- Shen, L.J. Fractional derivative models for viscoelastic materials at finite deformations. Int. J. Solids Struct. 2020, 190, 226–237. [Google Scholar] [CrossRef]
- Fichera, G. Sul principio della memoria evanescente. Rend. Semin. Mat. Della Univ. Padova 1982, 68, 245–259. [Google Scholar]
- Mainardi, F.; Spada, G. Creep, relaxation and viscosity properties for basic fractional models in rheology. Eur. Phys. J. Spec. Top. 2011, 193, 133–160. [Google Scholar] [CrossRef]
- Ciancio, A.; Flora, B.F.F. A Fractional Complex Permittivity Model of Media with Dielectric Relaxation. Fractal Fract. 2017, 1, 4. [Google Scholar] [CrossRef]
- Ciancio, A.; Ciancio, V.; d’Onofrio, A.; Flora, B.F.F. A Fractional Model of Complex Permittivity of Conductor Media with Relaxation: Theory vs. Experiments. Fractal Fract. 2022, 6, 390. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Tarasov, V.E.; Tarasova, S.S. Fractional derivatives and integrals: What are they needed for? Mathematics 2020, 8, 164. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A.; Valenza, A. Visco-elastic behavior through fractional calculus: An easier method for best fitting experimental results. Mech. Mater. 2011, 43, 799–806. [Google Scholar] [CrossRef]
- Ebaid, A.; El-Zahar, E.; Aljohani, A.; Salah, B.; Krid, M.; Machado, J.T. Analysis of the two-dimensional fractional projectile motion in view of the experimental data. Nonlinear Dyn. 2019, 97, 1711–1720. [Google Scholar] [CrossRef]
- Zener, C.M.; Siegel, S. Elasticity and Anelasticity of Metals. J. Phys. Chem. 1949, 53, 1468. [Google Scholar] [CrossRef]
- Bennewitz, K.; Rötger, H. Ueber die innere Reibung fester Körper; Absorptionsfrequenzen von Metallen im akustischen Gebiet. Physik. Zeitschr. 1936, 37, 578–588. [Google Scholar]
- Nowick, A.S. Internal friction in metals. Prog. Met. Phys. 1953, 4, 1–70. [Google Scholar] [CrossRef]
- Berry, B. Precise investigation of the theory of damping by transverse thermal currents. J. Appl. Phys. 1955, 26, 1221–1224. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Johansson, R. Numerical Python: A Practical Techniques Approach for Industry; Apress: Berkeley, CA, USA, 2015. [Google Scholar]
- SciPy v1.9.3 Manual. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html (accessed on 10 December 2022).




| i | ||||
|---|---|---|---|---|
| 1 | 1 | 0.440 | 0.205 | 0.910 |
| 2 | 2 | 0.570 | 0.325 | 0.780 |
| 3 | 3 | 0.650 | 0.435 | 0.735 |
| 4 | 4 | 0.725 | 0.520 | 0.725 |
| 5 | 5 | 0.770 | 0.620 | 0.720 |
| 6 | 10 | 0.975 | 0.975 | 0.770 |
| 7 | 20 | 1.200 | 1.530 | 1.070 |
| 8 | 25 | 1.213 | 1.650 | 1.150 |
| 9 | 30 | 1.180 | 1.880 | 1.380 |
| 10 | 40 | 1.065 | 2.090 | 1.691 |
| 11 | 46 | 1.025 | 2.100 | 1.775 |
| 12 | 50 | 0.975 | 2.080 | 1.965 |
| 13 | 60 | 0.900 | 1.965 | 2.180 |
| 14 | 70 | 0.840 | 1.840 | 2.360 |
| 15 | 80 | 0.790 | 1.740 | 2.450 |
| 16 | 93 | 0.750 | 1.605 | 2.510 |
| 17 | 100 | 0.730 | 1.575 | 2.505 |
| 18 | 200 | 0.590 | 1.090 | 2.040 |
| 19 | 300 | 0.540 | 0.860 | 1.675 |
| 20 | 400 | 0.495 | 0.690 | 1.375 |
| 21 | 500 | 0.480 | 0.565 | 1.140 |
| i | ||||
|---|---|---|---|---|
| 1 | 0.575515 | 0.001006 | 0.022103 | 172.96 |
| 2 | 0.360071 | 0.000229 | 0.077811 | 0.57 |
| i | ||||
|---|---|---|---|---|
| 1 | 994.035785 | 45.242727 | 1.000000 | 0.120119 |
| 2 | 4366.812227 | 12.851653 | 1.000000 | 19.272905 |
| i | ||||
|---|---|---|---|---|
| 1 | 0.561151 | 0.001453 | 0.072381 | 64.97 |
| 2 | 0.158946 | 0.005930 | 0.077555 | 0.99 |
| i | ||||
|---|---|---|---|---|
| 1 | 688.231246 | 13.815780 | 1.000000 | 0.127644 |
| 2 | 168.634064 | 12.894075 | 1.000000 | 12.952460 |
| i | ||||
|---|---|---|---|---|
| 1 | 0.806110 | 0.003680 | 0.069378 | 73.54 |
| 2 | 0.206638 | 0.000088 | 0.017235 | 0.03 |
| i | ||||
|---|---|---|---|---|
| 1 | 271.739130 | 14.413791 | 1.000000 | 0.014111 |
| 2 | 11,363.636364 | 58.021468 | 1.000000 | 257.802147 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciancio, A.; Ciancio, V.; Flora, B.F.F. A Fractional Rheological Model of Viscoanelastic Media. Axioms 2023, 12, 243. https://doi.org/10.3390/axioms12030243
Ciancio A, Ciancio V, Flora BFF. A Fractional Rheological Model of Viscoanelastic Media. Axioms. 2023; 12(3):243. https://doi.org/10.3390/axioms12030243
Chicago/Turabian StyleCiancio, Armando, Vincenzo Ciancio, and Bruno Felice Filippo Flora. 2023. "A Fractional Rheological Model of Viscoanelastic Media" Axioms 12, no. 3: 243. https://doi.org/10.3390/axioms12030243
APA StyleCiancio, A., Ciancio, V., & Flora, B. F. F. (2023). A Fractional Rheological Model of Viscoanelastic Media. Axioms, 12(3), 243. https://doi.org/10.3390/axioms12030243








