Modified Gravity Description of Neutron Star in the f(R) Framework
Abstract
1. Introduction
2. The Tolman–Oppenheimer–Volkoff Equation for Gravity
2.1. R as a Quadratic Function of Radius
2.2. R as an Exponential Function of Radius
2.3. R as a Linear Function of Radius
3. The Brans–Dicke Theory for Gravity
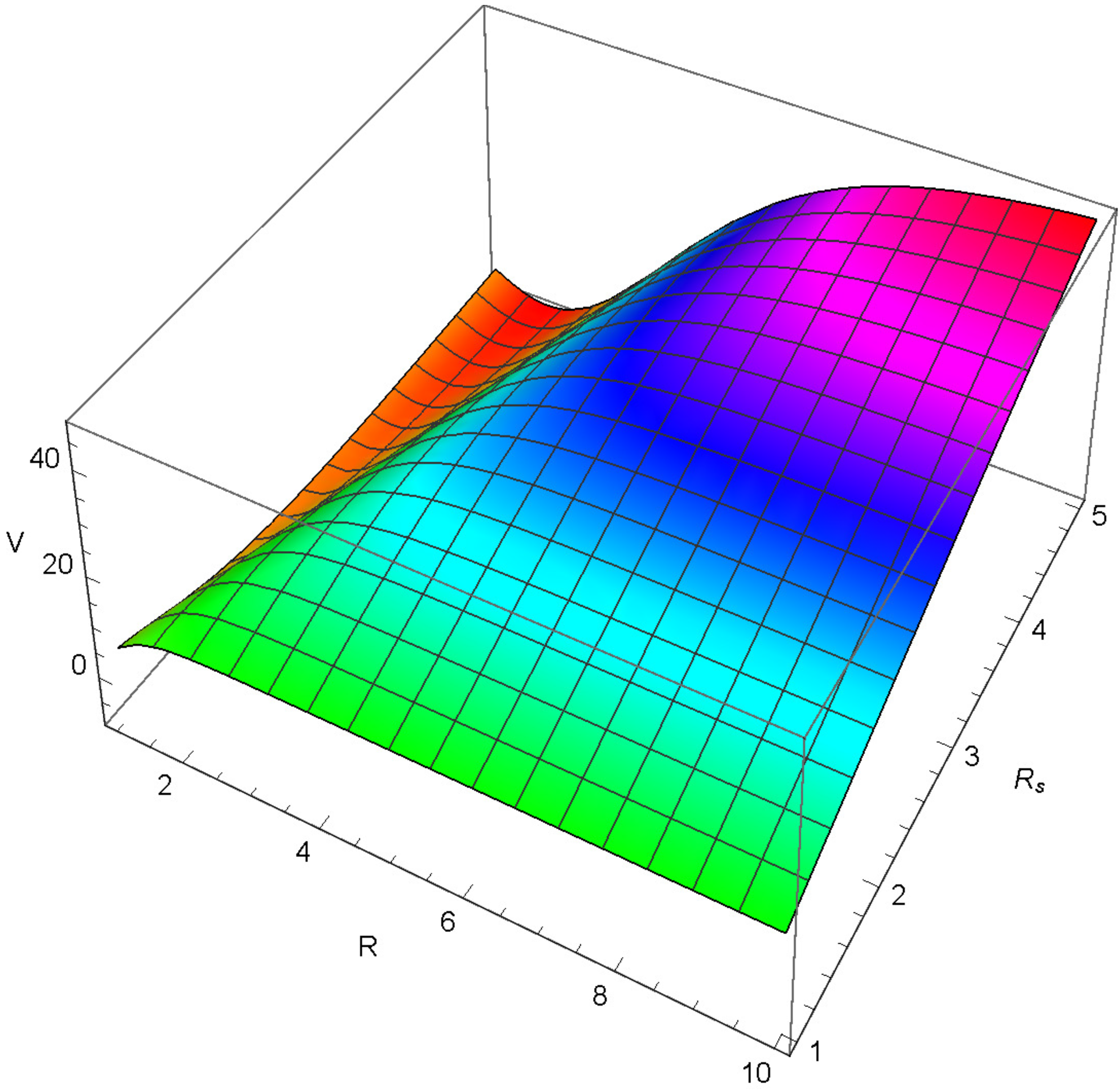
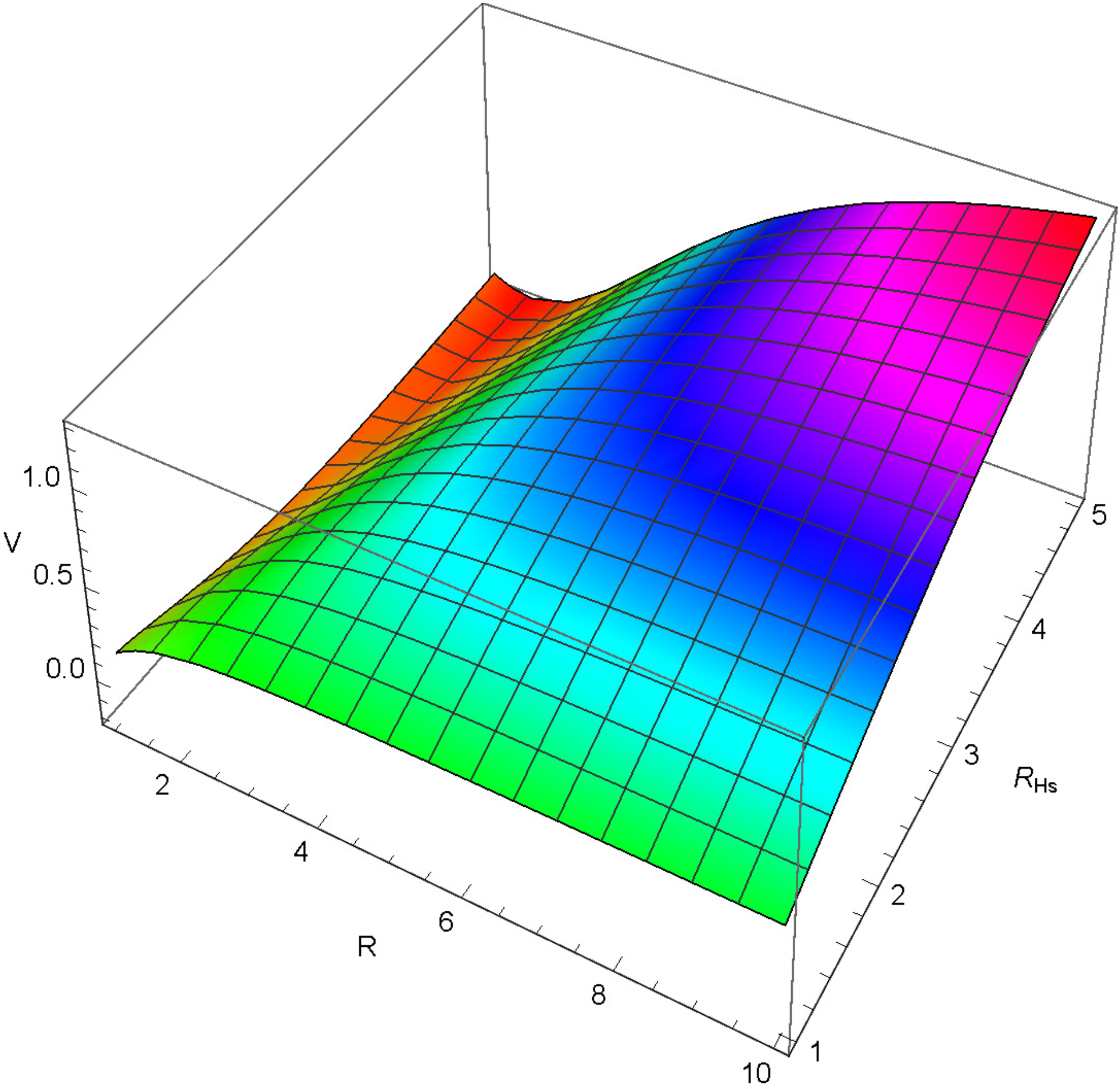
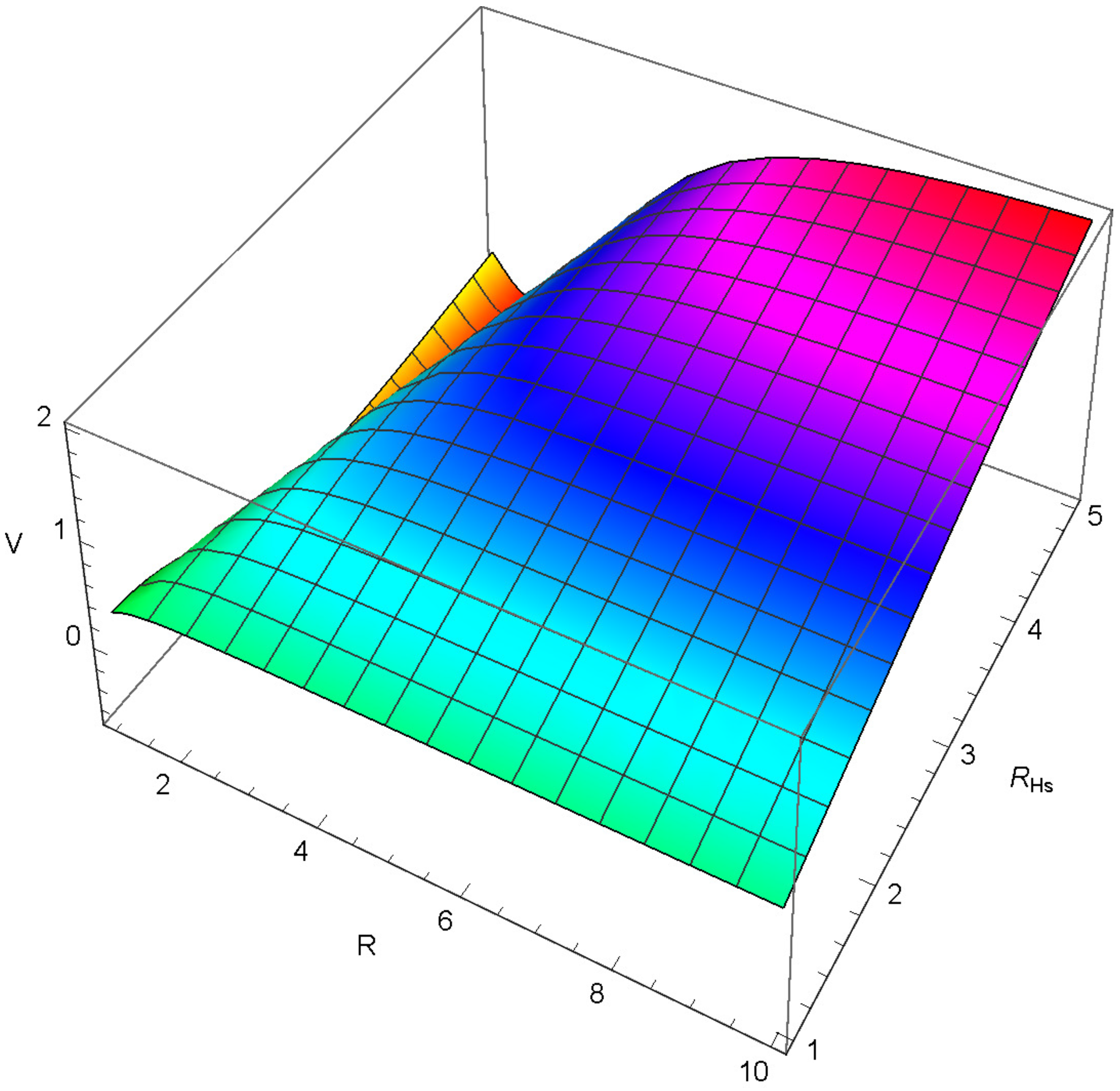
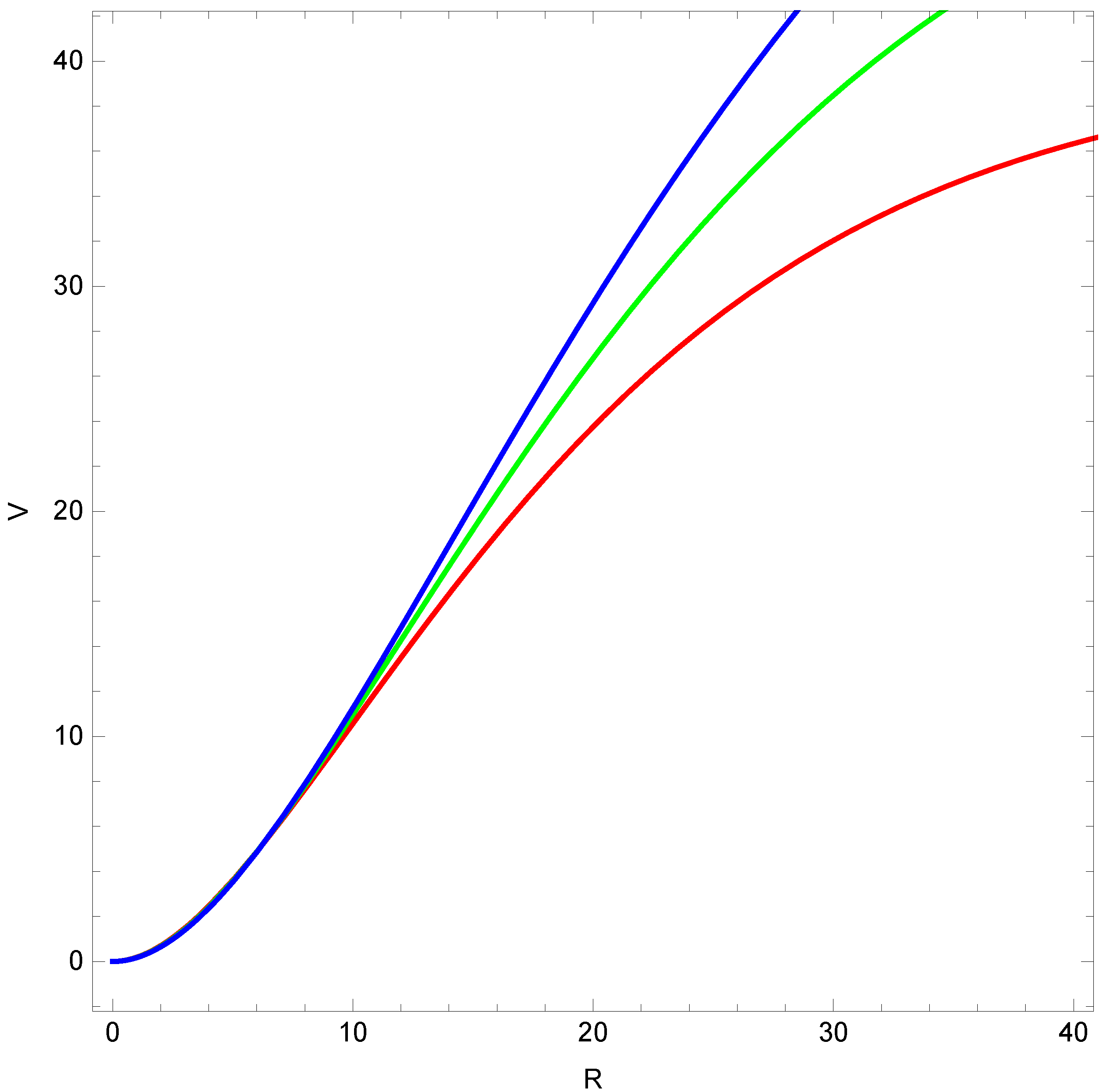
3.1. The Scalar Potential for R as a Quadratic Function of Radius
3.2. The Scalar Potential for R as an Exponential Function of Radius
3.3. The Scalar Potential for R as a Linear Function of Radius
4. Viable Gravity Models
4.1. Hu–Sawicki Model
4.2. Starobinsky Model
4.3. Tsujikawa Model
4.4. The Exponential Gravity Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Branch, D. Type Ia supernovae and the Hubble constant. Annu. Rev. Astron. Astrophys. 1998, 36, 17–55. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Doran, M. Cosmic microwave background and supernova constraints on quintessence: Concordance regions and target models. Phys. Rev. D 2004, 69, 103517. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Dark energy anisotropic stress and large scale structure formation. Phys. Rev. D 2006, 73, 083502. [Google Scholar] [CrossRef]
- Colless, M.; Dalton, G.; Maddox, S.; Sutherland, W.; Norberg, P.; Cole, S.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Collins, C.; et al. The 2df galaxy redshift survey: Spectra and redshifts. Mon. Not. R. Astron. Soc. 2001, 328, 1039–1063. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.I.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope cluster supernova survey. V. Improving the dark-energy constraints above z > 1 and building an early-type-hosted supernova sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The physics of cosmic Acceleration. Annu. Rev. Nucl. Part. Sci. 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Z.H. Interacting chaplygin gas. Phys. Rev. D 2006, 73, 043518. [Google Scholar] [CrossRef]
- Bilić, N.; Tupper, G.B.; Viollier, R.D. Unification of dark matter and dark energy: The inhomogeneous Chaplygin gas. Phys. Lett. B 2002, 535, 17–21. [Google Scholar] [CrossRef]
- Myung, Y.S. Holographic principle and dark energy. Phys. Lett. B 2005, 610, 18–22. [Google Scholar] [CrossRef]
- Karami, K.; Ghaffari, S. The generalized second law of thermodynamics for the interacting polytropic dark energy in non-flat FRW universe enclosed by the apparent horizon. Phys. Lett. B 2010, 688, 125–128. [Google Scholar] [CrossRef]
- Karami, K.; Ghaffari, S.; Fehri, J. Interacting polytropic gas model of phantom dark energy in non-flat universe. Eur. Phys. J. C 2009, 64, 85–88. [Google Scholar] [CrossRef]
- Bamba, K.; Matsumoto, J.; Nojiri, S.I. Cosmological perturbations in the k-essence model. Phys. Rev. D 2012, 85, 084026. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f (R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar]
- Nojiri, S.I.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom–non-phantom transition model and generalized holographic dark energy. Gen. Relativ. Gravit. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Bergmann, P.G. Comments on the scalar-tensor theory. Int. J. Theor. Phys. 1968, 1, 25–36. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Why to study teleparallel gravity. In Teleparallel Gravity; Springer: Dordrecht, The Netherlands, 2013; pp. 179–186. [Google Scholar]
- Sharif, M.; Rani, S. Entropy corrected holographic dark energy f (T) gravity model. Mod. Phys. Lett. A 2014, 29, 1450015. [Google Scholar] [CrossRef]
- Karami, K.; Abdolmaleki, A. f (T) modified teleparallel gravity as an alternative for holographic and new agegraphic dark energy models. Res. Astron. Astrophys. 2013, 13, 757. [Google Scholar] [CrossRef]
- Setare, M.R.; Darabi, F. Power-law solutions in f (T) gravity. Gen. Relativ. Gravit. 2012, 44, 2521–2527. [Google Scholar] [CrossRef]
- Karami, K.; Khaledian, M.S. Polytropic and Chaplygin f (R)-gravity models. Int. J. Mod. Phys. D 2012, 21, 1250083. [Google Scholar] [CrossRef]
- Güver, T.; Erkoca, A.E.; Reno, M.H.; Sarcevic, I. On the capture of dark matter by neutron stars. J. Cosmol. Astropart. Phys. 2014, 2014, 13. [Google Scholar] [CrossRef]
- Linder, E.V. Exponential gravity. Phys. Rev. D 2009, 80, 123528. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Nonsingular exponential gravity: A simple theory for early-and late-time accelerated expansion. Phys. Rev. D 2011, 83, 086006. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Further stable neutron star models from f (R) gravity. J. Cosmol. Astropart. Phys. 2013, 2013, 40. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Douchin, F. Equation of state of dense matter and the minimum mass of cold neutron stars. Astron. Astrophys. 2002, 385, 301–307. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81. [Google Scholar] [CrossRef]
- Oppenheimer, J.R. Volkoff. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- O’Hanlon, J. Intermediate-range gravity: A generally covariant model. Hysical Rev. Lett. 1972, 29, 137. [Google Scholar] [CrossRef]
- Chiba, T. 1/R gravity and scalar-tensor gravity. Phys. Lett. B 2003, 575, 1–3. [Google Scholar] [CrossRef]
- Fujii, Y.; Maeda, K.I. The Scalar-Tensor Theory of Gravitation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Uddin, K.; Mizuno, S.; Tavakol, R.; Yokoyama, J.I. Constraints on scalar-tensor models of dark energy from observational and local gravity tests. Phys. Rev. D 2008, 77, 103009. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f (R) theories. Living Rev. Relativ. 2010, 13, 1–161. [Google Scholar] [CrossRef]
- Bamba, K.; Geng, C.Q.; Lee, C.C. Generic feature of future crossing of phantom divide in viable f (R) gravity models. J. Cosmol. Astropart. Phys. 2010, 2010, 001. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From F (R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; Francaviglia, M. Extended theories of gravity and their cosmological and astrophysical applications. Gen. Relativ. Gravit. 2008, 40, 357–420. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended gravity description for the GW190814 supermassive neutron star. Physics Letters B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology; John Wiley & Sons Inc.: New York, NY, USA, 1972. [Google Scholar]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Nonperturbative models of quark stars in f (R) gravity. Phys. Lett. B 2015, 742, 160–166. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Jawad, A.; Rani, S. Holographic polytropic gravity models. Adv. High Energy Phys. 2015, 2015, 798902. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Maximal neutron star mass and the resolution of the hyperon puzzle in modified gravity. Phys. Rev. D 2014, 89, 103509. [Google Scholar] [CrossRef]
- Faber, J.A.; Grandclément, P.; Rasio, F.A. Mergers of irrotational neutron star binaries in conformally flat gravity. Phys. Rev. D 2004, 69, 124036. [Google Scholar] [CrossRef]
- Cooney, A.; DeDeo, S.; Psaltis, D. Neutron stars in f (R) gravity with perturbative constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Kase, R.; Tsujikawa, S. Neutron stars in f (R) gravity and scalar-tensor theories. J. Cosmol. Astropart. Phys. 2019, 2019, 054. [Google Scholar] [CrossRef]
- Branss, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Faraoni, V. Matter instability in modified gravity. Phys. Rev. D 2006, 74, 104017. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Classical Quantum Gravity 4, 695 (1987); V. Müller, H.-J. Schmidt, and AA Starobinsky. Phys. Lett. B 1987, 202, 198. [Google Scholar]
- Chiba, T.; Smith, T.L.; Erickcek, A.L. Solar System constraints to general f (R) gravity. Phys. Rev. D 2007, 75, 124014. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f (R) cosmic acceleration that evade solar system tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f (R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Tsujikawa, S. Observational signatures of f (R) dark energy models that satisfy cosmological and local gravity constraints. Phys. Rev. D 2008, 77, 023507. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f (R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Abdelwahab, M.; Carloni, S.; Dunsby, P.K.S. Cosmological dynamics of ‘exponential gravity’. Class. Quantum Gravity 2008, 25, 135002. [Google Scholar] [CrossRef]
- Bamba, K.; Geng, C.Q.; Lee, C.C. Cosmological evolution in exponential gravity. J. Cosmol. Astropart. Phys. 2010, 2010, 021. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V. Causal limit of neutron star maximum mass in f (R) gravity in view of GW190814. Phys. Lett. B 2021, 816, 136222. [Google Scholar] [CrossRef]
- Rincón, Á.; Panotopoulos, G.; Lopes, I. Anisotropic stars made of exotic matter within the complexity factor formalism. Eur. Phys. J. C 2023, 83, 116. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Interior solutions of relativistic stars with anisotropic matter in scale-dependent gravity. Eur. Phys. J. C 2021, 81, 63. [Google Scholar] [CrossRef]
- Tangphati, T.; Pradhan, A.; Banerjee, A.; Panotopoulos, G. Anisotropic stars in 4D Einstein–Gauss–Bonnet gravity. Phys. Dark Universe 2021, 33, 100877. [Google Scholar] [CrossRef]
- Andrade, J.; Contreras, E. Stellar models with like-Tolman IV complexity factor. Eur. Phys. J. C 2021, 81, 889. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F. Anisotropic fluid spheres in the framework of f (R, T) gravity theory. Ann. Phys. 2020, 414, 168070. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.; Radinschi, I.; Chattopadhyay, S. Modified Gravity Description of Neutron Star in the f(R) Framework. Axioms 2023, 12, 234. https://doi.org/10.3390/axioms12030234
Das S, Radinschi I, Chattopadhyay S. Modified Gravity Description of Neutron Star in the f(R) Framework. Axioms. 2023; 12(3):234. https://doi.org/10.3390/axioms12030234
Chicago/Turabian StyleDas, Samprity, Irina Radinschi, and Surajit Chattopadhyay. 2023. "Modified Gravity Description of Neutron Star in the f(R) Framework" Axioms 12, no. 3: 234. https://doi.org/10.3390/axioms12030234
APA StyleDas, S., Radinschi, I., & Chattopadhyay, S. (2023). Modified Gravity Description of Neutron Star in the f(R) Framework. Axioms, 12(3), 234. https://doi.org/10.3390/axioms12030234