RSVD for Three Quaternion Tensors with Applications in Color Video Watermark Processing

Abstract

In this paper, we study the restricted singular-value decomposition (RSVD) for three quaternion tensors under the Einstein product, and give higher-order RSVD over the quaternion algebra, which can achieve simultaneous singular value decomposition of three quaternion tensors. Moreover, we give the algorithm for computing the RSVD of for quaternion tensors. What is more, we present a new blind color video watermarking scheme based on the forth-order RSVD over the quaternion algebra, and our numerical example demonstrates the effectiveness of the framework.

1. Introduction

Higher-order tensor decomposition has a wide range of applications, such as signal processing, data mining, genomic signals and so on. Kolda and Bader, [1] in 2009, provided theoretical developments and applications of tensor decomposition. Moreover, a lot of papers discussing tensor decomposition and other fields of tensor theory have been presented [2,3,4,5,6,7,8,9,10,11,12].

Tensor equations have high application values in engineering and science, for example, modeling the problems for continuum physics and engineering, isotropic and anisotropic flexibility, and reducing order modeling [13]. In addition, there are also some papers using different approaches to investigate tensor equation over fields [4,14].

W.R. Hamilton [15] in 1843 first introduced the concept of quaternions. Quaternion algebra is an associative and noncommutative division algebra over the real number field. Many scholars have applied it to quantum physics, signal, computer science, and color image processing, etc. [16]. In particular, applications for quaternion matrix factorization in color signal processing, image processing, and recognition are also prominent [17,18].

It is well known that matrix decomposition has a wide range of applications, and at the same time, due to the quaternion structure, the quaternion matrix retains more information, which is especially well applied in image processing. However, for video or higher-dimensional signals, the quaternion matrix can no longer meet the storage requirements. Therefore, research on quaternion tensors becomes necessary.

Multi-tensor factorization on quaternion algebra is currently underdeveloped compared to tensor factorization on traditional algebra. It is very challenging to generalize results of real or complex numbers to quaternions due to their non-commutative properties. Tensor decomposition and quaternion algebra all have wide applications [19,20], and the theory of quaternion tensor theory is also in urgent need of development. Therefore, in this paper, we propose the restricted singular value decomposition (higher-order RSVD) of quaternion tensor triples. Our contributions are as follows:

• We give the structure for higher-order RSVD on quaternion algebra as wells as two special cases: singular value decomposition for one quaternion tensor and quotient singular value decomposition for two quaternion tensors (higher-order QSVD) under the isomorphic group structures and the Einstein product (Definition 1).
• We present a blind color video watermarking scheme based on the forth-order RSVD over the quaternion algebra.

The rest of the paper is organized as follows. In Section 2, we introduce some basic knowledge of tensor quaternions. In Section 3, we investigate the restricted singular value decomposition for three quaternion tensors. In Section 4, we give the application for RSVD. We finally give the conclusion in Section 5.

2. Preliminaries

The number of dimensions of a tensor is called the order. Matrices (tensors of order two) are written as capitals, e.g., A. Higher-order tensors (order three or higher) are written as calligraphic letters, e.g., $\mathcal{A}$. An order N tensor $\mathcal{A}={\left(a_{i_1\cdots i_N}\right)}_{1\le i_j\le I_j}(j=1,\dots ,N)$ is a multidimensional array with $I_1{I}_2\cdots I_N$ entries. Let ${\mathbb{R}}^{I_1\times \cdots \times I_N},{\mathbb{C}}^{I_1\times \cdots \times I_N}$ and ${\mathbb{H}}^{I_1\times \cdots \times I_N}$ be, respectively, for the sets of the order N dimension $I_1\times \cdots \times I_N$ tensors over the real number field $\mathbb{R}$, the complex number field $\mathbb{C}$ and the quaternion algebra

$$\mathbb{H}=\left\{q_0+q_1\mathbf{i}+q_2\mathbf{j}+q_3\mathbf{k}|{\mathbf{i}}^2={\mathbf{j}}^2={\mathbf{k}}^2=\mathbf{ijk}=-1,q_0,q_1,q_2,q_3\in \mathbb{R}\right\}.$$

As we all know, quaternion algebra is an associative and noncommutative division algebra. We refer the reader to the recent book [21] for more definitions and properties of quaternions. The symbol $\overline{q}$ stands for the conjugate transpose of a quaternion $q=q_0+q_1\mathbf{i}+q_2\mathbf{j}+q_3\mathbf{k},$ where $q_0,q_1,q_2,q_3\in \mathbb{R}$. Clearly, $\overline{q}=q_0-q_1\mathbf{i}-q_2\mathbf{j}-q_3\mathbf{k}.$

For a quaternion tensor $\mathcal{A}=\left(a_{i_1\cdots i_N{j}_1\cdots j_N}\right)\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N}$, let $\mathcal{B}=\left(b_{j_1\cdots j_N{i}_1\cdots i_N}\right)\in {\mathbb{H}}^{J_1\times \cdots \times J_N\times I_1\times \cdots \times I_N}$ be the conjugate transpose of $\mathcal{A}$, where $b_{j_1\cdots j_N{i}_1\cdots i_N}={\overline{a}}_{i_1\cdots i_N{j}_1\cdots j_N}$. The tensor $\mathcal{B}$ is denoted by ${\mathcal{A}}^{*}$. A “square” tensor $\mathcal{A}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$ is said to be Hermitian if $\mathcal{A}={\mathcal{A}}^{*}$. A “square” tensor $\mathcal{D}=\left(d_{i_1\cdots i_N{i}_1\cdots i_N}\right)\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$ is called a diagonal tensor if all its entries are zero except for $d_{i_1\cdots i_N{i}_1\cdots i_N}$. If all the diagonal entries $d_{i_1\cdots i_N{i}_1\cdots i_N}=1$, then $\mathcal{D}$ is a unit tensor, denoted by $\mathcal{I}$. The zero tensor with suitable order is denoted by 0. More detail regarding the basic definitions and properties of tensors are in [1].

The most common types of tensor multiplications are denoted by ${\ast }_N$ for the Einstein, ${\times }_n$ for the n-mode, ⊗ for the Kronecker, ⊙ for the Khatri–Rao, and ⊛ for the Hadamard products. We refer the reader to the paper [22] for the latter four definitions.

We only focus on the Einstein product in this paper. First of all, the definition of the Einstein product is as following.

Definition 1

(Einstein product [23]). For $\mathcal{A}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N}$ and $\mathcal{B}\in {\mathbb{H}}^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_M}$, the Einstein product of tensors $\mathcal{A}$ and $\mathcal{B}$ is defined by the operation ${\ast }_N$ via

$$\begin{array}{c}\hfill {\left(\mathcal{A}{\ast }_N\mathcal{B}\right)}_{i_1\cdots i_N{k}_1\cdots k_M}=\sum _{j_1\cdots j_N}{a}_{i_1\cdots i_N{j}_1\cdots j_N}{b}_{j_1\cdots j_N{k}_1\cdots k_M},\end{array}$$

(1)

where $\mathcal{A}{\ast }_N\mathcal{B}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times K_1\times \cdots \times K_M}$.

As a contracted product, the Einstein product has great applications for continuum mechanics [24] and the relativity theory [23]. The associative law of this tensor product is established. On the one hand, the Einstein product ${\ast }_1$ is the standard matrix multiplication. On the other hand, when specifying mode summation, the n-mode product ${\times }_n$ is the Einstein product ${\ast }_1$ A more general definition of contraction can be seen in [25].

In 2013, Navasca et al. [4] introduced the transformation f between the tensor and matrix over real number field. We give the following definition for the transformation f between the tensor and matrix over the quaternion.

Definition 2

(transformation [4]). Define the transformation $f:{\mathbb{T}}_{I_1,I_2,\cdots ,I_N,J_1,J_2,\cdots ,J_N}\left(\mathbb{H}\right)\to {\mathbb{M}}_{I_1·I_2\cdots I_{N-1}·I_N,J_1·J_2\cdots J_{N-1}·J_N}\left(\mathbb{H}\right)$ with $f\left(\mathcal{A}\right)=A$ defined component-wise as

$${\left(\mathcal{A}\right)}_{i_1{i}_2\cdots i_n{j}_1{j}_2\cdots j_n}\stackrel{f}{\to }{\left(A\right)}_{[i_1+{\sum }_{k=2}^N(i_k-1){\prod }_{s=1}^{k-1}{I}_s][j_1+{\sum }_{k=2}^N(j_k-1){\prod }_{s=1}^{k-1}{J}_s]},$$

(2)

where $\mathcal{A}\in {\mathbb{T}}_{I_1,I_2,\dots ,I_N,J_1,J_2,\dots ,J_N}\left(\mathbb{H}\right)$ and $A\in {\mathbb{M}}_{I_1·I_2\cdots I_N,J_1·J_2\cdots J_N}\left(\mathbb{H}\right)$. That is, the element has one-to-one correspondence between the quaternion matrix A and the quaternion tensor $\mathcal{A}.$

Lemma 1.

Let $\mathcal{A}\in {\mathbb{H}}^{I_1\times I_2\times \cdots I_N\times J_1\times J_2\times \cdots \times J_N}$, $\mathcal{B}\in {\mathbb{H}}^{J_1\times J_2\times \cdots \times J_N\times L_1\times L_2\times \cdots \times L_N}$ and f be the map defined in (2). Then the following properties hold:

1.

The map f is a bijection. Moreover, there exists a bijective inverse map $f^{-1}$:

$$\begin{array}{c}\hfill {\mathbb{M}}_{I_1·I_2\cdots I_{N-1}·I_N,J_1·J_2\cdots J_{N-1}·J_N}\left(\mathbb{H}\right)\stackrel{f^{-1}}{\to }{\mathbb{T}}_{I_1,I_2,\cdots ,I_N,J_1,J_2,\cdots ,J_N}\left(\mathbb{H}\right)\end{array}$$

(3)

2.

The map satisfies $f\left(\mathcal{A}{\ast }_N\mathcal{B}\right)=f\left(\mathcal{A}\right)·f\left(\mathcal{B}\right)$, where · refers to the usual matrix multiplication.

As can be seen from the Lemma 1, the Einstein product can be defined by the transformation:

$$\mathcal{A}{\ast }_N\mathcal{B}=f^{-1}\left[f\left(\mathcal{A}{\ast }_N\mathcal{B}\right)\right]=f^{-1}[f\left(\mathcal{A}\right)·f\left(\mathcal{B}\right)].$$

(4)

Consequently, the inverse map $f^{-1}$ satisfies

$$f^{-1}(A·B)=f^{-1}\left(A\right){\ast }_N{f}^{-1}\left(B\right),$$

(5)

where A and B are quaternion matrices with appropriate sizes.

The following lemma appears in [4] over the real number field. In addition, we can extend it to the quaternion algebra by using similar methods.

Lemma 2

([4]). Suppose $(\mathbb{M},·)$ is a group. Let $f:\mathbb{T}\to \mathbb{M}$ be any bijection. Then we can define a group structure on $\mathbb{T}$ by defining

$$\mathcal{A}{\ast }_N\mathcal{B}=f^{-1}[f\left(\mathcal{A}\right)·f\left(\mathcal{B}\right)]$$

for all $\mathcal{A},\mathcal{B}\in \mathbb{T}$. Moreover, the mapping f is an isomorphism.

3. Restricted Singular-Value Decomposition for Three Quaternion Tensors

In this section, we investigate the restricted singular value decomposition of three quaternion tensors $(\mathcal{A},\mathcal{B},\mathcal{C})$ based on the isomorphic group structures and the Einstein product.

De Moor introduced the RSVD for a matrix triplet over real field, and Golub [26] and Zha [27] further developed and discussed by Chu and De Moor [28,29]. Moreover, Chu, De Lathauwer, and De Moor [30] presented the CSD-based QR-type method to compute the RSVD for a real matrix triplet. More recently, He, Wang, and De Moor [31] presented the RSVD for a matrix triplet over the quaternion.

Lemma 3

(RSVD for three quaternion matrices [26,31]). Let $A\in {\mathbb{H}}^{m\times n},B\in {\mathbb{H}}^{m\times p}$ and $C\in {\mathbb{H}}^{q\times n}$ be given. There exist unitary matrices $U\in {\mathbb{H}}^{q\times q}$ and $V\in {\mathbb{H}}^{p\times p}$, and nonsingular matrices $P\in {\mathbb{H}}^{m\times m}$ and $Q\in {\mathbb{H}}^{n\times n}$ such that

$$\begin{array}{c}\hfill P^{*}AQ=S_a,P^{*}BV=S_b,U^{*}CQ=S_c,\end{array}$$

(6)

where

$$\left(\begin{array}{cc}{S}_a& S_b\\ S_c\end{array}\right)=\begin{array}{cccccccccccccc}& & r_1& r_2& r_3& r_4& r_6& & & & r_3& r_4& r_5& \\ \begin{array}{c}{r}_1\\ r_2\\ r_3\\ r_4\\ r_5\\ \\ \\ \\ r_2\\ r_4\\ r_6\end{array}& (& \begin{array}{c}I\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ I\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ I\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ I\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ S_{abc}\\ 0\\ 0\\ \\ 0\\ 0\\ I\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ I\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ 0\end{array}& & \begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ \\ \\ \\ \end{array}& \begin{array}{c}0\\ 0\\ I\\ 0\\ 0\\ 0\\ \\ \\ \\ \\ \end{array}& \begin{array}{c}0\\ 0\\ 0\\ I\\ 0\\ 0\\ \\ \\ \\ \\ \end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ I\\ 0\\ \\ \\ \\ \\ \end{array}& )\end{array},$$

(7)

and $S_{abc}=diag\{{\sigma }_1,\dots ,{\sigma }_{r_4}\}$ is square nonsingular diagonal with positive diagonal elements, ${\sigma }_1,\dots ,{\sigma }_{r_4}$ are defined to be the non-trivial restricted singular values of the matrix triplet $A,B,C.$ Expressions for the integers $r_1,\dots ,r_6$ are the following:

$$\begin{array}{c}\hfill r_1=r\left(\begin{array}{cc}A& B\\ C& 0\end{array}\right)-r\left(B\right)-r\left(C\right),\end{array}$$

(8)

$$\begin{array}{c}\hfill r_2=r(A,B)+r\left(C\right)-r\left(\begin{array}{cc}A& B\\ C& 0\end{array}\right),\end{array}$$

(9)

$$\begin{array}{c}\hfill r_3=r\left(B\right)+r\left(\begin{array}{c}A\\ C\end{array}\right)-r\left(\begin{array}{cc}A& B\\ C& 0\end{array}\right),\end{array}$$

(10)

$$\begin{array}{c}\hfill r_4=r\left(A\right)+r\left(\begin{array}{cc}A& B\\ C& 0\end{array}\right)-r\left(\begin{array}{c}A\\ C\end{array}\right)-r(A,B),\end{array}$$

(11)

$$\begin{array}{c}\hfill r_5=r(A,B)-r\left(A\right),r_6=r\left(\begin{array}{c}A\\ C\end{array}\right)-r\left(A\right),\end{array}$$

(12)

where the symbol $r\left(A\right)$ stands for the rank of the quaternion matrix A.

Now we give the definitions of the unitary quaternion tensor and quaternion tensor inverse.

Definition 3 (unitary quaternion tensor).

A tensor $\mathcal{U}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$ is unitary if $\mathcal{U}{\ast }_N{\mathcal{U}}^{*}={\mathcal{U}}^{*}{\ast }_N\mathcal{U}=\mathcal{I}.$

Definition 4 (inverse of an even order tensor).

A tensor $\mathcal{X}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$ is called the inverse of $\mathcal{A}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$ if it satisfies $\mathcal{A}{\ast }_N\mathcal{X}=\mathcal{X}{\ast }_N\mathcal{A}=\mathcal{I}.$ It is denoted by ${\mathcal{A}}^{-1}.$

Now we give the higher-order RSVD over the quaternion in the following theorem.

Theorem 1.

(higher-order RSVD over the quaternion tensor) Given $\mathcal{A}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N}$, $\mathcal{B}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times K_1\times \cdots \times K_N}$ and $\mathcal{C}\in {\mathbb{H}}^{L_1\times \cdots \times L_N\times J_1\times \cdots \times J_N}$. Then there exist unitary tensors $\mathcal{U}\in {\mathbb{H}}^{L_1\times \cdots \times L_N\times L_1\times \cdots \times L_N}$, $\mathcal{V}\in {\mathbb{H}}^{K_1\times \cdots \times K_N\times K_1\times \cdots \times K_N}$ and invertible tensors $\mathcal{P}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$, $\mathcal{Q}\in {\mathbb{H}}^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N}$ such that

$$\begin{array}{c}\hfill {\mathcal{P}}^{*}{\ast }_N\mathcal{A}{\ast }_N\mathcal{Q}={\mathcal{S}}_{\mathcal{A}},{\mathcal{P}}^{*}{\ast }_N\mathcal{B}{\ast }_N\mathcal{V}={\mathcal{S}}_{\mathcal{B}},{\mathcal{U}}^{*}{\ast }_N\mathcal{C}{\ast }_N\mathcal{Q}={\mathcal{S}}_{\mathcal{C}},\end{array}$$

where the tensors ${\mathcal{S}}_{\mathcal{A}}\in {\mathbb{R}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N}$, ${\mathcal{S}}_{\mathcal{B}}\in {\mathbb{R}}^{I_1\times \cdots \times I_N\times K_1\times \cdots \times K_N}$ and ${\mathcal{S}}_{\mathcal{C}}\in {\mathbb{R}}^{L_1\times \cdots \times L_N\times J_1\times \cdots \times J_N}$ have the following structures

$$\begin{array}{c}\hfill {\left({\mathcal{S}}_{\mathcal{A}}\right)}_{i_1\cdots i_N{j}_1\cdots j_N}=\left\{\begin{array}{c}1,if(i_1\cdots i_N{j}_1\cdots j_N)=(p_1^{a_1}\cdots p_N^{a_1}{q}_1^{a_1}\cdots q_N^{a_1}),\\ {\sigma }_{a_2},if(i_1\cdots i_N{j}_1\cdots j_N)=(p_1^{a_2}\cdots p_N^{a_2}{q}_1^{a_2}\cdots q_N^{a_2}),\\ 0,otherwise,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill {\left({\mathcal{S}}_{\mathcal{B}}\right)}_{i_1\cdots i_N{k}_1\cdots k_N}=\left\{\begin{array}{c}1,if(i_1\cdots i_N{k}_1\cdots k_N)=(h_1^b\cdots h_N^b{w}_1^b\cdots w_N^b),\\ 0,otherwise,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill {\left({\mathcal{S}}_{\mathcal{C}}\right)}_{l_1\cdots l_N{j}_1\cdots j_N}=\left\{\begin{array}{c}1,if(l_1\cdots l_N{j}_1\cdots j_N)=(u_1^{c_1}\cdots u_N^{c_1}{v}_1^{c_1}\cdots v_N^{c_1}),\\ 1,if(l_1\cdots l_N{j}_1\cdots j_N)=(u_1^{c_2}\cdots u_N^{c_2}{v}_1^{c_2}\cdots v_N^{c_2}),\\ 0,otherwise,\end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill a_1\in \{1,\dots ,r_1+r_2+r_3\},a_2\in \{r_1+r_2+r_3+1,\dots ,r_1+r_2+r_3+r_4\},\end{array}$$

$$\begin{array}{c}\hfill b\in \{1,\dots ,r_3+r_4+r_5\},c_1\in \{1,\dots ,r_2\},c_2\in \{r_2+1,\dots ,r_2+r_4+r_6\},\end{array}$$

$$\begin{array}{c}\hfill r_1=r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right)-r\left(f\left(\mathcal{B}\right)\right)-r\left(f\left(\mathcal{C}\right)\right),\end{array}$$

(13)

$$\begin{array}{c}\hfill r_2=r(f\left(\mathcal{A}\right),f\left(\mathcal{B}\right))+r\left(f\left(\mathcal{C}\right)\right)-r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right),\end{array}$$

(14)

$$\begin{array}{c}\hfill r_3=r\left(f\left(\mathcal{B}\right)\right)+r\left(\begin{array}{c}f\left(\mathcal{A}\right)\\ f\left(\mathcal{C}\right)\end{array}\right)-r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right),\end{array}$$

(15)

$$\begin{array}{c}\hfill r_4=r\left(f\left(\mathcal{A}\right)\right)+r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right)-r\left(\begin{array}{c}f\left(\mathcal{A}\right)\\ f\left(\mathcal{C}\right)\end{array}\right)-r(f\left(\mathcal{A}\right),f\left(\mathcal{B}\right)),\end{array}$$

(16)

$$\begin{array}{c}\hfill r_5=r\left(f\left(\mathcal{A}\right),f\left(\mathcal{B}\right)\right)-r\left(f\left(\mathcal{A}\right)\right),r_6=r\left(\begin{array}{c}f\left(\mathcal{A}\right)\\ f\left(\mathcal{C}\right)\end{array}\right)-r\left(f\left(\mathcal{A}\right)\right),\end{array}$$

(17)

${\sigma }_{a_2}$ are the non-trivial restricted singular values of the matrix triplet $f\left(\mathcal{A}\right),f\left(\mathcal{B}\right),f\left(\mathcal{C}\right)$, and f is the transformation in (2). Expressions for the subscripts $(p_1^{a_1}\cdots p_N^{a_1}{q}_1^{a_1}\cdots q_N^{a_1})$, $(p_1^{a_2}\cdots p_N^{a_2}{q}_1^{a_2}\cdots q_N^{a_2})$, $(h_1^b\cdots h_N^b{w}_1^b\cdots w_N^b)$, $(u_1^{c_1}\cdots u_N^{c_1}{v}_1^{c_1}\cdots v_N^{c_1})$ and $(u_1^{c_2}\cdots u_N^{c_2}{v}_1^{c_2}\cdots v_N^{c_2})$ are given in Theorem 2.

Proof. 

Let $A=f\left(\mathcal{A}\right)\in {\mathbb{H}}^{(I_1{I}_2\cdots I_N)\times (J_1{J}_2\cdots J_N)},$$B=f\left(\mathcal{B}\right)\in {\mathbb{H}}^{(I_1{I}_2\cdots I_N)\times (K_1{K}_2\cdots K_N)}$ and

$C=f\left(\mathcal{C}\right)\in {\mathbb{H}}^{(L_1{L}_2\cdots L_N)\times (J_1{J}_2\cdots J_N)}$. Applying the RSVD (Lemma 3) on the matrix triplet $(A,B,C)$, we obtain

$$\begin{array}{c}\hfill P^{*}AQ=S_a,P^{*}BV=S_b,U^{*}CQ=S_c,\end{array}$$

where

$$\left(\begin{array}{cc}{S}_a& S_b\\ S_c\end{array}\right)=\begin{array}{cccccccccccccc}& & r_1& r_2& r_3& r_4& r_6& & & & r_3& r_4& r_5& \\ \begin{array}{c}{r}_1\\ r_2\\ r_3\\ r_4\\ r_5\\ \\ \\ \\ r_2\\ r_4\\ r_6\end{array}& (& \begin{array}{c}I\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ I\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ I\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ I\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ S_{abc}\\ 0\\ 0\\ \\ 0\\ 0\\ I\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ I\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ 0\\ 0\\ 0\\ 0\end{array}& & \begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \\ \\ \\ \\ \end{array}& \begin{array}{c}0\\ 0\\ I\\ 0\\ 0\\ 0\\ \\ \\ \\ \\ \end{array}& \begin{array}{c}0\\ 0\\ 0\\ I\\ 0\\ 0\\ \\ \\ \\ \\ \end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ I\\ 0\\ \\ \\ \\ \\ \end{array}& )\end{array},$$

and $S_{abc}=diag\{{\sigma }_{r_1+r_2+r_3+1},\dots ,{\sigma }_{r_1+r_2+r_3+r_4}\}$ is square nonsingular diagonal with positive diagonal elements, ${\sigma }_{r_1+r_2+r_3+1},\dots ,{\sigma }_{r_1+r_2+r_3+r_4}$ are defined to be the non-trivial restricted singular values of the matrix triplet $(A,B,C),$ the expressions for $r_1,r_2,r_3,r_4,r_5,r_6$ are given by (13)–(17). The matrices $U\in {\mathbb{H}}^{(L_1{L}_2\cdots L_N)\times (L_1{L}_2\cdots L_N)}$ and $V\in {\mathbb{H}}^{(K_1{K}_2\cdots K_N)\times (K_1{K}_2\cdots K_N)}$ are unitary, and $P\in {\mathbb{H}}^{(I_1{I}_2\cdots I_N)\times (I_1{I}_2\cdots I_N)}$ and $Q\in {\mathbb{H}}^{(J_1{J}_2\cdots J_N)\times (J_1{J}_2\cdots J_N)}$ are invertible.

From the property of f in (5) and Lemma 2, we have

$$\begin{array}{c}\hfill f^{-1}\left(S_a\right)=f^{-1}\left(P^{*}AQ\right)=f^{-1}\left(P^{*}\right){\ast }_N\left(f^{-1}\left(A\right)\right){\ast }_N{f}^{-1}\left(Q\right)⟹{\mathcal{P}}^{*}{\ast }_N\mathcal{A}{\ast }_N\mathcal{Q}={\mathcal{S}}_{\mathcal{A}},\end{array}$$

$$\begin{array}{c}\hfill f^{-1}\left(S_b\right)=f^{-1}\left(P^{*}BV\right)=f^{-1}\left(P^{*}\right){\ast }_N\left(f^{-1}\left(B\right)\right){\ast }_N{f}^{-1}\left(V\right)⟹{\mathcal{P}}^{*}{\ast }_N\mathcal{B}{\ast }_N\mathcal{V}={\mathcal{S}}_{\mathcal{B}},\end{array}$$

$$\begin{array}{c}\hfill f^{-1}\left(S_c\right)=f^{-1}\left(U^{*}CQ\right)=f^{-1}\left(U^{*}\right){\ast }_N\left(f^{-1}\left(C\right)\right){\ast }_N{f}^{-1}\left(Q\right)⟹{\mathcal{U}}^{*}{\ast }_N\mathcal{C}{\ast }_N\mathcal{Q}={\mathcal{S}}_{\mathcal{C}},\end{array}$$

where ${\mathcal{P}}^{*}=f^{-1}\left(P^{*}\right),\mathcal{Q}=f^{-1}\left(Q\right)$ are invertible tensors, ${\mathcal{U}}^{*}=f^{-1}\left(U^{*}\right),\mathcal{V}=f^{-1}\left(V\right)$ are unitary tensors, ${\mathcal{S}}_{\mathcal{A}}=f^{-1}\left(S_a\right)$ is a real tensor whose nonzero entries are 1, and the non-trivial restricted singular values of the matrix triplet $\left(f\left(\mathcal{A}\right),f\left(\mathcal{B}\right),f\left(\mathcal{C}\right)\right)$, ${\mathcal{S}}_{\mathcal{B}}=f^{-1}\left(S_b\right)$, and ${\mathcal{S}}_{\mathcal{C}}=f^{-1}\left(S_c\right)$ are real tensors whose nonzero entries are 1.

Now we consider the subscripts of nonzero entries in the tensors ${\mathcal{S}}_{\mathcal{A}}$. Note that the subscripts of 1 and the non-trivial restricted singular values ${\sigma }_{a_2}$ in $S_a$ are $\left(a_1{a}_1\right)$ and $\left(a_2{a}_2\right)$, respectively, where

$$\begin{array}{c}\hfill a_1\in \{1,\dots ,r_1+r_2+r_3\},a_2\in \{r_1+r_2+r_3+1,\dots ,r_1+r_2+r_3+r_4\}.\end{array}$$

Suppose the subscripts of 1 and ${\sigma }_{a_2}$ in the tensor ${\mathcal{S}}_{\mathcal{A}}$ are $(p_1^{a_1}\cdots p_N^{a_1}{q}_1^{a_1}\cdots q_N^{a_1})$ and

$(p_1^{a_2}\cdots p_N^{a_2}{q}_1^{a_2}\cdots q_N^{a_2})$, respectively. Then, we have

$$\begin{array}{c}\hfill {\left({\mathcal{S}}_{\mathcal{A}}\right)}_{i_1\cdots i_N{j}_1\cdots j_N}=\left\{\begin{array}{c}1,if(i_1\cdots i_N{j}_1\cdots j_N)=(p_1^{a_1}\cdots p_N^{a_1}{q}_1^{a_1}\cdots q_N^{a_1}),\\ {\sigma }_{a_2},if(i_1\cdots i_N{j}_1\cdots j_N)=(p_1^{a_2}\cdots p_N^{a_2}{q}_1^{a_2}\cdots q_N^{a_2}),\\ 0,\mathrm{otherwise}.\end{array}\right.\end{array}$$

Similarly, we can give the structures of tensors of ${\mathcal{S}}_{\mathcal{B}}$ and ${\mathcal{S}}_{\mathcal{C}}$.    □

The direct expressions for the subscripts of nonzero entries in the tensors ${\mathcal{S}}_{\mathcal{A}}$, ${\mathcal{S}}_{\mathcal{B}}$, ${\mathcal{S}}_{\mathcal{C}}$ will be given in the following theorem.

Theorem 2.

Consider the above higher-order RSVD for three tensors $\mathcal{A}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N}$, $\mathcal{B}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times K_1\times \cdots \times K_N}$ and $\mathcal{C}\in {\mathbb{H}}^{L_1\times \cdots \times L_N\times J_1\times \cdots \times J_N}$. The expressions for the subscripts $(p_1^{a_1}\cdots p_N^{a_1}{q}_1^{a_1}\cdots q_N^{a_1})$, $(p_1^{a_2}\cdots p_N^{a_2}{q}_1^{a_2}\cdots q_N^{a_2})$, $(h_1^b\cdots h_N^b{w}_1^b\cdots w_N^b)$, $(u_1^{c_1}\cdots u_N^{c_1}{v}_1^{c_1}\cdots v_N^{c_1})$ and $(u_1^{c_2}\cdots u_N^{c_2}{v}_1^{c_2}\cdots v_N^{c_2})$ are given by:

$$\begin{array}{c}\hfill p_t^{a_1}=\left\{\begin{array}{c}⟦\frac{a_1-1}{{\prod }_{s=1}^{N-1}{I}_s}⟧+1,ift=N,\\ ⟦\frac{a_1-1-{\sum }_{k=t+1}^N(p_k^{a_1}-1){\prod }_{s=1}^{k-1}{I}_s}{{\prod }_{s=1}^{t-1}{I}_s}⟧+1,ift=2,\cdots ,N-1,\\ a_1-\sum _{k=2}^N(p_k^{a_1}-1)\prod _{s=1}^{k-1}{I}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill q_t^{a_1}=\left\{\begin{array}{c}⟦\frac{a_1-1}{{\prod }_{s=1}^{N-1}{J}_s}⟧+1,ift=N,\\ ⟦\frac{a_1-1-{\sum }_{k=t+1}^N(q_k^{a_1}-1){\prod }_{s=1}^{k-1}{J}_s}{{\prod }_{s=1}^{t-1}{J}_s}⟧+1,ift=2,\cdots ,N-1,\\ a_1-\sum _{k=2}^N(q_k^{a_1}-1)\prod _{s=1}^{k-1}{J}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill p_t^{a_2}=\left\{\begin{array}{c}⟦\frac{a_2-1}{{\prod }_{s=1}^{N-1}{I}_s}⟧+1,ift=N,\\ ⟦\frac{a_2-1-{\sum }_{k=t+1}^N(p_k^{a_2}-1){\prod }_{s=1}^{k-1}{I}_s}{{\prod }_{s=1}^{t-1}{I}_s}⟧+1,ift=2,\cdots ,N-1,\\ a_2-\sum _{k=2}^N(p_k^{a_2}-1)\prod _{s=1}^{k-1}{I}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill q_t^{a_2}=\left\{\begin{array}{c}⟦\frac{a_2-1}{{\prod }_{s=1}^{N-1}{J}_s}⟧+1,ift=N,\\ ⟦\frac{a_2-1-{\sum }_{k=t+1}^N(q_k^{a_2}-1){\prod }_{s=1}^{k-1}{J}_s}{{\prod }_{s=1}^{t-1}{J}_s}⟧+1,ift=2,\cdots ,N-1,\\ a_2-\sum _{k=2}^N(q_k^{a_2}-1)\prod _{s=1}^{k-1}{J}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill h_t^b=\left\{\begin{array}{c}⟦\frac{r\left(f\right(\mathcal{A}),f(\mathcal{B}\left)\right)-r\left(f\right(\mathcal{B}\left)\right)+b-1}{{\prod }_{s=1}^{N-1}{I}_s}⟧+1,ift=N,\\ ⟦\frac{r(f\left(\mathcal{A}\right),f\left(\mathcal{B}\right))-r\left(f\left(\mathcal{B}\right)\right)+b-1-{\sum }_{k=t+1}^N(h_k^b-1){\prod }_{s=1}^{k-1}{I}_s}{{\prod }_{s=1}^{t-1}{I}_s}⟧+1,ift=2,\cdots ,N-1,\\ r(f\left(\mathcal{A}\right),f\left(\mathcal{B}\right))-r\left(f\left(\mathcal{B}\right)\right)+b-\sum _{k=2}^N(h_k^b-1)\prod _{s=1}^{k-1}{I}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_t^b=\left\{\begin{array}{c}⟦\frac{{\prod }_{m=1}^N{K}_m-r\left(f\left(\mathcal{B}\right)\right)+b-1}{{\prod }_{s=1}^{N-1}{K}_s}⟧+1,ift=N,\\ ⟦\frac{{\prod }_{m=1}^N{K}_m-r\left(f\left(\mathcal{B}\right)\right)+b-1-{\sum }_{k=t+1}^N(w_k^b-1){\prod }_{s=1}^{k-1}{K}_s}{{\prod }_{s=1}^{t-1}{K}_s}⟧+1,ift=2,\cdots ,N-1,\\ \prod _{m=1}^N{K}_m-r\left(f\left(\mathcal{B}\right)\right)+b-\sum _{k=2}^N(w_k^b-1)\prod _{s=1}^{k-1}{K}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill u_t^{c_1}=\left\{\begin{array}{c}⟦\frac{{\prod }_{m=1}^N{L}_m-r\left(f\left(\mathcal{C}\right)\right)+c_1-1}{{\prod }_{s=1}^{N-1}{L}_s}⟧+1,ift=N,\\ ⟦\frac{{\prod }_{m=1}^N{L}_m-r\left(f\left(\mathcal{C}\right)\right)+c_1-1-{\sum }_{k=t+1}^N(u_t^{c_1}-1){\prod }_{s=1}^{k-1}{L}_s}{{\prod }_{s=1}^{t-1}{L}_s}⟧+1,ift=2,\cdots ,N-1,\\ \prod _{m=1}^N{L}_m-r\left(f\left(\mathcal{C}\right)\right)+c_1-\sum _{k=2}^N(u_t^{c_1}-1)\prod _{s=1}^{k-1}{L}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill v_t^{c_1}=\left\{\begin{array}{c}⟦\frac{r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right)-r\left(f\left(\mathcal{B}\right)\right)-r\left(f\left(\mathcal{C}\right)\right)+c_1-1}{{\prod }_{s=1}^{N-1}{J}_s}⟧+1,ift=N,\\ ⟦\frac{r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right)-r\left(f\left(\mathcal{B}\right)\right)-r\left(f\left(\mathcal{C}\right)\right)+c_1-1-{\sum }_{k=t+1}^N(v_k^{c_1}-1){\prod }_{s=1}^{k-1}{J}_s}{{\prod }_{s=1}^{t-1}{J}_s}⟧+1,ift=2,\cdots ,N-1,\\ r\left(\begin{array}{cc}f\left(\mathcal{A}\right)& f\left(\mathcal{B}\right)\\ f\left(\mathcal{C}\right)& 0\end{array}\right)-r\left(f\left(\mathcal{B}\right)\right)-r\left(f\left(\mathcal{C}\right)\right)+c_1-\sum _{k=2}^N(v_k^{c_1}-1)\prod _{s=1}^{k-1}{J}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill u_t^{c_2}=\left\{\begin{array}{c}⟦\frac{{\prod }_{m=1}^N{L}_m-r\left(f\left(\mathcal{C}\right)\right)+c_2-1}{{\prod }_{s=1}^{N-1}{L}_s}⟧+1,ift=N,\\ ⟦\frac{{\prod }_{m=1}^N{L}_m-r\left(f\left(\mathcal{C}\right)\right)+c_2-1-{\sum }_{k=t+1}^N(u_t^{c_2}-1){\prod }_{s=1}^{k-1}{L}_s}{{\prod }_{s=1}^{t-1}{L}_s}⟧+1,ift=2,\cdots ,N-1,\\ \prod _{m=1}^N{L}_m-r\left(f\left(\mathcal{C}\right)\right)+c_2-\sum _{k=2}^N(u_t^{c_2}-1)\prod _{s=1}^{k-1}{L}_s,ift=1,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill v_t^{c_2}=\left\{\begin{array}{c}⟦\frac{r\left(\begin{array}{c}f\left(\mathcal{A}\right)\\ f\left(\mathcal{C}\right)\end{array}\right)-r\left(f\left(\mathcal{C}\right)\right)+c_2-1}{{\prod }_{s=1}^{N-1}{J}_s}⟧+1,ift=N,\\ ⟦\frac{r\left(\begin{array}{c}f\left(\mathcal{A}\right)\\ f\left(\mathcal{C}\right)\end{array}\right)-r\left(f\left(\mathcal{C}\right)\right)+c_2-1-{\sum }_{k=t+1}^N(v_k^{c_2}-1){\prod }_{s=1}^{k-1}{J}_s}{{\prod }_{s=1}^{t-1}{J}_s}⟧+1,ift=2,\cdots ,N-1,\\ r\left(\begin{array}{c}f\left(\mathcal{A}\right)\\ f\left(\mathcal{C}\right)\end{array}\right)-r\left(f\left(\mathcal{C}\right)\right)+c_2-\sum _{k=2}^N(v_k^{c_2}-1)\prod _{s=1}^{k-1}{J}_s,ift=1,\end{array}\right.\end{array}$$

and $⟦a⟧$ is the greatest integer less than or equal to the real number a.

Now we give the following Algorithm 1 for computing the RSVD of three quaternion tensors.    

Algorithm 1: Computing the RSVD of quaternion tensors $\mathcal{A},\mathcal{B},$ and $\mathcal{C}$.

Input: $\mathcal{A}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N},\mathcal{B}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times K_1\times \cdots \times K_N},$$\mathcal{C}\in {\mathbb{H}}^{L_1\times \cdots \times L_N\times J_1\times \cdots \times J_N}$.

Output: $\mathcal{U}\in {\mathbb{H}}^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N},$$\mathcal{V}\in {\mathbb{H}}^{K_1\times \cdots \times K_N\times K_1\times \cdots \times K_N}$, $\mathcal{P}\in {\mathbb{H}}^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$,

${\mathcal{S}}_{\mathcal{A}}\in {\mathbb{R}}^{I_1\times \cdots \times I_N\times J_1\times \cdots \times J_N}$, ${\mathcal{S}}_{\mathcal{B}}\in {\mathbb{R}}^{I_1\times \cdots \times I_N\times K_1\times \cdots \times K_N}$ and ${\mathcal{S}}_{\mathcal{C}}\in {\mathbb{R}}^{L_1\times \cdots \times L_N\times J_1\times \cdots \times J_N}$.

1. $A=f\left(\mathcal{A}\right)$, $B=f\left(\mathcal{B}\right)$, $C=f\left(\mathcal{C}\right)$.

2. Give the RSVD of $A,B,$ and C by the method in [30],

$P^{*}AU=S_A$,

$P^{*}BU=S_B$,

$U^{*}CQ=S_C$,

3. ${\mathcal{S}}_{\mathcal{A}}=f^{-1}\left(S_A\right)$,  ${\mathcal{S}}_{\mathcal{B}}=f^{-1}\left(S_B\right)$, ${\mathcal{S}}_{\mathcal{C}}=f^{-1}\left(S_C\right)$,

$\mathcal{U}=f^{-1}\left(U\right)$,  $\mathcal{V}={bcirc}^{-1}\left(V\right)$,  $\mathcal{P}=f^{-1}\left(P\right),$  $\mathcal{Q}=f^{-1}\left(Q\right)$.

One numerical example is as following.

Example 1.

Consider the higher-order SVD for $2\times 2\times 3\times 2$-quaternion tensor $\mathcal{A}$ defined by

$$\begin{array}{c}\hfill a_{1111}=0,a_{1121}=0,a_{1131}=\frac{\sqrt{2}}{2}\mathbf{j},a_{1112}=\frac{\sqrt{2}}{2}\mathbf{j},a_{1122}=0,a_{1132}=0,\end{array}$$

$$\begin{array}{c}\hfill a_{2111}=-\mathbf{i},a_{2121}=-\mathbf{i},a_{2131}=0,a_{2112}=0,a_{2122}=0,a_{2132}=0,\end{array}$$

$$\begin{array}{c}\hfill a_{1211}=\mathbf{j},a_{1221}=-\mathbf{j},a_{1231}=-\mathbf{j},a_{1212}=\mathbf{j},a_{1222}=0,a_{1232}=0,\end{array}$$

$$\begin{array}{c}\hfill a_{2211}=\frac{\sqrt{2}}{2}(-1+\mathbf{i}+\mathbf{j}-\mathbf{k}),a_{2221}=\frac{\sqrt{2}}{2}(1-\mathbf{i}-\mathbf{j}+\mathbf{k}),a_{2231}=\frac{\sqrt{2}}{2}(-1+\mathbf{i}+\mathbf{j}-\mathbf{k}),\end{array}$$

$$\begin{array}{c}\hfill a_{2212}=\frac{\sqrt{2}}{2}(1-\mathbf{i}-\mathbf{j}+\mathbf{k}),a_{2222}=-1-\mathbf{i}+\mathbf{j}-\mathbf{k},a_{2232}=-1-\mathbf{i}+\mathbf{j}-\mathbf{k}.\end{array}$$

Then we have

$$\begin{array}{c}\hfill \mathcal{A}=\mathcal{U}{\ast }_2{\mathcal{S}}_{\mathcal{A}}{\ast }_2{\mathcal{V}}^{*},\end{array}$$

(18)

where $\mathcal{U}\in {\mathbb{H}}^{2\times 2\times 2\times 2}$ and $\mathcal{V}\in {\mathbb{H}}^{3\times 2\times 3\times 2}$ are unitary tensors and

$$\begin{array}{c}\hfill {\left({\mathcal{S}}_{\mathcal{A}}\right)}_{i_1{i}_2{j}_1{j}_2}=\left\{\begin{array}{c}1,if\left(i_1{i}_2{j}_1{j}_2\right)=\left(1111\right),\\ \sqrt{2},if\left(i_1{i}_2{j}_1{j}_2\right)=\left(2121\right),\\ 2,if\left(i_1{i}_2{j}_1{j}_2\right)=\left(1231\right),\\ 4,if\left(i_1{i}_2{j}_1{j}_2\right)=\left(2212\right),\\ 0,otherwise,\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{U}}_{1111}=\mathbf{i},{\mathcal{U}}_{1121}=0,{\mathcal{U}}_{1112}=0,{\mathcal{U}}_{1122}=0,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{U}}_{2111}=0,{\mathcal{U}}_{2121}=\mathbf{j},{\mathcal{U}}_{2112}=0,{\mathcal{U}}_{2122}=0,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{U}}_{1211}=0,{\mathcal{U}}_{1221}=0,{\mathcal{U}}_{1212}=\mathbf{k},{\mathcal{U}}_{1222}=0,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{U}}_{2211}=0,{\mathcal{U}}_{2221}=0,{\mathcal{U}}_{2212}=0,{\mathcal{U}}_{2222}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}\mathbf{j},\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{1111}^{*}=0,{\mathcal{V}}_{1121}^{*}=0,{\mathcal{V}}_{1131}^{*}=-\frac{\sqrt{2}}{2}\mathbf{k},{\mathcal{V}}_{1112}^{*}=-\frac{\sqrt{2}}{2}\mathbf{k},{\mathcal{V}}_{1122}^{*}=0,{\mathcal{V}}_{1132}^{*}=0,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{2111}^{*}=-\frac{\sqrt{2}}{2}\mathbf{k},,{\mathcal{V}}_{2121}^{*}=-\frac{\sqrt{2}}{2}\mathbf{k},,{\mathcal{V}}_{2131}^{*}=0,{\mathcal{V}}_{2112}^{*}=0,{\mathcal{V}}_{2122}^{*}=0,{\mathcal{V}}_{2132}^{*}=0,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{3111}^{*}=\frac{1}{2}\mathbf{i},{\mathcal{V}}_{3121}^{*}=-\frac{1}{2}\mathbf{i},{\mathcal{V}}_{3131}^{*}=-\frac{1}{2}\mathbf{i},{\mathcal{V}}_{3112}^{*}=\frac{1}{2}\mathbf{i},{\mathcal{V}}_{3122}^{*}=0,{\mathcal{V}}_{3132}^{*}=0,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{1211}^{*}=\frac{1}{4}(\mathbf{i}+\mathbf{j}),{\mathcal{V}}_{1221}^{*}=-\frac{1}{4}(\mathbf{i}+\mathbf{j}),{\mathcal{V}}_{1231}^{*}=\frac{1}{4}(\mathbf{i}+\mathbf{j}),{\mathcal{V}}_{1212}^{*}=-\frac{1}{4}(\mathbf{i}+\mathbf{j}),\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{1222}^{*}=\frac{\sqrt{2}}{4}(\mathbf{j}-\mathbf{k}),{\mathcal{V}}_{1232}^{*}=\frac{\sqrt{2}}{4}(\mathbf{j}-\mathbf{k}),{\mathcal{V}}_{2211}^{*}=\frac{1}{4}(1-\mathbf{k}),{\mathcal{V}}_{2221}^{*}=\frac{1}{4}(-1+\mathbf{k}),\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{2231}^{*}=\frac{1}{4}(1-\mathbf{k}),{\mathcal{V}}_{2212}^{*}=\frac{1}{4}(-1+\mathbf{k}),{\mathcal{V}}_{2222}^{*}=\frac{\sqrt{2}}{4}(\mathbf{j}+\mathbf{k}),{\mathcal{V}}_{2232}^{*}=\frac{\sqrt{2}}{4}(\mathbf{j}+\mathbf{k}),\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{V}}_{3211}^{*}=0,{\mathcal{V}}_{3221}^{*}=0,{\mathcal{V}}_{3231}^{*}=0,{\mathcal{V}}_{3212}^{*}=0,{\mathcal{V}}_{3222}^{*}=\frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4}\mathbf{i},{\mathcal{V}}_{3232}^{*}=-\frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4}\mathbf{i}.\end{array}$$

4. Some Applications

In this section, we give a watermarking scheme for blind color video based on the forth-order RSVD over the quaternion algebra. A fourth-order pure quaternion tensor $\mathcal{A}\in {\mathbb{H}}^{I_1\times I_2\times J_1\times 2}$ can represent a color video with the even frames, where $I_1$ and $I_2$ denote the height and width of each frame, respectively, and $2\ast J_1$ is the frame number of the video.

Moreover, the fourth-order pure quaternion tensor will save more information than the traditional method because of the advantages of quaternions in color image processing. Now we embed three color video watermarks simultaneously into one color video based on RSVD over the quaternion tensor, and extract these three watermarks using two keys. Now we simultaneously insert three color video watermarks into one color video by RSVD on quaternion tensors, and extract the three watermarks with two keys.

$\mathcal{H}\in {\mathbb{H}}^{M_1\times M_2\times N_1\times 2}$ denotes a color host video. $\mathcal{A}\in {\mathbb{H}}^{I_1\times I_2\times J_1\times 2}$, $\mathcal{B}\in {\mathbb{H}}^{I_1\times I_2\times J_1\times 2}$ and $\mathcal{C}\in {\mathbb{H}}^{I_1\times I_2\times J_1\times 2}$ denotes three color video watermarks ($J_1=I_1{I}_2/2$). Now we give the following procedures to plug three watermarks in the host video. Let $G=G_1+G_{2}i+G_{3}j+G4k\in {\mathbb{H}}^{m\times n}$, and $G_i\in R^{m\times n},i=1,2,3,4$. Then G is a pure quaternion matrix when $G_1$ is zero matrix.

The inserting process is as following:

Step 1. 

Decomposition three quaternion tensors $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{C}$ by RSVD,

$${\mathcal{P}}^{*}{\ast }_N\mathcal{A}{\ast }_N\mathcal{Q}={\mathcal{S}}_A,$$

$${\mathcal{P}}^{*}{\ast }_N\mathcal{B}{\ast }_N\mathcal{V}={\mathcal{S}}_B,$$

$${\mathcal{U}}^{*}{\ast }_N\mathcal{C}{\ast }_N\mathcal{Q}={\mathcal{S}}_C,$$

where $\mathcal{P}$ and $\mathcal{U}$ are two keys, which are stored for the process of watermark extraction.

Step 2. 

Transformation under map f:

$$H=f\left(\mathcal{H}\right),P=f\left(\mathcal{H}\right),Q=f\left(\mathcal{Q}\right),U=f\left(\mathcal{U}\right),V=f\left(\mathcal{V}\right),$$

$$A=f\left(\mathcal{A}\right),B=f\left(\mathcal{B}\right),C=f\left(\mathcal{C}\right),$$

$$S_A=f\left({\mathcal{S}}_A\right),S_B=f\left({\mathcal{S}}_B\right),S_C=f\left({\mathcal{S}}_C\right),$$

and

$$PAQ=S_A,PBV=S_B,UCQ=S_C,$$

where $H\in {\mathbb{H}}^{M_1{M}_2\times 2N_1}$ is a pure quaternion matrix.

Step 3. 

Obtaining the principal component of each video:

$$A^w\Leftarrow S_A{Q}^{-1},B^w\Leftarrow S_B{V}^{*},C^w\Leftarrow S_C{Q}^{-1}.$$

Step 4. 

Dividing $H_t,t=2,3,4$ into non-coinciding blocks and the size of the blocks is $m\times n$, where $m\ge \frac{M_1{M}_2}{I_1{I}_2}$, $n\ge \frac{N_1}{J_1}$. $T_{ij}^{\left(t\right)}\in {\mathbb{R}}^{m\times n}$ is the orthogonal transformed part for block position $(i,j)$, $i,j=1,\dots ,m$ of $H_t$, which is saved for the extraction.

Step 5. 

Getting the principal components $A_w$, $B_w$ and $C_w$ in step 3 in the transformed blocks in step 4:

$$T_{11}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{11}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)+\alpha A_1^w,$$

$$T_{12}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{12}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)+\alpha A_2^w,$$

$$T_{21}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{21}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)+\alpha A_3^w,$$

$$T_{22}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{22}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)+\alpha A_4^w,$$

$$T_{11}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{11}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)+\alpha B_1^w,$$

$$T_{12}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{12}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)+\alpha B_2^w,$$

$$T_{21}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{21}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)+\alpha B_3^w,$$

$$T_{22}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{22}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)+\alpha B_4^w,$$

$$T_{11}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{11}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)+\alpha C_1^w,$$

$$T_{12}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{12}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)+\alpha C_2^w,$$

$$T_{21}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{21}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)+\alpha C_3^w,$$

$$T_{22}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)\Leftarrow T_{22}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)+\alpha C_4^w,$$

where $\alpha$ is a scale factor, which can control watermarking strength. In particular, the larger $\alpha$ is, the stronger the robustness of watermark is, when the value of $\alpha$ is confirmed.

Step 6. 

The watermarked matrices $H_2^w$, $H_3^w$ and $H_4^w$ are obtained by the inverse orthogonal transformation, and $H^w=H_1+H_2^{w}i+H_3^{w}j+H_4^{w}k$.

Step 7. 

The inverse map gives the watermarked video

$${\mathcal{H}}^w=f^{-1}\left(H^w\right).$$

Next, the procedure of the extraction process is shown in the following.

Step 1. 

Map the watermarked video into a quaternion matrix

$$H^w=f\left({\mathcal{H}}^w\right).$$

Step 2. 

Split matrices $H_t^w,t=2,3,4$ into blocks ${\widehat{T}}_{i,j}^t$, which has size $m\times n$, $i,j=1,\dots ,m$ of $H_t$. In order to extract the video watermarks, save $T_{ij}^t$,$t=2,3,4,i,j=1,2$.

Step 3. 

The extracted principal components for each video are obtained by the following:

$${\widehat{A}}_1^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{11}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)-T_{11}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{A}}_2^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{12}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)-T_{12}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{A}}_3^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{21}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)-T_{21}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{A}}_4^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{22}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)-T_{22}^{\left(2\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{B}}_1^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{11}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)-T_{11}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{B}}_2^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{12}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)-T_{12}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{B}}_3^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{21}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)-T_{21}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{B}}_4^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{22}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)-T_{22}^{\left(3\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{C}}_1^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{11}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)-T_{11}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{C}}_2^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{12}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)-T_{12}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{C}}_3^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{21}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)-T_{21}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{C}}_4^w\Leftarrow \frac{1}{\alpha }({\widehat{T}}_{22}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)-T_{22}^{\left(4\right)}(1:,I_1{I}_2,1:2J_1)),$$

$${\widehat{A}}^w={\widehat{A}}_1^w+{\widehat{A}}_2^{w}i+{\widehat{A}}_3^{w}j+{\widehat{A}}_4^{w}k,$$

$${\widehat{B}}^w={\widehat{B}}_1^w+{\widehat{B}}_2^{w}i+{\widehat{B}}_3^{w}j+{\widehat{B}}_4^{w}k,$$

$${\widehat{C}}^w={\widehat{C}}_1^w+{\widehat{C}}_2^{w}i+{\widehat{C}}_3^{w}j+{\widehat{C}}_4^{w}k.$$

Step 4. 

The extracted color videos $\widehat{\mathcal{A}}$, $\widehat{\mathcal{B}}$, and $\widehat{\mathcal{C}}$ are obtained by:

$$\widehat{A}=P^{-1}{\widehat{A}}^w,\widehat{B}=P^{-1}{\widehat{B}}^w,\widehat{C}=U^{*}{\widehat{C}}^w,$$

$$\widehat{\mathcal{A}}=f^{-1}\left(\widehat{A}\right),\widehat{\mathcal{B}}=f^{-1}\left(\widehat{B}\right),\widehat{\mathcal{C}}=f^{-1}\left(\widehat{C}\right)$$

Note that we use the quaternion singular value decomposition method in [32] to get the inverse of a nonsingular quaternion matrix.

In the following experiment, our host video is the color video cars with 1024 frames and $64\times 64$ pixels, and watermarks are three color video with the same frame number 256 and the same size $16\times 16$. Taking $\alpha =0.5$, we plug our watermarks into the host video, and extract them from the watermarked host video by the above frameworks based on the discrete wavelet transform (DWT) [33], and results are shown in Figure 1.

Figure 1. Pictures of original host and watermarked host. Pictures in the first, third, and fifth lines are the frames of the original host video, and pictures in the second, fourth, and sixth lines are the frames of the watermarked video.

In Figure 1, we show some frames of original host video in the first, third and fifth lines, and the frames of the watermarked video in the second, fourth, and sixth lines. It can be seen visually that the original images and the watermarked images at the same number of frames are very similar. Therefore, we can conclude that the video watermarks are invisible in the watermarked video.

Next, three extracted watermark videos are separately shown in Figure 2, Figure 3 and Figure 4.

Figure 2. Pictures of watermark 1 and extracted watermark 1. Pictures in the first, third, and fifth lines are the frames in the original watermark video 1, and pictures in the second, fourth, and sixth lines are the frames in the extracted watermark video 1.

Figure 3. Pictures of watermark 2 and extracted watermark 2. Pictures in the first, third, and fifth lines are the frames in the original watermark video 2, and pictures in the second, fourth, and sixth lines are the frames in the extracted watermark video 2.

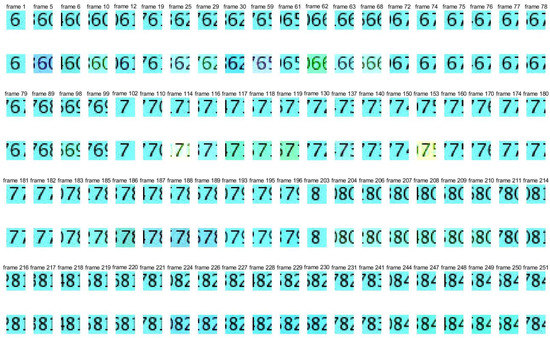
Figure 4. Pictures of watermark 3 and extracted watermark 3. Pictures in the first, third, and fifth lines are the frames in the original watermark video 3, and pictures in the second, fourth, and sixth lines are the frames in the extracted watermark video 3.

From Figure 2, Figure 3 and Figure 4, it can be seen that the quality of the extracted watermarks is very good, especially watermark 2, which is of particularly high quality.

The blind color video watermark processing framework based on RSVD over the quaternion tensor processes three color video waters simultaneously. In addition, only two keys are needed for the extraction process. Furthermore, it can be seen that the the reliable security of proposed blind color video watermarking scheme has been shown through numerical experiments.

5. Conclusions

In this paper, we have derived the restricted singular value decomposition for three quaternion tensors $(\mathcal{A},\mathcal{B},\mathcal{C})$ based on the isomorphic group structures and the Einstein product. As an application of RSVD, we present a blind color video watermarking scheme under the forth-order RSVD over the quaternion algebra. We plug three color video watermarks simultaneously into one host by the blind color video watermarking scheme, and extract the three watermarks by using two keys. Finally, numerical experiments show that the proposed blind color video watermarking scheme has reliable security. In the future, implementation algorithms based on quaternion tensors need to receive more attention. Due to the computational difficulty of quaternion and the high dimensionality of tensors, the design of a fast and effective quaternion tensor algorithm is a very meaningful research topic. This paper and future research content will provide new ideas and bring great improvements to video signal processing and high-dimensional signal processing.