A Fast Novel Recursive Algorithm for Computing the Inverse of a Generalized Vandermonde Matrix

Abstract

The main research object of this paper is to present a systematic computational procedure for computing the inverse of a generalized Vandermonde matrix. Short and rigorous proofs for the formulas of the determinant and the inverse of a generalized Vandermonde matrix are proposed. The computational cost of this method is $O\left(n^2\right)$. The proposed method can be used efficiently for hand calculation as well as for computer programming. Some examples are given for the sake of illustration. Furthermore, we present a simulation study to compare the time spent to calculate the inverse using the proposed algorithm and the inverse function in Maple.

1. Introduction and Objectives

Matrices arising in practice frequently have a distinguishing structure. The Vandermonde matrix (alternant matrix) is one of such matrices and appears in mathematics, engineering, and natural science. For example, they appear in the fields of statistics, in the derivation of explicit Rung-Kutta (ERK) and explicit Rung-Kutta-Nystrom (ERKN) methods in numerical analysis—see for instance [1,2,3]—and in the computing the inverse of a companion matrix [4].

In this paper, $\mathbf{x}$ denotes the following vector: $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {\mathbb{C}}^n,n\in \mathbb{N}$. We define a generalized Vandermonde matrix with distinct nodes $x_1,x_2,\dots ,x_n$, denoted by $V_{n,p}\left(\mathbf{x}\right),n\ge 1,p\in \mathbb{R}$ (for short, $V_{n,p}$) as $V_{n,p}={\left[x_j^{p+i-1}\right]}_{i,j=1}^n$. The classical Vandermonde matrix is a special case of the generalized Vandermonde $V_{n,p}$ when $p=0$. Some authors call $V_{n,p}^T$, rather than $V_{n,p}$, a Vandermonde matrix. Throughout this work, we will focus on the determinant and the inverse of the Vandermonde matrix $V_{n,p}$. The explicit formula of the determinant for the Vandermonde matrix, ${△}_{n,p}\equiv det\left(V_{n,p}\right)$, is given by the following compact formulas:

$${△}_{n,p}=\prod _{\ell =1}^n{x}_{\ell }^p\prod _{1\le j<i\le n}(x_i-x_j)=x_1^p\prod _{i=2}^n{x}_i^p\prod _{j=1}^{i-1}(x_i-x_j).$$

(1)

From (1), we see that ${△}_{n,p}\ne 0$, as long as $x_i\ne x_j$ for $i\ne j$. Furthermore, the determinant of the classical Vandermonde matrix is given by ${△}_{n,0}$, see [5]. In recent decades, there have been many fruitful research papers for computing the inverse of the classical Vandermonde matrix using different approaches. The interested reader may refer to [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In an article by El Mikkawy [21], an explicit formula for the inverse of a generalized Vandermonde matrix was given, which was proved from the inverse of a classical Vandermonde matrix, while, in this article, we provide another proof for that formula. However, what distinguishes the method in the current paper is the possibility of calculating the inverse of the Vandermonde matrix $V_{n,p}$ via hand calculation and also via computer programming with a computational cost of $O\left(n^2\right)$. Elementary symmetric polynomial (ESP) is a basic tool in computing the inverse of the Vandermonde matrix $V_{n,p}$, see for instance [21,22,23,24].

The current paper is organized as follows: In Section 2, we introduce a very simple proof for the determinant formula (1). Section 3 is mainly devoted to a new easy proof for the well-known explicit formula of the inverse of the Vandermonde matrix $V_{n,p}$. In Section 4, a recursive computational algorithm for computing the inverse of the Vandermonde matrix $V_{n,p}$ is presented. Section 5 focuses on a simulation study and some illustrative examples.

Symmetric polynomials appear in many fields such as representation theory [25] and combinatorics [26,27]. We introduce some basic definitions, notations, and well-known results which we will use in sequel and for further knowledge see, for instance [21,23,28,29].

Definition 1.

For a positive integer n, the i-th elementary symmetric polynomial (ESP) in n variables $x_1,x_2,\dots ,x_n$, denoted by ${\mathbf{e}}_i^{\left(n\right)}\left(\mathbf{x}\right)$ is defined by

$${\mathbf{e}}_i^{\left(n\right)}={\mathbf{e}}_i^{\left(n\right)}\left(\mathbf{x}\right)=\left\{\begin{array}{cc}0& \mathrm{if}\left(i>n\mathrm{or}i<0\right),\hfill \\ 1& \mathrm{if}i=0,\hfill \\ {\displaystyle \sum _{1\le r_1<r_2<\cdots <r_i\le n}}\prod _{\ell =1}^i{x}_{r_{\ell }}& \mathrm{if}i=1,2,\dots ,n.\hfill \end{array}\right.$$

(2)

It is worth noting that each ${\mathbf{e}}_i^{\left(n\right)}$ is a summation of $\left(\genfrac{}{}{0pt}{}{n}{i}\right)$ terms and is a homogeneous polynomial of degree i. The generating function $E\left(t\right)$ for the ESP ${\mathbf{e}}_i^{\left(n\right)}$ is given by

$$E\left(t\right)=\prod _{\ell =1}^n(1+x_{\ell }t)=\sum _{i=0}^n{\mathbf{e}}_i^{\left(n\right)}\left(\mathbf{x}\right)t^i.$$

(3)

From (3), we see that the ESP ${\mathbf{e}}_i^{\left(n\right)}$ satisfies the recurrence relation

$${\mathbf{e}}_i^{\left(n\right)}\left(\mathbf{x}\right)={\mathbf{e}}_i^{(n-1)}(x_1,x_2,\dots ,x_{n-1})+x_n{\mathbf{e}}_{i-1}^{(n-1)}(x_1,x_2,\dots ,x_{n-1}).$$

(4)

Due to symmetry, we see that the recurrence relation (4) can be written as

$$\begin{array}{c}\hfill {\mathbf{e}}_i^{\left(n\right)}\left(\mathbf{x}\right)={\mathbf{e}}_i^{(n-1)}\left({\widehat{\mathbf{x}}}_j\right)+x_j{\mathbf{e}}_{i-1}^{(n-1)}\left({\widehat{\mathbf{x}}}_j\right),\end{array}$$

(5)

for any $x_j,j=1,2,\dots ,n$, the notation ${\widehat{\mathbf{x}}}_j$ denotes the n − tuple where the component $x_j$ is absent.

Differentiating both sides of (5) partially with respect to $x_j$, we obtain the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\partial {\mathbf{e}}_i^{\left(n\right)}\left(\mathbf{x}\right)}{\partial x_j}={\mathbf{e}}_{i,j}^{\left(n\right)}\left(\mathbf{x}\right)& ={\mathbf{e}}_{i-1}^{(n-1)}\left({\widehat{\mathbf{x}}}_j\right)={\left.{\mathbf{e}}_{i-1}^{\left(n\right)}\left(\mathbf{x}\right)\right|}_{x_j=0}.\hfill \end{array}\end{array}$$

(6)

Also, by differentiating both sides of (3) partially with respect to $x_j$, we obtain

$${\mathbf{e}}_{i,j}^{\left(n\right)}\left(\mathbf{x}\right)={\mathbf{e}}_{i-1}^{\left(n\right)}\left(\mathbf{x}\right)-x_j{\mathbf{e}}_{i-1,j}^{\left(n\right)}\left(\mathbf{x}\right).$$

(7)

The following result, whose proof is given in [29], is an immediate consequence of (7) by repeated applications.

Lemma 1.

Let n be a positive integer and let ${\mathbf{e}}_i^{\left(n\right)}$ be the i − th ESP in $x_1,x_2,\dots ,x_n$. Then,

$${\mathbf{e}}_{i,j}^{\left(n\right)}\left(\mathbf{x}\right)=\sum _{\ell =1}^i{(-1)}^{\ell -1}{\mathbf{e}}_{i-\ell }^{\left(n\right)}\left(\mathbf{x}\right)x_j^{\ell -1},$$

(8)

for all $i,j=1,2,\dots ,n$.

Throughout this paper, let $f\left(x\right)$ be a monic polynomial of degree n with n distinct linear factors of the following form:

$$f\left(x\right)=\prod _{\ell =1}^n(x-x_{\ell }).$$

(9)

Furthermore, let $f_i\left(x\right),$ and $d_i,i=1,2,\dots ,n$ be defined by

$$f_i\left(x\right)=\prod _{\begin{array}{c}\ell =1\\ \ell \ne i\end{array}}^n(x-x_{\ell }),$$

(10)

and

$$d_i=x_i^p{f}_i\left(x_i\right)=x_i^p\prod _{\begin{array}{c}\ell =1\\ \ell \ne i\end{array}}^n(x_i-x_{\ell })\ne 0.$$

(11)

At this point it should be noted that the polynomials $f\left(x\right)$ and $f_i\left(x\right),i=1,2,\dots ,n$ in (9) and (10) can be written in terms of ESPs as follows:

$$f\left(x\right)=\sum _{\ell =0}^n{(-1)}^{n-\ell }{\mathbf{e}}_{n-\ell }^{\left(n\right)}\left(\mathbf{x}\right)x^{\ell },$$

(12)

and

$$f_i\left(x\right)=\sum _{\ell =1}^n{(-1)}^{n-\ell }{\mathbf{e}}_{n-\ell +1,i}^{\left(n\right)}\left(\mathbf{x}\right)x^{\ell -1},$$

(13)

having used (2) and (6), respectively. From (10), we see that

$$f_i\left(x_j\right)=0,\mathrm{if}j\ne i.$$

(14)

2. The Vandermonde Matrix ${\mathit{V}}_{\mathit{n},\mathit{p}}$ Determinant Formula—A Simple Proof

In this section, we provide a very simple proof for the determinant of the Vandermonde matrix $V_{n,p}$ that is given by the Formula (1).

Theorem 1.

Consider the generalized Vandermonde matrix $V_{n,p}$ with nodes $x_1,x_2,\dots ,x_n$. Then, the determinant, ${△}_{n,p}=det\left(V_{n,p}\right)$, is given by the Formula (1).

Proof. 

Consider the monic polynomial $\mathbf{h}\left(t\right)$ of degree $n-1$ defined by the n-th order determinant

$$\mathbf{h}\left(t\right)=\left|\begin{array}{cccccc}{x}_1^p& x_2^p& x_3^p& \cdots & x_{n-1}^p& 1\\ x_1^{p+1}& x_2^{p+1}& x_3^{p+1}& \cdots & x_{n-1}^{p+1}& t\\ x_1^{p+2}& x_2^{p+2}& x_3^{p+2}& \cdots & x_{n-1}^{p+2}& t^2\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ x_1^{p+n-2}& x_2^{p+n-2}& x_3^{p+n-2}& \cdots & x_{n-1}^{p+n-2}& t^{n-2}\\ x_1^{p+n-1}& x_2^{p+n-1}& x_3^{p+n-1}& \cdots & x_{n-1}^{p+n-1}& t^{n-1}\end{array}\right|.$$

(15)

We have $\mathbf{h}\left(x_i\right)=0$ for all $i=1,2,\dots ,n-1$. Therefore, we may write $\mathbf{h}\left(t\right)$ in the following form:

$$\mathbf{h}\left(t\right)=K\prod _{\ell =1}^{n-1}(t-x_{\ell }),$$

(16)

where K is a constant to be determined. Expanding $\mathbf{h}\left(t\right)$ in (15) in terms of its last column, we see that the coefficient of $t^{n-1}$ is ${△}_{n-1,p}$. Hence, $K={△}_{n-1,p}$. Consequently, we obtain

$$\mathbf{h}\left(t\right)={△}_{n-1,p}\prod _{\ell =1}^{n-1}(t-x_{\ell }).$$

(17)

Since $x_n^p\mathbf{h}\left(x_n\right)={△}_{n,p}$, from (17), we obtain

$${△}_{n,p}=x_n^p{△}_{n-1,p}\prod _{\ell =1}^{n-1}(x_n-x_{\ell })=\left(\prod _{i=n}^n{x}_i^p\prod _{\ell =1}^{i-1}(x_i-x_{\ell })\right){△}_{n-1,p}.$$

(18)

Repeated applications of (18) yields

$$\begin{array}{cc}\hfill {△}_{n,p}& =\left(\prod _{i=n-1}^n{x}_i^p\prod _{\ell =1}^{i-1}(x_i-x_{\ell })\right){△}_{n-2,p}\hfill \\ \hfill & =\left(\prod _{i=n-2}^n{x}_i^p\prod _{\ell =1}^{i-1}(x_i-x_{\ell })\right){△}_{n-3,p}\hfill \\ \hfill & =\cdots =\left(\prod _{i=2}^n{x}_i^p\prod _{\ell =1}^{i-1}(x_i-x_{\ell })\right){△}_{1,p}.\hfill \end{array}$$

Since ${△}_{1,p}=x_1^p$, the result follows. This completes the proof.    □

The importance of the determinant of the Vandermonde matrix $V_{n,p}$ appears in many fields of mathematics. For example, in linear algebra it can be used to prove that the eigenvectors corresponding to different eigenvalues are linearly independent, see [30].

3. Inversion of the Vandermonde Matrix ${\mathit{V}}_{\mathit{n},\mathit{p}}$—A New Easy Method for the Derivation

In this section, we are mainly concerned with introducing a simple proof for the inverse of the Vandermonde matrix $V_{n,p}$ with distinct nodes. For convenience of the reader, we state the following result.

Theorem 2

([21]). Consider the Vandermonde matrix $V_{n,p}$ with n distinct nodes $x_1,x_2,\dots ,x_n$. Then, $W_{n,p}=V_{n,p}^{-1}={\left[w_{ij}\right]}_{i,j=1}^n$, where

$$w_{ij}=\frac{{(-1)}^{n-j}{\mathbf{e}}_{n-j+1,i}^{\left(n\right)}\left(\mathbf{x}\right)}{d_i},$$

(19)

for all $i,j=1,2,\dots ,n$, where ${\mathbf{e}}_{n-j+1,i}^{\left(n\right)}\left(\mathbf{x}\right)$ and $d_i$ are defined by (8) and (11), respectively.

Proof. 

By (10) and (11), define the functions $g_i\left(x\right)$ for $i=1,2,\dots ,n$ as follows:

$$g_i\left(x\right)=\frac{x_i^p{f}_i\left(x\right)}{d_i}.$$

(20)

Consequently using (11) and (14), we have $g_i\left(x_j\right)={\delta }_{ij}=\left\{\begin{array}{cc}1,& i=j\hfill \\ 0,& i\ne j\hfill \end{array}\right.$. Therefore, by (13) we may write

$${\delta }_{ij}=\frac{{\sum }_{\ell =1}^n{(-1)}^{n-\ell }{\mathbf{e}}_{n-\ell +1,i}^{\left(n\right)}\left(\mathbf{x}\right)x_j^{p+\ell -1}}{d_i}.$$

(21)

Let

$$W_{n,p}={\left[\frac{{(-1)}^{n-i}{\mathbf{e}}_{n-j+1,i}^{\left(n\right)}\left(\mathbf{x}\right)}{d_i}\right]}_{i,j=1}^n.$$

(22)

Since $I_n={\left[{\delta }_{ij}\right]}_{i,j=1}^n$, then from (21), we obtain the matrix representation $I_n=W_{n,p}{V}_{n,p}$. Hence, $W_{n,p}=V_{n,p}^{-1}$. This completes the proof.    □

Notice that the denominators $d_i$ in any row of $W_{n,p}=V_{n,p}^{-1}$ are the same.

4. A Recursive Computational Algorithm for Inverting the Vandermonde Matrix ${\mathit{V}}_{\mathit{n},\mathit{p}}$

The main goal in the present section is to construct a systematic computational method for computing the inverse of the Vandermonde matrix. For this purpose it is convenient to consider the polynomials $f\left(x\right)$ and $f_i\left(x\right),i=1,2,\dots ,n$ defined in (9) and (10), respectively. Additionally, let

$$f\left(x\right)=\sum _{j=0}^n{a}_{n-j}{x}^j,$$

(23)

and

$$f_i\left(x\right)=\sum _{j=1}^n{b}_j^{\left(i\right)}{x}^{j-1},i=1,2,\dots ,n.$$

(24)

From (12) and (13), we obtain

$$a_j={(-1)}^j{\mathbf{e}}_j^{\left(n\right)}(x_1,x_2,\dots ,x_n),j=0,1,2,\dots ,n,$$

(25)

and

$$b_j^{\left(i\right)}={(-1)}^{n-j}{\mathbf{e}}_{n-j+1,i}^{\left(n\right)}\left(\mathbf{x}\right),i,j=1,2,\dots ,n.$$

(26)

It is time to give the following results.

Lemma 2.

Consider the monic polynomials $f\left(x\right)$ and $f_i\left(x\right),i=1,2,\dots ,n$ defined by (9) and (10), respectively. Then, for all $i=1,2,\dots ,n$, we have

$$d_i=x_i^p{f}_i\left(x_i\right)=\sum _{j=1}^{n}j{a}_{n-j}{x}_i^{p+j-1}.$$

(27)

Proof. 

Using (9) and (10), we see that $f\left(x\right)=(x-x_i)f_i\left(x\right)$. Therefore, differentiating both sides with respect to x we obtain $f^{\prime }\left(x\right)=(x-x_i)f_i^{\prime }\left(x\right)+f_i\left(x\right)$. Hence, $x_i^p{f}^{\prime }\left(x_i\right)=x_i^p{f}_i\left(x_i\right)=d_i={\sum }_{j=1}^{n}j{a}_{n-j}{x}_i^{p+j-1},i=1,2,\dots ,n$. This completes the proof.    □

Lemma 3.

Let n be a positive integer and let ${\mathbf{e}}_i^{\left(n\right)}$ be the i-th ESP in $x_1,x_2,\dots ,x_n$. Then, ${\mathbf{e}}_{i,j}^{\left(n\right)}$ satisfies

$${(-1)}^{n-j}{\mathbf{e}}_{n-j+1,i}^{\left(n\right)}=\sum _{\ell =0}^{n-j}{a}_{\ell }{x}_i^{n-j-\ell },$$

(28)

for all $i,j=1,2,\dots ,n$.

Proof. 

Following Lemma 1, we obtain

$$\begin{array}{cc}\hfill {(-1)}^{n-j}{\mathbf{e}}_{n-j+1,i}^{\left(n\right)}\left(\mathbf{x}\right)& ={(-1)}^{n-j}\sum _{\ell =1}^{n-j+1}{(-1)}^{\ell -1}{\mathbf{e}}_{n-j-\ell +1}^{\left(n\right)}\left(\mathbf{x}\right)x_i^{\ell -1}\hfill \\ \hfill & =\sum _{\ell =1}^{n-j+1}{(-1)}^{n-j-\ell +1}{\mathbf{e}}_{n-j-\ell +1}^{\left(n\right)}\left(\mathbf{x}\right)x_i^{\ell -1}\hfill \\ \hfill & =\sum _{\ell =0}^{n-j}{(-1)}^{\ell }{\mathbf{e}}_{\ell }^{\left(n\right)}\left(\mathbf{x}\right)x_i^{n-j-\ell }=\sum _{\ell =0}^{n-j}{a}_{\ell }{x}_i^{n-j-\ell },\hfill \end{array}$$

having used (25). This completes the proof.    □

We may now formulate the following result.

Theorem 3.

Consider the Vandermonde matrix $V_{n,p}$ with n distinct nodes $x_1,x_2,\dots ,x_n$. Then, we have $W_{n,p}=V_{n,p}^{-1}={\left[w_{ij}\right]}_{i,j=1}^n$, where

$$w_{ij}=\frac{N_{ij}}{d_i}=\frac{{\sum }_{\ell =0}^{n-j}{a}_{\ell }{x}_i^{n-j-\ell }}{{\sum }_{\ell =1}^n\ell a_{n-\ell }{x}_i^{p+\ell -1}}.$$

(29)

Proof. 

Using Theorem 2 yields $N_{ij}={(-1)}^{n-j}{\mathbf{e}}_{n-j+1,i}^{\left(n\right)}\left(\mathbf{x}\right)=b_j^{\left(i\right)}$ (in favor of (26)). Applying Lemmas 1–3, respectively, the required result follows.    □

According to Lemma 1 in [31], we can deduce the following result for a particular case of the Vandermonde matrix $V_{n,p}\left(x_1,x_2,\dots ,x_{\frac{n}{2}},-x_1,-x_2,\dots ,-x_{\frac{n}{2}}\right)$.

Corollary 1.

Consider the Vandermonde matrix $V_{n,p}$ with an even n distinct nodes $x_1,x_2,\dots ,x_{\frac{n}{2}},-x_1,-x_2,\dots ,-x_{\frac{n}{2}}$. Then, we have $W_{n,p}=V_{n,p}^{-1}={\left[w_{ij}\right]}_{i,j=1}^n$, where

$$w_{ij}=\frac{N_{ij}}{d_i}=\frac{{\displaystyle \sum _{\begin{array}{c}\ell =0\\ \ell \equiv 0\left(\mathrm{mod}2\right)\end{array}}^{n-j}}{a}_{\ell }{x}_i^{n-j-\ell }}{{\displaystyle \sum _{\begin{array}{c}\ell =2\\ \ell \equiv 0\left(\mathrm{mod}2\right)\end{array}}^n}\ell a_{n-\ell }{x}_i^{p+\ell -1}},$$

(30)

with

$$a_{\ell }=\left\{\begin{array}{cc}{(-1)}^{\frac{3\ell }{2}}{\mathbf{e}}_{\frac{\ell }{2}}^{\left(\frac{n}{2}\right)}\left(x_1^2,x_2^2,\dots ,x_{\frac{n}{2}}^2\right)& ,\ell \equiv 0\left(\mathrm{mod}2\right),\hfill \\ & \\ 0& ,\ell \equiv 1\left(\mathrm{mod}2\right).\hfill \end{array}\right.$$

(31)

Following Lemma 2 in [31], we can deduce the following result for a particular case of the classical Vandermonde matrix $V_{n,0}\left(x_1,x_2,\dots ,x_{\frac{n-1}{2}},0,-x_1,-x_2,\dots ,-x_{\frac{n-1}{2}}\right)$ with the first row inputs as ones.

Corollary 2.

Consider the classical Vandermonde matrix $V_{n,0}$ with an odd n distinct nodes $x_1,x_2,\dots ,x_{\frac{n-1}{2}},0,-x_1,-x_2,\dots ,-x_{\frac{n-1}{2}}$. Then, we have $W_{n,0}=V_{n,0}^{-1}={\left[w_{ij}\right]}_{i,j=1}^n$, where

$$w_{ij}=\frac{N_{ij}}{d_i}=\frac{{\displaystyle \sum _{\begin{array}{c}\ell =0\\ \ell \equiv 0\left(\mathrm{mod}2\right)\end{array}}^{n-j}}{a}_{\ell }{x}_i^{n-j-\ell }}{{\displaystyle \sum _{\begin{array}{c}\ell =2\\ \ell \equiv 0\left(\mathrm{mod}2\right)\end{array}}^n}\ell a_{n-\ell }{x}_i^{\ell -1}},$$

(32)

with

$$a_{\ell }=\left\{\begin{array}{cc}{(-1)}^{\frac{3\ell }{2}}{\mathbf{e}}_{\frac{\ell }{2}}^{\left(\frac{n-1}{2}\right)}\left(x_1^2,x_2^2,\dots ,x_{\frac{n-1}{2}}^2\right)& ,\ell \equiv 0\left(\mathrm{mod}2\right),\hfill \\ & \\ 0& ,\ell \equiv 1\left(\mathrm{mod}2\right).\hfill \end{array}\right.$$

(33)

The following result gives a recurrence relation for the numerator of the formula (29).

Lemma 4.

Let n be a positive integer, for $i=1,2,\dots ,n$ and $j=n-1,n-2,\dots ,1$. The numerator of (29) satisfies the following recurrence relation

$$N_{ij}=x_i{N}_{i(j+1)}+a_{n-j},$$

(34)

with $N_{in}=1$.

Proof. 

Following the numerator of (29), we have

$$\begin{array}{cc}\hfill x_i{N}_{i(j+1)}+a_{n-j}& =x_i\sum _{\ell =0}^{n-j-1}{a}_{\ell }{x}_i^{n-j-\ell -1}+a_{n-j}\hfill \\ \hfill & =\sum _{\ell =j+1}^n{a}_{\ell -j-1}{x}_i^{n-\ell +1}+a_{n-j}\hfill \\ \hfill & =\sum _{\ell =j}^{n-1}{a}_{\ell -j}{x}_i^{n-\ell }+a_{n-j}\hfill \\ \hfill & =\sum _{\ell =j}^n{a}_{\ell -j}{x}_i^{n-\ell }=\sum _{\ell =0}^{n-j}{a}_{\ell }{x}_i^{n-j-\ell }=N_{ij}.\hfill \end{array}$$

This completes the proof.    □

Remark 1.

We can easily observe that

• Using matrix representation, we see that Lemma 2 together with Lemma 3 introduce a very simple, direct proof and generalizes Theorem 2.1 in [17], which can be written as $V_{n,p}^{-1}={\mathsf{\Omega }}_{n,p}A$, where

  $${\left({\mathsf{\Omega }}_{n,p}\right)}_{ij}=\frac{x_i^{n-j}}{d_i}\mathit{and}{\left(A\right)}_{ij}=\left\{\begin{array}{cc}{a}_{i-j},& \mathrm{if}i\ge j\hfill \\ & \\ 0,& \mathrm{if}i<j\hfill \end{array}\right.,$$

  for $i,j=1,2,\dots ,n$. The relation $V_{n,p}^{-1}={\mathsf{\Omega }}_{n,p}A$ enables us to give another proof that $N_{ij}$ in Theorem 3 satisfies $N_{ij}={\sum }_{\ell =0}^{n-j}{a}_{\ell }{x}_i^{n-j-\ell }$.
• Following [32], we obtain $V_{n,0}^{-1}=UL$, where

  $$\begin{array}{cc}\hfill {\left(L\right)}_{ij}& =\left\{\begin{array}{cc}{(-1)}^{i-j}{\mathbf{e}}_{i-j}^{(i-1)}(x_1,x_2,\dots ,x_{i-1})& \mathit{if}i\ge j\hfill \\ & \\ 0& \mathit{if}i<j\hfill \end{array}\right.\hfill \\ \hfill {\left(U\right)}_{ij}& =\left\{\begin{array}{cc}\frac{1}{{\prod }_{\begin{array}{c}\ell =1\\ \ell \ne i\end{array}}^j(x_i-x_{\ell })}& \mathit{if}i\le j\hfill \\ & \\ 0& \mathit{if}i>j\hfill \end{array}\right.,\hfill \end{array}$$

  for $i,j=1,2,\dots ,n$, see also Theorem 2.1 in [13].
• Since $f_i\left(x\right)=f\left(x\right)÷(x-x_i),i=1,2,\dots ,n$, and applying the Horner’s scheme for synthetic division, we obtain

  $$\begin{array}{ccccccc}{x}_i& a_0=1& a_1& a_2& \cdots & a_{n-1}& a_n\\ & & x_i{N}_{in}& x_i{N}_{i(n-1)}& \cdots & x_i{N}_{i2}& x_i{N}_{i1}\\ & a_0=N_{in}& N_{i(n-1)}& N_{i(n-2)}& \cdots & N_{i1}& r_i=a_n+x_i{N}_{i1}\end{array}$$
• The denominators $d_i,i=1,2,\dots ,n$ can be computed recursively as follows

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill z_0& =n{a}_0=n,\hfill \\ \hfill z_j& =(n-j)a_j+x_i{z}_{j-1},\hfill \end{array}\end{array}$$

  (35)

  for $j=1,2,\dots ,n-1$. Meanwhile, $d_i=z_{n-1}{x}_i^p$. In conclusion, the rows of $W_{n,p}=V_{n,p}^{-1}$ can be computed recursively using (34) and (35). This is always a good habit in computation.
• For $i=1,2,\dots ,n$, $d_i=x_i^p{f}_i\left(x_i\right)$ can also be computed using the recurrence

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill y_0& =1,\hfill \\ \hfill y_{\ell }& =x_i{y}_{\ell -1}+N_{i(n-\ell )},\hfill \end{array}\end{array}$$

  (36)

  for $\ell =1,2,\dots ,n-1$. Hence, $d_i=y_{n-1}{x}_i^p$.

By means of the above discussion and results, we are now able to present a systematic computational algorithm for inverting the Vandermonde matrix $V_{n,p}$.

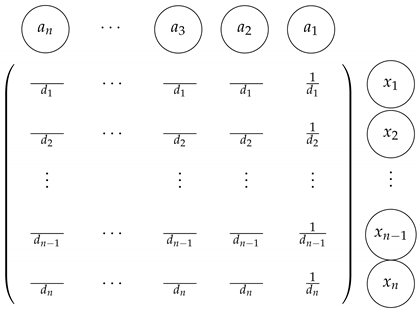
Algorithm 1 A recursive algorithm for inverting $V_{n,p}$

Consider the Vandermonde matrix $V_{n,p}$ with n distinct nodes $x_1,x_2,\dots ,x_n$ (real or complex). Let $W_{n,p}=V_{n,p}^{-1}=\left[C_1{C}_2\cdots C_n\right]$, where $C_j$ is the j-th column in $W_{n,p}=V_{n,p}^{-1}$. To compute the inverse $W_{n,p}=V_{n,p}^{-1}$, we may proceed as follows:

INPUT: The nodes $x_1,x_2,\dots ,x_n$ of $V_{n,p}$.

OUTPUT: The inverse $W_{n,p}=V_{n,p}^{-1}$.

Step 1:  Compute $a_i,i=0,1,\dots ,n$ and $d_i,i=1,2,\dots ,n$ using (25) and (27), respectively. Arrange the values of $a_1,a_2,\dots ,a_n$ and the nodes $x_1,x_2,\dots ,x_n$ as follows

Step 2:  Compute the numerators $N_{ij}$ in columns $C_{n-1},C_{n-2},\dots ,C_1$ in the same order using (34). Then, compute the components of the remainder vector, $\mathbf{r}$, and make sure that $$\mathbf{r}=\left(x_1{N}_{11}+a_n,x_2{N}_{21}+a_n,\dots ,x_n{N}_{n1}+a_n\right)$$ is actually the zero vector. Eventually, simplify the values of all entries of $W_{n,p}=V_{n,p}^{-1}$ in its simplest forms.

This algorithm can be used directly for obtaining any particular row of the inverse $W_{n,p}=V_{n,p}^{-1}$. The algorithm will be referred to as “$\mathrm{VMIEA}$” for a MAPLE procedure for inverting the Vandermonde matrix, see Appendix A. Regarding the complexity of the proposed technique, we can observe that to accomplish each step in Algorithm 1, we need two nested loops which means that the computational cost is $O\left(n^2\right)$.

5. Illustrative Examples and Simulation Study

Now, we give some illustrative examples to clarify the technique discussed in the current paper, the $\mathrm{VMIEA}$ algorithm. One important special case of a Vandermonde matrix $V_{n,0}$ is the so-called discrete Fourier transform (for short, DFT) matrix, $F_n=F_n\left(\omega \right)$. The nodes of $F_n\left(\omega \right)$ are the n-th roots of unity, i.e., $1,\omega ,{\omega }^2,\dots ,{\omega }^{n-1}$, where $\omega =exp\left(\frac{2\pi \mathrm{i}}{n}\right)$ and $\mathrm{i}=\sqrt{-1}$. It is given by

$$F_n\left(\omega \right)={\left[{\omega }^{(j-1)(\ell -1)}\right]}_{j,\ell =1}^n.$$

(37)

The inverse of $F_n\left(\omega \right)$ is given by the following result.

Corollary 3.

Let $F_n\left(\omega \right)$ be the DFT matrix defined by (37). Then, we have $F_n^{-1}\left(\omega \right)=\frac{1}{n}{F}_n\left(\frac{1}{\omega }\right)={\left[{\alpha }_{j\ell }\right]}_{j,\ell =1}^n$, where

$${\alpha }_{j\ell }=\frac{1}{n}{\omega }^{-(j-1)(\ell -1)}.$$

(38)

Proof. 

The nodes of $F_n$ are $1,\omega ,{\omega }^2,\dots ,{\omega }^{n-1}$. Hence, $f\left(x\right)=x^n-1$. From (23), we deduce that $a_0=1,a_n=-1$ and $a_j=0$ for all $j=1,2,\dots ,n-1$. Using (29), then we have $N_{j\ell }={\omega }^{(j-1)(n-\ell )}$ and $d_j=n{\omega }^{(j-1)(n-1)}$. The required result follows on simplification.    □

Now, we will invoke the following numerical examples.

Example 1.

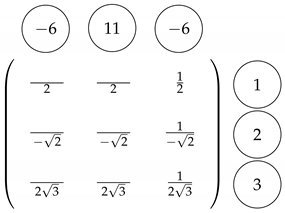
Use the $\mathrm{VMIEA}$ algorithm to find the inverse of the following matrix

$$V_{3,\frac{1}{2}}(1,2,3)=\left(\begin{array}{ccc}1& 2^{1/2}& 3^{1/2}\\ 1& 2^{3/2}& 3^{3/2}\\ 1& 2^{5/2}& 3^{5/2}\end{array}\right).$$

Apply the $\mathrm{VMIEA}$ algorithm as follows:

Step 1

Using (25), we obtain $a_0=1,$$a_1=-6$, $a_2=11$ and $a_3=-6$. Following (27), we have $d_1=2,d_2=-\sqrt{2}$ and $d_3=2\sqrt{3}$. Arrange $a_1,a_2,a_3$ and the nodes $x_1,x_2,x_3$ as follows

Step 2

Furthermore, we can use the recurrence relation (34) to compute the numerators $N_{ij}$ in columns $C_2,C_1$ in the same order. Thus, the inverse is given by

Hence, simplifying the entries for the previous matrix, we obtain the inverse of the Vandermonde matrix $V_{3,\frac{1}{2}}(1,2,3)$.

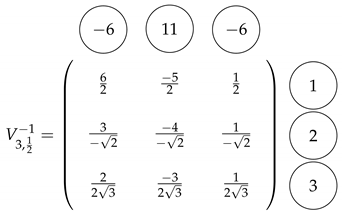
In the next example we compute the inverse of a generalized Vandermonde matrix of dimension $n=5$.

Example 2.

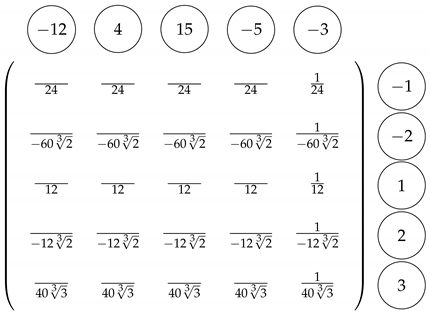
Use the $\mathrm{VMIEA}$ algorithm to find the inverse of the following matrix:

$$V_{5,\frac{1}{3}}(-1,-2,1,2,3)=\left(\begin{array}{ccccc}-1& -\sqrt[3]{2}& 1& \sqrt[3]{2}& \sqrt[3]{3}\\ 1& 2\sqrt[3]{2}& 1& 2\sqrt[3]{2}& 2\sqrt[3]{3}\\ -1& -4\sqrt[3]{2}& 1& 4\sqrt[3]{2}& 9\sqrt[3]{3}\\ 1& 8\sqrt[3]{2}& 1& 8\sqrt[3]{2}& 27\sqrt[3]{3}\\ -1& -16\sqrt[3]{2}& 1& 16\sqrt[3]{2}& 81\sqrt[3]{3}\end{array}\right).$$

Apply the $\mathrm{VMIEA}$ algorithm as follows:

Step 1 

Applying (25), we get $a_0=1,a_1=-3,a_2=-5,$$a_3=15$, $a_4=4$ and $a_5=-12$. By using (27), w obtain $d_1=24,d_2=-60\sqrt[3]{2},d_3=12,d_4=-12\sqrt[3]{2}$ and $d_5=40\sqrt[3]{3}$. Arrange $a_1,a_2,\dots ,a_5$ and the nodes $x_1,x_2,\dots ,x_5$ as follows

Step 2 

Using (34) to compute the numerators $N_{ij}$ in columns $C_4,C_3,C_2,C_1$ in the same order. Thus, the inverse is given by

Furthermore, we can compute $N_{ij}$ via Horner’s scheme Remark 1. Hence, simplifying the entries for the previous matrix, we obtain the inverse of the Vandermonde matrix $V_{5,\frac{1}{3}}(-1,-2,1,2,3)$.

The following example shows the power of Corollary 1 to reduce the effort of the calculations.

Example 3.

Use the $\mathrm{VMIEA}$ algorithm to find the inverse of the following matrix

$$V_{6,0}(-3,-2,-1,1,2,3)=\left(\begin{array}{cccccc}1& 1& 1& 1& 1& 1\\ -3& -2& -1& 1& 2& 3\\ 9& 4& 1& 1& 4& 9\\ -27& -8& -1& 1& 8& 27\\ 81& 16& 1& 1& 16& 81\\ -243& -32& -1& 1& 32& 243\end{array}\right).$$

We have $x_1=-3,x_2=-2,x_3=-1,x_4=1,x_5=2$ and $x_6=3$. We apply the $\mathrm{VMIEA}$ algorithm as follows:

Step 1 

Following Corollary 1, we obtain $a_1=a_3=a_5=0$ and

$$a_j={(-1)}^{\frac{3j}{2}}{\mathbf{e}}_{\frac{j}{2}}^{\left(3\right)}(9,4,1),j=0,2,4,6,$$

furthermore, $a_0=1,a_2=-14,a_4=49$ and $a_6=-36$. Moreover, we have for $i=1,2,3,4,5,6$

$$d_i=2a_4\left(x_i\right)+4a_2{\left(x_i\right)}^3+6a_0{\left(x_i\right)}^5,$$

so, $d_1=-240,d_2=60,d_3=-48,d_4=48,d_5=-60$ and $d_6=240$. Arrange $a_1,a_2,\dots ,a_6$ and the nodes $x_1,x_2,\dots ,x_6$ as follows

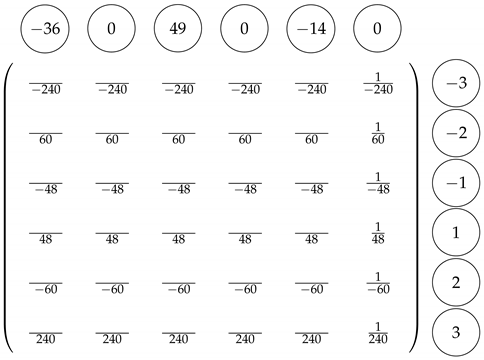
Step 2 

Using (34) to compute the numerators $N_{ij}$ in columns $C_5,C_4,C_3,C_2,C_1$ in the same order. Thus, the inverse is given by

Furthermore, we can compute $N_{ij}$ via Horner’s scheme Remark 1. Hence, simplifying the entries for the previous matrix, we obtain the inverse of the Vandermonde matrix $V_{6,0}(-3,-2,-1,1,2,3)$.

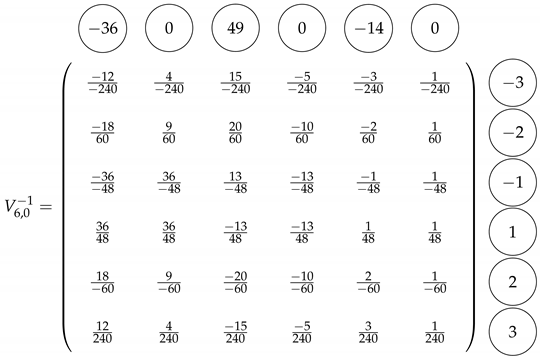
Now, we provide a simulation to make a comparison between the time spent to compute the inverse of the Vandermonde matrix through the inverse function in Maple and the $\mathrm{VMIEA}$ algorithm. The mathematical software used is Maple 2020, and the specifications of the device used in the simulation are MacBook Pro with 2.6 GHz Intel Core i5, and 8 GB 1600 MHz DDR3 RAM.

We divided the simulation for computing the inverse for both symbolic and numerical Vandemonde matrix with different orders. For the symbolic Vandermonde matrix $V_{n,0}(x_1,x_2,\dots ,x_n)$, where n denotes the matrix dimension, we did the simulations only for orders $n=2,\dots ,10$. Whereas, for the numerical Vandermonde matrix $V_{n,0}(x_1,x_2,\dots ,x_n)$ and $V_{n,0.25}(x_1,x_2,\dots ,x_n)$, we did the simulation for orders $n=2,\dots ,20$. For each n, we repeated the simulation 50 times, and then we found the average running time. Furthermore, we have checked the proposed $\mathrm{VMIEA}$ algorithm for the higher order of numerical Vandermonde matrix, for instance, $n=100,200,300,400$. We observed that the $\mathrm{VMIEA}$ algorithm is faster than the Maple inverse function. Figure 1 clarifies that the running time for computing the inverse of symbolic Vandermonde matrix by Maple inversion function for matrices is much more than that by $\mathrm{VMIEA}$ algorithm. Furthermore, Figure 2 and Figure 3 show the efficiency of the $\mathrm{VMIEA}$ algorithm for computing the inverse of the numerical Vandermonde matrix, where the proposed algorithm is faster than the Maple inverse function.

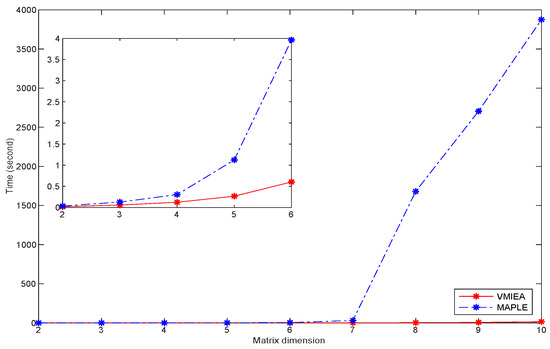
Figure 1. Running time for computing the inverse of symbolic Vandermonde matrix $V_{n,0}\left(\mathbf{x}\right)$ via $\mathrm{VMIEA}$ algorithm (in red color) and Maple inversion function for matrices (in blue color).

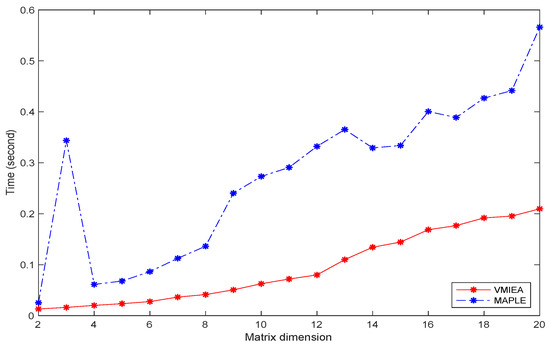
Figure 2. Running time for computing the inverse of numerical Vandermonde matrix $V_{n,0}(1,2,\dots ,n)$ via $\mathrm{VMIEA}$ algorithm (in red color) and Maple inversion function for matrices (in blue color).

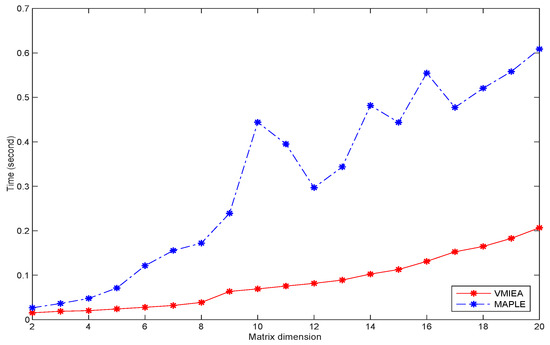
Figure 3. Running time for computing the inverse of numerical Vandermonde matrix $V_{n,0.25}(1,2,\dots ,n)$ via $\mathrm{VMIEA}$ algorithm (in red color) and Maple inversion function for matrices (in blue color).

6. General Conclusions

In this paper, we have presented a novel recursive algorithm for computing the inverse of the generalized Vandermonde matrix $V_{n,p}$. The proposed method is simple for hand calculation and computer programming as well. From the provided comparison, it is clear that with the increase in matrix dimension, the difference in running time between Maple inversion function and $\mathrm{VMIEA}$ algorithm is increasing as well. In summary, we can observe that the proposed method for computing the inverse of the Vandermonde matrix is more efficient than Maple’s inverse function for both types, symbolic and numerical Vandermonde matrix.