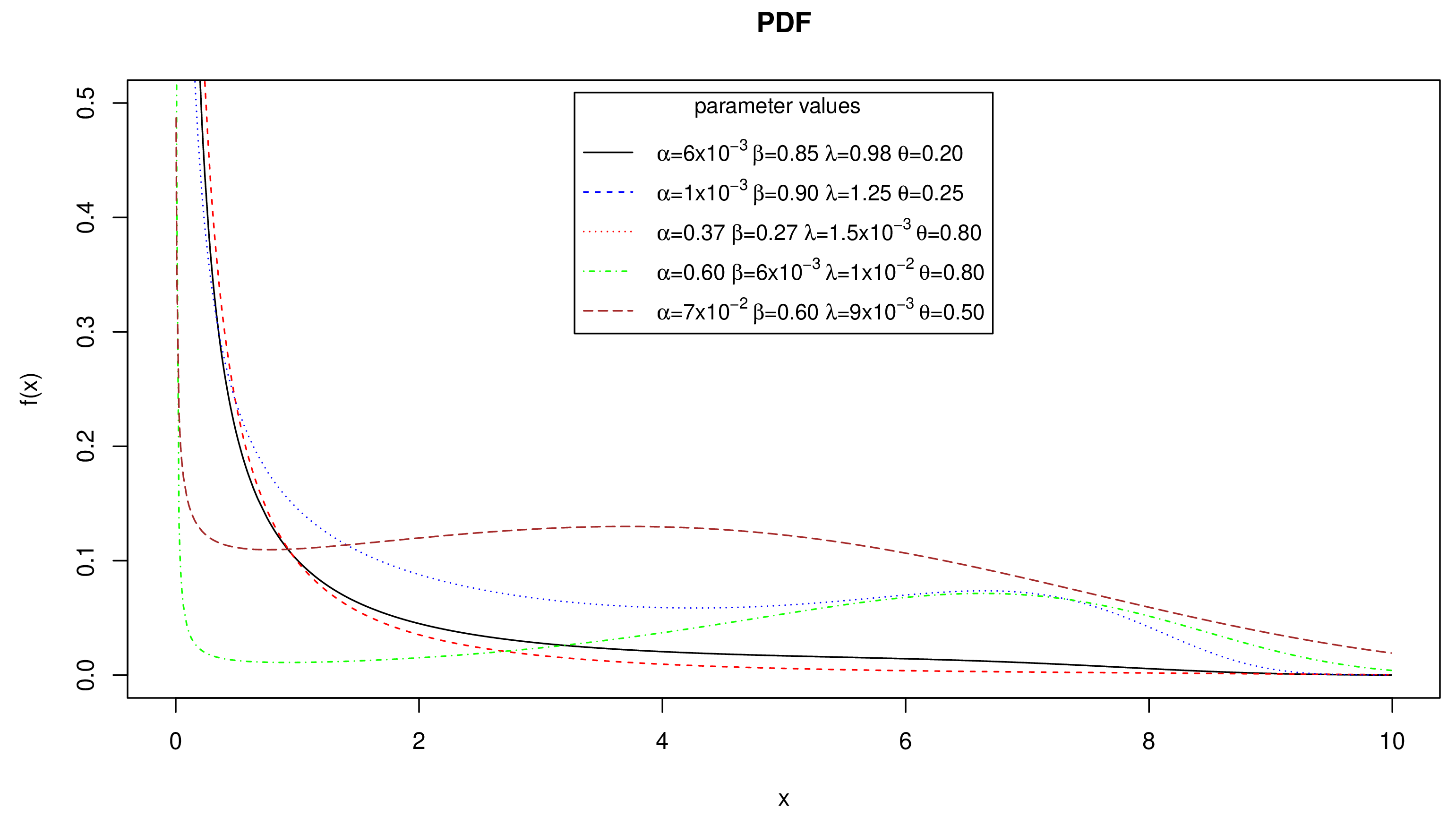
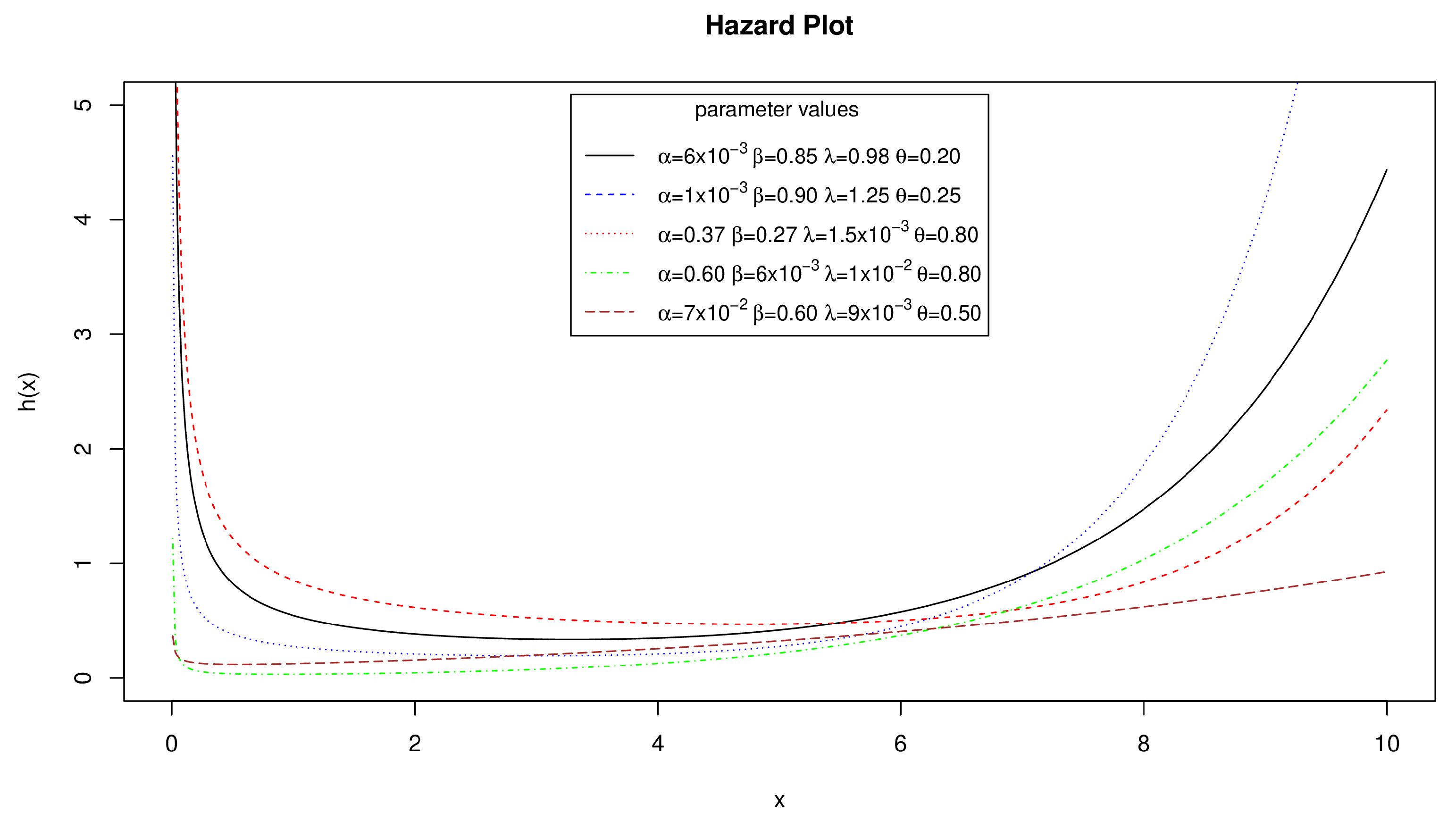
1. Introduction
Reliability analysis determines a device’s behavior by the bathtub curve, which establishes the stages a product passes throughout its useful life. To verify whether the device follows a bathtub curve behavior, practitioners use statistical probability distributions and analyze the behaviors to determine essentials such as warranty and optimal maintenance times. Due to mathematical flexibility, classical probability distributions, such as the Weibull, Exponential or Lognormal distribution, are commonly used to describe this behavior. Nevertheless, this type of distribution cannot fit the data well if they have a non-monotonic behavior, such as the bathtub curve. The above causes uncertainty in the description of the information, and sometimes the conclusions of the analysis drop off due to the properties of certain distributions before different types of data.
Some researchers have proposed different methodologies to solve the problem of data representation with non-monotonic behavior. For example, refs. [
1,
2,
3,
4,
5,
6,
7] developed models based on the additive methodology, which consists of adding the hazard functions of two statistical distributions, this to combine properties of the distributions. Other authors established the use of mathematical transformations to make the behavior of base distributions more flexible. By making the parameters of the distributions more flexible, it is possible to cover a more significant number of behaviors, including non-monotone. Examples of these works can be appreciated in [
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. Finally, another current of researchers has chosen to modify classical distributions such as the Weibull. The modifications presented consist of exponentiating parameters or adding a parameter to the distribution under analysis. These modifications have been popular since they allow mathematical flexibility with which the analysis is simplified. Examples of these distributions can be seen in [
20,
21,
22,
23,
24,
25].
One of the main disadvantages of the work presented above is that the non-monotonic representation of the data resembles a “J” or “V” shape, which biases the complete information of the subject under analysis. This problem can be seen reflected in the design and quality of the product. Therefore, the device’s behavior representation must be close to the bathtub curve and the designed specifications.
On the other hand, Chen [
26] proposed distribution with two parameters, with which it is possible to represent data with a tendency to have incremental, decremental, or bathtub-shaped behavior. The hazard function of the Chen distribution (ChD) is defined as:
where
and
are the shape parameters. The ChD problem is that the representation of the failure rate is not symmetric to a bathtub shape, leading to the ChD being modified; this is because the ChD does not have a scale parameter that can make the distribution more flexible. For example, Thanh Thach and Briš [
27], Tarvirdizade and Ahmadpour [
28] presented the Additive Chen-Weibull (ACW), which combines the properties of the ChD and Weibull to obtain a hybrid model that offers very competitive results for survival analysis. Other studies proposed an extension of ChD based on transformations o generalizations; these works can be seen in [
29,
30,
31,
32]. The transformations mentioned above represent an alternative for reliability analysis but may not be a good option to determine the behavior of the lifetimes of the devices under analysis.
Therefore, this paper aims to present a new variant of the ChD, with which practitioners can represent the behavior of data with non-monotonic behavior in a way closer to that established by the bathtub curve. The proposed distribution is based on the additive methodology presented by Xie and Lai [
1]. Thus, the Additive Chen Distribution (AddC) is preset and has two extra parameters to the base ChD. The extra parameters of AddC allow more flexibility for representing data with trends to be increasing, decreasing, or bathtub shaped. In turn, the MLE was used to estimate the parameters of the new distribution. On the other hand, to verify the properties of AddC, three case studies were designed, where AddC is compared against other distributions that have the property of modeling non-monotone or bathtub-shaped behavior. The Akaike information criterion (AIC), the Bayesian information criterion (BIC), the Kolmogorov Smirnov test (K-S), and the
p-value were used to derive the conclusions of the case studies. The importance of AddC lies in offering competitive results concerning other distributions with similar properties, which helps practitioners to consider new analysis perspectives when performing reliability tests. For this new distribution, some functional statistical and mathematical properties are presented and discussed to demonstrate that AddC can be considered in real applications to determine the reliability of some devices’ underperformance or acceleration life testing.
Finally, this paper is organized as follows.
Section 2 presents the general equations of AddC.
Section 3 presents the Measures of Central Tendency of APD.
Section 4 presents the moments and Incomplete Moments.
Section 5 presents the order statistics.
Section 6 presents the mean residual lifetime function.
Section 7 presents the Rényi Entropy.
Section 8 presents the Stress Strength Reliability.
Section 9 presents the likelihood function to calculate the parameters proposed in
Section 2.
Section 10 presents the case studies of the paper. The last section provides concluding remarks and future work about the proposed model.
9. Maximum Likelihood Estimator
A primordial aspect of statistical models is the formulation of a method that will estimate the values of each parameter in the distribution. For the case of AddC, the use of the MLE is proposed. Let
be a random sample from the lifetime distribution with PDF
and based on a sample of size
m. Then the likelihood function of Equation (
3) is written as follows:
If we compute the natural logarithm of the above equation, the log-likelihood
function becomes:
By taking the first partial derivative of Equation (
22), the estimation for each parameter
, and
can be calculated as follow:
From Equations (
23)–(
26), we can derive the Fisher observation matrix, with which it is possible to obtain the Hessian. In
Appendix A, the elements of the Fisher matrix are presented.
10. Case of Study
In this section, the behavior of AddC is analyzed in three case studies where the data has non-monotonic behavior. To verify the methodology established in this paper, a comparative study was designed between AddC and other distributions with similar properties. The distributions considered were the ACW proposed by Thanh Thach and Briš [
27], Tarvirdizade and Ahmadpour [
28], the Additive Weibull Distribution (AWD) proposed by Xie and Lai [
1], the Additive Perks-Weibull (APW) proposed by Singh [
5], Perks4 proposed by Zeng et al. [
34], Modified Weibull Distribution (MW) proposed by Almalki and Yuan [
22], and the Sarhan and Zaindin modified Weibull (SZMW) proposed by Zaindin and Sarhan [
23].
Table 1 shows the hazard functions of each distribution used for the comparative analysis.
In all of the proposed case studies, the parameters were estimated through the MLE. This algorithm was programmed through R using the MaxLik package [
35]. In turn, the AIC, BIC, K-S, and
p-Value were calculated for each distribution to establish the discussion and draw conclusions from the results.
10.1. Case Study 1: Lifetime of 50 Devices
This case study focuses on determining the behavior of the failure times of 50 devices. The data was obtained by Aarset [
36] and is presented in
Table 2.
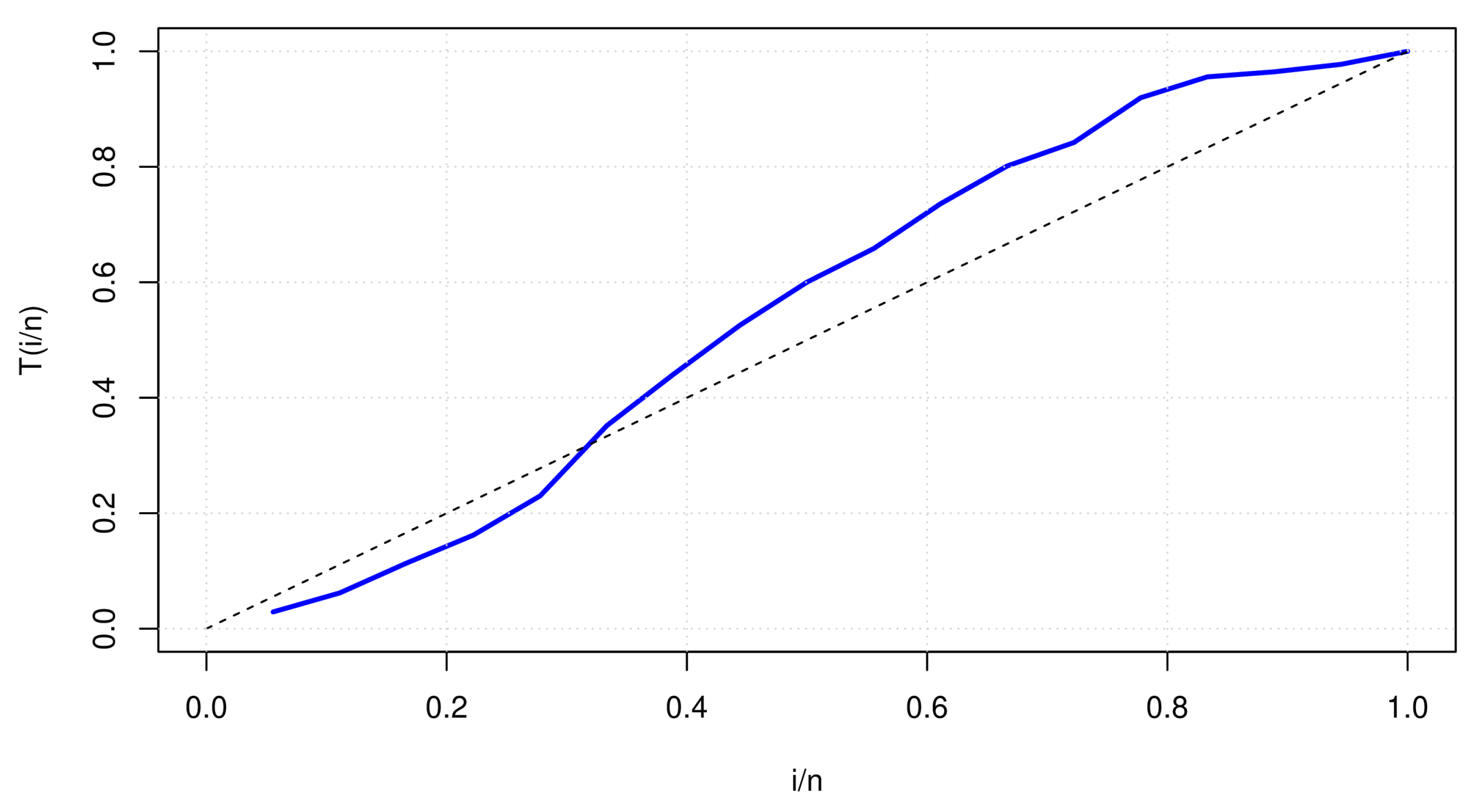
To identify the behavior of the data, the total test time (TTT) curve is used. Therefore, in
Figure 3, the TTT of the data presented in
Table 2 is presented.
The results shown in
Figure 3, show that the data presented in
Table 2 exhibit a non-monotonic behavior.
On the other hand,
Table 3 shows the estimation of each parameter for each of the models presented in
Table 1 and AddC. The information presented in
Table 3 shows statistical evidence that AddC offers a better description of the behavior of device failure times concerning the distributions listed in
Table 1. The previous is based on the AIC and BIC criteria, where AddC has the smallest value of these criteria concerning the other distributions compared within the analysis carried out, which indicates that AddC may be a good candidate for the description of the data in
Table 2. On the other hand, AddC shows a better fit in the data representation, based on the
p-value described in
Table 3. This
p-value represents that the data will be as close as possible to the device’s behavior under the operating conditions that the manufacturer has described.
In turn, with the information obtained in
Table 3, it is possible to make a graphic description of the behavior of the devices over time, for which
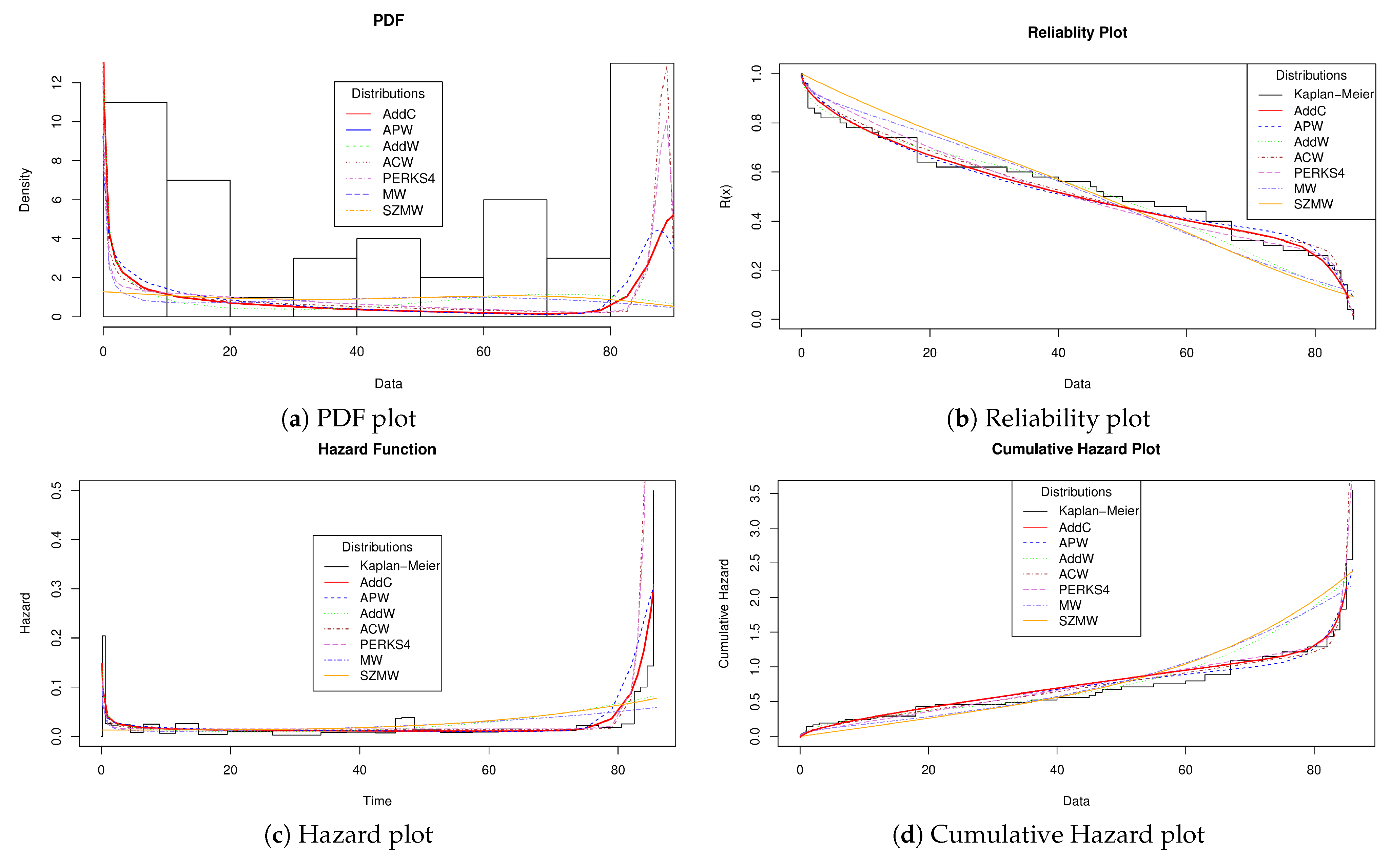
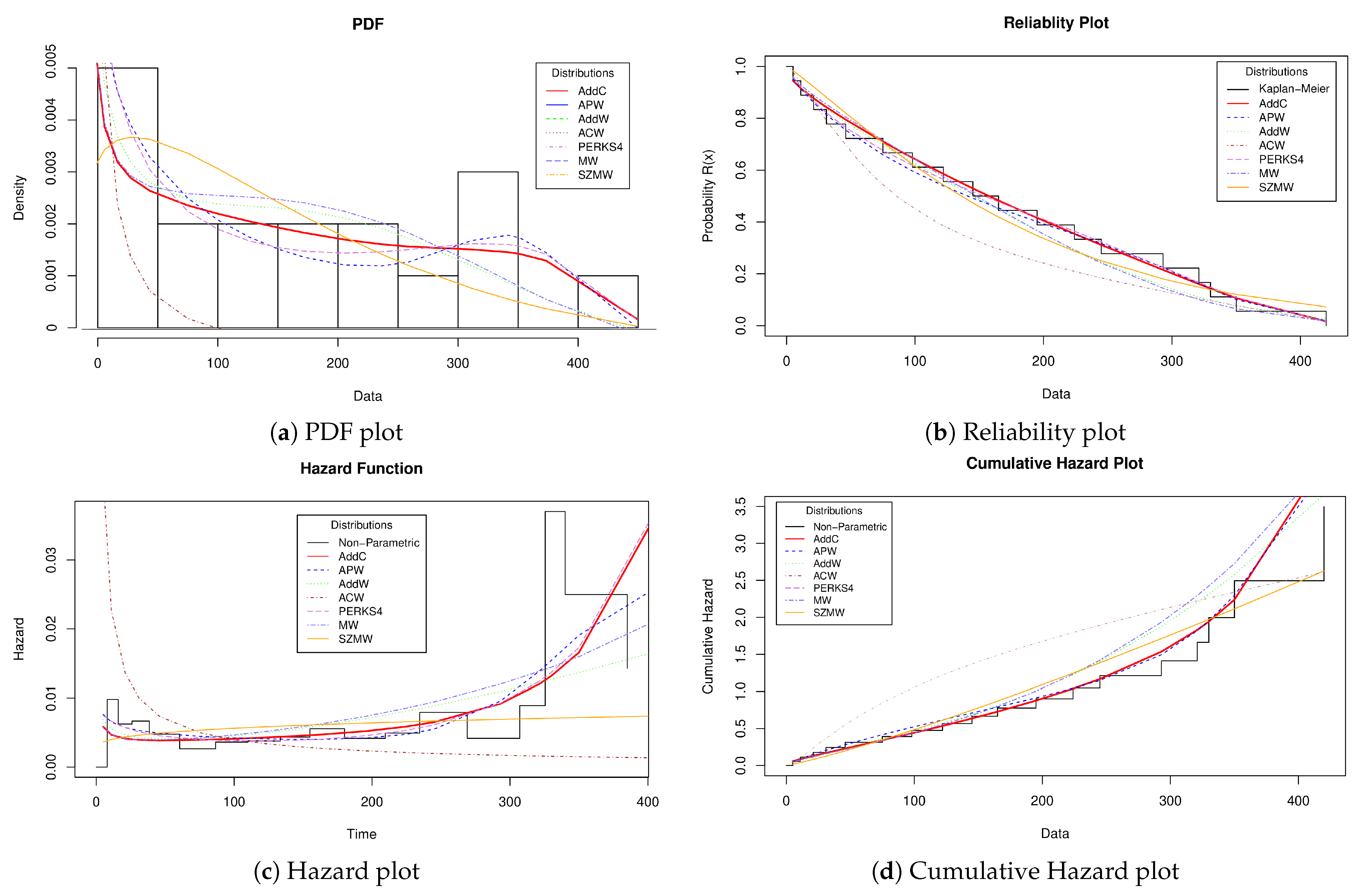
Figure 4 shows the representation of the PDF, Reliability, Hazard, and Cumulative Hazard.
Figure 4a shows the PDF behavior for each distribution under analysis by considering how the data histogram in
Table 2, Perks4, AWC, APW, and AddC offer a good representation of the distribution of lifetimes. Although the above does not represent convincing evidence, it can give an idea of which distributions can offer behaviors close to the reality of the device under analysis.
Figure 4b shows the behavior of the lifetimes of
Table 2 concerning the reliability equation of each distribution under analysis. The graph mentioned above is used within reliability engineering to determine essential aspects such as determining the estimated lifetime of the device under analysis or maintenance times to extend the product’s life. For the specific case and considering the Kaplan–Meier empirical reliability, AddC offers a better fit concerning the other distributions used in the comparative analysis. That means AddC will more accurately describe lifetimes, maintenance times, and MTTF; those metrics are essential in reliability analysis.
Figure 4c shows the form taken by the failures of the device under analysis. As seen in the vast majority of the distributions, a behavior similar to the bathtub curve can be observed, which confirms the empirical behavior obtained by the TTT plot (see
Figure 3). Now, suppose we visually contrast the behavior of the distributions and compare it against the results of
Table 3. In that case, we can conclude that AddC touches the empirical behavior in more points, which indicates that AddC offers a more competitive representation of failures within the device. Product engineers can consider the above information to improve designs, reduce manufacturing, and estimate maintenance costs. Finally,
Figure 4d shows the behavior of the accumulated hazard. In this graph, it can be seen that AddC is closer to the Kaplan–Meier empirical representation. The preceding indicates that AddC will better model the failures of the device as its useful life elapses.
10.2. Case of Study 2: Field-Tracking Study of a Larger System
This case study analyzed the behavior of 30 devices inserted into the primary electrical system after a series of determined conditions and time had elapsed. These data were presented by Meeker et al. [
37]. In turn, the failures were classified into two types; failures due to wear or electrical variation produced by the electrical source. The result of the failure cycles are presented in
Table 4.
The form that the data takes, as established in the TTT plot of
Figure 5, indicates that the data of
Table 4 have a behavior similar to that of a bathtub curve. Therefore, it is submitted to the analysis with the distributions established in
Table 1.
Table 5 shows the results obtained from the estimates of each parameter for the models under analysis.
Table 5 shows that AddC offers a better fit than the other distributions under analysis. However, the adjustment of AddC is not the best since the
p-Value reaches a value above 0.7, which is possible that for this specific case, AddC may not represent all the data presented in
Table 4. Those mentioned above can be better exposed when representing the behavior of the estimates and the data of this case study, so
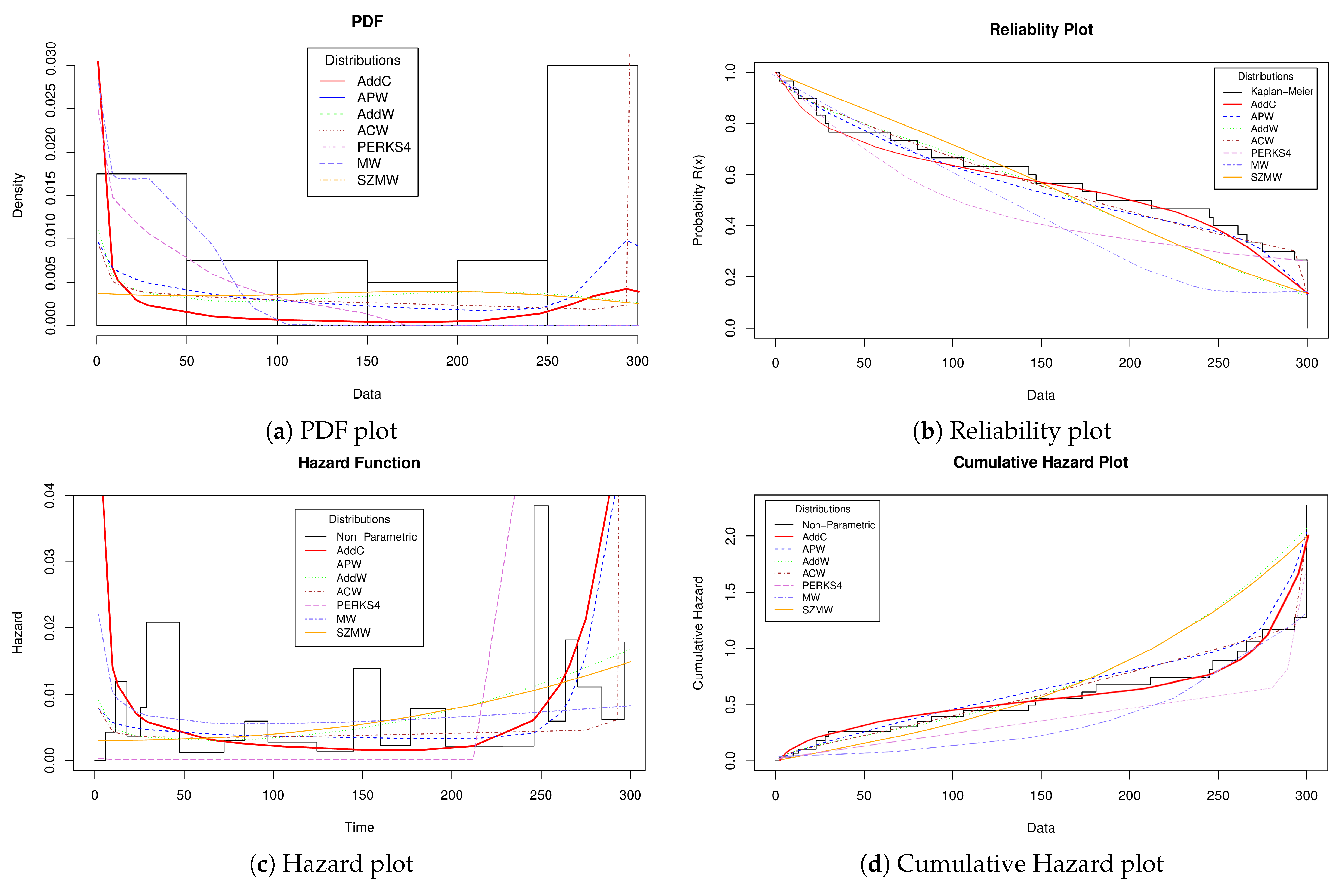
Figure 6 shows the behavior graphs of the data presented in
Table 4.
Figure 6a shows the behavior of the PDF for each of the distributions established in the comparative analysis. As can be seen, AddC represents more competitively the behavior of the data density. The previous offer AddC a competitive advantage that reliability practitioners make decisions about what kind of distributions they can use to obtain analyzes closer to the reality of the product they are analyzing. In
Figure 6b, the behavior of the distributions’ reliability curve is observed and compared concerning the Kaplan–Meier representation. The conclusion obtained from
Figure 6b is that AddC passes the Kaplan–Meier representation through a more significant number of points concerning the distributions listed in
Table 1; This means that AddC can get closer to the device operation times such as warranty times, MTTF and maintenance times. These times are vital in the design of the product since, with these times, it is possible to establish substantial improvements.
On the other hand,
Figure 6c shows the behavior of the hazard function of failure times, where it is notable that despite the data described in
Table 4 being known to behave similarly to a bathtub curve. Some distributions that possess the above property cannot reliably represent non-monotonic behavior. The above described leads to an essential loss of information in describing the behavior of the device under analysis, so practitioners must consider this when choosing the distribution that will describe the failure times.
The AddC shows a very competitive fit concerning the non-parametric representation of the data presented in
Table 4 and the distributions presented in
Table 1. So It can be concluded that AddC is the best option to describe the failure times in this case study. Finally,
Figure 6d shows the behavior of the cumulative hazard. As in the previous cases, if we compare each distribution’s form concerning the non-parametric representation. We can observe that AddC better adjusts the faults accumulated in the device, which gives an idea more precise to the practitioners of how it is that the faults are presented throughout the useful life of the device under analysis.
10.3. Case of Study 3: Lifetime of 18 Electronic Devices
The following case study is based on the results obtained by Wang [
7], who tested 18 electronic devices. The failure times obtained are shown in
Table 6.
The TTT plot is obtained to verify the behavior of the data presented in
Table 6. Therefore,
Figure 7 shows the behavior of the data presented by Wang [
7].
As shown in
Figure 7, empirically, the TTT plot indicates that the data presented in
Table 6 show behavior resembling the bathtub curve. Therefore, the estimation of the parameters is carried out through the MLE for all the distributions placed under analysis.
Table 7 presents the results of the parameters’ estimations and the statistical decision criteria.
Based on the evidence shown in
Table 7, it can be established that AddC has good results for describing the data established in
Table 6. Although, it should be noted that in this case study, some of the distributions established for the analysis offer very competitive results, where the difference is minimal concerning AddC. Nevertheless, this slight difference can establish a decision criterion regarding which distribution to use in the analysis.
The graphical representation of the results obtained in
Table 7 is shown in
Figure 8.
As in the two previous case studies,
Figure 8 shows the device’s behavior under the different reliability representations. The representation of the PDF is shown in
Figure 8a, where it can be seen that the distributions under analysis offer a good representation of the histogram of the data presented in
Table 6. So, in this case, the PDF cannot draw a satisfactory conclusion about which distribution can be used practically. The reliability graph presented in
Figure 8b shows that the adjustment of AddC touches the Kaplan–Meier representation in a more significant number of points. This aspect shows that AddC could express closer to the operating environments the behavior of the device under analysis.
The shape taken by the failure times in
Figure 8c shows that AddC manages to get closer to the shape of the bathtub curve. In turn, the other distributions listed in
Table 1 exhibit a non-monotonous behavior but without a defined bathtub curve shape. In this case, AddC could be a good choice for practitioners of reliability engineering.
Finally,
Figure 8d shows the shape of the cumulative hazard plot of each distribution included in the analysis. In this case, we can see that AddC and the APW have a good fit, but AddC shows slightly closer to the non-parametric representation, with which AddC can establish the representation of device faults.
11. Conclusions
In this paper, a statistical distribution with applications to reliability engineering for the description of device failure times was presented. The distribution was based on the Chen distribution and the additive methodology, thus introducing AddC, with two shape and scale parameters. The AddC has the property of competitively describing non-monotonic behaviors, especially in the form of a bathtub curve, which theoretically represents the useful life of any device.
The statistical properties analyzed show the flexibility that AddC can have in different analysis scenarios, which allows AddC to approach describing the real behavior of the devices under analysis. In turn, it allows reliability practitioners to determine essential aspects in the analysis, such as warranty and maintenance times. With this information, it is possible to improve device designs and reduce manufacturing costs. The assumptions or conditions for the use of AddC are similar to those of any probability distribution. So the results that AddC yields are based on the quality of the data put under analysis; therefore, there are no special conditions for AddC application.
The competitiveness of AddC was tested on three case studies designed where the failure times of the devices are non-monotonic. In all case studies, the results obtained from AddC were compared against other statistical distributions with similar mathematical properties. This comparative study aimed to demonstrate that AddC can be a good option for reliability analysis in different devices.
In future work to extend the applications of AddC, Bayesian techniques are proposed to know the differences between the results obtained by MLE and the Bayes techniques. On the other hand, AddC can be modified to be used in accelerated life tests, which is one of the most used techniques in reliability for obtaining information in short times through the acceleration of some variable that directly affects the life of the devices under analysis.