Abstract
As traditional models and algorithms are less effective in dealing with complex and irregular temporal data streams, this work proposed a fuzzy temporal association model as well as an algorithm. The core idea is to granulate and fuzzify information from both the attribute state dimension and the temporal dimension. After restructuring temporal data and extracting fuzzy features out of information, a fuzzy temporal event association rule mining model as well as an algorithm was constructed. The proposed algorithm can fully extract the data features at each granularity level while preserving the original information and reducing the amount of computation. Furthermore, it is capable of efficiently mining the possible rules underlying different temporal data streams. In experiments, by comparing and analyzing stock trading data in different temporal granularities, the model and algorithm identify association events in disorder trading. This not only is valuable in identifying stock anomalies, but also provides a new theoretical tool for dealing with complex irregular temporal data.
Keywords:
fuzzy temporal data mining; fuzzy temporal association rules; fuzzy temporal event; temporal type MSC:
68Q32; 62G08; 03B52
1. Introduction
Temporal data stream (also known as time-varying data streams) mining is currently of great importance in the field of data mining, where the discovery of implicit knowledge (associative features, categorical features, etc.) in irregular temporal data streams is critical. First, each record in a temporal data stream varying irregularly over time displays multiple granularities, magnitudes and dimensions, as shown by data in finance. Second, in the same data bank there are different types of data, i.e., qualitative vs. quantitative, and structured vs. unstructured, e.g., trading data vs. public opinion data in the stock market, consultation data vs. medical records in hospitals, and weather detection data vs. body sensory data in describing temperature, etc. Finally, features and patterns of the data flowing in temporal data streams are obscured by the overwhelming amount and complexity of the data. All of these make it extremely difficult to build effective knowledge-discovery algorithms [1], such as those for urban traffic management, medical systems, stock market trading, and social networks. The current widely used mining algorithms, including Apriori, SVM, BP, and deep learning, focus on non-temporal association rules, classification, and feature recognition [2,3]. For temporal data streams, there is still a lack of effective models and algorithms. Therefore, the study of temporal data stream mining models and algorithms is extremely valuable and challenging.
Since it is difficult to discover the information features and patterns in complex time data, deformation processing methods are needed. As early as 1979, for example, LA Zadeh proposed a theory of information granulation [4] to deal with complex data. Subsequently, the idea was further developed into the theory of granular computing. With it, complex data (e.g., unstructured verbal text, time series data, etc.) are translated into digital information at different granularity, which reveals features and patterns at different scales [5]. Based on this, this paper reconstructed the information in the raw data under different time granularity combining fuzzy theory, which helps rebuild the problem from multi-granularity spaces and establish a fuzzy feature-discovery model for multi-granularity data. Wang Guoyin et al. [6] indicated that multi-grain hierarchical thinking is consistent with human cognitive mechanisms, which helps human–computer cognitive mechanism integration. In this way, it enhances the computability of information and the interpretability of results. Particularly for the information granularity processing of time series, Yu Fusheng et al. [7] summarized previous experiences and proposed that information granularity processing should preferably be based on both temporal granularity and value granularity. Therefore, processing temporal data streams should be a multi-granular parallel processing work. Thus, knowledge-discovery models and algorithms with multiple granularities or different scales play an important role in solving complex temporal data streams.
Research on mining the original timestamp data is divided into two main categories: one is to directly build models and algorithms without partitioning the data at any granularity, with the argument that data deformation will lose the features inherent in the raw information. It is mainly shown by econometric models such as AMAR and panel models, etc. However, it has proved to be extremely problematic for complex time series. Therefore, another category dealing with complex time series data has risen, i.e., the construction of temporal data models and algorithms using different time granularity information, which has become an important research direction for temporal data mining. The methods in the second category have been successfully applied in many fields where there are strong systematic associations with historical data, such as in transport, medical, insurance, finance, and meteorology. Temporal data-mining methods have already achieved many research results in terms of association rule mining, data trend analysis, pattern analysis, causality analysis, and periodic pattern analysis [8].
The following discussion focuses on five aspects concerning data mining of time or temporal divisions and fuzzy temporal mining.
- (1)
- Some researchers have adopted temporal-segmentation methods to perform temporal data mining, such as Lovrić who pointed out that temporal segmentation is considered as a pre-processing step and a core task for various temporal data mining methods [9], the core problem being solving the theory of temporal data-mining models. For example, some scholars proposed generating subsequences by using the sliding window method on the raw time series, and then mine association rules based on operations such as feature–symbol transformation or similarity analysis on the subsequences [10,11]. Some scholars have also proposed to segment the subsequence separately and extract features based on item lifespans, and then mine the association rules between them [12,13].
- (2)
- Other researchers focused on diversity treatment of time granularity: raw time is organized into granular pieces of fixed time length, and the reconstructed data are mined separately for different time granularity, such as the periodical association rule mining based on the calendar [14]. However, this kind of time granularity segmentation is relatively rough. Usually day-, month-, or year- scales are adopted for the segmentation standard and sometimes the length of the segmentation is even not consistent, which all bring problems to the accuracy of the following mining. There is research showing the importance of temporal data mining for the discovery of temporal correlations or approximate periodic phenomena, but in practice there is the problem that it is difficult to precisely distinguish feature changes. Therefore, in this paper, based on the existing temporal type definition [15], combined with the fuzzy set theory [16], a new temporal fuzzy correlation model and algorithm were reconstructed.
- (3)
- In the area of fuzzy data mining with time series, fuzzy theory was introduced as early as 20 years ago to handle the relationship between fuzzy and temporal data [17]. Fuzzy theory mainly deals with imprecise, non-quantitative common information, and through abstracting and generalizing quantitative attributes, concise and easily-understood conclusions with a certain degree of precision are reached. Therefore, fuzzy data mining has shown its effectiveness in financial data prediction and traffic flow control, as well as in medical diagnosis [18,19,20].
- (4)
- The research on fuzzy temporal data mining is mainly divided into two classes, namely time fuzzy and attribute feature fuzzy. More research focused on the fuzziness while taking into account the time attribute of the dataset, i.e., the fuzzy treatment of time. For example, Mazarbhuiya et al. uncovered interesting time-dependent patterns using Tire algorithm to deal with a dataset with fuzzy trading times [21,22]. The fuzziness also works on time constraints, especially the backward and forward association constraints of items. Fuzzy temporal logic is used to deal with time-constrained incomplete information, and performs mining, for example, fuzzy periodic association rules for items [23,24,25]. Additionally, fuzziness works on the duration of rules, where the association rules may only hold for a fuzzy period of time instead of the entire data set [22,26].
- (5)
- Besides time fuzzy, another research point is that temporal data-mining models introduce fuzziness into attributes [17,27]. When mining temporal databases with quantitative attributes, fuzzy sets can be used to represent their quantitative values, thus defining smoother transitions between adjacent values [24]. A common operation mode is to convert non-temporal quantitative values from temporal data into symbols or linguistic terms to make it easier for further analysis and interpretation. Many other researchers have also contributed to the exploration of suitable fuzzy affiliation functions [28,29,30] and mining algorithms [31] for fuzzy temporal mining. Some examples are neuro-fuzzy systems [32,33] and fuzzy clustering [34] that combine intensive machine learning.
In summary, the time or temporal fuzzy data mining mainly involves two models of temporal fuzzy and attribute feature fuzzy. Therefore, based on information granularity reconstruction and combining fuzzy mathematics and temporal approaches, this paper reconstructed time-varying data sets in a multi-dimensional and multi-granularity fashion by simulating human perception. In this paper, a fuzzy temporal event was defined, associated properties of the fuzzy temporal approach as well as operations were given, and a fuzzy temporal event association rule mining model and algorithm were proposed to discover the knowledge and patterns hidden in the raw time-varying data. Numerical experiments indicated that the fuzzy temporal event mining model can detect the correlations hidden in daily trading events, which proves its effectiveness.
This paper presents three main innovations: (1) defining the fuzzy temporal type and fuzzy temporal granularity; (2) building a fuzzy temporal event model; and (3) proposing a fuzzy temporal event association rule model and algorithm.
Section 2 defines fuzzy temporal events and their operational rules and the associated properties. Section 3 constructs a fuzzy temporal event mining model based on fuzzy temporal events. In Section 4 stock trading data on the Lung Fu Bong (a Chinese stock daily winners list) is mined to show the effectiveness of the proposed fuzzy temporal even-association mining model.
2. Definition and Arithmetic of the Fuzzy Temporal Event
In this section, the definition and operations of the fuzzy temporal event are given to reveal features of temporal data streams at different temporal granularities. To better illustrate these, stocks were taken as an example.
Definition 1.
Leta finite set of m objects. Let,be the set of attributes of the objects containing a subset ofspecific attributes. The set of state variables corresponding to attributeis defined as , whereare highly fuzzy due to decisions made by humans.
Definition 2.
The fuzzy threshold interval corresponding to each attribute state variableis defined as(s can be omitted), whereis the worst andis the best for. Letbe called the set of fuzzy intervals corresponding toof attribute. When fuzzy state variabletakes an actual value, fuzzy membership functionat stateis defined by:
Definitions 1 and 2 describe the state transformation degree of a transaction attribute. The following example illustrates the abovementioned concepts.
Example 1.
The price of stockhas three attributes{Open price, Close price, Trading volume} in the stock market. Trading volume, an attribute of stock, is often described by vague conceptual terms such as {Low, Medium, High} to depict its states. Corresponding the states Low, Medium, and High to, VOL is depicted asby Definition 1. In addition, stock prices, another attribute of stock, are often depicted as {Rise, Fall, Unchanged} or {Great Rise, Small Rise, Shock, Small Drop, Large Drop}.
Furthermore by Definition 2, when are defined as low, and high VOL, respectively, and let its corresponding fuzzy interval be abbreviated as , such as ; for -medium volume, ; for -high volume, . By (1), for a VOL of , when , , which means that a VOL of 45 is associated with 0% of the state Low. The value of indicates that a VOL of 45 is 100% in the medium state. A value of means a VOL of 45 is 25% in the high state. Then, a conclusion that stock is currently experiencing medium–high trading volume is drawn.
In the real world, everything changes over time. Let be the time variable, i.e., a temporal dimension added to the description of object and the attribute . To further explore the interactions among , it is necessary to define temporal type and some associated concepts as follows:
Definition 3.
For any absolute moment, when the following conditions are satisfied: (1) non-emptiness:; (2) monotonicity: ifand , for anyand, there is, and hence; (3) homogeneity: for any, there is; (4) boundedness: for any, there is, and thenis defined as a temporal type andis called the temporal factor of the temporal type [15]. A temporal type is called temporal granularity when it has a temporal factor of the same length.
In Definition 3, for example, second, minute, hour, day, month, and year are the most common temporal types. A specific day is a day temporal factor if day is the temporal type. Additionally, quarter of an hour, seven hours, five days, week, quarter of a year, and other time intervals can be temporal types. Temporal type is the concept of temporal factors, and temporal granularity is the concept of time factors with the same length, for example, day and hour, are temporal granularity, but month is temporal type, not temporal granularity. Definition 1 are all temporal types. Additionally, when raw datasets are reconstructed from different temporal type perspectives, new patterns may be revealed, which may broaden and deepen temporal data mining.
Property 1.
Given an absolute time period , and the temporal type which divides the time periodintosegments, whereis the starting point and is the ending point, then there exists, such thatholds, where ,.
Property 2.
Forand any temporal factor, there exists an upper boundand a lower bound. From Definition 1, the length of the temporal factoris. When, the value ofdetermines the value of, so a larger value indicates a smaller temporal granularity and vice versa.
Therefore, different granularity of the temporal type means a huge difference when describing the features of even the same period of time, by Property 2.
For example, if a factory operates on an hourly basis, there is a temporal length of one hour, while for a two-shift factory there is a temporal length of twelve hours and for a three-shift manufacturer there is a temporal length of eight hours.
Definition 4.
For temporal typeat given time intervaland the fuzzy features of objectsand attribute set,is defined as the space of fuzzy temporal events in. A specific fuzzy temporal event can be denoted as, which means a fuzzy state of the event atoffor temporal factorof object. The event function is defined by:
and various states for the same temporal factor at the same attribute state are defined by:
Then E is called the event function. Its value is determined by, and obtained by computing the attribute state valuewith the setcorresponding to the state.
Example 2.
In Definition 4, when the VOL of stockis 45 at 13:01 on 8 October 2020, with the temporal type of minute, E is calculated:,,. In terms of attribute VOL, this event can be noted as, which means the event (, medium to high in trading volume, 25% of High, 13:01) occurs.
Property 3.
Given, then the sequence of fuzzy temporal eventsforms of the following fuzzy temporal matrix:
Example 3.
Whenis given a different value, a different set of fuzzy temporal events is generated for the same time period. Again take stocks. For attribute VOL of stock, three fuzzy attribute states i.e., Low, Medium and High, are used, with its fuzzy attribute states as D = {Low, Medium, High} and the corresponding set of fuzzy state intervals:. If VOL of stockfor the past three days is 20, 30, and 45, respectively, a fuzzy temporal event sequenceis created. Three fuzzy membership degrees combined in one temporal factor for each fuzzy temporal event are as follows:,,. These events are combined to form a fuzzy state matrix:
Definition 5.
For a temporal event, let a fuzzy threshold exist for the corresponding attribute; whenand , it meansofat temporal factoroccurs, otherwisemeans it does not occur. So the occurrence of a fuzzy state event can be recorded by the occurring attribute stateafter code conversion (s can be omitted in expressions), while non-occurrence is recorded as 0:
Example 4.
In Definition 5, assuming the fuzzy thresholdbeing 0.25 for attribute VOL, for the above three days, the fuzzy temporal events are transcribed as follows:,,, with an updated fuzzy state code matrix:
Definition 6.
Letbe the support rate (or frequency) ofof objectfor the temporal state typeover the time period:
Given a frequent threshold, if, thenis said to be a frequent fuzzy temporal event with respect to thresholdover time period, and the validity value of the event occurring during that time period is.
Definition 6 depicts the correlation or connection of events in different temporal factors.
Example 5.
In Definition 6, with, a further calculation ofassumes the support rate of Low, Medium, and High as 1/3, 2/3, and 1/3 for a VOL of, respectively. When, then (, (medium trading volume), day) is a frequent fuzzy temporal event during the three days.
Property 4.
Given, a frequent fuzzy temporal event aboutover time period, when there existsand, the event is also a frequent fuzzy temporal event aboutover time period.
Definition 7.
With two fuzzy temporal events,in, the operations of fuzzy events in the fuzzy temporal event space are as follows:
- (1)
- The operation “AND”, notated as ““:If bothandoccur, thenwhich indicates that fuzzy temporal eventsandare logically AND correlated onand.
- (2)
- The operations “OR”, notated as ““:Iforoccurs, thenwhich indicates fuzzy temporal eventsandare logically OR correlated onand.
Definition 7 depicts the correlation or connection between two different fuzzy temporal events. Through Definition 7 we obtain the following results.
Property 5.
There exists, satisfying, which makes
Additionally, if,
The threshold for the logical AND relationship between eventsandis.
Property 6.
There existssatisfyingand making
Additionally, if,. The threshold for the logical OR relationship between eventsandis.
Axiom 1.
In, for any three fuzzy temporal events,,, the following hold:
- Exchange law:
- Combination law:
- Distribution ratio:,
If, it is denoted ascalled the fuzzy temporal association rule. Moreover, there are following properties:
Property 7.
If, then,
Property 8.
If , then.
Property 9.
If,, then .
The definitions and properties of the abovementioned fuzzy temporal event model can be used to study the correlation between pricing, trading volume, etc. In Section 3, a fuzzy temporal event mining model and algorithm are proposed.
3. Fuzzy Temporal Event Mining Model and Algorithm
Based on the abovementioned, it is possible to describe the behavior of more complex fuzzy temporal events so as to find associations between them.
3.1. Fuzzy Temporal Event Association Rule Model
Definition 8.
Letand be integers, and let, where are adjacent temporal factors and they are of an increasing relationship: is abbreviated asor.
Define an operation:
For,
i.e., ,
indicates when eventoccurs, one of the subsequent eventsafter temporal factor would occur, i.e., the fuzzy temporal event association ruleholds. Otherwise,and the rule does not hold.
Definition 9.
Let denote the number of repetitions of event occurring in the time period:
Similarly, the number of recurrences of rulein time periodis expressed as:
The occurrence of such a correlation is common in life. For example, prices of stocks rise sharply to form a high opening price, followed by a high probability of the price falling within a few days afterwards.
To mark the time interval during which event frequently occurs in , the concept of the lifespan of an event is defined.
Definition 10.
Lifespan is defined as the period between the first temporal factorand the last temporal factorwhen eventoccurs in the database in, and is denoted aswith its lengthwhere.
The lifespan length ofis calculated as follows: , with the unit of measurement being temporal type.
For example, when there is a great rise in the opening price (at an association of 0.6) for stock on 20 October and another rise on 20 December during the observation period October to December, if day is chosen as the temporal type, then the lifespan length of the event is 61 days.
Corollary 1.
Starting temporal factorand ending temporal factorof the lifespan offor the same temporal type inare determined by the threshold. The length of lifespan is determined similarly.
Corollary 2.
Whenoccurs inat, there exists,, making. Similarly there exists,, making.
For the above stock , when the threshold is reduced from 0.6 to 0.4, the first date to observe great rise in opening price will probably be earlier, i.e., on or before 20 October; similarly, the last day to observe another great rise will most likely be later, i.e., on or after 20 December. Then lifespan of the event is conceivably extended. Similarly, when the affiliation threshold increases, in contrast, the lifespan may be shortened.
Definition 11.
With the fuzzy temporal event association rule , abbreviated as,is defined as the support of the fuzzy temporal event association rulein:
is defined as the confidence level of the fuzzy temporal event association rulein:
The distinctive feature of the fuzzy temporal event association rule is that it has both a fuzzy property and temporal dimension, so the confidence level and support of a fuzzy temporal event association rule can be used to measure the validity of the rule.
Giventhe number of temporal factors in interval, and let thresholdssuch that
The support and confidence level of all fuzzy temporal event association rules on the event space that satisfies the threshold requirement is obtained. Such a situation that satisfies fuzzy temporal event association rule is common in the stock market. For example, when the price of stock jumps high followed by a low in 2 days after an interval of 3 days and there are 7 such jumps out of all 20 opening high in a year for that stock, the annual validity is 7/20.
For the support and confidence level, clearly the following property holds:
Property 10.
Ifand all the others remain unchanged, then
Definition 12.
The effective lifespan of the fuzzy temporal event association ruleis determined by the temporal interval, wheremeans the first time whenand the fuzzy temporal event association rule are satisfied andthe last time. Similarly, the length of the lifespan is also determined by temporal factor, measured by temporal type.
3.2. Fuzzy Temporal Event Association Rule Mining Algorithm
The fuzzy temporal event rule mining algorithm (FTEAM algorithm) proposed in this paper includes three parts: attribute fuzzification, temporal type transformation, and fuzzy association rule mining.
In real world, the same database depicted by different temporal types may display different amounts of information. Taking stock trading data as an example, for the same trading period, if smaller temporal granularity is taken, it will have more temporal factors, i.e., more total data, which will give a more detailed view of the changing pattern of stock transaction with more dynamic information and, of course, more noise. In this case it may be possible to extract more features and retain more details of the transaction. In contrast, with larger temporal granularity, trading data are more noise tolerant and more likely to show features and trends. In particular, Ouyang Weiming et al. [35] demonstrated that the validity of association rules relates to temporal type. The choice of temporal type is critical to the validity of association rules. By selecting different temporal types, the database can be temporally transformed and reorganized into different temporal granularities, and correlation is mined at each granularity while considering commonality and individuality. The mining steps and algorithm are as follows.
The FTEAM algorithm:
Step 1 For one or more objects in , select specific attributes to mine, based on the object’s features.
Step 2 Based on practical experience and circumstances, select one or more suitable temporal types and transform and reorganize the raw data to form temporal events.
Step 3 Based on the actual situation of specific attributes and mining requirements, predetermine the number of of the attribute state. Assume that domain covers the values of attribute in all temporal events of the specific temporal type in , where and are respectively the minimum and maximum values of . With the K-means clustering algorithm clustering values of the selected attribute with a pre-determined number , cluster centroids are obtained, on which basis the domain of the attributes is delimited into k attribute state intervals , .
Step 4 The midpoint of two adjacent clustering centers is taken as the boundary point between two adjacent state intervals. Considering the fuzziness of the attribute state, set the proportion of interval cross-boundary part to 2c% (c-value is the extension ratio of the boundary point), then and . Combing and , the attribute domain is divided into intersecting attribute state subintervals , which correspond to the fuzzy states of the attribute .
Step 5 Select the fuzzy membership function, and calculate the fuzzy membership degree of the attribute value of each temporal factor on each fuzzy attribute state interval in , to obtain the new fuzzy temporal state event . Then set the fuzzy threshold to transform events into a fuzzy temporal event set .
Step 6 Apriori algorithm [24,35] is applied to mine possible frequent sets and association rules among the fuzzy temporal event sets in Steps 6.1 to 6.3.
Step 6.1 Scan the fuzzy temporal event set to obtain a set of non-duplicate fuzzy temporal events, noted as (called pre-1 sized frequent set). Scan the event set again and count the occurrences of all fuzzy events in to calculate their . Remove the items from that do not achieve the minimum support threshold (minsup) by (3.7), thus obtaining the fuzzy state 1-sized frequent set .
Support:
Step 6.2 Set (pre-2 frequent sets) containing two states is formed after combination and permutation of frequent set . The AND operation ““ is performed on all fuzzy temporal events two-by-two, scanning all combinations of events and counting the occurrences of items in . The items that do not achieve the minsup are dropped, resulting in the 2-sized frequent set of fuzzy jointly state events. Repeat the above steps to generate a 3-sized pre-frequent set based on the permutation of , and then obtain the 3-sized frequent set by minsup value deletion, and so on until the p-sized frequent set is obtained as a cut-off.
Step 6.3 Finally, based on the frequent sets of to , confidences are calculated for fuzzy joint state events that occur frequently within the frequent set, and if the minimum support requirement (11) and minimum confidence threshold (12) are met, the association rule holds.
Since the number of fuzzy temporal events is limited, the FTEAM algorithm stops after a finite step operation.
4. Numerical Experiments and Analysis of Results
To demonstrate the effectiveness of fuzzy-temporal data association rule mining model and algorithm (FTEAM algorithm), in this part, intra-day trading data of stocks on Lung Fu Bong are mined.
4.1. Description of the Experimental Data
Stocks on Lung Fu Bong are identified as typical outliers in the Chinese stock market, which meet any of the following criteria and should to be one of the top 3: (1) daily price deviation: ±7%; (2) daily turnover rate: 20%; (3) daily price amplitude: 15%; and (4) cumulative price deviation in three consecutive trading days: 20%. So when any stock is on the list, it indicates there is an obvious anomaly. The period from 1 October 2020 to 31 December 2020 was selected as the statistical time period. For the validity of the sample it is necessary to select the most representative stocks of lung fu bong. Therefore, Lanzi (002612.SZ) was selected, which was listed 36 times during 10 November 2020–31 December 2020, very frequently, indicating the complexity and irregularity of the selected temporal data.
Five temporal types were selected, with temporal granularity from small to large, including 1 min temporal, 5 min temporal, 10 min temporal, 15 min temporal, and 30 min temporal, based on which two comparison groups were formed, i.e., 5 min apart and 15 min apart. K-line data for 002612.SZ is exported from Comstar Financial Terminal for the period 2 November 2020–31 December 2020. By FTEAM algorithm, Python 3.8 and Excel 2016 were used to handle attribute states, dimensionless normalization, and code conversion of raw stock data. Table 1 illustrates fuzzy intervals and corresponding codes of the attribute states, where the first five attributes show the comparison of adjacent longitudinal temporal factors, and the last three reflect the inner trend within a transverse temporal factor.

Table 1.
The fuzzy intervals and corresponding codes of the attribute states.
Our first experiment was to mine the association rules in the raw daily data of Lanzi. After code-transforming the daily data using the same intervals, a total of 85 1-sized association rules were mined using Apriori algorithm, yet all of which implied a traversal correlation between the extreme states (Great Rise, Great Drop) of eight attributes, which has no real meaning. Due to the fact that the number of data mined was too small at only 43 items, the experiment was extended to the full year of 2020, where the association rules mined were still insubstantial. So, this is to say it is not feasible to find trade rules just based on raw daily data of stocks.
4.2. Results and Analysis
The FTEAM algorithm was applied to mine the adjacent association rules between different attributes of the same object (a special form as defined by Definition 8), which led to the following conclusions.
4.2.1. Discoverability of Fuzzy Temporal Association Features
Experiments show that these parameter thresholds directly affect the discovery of association rules at each temporal granularity, as conjectured from the nature of affiliation (Properties 4–6) and the definitions of support and confidence (Definitions 9 and 11). The threshold (as shown in Figure 1) flexibly adjusts the mined content. As it decreased from 0.7 to 0.5, the content and number of attribute state features mined under the same temporal type differed greatly, which demonstrates the necessity of mining data at different levels of granularity. Figure 1 and Table 2 indicate that the number of fuzzy temporal association rules decreased as the granularity increased, inferring that large temporal granularity makes it difficult to detect stock anomalies.
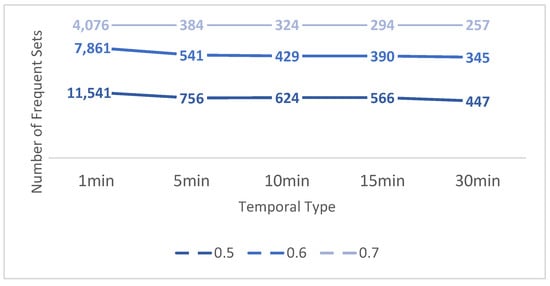
Figure 1.
Number of frequent sets for different temporal types at different thresholds.

Table 2.
Number of association rules for each temporal type at different support and confidence levels.
With all other parameters unchanged, minsup rose from 0.1 to 0.2, as shown in rows 1 and 3 of Table 2; additionally, minconf rose from 0.5 to 0.6 as shown in rows 1 and 2. It can be concluded that for the same stock trading data (at the same fuzzy affiliation threshold), the main factor affecting the mining of fuzzy temporal event association rules is the minsup, while minconf plays a role of fine-tuning the number of association rules.
Figure 2 gives the number of the frequent set mined under different temporal types. When small temporal granularity was taken, the attribute states concentrated more obviously in smooth or fluctuating states (right); yet, when large temporal granularity was taken, the attribute states diverged more greatly in great-rise and great-drop state (left). In terms of Lanzi, when temporal granularity changed from small to large, the extreme distribution of attribute states became more apparent. Furthermore, fuzzy temporal trading data at small granularity are more sensitive to changes in stock characteristics, making it easier to detect abnormal trading patterns.
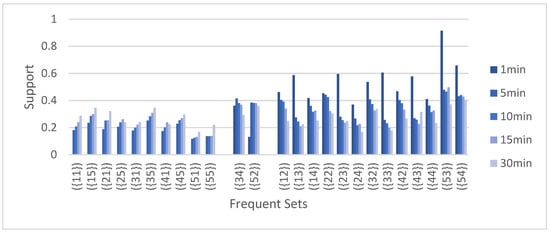
Figure 2.
Frequent set distribution at different temporal granularity.
By mining the trading data of Lanzi, the association rules common to all temporal granularity are shown in Table 3, where Rule 1 and 2 (line 1-2) illustrate that the states of the closing price, i.e., rise or drop, can reflect the state of the highest price and VOL. Support for the temporal association rule is higher at smaller granularity, indicating that smaller granularity is more effective in portraying the association between features and that small granularity reveals a stock’s anomaly. Rule 3 (line3) says lowest price shock (33) usually accompanies a slight drop in lowest price (32). This implies that when Lanzi’s price fluctuates slightly, especially around lowest price, the longer the fight between the long and short sides, and the more likely there will be a downward trend of the price. This is more evident in large granularity temporal type, which indicates that stock trading trends are more specific and visible in large granularity data.

Table 3.
Comparison of support for association rules at different temporal granularity of Lanzi.
4.2.2. Predictability of Fuzzy Temporal Event Association Rules
The inclusion of temporal granularity makes it possible to predict trading events that may be hidden when using standard approaches. Setting the following parameters, threshold = 0.6, minsup = 0.1, minconf = 0.6, experiment, yields 15 association rules between adjacent disparate attribute states (see Table 4). The rules are roughly divided into two categories, one with three rules concentrating on opening price and price trend: (1) small drop in opening price (12) in the previous temporal factor leads to a small drop in price trend (62) in the following temporal factor; (2) a shock in opening price (13) in the previous temporal leads to a stable fluctuation in price trend (63) in the following temporal; (3) a small rise in opening price (14) in previous temporal state corresponds to a small increase in price trend (64) in the following temporal state. These association rules have a relatively high degree of confidence in all temporal types, with validity generally reaching around 0.9, where associations very clearly occur. This suggests that for the five-day temporal type, the state of opening price of the previous temporal factor can be used to predict the state of Lanzi’s Price Trend of the following temporal factor. The following 12 rules mean small fluctuations in volume and price in the previous temporal factor easily lead to a low turnover state immediately following. Further, it demonstrates that volume states in the previous temporal factor are highly relevant to the trend of turnover rate in the immediate following temporal factor.

Table 4.
Comparison of confidence for 1-sized fuzzy temporal adjacency association rules.
In experiments of raw daily data, these rules do not hold at all. Moreover, it illustrates that FTEAM algorithm is capable of identifying valid correlations between features at multiple temporal granularities, and thus provides appropriate predictions, which is crucial for the identification of some special stocks, such as the stocks on Lung Fu Bong.
4.2.3. Lifespan Validity of Fuzzy Temporal Event Association Rules
It is found that confidence of association rules for the same lifespan (see Definition 10) is different for different temporal granularities. It is not true that that the smaller or larger the granularity, the more effective the fuzzy temporal event association rules (see Definition 12). For example, as shown by the fuzzy temporal adjacency association rule (12→62) in Table 5, even though the rule holds in the time period, 2 November 2020–31 December 2020, in all five temporal types, the confidence is different. The results showed that confidence was best at 5 min and 10 min, and association rules were significantly more effective at the 5 min temporal type. In real stock trading, this finding can help grid strategies to find the optimal grid size and achieve maximum grid arbitrage returns with minimum capital. It is also a helpful reference for other intraday quantitative trading strategies.

Table 5.
Comparison of confidence for different temporal granularities of rule (12→62).
4.3. Conclusions of the Data Experiment
By effectively granularizing the raw data from multiple attribute dimensions (including the temporal dimension), the FTEAM algorithm can uncover hidden association rules and phenomena, including:
- (1)
- Small granularity of minute-level temporal type can mine many valid temporal association rules;
- (2)
- Large granularity of minute-level temporal type gives a better indication of the trend in the data;
- (3)
- When different temporal types are taken, it is possible to uncover both common and unique association rules, and common association rules have different lifespans and validity under different temporal types, as well as different meanings;
- (4)
- The choice of affiliation intervals and affiliation thresholds for fuzzy code transformation affects the discovery of temporal association rules;
- (5)
- The settings of thresholds for the fuzzy temporal association rule, consisting of those of minsup and minconf, should be based on the stringency of the realistic need for the validity of rules. Generally, when the settings are small, more rules will be acquired. Larger settings may result in rules not mined. Furthermore, the adjustment of support has a significant impact on the number of association rules mined;
- (6)
- There exists a very niche association event with low support for the previous event, but a high level of confidence in the overall association rules.
Experimental results show that the fuzzy temporal event mining model has significant academic value in theory and application, mainly insofar as (1) the model can discover the anomalous characteristics of special stocks under different granularity. For example, there is a clear tendency for Lanzi to have minute price swings in the same direction by small margins, which will manifest itself in the form of broad price oscillations over a longer temporal period; (2) the model has significant effectiveness in predicting stock trends at different levels of granularity. For example, it was found that in Lanzi’s case previous temporal state of volume and price directly affects the trend of trading volume in the immediate following temporal state; (3) the model and algorithm are capable of discovering frequent features and association rules at various levels of temporal granularity, which, however, cannot be found in conventional data analysis.
5. Conclusions
To efficiently handle temporal data streams, this paper proposed to pre-process and re-structure raw data from a perspective of attribute state fuzziness and temporal type. Fuzzy temporal events were defined, their properties and operations deduced, and a rule mining mode with a fine algorithm was proposed to mine fuzzy temporal event associations. This work extends models for temporal data mining and enhances the performance and quality of temporal data association rule mining algorithms. The original information contained in the data was preserved, and flexible control of its volume and precision through temporal and state granularities is gained when multi-level and all-round data features were extracted and hidden knowledge was discovered from temporal data streams. Experimental results on intraday trading data of stocks on Lung Fu Bong indicate that the model and algorithm are highly sensitive to abnormal stock trading, as it uncovers trends hidden in daily trading data as well as related events. Statistically, these are useful in guiding the decision making of quantitative trading with high intraday frequency.
The fuzzy temporal event mining model mode studied in this paper is primarily concerned with raw data reconstruction. When it comes to temporal types, fuzzy temporal event association rules (see Definition 8) can still be further studied in a number of ways:
- (1)
- In life, a large number of correlations among events do not occur immediately afterwards, as there is a buffer period. The adjustment of r-value in the fuzzy temporal association rules will uncover more undiscovered correlations.
- (2)
- There may be more undiscovered correlations mined with adjusting of h, which does not restrict itself to the following temporal factor.
- (3)
- Models for mining association rules do not necessarily restrict themself within the same object . Take stock as an example. A great rise in the price of stock may lead to a small drop in the price of stock and stock .
- (4)
- Based on actual experience and transaction need, the number of can take different values. In Lanzi’s case, five were taken. However, the rise and drop of prices can be further divided into more distinct groups, and then a richer set of correlation rule events may be gained.
- (5)
- Currently only event attributes are fuzzified, but time is also a key attribute dimension. Fuzzifying temporal states is also extremely useful, in, e.g., mining and discovering fuzzy periodic rules.
In addition, all other parameters in the model need further exploration and should be reasonably set based on actual trading data. A more effective and specific method of parameter moderation still needs to be found, as reasonable parameter setting helps improve the speed and accuracy of the algorithm, as well as the effectiveness and practicality of association rules.
Author Contributions
Conceptualization, A.Z. and Z.M.; methodology, software and validation, A.Z.; writing—original draft preparation, A.Z. and Z.M.; writing—review and editing, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NO.11871434).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: [http://vip.stock.finance.sina.com.cn/q/go.php/vInvestConsult/kind/lhb/index.phtml and https://tushare.pro/document/2?docid=24].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laxman, S.; Sastry, P.S. A survey of temporal data mining. Sadhana 2006, 31, 173–198. [Google Scholar] [CrossRef]
- Lin, W.; Orgun Mehmet, A.; Williams Graham, J. An Overview of Temporal Data Mining. AusDM 2022, 8, 83–90. [Google Scholar]
- Lim, B.; Zohren, S. Time Series Forecasting with Deep Learning: A Survey. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy Sets and Information Granularity. Adv. Fuzzy Set Theory Appl. 1979, 11, 3–18. [Google Scholar]
- Li, X.; Zhou, J.; Pedrycz, W. Linking granular computing, big data and decision making: A case study in urban path planning. Soft Comput. 2020, 24, 7435–7450. [Google Scholar] [CrossRef]
- Wang, G.; Hong, Y. Multi-Granularity Cognitive Computing—A New Model for Big Data Intelligent Computing. Front. Data Domputing 2020, 1, 75–85. [Google Scholar] [CrossRef]
- Yu, F.; Cai, R. Optimized fuzzy information granulation of temporal data. In Proceedings of the 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery, Shandong, China, 10–12 August 2010; Volume 1, pp. 419–423. [Google Scholar] [CrossRef]
- Mitsa, T. Temporal data mining. In Chapman & Hall/CRC Data Mining and Knowledge Discovery Series; Chapman & Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lovrić, M.; Milanović, M.; Stamenković, M. Algoritmic methods for segmentation of time series: An overview. J. Contemp. Econ. Bus. Issues 2014, 1, 31–53. [Google Scholar]
- Rawassizadeh, R.; Momeni, E.; Dobbins, C.; Gharibshah, J.; Pazzani, M. Scalable Daily Human Behavioral Pattern Mining from Multivariate Temporal Data. IEEE Trans. Knowl. Data Eng. 2016, 28, 3098–3112. [Google Scholar] [CrossRef]
- Chen, C.-H.; Hong, T.-P.; Tseng, V.S. Fuzzy data mining for time-series data. Appl. Soft Comput. 2012, 12, 536–542. [Google Scholar] [CrossRef]
- Chen, C.-H.; Hong, T.-P.; Lin, S.-B. Mining fuzzy temporal knowledge from quantitative transactions. In Proceedings of the 2011 International Conference on System Science and Engineering, Macau, China, 8–10 June 2011; pp. 405–409. [Google Scholar] [CrossRef]
- Chen, C.-H.; Lan, G.-C.; Hong, T.-P.; Lin, S.-B. Mining fuzzy temporal association rules by item lifespans. Appl. Soft Comput. 2016, 41, 265–274. [Google Scholar] [CrossRef]
- Hong, T.-P.; Lan, G.-C.; Su, J.-H.; Wu, P.-S.; Wang, S.-L. Discovery of temporal association rules with hierarchical granular framework. Appl. Comput. Inform. 2016, 12, 134–141. [Google Scholar] [CrossRef]
- Meng, Z.; Jiang, H.; Jiang, M.; Liu, Y. An Algorithm of Discovering Approximate Periodicity Based on Self-Organizing Map for Temporal Data. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Hainan, China, 24–27 August 2007; Volume 3, pp. 293–297. [Google Scholar] [CrossRef]
- Mahmood, N.; Burney, A. Advances in Fuzzy Temporal Relational Databases: A Review. WSEAS Trans. Inf. Sci. Appl. 2011, 8, 171–184. [Google Scholar]
- Wu, H.; Long, H.; Wang, Y.; Wang, Y. Stock index forecasting: A new fuzzy time series forecasting method. J. Forecast. 2021, 40, 653–666. [Google Scholar] [CrossRef]
- Chen, W.; An, J.; Li, R.; Fu, L.; Xie, G.; Alam, B.M.Z.; Li, K. A novel fuzzy deep-learning approach to traffic flow prediction with uncertain spatial–temporal data features. Future Gener. Comput. Syst. 2018, 89, 78–88. [Google Scholar] [CrossRef]
- Xiao, F.; Ding, W. Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl. Soft Comput. 2019, 79, 254–267. [Google Scholar] [CrossRef]
- Mazarbhuiya, F.A. An Efficient Algorithm for Mining Fuzzy Temporal Data. Int. J. Math. Trends Technol. 2016, 37, 1–5. [Google Scholar] [CrossRef]
- Mazarbhuiya, F.A.; Shenify, M. Finding Local and Periodic Association Rules from Fuzzy Temporal Data. In Proceedings of the 2014 International Conference on Advances in Big Data Analytics, Beijing, China, 4–7 August 2014; Volume 9, pp. 21–24. [Google Scholar]
- Lee, W.-J.; Jiang, J.-Y.; Lee, S.-J. Mining fuzzy periodic association rules. Data Knowl. Eng. 2008, 65, 442–462. [Google Scholar] [CrossRef]
- Purificación, C. Fuzzy temporal association rules: Combining temporal and quantitative data to increase rule expressiveness: Fuzzy temporal association rules. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 64–70. [Google Scholar] [CrossRef]
- Owuor, D.; Laurent, A.; Orero, J. Mining Fuzzy-Temporal Gradual Patterns. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; IEEE: New Orleans, LA, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Alom, M.F. Mining Local Patterns from Fuzzy Temporal Data. Int. J. Eng. Appl. Sci. 2016, 2, 257768. [Google Scholar]
- Dogan, O.; Kem, F.C.; Oztaysi, B. Fuzzy association rule mining approach to identify e-commerce product association considering sales amount. Complex Intell. Syst. 2022, 8, 1551–1560. [Google Scholar] [CrossRef]
- Keyvanpour, M.R.; Mehrmolaei, S.; Etaati, A. PLI-X: Temporal Association Rules Mining in Customer Relationship Management Systems. Comput. Knowl. Eng. 2020, 2, 29–48. [Google Scholar] [CrossRef]
- Sharmila, S.; Vijayarani, S. Association rule mining using fuzzy logic and whale optimization algorithm. Soft Comput. 2021, 25, 1431–1446. [Google Scholar] [CrossRef]
- Chen, C.-H.; Chou, H.; Hong, T.-P.; Nojima, Y. Cluster-Based Membership Function Acquisition Approaches for Mining Fuzzy Temporal Association Rules. IEEE Access 2020, 8, 123996–124006. [Google Scholar] [CrossRef]
- Poli, V.S.R. Fuzzy Temporal Data Mining Algorithms. EasyChair, No. 3560. 2020. [Google Scholar]
- de Campos, S.P.V. Fuzzy neural networks and neuro-fuzzy networks: A review the main techniques and applications used in the literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- El Meftahy, M.; El Kabbouri, M. Application of neuro-fuzzy methods for stock market forecasting: A systematic review. Int. J. Account. Finance Audit. Manag. Econ. 2022, 3, 437–454. [Google Scholar]
- Li, H.; Wei, M. Fuzzy clustering based on feature weights for multivariate time series. Knowl.-Based Syst. 2020, 197, 105907. [Google Scholar] [CrossRef]
- Ouyang, W.-M.; Cai, Q.-S. Discovering association rules with temporal constraints in databases. J. Softw. 1999, 10, 527–532. [Google Scholar]
- Rahman, T.; Kabir, M.M.J.; Kabir, M. Performance Evaluation of Fuzzy Association Rule Mining Algorithms. In Proceedings of the 2019 4th International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 20–22 December 2019; IEEE: Khulna, Bangladesh, 2019; pp. 1–4. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).