Abstract
The social, scientific and technological development of recent years has encouraged the incorporation of computational thinking in the school curriculum of various countries progressively, starting from early childhood education. This research aims to characterize future kindergarten teachers’ traits of didactic-mathematical and computational knowledge presented when solving and posing robotics problems. Firstly, aspects of the mathematical and computational knowledge of the participants (97 students of the subject of Didactics of Mathematics of the Degree in Early Childhood Education at a Spanish university) were identified when they solved problems as users of the Blue-Bot didactic robot. Secondly, we analyzed their justifications for reflecting on the design of robotics problems. The results indicate that future teachers present characteristics of didactic-mathematical knowledge when solving and designing robotics problems, although errors and ambiguities are evident, especially in the procedures and representations of the programming. These shortcomings significantly influence the didactic suitability of the robotics problems they design. From a future perspective, in the training of future teachers, it is considered relevant to incorporate didactic-mathematical and computational knowledge that allows them to develop logical, spatial and computational thinking.
Keywords:
computational thinking; early childhood education; mathematical thinking; robotics problems; teachers in training; ontosemiotic approach (OSA) MSC:
97D40; 97D50; 97P40
1. Introduction
The social, scientific and technological development of recent years has fostered changes in the global educational system, supporting the incorporation of computational thinking (CT) as a key aspect for students living and acting in the contemporary world; according to Wing [1] and Zapata-Ros [2], this incorporation must occur progressively starting from an early age from the notion of unplugged CT.
Different Latin American countries [3] have introduced CT in the school curriculum, starting from early childhood education [4], either through a specific subject or by introducing CT in the subject of mathematics. The current curricular reform of basic education in Spain, specifically the new curriculum of the autonomous region of Catalonia, makes explicit that one of the specific competences that the student must develop in the subject of mathematics at the end of basic education is to use CT for the development of mathematical processes, in particular, to solve problems and model efficiently [5]. In the case of the second cycle of early childhood education (students from 3 to 6 years old), the current Spanish curriculum (as well as, soon, the one of Catalonia that is currently in preparation) [6], for the first time, incorporates CT in the area of discovery and exploration of the environment, with the purpose, among others, of developing the problem-solving process in students [7,8]. This approach allows us to interpret that there is an integration between computational thinking (CT) and mathematical thinking (MT) in the curricular definition of the Ministry of Education of Spain at the most diverse educational levels.
To attend to this regulatory demand, there is a need to introduce teacher training programs that promote CT from early childhood education [9]. Therefore, it is necessary to guide teachers and future teachers of early childhood education to develop MT through CT and reflect on it, either from the resolution of programming problems with the use of educative robots [10] or from the design of problems or a didactic sequence with the use of educative robots (Blue-Bot or similar) adapted to the first ages ([11,12,13,14,15,16]).
In the last five years, we can find research that studies the pedagogical practices and conceptions of teachers regarding the use of robots or the development of CT through robotics in the classroom [17,18,19] and, in particular, those related to the use of educative robots in early ages [20,21,22,23]. These studies have highlighted the research agenda that aims to study what knowledge teachers must possess for the exercise of teaching, which, beyond the pedagogical knowledge of the content [24], must be endowed with technological knowledge [25]. Within the framework of the ontosemiotic approach (OSA) [26], there is a model of didactic-mathematical knowledge (DMK) which, in Latin terms, refers to teachers’ knowledge about mathematical content (MK) and about their teaching (DK)—didactic and pedagogical aspects of the teaching and learning processes. This model interprets and characterizes the teacher’s knowledge from three dimensions: the mathematical dimension, the didactic dimension and the meta-didactic-mathematical dimension [27].
On the one hand, for Pino-Fan and Godino [27], the mathematical dimension of the DMK includes two subcategories of knowledge: common knowledge of the content (knowledge about a specific mathematical object that is considered sufficient to solve problems or tasks proposed in the mathematics curriculum of a given educational level) and expanded knowledge of the content (it is further on in the curriculum of the educational level in question, or at a next level). On the other hand, the didactic dimension of DMK includes the following subcategories of knowledge: specialized knowledge of the mathematical dimension (epistemic facet); knowledge about the cognitive aspects of students (cognitive facet); knowledge about the affective, emotional and attitudinal aspects of students (affective facet); knowledge about the interactions that arise in the classroom (interactional facet); knowledge about resources and means that can enhance student learning (mediational facet); and knowledge about the curricular, contextual, social, political and economic aspects which influence the management of student learning (ecological facet). Finally, the meta-didactic-mathematical dimension characterizes the knowledge that teachers need to reflect on their practice, identify and analyze the set of norms and meta-norms that regulate the teaching and learning processes of mathematics, and evaluate the didactic suitability to find possible improvements in the design and implementation of these processes [28,29].
For each of the components of didactic-mathematical knowledge, the OSA has “theoretical and methodological” tools that have been described and used in several investigations [26,30,31]. For example, for the development of instruments that allow the evaluation and systematic analysis of the knowledge of teachers regarding the mathematical dimension (common and expanded knowledge) and the epistemic facet of DMK. The “ontosemiotic configuration” tool allows the description and characterization of the primary mathematical objects—representations/language (terms, expressions, notations, graphs) in their diverse registers; problem situations (intra- or extra-mathematical applications, exercises); concepts and definitions (introduced through definitions or descriptions); propositions (statements about concepts); procedures (algorithms, operations, calculation techniques); and arguments/justifications (statements used to validate or explain propositions or procedures)—that are produced through the respective mathematical processes of communication, problematization, definition, enunciation, elaboration of procedures (creation of algorithms and routines) and argumentation that are activated in the mathematical practices that teachers develop in solving a problem [32,33], or as part of a problem planning (or problem sequence) for the classroom [34,35]. In addition, mathematical knowledge includes the description of errors and ambiguities committed by teachers from a mathematical point of view.
For the development of instruments that allow the systematic evaluation and analysis of the knowledge of teachers regarding the meta-didactic-mathematical dimension, the didactic suitability criteria (DSC) tool is operational. According to Font, Planas and Godino [36], the DSC are characterized as follows: Epistemic Suitability, to assess if the mathematics being taught is “good mathematics”; Cognitive Suitability, to assess, before starting the instructional process, if what one wants to teach is at a reasonable distance from what students know, and after the process, if the acquired learning is close to what was intended to be taught; Interactional Suitability, to assess if interactions resolve students’ doubts and difficulties; Mediational Suitability, to assess the adequacy of the material and temporal resources used in the instructional process; Affective Suitability, to assess the involvement (interests and motivations) of students during the instructional process; Ecological Suitability, to assess the adequacy of the instructional process for the educational project of the school or institution, the curricular guidelines, and the conditions of the social and professional environment. These criteria are split into components and indicators to become operational in the exercise of analysis and assessment of instructional processes. The criteria and components of didactic suitability are detailed in Table 1. The full table with the indicators can be found in Breda, Pino-Fan and Font [28].

Table 1.
Didactic suitability criteria and components.
The notion of didactic suitability has had a relevant impact on teacher training in several countries; such impact evidences the use of DSC in several investigations on teacher training who teach mathematics, in which this construct is used. However, it is not used within the framework of a training device expressly designed to teach didactic suitability as a tool to organize reflection and the development of the teachers’ meta-didactic-mathematical knowledge about their own practice, both in primary and secondary teacher training courses [37,38,39] and for future early childhood teachers in the context of Catalonia and future primary school teachers for the use of educative robots.
Some authors propose models of teacher training programs that allow teachers to acquire the necessary knowledge to develop CT in students [40,41]. In particular, Estebanell et al. [40] propose a model for initial teacher training that contemplates four levels for the development of CT: (1) User: aims to make teachers ask questions about how to use a given computational language to address problems with a robot, video game, application, etc.; (2) Reflective User: teachers that reflect on what they have done when developing a computational problem; (3) Teacher: teachers facing the challenge of deciding what to teach, what they expect their students to learn from CT and what resources and strategies will be implemented; and (4) Reflective Teacher: teachers reflecting on the teaching and learning process related to CT.
Regarding the User level, Seckel, Vásquez, Samuel and Breda [10] propose a classification in relation to the errors that teachers make in programming planning, which are the following: (a) error due to the absence of a function in the programming, not programming one or more functions to respond to a statement, or not clearing the programming to resolve a second statement; (b) error due to excessive quantification of a function in programming, the user does not understand the relationship between the characteristics of the carpet (scheme or grid with possible robot routes) and the displacement of the robot, e.g., the user programming by estimating without considering the measurements of the grids of the carpet and the 15 cm that the robot advances; (c) error due to misunderstanding of a type of programming, e.g., the user does not understand that the rotation of the robot is 90°, believes that it rotates and advances at the same time, or does not consider that the programming of each pause corresponds to a second; and (d) error when applying previous knowledge, e.g., the user presents difficulties in applying his or her knowledge of spatial orientation, making misuse of the planning cards of the programming.
Moreover, it is necessary for teachers to recognize two basic aspects when designing problems [42]. The first aspect is related to the idea of a robotics problem-type task, the resolution of which implies that the robot passes from an initial state to a final one, through the planning of a sequence of actions (intermediate states that are programmed). The second aspect is related to the criteria that should guide the approach of a problem or a sequence of problems; these are as follows: (1) present progressive complexity, (2) refer to known and unknown aspects and (3) place the problem in an environment (scenario). Although there are several investigations that try to infer the knowledge of teachers who teach mathematics, there are few that try to investigate the characteristics of didactic-mathematical knowledge and computational knowledge of teachers who work with students of the first ages. In this sense, the general objective of this research is to characterize the traits of didactic-mathematical and computational knowledge presented by future early childhood education teachers solving and posing robotics problems. To do this, first, we identified aspects of mathematical and computational knowledge presented by future teachers when they solved problems as users of the educative robot Blue-Bot; secondly, we analyzed their justifications when they reflected on their design of robotics problems.
2. Materials and Methods
This research is part of a qualitative and interpretive paradigm [43] that, based on a case study [44], sought to understand and explain features of the didactic-mathematical-computational knowledge presented by 97 students of the Early Childhood Education Degree in a Spanish university when developing a didactic sequence of computational education (using educative robots), designed by the authors of the article, as well as to analyze the didactic suitability of their designs of robotics problems.
2.1. Description of the Educative Robot Used
The educative robot used was marketed under the name Blue-Bot (see Figure 1). It is an analog robot (although it has a mobile application, it was not used in this case); that is, to indicate the instructions for the movements the user wants to perform, he or she must press the keys that it has on its back. The robot memorizes the sequence of keystrokes that the user has made; every time one wants to start a new sequence of orders, one must press the delete key. Otherwise, the new orders are added to the previously memorized ones. With each press forward (or backward), the robot advances (or retreats) 15 cm. With the press to turn (right or left), the robot only rotates and does not advance. The programming can consider that the robot makes stops in its route by including pressing the “Pause” key.

Figure 1.
Educative robot used in the implementation.
To write or represent the commands (keystrokes) or algorithms that the robot must follow, the manipulative material shown in Figure 2a can be used. These are small, plasticized cards that represent each of the keys of the robot. Each card is played as many times as necessary so that students can write or represent the algorithm of their program so that the robot completes the required route, before or after running the program.
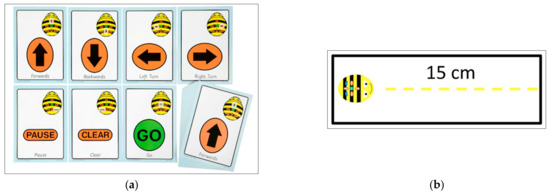
Figure 2.
(a) Cards to represent the program’s algorithm. (b) Rectangle card, a resource that represents the distance that the robot covers with each press of forward or backward.
Another manipulative resource that can be used by both students and teachers is a rectangular card with the longest side length of 15 cm (Figure 2b). It is useful to be able to count how many keystrokes must be given to the forward (or backward) key so that the robot moves from one specific point to another.
2.2. Context and Participants
The Early Childhood Education Degree in the Spanish university where the study was carried out is composed of four courses of 240 European Credit Transfer and Accumulation System (ECTS) credits, and one ECTS credit is equivalent to 25 h of student work, which includes everything (lectures, theoretical or practical classes, personal study, participation in seminars, work in tasks or projects, preparation and performance of assessment tests). In the 1st and 2nd years, the students should pass 120 ECTS credits of basic training in subjects such as psychology, music, art, languages, syllabus, educative system, mathematics and science. Concretely, the basic training includes 6 ECTS credits of an interdisciplinary subject that involves mathematics and science (in 2nd level), among others. This is the first time in the degree that students are in contact with mathematics. In the 3rd and 4th years, students take 120 ECTS credits, 99 of which correspond to compulsory subjects focused on the pedagogical knowledge aspects and 21 to diverse elective subjects. The basic training and the compulsory training both include some credits of practice subjects that involve students going to schools or training centers to learn with teachers and their pupils.
In the 3rd level, students are involved in the compulsory subject called Didactics of Mathematics in which this study is developed. The participants of the study were two groups of students of the subject of Didactics of Mathematics of the Degree of Early Childhood Education at a Catalan university (Catalonia, Spain), a group of 50 students who study in the morning shift and a group of 47 students who study in the afternoon shift, in total 97 people.
Since this research is about the study of a case, qualitatively analyzed in its depth, a sampling process of the participating subjects was not carried out. However, all the students in two groups of the Early Childhood Education Degree who were studying the Didactics of Mathematics subject were considered.
The participating future teachers were organized into work teams to carry out the didactic sequence that was proposed to them (designed by the authors); in total, there were 17 work teams called A1, A2, A3, A4, A5, A6, A7, A8, A9, B1, B2, B3, B4, B5, B6, B7 and B8.
The data were obtained from the recordings of some of the sessions implemented (detailed below); from the field notes of the first and second authors, who acted as teachers of the group making a participant observation; and from the documents written by the future teachers, called D1, D2 and D3.
2.3. Description of the Didactic Sequence Implemented
The didactic sequence implemented with future teachers of early childhood education was designed by the authors of the article based on the CDS and considering an active and interactional perspective of teaching and learning.
Learning is not a simple reproduction of contents that must be learned; pupils play a decisive role in the process of learning to build and rebuild their knowledge. However, the contents which pupils have to learn are the result of a widely accepted social elaboration. In this sense, the role of the teacher is complex; he or she should connect the pupils’ construction processes with culturally organized collective meanings.
In the field of mathematical learning, according to Abtahi [45] with a Vygotskian perspective [46], learning is not possible without interactions, especially social interactions. Pupils live and interact in several social worlds of mathematical tools and signs, but considering the syllabus or, more generally, the knowledge demands of system schools, there are mathematical worlds that pupils cannot interact with because they do not know them, such as the computational knowledge that we would like to teach in this case. Vygotsky [46] introduce the idea of the zone of proximal development (ZPD) which is located among the mathematical worlds that pupils can interact with and the others that they cannot. The interactions among the worlds, inside the ZPD, are not possible without a person with more knowledge who is also participating. In the ZPD, pupils can construct higher-level knowledge with their peers, some of them with more advanced knowledge, or with the teacher than they can alone. This fact allows them to learn mathematics independently.
According to Font [47], the most effective teaching is that which is based on the learner’s effective development, not in order to adapt to it, but to make it progress through the zone of proximal development and in this way generate new zones of proximal development.
The didactic sequence included several sessions and the autonomous work of the teams. The implementation of the didactic sequence was carried out following the same scheme and indications with the group of students of the morning shift as with the group of the afternoon shift. Session 1 was implemented on the date indicated in Table 2 with half a group and on the following date with the other half group, to have a suitable ratio of participants to make the necessary observations.

Table 2.
Outline of the implemented didactic sequence.
Table 2 also includes an outline of the deployment sessions performed with each of the groups in the two shifts.
2.3.1. Session 1 and Following Autonomous Work
The didactic objective of session 1 focused on the development of the skills related to logical–mathematical and computational thinking of children aged 5–6 years by solving problems with an educative robot. In this session, held in the classroom (and in the corridors of the Faculty) students had to “live” the activity developed in it as users of the robot, that is, they were expected to act like children aged 5 or 6 years [40].
With the presentation of the tasks, each of the work teams was given a Blue-Bot, a pack of cards to represent the programming planning algorithms, a package of rectangles of 15 cm and a dossier with the tasks to be performed. We only explained that they had to address and answer the questions in the dossier and explain what they had done to answer them, and no further information on the workings of Blue-Bot or on the use of the other resources released was given.
Each page of the dossier contained a task, and each task consisted of answering several questions based on the use and manipulation of the Blue-Bot and explaining the actions taken to answer them (at that time, the future teachers would be acting as reflective users of the robot) [40]. On the one hand, as one moves through the pages of the dossier, the complexity of the task increases in relation to the actions that must be taken to answer the questions. On the other hand, each task of the dossier, in turn, responds to certain specific objectives of development of the CT that connects various contents such as argumentation, logical–mathematical reasoning, and spatial and metric reasoning in a transversal way. The questions in the dossier are indicated in Table 3:

Table 3.
Questions for each task included in the dossier.
The questions in task 1 were answered only by teams that did not know at all about the use of Blue-Bot. If they had had any previous experience, they could skip that task.
Each work team presented a PDF document including the answers to the questions of the dossier together with the explanation of the actions carried out with the Blue-Bot to answer them. We have called this document D1.
2.3.2. Session 2 and Following Autonomous Work
This session, held in the classroom in a large group, aimed to help participants identify key aspects of the characteristics that a problem must have and the subprocesses that must be carried out to solve it. To do this, a video is watched about a children’s story where the characters encounter a problem in which the processes that they must follow to solve it are shown. The expectation was that from the visualization and following reflection in the large group they could make inferences so that some of these characteristics could be agreed upon through sharing.
The video watched is named “Per quatre cantonades de no res” and is available at the following link https://www.youtube.com/watch?v=H5fVi0qMhVc&ab_channel=Coronacontes (accessed on 8 January 2023). The official language of the Faculty is Catalan, so the video was viewed in this language. However, there is an English version with the title “Four Little Corners” that is available at the following link https://www.youtube.com/watch?v=LHgdj3piX3Q (accessed on 8 January 2023).
The author of the book on which the video is based is Jerome Ruillier, and the original French title of the book, from 2004, is “Quatre petits coins de rien du tout”. This story is usually used in education on inclusion issues, although it is a clear example of how a problem should be to become meaningful and close to the participants since they are interested in solving it, and how the actions for its resolution should be developed: present a problematic context; establish a specific question; meet to brainstorm that leads to the proposal of possible solutions (hypothesis); discard some of the possible solutions for various reasons; repropose others; try to implement them (and so on until finding one that seems to work); check that the found solution works; congratulate ourselves on the cooperative work done; and celebrate having been able to solve the problem (in the story, the part of reviewing what we could have done better does not appear).
After watching the video, students in teams are prompted to think about characteristics or relevant aspects of a good problem to use for didactic purposes. Next, a large group shares in listing these aspects. Then, each group presents a document with their list in a forum of the subject platform to share it. This document has been named D2.
After this session, participants are asked to work as a team to design a session for children aged 5–6 years with educative robots that include elements of the didactic use of the problems identified in session 2 and the experience lived in session 1. The participants must decide what aspects they should contemplate and include in an explanatory document that they must deliver (according to the categories proposed by Estebanell et al. [40], the future teachers would be acting as teachers in the use of the robot). The document had to be sent to a forum on the subject so that the other teams could read it. This document has been named D3.
2.4. Analysis Tools
To identify aspects of mathematical and computational knowledge presented by future childhood education teachers when solving problems as users of the educative robot Blue-Bot, we consider two instruments of data collection obtained in the development of session 1 (Table 2). The first was the document D1 with the answers of the future teachers to the problems raised in the dossier and the explanation of the actions taken to achieve them. In particular, for the analyses, questions 3a, 3b, 3c, 4b, 4c, 5b, 5c and 6a were considered, as they are those in which some primary mathematical objects can emerge. In addition, the recordings of the development and resolution of the problems in the dossier when the future teachers manipulated the Blue-Bot robot were considered.
Both the document D1 and the recordings were analyzed using two theoretical contributions explained in the introduction. That is, to identify characteristics of mathematical and computational knowledge, the notion of ontosemiotic configuration present in the DMK model of the OSA was used [27]. Specifically, we sought to identify which primary mathematical objects—representations/languages, concepts and definitions, propositions, procedures and arguments/justifications—emerged in the mathematical practices developed by the teachers in solving the problems proposed in the questions of the dossier D1 specified above and when manipulating the Blue-Bot. In addition, the categories of the errors made by teachers when programming the educative robot Bee-Bot proposed by Seckel, Vásquez, Samuel and Breda [10] were used.
In session 2 (Table 2), all the teams wrote a document that we have called D2, with the characteristics that they believed should have a problem for didactic objectives. To collect all the characteristics, a content analysis of this document was carried out, the emerging characteristics were identified and the emerging characteristics that were coincident between the different teams were identified. The design of a robotics problem and its possible implementation with 5-year-olds carried out by the participants (in the document D3) were then considered. This document was analyzed, first, to identify which of the emerging characteristics resulting from the analysis of D2 appeared in D3, that is, if the key aspects of the characteristics that a robotics problem must have had been considered. In addition, it has been observed whether the characteristics that a robotics problem should present proposed by Arlegui and Pina [42] were contemplated.
Finally, to identify the suitability of the designs of the teams of research participants and determine their meta-didactic-mathematical knowledge, the DSC categories were used (Table 1).
Finally, from a triangulation of the analyses among the most expert authors in the use of the instruments, from the aspects of mathematical and computational knowledge and the meta-didactic-mathematical knowledge emerging in the previous analyses, it was possible to infer aspects of the didactic-mathematical and computational knowledge displayed by the participants when posing and solving robotics problems. This inference was triangulated with an expert in the theoretical framework of the ontosemiotic approach.
3. Results
In this section, we present the results referring to the analyses of sessions 1 and 2.
3.1. Results of Session 1
To infer traits of the mathematical and computational knowledge of the participants, after analyzing their answers to questions (3a), (3b), (3c), (4b), (4c), (5b), (5c) and (6a) of Table 3, from the notion of the epistemic configuration of the DMK model of the OSA, the evidence of the primary objects that emerged is presented in Table 4.

Table 4.
Emerging primary objects in solving robotics problems.
Related to the objects that emerge from robotics problem-solving practices, we find arguments and justifications. In particular, the arguments are related to the notion of a sequence. For example, to answer the question of whether different orders could help the robot arrive at the same place, 47% (8 out of 17) of the teams argued that they could, and five teams argue that this could occur not through different algorithms (or orders) but could occur through different paths. On the other hand, concerning the arguments related to the notion of measurement, to know how much distance the robot runs with each order to advance, a team argues that it can be known through the measurement by measuring instruments (meter or ruler) and four other teams argue that the distance is verified by the length of 15 cm of the rectangular card (Figure 2b).
In each order of advance, the robot runs 15 cm. We verified it by advancing the robot next to a 15 cm card, seeing that the distances coincided(B7)
However, a considerable number of teams (8 out of 17) only answer “15 cm” without arguing or justifying any reasoning. On the other hand, for problem 4c “How could we know how far the robot can go? Could the robot arrive at the class of…?”, some teams argued that it could be reached from programming with the cards, the measurement with the 15 cm card, the calculation of the distance between the two classes or the calculation of the number of movements made by the robot. However, most teams answered that another class could be reached by testing and checking different orders and/or different calculations; that is, they argued from the trial and error procedure.
To know where it can arrive, we must try different orders and calculate how much it can advance. In our case, we calculated it with the cards, and it was able to get from one class to another covering a distance of 8 m(A1)
Some comments are not related to the arguments of the procedures used, but to the characteristics of the electronic device; for example, 5.9% (1 out of 17) of teams argue that the reason that the robot stops walking is the lack of battery and not a limited number of movements.
Another emerging primary object in participants’ responses is propositions. For example, to know if the robot takes the same time to arrive with one algorithm as with a different one, several propositions have emerged; for example, it takes less time if it walks in a straight line, it takes longer when it turns, it always takes the same because it always advances at the same distance, it takes more or less depending on the number of orders given to the robot, and it takes more or less time depending on the planned algorithm. This last proposal was evidenced by 41.2% (7 out of 17) of the teams, according to the following evidence:
No, depending on the algorithm it will take more or less time to arrive. It is not the same to make a route all in a straight line as if we do it turning, etc.(B8)
Propositions also arise when answering problem 5c “Where is it better for the robot to run? What is the best itinerary?” Although the proposition has emerged that the best itinerary is the one that arrives fastest at the destination and that there is only one possible itinerary, the proposition that the best itinerary is in a straight line was assumed by 47% (8 out of 17) of the work teams. However, some participants, instead of explaining the best itinerary referring to the shortest distance or the shortest time, refer to the characteristics of the surface, as the following comment exemplifies:
The robot is better to run over a smooth surface, that is, there are no potholes, as this makes it difficult for the robot to walk(B1)
The language/representation object emerges in three of the problems posed to future teachers. Concerning the resolution of how the orders they give to the robot could be represented, the verbal–written representation appears, as does the iconic representation, and most teams (64.7%, 11 out of 17) report the symbolic representation through the cards offered by the Blue-Bot didactic package.
On the other hand, the iconic type of representation emerges to represent that different orders of the robot could serve to reach the same place. However, the representation is erroneous and ambiguous. It is erroneous because, considering that the robot leaves the same starting point, the two representations made do not take the robot to the same final destination, according to Figure 3a. In addition, the horizontal arrows are represented ambiguously because it is not known whether it represents the left or right turn. A similar error was observed in the representation made by the same team when explaining the robot’s round-trip algorithm (Figure 3b).
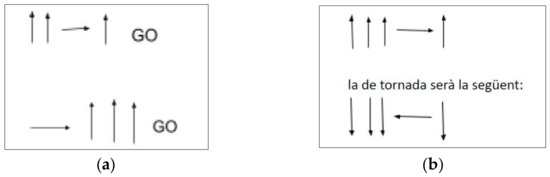
Figure 3.
(a) Representation of group B3 to explain that the robot arrives at the same destination from different routes. (b) Representation of group B3 to explain the way to and from the destination running by the robot. In the image, you can read “the way back is the following”.
At different times during the development of the activities, several groups made mistakes in the representation of the route from the programming cards, due to a lack of good spatial orientation, as shown in Figure 4.

Figure 4.
Inappropriate use of the programming cards.
It was also possible to observe the emergence of procedures. In particular, errors were observed in the procedure of programming the sequence that the robot should perform to reach a certain arrival point. According to the categories of Seckel, Vásquez, Samuel and Breda (2022), the most recurrent errors were those of error due to the absence of a function in programming, error due to excessive quantification of a function in programming and error due to misunderstanding of a type of programming. For example, there were cases in which participants did not delete the previous programming to perform new programming (they did not consider that the robot has memory); other cases were an excess of commands to reach the final destination and a failure to respect the distance of 15 cm that the robot walks in each section (Figure 5a); finally, there were cases in which the participants did not understand that the robot does not advance when turning 90 degrees (Figure 5b). These aspects were decisive in the low success of the robot arriving correctly at the destination of the route previously established by each team.

Figure 5.
(a) Error due to excessive commands. (b) Error due to misunderstanding of a type of programming.
Related to the procedures that appear to establish what distance there is from one class to the other class from the use of the robot, the emergence of distance calculation is observed from the estimation, the orders given to the robot, the measure of the length of the diagonal of the tiles of the class multiplied by the number of tiles traveled by the robot and, mostly, the arithmetic calculation that multiplies the number of movements that the robot performs by the length of the rectangular card (15 cm). On the other hand, considering the procedures contemplated by future teachers to answer how the way back (to go back) could be programmed and if part of the previous programming (to go) could be reused, ambiguities and errors are observed in the programming procedures of 88.2% (15 out of 17) of the work teams.
It will be in the same way as the trip to go but in reverse. That is, if we make two movements forward then we must give two backwards […]. No, because the robot has memory, therefore, we cannot reuse a specific part, since the entire sequence would be repeated(A2)
3.2. Results of Session 2
In session 2, the described work was carried out in the classroom, referring to the characteristics of a problem to be used for didactic purposes. The teams prepared the document D2 with the characteristics and shared it with the other teams of the same group through a forum on the Moodle platform of the course. Then, as autonomous work outside the classroom, they elaborated the design of a robotics problem in a document called D3.
This section presents the results regarding the analysis of these two documents.
3.2.1. Results Related to the Characteristics of the Problems
To identify the characteristics that the participating teams considered that the problems should have to be used for didactic objectives, the D2 documents prepared in search of the emerging characteristics, which are detailed in Table 5, were analyzed.

Table 5.
Characteristics of didactic problems in robotics problem designs.
Characteristics 1 to 12, the majority, refer to the stages of solving a problem, and items 13-16 refer to characteristics about the nature of the problems. The characteristics that have more consensus (80% of the work teams mention them) are as follows: 4. make a meeting and think of group solutions/brainstorm; 12. reflect on possible process improvements; 2. raise the problematic problem/situation; 8. propose a hypothesis and carry it out to see if it is correct/test the hypothesis; 11. celebrate successes; and 5. consider different hypotheses that respond to the problem.
After that, the D3 documents were analyzed to identify which of these emerging features were considered by the participating teams when making their robotics problem designs. This analysis also sought to identify whether the designs consider the robotics problem characteristics set out in Section 1 of this article: (1) be of progressive complexity, (2) refer to known and unknown aspects and (3) place the problem in an environment (scenario). The results of this analysis are shown in Table 5.
The work done in the classroom during session 2 on the characteristics of the didactic problems, as well as the fact that the teams shared their D2 documents through a forum in the classroom, had a great influence on the D3 designs of the robotics problem.
As can be seen in Table 5, virtually all of the emerging features identified by some of the teams increased in presence in the designs. For example, characteristic 2 “pose the problem/problem situation”, which had been mentioned by 88.2% of the teams in D2, was taken into account by all teams in their D3 designs. There are two characteristics, 11 and 12, referring to attitudinal and motivational aspects, which considerably lower the percentage in the designs. Characteristic 1, stated in D2 by two teams, is not contemplated in any of the D3 designs, possibly because all the problems arise from explaining a contextualized situation and presenting an oral question.
The characteristics referring to the nature of the problems, 13 to 16, considerably increase in presence in the D3 designs. Most teams did not list them in D2 but nevertheless took them into account in their designs.
On the other hand, the analysis of the characteristics of robotics problems, 17 to 19, reveals that only 23.5% (corresponding to three designs) consider that the problems present a progressive complexity (characteristic 17). Instead, all designs place problems in a scenario in a contextualized manner (feature 19) and also reference known and unknown aspects (feature 18).
3.2.2. Results Related to the Didactic Suitability of the Designs
To know the didactic suitability of the designs of each team, in total 17 designs, the evidence of the different indicators of each of the components of the DSC of the OSA have been analyzed.
Table 6 was prepared by counting the number of designs that show evidence of each of the components of DSC and calculating the percentage of the 17 total designs that the number represents. In general, it can be observed that there is more evidence of indicators of affective suitability (in 64.7% of the designs); secondly, the designs are concerned with evidencing interactional suitability (in 52.9% of the designs), followed by epistemic suitability (43.5% of the designs) and mediational suitability (41.2%). Where we obtain less evidence is ecological suitability (in 11.8% of designs).

Table 6.
Percentage of designs considering each of the DSC components.
Related to epistemic suitability, half of the designs (9 out of 17) show errors regarding the computational language when they describe the instructions that students should give to the robot to make the programmed path. For example, when explaining the movements that the robot must make, they use “straight” or “up” instead of the instruction “move forward”, “down” instead of the instruction “go back”, and “right” instead of “turn right”:
Guide the robot straight twice, once to the right, and once straight(A8)
Children must count how many movements they have to make in each direction (3 up, two right, and one down)(A7)
Accordingly, almost two-thirds of the designs (11 out of 17) present ambiguities, either of didactic aspects in the design of the activity or of mathematical aspects. For example, six of the designs refer to the robot having to make the path “shorter”, “faster” or “easier” but do not define what they mean by this type of trajectory. Sometimes they use, regarding trajectories, “short”, “fast” and “simple” as synonyms.
They do not refer to the programming sequence or algorithm for defining the programmed route, for example:
Students will have to use the Blue-Bot’s directions to check it [if the route is correct] and thus find the final solution to the problem(A7)
Sometimes, they do not take into account their programming, nor do they consider instructions other than “moving forward”. For example:
The carpet is designed so that each frame is a movement of the Blue-Bot, which is 15 cm, and so children can count how many squares are needed to reach their goal(B1)
However, all designs from all teams promote a wealth of relevant processes, such as problem-solving, direct modeling to respond with more than one possible solution, and argumentation, although only 10 of the designs make a direct allusion to “programming”.
Two-thirds of the designs (12 out of 17) only provide for the use of oral language to say aloud the robot’s programming sequence so that it runs the desired path before pressing the keys on the robot. The A4 team, in addition to that, suggests that children represent the trajectory on the floor with the 15 cm rectangular cards and/or draw it on a blank sheet. The B8 team proposes that students use paper and pencil to draw a “map” of the route that the robot must take. The A8 and B3 teams are the only ones that propose that students can “write” the algorithm with instruction cards, although they propose it optionally.
Related to cognitive suitability, only four of the designs explicitly state that the previous knowledge of the students is considered, and of these, only two refer directly to the use of educative robots. Only one of the designs explains that the intended meanings have a manageable difficulty for students, and another anticipates certain didactic variables that progressively increase the difficulty of the task:
The elements that hinder the route can be changed [of place] to pose various challenges, also the start and end square [of the carpet](A7)
Only three of the designs include complementary activities that could be considered extension and reinforcement to adapt the curriculum to the individual differences of the students. On the other hand, this highlights that none of the team designs includes the planning of any type of evaluation of student learning.
In general, all designs pose activities of high cognitive demand since they activate processes such as the formulation and testing of hypotheses, and two of them propose changes in representation. In more than half of the designs (11 out of 17), moments of reflection on the activity carried out and what has been learned, on how to improve the process, on other possible responses, etc., are planned. These moments of reflection are intended to promote metacognitive processes.
It is important to note that none of the designs includes the teaching and learning objectives of the activity, nor do they specify the specific knowledge (about mathematics, about CT, for example) that students are expected to be able to develop through the programmed activity.
All teams are concerned about high interactional suitability. In the first place, all the works are concerned to a greater or lesser extent with how the student–teacher interaction should be. Only a single design does not describe the presentation of the problem that the teacher must perform to contextualize it. In more than half (10 out of 17) of the designs, in addition to indicating how the problematic situation should be presented, the specific question that the teacher must ask is explicit so that the problem posed is clear. In one-fourth (6 out of 17) of the designs, it is established that the teacher must observe the students, supervise and guide the development of the activity, resolve conflicts, ask good questions and engage in dialogue that helps the students understand.
The teacher will adopt an understandable, rich, and explanatory dialogue. You must include in your explanation examples that help to understand the objective of the activity(A6)
In the case that the hypothesis is wrong, the teachers will have to pose questions so that the children realize why they have made a mistake and can formulate a new hypothesis(B4)
All designs promote interaction between students; in addition, in more than two-thirds of the designs (13 out of 17), there are spaces for discussion or assembly for students to share ideas, and in one-third of the designs (6 out of 17), students are expected to reach a consensus among themselves, either in large groups or among the students of each small workgroup.
Later, all the children will decide which is the easiest and fastest way to get there(A2)
Together a final hypothesis is decided to reach the other class(A4)
Some of the designs (3 out of 17) are very directed, giving the teacher a strong interventionist role. However, more than two-thirds of the designs (12 out of 17) contemplate moments when students take responsibility for the activity (exploration with robots, formulation of hypotheses, validation of hypotheses using robots, group argumentation, etc.), thus favoring the autonomy of students.
Mediational suitability has been analyzed in the designs that refer both to the material resources that are made available to the students and the ideal organization of the students, considering the conditions of the classroom. All designs plan the use of Blue-Bot as it was a condition of the session 2 task; therefore, it has been identified that other material resources were indicated.
Although the carpets that exist in the market for the use of Blue-Bot or Bee-Bot type robots were not mentioned or used in the experience of session 1, almost two-thirds of the designs (11 of 17) propose the use of these carpets with different objectives, but always to limit the possible trajectories of the robot. Examples are given in Figure 6a,b. We wonder if this may be due to the deep-rooted habit in students of consulting the Internet for inspiration and ideas when creating their designs.
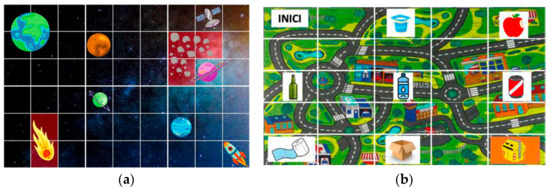
Figure 6.
(a) Carpet in the design of team A1. (b) Carpet in the design of team B1.
The participants in session 1, under the supervision of the teachers, practiced with the programming cards to represent their algorithms, before or after performing the keystrokes on the robot. They went from saying the algorithm orally while pressing the robot keys to representing the algorithm with the cards, progressively: placing them first following the shape of the desired route for the robot and then, with practice, horizontally (regardless of the shape of the route). They also compared different algorithms represented with the cards. The teachers emphasized the role of algorithm representation in institutionalizing concepts related to the development of CT. Thus, it is surprising that only three of the designs propose the use of the representation cards of the programming algorithm, and, of these three, the representation cards are part of the activity in one since the other two propose it as an optional use resource.
Other resources were incorporated in the designs: different cards with images of objects related to the theme of the context to be put on the carpet as obstacles or objectives for the robot; the 15 cm rectangle card; pen and paper; a children’s story and its main characters (Hansel and Gretel, for example); treasure map and treasure (chocolate coins); and lyrics of children’s songs, among others. All these material resources show an effort to contextualize the activity designed to favor the use of models and concrete visualizations for the programming of robot actions.
On the other hand, half of the designs (9 out of 17) make explicit the organization of the students during the activity, always in small groups during the development of the activity that requires the manipulation of the robot and with other moments of sharing in a large group to share ideas and reflect on the work done. One of the designs also states that half of the group would be worked on, which indicates a concern to be able to develop an educational practice with the best possible conditions in terms of the number of children to attend and the resources to put at their disposal:
This activity is designed to be carried out in the “Mathematics Environment” or the mathematics class, with the group split, that is, with 12–13 children (…) in groups of 4 children(A8)
In the designs, great attention is paid to affective suitability, selecting tasks that arouse interest and motivation, as well as keeping students motivated. Of the 17 designs, 7 are based on an uncompetitive game, some with a “prize” (a “real” treasure composed of chocolate coins); 6 on a problem from an everyday context known to children (problem with the class fish tank, looking up words from a nursery rhyme, finding the key to the classroom cupboard, etc.); 2 on centers of interest (space and planets and pirates); and 2 on a children’s story and its characters. The problems posed challenge students to feel involved and motivated to participate in solving them. Some designs appeal to the empathy of the students with the characters of the stories or games so that they want to help them, and in others, a need is created to solve the problem cooperatively because it affects elements that belong to the group (the keys of the cupboard do not appear, the fish of their fish tank have been lost, the robot is running out of battery) In addition, in half of the designs (9 out of 17), it is explicit that the teacher will encourage students to formulate and test several hypotheses until the solution is found.
In the line of generating positive attitudes and feelings of participation in the task, two-thirds of the designs (12 out of 17) include scheduled moments of debate and reflection in a small group where it is expected that children intervene in inequality to contribute their ideas, argue different hypotheses or possible solutions and make comments that other students should actively listen to.
Children will also give their opinion on what improvements they would propose to solve the problem(A8)
(…) and each student will be able to explain their hypothesis(A9)
We will motivate children to continue to have an interest in learning and acquiring new knowledge(B8)
Finally, regarding ecological suitability, the evidence in the designs of the aspects related to the adaptation to the curriculum and the intra- and interdisciplinary connections have been analyzed. On the one hand, the contents that are treated, although, as mentioned above, they are not explicit in any of the designs, are framed in the guidelines of the current curriculum for the stage of early childhood education in Catalonia [6] that incorporates explicitly, for the first time, the development of CT.
On the other hand, the core content is CT, and in most of the designs (13 out of 17), it is not explicitly expressed that the design relates to any other content. However, almost a quarter of the designs (4 out of 17) make it explicit that the activity is related to other content: two designs are related to other mathematical content (numerical thinking and spatial thinking); one design is explicitly related to the environment; and another is related to music.
4. Results and Discussion
First, we could find the following primary objects that emerge from the answers of future teachers when they proposed robotics problems: arguments/justifications, representations/language, propositions and procedures concerning the sequence and measure mathematical objects. It was not possible to identify, for example, definitions or concepts referring to a specific mathematical object.
When participants argue and justify whether different orders can take the robot to the same place, although some teams already establish a justification based on the sequencing related to CT, many teams do not reach that level and argue that the robot arrives at a certain place from the concrete idea of the route (not referring to the programming of the robot). Regarding the procedures indicated by the teams for the calculation of distance between one class and another, although the procedure of estimation and arithmetic calculation of multiplication appears, for example, the idea of measurement by comparison (once working with medium-scale distances) does not appear. This result is reaffirmed by the results found by Sala-Sebastià and Farsani [48] when working on the notion of measurement with future teachers of early childhood education. In addition, most teams had errors in the programming procedure when they had to give instructions for the robot to return on the outward trajectory. Related to the representations that the participants made to represent the orders that are given to the Blue-Bot, although the verbal–written, the symbolic and the iconic appear, they present errors in the representation of the sequence that the robot runs and also ambiguities in the drawing of the arrows made in the iconic representation.
Although studies present positive levels of interest, knowledge, problem-solving and self-efficacy of future teachers working on robotics and CT in basic education [49], this study observes a lack of mathematical (sequence and measurement) and computational (sequence programming) knowledge in the solving of robotics problems at the level of users and reflective users, which corroborates the studies of Caviedes, De Gamboa and Badillo [50] carried out with future primary school teachers solving tasks that involve the mathematical object area and, mainly, with the studies of Seckel, Vásquez, Samuel and Breda [10] which present different typologies of errors made by future kindergarten teachers when solving robotics problems, both in the use of robot commands and in their respective representation of programming.
In the same way that the results referring to the analysis of the mathematical and computational knowledge of the participants show errors and ambiguities in the programming procedures, the designs lack didactic objectives focused on the teaching and learning of computational knowledge. The representation or writing of robot programming algorithms is not promoted as an essential element for the development of CT. It can be inferred that future teachers do not contemplate it in their designs either because they do not master it (since they make mistakes) or because they are not aware of the importance of promoting the writing or representation of algorithms as an institutionalization of CT knowledge. This is reflected in the epistemic and cognitive suitability of the designs.
The designs take special care of the aspects concerning affective suitability and include many elements to motivate and involve students in a fun activity that generates positive emotions. For this, mainly, problem contexts that encourage the involvement of the students in the activity are provided (e.g., centers of interest of the students; very close, everyday and known situations; games with prizes; children’s stories). The resources identified in the analysis of mediational suitability corroborate this focus on the emotional part of the design, since, in general, most of the resources are used to enrich the context (carpets decorated with motifs of the theme of the center of interest, children’s stories, etc.). On the other hand, the programming cards that could have been proposed as facilitating resources for the learning and development of CT have no central role, since they are included only for optional use. To achieve involvement in the designed activities, students are given an active and leading role in decision-making and the expression of justifications and arguments. To do this, they are organized into small workgroups that facilitate the necessary interaction (interactional suitability) so that these situations of debate and reflection that the teacher will lead occur. This type of design of future teachers of early childhood education with great concern to obtain high affective suitability was also found in the work of Sala-Sebastià and Farsani [48].
According to the results, ecological suitability is of the least concern to future teachers since it seems that none of the participants consulted the curriculum to ensure that their proposal complied with legal guidelines. In addition, although all designs present contextualized problems, none of them presents an interdisciplinary approach. Only one treats the environment transversally and with little depth, and a couple of them are concerned with establishing connections with other contents within mathematics (numerical and spatial thinking).
When future teachers design educative practices without being given a detailed guide of how the designs should be, many of the elements of consensus of the educational community emerge, such as that the task must involve and motivate students and that students must interact, share ideas and help each other [37]. However, other equally important aspects do not always emerge, such as establishing didactic objectives and evaluation criteria, establishing a sequence of activities of progressive difficulty and establishing mechanisms for institutionalizing the core contents that are the objective of educative practice [14].
5. Conclusions
The originality and innovation of the research presented are framed in two aspects. The first is the characteristics of the didactic sequence which was designed and implemented with the future teachers. In this study, CT is considered as the thought process involved in formulating problems so their solutions can be represented as computational steps and algorithms. An important part of this process is finding appropriate models of computation with which to formulate the problem and derive its solutions [51]. Thus, the authors designed a sequence of tasks that could imply the development of CT understood from this perspective based on open robotics problems, the resolution of which is not limited to the use of a robotic carpet or any previously specified strategy.
The second aspect is the theoretical and methodological approach of the article based on the DMK model of the OSA to search for the features of didactic-mathematical and computational knowledge of future early childhood education teachers. This is a new approach, not carried out in other investigations about this issue, which points us to novel results.
The results indicate that future teachers present characteristics of didactic-mathematical and computational knowledge since aspects of this knowledge are observed timidly in the participants’ answers. However, they show certain deficiencies of mathematical and computational knowledge that are reflected in the results on the didactic suitability of the designs made. This leads us to wonder if it would not be necessary to include these future teachers’ basic mathematical knowledge and, specifically, computational thinking in training to guarantee the quality of their future educative practices and comply with the current guidelines of the Spanish and Catalan curriculum. This should mean enabling future teachers to design innovative and learner-centered educational practices that involve the development of CT. When these teachers in training become teachers in service, they will have to be able to implement this kind of innovative sequence of tasks with their kindergarten pupils. From here, a new approach to MT teaching in which mathematics could be considered something more than a tool of calculation would be promoted.
If the DSC, which in this work has been used as a methodological element to carry out the analysis of the data, is made available to future teachers through training in their degree, they could use it as a design instrument and implementation guide to help them to keep in mind the several didactic facets of educative practice and balance them. In this way, the development of didactic knowledge in future teachers could be improved.
The results of the study, determined from a particular context, present limitations since they are directed to future kindergarten teachers in a specific region of Spain. Different results could be obtained if the study were carried out with future primary school teachers or with active teachers from another locality or country. It is also important to emphasize that the proposed robotics problems also conditioned certain types of response. Changing the problems could imply some subtle modifications in the results found.
From a future perspective, it is considered that the future teachers participating in the study should perform a kind of simulation with their peers, implementing the problems designed with the objective to characterize the didactic knowledge not being contemplated in their theoretical designs. In addition, it is considered relevant to incorporate mathematical and computational knowledge into the training of future teachers in operating the Blue-Bot robot and developing logical, spatial, and computational thinking. Consideration is also given to incorporating DSC into training to develop teaching skills.
Finally, it is considered that this study is aimed at training programs and trainers of future teachers of early childhood education. Evidence is presented that in the training of future teachers, it would be necessary not only to include tasks with educative robots, but also to promote the development of didactic and mathematical knowledge for the incorporation of logical, spatial and computational thinking in the early ages.
Author Contributions
Conceptualization, G.S.-S., A.B., M.J.S. and À.A.; methodology, G.S.-S. and A.B.; validation, G.S.-S., A.B., M.J.S., D.F. and À.A.; formal analysis, G.S.-S., A.B. and M.J.S.; investigation, G.S.-S., A.B., M.J.S., D.F. and À.A.; resources, G.S.-S. and A.B.; data curation, G.S.-S. and A.B.; writing—original draft preparation, G.S.-S., A.B., M.J.S. and À.A.; writing—review and editing, M.J.S. and D.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish R&D project PID2021-127104NB-I00 (MINECO/FEDER, EU) and the Fondecyt (Chile) research project No. 11190547.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge the active participation of the future teachers of childhood education in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wing, J.M. Computational Thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Zapata-Ros, M. Pensamiento Computacional Desenchufado. Educ. Knowl. Soc. EKS 2019, 20, 29. [Google Scholar] [CrossRef] [PubMed]
- Jara, I.; Hepp, P. Enseñar Ciencias de La Computación: Creando Oportunidades Para Los Jóvenes de América Latina. Available online: www.microsoft.com/es-es/education (accessed on 27 July 2022).
- Grover, S.; Pea, R. Computational Thinking in K–12: A Review of the State of the Field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Department of Education Decree 175/2022, of 27 September, on the Organisation of Basic Education Teaching. Available online: https://dogc.gencat.cat/ca/document-del-dogc/?documentId=938401 (accessed on 10 January 2023).
- Department of Education Decree (pending legislation) on the Organization of the Teachings of Early Childhood Education. Available online: https://projectes.xtec.cat/nou-curriculum/educacio-infantil/#esborrany (accessed on 10 January 2023).
- Alsina, À. Transformando El Currículo Español de Educación Infantil: La Presencia de La Competencia Matemática y Los Procesos Matemáticos. Números Rev. Didáct. Mat. 2022, 111, 33–48. [Google Scholar]
- Ministry of Education and Vocational Training (MEFP) Royal Decree 95/2022, of 1 February, Which Establishes the Ordination and the Minimum Education of the Early Childhood Education. Available online: https://eurydice.eacea.ec.europa.eu/national-education-systems/spain/national-reforms-early-childhood-education-and-care (accessed on 10 January 2023).
- Ribeiro, C.R.; Coutinho, C.P.; Costa, M.F.M. A Robótica Educativa Como Ferramenta Pedagógica Na Resolução de Problemas de Matemática No Ensino Básico. In Proceedings of the 6a Conferência Ibérica de Sistemas e Tecnologias de Informação (CISTI), Chaves, Portugal, 15–18 June 2011; pp. 15–18. [Google Scholar]
- Seckel, M.J.; Vásquez, C.; Samuel, M.; Breda, A. Errors of Programming and Ownership of the Robot Concept Made by Trainee Kindergarten Teachers during an Induction Training. Educ. Inf. Technol. 2022, 27, 2955–2975. [Google Scholar] [CrossRef]
- Benton, L.; Hoyles, C.; Kalas, I.; Noss, R. Bridging Primary Programming and Mathematics: Some Findings of Design Research in England. Digit. Exp. Math. Educ. 2017, 3, 115–138. [Google Scholar] [CrossRef]
- Leidl, K.D.; Bers, M.U.; Mihm, C. Programming with ScratchJr: A Review of the First Year of User Analytics. In Proceedings of the International Conference on Computational Thinking Education, Hong Kong, China, 13–15 July 2017; Kong, S.C., Sheldon, J., Li, K.Y., Eds.; The Education University of Hong Kong: Hong Kong, China, 2017; pp. 116–121. [Google Scholar]
- Sáez, J.M.; Cózar, R. Pensamiento Computacional y Programación Visual Por Bloques En El Aula de Primaria | Educar. Educar 2017, 53, 129–146. [Google Scholar] [CrossRef]
- Seckel, M.J.; Breda, A.; Farsani, D.; Parra, J. Reflections of Future Kindergarten Teachers on the Design of a Mathematical Instruction Process Didactic Sequences with the Use of Robots. EURASIA J. Math. Sci. Technol. Educ. 2022, 18, em2163. [Google Scholar] [CrossRef]
- Sullivan, A.; Bers, M.U.; Mihm, C. Imagining, Playing, and Coding with KIBO: Using Robotics to Foster Computational Thinking in Young Children. In Proceedings of the International Conference on Computational Thinking Education, Hong Kong, China, 13–15 July 2017; Kong, S.C., Sheldon, J., Li, K.Y., Eds.; The Education University of Hong Kong: Hong Kong, China, 2017; pp. 110–115. [Google Scholar]
- Sullivan, A.; Strawhacker, A.; Bers, M.U. Dancing, Drawing, and Dramatic Robots: Integrating Robotics and the Arts to Teach Foundational STEAM Concepts to Young Children. In Robotics in STEM Education: Redesigning the Learning Experience; Khine, M.S., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 231–260. ISBN 9783319577869. [Google Scholar]
- Tang, A.L.L.; Tung, V.W.S.; Cheng, T.O. Dual Roles of Educational Robotics in Management Education: Pedagogical Means and Learning Outcomes. Educ. Inf. Technol. 2020, 25, 1271–1283. [Google Scholar] [CrossRef]
- Yang, Y.; Long, Y.; Sun, D.; van Aalst, J.; Cheng, S. Fostering Students’ Creativity via Educational Robotics: An Investigation of Teachers’ Pedagogical Practices Based on Teacher Interviews. Br. J. Educ. Technol. 2020, 51, 1826–1842. [Google Scholar] [CrossRef]
- Casey, J.E.; Pennington, L.K.; Mireles, S.V. Technology Acceptance Model: Assessing Preservice Teachers’ Acceptance of Floor-Robots as a Useful Pedagogical Tool. Technol. Knowl. Learn. 2021, 26, 499–514. [Google Scholar] [CrossRef]
- Caballero-González, Y.A.; Muñoz-Repiso, A.G.V. Robots En La Educación de La Primera Infancia: Aprender a Secuenciar Acciones Usando Robots Programables. RIED-Rev. Iberoam. Educ. Distancia 2021, 24, 77–94. [Google Scholar] [CrossRef]
- Schina, D.; Esteve-Gonzalez, V.; Usart, M. Teachers’ Perceptions of Bee-Bot Robotic Toy and Their Ability to Integrate It in Their Teaching. In Proceedings of the International Conference on Robotics in Education (RiE), Vienna, Austria, 10–12 April 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 121–132. [Google Scholar]
- Papadakis, S. Robots and Robotics Kits for Early Childhood and First School Age. Int. J. Interact. Mob. Technol. iJIM 2020, 14, 34–56. [Google Scholar] [CrossRef]
- Seckel, M.J.; Breda, A.; Font, V.; Vásquez, C. Primary School Teachers’ Conceptions about the Use of Robotics in Mathematics. Mathematics 2021, 9, 3186. [Google Scholar] [CrossRef]
- Shulman, L.S. Those Who Understand: Knowledge Growth in Teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Mishra, P.; Koehler, M.J. Technological Pedagogical Content Knowledge: A Framework for Teacher Knowledge. Teach. Coll. Rec. 2006, 108, 1017–1054. [Google Scholar] [CrossRef]
- Godino, J.D.; Batanero, C.; Font, V. The Onto-Semiotic Approach to Research in Mathematics Education. ZDM-Int. J. Math. Educ. 2007, 39, 127–135. [Google Scholar] [CrossRef]
- Pino-Fan, L.R.; Godino, J.D. Perpectiva Ampliada Del Conocimiento Didáctico-Matemático Del Profesor. Paradigma 2015, 36, 87–109. [Google Scholar]
- Breda, A.; Pino-Fan, L.R.; Font, V. Meta Didactic-Mathematical Knowledge of Teachers: Criteria for the Reflection and Assessment on Teaching Practice. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 1893–1918. [Google Scholar] [CrossRef]
- Pino-Fan, L.R.; Godino, J.D.; Font, V. Assessing Key Epistemic Features of Didactic-Mathematical Knowledge of Prospective Teachers: The Case of the Derivative. J. Math. Teach. Educ. 2016, 21, 63–94. [Google Scholar] [CrossRef]
- Godino, J.D. Categories for Analysing the Knowledge of Mathematics Teachers. Unión Rev. Educ. Mat. 2009, 20, 13–31. [Google Scholar]
- Godino, J.D. Origen y Aportaciones de La Perspectiva Ontosemiótica de Investigación En Didáctica de La Matemática. In Proceedings of the Investigación en Educación Matemática XVI, Baeza, Spain, 20–22 September 2012; Estepa, A., Contreras, A., Deulofeu, J., Penalva, M.C., García, F.J., Ordóñez, L., Eds.; Universidad de Granada: Granada, Spain, 2012; pp. 49–68. [Google Scholar]
- Badillo, E.; Font, V.; Edo, M. Analyzing the Responses of 7–8 Year Olds When Solving Partitioning Problems. Int. J. Sci. Math. Educ. 2015, 13, 811–836. [Google Scholar] [CrossRef]
- Malaspina, U.; Font, V. The Role of Intuition in the Solving of Optimization Problems. Educ. Stud. Math. 2010, 75, 107–130. [Google Scholar] [CrossRef]
- Malaspina, U. The Creation of Problems as a Means to Enhance the Articulation of Skills and Knowledge of the Mathematics Teacher. In Proceedings of the Actas del Segundo Congreso Internacional Virtual sobre el Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos, Granada, Spain, 23–26 March 2017; Contreras, J.M., Arteaga, P.G.R.C., Gea, M.M., Giacomone, B., López-Martín, M.M., Eds.; Enfoque Ontosemiótico: Granada, Spain, 2017. [Google Scholar]
- Malaspina, U.; Torres, C.; Rubio, N. How to Stimulate In-Service Teachers’ Didactic Analysis Competence by Means of Problem Posing. In Mathematical Problem Solving; Springer: Berlin/Heidelberg, Germany, 2019; pp. 133–151. [Google Scholar]
- Font, V.; Planas, N.; Godino, J.D. Modelo Para El Análisis Didáctico En Educación Matemática. Infanc. Aprendiz. 2010, 33, 89–105. [Google Scholar] [CrossRef]
- Breda, A. Características Del Análisis Didáctico Realizado Por Profesores Para Justificar La Mejora En La Enseñanza de Las Matemáticas. Bolema Bol. Educ. Mat. 2020, 34, 69–88. [Google Scholar] [CrossRef]
- Morales-López, Y.; Font, V. Valoración Realizada Por Una Profesora de La Idoneidad de Su Clase de Matemáticas. Educ. Pesqui. 2019, 45, 1–19. [Google Scholar] [CrossRef]
- Moreira, C.B.; Gusmão, T.C.R.S.; Moll, V.F. Tarefas Matemáticas Para o Desenvolvimento Da Percepção de Espaço Na Educação Infantil: Potencialidades e Limites. Bolema Bol. Educ. Mat. 2018, 32, 231–254. [Google Scholar] [CrossRef]
- Estebanell, M.; López, V.; Peracaula, M.; Simarro, C.; Cornellà, P.; Couso, D.; González, J.; Alsina, A.; Badillo, E.; Heras, R. Pensament Computacional En La Formació de Mestres; Servei de Publicacions UdG: Girona, Spain, 2018. [Google Scholar]
- Kong, S.C.; Lai, M.; Sun, D. Teacher Development in Computational Thinking: Design and Learning Outcomes of Programming Concepts, Practices and Pedagogy. Comput. Educ. 2020, 151, 103872. [Google Scholar] [CrossRef]
- Arlegui, J.; Pina, A. Didáctica de La Robótica Educativa: Un Enfoque Constructivista; Dextra Editorial S.L.: Madrid, Spain, 2016; ISBN 978-84-16277-90-2. [Google Scholar]
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education, 6th ed.; Routledge: Oxford, UK, 2007. [Google Scholar]
- Stake, R.E. Investigación Con Estudio de Casos; Ediciones Morata: Madrid, Spain, 1998; ISBN 847112422X. [Google Scholar]
- Abtahi, Y. Una Exploración Teórica: La Zona de Desarrollo Próximo Como Zona Ética Para Enseñar Mate-Máticas. Av. Investig. Educ. Mat. 2021, 20, 7–21. [Google Scholar]
- Vygotsky, L.S. Thinking and Speech. In The Collected Works of L. S. Vygotsky, Problems of General Psychology; Rieber, R.W., Carton, A.S., Eds.; Original Work Published 1934; Plenum Press: New York, NY, USA, 1987; Volume 1, pp. 39–285. [Google Scholar]
- Font, V. Una Organización de Los Programas de Investigación En Didáctica de Las Matemáticas. Rev. Ema 2002, 7, 127–170. [Google Scholar]
- Sala-Sebastià, G.; Farsani, D. Reflexiones de Futuros Maestros de Infantil Sobre Una Tarea de Medida. Caminhos Educ. Mat. Em Rev. Online 2022, 12, 213–228. [Google Scholar]
- Piedade, J.M.N. Interesse, Conhecimento e Autoconfiança de Futuros Professores e Professores Em Serviço No Uso de Robótica Educacional Em Atividades de Aprendizagem. Educ. Form. 2021, 6, e3345. [Google Scholar] [CrossRef]
- Caviedes, S.; de Gamboa, G.; Badillo, E. Conocimiento Movilizado Por Estudiantes Para Maestro, al Comparar Áreas de Figuras 2D. Uniciencia 2022, 36, 639–658. [Google Scholar] [CrossRef]
- Aho, A. Computation and Computational Thinking. Comput. J. 2012, 55, 832–885. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).