Abstract
Due to the importance of cutting-edge nanomaterials applications in energy generation and storage devices, electrochemical impedance spectroscopy (EIS) has been adopted to fully understand the electronic and chemical reactions occurring inside these emerging technologies. Electronic behavior can be correlated with electrochemical properties such as electron transfer resistance, rate of mass diffusion, and the number of electrons in the electrochemical reaction. Although there is a lot of information about the electronic diagrams and methods for parameter estimation, some readers have difficulty analyzing and interpreting EIS curves. Thus, this work proposed using a heuristic approach and genetic algorithms to successfully estimate the resistance and capacitance value of a previously defined circuit model. To assess the potential of the genetic algorithm in electrochemical parameters estimation, we carried out practical measurements with known elements, and then the experimental and theoretical values were compared. Furthermore, the versatility and effectiveness of the algorithm were validated by determining the parameters in an Li-ion battery. The results revealed that the heuristic genetic algorithm (HGA) is a powerful tool for EIS parameters estimation because it can handle large below and upper limits with more pragmatic results in a shorter computational time.
1. Introduction
Nowadays, nanomaterials are crucial in developing sustainable technologies, such as batteries, fuel cells, supercapacitors, electrolyzes, and solar cells [1,2,3,4,5,6]. Modeling and simulation are commonly adopted tools that scientific communities use to understand and avoid accelerated degradation, undesired electrochemical reaction, and safety management in recent electronic and electrochemical devices [7,8]. Obviously, improving the technologies mentioned above is mandatory to face the challenge of energy generation, and a parameter estimation is a promising approach to fully understanding the internal electrochemical process. Additionally, EIS can be used to determine the lifetime, diagnose the device’s health, and predict its dynamic behavior over a large period of time [9,10,11]. As is well known, the electrochemical processes in nanomaterials can be studied by considering the charge transfer resistance and diffusion mass control of species, in other words, by modelling the system by interconnected resistors, capacitors, and inductors [12,13]. EIS is a powerful tool to assess the physical characteristic of nanomaterials under practical operational conditions of the cited technologies [14,15,16]. This non-destructive method is based on frequency modulation of the sine voltage input signal while measuring the generated flowing current through the system. From a mathematical point of view, impedance is the ratio between the voltage and current, and this is also referred to as the transfer function of one electrical system. Under the control argot, impedance is studied by constructing the Nyquist diagram consisting of a complex plane where real impedance and imaginary impedance are plotted under a given set of frequencies [17]. Thus, the modeling equation is usually written in complex form by making some mathematical arrangements. The final function depends on the perturbation frequency and the value of the interconnected electrical devices. The most important part of EIS characterization is the parameter estimation of the unknown variables. Although there are many methods to model it, accuracy and reliability can be difficult because multiple values can fit the experimental measurements well. In addition, due to the fact that EIS is a multivariable system, the dynamics are truly complex to solve. There are many mathematical procedures to solve the transfer function of the electrical diagram and estimate the value of each element, and non-linear regression analysis is usually selected. Levenberg–Marquardt is another numerical optimization algorithm that has been used to solve non-linear equations but still suffers from numerous local minima [18,19]. As the system becomes complex, the algorithms mentioned above are computationally expensive and inaccurate, even with few elements or variables. One of the most used numerical methods to solve multivariable models is the Newton–Raphson method [20]. This method has the ability to handle non-linear systems, and guess values are only required to start the iterations. The main drawback of Newton–Raphson is that it is highly mathematical, and the convergence times truly depend on the initial guess values. Another challenge of Newton–Raphson is the existence of inflection points where slope change is observed, which has the problem of multiple local minima.
Ruan et al. proposed an EIS based on the multi-time-scale-fractional-order model to simulate the internal dynamic of lithium-ion batteries in both short and long-time intervals [21]. Even though this group modeled the EIS with high accuracy and adaptability, the mathematical expression and the resolution method were not friendly to handle, and errors due to the linear model assumption and time-consuming parameter identification were the main challenges. Fractional-order EIS was also implemented by Caponetto et al. to study the electrochemical process in a fuel cell [10]. They used mathematical interpolation laws to identify three parameters while fixing the other two parameters.
The internal impedance of batteries has been a topic of interest because it can obtain this device’s state of health and function [9]. Significant work was done by the research group of Middlemiss [22]) where EIS measurements were conducted in order to elucidate information on battery degradation. This group highlighted the primary processes for metal-ion battery degradation: loss of active metal, loss of cathode, and deterioration of ionic transport. They recognized that although EIS is easy to use, the issue resides in the data interpretation.
The Randles circuit is one of the most useful models to simulate physical and chemical processes in energy devices such as batteries [23]. For instance, Rong et al., studied a hole-conductor-free TiO2/CH3NH3PbI3 heterojunction solar cell by EIS to further understand the charge-transport process in the perovskite device [24]. They used two Randles circuits, conformed by resistance and capacitance in parallel. At high frequency, a semicircle was observed, attributed to the perovskite-counter electrode interaction. At the same time, the second Randles model represents the charge transfer resistance and recombination at TiO2/perovskite interface occurring at low frequency. The EIS measurements were consistent with the previously recorded J–V curve and the differences in open-circuit potential. Another application of the Randles circuit can be found in the area of corrosion [25,26]. A nanocompound of ZnO–Cr2O3/epoxy was studied as a protective layer for mild steel in a 3.5% NaCl solution [27]. The EIS technique was used to elucidate the anti-corrosion mechanism of the nano compound. The author observed a single depressed semicircle with the center under the real axis from the Nyquist plot. The fitness of the spectra was achieved by using a Randles circuit consisting of a resistance and capacitance representing the charge transfer resistance and the double-layer capacitance. Also, series resistance was considered to model the solution resistance.
Due to the aforementioned limitations of traditional mathematics for parameter estimation on multiple equations, the scientific community has been adopting the population-based approach to solve a multi-objective optimization problem [19]. Zhu and coworkers developed interesting work. They used a support vector machine (SVM) learning algorithm to obtain the values for electrical components in an equivalent circuit model [28]. They stated that SVM efficiently figures out the equivalent circuit model of the studied EIS spectrum. The SVM code was written in Python and Scikit-learn package. The basis of this method consists of finding the minimum value of a geometrical interval (distance between the support vector and the hyperplane). The proposed algorithm was tested by fitting EIS extracted from the literature and discretized in data points. Compared with the decision tree and random forest algorithm SVM presents the highest reliability, and the error was mainly attributed to the small amount of the collected raw data.
Genetic algorithms (GA) are a versatile learning tool based on the biological evolution algorithm. GA have been used to solve engineering models such as solar cells, robots, and fuel cells [29,30,31]. This method is based on the optimization of genes that satisfy the equation under some limits and constraints for precise parameter estimation. It is capable of handling the global optima in less computing time [32]. One attempt to use evolutionary algorithms was conducted by Haeverbeke et al., where this group used gene expression programming to achieve circuit model identification and then remove the components that do not contribute significantly [33]. Nonetheless, the objective function was solved by the Nelder–Mead simplex numerical algorithm. The method mentioned above is a non-constraint direct search method based on constructing N + 1 vertices that will be replaced by new optimal ones [34]. The main drawback of this algorithm is the time computing and that, at near local minima, the algorithm could not converge in a single value [35]. The challenge of GA is the creation of the initial population and the crossover and mutation of the individual, resulting in the rejection of a considerable number of genes [36]. It should be mentioned that meta-heuristic methods can optimize the problem even when the initial guesses are very distant from the actual values and the probability of the global optima is higher [20]. A recently published work showed the potential of the adoption of GA to solve practical engineering problems [37]. Wang et al., developed a deep comparison of several machine-learning algorithms to minimize the nitrogen crossover in polymer electrolyte fuel cells [38]. Reactant crossover is critical because it can provoke low performance and irreversible component damage. This group used a surrogate machine learning model to successfully reduce the nitrogen crossover by 49.5%. On the other hand, Luo et al., critically reviewed machine learning as a strategy to predict the state of health and charge of lithium-ion batteries [39]. The authors concluded that battery prognosis is critical in determining the second-lifetime application or recycling route. The non-linear model can be predicted using machine learning algorithms. Meanwhile, Yang and coworkers used five machine-learning algorithms to unravel the complex relationship of organic molecules in solar cell performance [40]. To this end, they used the open circuit voltage loss and dielectric constant as molecular descriptors. The results demonstrated that machine learning could help scientists develop novel and efficient organic photovoltaic materials.
This study considered a Randles circuit to determine the EIS and estimate the optimal parameters. Specifically, the objective functions were determined using the transfer function concept, and this mathematical equation was rearranged to separate the real and imaginary parts. Then, the equations were solved by using GA under heuristic considerations. A real-Randles circuit was constructed with a Rs, Rp and Cp. EIS measurements were conducted in a GillAC potentiostat–Galvanostat with a two-electrode cell configuration. The obtained measured impedance data were used as inputs for the multi-objective function. In order to solve the heuristic algorithms of the non-linear multi-objective optimization problem, the Matlab optimization toolbox was used. The adopted HGA approach exhibited good accuracy and convergence in a short time, indicating that it is a promising candidate for the simulation of complex circuits in the area of nanomaterials. Furthermore, the proposed GA was used to identify the parameters in an Li-ion battery, and the results were compared with the pattern search algorithm.
Last but not least, HGA is an excellent tool for solving complex mathematical models. This could help face the main drawbacks of engineering by conducting high-fidelity model simulations. The contribution of this research work is the proposal of a straightforward methodology where the practitioner can use the Matlab optimization toolbox to determine or extract physical parameters through GA. The latter is relevant because the use of GA has been achieved only by experienced and trained researchers. Therefore, the scientific community can adopt the proposed pathway to solve engineering problems and focus on analyzing and interpreting the information obtained from the genetic algorithm.
2. Materials and Methods
2.1. Mathematical Model
Due to its simplicity and deployment, Randles equivalent circuit was considered to assess the power of heuristic HGA for EIS model estimation. Figure 1 displays the interconnection of resistances and capacitance in the Randles configuration. An alternating voltage source is considered as the input signal for the electrical circuit.
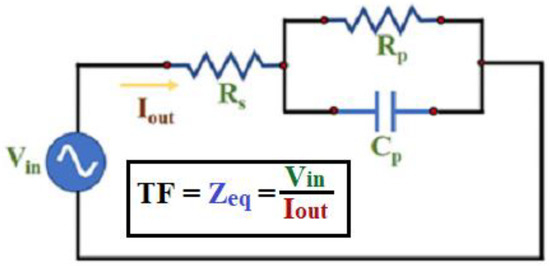
Figure 1.
Representation of the Randles equivalent circuit.
From the above-mentioned literature, the series resistance (Rs) usually represents the internal resistance or electrolyte resistance of the electrochemical process, while the parallel topology of Rp and Cp describes the charge transfer resistance and the electrical double layer, respectively. In order to corroborate the versatility of HGA in the EIS parameter estimation, we conducted experimental measurements in a GillAC potentiostat–Galvanostat with a two-electrode cell configuration. Commercially available resistors and capacitors were interconnected in the Randles configuration. The EIS spectra were measured with a 10 mV of sine wave signal over the range of 80,000 Hz to 1 Hz. Three circuit models labeled circuits A, B and C were constructed and measured under the EIS configuration setup. The obtained data were used to construct a Nyquist plot.
We first obtained the mathematical equations for the proposed circuit to identify model parameters. First, the equivalent impedance was obtained in the frequency domain by the following equation:
where s is the complex plane in the frequency domain. The latter equation can be expressed in terms of angular frequency by changing s = jw; the equation can be written as:
The EIS real dynamic of the equivalent circuit is described by:
where w is the angular frequency and Rs, Rp and Cp are the three parameters that need to be obtained by the proposed heuristic GA. It can be observed that the Zeq is composed of a real and imaginary part, and this can be useful because by each value of w we can have two different equations to solve.
2.2. Parameter Estimation Using HGA
The genetic algorithm is based on evolution theory and was formulated by John Holland in 1975 [41]. This method has been widely used in various engineering fields to solve complex mathematical equations. The first step of GA is the creation of a random population composed of individuals that form the first generation. Then, these individuals can mate at the next level, and the selection process is achieved to have a new, improved generation. Generally, the number of members is adopted as an estimate of the minimizer. In our case, we used a minimization process to obtain the local minima and, in this way, calculate the three parameters or variables.
To this end, the non-linear system equation for the Randles circuit was converted to a multi-objective optimization model as follows:
In this way, Equation (3) was re-written as a multi-objective function where two equations were obtained for each w value, the Zreal and Zim. For example, considering the experimental results at the w = 1000, the multi-objective function is as follows:
where 5.999 × 102 and 7.4983 are the measured Zreal and Zim values, respectively.
The latter function helps to obtain the global optima, and constraints were not necessary to consider. Lower and upper bound were defined in order to estimate the optimal values for Rs, Rp, and Cp. The GA is based on selecting the next generations that fit the 3-variables multi-objective function.
The heuristic crossover was implemented to combine chromosomes or parents to produce a new offspring at a small distance from the parent with the best fitness value. Equation (6) was used to compute the heuristic crossover [42,43]
where βif1 is the best parent and βif2 is the worst parent. It is worth mentioning that the crossover operator plays a critical role because if the crossover process is inadequate, all the reproduced generation is disrupted.
After the crossover application, a mutation operator was applied to guarantee adequate diversity in the generation and avoid convergence at the local minimum [44]. Figure 2 displays the adopted HGA procedure to obtain the numerical values of Rs, Rp, and Cp.
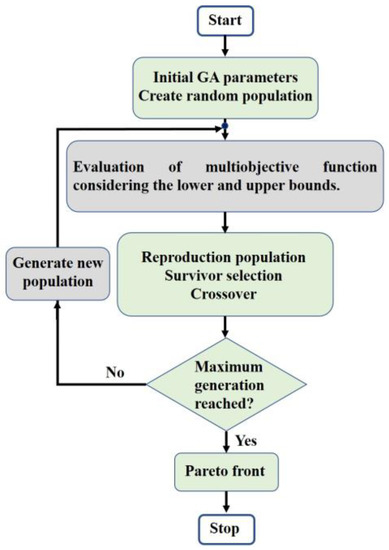
Figure 2.
Heuristic genetic algorithm procedure to estimate EIS parameters.
2.3. Matlab Optimization Toolbox
It is a package designed to optimize solution problems using methods such as pattern search, surrogate optimization, particle swarm optimization, genetic algorithm, etc. Users can access this toolbox by selecting the app menu and opening the optimization windows. The first step in the optimization setup is defining the problem type. In our case, we used the constrained non-linear configuration with lower and upper bounds. The second step is declaring the objective function (as shown in Equation (5)). It is recommended to write the code in a new script. The next stage is the selection of the population, algorithm, and tolerance settings.
3. Results
Attainment of EIS Characteristics Using Heuristic Genetic Algorithms
Three different case studies were considered in order to assess the versatility of the proposed heuristic GA in the parameter estimation of a three-variables multi-objective function. In the first case, we constructed a Randles circuit by interconnecting the Rs, Rp, and Cp with commercial values of 2 × 220 Ω, 1 kΩ and 10 nF, respectively. Table 1 lists the case studies and the commercial values for the resistance and capacitance.

Table 1.
Summary of circuit model characteristics and parameter estimation by HGA.
The EIS measurement for each case model was conducted under the same dataset, such as the sinewave amplitude and frequency range. The obtained raw data were used to construct the Nyquist plot, and the magnitude of the Zreal and Zim at different frequencies were used to optimize the EIS parameters. In order to study the versatility of the heuristic GA, a wide range of lower bound and upper limits was used. It is worth mentioning that the upper and lower bound range may significantly affect the iteration time and the calculated error. In our case, the large upper bound does not significantly impact the computer solution because the ideal capacitor model is used. However, when the constant phase element and Warburg element are implemented, the upper limit plays a crucial role in computer time. So, practitioners need to know the physical characteristics of the system under study to close the upper and lower limit range. By applying the process described in Figure 2, and after performing enough iterations, we obtained the sets of optimized parameters shown in Table 1. In all cases, the simulated curve matched the experimental values well. It is worth mentioning that crossover type has a great effect on the final optimized values; at the beginning of the simulation, we used one-point and two-point crossover, but the results were not optimal. Nevertheless, the heuristic crossover shows a uniform distribution. Note that the slight discrepancies between the experimental curve and the simulated one could be due to the tolerance of the commercial electrical elements and the equipment’s accuracy.
Figure 3 shows the target and the obtained simulated Nyquist plot using the heuristic GA to solve the optimization problem. It can be seen that the simulated curve has a reasonably good fit at frequencies more than 18 kHz. The slightly lower performance at high frequencies could be due to the equipment’s precision under the operational conditions and small capacitance. According to the data provided by Li and coworkers, some electronic devices present high-frequency noise [45] that can influence the measurement. They incorporated a Butterworth low-pass filter in the AD9834DDS digital-analog converter to improve EIS resolution. The estimated parameters at low frequency, on the other hand, not only showed a good fit, but the calculated values were changing with a regular pattern. From Equation (3) it can be deduced that the curve will intersect the real axis in Rs + Rp value at a lower frequency. A relevant point is the extended lower and upper limits that the HGA can handle without affecting parameter estimation accuracy.
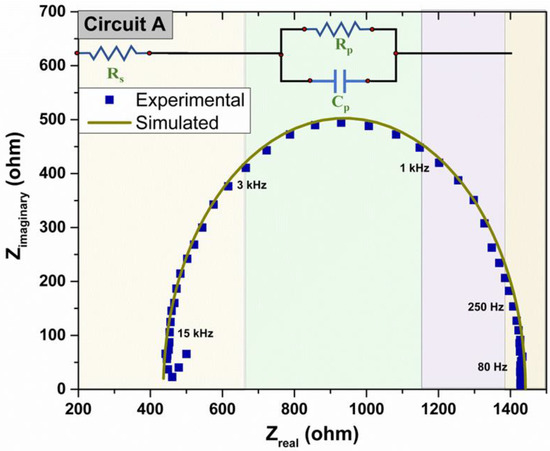
Figure 3.
Experimental and simulated Nyquist plot for Circuit A.
The second case study was a circuit with a commercial value of Rs, Rp, and Cp of 2 × 220 Ω, 200 Ω, and 1 µF, respectively. Figure 4 displays the EIS curve for circuit B. This model also shows an erratic fluctuation at high frequencies. It can be observed that the Nyquist plot enables the parameterization of R, C values [46]. For example, the semicircle begins close to the Rs value, 441 Ω, and from the Nyquist diagram, it can be inferred that its diameter is equal to Rp, close to 208 Ω. Meanwhile, the capacitive value can be estimated by the following equation [47]:
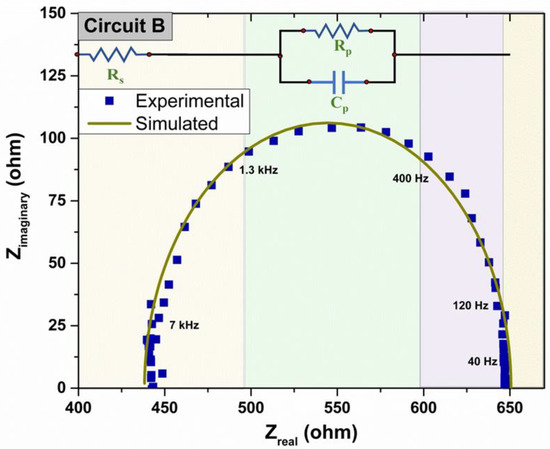
Figure 4.
Experimental and simulated Nyquist plot for Circuit B.
These values correlate well with the optimized values obtained by the heuristic GA procedure. The former reveals the usefulness and power of evolutionary algorithms in the analysis and parameter estimation of EIS measurements.
The last case study is presented in Figure 5. The high-frequency region of the semicircle deviates from the reported shape of the Randles circuit. As mentioned before, this could be due to high-frequency noise, but this does not affect the general behavior of the circuit. Due to the high capacitance, the semicircle starts at the intersection of the real axis at a lower frequency, c.a. 500 Hz. From Table 1, it can be seen that the estimated parameters are very close to the used electrical elements. Thus, the simulated curve fits the target data very well. HGA has an advantage over analytical methods and deterministic techniques such as the Lambert W-function because it can handle wrong guesses or limits and avoid local optimum [30,48]. From Figure 5, it is clearly observed that the capacitor has no contribution at high and low frequencies, and only Rs and Rp represent an impedance to the system. From an electrochemical point of view, we can say that the internal or electrolyte resistance, Rs, is high with a value c.a of 1000 Ω. Compared with Circuit B, the wide semicircle indicates the high resistance the material offers to the current flow.
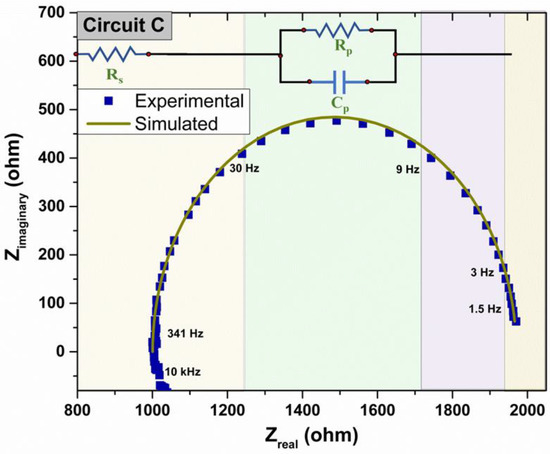
Figure 5.
Experimental and simulated Nyquist plot for Circuit C.
From Table 1 it can be observed that all the case studies have an error below 3.5%. This is a relevant result because other algorithms implemented for EIS parameter estimation, such as artificial neuronal networks, have an average error close to 6.2% [49]. Actually, from the literature, it can be seen that other evolutionary algorithms were compared with a ZsimpWin package, and they showed an extensive range of errors [50]. Thus, the already implemented HGA has an advantage over the abovementioned algorithms.
It should be mentioned that in multi-objective problems, a single objective is optimized simultaneously, and the optimization process is a set of more than one best individual that is represented as the Pareto optimal solution [51,52]. Figure 6 shows the Pareto front for the best individual obtained by the heuristic GA. The red spheres form a three-dimensional curve surface. It can be seen that the multi-objective approach for EIS parameter optimization presents good results because the individuals are concentrated in one region that follows a consistent trajectory. From the curve surface, a direct relationship between the estimated parameters can be seen. For example, an increase in capacitance also increases the value of Rs and Rp. Therefore, this helps to make all parameters optimal at the same time. Thus, it demonstrates that heuristic crossover enhances optimization by producing the best individual fitness for the multi-objective problem.
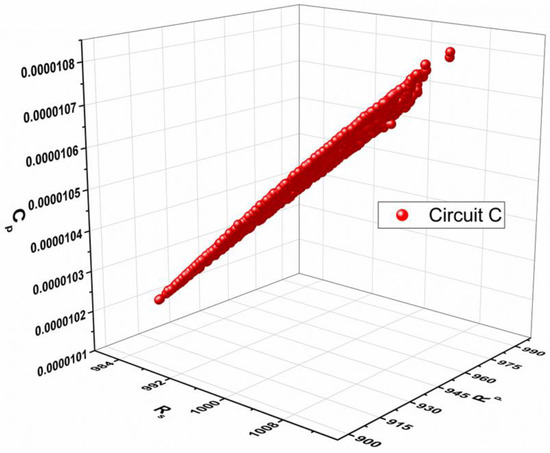
Figure 6.
Pareto frontier for Circuit C EIS optimization.
The validity and accuracy of the proposed HGA procedure are demonstrated by analyzing the experimental EIS data of Li-ion battery recorded at 35 °C, obtained from Zhang et al. [53]. The data were used to construct the Nyquist plot and then analyzed to determine the best equivalent circuit model. The already explained HGA procedure was adopted to estimate the value of each variable (see Figure 2). To this end, the experimental data were fitted with the equivalent circuit proposed in the literature [54,55]. Figure 7 displays the elements of this model that simulate the electrochemical process in batteries. As can be seen, this equivalent electric circuit contemplates a series of electric resistance at high frequencies. Two Randles circuits with a constant phase element (ZCPE = Q−1(jw)−α) that simulate the behavior of non-ideal capacitors were proposed at intermediate frequencies to simulate electrolyte and charge transfer processes. Meanwhile, a constant phase element was implemented at low frequencies to simulate the diffusion mechanism.
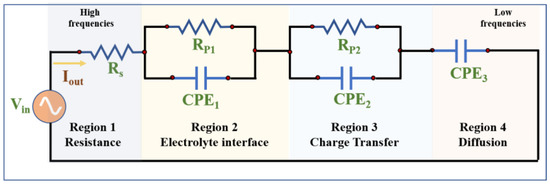
Figure 7.
Adopted equivalent electric circuit for parameter estimation in the Li-ion battery.
The impedance of the model was determined by following the same analytical procedure previously explained, but in this case, a constant phase element was considered. The obtained equation was written in its complex form and then was used to find the nine unknown variables, see Equations (8) and (9).
The equations mentioned above were expressed as a multi-objective problem and were solved by using the HGA. This way, each unknown variable’s values were obtained with reasonable accuracy. After computing and data analysis, it was concluded that the value for the best individuals that satisfy the proposed model were 0.3219, 0.2454 and 0.4063 Ω for Rs, RP1 and RP2, respectively. Meanwhile, the values for QP1, QP2 and QP3 were 0.0175, 0.0651, 6.8987 with α1 = 0.65, α2 = 0.85, and α3 = 0.82, respectively.
Figure 8 presents the experimental Nyquist plot and the simulated curve computed using the parameters obtained from the HGA. It is evident that the estimated parameters fit well with the experimental curve, indicating that the implemented HGA procedure is versatile and can estimate parameters with appropriate accuracy. The effectiveness of the proposed HGA in estimating the parameters of Li-ion battery is demonstrated by comparing this algorithm with the patterns search (PS) algorithm available in the Matlab optimization toolbox. The former algorithm is based on iteratively searching space computing for a set of points close to the Pareto front without any analytical information about the function under study and converging to the optimal global solution without needing any derivative calculations [56]. The estimated error (Root Mean Square, RMS) for the HGA was 0.0116, while the PS algorithms presented an RMS error of 0.021. It should be mentioned that those values are close to those reported in the literature. For example, Li et al., obtained an RMS error of 0.0145 using an improved particle swarm optimization algorithm to determine Li-ion battery parameters [57]. Thus, this confirmed the effectiveness of HGA in estimating the Li-ion battery parameters. It should be mentioned that practitioners require knowledge about the electrochemical process under study to correctly propose the equivalent model elements, especially when a constant phase element and Warburg diffusion elements are required.
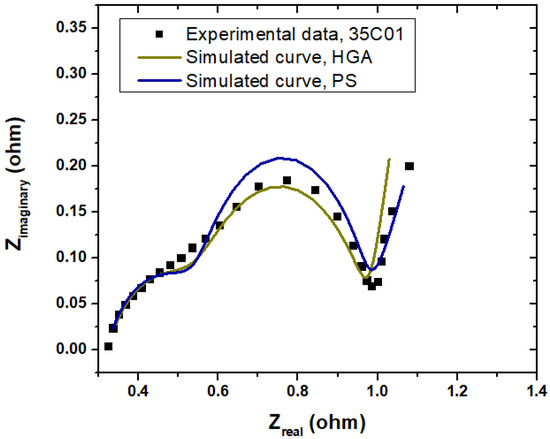
Figure 8.
Experimental and simulated Nyquist plot for the Li-ion battery under study.
4. Conclusions
In this work, the successful application of genetic algorithms was achieved to solve the multi-objective model, providing a more accurate fitness function for the EIS curve. In contrast with other studies, a heuristic crossover operator was implemented to solve the optimization problem. The latter enhances the accuracy of estimated parameters with less computing time. The optimization process involves the resolution of the EIS equation using GA to obtain the best value for each variable iteratively. The methodology presented in this work was validated for three different circuit models, and further studies were conducted by estimating the electrical parameters in batteries. One main advantage of the procedure is that all the simulations were achieved in the Matlab Toolbox, which is a relevant point because scientists do not need great expertise as programmers in evolutionary algorithms.
5. Future Work
In future work, we will consider extending the proposed methodology to estimate electrochemical parameters in systems that consider non-ideal capacitor behavior and inductive elements. Thus, circuit models that contemplate the use of constant phase elements and the Warburg impedance, to model the diffusion-controlled process, will be implemented. Furthermore, we plan to explore the potential of genetic algorithms to solve electrochemical equations such as the Butler–Volmer equation.
Author Contributions
Conceptualization, W.J.P.-R. and G.G.S.-V.; methodology, W.J.P.-R.; vali-dation, E.N.A.-M., G.G.S.-V. and C.A.C.-A.; formal analysis, W.J.P.-R. and E.R.-R.; investigation, W.J.P.-R., G.G.S.-V. and E.R.-R.; resources, W.J.P.-R., G.G.S.-V. and E.R.-R.; data curation, E.N.A.-M. and C.A.C.-A.; writing—original draft preparation, W.J.P.-R. and G.G.S.-V.; writing—review and editing, E.R.-R.; visualization, W.J.P.-R., G.G.S.-V. and E.R.-R.; supervision, W.J.P.-R. and E.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We appreciate the Polytechnic University of Victoria for the given time to develop this research.
Conflicts of Interest
The authors declare that there is no competing financial or personal interest.
References
- Pech-Rodríguez, W.J.; Rodríguez-Varela, F.J.; Rocha-Rangel, E.; González-Quijano, D.; Martínez-Loyola, J.C.; Vargas-Gutiérrez, G.; Suarez-Velazquez, G.; Morais, C.; Napporn, T. Cost-effective functionalization of Vulcan XC-72 by using the intermittent microwave heating process as nanocatalyst support for ethanol electrooxidation in acid media. Rev. Mex. Ing. Quím. 2021, 20, 955–973. [Google Scholar] [CrossRef]
- Zapata-Cruz, J.R.; Armendáriz-Mireles, E.N.; Rocha-Rangel, E.; Suarez-Velazquez, G.; González-Quijano, D.; Pech-Rodríguez, W.J. Implementation of Taguchi method to investigate the effect of electrophoretic deposition parameters of SnO2 on dye sensitised solar cell performance. Mater. Technol. 2019, 34, 549–557. [Google Scholar] [CrossRef]
- Bredar, A.R.C.; Chown, A.L.; Burton, A.R.; Farnum, B.H. Electrochemical Impedance Spectroscopy of Metal Oxide Electrodes for Energy Applications. ACS Appl. Energy Mater. 2020, 3, 66–98. [Google Scholar] [CrossRef]
- Dsoke, S.; Pfeifer, K.; Zhao, Z. The role of nanomaterials for supercapacitors and hybrid devices. In Frontiers of Nanoscience; Raccichini, R., Ulissi, U., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 19, pp. 99–136. [Google Scholar] [CrossRef]
- Zhao, W.; Ci, S. Nanomaterials as Electrode Materials of Microbial Electrolysis Cells for Hydrogen Generation. In Nanomaterials for the Removal of Pollutants and Resource Reutilization; Luo, X., Deng, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 213–242. [Google Scholar] [CrossRef]
- AbdelHamid, A.A.; Mendoza-Garcia, A.; Ying, J.Y. Advances in and prospects of nanomaterials’ morphological control for lithium rechargeable batteries. Nano Energy 2022, 93, 106860. [Google Scholar] [CrossRef]
- Choi, W.; Shin, H.-C.; Kim, J.M.; Choi, J.Y.; Yoon, W.S. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-ion Batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Han, S.B.; Oh, H.; Lee, W.Y.; Won, J.; Chae, S.; Baek, J. On-Line EIS Measurement for High-Power Fuel Cell Systems Using Simulink Real-Time. Energies 2021, 14, 6133. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Source 2020, 480, 228742. [Google Scholar] [CrossRef]
- Caponetto, R.; Matera, F.; Murgano, E.; Privitera, E.; Xibilia, M.G. Fuel Cell Fractional-Order Model via Electrochemical Impedance Spectroscopy. Fractal Fract. 2021, 5, 21. [Google Scholar] [CrossRef]
- Baldinelli, A.; Staffolani, A.; Bidini, G.; Barelli, L.; Nobili, F. An extensive model for renewable energy electrochemical storage with Solid Oxide Cells based on a comprehensive analysis of impedance deconvolution. J. Energy Storage 2021, 33, 102052. [Google Scholar] [CrossRef]
- Qu, D.; Wang, G.; Kafle, J.; Harris, J.; Crain, L.; Jin, Z.; Zheng, D. Electrochemical Impedance and its Applications in Energy-Storage Systems. Small Methods 2018, 2, 1700342. [Google Scholar] [CrossRef]
- George, K.; Van Berkel, M.; Zhang, X.; Sinha, R.; Bieberle-Hütter, A. Impedance Spectra and Surface Coverages Simulated Directly from the Electrochemical Reaction Mechanism: A Nonlinear State-Space Approach. J. Phys. Chem. C 2018, 123, 9981–9992. [Google Scholar] [CrossRef]
- Nara, H.; Yokoshima, T.; Osaka, T. Technology of electrochemical impedance spectroscopy for an energy-sustainable society. Curr. Opin. Electrochem. 2020, 20, 66–77. [Google Scholar] [CrossRef]
- Losantos, R.; Montiel, M.; Mustata, R.; Zorrilla, F.; Valiño, L. Parameter characterization of HTPEMFC using numerical simulation and genetic algorithms. Int. J. Hydrogen Energy 2022, 47, 4814–4826. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Tran, T.N. Parameter estimation of photovoltaic cell and module models relied on metaheuristic algorithms including artificial ecosystem optimization. Neural Comput. Appl. 2022, 34, 12819–12844. [Google Scholar] [CrossRef]
- Caliandro, P.; Nakajo, A.; Diethelm, S.; Van Herle, J. Model-assisted identification of solid oxide cell elementary processes by electrochemical impedance spectroscopy measurements. J. Power Source 2019, 436, 226838. [Google Scholar] [CrossRef]
- Kim, H.; Park, C.; Kang, Y. Distribution-guided heuristic search for nonlinear parameter estimation with an application in semiconductor manufacturing. IISE Trans. 2020, 52, 1246–1261. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; El-Refaey, A.M. Hybridization of Grasshopper Optimization Algorithm with Genetic Algorithm for Solving System of Non-Linear Equations. IEEE Access 2020, 8, 220944–220961. [Google Scholar] [CrossRef]
- Zain, U.-A.; Mahmood, T.; Shorfuzzaman, M.; Xiong, N.N.; Mehmood, R.M. Aiding Prosumers by Solar Cell Parameter Optimization Using a Hybrid Technique for Achieving Near Realistic P-V Characteristics. IEEE Access 2020, 8, 225416–225423. [Google Scholar] [CrossRef]
- Ruan, H.; Sun, B.; Jiang, J.; Zhang, W.; He, X.; Su, X.; Bian, J.; Gao, W. A modified-electrochemical impedance spectroscopy-based multi-time-scale fractional-order model for lithium-ion batteries. Electrochim. Acta 2020, 394, 139066. [Google Scholar] [CrossRef]
- Middlemiss, L.A.; Rennie, A.J.R.; Sayers, R.; West, A.R. Characterisation of batteries by electrochemical impedance spectroscopy. Energy Rep. 2020, 6, 232–241. [Google Scholar] [CrossRef]
- Abdulrahim, S.M.; Ahmad, Z.; Bahadra, J.; Al-Thani, N.J. Electrochemical Impedance Spectroscopy Analysis of Hole Transporting Material Free Mesoporous and Planar Perovskite Solar Cells. Nanomaterials 2020, 10, 1635. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Ku, Z.; Mei, A.; Liu, T.; Xu, M.; Ko, S.; Li, X.; Han, H. Hole-Conductor-Free Mesoscopic TiO2/CH3NH3PbI3 Heterojunction Solar Cells Based on Anatase Nanosheets and Carbon Counter Electrodes. J. Phys. Chem. Lett. 2014, 5, 2160–2164. [Google Scholar] [CrossRef] [PubMed]
- Feliu, S. Electrochemical Impedance Spectroscopy for the Measurement of the Corrosion Rate of Magnesium Alloys: Brief Review and Challenges. Metals 2020, 10, 775. [Google Scholar] [CrossRef]
- Saady, A.; El-Hajjaji, F.; Taleb, M.; Ismaily Alaoui, K.; El Biache, A.; Mahfoud, A.; Alhouari, G.; Hammouti, B.; Chauhan, D.S.; Quraishi, M.A. Experimental and theoretical tools for corrosion inhibition study of mild steel in aqueous hydrochloric acid solution by new indanones derivatives. Mater. Discov. 2018, 12, 30–42. [Google Scholar] [CrossRef]
- Hajiyan Pour, F.; Rajabi, M.; Behpour, M.; Jafari, Y. Investigation of corrosion protection performance of epoxy coatings modified by ZnO-Cr2O3 nanocomposites on mild steel surfaces. Appl. Chem. 2018, 13, 45–52. [Google Scholar] [CrossRef]
- Zhu, S.; Sun, X.; Gao, X.; Wang, J.; Zhao, N.; Sha, J. Equivalent circuit model recognition of electrochemical impedance spectroscopy via machine learning. J. Electroanal. Chem. 2019, 855, 113627. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Yu, L.; Shu, H.; Yu, T.; Zhang, X.; Yao, W.; Sun, L. A critical survey on proton exchange membrane fuel cell parameter estimation using meta-heuristic algorithms. J. Clean. Prod. 2020, 265, 121660. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Guo, Y.; Hu, W.; Chang, X.; Wu, P.; Han, C.; Li, J. Accurate Solar Cell Modeling via Genetic Neural Network-Based Meta-Heuristic Algorithms. Front. Energy Res. 2021, 9, 1–14. [Google Scholar] [CrossRef]
- Ohenoja, M.; Leiviskä, K. Observations on the Parameter Estimation Problem of Polymer Electrolyte Membrane Fuel Cell Polarization Curves. Fuel Cells 2020, 20, 516–526. [Google Scholar] [CrossRef]
- Maghawry, A.; Hodhod, R.; Omar, Y.; Kholief, M. An approach for optimizing multi-objective problems using hybrid genetic algorithms. Soft Comput. 2021, 25, 389–405. [Google Scholar] [CrossRef]
- Haeverbeke, M.V.; Stock, M.; Baets, B.D. Practical Equivalent Electrical Circuit Identification for Electrochemical Impedance Spectroscopy Analysis with Gene Expression Programming. IEEE Trans. Instrum. Meas. 2021, 70, 2514612–2514623. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Maia, A.; Ferreira, E.; Oliveira, M.C.; Menezes, L.F.; Andrade-Campos, A. Numerical optimization strategies for springback compensation in sheet metal forming. In Computational Methods and Production Engineering; Paulo Davim, J., Ed.; Woodhead Publishing: Sawston, UK, 2013; pp. 51–82. [Google Scholar] [CrossRef]
- Jakus, D.; Čađenović, R.; Vasilj, J.; Sarajčev, P. Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm. Energies 2020, 13, 1544. [Google Scholar] [CrossRef]
- Baskin, I.; Ein-Eli, Y. Electrochemoinformatics as an Emerging Scientific Field for Designing Materials and Electrochemical Energy Storage and Conversion Devices—An Application in Battery Science and Technology. Adv. Energy Mater. 2022, 1, 2202380–2202403. [Google Scholar] [CrossRef]
- Wang, J.; Ding, R.; Cao, F.; Li, J.; Dong, H.; Shi, T.; Xing, L.; Liu, J. Comparison of state-of-the-art machine learning algorithms and data-driven optimization methods for mitigating nitrogen crossover in PEM fuel cells. Chem. Eng. J. 2022, 442, 136064–136070. [Google Scholar] [CrossRef]
- Luo, K.; Chen, X.; Zheng, H.; Shi, Z. A review of deep learning approach to predicting the state of health and state of charge of lithium-ion batteries. J. Energy Chem. 2022, 74, 159–173. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, C.-R.; Wang, Y.; Zhao, M.; Yu, H.-Y.; Liu, Z.-J.; Liu, X.-M.; Chen, Y.-H.; Wu, Y.-Z.; Chen, H.-S. Open-circuit voltage loss and dielectric constants as new descriptors in machine learning study on organic photovoltaics. Int. J. Quantum Chem. 2022, 1, e27039. [Google Scholar] [CrossRef]
- Jamilla, C.U.; Mendoza, R.G.; Mendoza, V.M.P. Parameter Estimation in Neutral Delay Differential Equations Using Genetic Algorithm with Multi-Parent Crossover. IEEE Access 2021, 9, 131348–131364. [Google Scholar] [CrossRef]
- Hakimi, D.; Oyewola, D.O.; Yahaya, Y. Bolarin, G. Comparative analysis of genetic crossover operators in knapsack problem. J. Appl. Sci. Environ. Manag. 2016, 20, 593–596. [Google Scholar]
- Saxena, D.; Singh, A.K. Auto-adaptive learning-based workload forecasting in dynamic cloud environment. Int. J. Comput. Appl. 2020, 44, 541–551. [Google Scholar] [CrossRef]
- Câmara, D. Evolution and Evolutionary Algorithms. In Bio-Inspired Networking; Câmara, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1–30. [Google Scholar] [CrossRef]
- Li, J.; Jiang, X.; Khan, F.; Ye, X.; Wang, S.; Chen, J. Field deployable impedance-based corrosion sensor. Sci. Rep. 2022, 12, 236. [Google Scholar] [CrossRef] [PubMed]
- Lukács, Z.; Kristóf, T. A generalized model of the equivalent circuits in the electrochemical impedance spectroscopy. Electrochim. Acta 2020, 363, 137199. [Google Scholar] [CrossRef]
- Wan, C.; Liyang, Y.; Shen, H. Effects of Electrode Mass-loading on the Electrochemical Properties of Porous MnO2 for Electrochemical Supercapacitor. Int. J. Electrochem. Sci. 2014, 9, 4024–4038. [Google Scholar]
- Montano, J.J.; Grisales Noreña, L.F.; Tobon, A.F.; Gonzalez Montoya, D. Estimation of the parameters of the mathematical model of an equivalent diode of a photovoltaic panel using a continuous genetic algorithm. IEEE Lat. Am. Trans. 2021, 20, 616–623. [Google Scholar] [CrossRef]
- Luo, Y.F. A Multi-Frequency Electrical Impedance Spectroscopy Technique of Artificial Neural Network-Based for the Static State of Charge. Energies 2021, 14, 2526. [Google Scholar] [CrossRef]
- González, F.; Greiner, D.; Mena, V.; Souto, R.M.; Santana, J.J.; Aznárez, J.J. Fitting procedure based on Differential Evolution to evaluate impedance parameters of metal–coating systems. Eng. Comput. 2019, 36, 2960–2982. [Google Scholar] [CrossRef]
- Alhammadi, H.Y.; Romagnoli, J.A. Chapter B4—Process design and operation: Incorporating environmental, profitability, heat integration and controllability considerations. In Computer Aided Chemical Engineering; Seferlis, P., Georgiadis, M.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; Volume 17, pp. 264–305. [Google Scholar] [CrossRef]
- Bejarano, L.A.; Espitia, H.E.; Montenegro, C.E. Clustering Analysis for the Pareto Optimal Front in Multi-Objective Optimization. Computation 2022, 10, 37. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, J.; Cao, B.; Li, X. A simplified fractional order impedance model and parameter identification method for lithium-ion batteries. PLoS ONE 2017, 12, 172424. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, Z.; Lai, Y.; Liu, J.; Li, J.; Liu, Y. Electrochemical Impedance Spectroscopy Study of a Lithium/Sulfur Battery: Modeling and Analysis of Capacity Fading. J. Electrochem. Soc. 2013, 160, A553–A558. [Google Scholar] [CrossRef]
- Theodorokatos, N.; Lytras, M.; Babu, R. A Generalized Pattern Search Algorithm Methodology for solving an Under-Determined System of Equality Constraints to achieve Power System Observability using Synchrophasors. J. Phys. Conf. Ser. 2021, 2090, 012125. [Google Scholar] [CrossRef]
- Li, D.; Yang, D.; Li, L.; Wang, L.; Wang, K. Electrochemical Impedance Spectroscopy Based on the State of Health Estimation for Lithium-Ion Batteries. Energies 2022, 18, 6665. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).