Application of Fuzzy Simple Additive Weighting Method in Group Decision-Making for Capital Investment

Abstract

Investment management is a common process and practice used for achieving a desirable investment goal or outcome. Unfortunately, the systematic variation of economic situations in the marketplace effects the continuous and frequent change of investment conditions and environment in which the investor should act and operate. Hence, the rules required for providing a reasonable quality of investment projects can be based only on the investor’s management strategy, intuition and practice. There exists various decision-making approaches to investment management, and simple additive weighting (SAW) is one of the most well-known multicriteria decision-making (MCDM) methods aiming to provide an optimal decision for the decision-maker when solving various real-life problems, particularly investment problems. In this paper, the fuzzy simple additive weighting (FSAW) method is applied in group decision-making to undertake capital investment expenditure for purchasing cars with the purpose of renting them out to the public. A numerical example illustrates the importance and effectiveness of the suggested approach with the aim of ranking alternatives, and, hence, determining the preferred alternative in the MCDM problem.

1. Introduction

Capital investment, as a decision-making process, is very significant when making managerial decisions. The optimal allocation of capital is an essential issue for a company’s portfolio evaluation in achieving profit maximization, as well as taking advantage of prospective profit opportunities. This study addresses the problem of ranking alternatives, as well as the selection of the most desirable alternative, providing a maximum return from the company’s capital investment. For this reason, applying an appropriate decision-making technique is an indispensable requirement.

Decision-making is a process in which certain steps should be taken to choose the most-sensible option among the available courses of action, and the best decision should meet all stipulated requirements. For this reason, the problem should be specified, the necessary information about the problem should be collected, and finally, the feasible solution should be determined.

In cases dealing with complex and unclear problems, many factors should be taken into consideration to make a pragmatic, rational, and logical decision. This requires the involvement of experts with diverse points of view to make a strategic decision.

Most real-life decision-making processes take place in environments that are fuzzy or uncertain in nature, and consequently, are described using linguistic fuzzy terms. When dealing with fuzzy decision-making, certain outcomes are scarce, and the final decision to be made occurs under imprecise conditions. This form of decision-making mostly involves the ambiguity and intangibility of information and knowledge, and the implementation of fuzzy decision-making techniques, which can overcome the above drawbacks, is up to date.

In the initial stage of application of the fuzzy decision-making procedure, all crisp values are converted into fuzzy values, and this process is called fuzzification. Then, fuzzy rules, which mostly represent information in linguistic form with a set of IF…THEN rules, are implemented. In the last stage, the defuzzification process is carried out to convert fuzzy output values into crisp output values.

Group decision-making is a process involving acceptance of a strategy that will be beneficial for coming to a consensus on all necessary issues. Most managerial decisions are related to group decision-making.

Evidence shows that, on average, groups make better decisions than individuals, especially when dealing with complex problems. Obviously, this should not mean that any group will necessarily be more successful than any individual in making a final decision, yet group decisions mostly predominate over decisions made by individuals. The advantages of group decision-making over individual decision-making are stipulated by several factors as follows: experts have different perspectives, skills, and knowledge about the problem; experts can generate various ideas, brainstorm, and choose the best outcome that can avoid errors and reach a good-quality final decision; all experts involved in a group decision-making process have a chance to influence the decision; all experts are responsible for the consequences of the final decision; experts can come to an agreement, which is important for the final acceptability of the decision; and experts can be risk takers, risk-neutral, or risk avoiders, which is useful from the viewpoint of balancing risk before the final decision is accepted.

The quality of group decision-making is significantly dependent on the number of experts taking part in the decision-making process; in other words, the larger the number of experts in the group, the better the quality and efficiency of the decision made. In any case, when moving to the generalizing opinion of the group, a preliminary analysis of experts’ preferences, as well as differences in their opinions, should be carefully investigated.

A holistic theory of investment management in business and economics does not yet exist. However, by studying the experience of entrepreneurship in various countries, the first theoretical development in risk assessment and management help us outline different ways to solve investment problems. Currently, there is enough information present to solve problems associated with possible manifestations of investment risk. The relationships between behavioral risk variables and capital budgeting methods in firms operating in environments with different levels of uncertainty are presented in [1]. An analysis of risk management in capital budgeting shows that managers with high risk-taking behavior generally work in organizations that encourage a high degree of risk when running long-term projects and functioning under a high level of uncertainty of economic and social factors [2]. The relationship between financial uncertainty in investment decision and the sophisticated capital budgeting of numerous Dutch organizations is investigated in [3].

The determination of sufficient and reliable quantitative and qualitative assessments of the effectiveness of investments is a complex and difficult task to perform. In most cases, every investment project has several performance indicators to be considered in the process of choosing the best objects among a set of available ones.

In the decision-making process, the role of risk assessment is incredibly significant. When solving the problems of multipurpose selection of efficient resource-saving investment decisions from a certain set of possible options, various decision-making methods are used (TOPSIS, SAW, COPRAS, AHP, etc.). The information that an investor or project manager (decision-maker) possesses when solving the problems of preparing a construction investment project and performing construction processes is distinguished by its structure and level of certainty. When solving most problems, cardinal (quantitative) information is used. However, in practice, there are tasks that require information of an ordinal (qualitative) nature, or information of both types simultaneously. The practical tasks of a construction investment project are solved in the presence or absence of information about the significance of performance indicators. The main problem that decision-makers face in situations, which are difficult to analyze is the presence of information handled by fuzzy sets. Therefore, the decision-makers deal with situations that might be uncertain and vague in nature. The uncertainty may include imperfect information, insufficient understanding, and undifferentiated alternatives.

In [4], experts used fuzzy numbers to express their preferences, and the opinions were used to perform the fuzzy arrangement of alternatives by applying certain criteria. The fuzzy preference relations of each expert were collected to enable group decision-making in [5], and the fuzzy linguistic expression was analyzed to build a fuzzy majority rule that derived solution concepts of different types. In [6], the fuzzy majority rule was represented to prove the impossibility theorem for pure mixed rules. In [7], the properties of choice functions based on t-norms and rationality conditions were presented. Group choices with fuzzy preference relations were investigated in [8] to obtain the best alternative. The Multiple-Attribute Decision-Making techniques and their applications were analyzed in [9]. In [10], the evaluation of airline competitiveness was carried out by implementing three methods: SAW, weighted product (WP), and TOPSIS, and the evaluation outcome was chosen with respect to the minimum expected value loss. In [11], the reasoning of a graphical user interface (GUI) named the Intelligent File Manipulator (IFM) was compared with the human experts’ reasoning, and the synergy of Human Plausible Reasoning (HPR) and SAW theories was presented to obtain the most convenient action to be recommended to the user. A fuzzy set-based facility site selection algorithm was suggested in [12] to take into consideration the fuzzy assessments of decision-makers in the process of aggregation.

As for the issue of investments, the level of vagueness increases due to the difficulty of assessing the impact of unexpected changes on public relations (PR) opinions. The focus is on obtaining subjective judgments from the decision-makers, which may be uncertain or imperfect, to select the best option from a set of accessible alternatives.

Many real-life short-term or long-term investment projects run under the presence of imprecise and vague information, and maximizing investment returns and minimizing investment risks are aspects of objective optimization. In most cases, the opinions of experts acting collaboratively in a group are represented by linguistic terms in natural language, enabling achievement of more rational decisions. In this respect, FSAW is one of the major fuzzy-logic-based decision-making techniques vital for considering uncertainty in investment decisions.

The selection of appropriate alternatives and their ranking in investment analysis can be better realized using FSAW. This technique can make up the subjectivism of fuzzy criteria weights, reach an optimal solution under each subjective criterion, provide simplicity in a calculation process, and show effective validity in case of increasing the number of alternatives.

The FSAW method is based on the weighted average, which is an arithmetic mean value in which some numbers carry more significance or weight than others. The FSAW method has a wide range of application areas. The selection process of the appropriate maintenance of a material handling equipment strategy is an important issue in increasing plant productivity, and the FSAW method has been used to assign experts’ weights to linguistic variables, which were represented in triangular fuzzy number form [13]. Six types of maintenance strategies and 10 maintenance decision criteria were investigated. The breakdown and predictive strategies were shown, respectively, to be the best and worst maintenance strategies for material handling equipment. In [14], the FSAW method was applied to make the best decision when selecting students with high achievements, and for this reason, six criteria defined with fuzzy numbers of priority assessment weights were taken into consideration. In [15], a fuzzy multi-attribute decision-making–simple additive weighting (MADM-SAW) model was proposed for information retrieval to help buyers to make decisions when choosing their optimal e-commerce site. Five criteria with different scales of values were used to identify a reputable online shop.

The basic principle of the SAW method in group decision-making is to obtain a weighted sum of ratings of the performance of each alternative in terms of all the criteria and opinions of decision-makers.

In this paper, the FSAW method is considered in order to enable investment efficiency to be determined by choosing the most effective capital investment option in terms of purchasing cars with the purpose of hiring them out to the public. Investment efficiency is evaluated to rank the available alternatives from the best to the worst.

Group decision-making under uncertainty on the capital investment problem in the existing literature is very scarce. In this paper, we consider a comprehensive approach to group decision-making using fuzzy information for the investment problem on cars purchasing to be leased afterwards.

The maintenance content introduced in this paper is structured as follows. Section 2 presents the preliminaries required to understand the main steps of the FSAW method in group decision-making. In Section 3, we consider and solve the problem for capital investment to demonstrate the efficiency of the suggested technique. In Section 4, a discussion about the suggested method is carried out, and the conclusions are given in Section 5.

2. Preliminaries

Definition 1.

Fuzzy set theory can be considered as the extension of conventional or classical set theory and was introduced by Zadeh with the purpose of handling ambiguous, uncertain, subjective, and imprecise types of information. Fuzzy set theory gained huge popularity around the world because it has the ability to deal with problems that are difficult or even sometimes impossible to solve by implementing classical set theory. This is because classical set theory is unable to provide an effective way to describe human belief and reasoning. In classical set theory, elements or members contained in the set hold a degree of membership equal to 1, and elements that are not contained in the set have a degree of membership equal to 0. Hence, the degree of membership of elements in a classical set are binary values (either one or zero). Fuzzy sets allow elements in the set to have partial degrees of membership; in other words, elements of a fuzzy set can be described by certain membership functions. Fuzzy sets contain elements with degrees of membership, or membership functions, in the interval [0,1]. It should be clarified that the degree of membership of an element in the fuzzy set is not same as the probability distribution function.

Definition 2.

Fuzzy numbers can be defined as the extension of real numbers. In other words, a fuzzy number is a specific type of fuzzy set that defines a fuzzy interval in the real number. Fuzzy numbers were proposed by Zadeh with the purpose of dealing optimally with inaccurate numerical values. A fuzzy number must satisfy the following conditions: the fuzzy set must be convex; the fuzzy set must be normalized, i.e., there must be an element in the fuzzy set with a maximal degree of membership (also called the height of the fuzzy set) equal to one; and the degree of membership of the fuzzy set must be piecewise continuous.

Different shapes of fuzzy numbers, such as triangular, trapezoidal, and Gaussian fuzzy numbers, exist. In fact, the trapezoidal fuzzy number is a superset of the triangle fuzzy number. If the trapezoidal and triangular fuzzy numbers are denoted as $l,{\mathrm{m}}_1,{\mathrm{m}}_2,\mathrm{r}$, and $l,\mathrm{m},\mathrm{r}$, respectively, then the conversion of the trapezoidal fuzzy number into the triangle fuzzy number can occur if the condition ${\mathrm{m}}_1={\mathrm{m}}_2$ is fulfilled. It should also be mentioned that in the trapezoidal fuzzy number denoted as $l,{\mathrm{m}}_1,{\mathrm{m}}_2,\mathrm{r}$, the condition $l\le {\mathrm{m}}_1\le {\mathrm{m}}_2\le \mathrm{r}$ must be met.

In this paper, we use a trapezoidal fuzzy number.

Definition 3.

In the case of emphasizing the priority and weight of each expert, fuzzy weights ${\stackrel{\sim }{\omega }}_t, t=1,2,\dots ,k$ of experts are appointed consequent to the importance defined by the final expert’s interview. Eventually, the rate of importance $I_t$ is determined as follows [16]:

$$I_t=\frac{d\left({\stackrel{\sim }{\omega }}_t\right)}{{\displaystyle {\sum }_{t=1}^{k}d\left({\stackrel{\sim }{\omega }}_t\right)}}, t=1,2,\dots ,k$$

(1)

where  $d\left({\stackrel{\sim }{\omega }}_t\right)$ is the defuzzified or crisp value of the fuzzy weight determined by applying the oriented distance.

Definition 4.

Let ${\stackrel{\sim }{W}}_{jt}=\left(a_{jt},b_{jt},c_{jt},d_{jt}\right)$, $j=1,2,\dots ,n$, and $t=1,2,\dots ,k$ be the linguistic weight of subjective criteria—$C_1,C_2,\dots ,C_h$, and objective criteria—$C_{h+1},C_{h+2},\dots ,C_n$ provided by experts $D_t$. The aggregated fuzzy criteria weight ${\stackrel{\sim }{W}}_j=\left(a_j,b_j,c_j,d_j\right), j=1,2,\dots ,n$ of criteria $C_j$ assessed by a group of $k$ experts is determined in the following form [16]:

$${\stackrel{\sim }{W}}_j=\left(I_1\otimes {\stackrel{\sim }{W}}_{j1}\right)\oplus \left(I_2\otimes {\stackrel{\sim }{W}}_{j2}\right)\oplus \cdots \oplus \left(I_k\otimes {\stackrel{\sim }{W}}_{jk}\right)$$

(2)

where $a_j={\displaystyle {\sum }_{t=1}^k{I}_t}{a}_{jt}$, $b_j={\displaystyle {\sum }_{t=1}^k{I}_t}{b}_{jt}$, $c_j={\displaystyle {\sum }_{t=1}^k{I}_t}{c}_{jt}$, $d_j={\displaystyle {\sum }_{t=1}^k{I}_t}{d}_{jt}$.

Definition 5.

The fuzzy rating matrix $\stackrel{\sim }{M}$ is described as follows [17]:

$$\stackrel{\sim }{M}=\left[\begin{array}{cccc}{\stackrel{\sim }{x}}_{11}& {\stackrel{\sim }{x}}_{12}& \cdots & {\stackrel{\sim }{x}}_{1n}\\ {\stackrel{\sim }{x}}_{21}& {\stackrel{\sim }{x}}_{22}& \cdots & {\stackrel{\sim }{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{x}}_{m1}& {\stackrel{\sim }{x}}_{m2}& \cdots & {\stackrel{\sim }{x}}_{mn}\end{array}\right]$$

(3)

where ${\stackrel{\sim }{x}}_{ij}, \forall i, j$ indicates the aggregated fuzzy rating for the alternative $A_i, i=1,2,\dots ,m$ with the appropriate criteria $C_j$.

Definition 6.

The weighted fuzzy matrix is determined by the multiplication of the fuzzy rating matrix $\stackrel{\sim }{M}$ and weight vector $W$ [16], i.e.,

$$\stackrel{\sim }{F}=\stackrel{\sim }{M}\otimes W=\left[\begin{array}{cccc}{\stackrel{\sim }{x}}_{11}& {\stackrel{\sim }{x}}_{12}& \cdots & {\stackrel{\sim }{x}}_{1n}\\ {\stackrel{\sim }{x}}_{21}& {\stackrel{\sim }{x}}_{22}& \cdots & {\stackrel{\sim }{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{x}}_{m1}& {\stackrel{\sim }{x}}_{m2}& \cdots & {\stackrel{\sim }{x}}_{mn}\end{array}\right]\otimes \left[\begin{array}{c}{W}_1\\ W_2\\ ⋮\\ W_n\end{array}\right]=\left[\begin{array}{cccc}{\stackrel{\sim }{x}}_{11}\otimes W_1& {\stackrel{\sim }{x}}_{12}\otimes W_2& \cdots & {\stackrel{\sim }{x}}_{1n}\otimes W_n\\ {\stackrel{\sim }{x}}_{21}\otimes W_1& {\stackrel{\sim }{x}}_{22}\otimes W_2& \cdots & {\stackrel{\sim }{x}}_{2n}\otimes W_n\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{x}}_{m1}\otimes W_1& {\stackrel{\sim }{x}}_{m2}\otimes W_2& \cdots & {\stackrel{\sim }{x}}_{mn}\otimes W_n\end{array}\right]$$

(4)

3. Statement and Solution of the Problem

The case study in this paper describes a capital investment regarding a purchase of cars by a small company with the purpose of hiring them out to the public. A company spent GBP 100,000 on purchasing cars. The car purchase took place in the UK, and we assume that four decision-makers (denoted as $D_1$, $D_2$, $D_3$, and $D_4$) were involved in the process of expressing opinions to determine the car models, which are most commonly used for rental purposes. Finally, the following three alternatives (car models) were chosen by the decision-makers: Proton Persona, Vauxhall Merit, and Daewoo Lanos, denoted as $A_1$, $A_2$, and $A_3$, respectively. In choosing the above-mentioned alternatives, the following four criteria were taken into consideration by the decision-makers: equipment quality ($C_1$), comfort ($C_2$), car parts and component reliability ($C_3$), and safety ($C_4$) [18].

The following steps of the FSAW method were used to rank the alternatives, resulting in the determination of the best (winning) alternative.

Step 1: An expert group must be created. The criteria are selected and promising alternate feature investments are determined. A group of decision-makers is responsible for determining the most-suitable alternative. In this paper, we used four subjective criteria as mentioned above in the case study part.

In the process of group decision-making, a large role is given to expert assessments that reflect the opinions of the involved specialists. For forming expert assessments, an expert commission is created, including all experts as well as the special working group, which coordinates the activities of the expert commission.

The expert group is formed based on the need to ensure its representativeness. This means that during the formation of the expert group, resolving issues related to assessing the competence of experts and determining the expert group size are obligatory.

The mandatory similarity of experts’ opinions can be considered from two points of view. On the one hand, when aggregating the preferences of experts involved in a group decision-making process, their differences in views will be averaged. On the other hand, the aggregated opinion of experts in several cases may practically not differ from the opinion of a group of less qualified experts.

Step 2: The importance rate of decision-makers should be defined. The above-mentioned four group decision-makers $D_1$, $D_2$,$D_3$, and $D_4$ are accountable for evaluating the three alternatives $A_1$, $A_2$, and $A_3$ under each of the four criteria $C_1$, $C_2$, $C_3$, and $C_4$, as well as the significance of the criteria. The importance degrees of the decision-makers are $I_1, I_2, I_3, I_4$ ($I_t, t=1,2,\dots ,k$), where $I_t\in \left[0,1\right]$ and ${\displaystyle {\sum }_{t=1}^k{I}_t}=1$. The decision-makers’ group is a homogeneous group if $I_1=I_2=\cdots =I_k=\frac{1}{k}$; otherwise, the decision-makers’ group is a heterogeneous group. In a homogeneous group, subjects have similarities in qualifications and experiences. A homogenous group contributes to the satisfaction of its subjects and reduces the conflict between them. In this case, there is a guarantee that during the joint activity of the group, none of its subjects would dominate. Assuming that the decision-makers’ group is homogeneous: $I_1=I_2=I_3=I_4=\frac{1}{4}=0.25$.

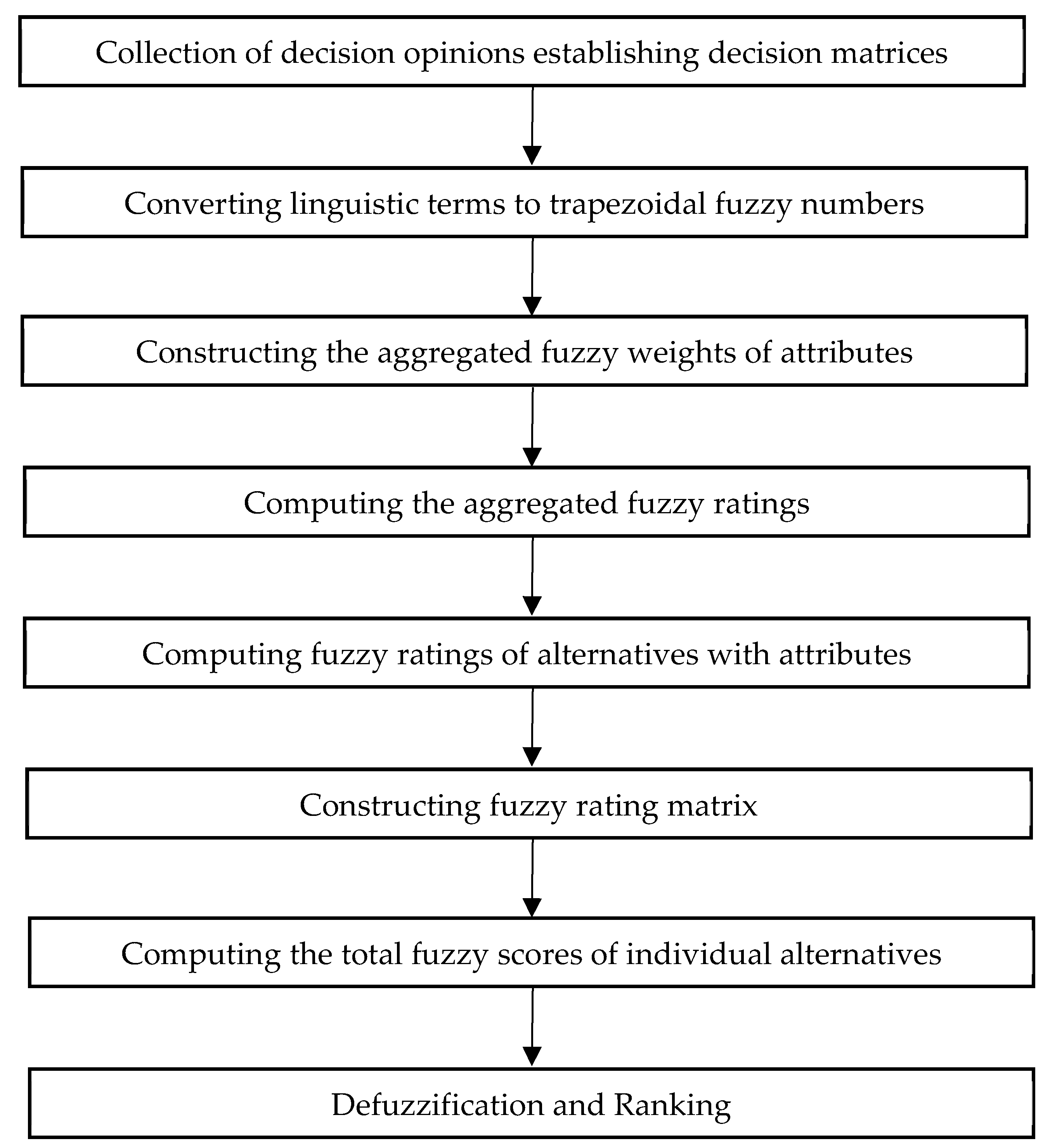
The flowchart of the FSAW method is represented in Figure 1.

Step 3: Linguistic weighting terms are entered to enable decision-makers to evaluate the importance of the criteria and to calculate aggregated fuzzy weights for individual criteria. Linguistic terms and fuzzy numbers for importance weights are represented as follows [12]:

Very low (VL)—(0,0,0,3);

Low (L)—(1,3,3,5);

Medium (M)—(2,5,5,8);

High (H)—(5,7,7,10);

Very high (VH)—(7,10,10,10).

We used linguistic weighting terms and their respective fuzzy numbers to assess the significance weights for each criterion. Using Formula (2), we determined the aggregated fuzzy weight for each criterion (

Table 1. Aggregated fuzzy weight for each criterion.

Criteria	Decision-Makers
	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$	${\mathit{D}}_4$	Aggregated Fuzzy Weight
$C_1$	(2,5,5,8)	(5,7,7,10)	(5,7,7,10)	(2,5,5,8)	(3.5,6,6,9)
$C_2$	(2,5,5,8)	(5,7,7,10)	(2,5,5,8)	(1,3,3,5)	(2.5,5,5,7.75)
$C_3$	(2,5,5,8)	(2,5,5,8)	(2,5,5,8)	(7,10,10,10)	(3.25,6.25,6.25,8.5)
$C_4$	(7,10,10,10)	(2,5,5,8)	(1,3,3,5)	(2,5,5,8)	(3,5.75,5.75,7.75)

). For example, the aggregated fuzzy weight for $C_1$ is calculated as follows:

$$C_1=\left(\left(2+5+5+2\right)/4,\left(5+7+7+5\right)/4,\left(5+7+7+5\right)/4,\left(8+10+10+8\right)/4\right)=\left(3.5,6,6,9\right)$$

Step 4: The fuzzy weights of individual criteria must be defuzzified to determine weights in normalized form and to state the weight vector. For defuzzification weights of fuzzy criteria, the oriented distance is determined. The defuzzification of ${\stackrel{\sim }{W}}_j$, indicated as $d\left({\stackrel{\sim }{W}}_j\right)$, is represented by $d\left({\stackrel{\sim }{W}}_j\right)=\frac{1}{4}\left(a_j+b_j+c_j+d_j\right), j=1,2,\dots ,n$ [18]. For the different criteria, the calculations will be as follows:

$$C_1=\left(3.5+6+6+9\right)/4=6.125$$

$$C_2=\left(2.5+5+5+7.75\right)/4=5.0625$$

$$C_3=\left(3.25+6.25+6.25+8.5\right)/4=6.0625$$

$$C_4=\left(3+5.75+5.75+7.75\right)/4=5.5625$$

Then, the defuzzified value of the normalized weight for criteria $C_j$, indicated as $W_j$, is calculated in the following form [16]:

$$W_j=\frac{d\left({\stackrel{\sim }{W}}_j\right)}{{\displaystyle {\sum }_{j=1}^{n}d\left({\stackrel{\sim }{W}}_j\right)}}, j=1,2,\dots ,n$$

where ${\displaystyle {\sum }_{j=1}^n{W}_j}=1$. The weight vector, denoted as $W=\left[W_1,W_2,\dots ,W_n\right]$, is consequently determined. For example, the normalized weight for the first criterion is $C_1=6.125/\left(6.125+5.0625+6.0625+5.5625\right)=0.27$. After realization of the defuzzification process, the aggregated fuzzy weight values become crisp (defuzzified). These values and weights in normalized form are depicted in

Table 2. Aggregated fuzzy weight values after defuzzification and weights in normalized form.

Process	Criteria
	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
Aggregated fuzzy weight values after defuzzification	6.125	5.0625	6.0625	5.5625
Weights in normalized form	0.27	0.22	0.27	0.24

.

$W=[0.27,0.22,0.27,0.24]$

Step 5: Linguistic terms are applied, and the decision-makers evaluate the fuzzy ratings of alternatives regarding individual subjective criteria, and the combination of these criteria enables us to obtain the aggregated fuzzy rates. Assuming that ${\stackrel{\sim }{x}}_{ijt}=\left(o_{ijt},p_{ijt},q_{ijt},s_{ijt}\right)$, $i=1,2,\dots ,m,$ $j=1,2,\dots ,h, t=1,2,\dots ,k$ is the linguistic conformity rate appointed to alternative $A_i$ by considering subjective criteria $C_j$ by decision-maker $D_t$. ${\stackrel{\sim }{x}}_{ij}$ is computed to be the aggregated fuzzy rating of alternative $A_i$ under subjective criteria $C_j$, so that [16]

$${\stackrel{\sim }{x}}_{ij}=\left(I_1\otimes {\stackrel{\sim }{x}}_{ij1}\right)\oplus \left(I_2\otimes {\stackrel{\sim }{x}}_{ij2}\right)\oplus \cdots \oplus \left(I_1\otimes {\stackrel{\sim }{x}}_{ijk}\right)$$

which can afterward be represented and defined as

$${\stackrel{\sim }{x}}_{ij}=\left(o_{ij},p_{ij},q_{ij},s_{ij}\right), i=1,2,\dots ,m, j=1,2,\dots ,h$$

where $o_{ij}={\displaystyle {\sum }_{t=1}^k{I}_t}{o}_{ijt}$, $p_{ij}={\displaystyle {\sum }_{t=1}^k{I}_t}{p}_{ijt}$, $q_{ij}={\displaystyle {\sum }_{t=1}^k{I}_t}{q}_{ijt}$, $s_{ij}={\displaystyle {\sum }_{t=1}^k{I}_t}{s}_{ijt}$.

We need to evaluate the fuzzy rates of three alternatives. For this reason, we applied linguistic terms and fuzzy numbers with regard to these terms by considering every subjective criterion. Afterwards, the aggregated fuzzy rate was determined for each alternative–criterion combination by using ${\stackrel{\sim }{x}}_{ij}=\left(I_1\otimes {\stackrel{\sim }{x}}_{ij1}\right)\oplus \left(I_2\otimes {\stackrel{\sim }{x}}_{ij2}\right)\oplus \cdots \oplus \left(I_1\otimes {\stackrel{\sim }{x}}_{ijk}\right)$ (

Table 3. Estimation of subjective criteria of decision-makers.

Criteria	Alternative	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$	${\mathit{D}}_4$	Aggregated Ratings
$C_1$	$A_1$	(30, 50, 80, 100)	(60, 80, 80, 100)	(80, 100, 100, 100)	(30, 50, 50, 70)	(50, 70, 77.5, 92.5)
	$A_2$	(30, 50, 50, 70)	(60, 80, 80, 100)	(30, 50, 80, 100)	(60, 80, 80, 100)	(45, 65, 72.5, 92.5)
	$A_3$	(60, 80, 80, 100)	(30, 50, 80, 100)	(60, 80, 100, 100)	(30, 50, 50, 70)	(45, 65, 77.5, 92.5)
$C_2$	$A_1$	(60, 80, 80, 100)	(60, 80, 100, 100)	(30, 50, 50, 70)	(30, 50, 50, 70)	(45, 65, 70, 85)
	$A_2$	(30, 50, 50, 70)	(60, 80, 100, 100)	(30, 50, 80, 100)	(60, 80, 80, 100)	(45, 65, 77.5, 92.5)
	$A_3$	(30, 50, 50, 70)	(80, 100, 100, 100)	(60, 80, 100, 100)	(30, 50, 80, 100)	(50, 70, 82.5, 92.5)
$C_3$	$A_1$	(60, 80, 100, 100)	(30, 50, 50, 70)	(60, 80, 80, 100)	(30, 50, 50, 70)	(45, 65, 70, 85)
	$A_2$	(30, 50, 80, 100)	(60, 80, 100, 100)	(60, 80, 80, 100)	(60, 80, 100, 100)	(52.5, 72.5, 90, 100)
	$A_3$	(60, 80, 80, 100)	(30, 50, 50, 70)	(60, 80, 80, 100)	(30, 50, 80, 100)	(45, 65, 72.5, 92.5)
$C_4$	$A_1$	(60, 80, 100, 100)	(30, 50, 50, 70)	(60, 80, 80, 100)	(80, 100, 100, 100)	(57.5, 77.5, 82.5, 92.5)
	$A_2$	(30, 50, 80, 100)	(60, 80, 80, 100)	(30, 50, 50, 70)	(60, 80, 100, 100)	(45, 65, 77.5, 92.5)
	$A_3$	(60, 80, 80, 100)	(60, 80, 100, 100)	(30, 50, 80, 100)	(60, 80, 80, 100)	(52.5, 72.5, 85, 100)

).

The linguistic terms for the ratings are represented below [12]:

Very poor (VP)—(0, 0, 0, 20);

Poor (P)—(0, 0, 20, 40);

Slightly poor (SP)—(0, 20, 20, 40);

Very fair (VF)—(0, 20, 50, 70);

Fair (F)—(30, 50, 50, 70);

Slightly fair (SF)—(30, 50, 80, 100);

Slightly good—(SG) (60, 80, 80, 100);

Good (G)—(60, 80, 100, 100);

Very good—(VG) (80, 100, 100, 100).

Step 6: The group decision-maker evaluation should be performed. Group decisions can involve interacting and managing the huge amount of available information, exploring different ideas related to the problem, and tapping into many strands of experience. Group decision-making depends on such factors as social influence, group dynamics, etc. The group of experts can make decisions by adopting a majority rule strategy to choose the option supported by most of them.

Group decision-makers evaluate the fuzzy costs and profits related to different alternatives referring to objective criteria and then determine the fuzzy rates of alternatives by considering the above criteria for individuals. These criteria are defined in different items and should be converted into nondimensional indexes to provide reconcilability with the linguistic rates of subjective criteria. Alternatives with the lowest cost or greatest profit have the largest rating. Let ${\stackrel{\sim }{r}}_{ij}=\left(a_{ij},b_{ij},c_{ij},d_{ij}\right)$, $i=1,2,\dots ,m$, $j=q, q+1,\dots ,n$, $q=h+1$ be the fuzzy cost or profit represented by different alternatives $A_i$ for objective criteria $C_j$. The transforming objective criteria are defined as follows [16]:

$${\stackrel{\sim }{x}}_{ij}=\left\{{\stackrel{\sim }{r}}_{ij}/\max \left\{d_{ij}\right\}\right\}\otimes 100, i=1,2,\dots ,m, j=q,q+1,\dots ,n$$

where $\max \left\{d_{ij}\right\}>0$, and ${\stackrel{\sim }{x}}_{ij}$ represents the converted fuzzy rating of fuzzy profit ${\stackrel{\sim }{r}}_{ij}$. ${\stackrel{\sim }{x}}_{ij}$ should also be described by the fuzzy number ${\stackrel{\sim }{x}}_{ij}=\left(o_{ij},p_{ij},q_{ij},s_{ij}\right)$, $i=1,2,\dots ,m,$$j=q, q+1,\dots ,n$. In addition, ${\stackrel{\sim }{x}}_{ij}$ becomes larger as ${\stackrel{\sim }{r}}_{ij}$ becomes larger:

$${\stackrel{\sim }{x}}_{ij}=\left\{\min \left\{a_{ij}\right\}/{\stackrel{\sim }{r}}_{ij}\right\}\otimes 100, i=1,2,\dots ,m, j=q, q+1,\dots ,n$$

where $\min \left\{a_{ij}\right\}>0$, and ${\stackrel{\sim }{x}}_{ij}$ represents the converted fuzzy rating of fuzzy cost ${\stackrel{\sim }{r}}_{ij}$. ${\stackrel{\sim }{x}}_{ij}$ can also be described by the fuzzy number ${\stackrel{\sim }{x}}_{ij}=\left(o_{ij},p_{ij},q_{ij},s_{ij}\right)$, $i=1,2,\dots ,m,$$j=q, q+1,\dots ,n$, $q=h+1$, but ${\stackrel{\sim }{x}}_{ij}$ becomes smaller as ${\stackrel{\sim }{r}}_{ij}$ becomes larger. Our criteria are subjective, and we will state the fuzzy matrix, which is based on fuzzy ratings.

Step 7: The fuzzy matrix is defined on a base of fuzzy ratings. The fuzzy rating matrix $\stackrel{\sim }{M}$ is represented as in Formula (3).

Using aggregated ratings, the fuzzy rating matrix is structured as shown in

Table 4. The fuzzy rating matrix.

${\mathit{A}}_{\mathit{i}}$	Criteria
	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
	$w_1=0.27$	$w_2=0.22$	$w_3=0.27$	$w_4=0.24$
$A_1$	(50, 70, 77.5, 92.5)	(45, 65, 70, 85)	(45, 65, 70, 85)	(57.5, 77.5, 82.5, 92.5)
$A_2$	(45, 65, 72.5, 92.5)	(45, 65, 77.5, 92.5)	(52.5, 72.5, 90, 100)	(45, 65, 77.5, 92.5)
$A_3$	(45, 65, 77.5, 92.5)	(50, 70, 82.5, 92.5)	(45, 65, 72.5, 92.5)	(52.5, 72.5, 85, 100)

.

Step 8: Normalization of the decision matrix should be performed. Normalization is a method of preprocessing numerical features in the training dataset to bring them to a common scale without losing information about the difference in ranges. Normalizing a matrix means scaling the values so that the range of values in a row or column is between 0 and 1. The decision matrix is normalized by using the formula given below [19]:

$$\stackrel{\sim }{R}={\left[{\stackrel{\sim }{r}}_{ij}\right]}_{m\times n}, i=1,2,3,\dots ,m; j=1,2,3,\dots ,n$$

$${\stackrel{\sim }{r}}_{ij}=\left(\frac{a_{ij}}{d_j^{\max }},\frac{b_{ij}}{d_j^{\max }},\frac{c_{ij}}{d_j^{\max }},\frac{d_{ij}}{d_j^{\max }}\right) (j \mathrm{is} \mathrm{a} \mathrm{Profit} \mathrm{Criteria})$$

$${\stackrel{\sim }{r}}_{ij}=\left(\frac{a_j^{\min }}{d_{ij}},\frac{a_j^{\min }}{c_{ij}},\frac{a_j^{\min }}{b_{ij}}, \frac{a_j^{\min }}{a_{ij}}\right) (j \mathrm{is} \mathrm{a} \mathrm{Cost} \mathrm{Criteria})$$

Thus, we have the normalized fuzzy decision matrix as depicted in

Table 5. The normalized fuzzy decision matrix.

${\mathit{A}}_{\mathit{i}}$	Criteria
	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
	$w_1=0.27$	$w_2=0.22$	$w_3=0.27$	$w_4=0.24$
$A_1$	(0.541, 0.757, 0.838, 1)	(0.529, 0.765, 0.824, 1)	(0.529, 0.765, 0.824, 1)	(0.622, 0.838, 0.892, 1)
$A_2$	(0.486, 0.703, 0.784, 1)	(0.486, 0.703, 0.838, 1)	(0.525, 0.725, 0.9, 1)	(0.486, 0.703, 0.838, 1)
$A_3$	(0.486, 0.703, 0.838, 1)	(0.541, 0.757, 0.892, 1)	(0.486, 0.703, 0.784, 1)	(0.525, 0.725, 0.85, 1)

.

Step 9: The total fuzzy estimation for individual alternatives is determined by multiplication of the fuzzy rating matrix and its respective weight vector $W=\left[0.27,0.22,0.27,0.24\right]$. In other words, by using Formula (4), we obtain the determined total fuzzy estimation vector by multiplication of the fuzzy rating matrix $\stackrel{\sim }{M}$ and the corresponding weight vector $W$.

The weighted fuzzy rating matrix is represented in

Table 6. The weighted fuzzy rating matrix.

${\mathit{A}}_{\mathit{i}}$	Criteria
	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
$A_1$	(0.146, 0.204, 0.226, 0.27)	(0.116, 0.168, 0.181, 0.22)	(0.143, 0.207, 0.222, 0.27)	(0.15, 0.201, 0.214, 0.24)
$A_2$	(0.131, 0.19, 0.212, 0.27)	(0.107, 0.155, 0.184, 0.22)	(0.142, 0.196, 0.243, 0.27)	(0.117, 0.169, 0.201, 0.24)
$A_3$	(0.131, 0.19, 0.226, 0.27)	(0.119, 0.167, 0.196, 0.22)	(0.131, 0.19, 0.212, 0.27)	(0.126, 0.174, 0.204, 0.24)

.

Step 10: The defuzzified (crisp) value for each total score is determined. The defuzzification process is the inverse of the fuzzification process. In the defuzzification process, fuzzy numbers are transformed into crisp numbers. Defuzzification is used to transform the fuzzy inference output into the crisp output. The crisp output is used as the output of the decision-making process by taking the best course of action. Thus, we apply the defuzzification technique and choose the alternative that has the highest total score. The total fuzzy scores ${\stackrel{\sim }{f}}_1,{\stackrel{\sim }{f}}_2,\cdots ,{\stackrel{\sim }{f}}_m$ are ordered by the oriented distance to define the best alternative. We define the defuzzified total scores of individual locations using the defuzzification formula represented below [20]:

$$d\left(f_i\right)=\frac{1}{4}\left(r_i+s_i+t_i+u_i\right), i=1,2,\dots ,m$$

where $d\left(f_i\right)$ is the crisp or defuzzified value of the total fuzzy score of alternative $A_i$ by using the oriented distance. The ordering of alternatives can then be forerun with the above-defined defuzzified value of total scores for individual alternatives.

The fuzzy numbers and defuzzified (crisp) values of the alternatives’ total fuzzy scores are presented in

Table 7. The fuzzy numbers and defuzzified (crisp) values of the alternatives’ total fuzzy scores.

${\mathit{A}}_{\mathit{i}}$
$A_1$	Fuzzy numbers Defuzzified value (crisp)	(0.139, 0.195, 0.211, 0.25)
		0.199
$A_2$	Fuzzy numbers Defuzzified value (crisp)	(0.124, 0.178, 0.21, 0.25)
		0.191
$A_3$	Fuzzy numbers Defuzzified value (crisp)	(0.127, 0.18, 0.21, 0.25)
		0.192

.

The comparison of defuzzified values depicted in Table 7 can yield the result in the ranking form of alternatives as $A_1>A_3>A_2$. So, the best alternative is determined as $A_1$.

4. Discussion

Investment risk management implies the effective control of all procedures and monitoring of risks in all phases of the investment project. Because a single indicator in the probability calculation of achieving an optimal return from the investment does not exist, performing sufficiently reliable estimates of the quality of investments becomes a tedious task. There are many indicators, factors, and criteria required to be considered in order to reach an effective solution to the investment problem.

The importance of classification in investment management and the decision-making process is undeniable. The objects to be classified are described using assessments in accordance with various criteria, which can be both quantitative and qualitative. With a competent formulation of the investment process, both methods are used in parallel.

MCDM is one of the most accurate and reliable approaches to problem evaluation. For this reason, investigations into MCDM techniques and concepts have been making continuous progress over the years. MCDM techniques differ by implementing various criteria-weighting methods, expressing the evaluation criteria of preferences for decision-making problems, a variety of procedures for aggregating experts’ opinions, etc.

In MCDM problems, the decision-making process involves multiple criteria that should be evaluated and considered together to rank them in order of priority from the most preferable to the least preferable.

In many real-life MCDM problems, data are vague and imprecise. This is one of the main constraints and difficulties that MCDM techniques can face during problem-solving and decision-making activities. Fuzzy set theory dealing with uncertainty in human belief and judgment, in combination with MCDM, can provide more realistic and accurate solutions to a problem and is strictly recommended by experts for practical use in a wide range of application areas for making an optimal decision.

MCDM methods, which are based on linguistic evaluations like FSAW, help to make the best selection of a decision using a weighting process within the scope of the available alternatives under the paired comparisons. The criteria should be evaluated and weighted, and then an evaluation of alternatives performed.

In conventional SAW and other analog methods, the evaluation of criteria is performed by using the numerical values of linguistic variables. In cases where an environment requires fuzzy decision-making, using fuzzy numbers for the evaluation of the deviations of decision-makers becomes essential. At present, particularly in complicated economic situations, most decisions are made in fuzzy environments. Hence, the fuzzy model of SAW is very suitable for application in such situations.

In this study, a car purchasing investment problem with a rental purpose was investigated. The group decision-making procedure was carried out in a fuzzy environment. The suggested approach is theoretically grounded and the test analysis shows its validity and effectiveness.

5. Conclusions

This study attempted to use the comprehensive and detailed analysis of the FSAW method, which includes the use of the power analysis method and group decision-making. The FSAW technique was applied to solve a capital investment decision-making problem involving purchasing cars to be rented to the public, where the significant weights of all criteria and the ranking of various alternatives with respect to subjective criteria were evaluated in linguistic terms defined by fuzzy numbers. As a result of the ranking process, the alternatives were ordered and, consequently, the optimal alternative was defined.

Throughout this paper, a balance exists between the size of the problem under consideration and the development of the existing FSAW methodology used, and as such, there is a level of exposure approach to the application under investigation.

An analysis of the suggested approach considers the following factors: a comprehensive approach to group decision-making in capital investment is applied to the example of a car purchasing investment with leasing intention. Specifically, the procedure for group decision-making can be applied for investment problems of different types, and the obtained results coincide with the opinions of different investors and experts.