Fractional Dynamics of a Measles Epidemic Model
Abstract
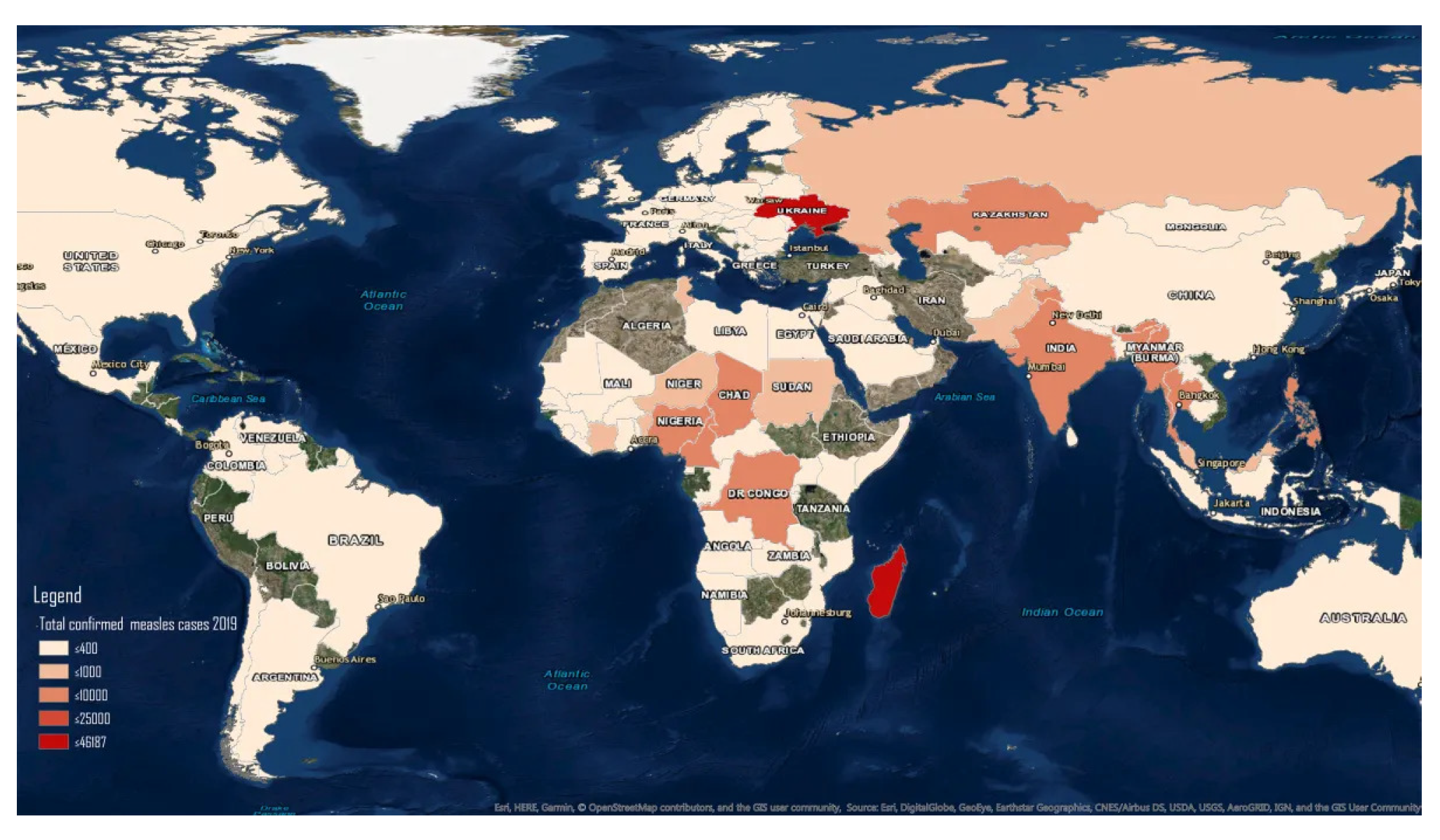
:1. Introduction
| Rank | Country | Number of Cases | Rank | Country | Number of Cases |
|---|---|---|---|---|---|
| 1 | Nigeria | 17,794 | 6 | Democratic Republic of the Congo | 1907 |
| 2 | India | 5874 | 7 | Afghanistan | 1621 |
| 3 | Somalia | 4772 | 8 | Liberia | 1495 |
| 4 | Ethiopia | 3403 | 9 | Cameroon | 1373 |
| 5 | Pakistan | 2677 | 10 | Ivory Coast | 1152 |
2. Model Formulation and Basic Results
- (ii)
- The unique endemic equilibrium point is locally stable whenever .
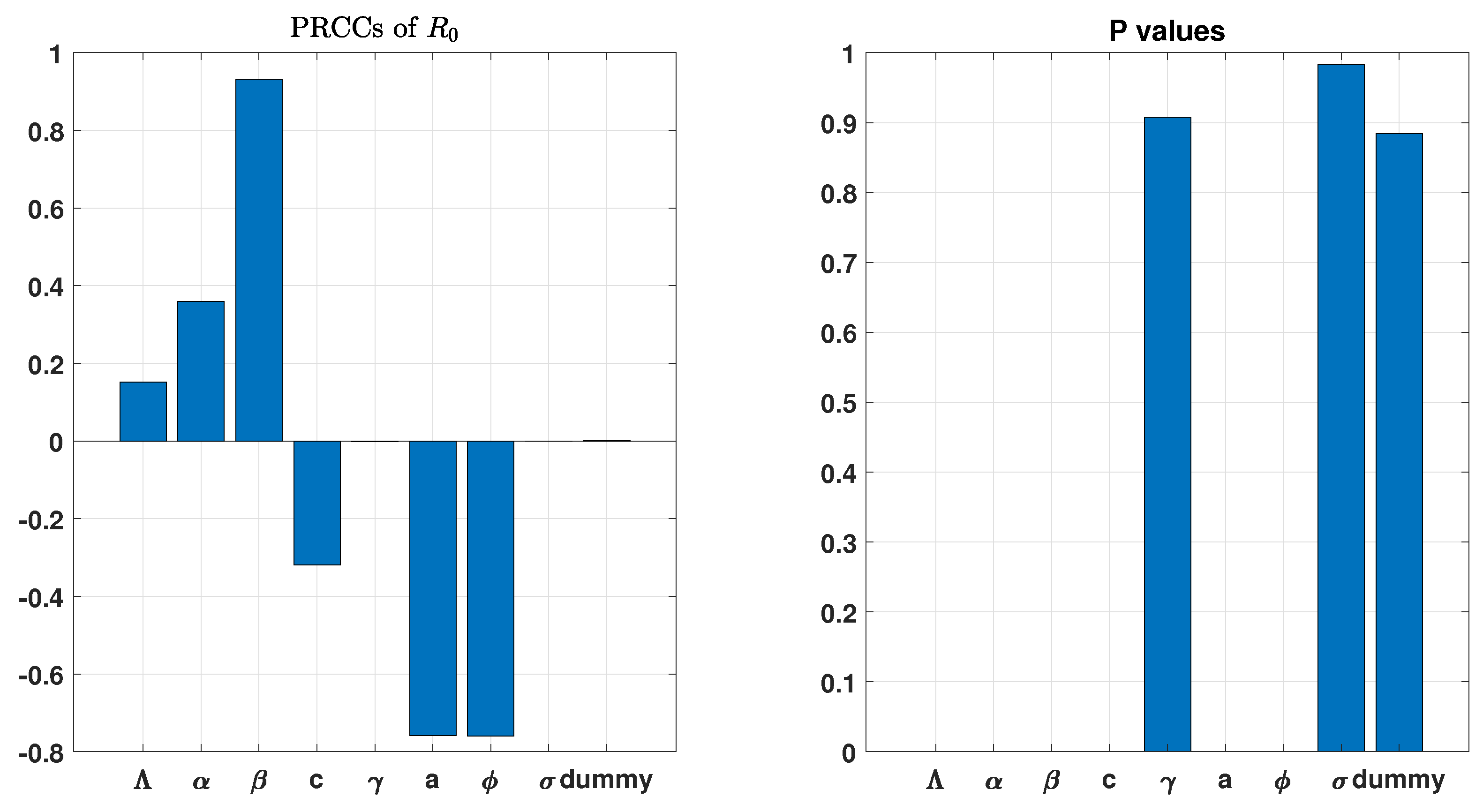
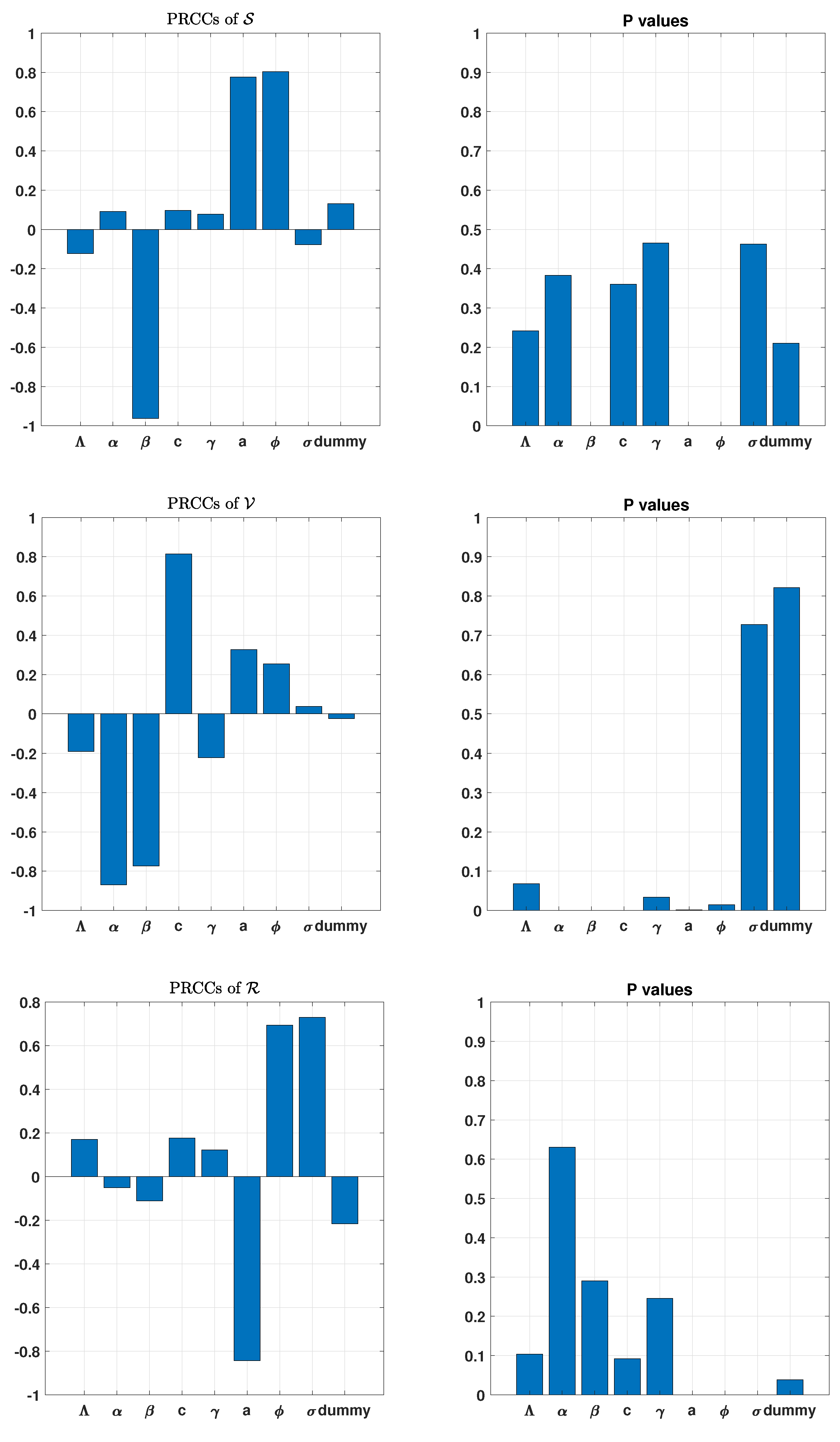
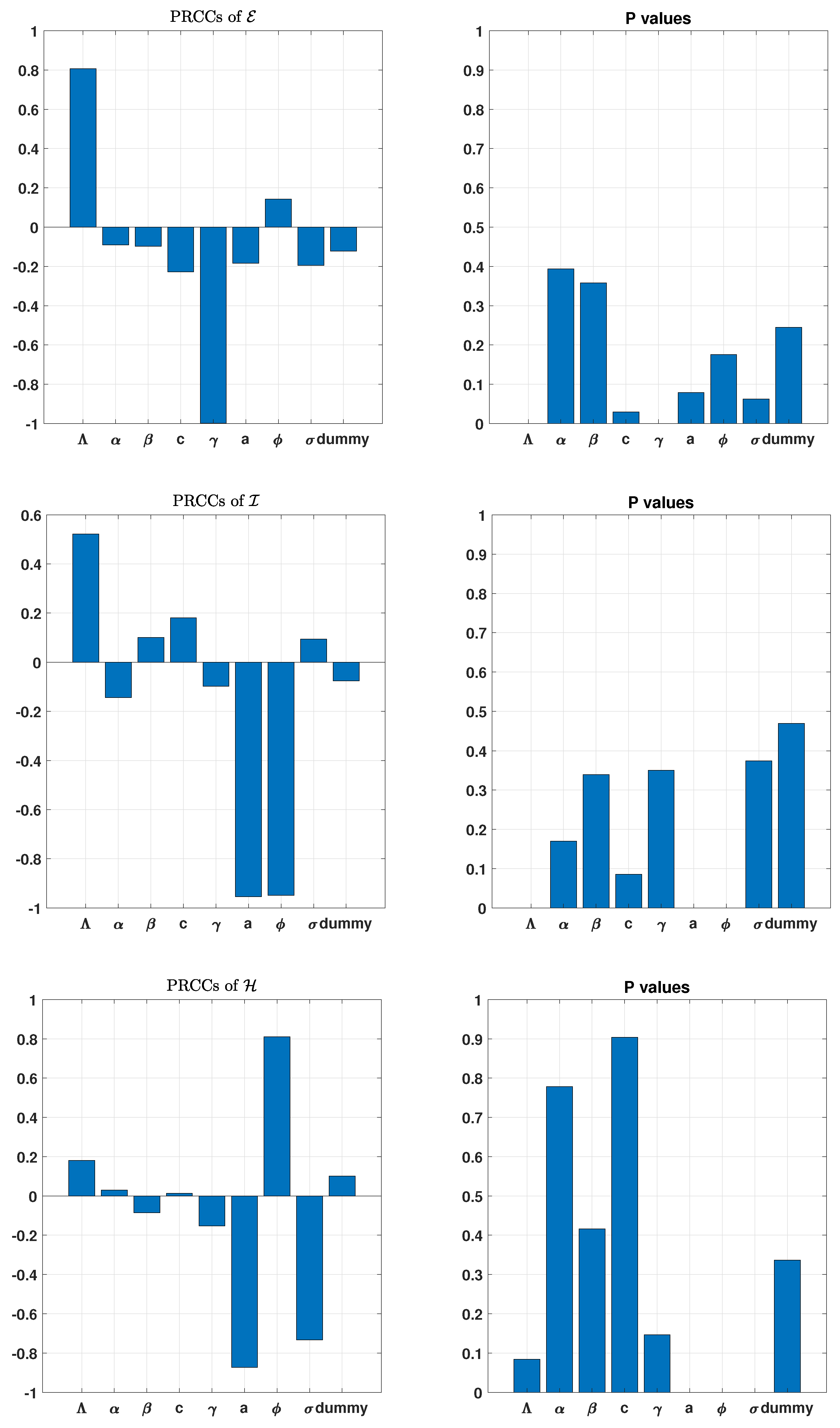
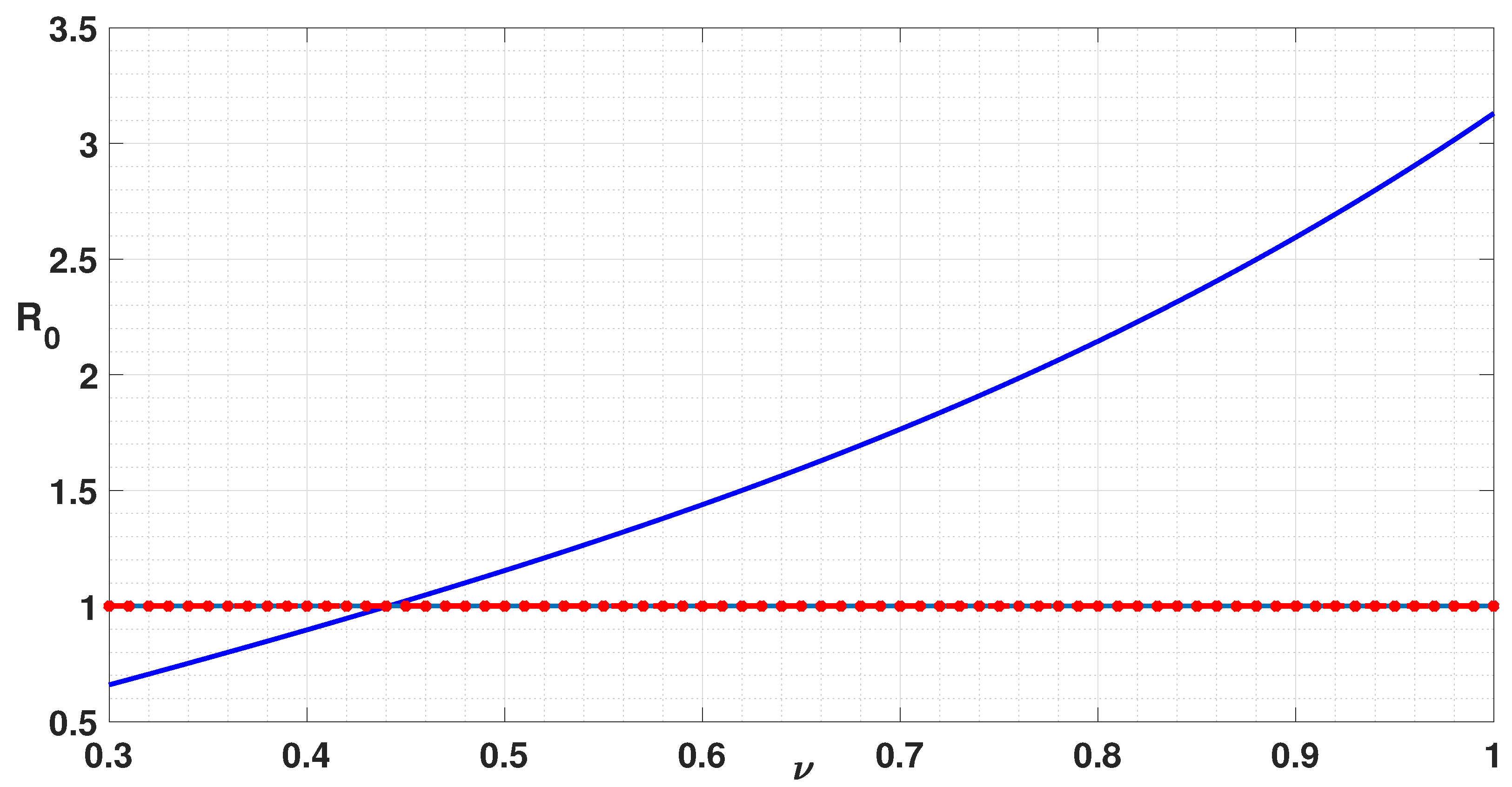
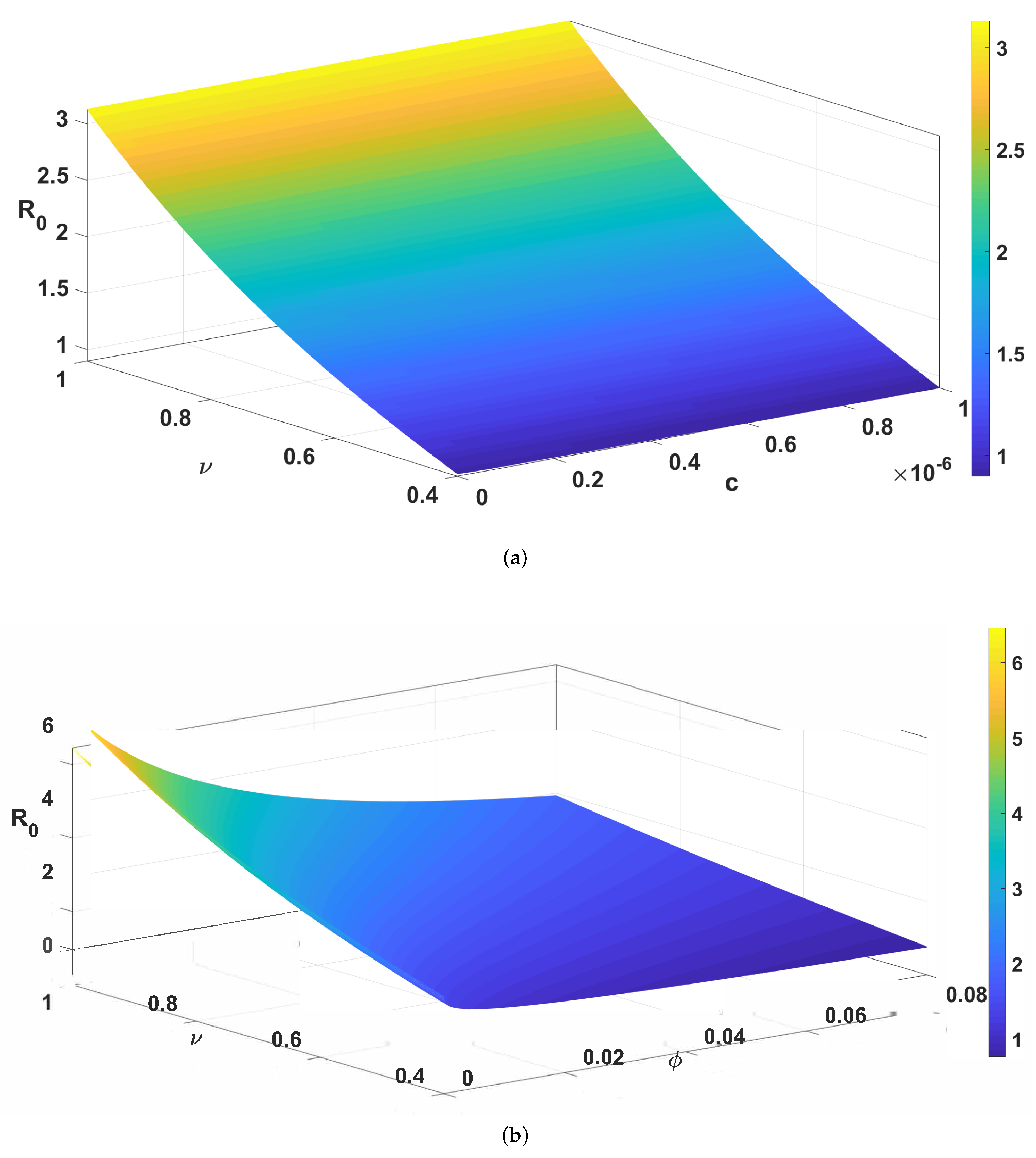
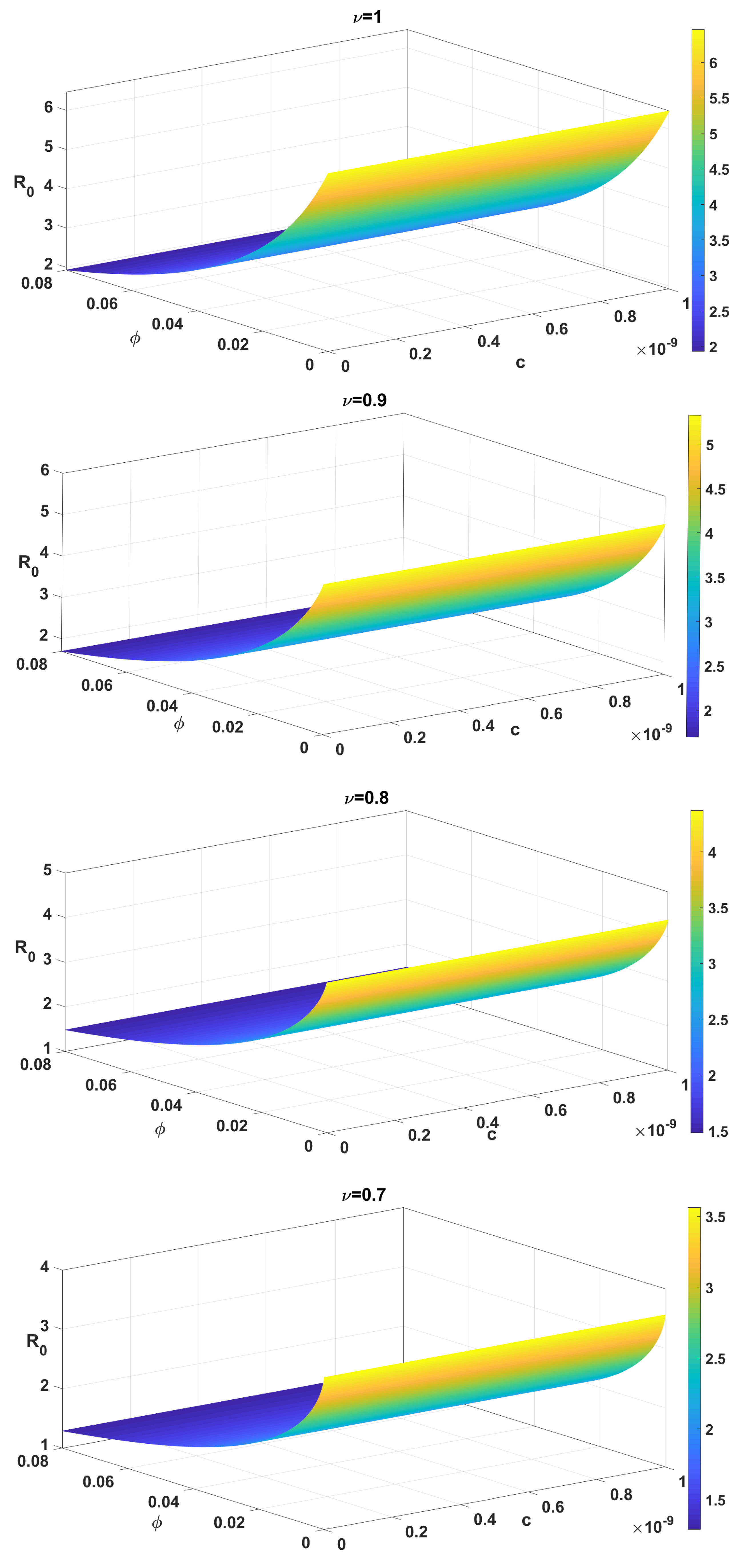
3. Uncertainty and Global Sensitivity Analysis
4. The Fractional Model and Its Analysis
4.1. Primarily Definition and Results of Fractional Calculus
4.2. The Fractional Model with Caputo Operator
4.2.1. Asymptotic Stability of the Disease-Free Equilibrium
4.2.2. Existence and Uniqueness of Solution
4.3. Global Stability of the Fractional Model
- ;
- , .
4.4. Numerical Scheme
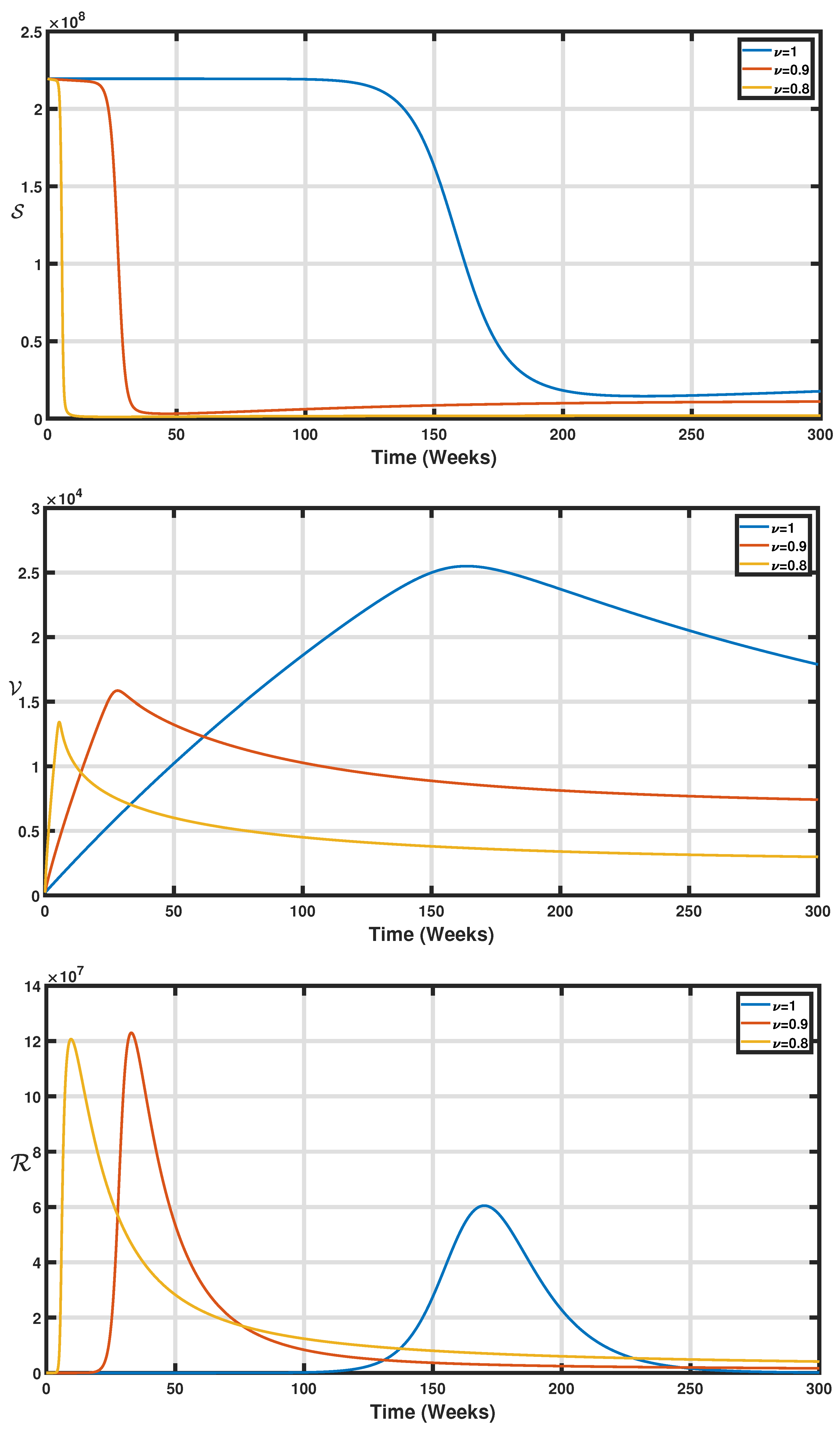
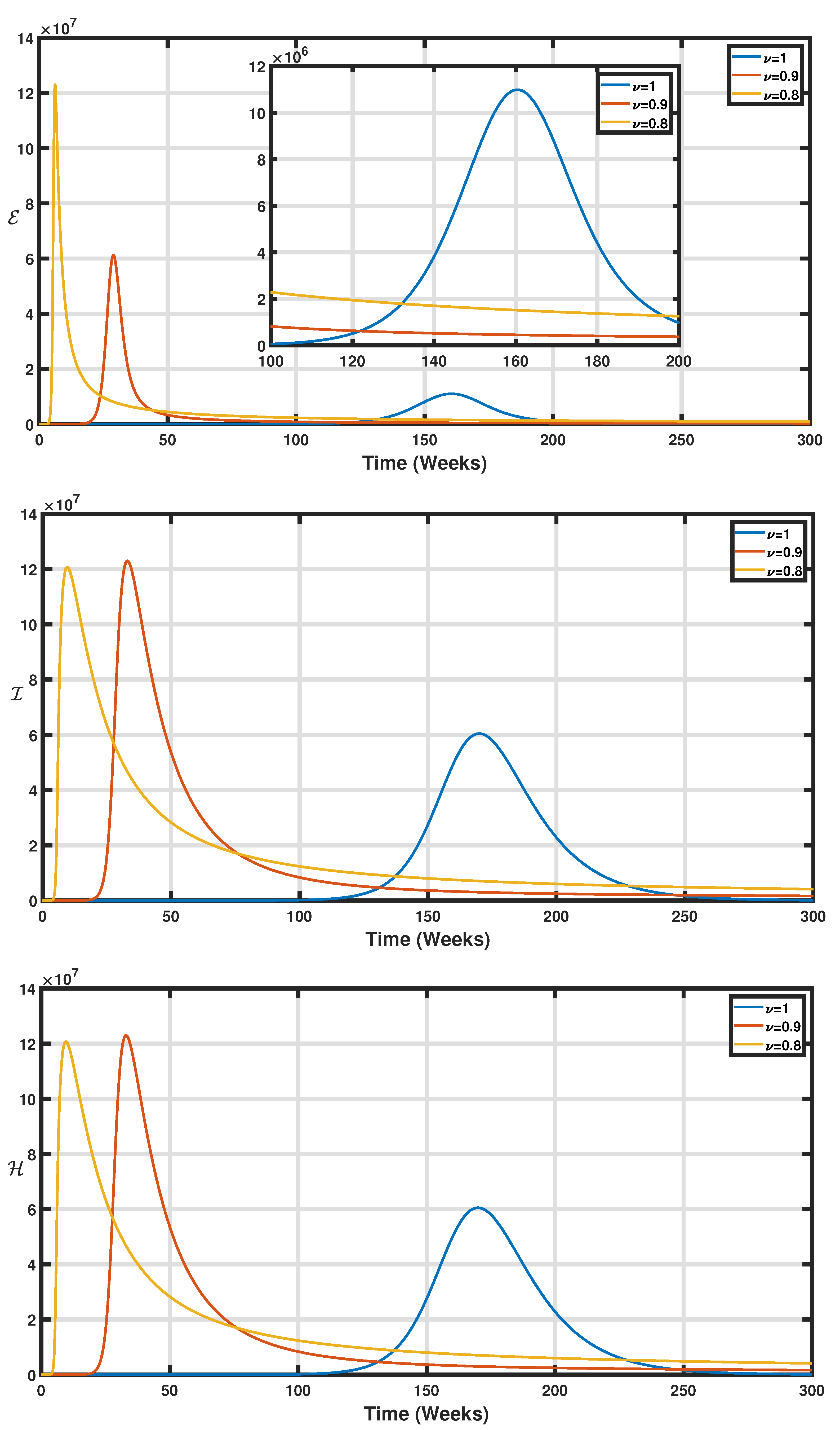
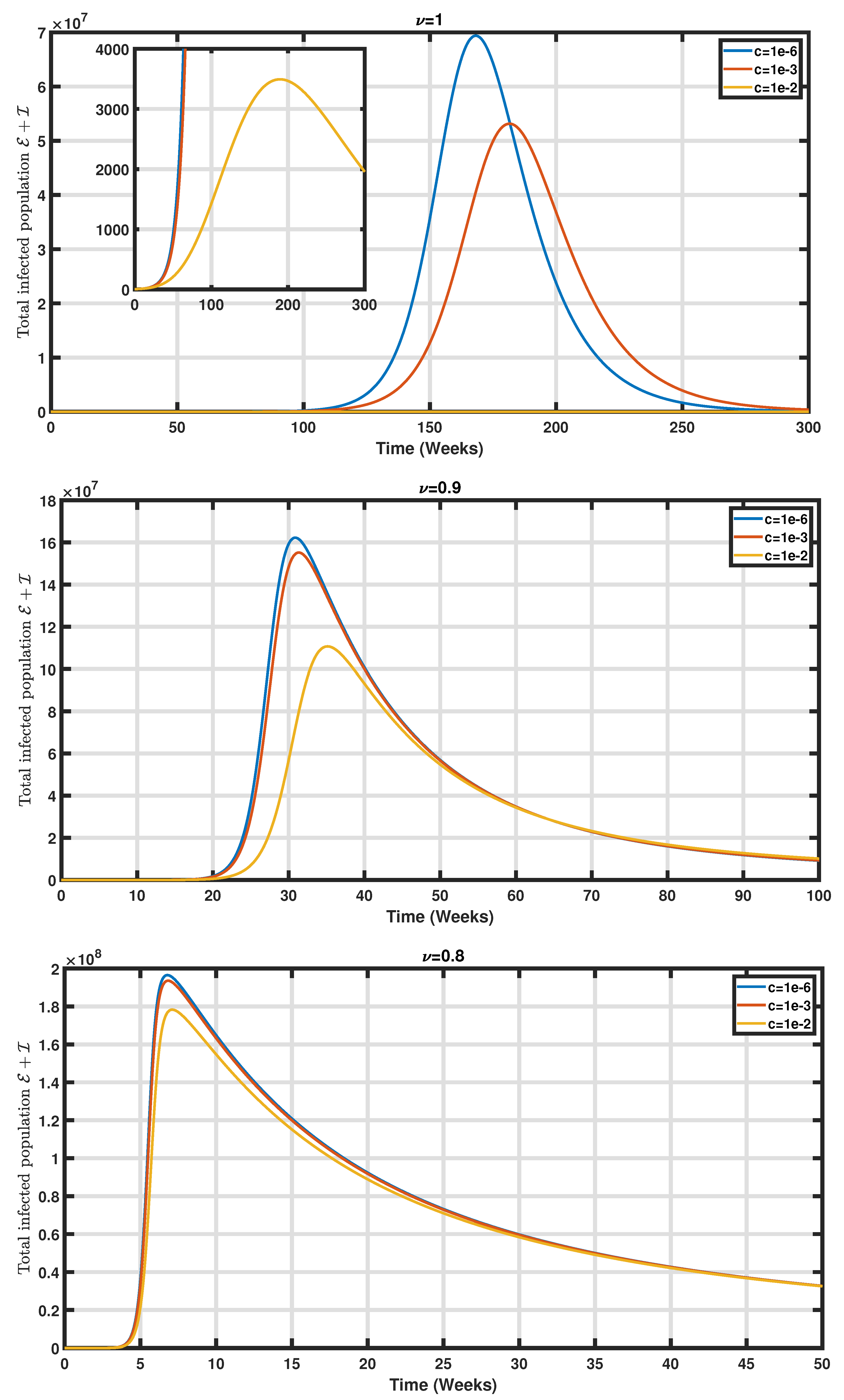
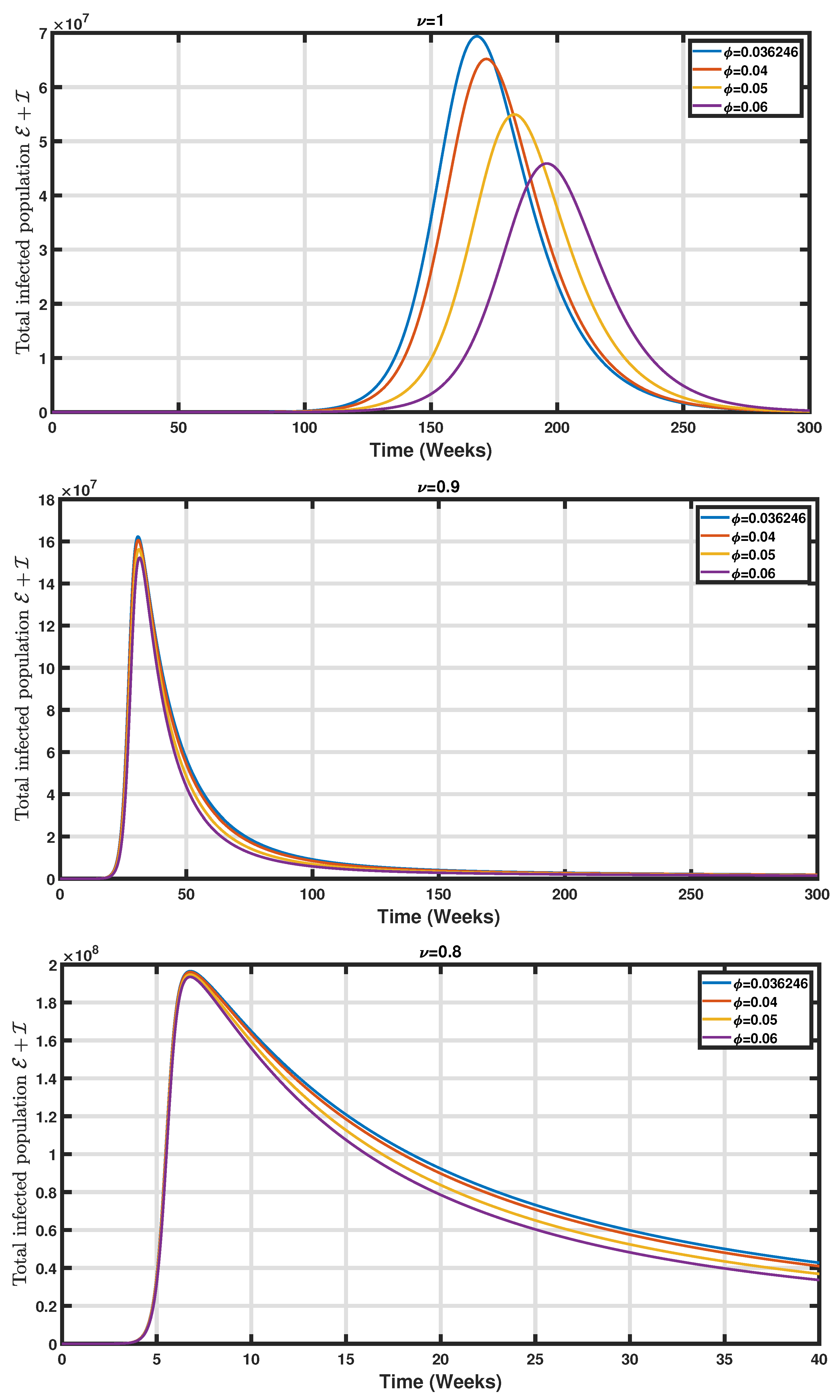
5. Numerical Simulations
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Griffin, D.E. The immune response in measles: Virus control, clearance and protective immunity. Viruses 2016, 8, 282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- James Peter, O.; Ojo, M.M.; Viriyapong, R.; Abiodun Oguntolu, F. Mathematical model of measles transmission dynamics using real data from Nigeria. J. Differ. Equ. Appl. 2022, 1–18. [Google Scholar] [CrossRef]
- Roberts, M.; Tobias, M. Predicting and preventing measles epidemics in New Zealand: Application of a mathematical model. Epidemiol. Infect. 2000, 124, 279–287. [Google Scholar] [CrossRef] [PubMed]
- Subaiya, S.; Tabu, C.; N’ganga, J.; Awes, A.A.; Sergon, K.; Cosmas, L.; Styczynski, A.; Thuo, S.; Lebo, E.; Kaiser, R.; et al. Use of the revised World Health Organization cluster survey methodology to classify measles-rubella vaccination campaign coverage in 47 counties in Kenya, 2016. PLoS ONE 2018, 13, e0199786. [Google Scholar] [CrossRef] [Green Version]
- Nabi, K.N.; Abboubakar, H.; Kumar, P. Forecasting of COVID-19 pandemic: From integer derivatives to fractional derivatives. Chaos Solitons Fractals 2020, 141, 110283. [Google Scholar] [CrossRef]
- Inaba, H. Kermack and McKendrick revisited: The variable susceptibility model for infectious diseases. Jpn. J. Ind. Appl. Math. 2001, 18, 273–292. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. II.—The problem of endemicity. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1932, 138, 55–83. [Google Scholar]
- Raza, A.; Rafiq, M.; Baleanu, D.; Shoaib Arif, M.; Naveed, M.; Ashraf, K. Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population. IET Syst. Biol. 2019, 13, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, Y.G.; Sabir, Z.; Guirao, J.L. Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (COVID-19). Fractals 2020, 28, 2040026. [Google Scholar] [CrossRef]
- Shoaib, M.; Anwar, N.; Ahmad, I.; Naz, S.; Kiani, A.K.; Raja, M.A.Z. Intelligent networks knacks for numerical treatment of nonlinear multi-delays SVEIR epidemic systems with vaccination. Int. J. Mod. Phys. B 2022, 2250100. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Zahoor Raja, M.A.; Gupta, M.; Le, D.N.; Aly, A.A.; Guerrero-Sánchez, Y. Computational intelligent paradigms to solve the nonlinear SIR system for spreading infection and treatment using Levenberg–Marquardt backpropagation. Symmetry 2021, 13, 618. [Google Scholar] [CrossRef]
- Umar, M.; Kusen; Raja, M.A.Z.; Sabir, Z.; Al-Mdallal, Q. A computational framework to solve the nonlinear dengue fever SIR system. Comput. Methods Biomech. Biomed. Eng. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Arsal, S.R.; Aldila, D.; Handari, B.D. Short review of mathematical model of measles. AIP Conf. Proc. 2020, 2264, 02003. [Google Scholar]
- Aldila, D.; Asrianti, D. A deterministic model of measles with imperfect vaccination and quarantine intervention. J. Phys. Conf. Ser. 2019, 1218, 012044. [Google Scholar] [CrossRef]
- Bashir, A.; Mushtaq, M.; Zafar, Z.U.A.; Rehan, K.; Muntazir, R.M.A. Comparison of fractional order techniques for measles dynamics. Adv. Differ. Equ. 2019, 2019, 334. [Google Scholar] [CrossRef]
- Berhe, H.W.; Makinde, O.D. Computational modelling and optimal control of measles epidemic in human population. Biosystems 2020, 190, 104102. [Google Scholar] [CrossRef] [PubMed]
- Memon, Z.; Qureshi, S.; Memon, B.R. Mathematical analysis for a new nonlinear measles epidemiological system using real incidence data from Pakistan. Eur. Phys. J. Plus 2020, 135, 378. [Google Scholar] [CrossRef]
- Momoh, A.; Ibrahim, M.; Uwanta, I.; Manga, S. Mathematical model for control of measles epidemiology. Int. J. Pure Appl. Math. 2013, 87, 707–718. [Google Scholar] [CrossRef] [Green Version]
- Mossong, J.; Muller, C.P. Modelling measles re-emergence as a result of waning of immunity in vaccinated populations. Vaccine 2003, 21, 4597–4603. [Google Scholar] [CrossRef]
- Obumneke, C.; Adamu, I.I.; Ado, S.T. Mathematical model for the dynamics of measles under the combined effect of vaccination and measles therapy. Int. J. Sci. Technol. 2017, 6, 862–874. [Google Scholar]
- Okyere-Siabouh, S.; Adetunde, I. Mathematical model for the study of measles in cape coast metropolis. Int. J. Mod. Biol. Med. 2013, 4, 110–133. [Google Scholar]
- Qureshi, S. Real life application of Caputo fractional derivative for measles epidemiological autonomous dynamical system. Chaos Solitons Fractals 2020, 134, 109744. [Google Scholar] [CrossRef]
- Center of Disease Control and Prevention. Global Measles Outbreaks. Available online: https://www.cdc.gov/globalhealth/measles/data/global-measles-outbreaks.html (accessed on 12 June 2022).
- Relief, D. The Global Measles Epidemic Isn’t (Just) About Measles. Available online: https://reliefweb.int/report/world/global-measles-epidemic-isn-t-just-about-measles (accessed on 21 April 2022).
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Abboubakar, H.; Kom Regonne, R.; Sooppy Nisar, K. Fractional Dynamics of Typhoid Fever Transmission Models with Mass Vaccination Perspectives. Fractal Fract. 2021, 5, 149. [Google Scholar] [CrossRef]
- Neirameh, A. New fractional calculus and application to the fractional-order of extended biological population model. Bol. Soc. Parana. Matemática 2018, 36, 115–128. [Google Scholar] [CrossRef]
- He, J.H.; Ji, F.Y. Two-scale mathematics and fractional calculus for thermodynamics. Therm. Sci. 2019, 23, 2131–2133. [Google Scholar] [CrossRef]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Derbazi, C.; Baitiche, Z.; Abdo, M.S.; Shah, K.; Abdalla, B.; Abdeljawad, T. Extremal Solutions of Generalized Caputo-Type Fractional-Order Boundary Value Problems Using Monotone Iterative Method. Fractal Fract. 2022, 6, 146. [Google Scholar] [CrossRef]
- Haidong, Q.; Arfan, M. Fractional model of smoking with relapse and harmonic mean type incidence rate under Caputo operator. J. Appl. Math. Comput. 2022, 1–18. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. Int. Sci. Res. Publ. 2017. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Liu, J.G. A generalized definition of Caputo derivatives and its application to fractional ODEs. SIAM J. Math. Anal. 2018, 50, 2867–2900. [Google Scholar] [CrossRef] [Green Version]
- Odibat, Z.; Baleanu, D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl. Numer. Math. 2020, 156, 94–105. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P.; Guo, Y.; Liu, Z. Bifurcation properties for fractional order delayed BAM neural networks. Cogn. Comput. 2021, 13, 322–356. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Aouiti, C.; Liu, Z.; Yao, L. Further analysis on dynamical properties of fractional-order bi-directional associative memory neural networks involving double delays. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P.; Yuan, S. Impact of leakage delay on bifurcation in fractional-order complex-valued neural networks. Chaos Solitons Fractals 2021, 142, 110535. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and Application to Heat Transfer Model. arXiv 2016, arXiv:1602.03408. [Google Scholar]
- Liu, X.; Arfan, M.; Ur Rahman, M.; Fatima, B. Analysis of SIQR type mathematical model under Atangana-Baleanu fractional differential operator. Comput. Methods Biomech. Biomed. Eng. 2022, 3, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Zifan, A.; Saberi, S.; Moradi, M.H.; Towhidkhah, F. Automated ECG segmentation using piecewise derivative dynamic time warping. Int. J. Biol. Med. Sci. 2006, 1. Available online: https://www.researchgate.net/publication/228734344_Automated_ECG_Segmentation_Using_Piecewise_Derivative_Dynamic_Time_Warping (accessed on 26 June 2022).
- Abboubakar, H.; Kumar, P.; Rangaig, N.A.; Kumar, S. A malaria model with Caputo–Fabrizio and Atangana–Baleanu derivatives. Int. J. Model. Simulation, Sci. Comput. 2021, 12, 2150013. [Google Scholar] [CrossRef]
- Atangana, A. Mathematical model of survival of fractional calculus, critics and their impact: How singular is our world? Adv. Differ. Equ. 2021, 2021, 403. [Google Scholar] [CrossRef]
- Abdulazeez, S.T.; Modanli, M. Solutions of fractional order pseudo-hyperbolic telegraph partial differential equations using finite difference method. Alex. Eng. J. 2022, 61, 12443–12451. [Google Scholar] [CrossRef]
- Farman, M.; Saleem, M.U.; Ahmad, A.; Ahmad, M. Analysis and numerical solution of SEIR epidemic model of measles with non-integer time fractional derivatives by using Laplace Adomian Decomposition Method. Ain Shams Eng. J. 2018, 9, 3391–3397. [Google Scholar] [CrossRef]
- Ogunmiloro, O.M.; Idowu, A.S.; Ogunlade, T.O.; Akindutire, R.O. On the Mathematical Modeling of Measles Disease Dynamics with Encephalitis and Relapse Under the Atangana–Baleanu–Caputo Fractional Operator and Real Measles Data of Nigeria. Int. J. Appl. Comput. Math. 2021, 7, 185. [Google Scholar] [CrossRef]
- Qureshi, S. Monotonically decreasing behavior of measles epidemic well captured by Atangana–Baleanu–Caputo fractional operator under real measles data of Pakistan. Chaos Solitons Fractals 2020, 131, 109478. [Google Scholar] [CrossRef]
- Qureshi, S.; Jan, R. Modeling of measles epidemic with optimized fractional order under Caputo differential operator. Chaos Solitons Fractals 2021, 145, 110766. [Google Scholar] [CrossRef]
- Diethelm, K. An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal 1997, 5, 1–6. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Dhingra, R.; Gambhir, M.; Remais, J.V. Sensitivity analysis of infectious disease models: Methods, advances and their application. J. R. Soc. Interface 2013, 10, 20121018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Bozkurt, F.; Yousef, A.; Abdeljawad, T.; Kalinli, A.; Al Mdallal, Q. A fractional-order model of COVID-19 considering the fear effect of the media and social networks on the community. Chaos Solitons Fractals 2021, 152, 111403. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef] [Green Version]
- Akindeinde, S.O.; Okyere, E.; Adewumi, A.O.; Lebelo, R.S.; Fabelurin, O.O.; Moore, S.E. Caputo fractional-order SEIRP model for COVID-19 Pandemic. Alex. Eng. J. 2022, 61, 829–845. [Google Scholar] [CrossRef]
- Jung, S.M. Hyers-Ulam-Rassias Stability of Functional Equations in Nonlinear Analysis; Springer: Berlin/Heidelberg, Germany, 2011; Volume 48. [Google Scholar]
- Li, C.; Zeng, F. The finite difference methods for fractional ordinary differential equations. Numer. Funct. Anal. Optim. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Kumar, P.; Rangaig, N.A.; Abboubakar, H.; Kumar, A.; Manickam, A. Prediction studies of the epidemic peak of coronavirus disease in Japan: From Caputo derivatives to Atangana–Baleanu derivatives. Int. J. Model. Simul. Sci. Comput. 2022, 13, 2250012. [Google Scholar] [CrossRef]
- van Boven, M.; Kretzschmar, M.; Wallinga, J.; O’Neill, P.D.; Wichmann, O.; Hahné, S. Estimation of measles vaccine efficacy and critical vaccination coverage in a highly vaccinated population. J. R. Soc. Interface 2010, 7, 1537–1544. [Google Scholar] [CrossRef]

| Parameter | Description | Values (per Week) |
|---|---|---|
| Recruitment rate | 68,027 | |
| Rate of loss of vaccine immunity | ||
| Transmission Rate | ||
| c | Vaccination rate | |
| d | Natural death rate | |
| Rate of progression from to | ||
| a | Disease-induced rate | |
| Rate of progression from to | ||
| Rate of progression from to |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abboubakar, H.; Fandio, R.; Sofack, B.S.; Ekobena Fouda, H.P. Fractional Dynamics of a Measles Epidemic Model. Axioms 2022, 11, 363. https://doi.org/10.3390/axioms11080363
Abboubakar H, Fandio R, Sofack BS, Ekobena Fouda HP. Fractional Dynamics of a Measles Epidemic Model. Axioms. 2022; 11(8):363. https://doi.org/10.3390/axioms11080363
Chicago/Turabian StyleAbboubakar, Hamadjam, Rubin Fandio, Brandon Satsa Sofack, and Henri Paul Ekobena Fouda. 2022. "Fractional Dynamics of a Measles Epidemic Model" Axioms 11, no. 8: 363. https://doi.org/10.3390/axioms11080363
APA StyleAbboubakar, H., Fandio, R., Sofack, B. S., & Ekobena Fouda, H. P. (2022). Fractional Dynamics of a Measles Epidemic Model. Axioms, 11(8), 363. https://doi.org/10.3390/axioms11080363






