Home Health Care Planning with the Consideration of Flexible Starting/Ending Points and Service Features

Abstract

One of the recently proposed strategies in health systems is providing services to patients at home and improving the service quality in addition to reducing the health system costs. In the real world, some services, such as biological tests or blood sampling, force the nurses to start or end his/her route from/at the laboratory instead of the depot, changing the whole optimal planning. The effect of these special service requirements and features has not been considered so far. In this study, a new mathematical model is suggested considering the flexibility of starting/ending places of each nurse’s route according to the specific characteristics of each service. Then, several sets of problems in various sizes are solved using the proposed model, where the results confirm the efficiency of the proposed approach. In addition, some sensitivity analyses are performed on the parameters of the required features of the services, followed by some managerial insights and directions for future studies.

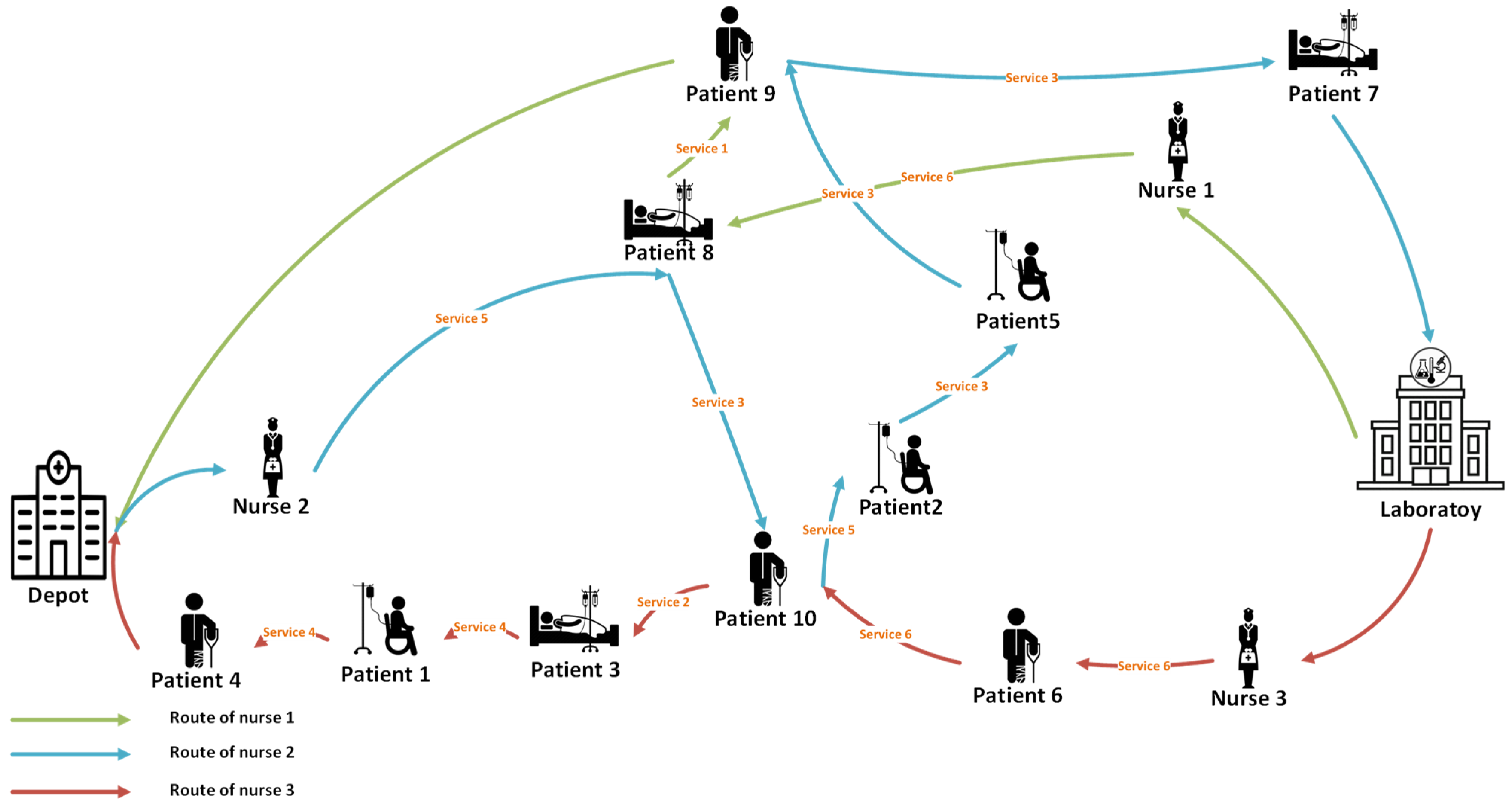
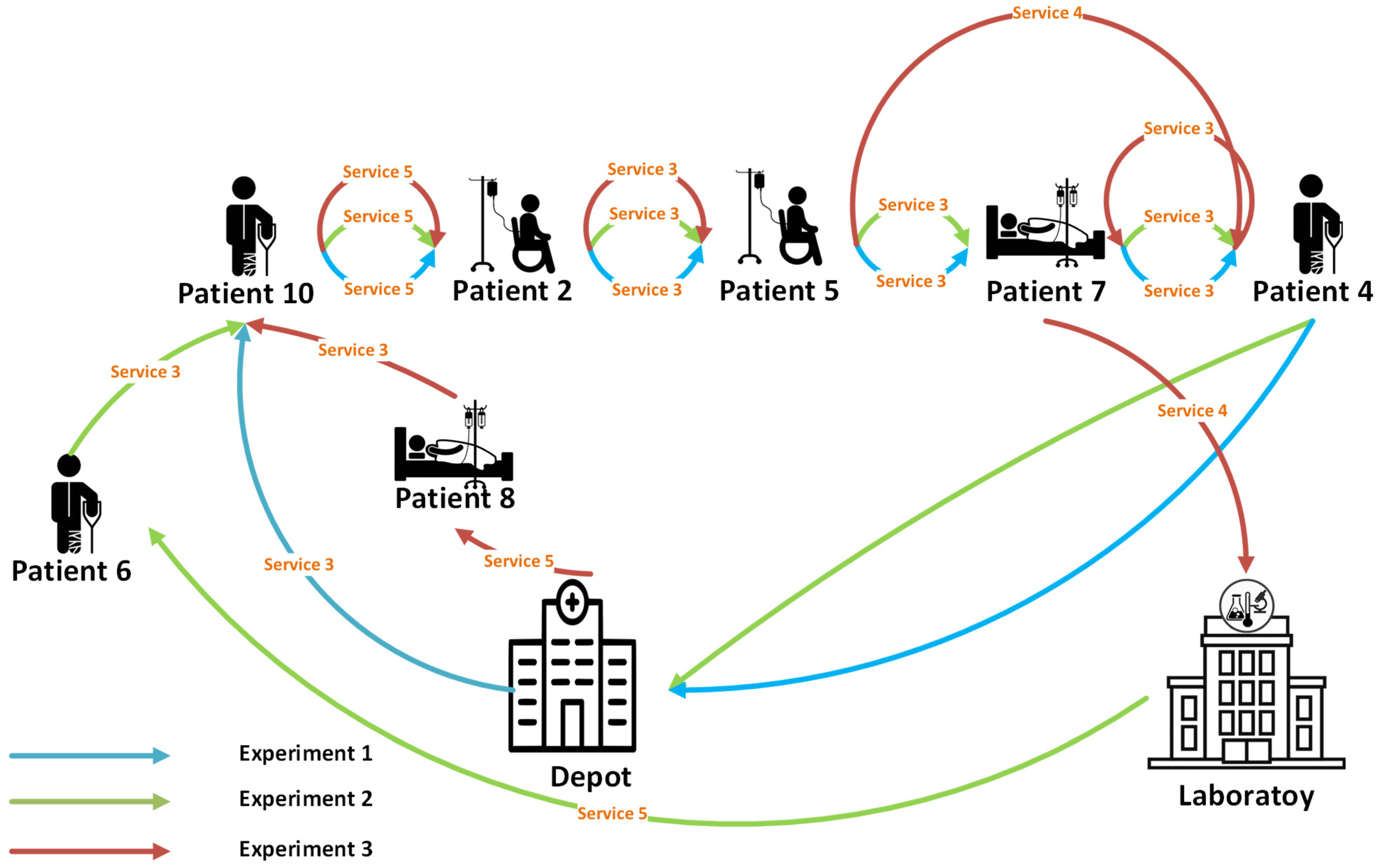
1. Introduction

Health has always been one of the most important human concerns from the past, and there has been a lot of efforts to create stable health in communities. Today, with an increase in life expectancy and a decline in birth rates in most societies, we are seeing a rise in the average age of the population, which has imposed a lot of costs on health systems around the world, and a significant share of a country’s budget is spent on health care [1].

In the current situation, creating a plan to use the resources optimally seems to be necessary due to resource limitations. For example, human resource shortages and shortage of hospitals are a limiting factor in health services. On the other hand, one can also see an individual life pattern of elderly people in the developed and developing countries that makes it necessary to focus on this group of individuals. Developing a framework for offering health care to individuals at their home effectively could be a good solution to this problem. In this context, home health care (HHC) companies are usually faced with conflicts in their targets such as maximizing the offering service level and minimizing the operating costs, which usually should be simultaneously optimized. With the attendance of various companies in this field, new angles of existing costs have been clarified, which have encouraged researchers to use optimization techniques in this field. One of the most related issues for companies consists in finding an optimal plan for offering services. This problem is called the home health care routing and scheduling problem (HHCRSP), which has attracted a lot of attention recently among researchers [2].

In the HHCRSP, there are a set of patients in different geographical regions who need a diverse range of health care services at their home. These service requirements should be handled by some specialized companies and their highly skilled nurses. In this context, most researchers assume that each nurse’s route is started from and ended in the depot. The word depot is used to indicate the starting or ending point of the routes, which is usually the HHC company’s office. Active organizations in this field should make a tradeoff between reducing their operational costs and providing high quality services to customers. Therefore, the HHCRSP focuses on planning a set of routes to deliver the scheduled care services within a planning horizon, which minimizes a criterion such as cost or maximizes the service quality by taking into account a number of constraints [3].

Fernandez, Gregory, Hindle, and Lee [4] were the first to study routing and scheduling in the HHC context. They investigated a working day of community nurses in their research. Their plan divides the county into a number of nursing districts. Then, they estimated the number of calls that can be made on average to measure the effectiveness of the proposed plan on the community. Hindle, Hindle, and Spollen [5] and Hindle, Hindle, and Spollen [6] extended the problem of Fernandez et al. [4] by considering resource allocations and travel cost estimation aspects. Decision support systems (DSSs) in this context were first considered by Bertels and Fahle [7] and Eveborn, Flisberg, and Rönnqvist [8]. This problem was developed as an extension of the vehicle routing problem by Akjiratikarl, Yenradee, and Drake [9] and solved by using a particle swarm optimization (PSO) algorithm.

In recent years, the HHCRSP has attracted the attention of many researchers, and various studies have been implemented in this field. Recent research in this field can be classified into two categories: deterministic and uncertain studies. In the category of recent deterministic studies, Mankowska, Meisel, and Bierwirth [10] provided a daily planning with regard to the specific needs of each patient, the particular skills of each nurse, as well as the relationships between different services. They developed a new heuristic to handle such requirements. Their solutions indicated that the method can achieve a fair distribution of inevitable tardiness, low average waiting times for the patients, and low traveling costs for the nurses. Liu et al. [11] applied the research of Mankowska et al. [10] to the logistics domain of home health care. They noted that nurses may need to transfer medicines and medical supplies from the company center to the patients’ home and return the laboratory samples, unused drugs, and medical equipment to the center. Liu et al. [11] extended the problem of the multiperiod vehicle routing problem with time windows (PVRPTWs) to three different patient demand types. They proposed a Tabu Search method combined with different local search schemes including both feasible and infeasible local searches. Their experiments showed that the proposed approach balances better the workloads of vehicles and reduces the total cost.

Decerle, Grunder, El Hassani, and Barakat [12] addressed the problem of home health care by considering a few objectives simultaneously and focusing on the applicability of the planning. They employed a memetic algorithm to solve this problem. They conducted several experiments and showed that the developed methods had a good performance for small-sized instances. However, Simulated Annealing (SA) was slightly better than Tabu Search (TS) for large-sized problems. Fathollahi-Fard, Hajiaghaei-Keshteli, and Tavakkoli-Moghaddam [13] presented a biobjective green home health care problem that considers environmental pollution. They developed a new modified multiobjective version of a social engineering optimizer (SEO) by using an adaptive memory strategy, so-called AMSEO. Based on their analyses, AMSEO performs significantly better than SEO, NSGA-II, and SA when all methods were tuned by the response surface methodology (RSM) and compared across four popular evaluation metrics. The conventional HHCRSP is extended to demand and capacity management by Nasir and Dang [14]. A mixed integer programming (MIP) model is suggested by considering workload balancing. To solve this model, some heuristics, including a variable neighborhood search (VNS) algorithm, were applied. They compared the results obtained by VNS with a CPLEX-based solution. Performing the model on different datasets showed the efficiency and effectiveness of the solution methods to handle the considered problem. Nasir, Hussain, and Dang [15] developed a mathematical model to consider group-based and telehealth-based care services. Three different goals were considered in their model to achieve this target. The first goal was to select an optimal location for the HHC centers, staff and group patient centers considering the required specifications. The second goal of their study was to schedule the group patient sessions in specific time windows by pairing each nurse with a telephone service staff. Finally, as their third goal, the violation from good quality services and the dissatisfaction of the patients were considered. They employed Fuzzy c-means in order to validate the effectiveness of the proposed integration approach. Then, a sensitivity analysis was conducted to explore the model behavior against the variation in the values. The detailed analysis of the results showed the effectiveness of the proposed model and its behavior with respect to different types of cost.

Fikar and Hirsch [16] introduced the concept of car and trip sharing within home health care nurses. They also considered the option that the nurses are allowed to walk to the patient’s home. They investigated different geographic distributions to identify beneficial settings for a successful implementation considering various goals of the decision makers. Their evaluation showed that trip sharing performs best if long service durations exist and long delays for parking occur and in areas where clients are both geographically distributed randomly and in clusters. Lin, Hung, Liu, and Tsai [17] presented a modified harmony search (MHS) algorithm that considers the three problems of nurse rostering, nurse routing, and nurse rerostering simultaneously. They specified that past studies had considered the issues of the nurse rostering problem (NRP) and VRPTWs independently; in this study, it was investigated at the same time. Then, they formulated the model by MIP and solved it by the commercial solver CPLEX. They also adopted a real dataset extracted from an existing HHC institution. The numerical results showed an efficient computing performance for an optimal solution of small, medium, and large sizes.

The home health care problem in Chinese communities was considered by Zhang, Yang, Chen, Bai, and Chen [18]. These communities have an intense distribution of patients. They formulated the problem by MIP and considered three main factors, including match qualities, uncertain service times, and time windows. Therefore, they applied a modified ant colony optimization and analyzed it in four instances. Liu, Yang, Su, and Xu [19] developed a biobjective model with the objective to minimize the costs of the company and to improve patient satisfaction. In their study, multiple weeks of planning and medical teams were considered. To solve such a problem, the epsilon-constraint method was used to obtain the Pareto fronts of the problem. They conducted computational experiments, and the results showed the efficiency of the approaches.

Shanejat-Bushehri, Tavakkoli-Moghaddam, Momen, Gasemkhani, and Tavakkoli-Moghaddam [20] considered the HHCRSP problem with temporarily precedence and synchronization constraints as well as limited allowable times for transferring the collected biological samples to the laboratory. The goal was to minimize the cost related to the transportation and the idle time of the nurses. They presented a mathematical model and applied Simulated Annealing and Tabu Search in two phases. They performed several comparative experiments and showed that the developed methods had a good performance for small-sized instances. However, SA was slightly better than TS for large-sized problems. Grenouilleau, Legrain, Lahrichi, and Rousseau [21] presented a method for the HHCRSP problem, which is based on a set partitioning formulation as well as a variable neighborhood search framework. Their algorithm solved first a linear relaxation, and then a constructive heuristic was applied to generate an integer solution. They applied the algorithm to real instances and showed that the proposed method is able to provide an increase of more than 16% in the continuity of care and a reduction in travel times by 37%. Euchi, Zidi, and Laouamer [22] presented a distributed optimization approach for the HHCRSP problem, which used artificial intelligence techniques. They integrated automatic learning and search techniques to optimize the assignment of nurses to patients. Their results proved the efficiency of the proposed approach, which can offer a decision support for medical executives of HHC. Khodabandeh, Kayvanfar, Rafiee, and Werner [3] included downgrading aspects into the classical HHCRSP problem. They considered the additional goal to minimize also the difference between the actual and the potential skills of the nurses. To solve the derived biobjective model, the authors used the epsilon-constraint method. They also performed a sensitivity analysis on the epsilon parameter. Ghiasi, Yazdani, Vahdani, and Kazemi [23] considered the HHCRSP problem with two transportation modes, namely public and private modes under the multidepot version. The objective was the minimization of the sum of the travel distance and overtime costs. After presenting a mixed integer programming model, three metaheuristic algorithms including Invasive Weed Optimization (IWO), Grasshopper Optimization Algorithm (GOA), and Simulated Annealing (SA) were given for solving large instances. Their computational results showed that the suggested IWO performed better than the other algorithms. Xiang, Li, and Szeot [24] considered the HHCRSP problem by minimizing total costs and maximizing patient preference satisfaction. They formulated a biobjective mixed integer linear programming model. For solving this problem, a local search algorithm was embedded into the basic framework of a nondominated sorting genetic algorithm. The algorithm obtained approximate Pareto-optimal solutions for small instances in a shorter computation time than the epsilon-constraint method.

In the category of recent uncertain studies, Yuan, Liu, and Jiang [25] addressed the HHCRSP with stochastic service times. The problem was modeled in the form of a stochastic programming problem with recourse in which the expected value of late arrivals of the nurses was considered. Then, the branch and price (B&P) method was used to solve this problem. They validated the effectiveness of their proposed algorithm through numerical experiments. In Liu, Yuan, and Jiang [26], stochastic service and travel times were considered in their problem. They employed a chance constraint in order to guarantee the probability of on-time services. In their study, a route-based mathematical model was developed, and the branch and cut (B&C) algorithm was used with the discrete estimation method to solve it. Moreover, labeling algorithms and acceleration methods were also employed for solving the proposed model. The performance of the proposed B&P algorithm was validated on test instances and demonstrated the necessity of considering the stochasticity of the travel times of the nurses and the service times. Lanzarone and Matta [27] presented a robust strategy for home health care, in which random patient requests were considered, and the nurse allocation to the patients was investigated as well. The policy of this paper is compared to other previously developed approaches and applied to a relevant real case. Rodriguez, Garaix, Xie, and Augusto [28] modeled the HHC problem considering a stochastic demand for patients and handled it through stochastic programming. Then, the B&C method was used to solve their proposed model. The analysis of their computational experiments showed that routing evaluation can help to obtain a more precise working time, especially in geographical areas assuming rural or semi-urban patterns. Their solutions and the computed Pareto optimal sets indicate that their approach can help the decision maker before opening a HHC service or before hiring an employee. Shi, Boudouh, and Grunder [29] addressed the HHC problem with a fuzzy demand for the patients. They employed a fuzzy chance constraint method as well as a hybrid genetic algorithm (GA) for the solution of the model. Their experiments on the fuzzy version model were undertaken by considering a variable value of the Dispatcher Preference Index (DPI) parameter between [0, 1]. Finally, the influence of DPI on the final objective and the indicators of the problem were discussed using stochastic simulation, and the best value of DPI was obtained. Shi, Boudouh, Grunder, and Wang [30] investigated the HHC problem considering stochastic travel and service times through stochastic programming with recourse. Then, they applied a simulated annealing (SA) algorithm to obtain the solutions of the problem. Comparisons between the solutions obtained by the stochastic model and the deterministic one have validated the advantages and robustness of considering stochastic travel and service times. Issabakhsh, Hosseini-Motlagh, Pishvaee, and Saghafi Nia [31] presented a robust optimization model for patients in need of dialysis in which the travel times of nurses are uncertain. Their results showed that the proposed method has less than a 30% variation in the results at the maximum uncertainty level, and, in comparison to the deterministic model, the costs increased only by 1.2%. An innovative approach to accept or reject new patients by a nurse was recently investigated in Demirbilek, Branke, and Strauss [32]. The objective was to maximize the average number of daily visits for a single nurse. They proposed a new heuristic-based approach, and then, random scenarios were created to present this simple and fast method. Their approach was compared with two greedy heuristics from the literature and showed that it achieves significantly better results compared to other methods. Carello, Lanzarone, and Mattia [33] proposed a multicriteria optimization approach to consider different goals of the stakeholders with regard to the need for continuity of the care and considering certain and uncertain patient demands. The three stakeholder perspectives were modeled as alternative objective functions of an integer linear programming (ILP) model, and a threshold method to include all of them is proposed. The approach was then validated on real-life instances, and they considered both deterministic and uncertain patient demands. Khodaparasti, Bruni, Beraldi, Maleki, and Jahedi [34] presented a multiperiod allocation method through a robust approach in which the patient demand was considered to be uncertain. The problem was formulated as a covering model in which the capacity of the facilities as well as the demand elasticity were considered. Then, they applied the proposed model to a real case study.

Bazirha, Kadrani, and Benmansour [35] dealt with the HHCRSP problem with stochastic travel and care times and the goal to minimize the transportation costs of the nurses and the expected value of recourse caused by delayed services and the overtime of the nurses. The performance of the developed genetic algorithm with an embedded Monte Carlo simulation was discussed. Later in an extended paper, Bazirha, Kadrani, and Benmansour [36] proposed a stochastic programming model with recourse for solving the HHCRSP problem, where the goal was the minimization of the transportation costs and the expected value of recourse, and also multiple services and their synchronization were considered. While the underlying deterministic problem was solved by CPLEX, a genetic algorithm and a general variable neighborhood search heuristic, the stochastic problem was solved by Monte Carlo simulation embedded into their genetic algorithm. Recently, Bazirha [37] applied a similar approach to the HHCRSP problem with additional hard/fixed time windows and the objective to minimize the traveling costs of the nurses and the average number of unvisited patients. Very recently, Di Mascolo, Martinze, and Espinouse [38] presented a survey of the relevant literature and a bibliometric analysis in the field of home health care. They reviewed and analyzed the current state-of-the-art with a focus particularly on uncertain and dynamic aspects.

To the best of the authors’ knowledge and as it can be seen from the discussed literature, most of the studies assumed that each nurse should start her/his journey from the depot and end it at the laboratory. In home health care’s real world, there are some services, which need special instruments and force the nurse to start her/his route from the laboratory. On the other hand, if a nurse has to take a biological test or a blood test, she/he should end her/his route at the laboratory instead of the depot [11]. Such requirements inspired us to develop conventional models to a more flexible model, which can consider different options for the origin and the destination of nurse routes.

The rest of the paper is organized as follows. The description of the problem and the mathematical model are given in Section 2. The methodological background of the paper is stated in Section 3. Section 4 discusses the computational experiments. The results of a sensitivity analysis are explained in Section 5. Section 6 offers some managerial insights, and, finally, study limitations, conclusions, and future studies are presented in Section 7.

2. Problem Description

One of the most important issues that has always been a focus of attention in the HHCRSP is to make the problem conditions closer to the real world of the health industry. In home health care, there are many different types of services with different features that play an important role in the real world. Therefore, they should always be considered by the planners. Each of these services needs to take into account their own particular considerations according to their characteristics. On the other hand, each of the nurses has special skills and to provide the appropriate services to any patient, these services should be offered with a set of these skills [10].

In home health care, many patients require several different services, which may be provided by a nurse or several nurses with relevant skills. One of the most important assumptions existing in the home health care literature was that each patient needs only one service. Such a problem with this assumption is very simple. However, it does not seem to be valid in the real world since some patients need several services. The services provided to patients in the field of home health care are very diverse, including services with specific characteristics that are necessary to satisfy their anterior and posterior requirements. Some services require specific equipment, materials, and supplies that the nurse must obtain at the start of her/his journey from the lab, while other services do not require such an action. Moreover, some services require equipment that must be delivered to the laboratory upon the completion of the nurse’s route, or some vital services, such as biological tests, are required to be delivered to the laboratory at the end of the day. Due to such real-world requirements, it seems to be necessary to create flexibility at the starting and ending points of the nurse’s route. This flexibility is determined depending on the specific features of the services [11].

In this study, a mathematical model is proposed with the consideration of flexible starting and ending points of the routes that are determined depending on the features of the required services. This problem has also been developed by a simultaneous consideration of different services for the patients, the patient time windows, the correct sequence of the patient services as well as the rest of the other constraints required for the VRP problems. The effectiveness of this proposed novel model in the optimal planning and scheduling process is demonstrated through solving some sample problems.

2.1. Assumptions

• Each patient may need several services, where all of these needs should be satisfied by the company through its nurses.
• Each nurse is only qualified for some set of services and has her/his own qualifications matrix.
• The starting and ending points of each nurse’s route (depot or laboratory) are determined by the features of the services that are included in the route.
• Every patient has a desirable time window that must be respected.
• Each patient’s service could begin after the end of the previous patient’s service in addition to the time that is needed to travel to the place of the second patient.
• The travel time, the service time, and the demand of each patient are deterministic, and the planner knows them before the beginning of the planning.
• The planning is performed daily.
• Each nurse has a car for traveling between the patients, and multimode traveling and travel sharing concepts are not considered.
• Urgent service calls and emergent situations are not considered in the planning.

2.1.1. Subscripts

i	Starting point of each transfer (i = 1,2,..., n + 1), where n is the number of patients. In this context, transfer means the act of moving a nurse from each beginning node to the next destination node, for example from patient 1 to patient 2.
j	Ending point of each transfer (j = 2,3,..., n + 2); where n is again the number of patients.
k	Nurse index (k = 1, 2, …, K), where K is the number of nurses.
s	Service index (s = 1, 2, …, S), where S is the number of different services in the planning.

2.1.2. Sets

P	Set of patients.
N	Set of all nodes that includes the depot, the patients, and the laboratory.
K	Set of nurses.
S	Set of services.

2.1.3. Input Parameters

tij	Traveling time from node i to node j.
tis	Needed time for giving service s to patient i.
[li, ui]	Acceptable time window of patient i.
aks	Nurse qualification matrix; 1 means that nurse k has the qualification of service s.
gjs	Patient’s service needs matrix; 1 means that service s is needed by patient j.
Rs	Service starting requirements matrix; 1 means that service s needs to start from the laboratory.
Rs′	Service ending requirements matrix; 1 means that service s needs to end at the laboratory.

2.2. Decision Variables

xijks	1 if nurse k travels from node i to node j for giving service s; 0 otherwise.
Sis	Starting time of giving service s to patient i.
δk1	1 if nurse k needs to start her/his route from the laboratory; 0 otherwise.
δk2	1 if nurse k needs to finish her/his route at the laboratory; 0 otherwise.

2.3. The Mathematical Model

Objective Function

$$Minz={\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}{\displaystyle \sum _{s\in S}{t}_{ij}.x_{ijks}}}}}$$

(1)

Constraints:

$$\epsilon .{\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{s\in S}{R}_s{x}_{ijks}}\le {\delta }_k{}_1}}\le {\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{s\in S}{R}_s{x}_{ijks}}}}\forall k\in K$$

(2)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{1iks}}}+M.{\delta }_k{}_1\ge 1\forall k\in K$$

(3)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{1iks}}}-M.{\delta }_k{}_1\le 1\forall k\in K$$

(4)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{(n+2)iks}}}+M.(1-{\delta }_{k1})\ge 1\forall k\in K$$

(5)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{(n+2)iks}}}-M.(1-{\delta }_{k1})\le 1\forall k\in K$$

(6)

$$\epsilon .{\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{s\in S}{R}_s{}^{\prime }{x}_{ijks}}\le {\delta }_k{}_2}}\le {\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{s\in S}{R}_s{}^{\prime }{x}_{ijks}}}}\forall k\in K$$

(7)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{i1ks}}}+M.{\delta }_k{}_2\ge 1\forall k\in K$$

(8)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{i1ks}}}-M.{\delta }_k{}_2\le 1\forall k\in K$$

(9)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{i(n+2)ks}}}+M.(1-{\delta }_{k2})\ge 1\forall k\in K$$

(10)

$${\displaystyle \sum _{i\in P}{\displaystyle \sum _{s\in S}{x}_{i(n+2)ks}}}-M.(1-{\delta }_{k2})\le 1\forall k\in K$$

(11)

$${\displaystyle \sum _{i\in N}{\displaystyle \sum _{s\in S}{x}_{ijks}-}}{\displaystyle \sum _{i\in N}{\displaystyle \sum _{s\in S}{x}_{jiks}=0}}\forall j\in P,k\in K$$

(12)

$$S_{i{s}_1}+t_{i{s}_1}+t_{ij}-M(1-x_{ijk{s}_2})\le S_{j{s}_2}\begin{array}{c}\forall i,j\in N,k\in K,\hfill \\ s_1\in S,s_2\in S\hfill \end{array}$$

(13)

$$l_i\le S_{is}\le u_i\forall i\in P,s\in S$$

(14)

$${\displaystyle \sum _{k\in K}{\displaystyle \sum _{i\in N}{a}_{ks}.x_{ijks}=g_{js}}}\forall j\in P,s\in S$$

(15)

$$x_{ijks}=a_{ks}.g_{js}\forall i,j\in N,k\in K,s\in S$$

(16)

Equation (1) presents the optimization criterion of the model, i.e., to minimize the total traveling time that the nurses of the company need for providing suitable care to the patients. Constraints (2) to (6) are used to determine the starting point of the routes of the nurses. The initial position of each nurse is decided with respect to the features of all services that should be applied in that route. If there is a service in a route, which forces the nurse to start her/his journey from the laboratory instead of the depot, the variable δ_k1 will become 1 by constraint (2). In this situation, constraints (3) and (4) are deactivated, and constraints (5) and (6) are activated and guarantee that the nurse must start her/his route from the laboratory. Contrariwise, constraints (3) and (4) are activated and enforce the nurse to start her/his journey from the depot. Constraints (7) to (11) are used to determine the ending place of the routes of the nurses. The finishing point of each nurse is decided with respect to the features of all services that should be applied in that route. If there is a service in a given route, which forces the nurse to finish her/his journey from the laboratory instead of the depot, the variable δ_k2 will become 1 by constraint (7). In this situation, constraints (8) and (9) are deactivated, and constraints (10) and (11) are activated and guarantee that the nurse must finish her/his route at the laboratory. Inversely, constraints (8) and (9) are activated and enforce the nurse to finish the journey at the depot. Constraint (12) ensures that each nurse should depart from the patient’s place after giving care and go to another patient’s home. Constraint (13) states that a service could be initiated after ending the previous service as well as the needed time for traveling the nurse to the new place. Constraint (14) indicates that each patient’s service should be started in her/his desirable time window. Constraint (15) is used to ensure that, if patient j needs service s, exactly one of the nurses with the required qualifications should go to the patient’s home and serve her/him. Constraint (16) ensures that for giving service s by nurse k to patient j, the patient must need the service s, and, of course, the nurse must have the required qualifications.

3. Methods

In this study, the code for the mathematical model was implemented in IBM ILOG CPLEX Optimization Studio. The branch and cut (B&C) algorithm was used to solve the problem. This algorithm is one of the most famous methods of combinatorial optimization that is used to solve a series of linear programming (LP) and subproblems, where some or all the parameters are constrained to integer values. B&C comprises running a branch and bound technique and using cutting planes in order to tighten the LP relaxations. The pseudocode of the general B&C technique is presented in Figure 1 [39]:

4. Computational Experiments

In this study, in order to demonstrate the effectiveness of the proposed model in the real world, first a small example was implemented, and the results are then explained accompanied by a discussion regarding the verification of the proposed model. Next, some benchmark instances that were obtained from [10] were applied to the model, and IBM ILOG CPLEX Optimization Studio Version 12.6.0.0 was used to solve the model. In this study, a computer with an Intel i7-4710HQ processor, 8 GB of RAM, and 2.5 GHz core speed was used for the computational experiments.

4.1. Model Verification

In this subsection, first a small instance was solved to demonstrate the effectiveness of the proposed model and to clarify the benefits of this model in comparison to the traditional home health care routing and scheduling models. In the solved problem, there were 10 patients, 3 nurses, and 6 service types. The characteristics and full details of the parameters are provided in Appendix A.

In this problem, the nurses have different qualifications, and, on the other hand, the patients have different service needs. There are 6 different services and qualifications, where service #3 means finishing the route at the laboratory, and where service #6 means starting the route from the laboratory.

In this section, to show the importance of the new model compared to the old home health care routing and scheduling models, the problem without considering flexibility in the starting and ending points was first solved, and then it was solved using the proposed model in this paper. Finally, the differences and benefits of the proposed novel model are presented. The results of the classic and the proposed model are given in

Table 1. Optimal routes without considering flexibility in the model.

Optimal Routes of the Nurses without Considering Flexible Starting and Ending Points
Nurse1	Services			S6 **		S1
	Route	Depot	→	8	→	9	→	Depot
Nurse2	Services			S3		S5		S3		S3		S4
	Route	Depot	→	10	→	2	→	5	→	7	→	4	→	Depot
Nurse3	Services			S5		S6		S5		S2		S4		S3
	Route	Depot	→	8	→	10	→	6	→	3	→	1	→	9	→	Depot

** In this table, “S” stands for the word “Service”. For example, “S6” stands for “Service #6”.

and

Table 2. Optimal routes considering flexibility in the model (the proposed model).

Optimal Routes of the Nurses Considering Flexible Starting and Ending Points
Nurse1	Services			S6 **		S1
	Route	Lab	→	8	→	9	→	Depot
Nurse2	Services			S5		S3		S5		S3		S4		S3
	Route	Depot	→	8	→	10	→	2	→	5	→	9	→	7	→	Lab
Nurse3	Services			S5		S6		S2		S4		S4
	Route	Lab	→	6	→	10	→	3	→	1	→	4	→	Depot

** In this table, “S” stands for the word “Service”. For example, “S6” stands for “Service #6”.

, respectively. The classic model is the traditional model that considers static locations for the starting and ending points of the nurse routes. In the following tables, the provided service to each patient is shown above the patient number. For example, S6 above patient number 8 states that nurse number 1 provides service 6 to patient 8. For a better illustration of the results of the new model, the optimal routes for each nurse are demonstrated in Figure 2.

By comparing Table 1 and Table 2, one can obviously observe that in addition to the existence of starting and ending points from and to the laboratory, the whole routes of the nurses are changed. Nurse #1 started her/his route from the lab and after giving service to patients 8 and 9, her/his route ended at the depot. In fact, because of the existence of service 6, the route was started from the laboratory. The initial place of nurse #2 was the depot, and her/his route ended at the laboratory after giving service to patients 8, 10, 2, 5, 9, and 7. Nurse #3 started her/his route from the laboratory, and after giving service to patients 6, 10, 3, 1, and 4, her/his route ended at the depot.

As it can be observed from these new results, nurse #2 visited patients 8 and 9 instead of patient 4 in the old planning. This new and different planning is owing to the attendance of service 3 in the nurse’s journey. In addition, one can see that the route of nurse #3 was changed, and she/he visited patient 4 instead of patients 8 and 9.

Considering the differences between the flexible proposed model and the traditional model based on the obtained results of this example, one can conclude that the service features that force our planning to start from or end at different places could be managed and taken into account by applying the novel model. These different service features affect not only individual services having these features, but also strongly affect the whole journey of each nurse. In fact, some nurses should visit different patients compared to the old planning.

4.2. Results

In this subsection, three different categories of instances were employed to demonstrate the effectiveness of the suggested model. In

Table 3. Characteristics of the benchmark instances.

Characteristics of the Instances
Instance Type	Instance Number	Number of Patients	Number of Nurses	Number of Services
Small	#1–#5	10	3	6
Medium	#6–#10	15	5	6
Large	#11–#15	25	5	6

, the characteristics of the benchmark instances are presented. In this table, the instance type states the number of patients and nurses that should be planned in the model. Note that in initial tests, it was found that the problem can be solved exactly if the ratio of the number of patients to the number of nurses is up to around 5. By increasing the values of these parameters, the problem will be more complicated and force a more computational workload to find a feasible and optimal solution.

To the best of the authors’ knowledge, this is the first study to consider different features of services in the routing and scheduling of home health care. Accordingly, the value of parameter R was assumed by the authors. The service requirements of starting from the depot or laboratory and finishing at the depot or laboratory are summarized in

Table 4. Starting and ending features of the services.

Starting and Ending Requirements of the Services
Services	Needs to start from the lab	Needs to finish at the lab
Service 1
Service 2
Service 3		yes
Service 4
Service 5
Service 6	yes

.

The obtained solutions of solving the small-sized, medium-sized, and large-sized instances are presented in

Table 5. The results for the small instances.

Instance Number	Optimal Function Value	Nurses with Starting Point at the Depot	Nurses with Starting Point at the Laboratory	Nurses with Ending Point at the Depot	Nurses with Ending Point at the Laboratory	Computational Time (Seconds)
#1	654.596	Nurse1	Nurse2, Nurse3	Nurse2, Nurse3	Nurse1	0.43
#2	724.654	Nurse1, Nurse2	Nurse3	Nurse2, Nurse3	Nurse1	0.28
#3	533.423	Nurse1, Nurse2	Nurse3	Nurse2, Nurse3	Nurse1	2.06
#4	568.63	Nurse1	Nurse2, Nurse3	Nurse2, Nurse3	Nurse1	2.56
#5	596.976	Nurse1	Nurse2, Nurse3	Nurse2, Nurse3	Nurse1	1.91

,

Table 6. The results for the medium instances.

Instance Number	Optimal Function Value	Nurses with Starting Point at the Depot	Nurses with Starting Point at the Laboratory	Nurses with Ending Point at the Depot	Nurses with Ending Point at the Laboratory	Computational Time (Seconds)
#6	1079.436	Nurse1, Nurse2, Nurse4	Nurse3, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	3.73
#7	623.756	Nurse1, Nurse2	Nurse3, Nurse4, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	6.55
#8	623.756	Nurse1, Nurse2	Nurse3, Nurse4, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	6.51
#9	880.249	Nurse1, Nurse2, Nurse3, Nurse5	Nurse4	Nurse2, Nurse3, Nurse4, Nurse5	Nurse1	2.65
#10	964.402	Nurse1, Nurse2	Nurse3, Nurse4, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	4.61

and

Table 7. The results for the large instances.

Instance Number	Optimal Function Value	Nurses with Starting Point at the Depot	Nurses with Starting Point at the Laboratory	Nurses with Ending Point at the Depot	Nurses with Ending Point at the Laboratory	Computational Time (Seconds)
#11	1244.058	Nurse1, Nurse2	Nurse3, Nurse4, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	22
#12	1291.087	Nurse1, Nurse2	Nurse3, Nurse4, Nurse5	Nurse2, Nurse3, Nurse4, Nurse5	Nurse1	9.92
#13	1058.956	Nurse1, Nurse2	Nurse3, Nurse4, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	19.01
#14	977.501	Nurse1, Nurse2, Nurse4	Nurse3, Nurse5	Nurse1, Nurse3, Nurse4, Nurse5	Nurse2	15.73
#15	978.898	Nurse1, Nurse2, Nurse5	Nurse3, Nurse4	Nurse1, Nurse3, Nurse4	Nurse2, Nurse5	2880

, respectively.

It can be understood from the mentioned results that this model can be well applied for the daily planning process of home health care organizations in different sizes and can assist them in their decisions as well.

5. Sensitivity Analysis

In this section, a sensitivity analysis on the special parameter of the studied problem was carried out in order to yield a better vision about the effects of changing an important parameter over the outputs. The parameter R was chosen for the sensitivity analysis, which is directly related to the flexibility of the planning at the starting and ending points of the routes. In each experiment, it was assumed that the parameter R has a specified value for service #4, and then the results for the routes of nurse #2 are explained. Different optimal routes for each experiment are shown in

Table 8. Sensitivity analysis on parameter R for small instances.

Sensitivity Analysis on Parameter R for Small Instances
#	Number of Patients	Feature of Service #4	Optimal Function Value	Route of Nurse #2
#1	10		561.813			S3 **		S5		S3		S3		S4
				D	→	10	→	2	→	5	→	7	→	4	→	D
#2	10	Needs to start from the lab	536.422			S5		S3		S5		S3		S3		S4
				L	→	6	→	10	→	2	→	5	→	7	→	4	→	D
#3	10	Needs to end at the lab	609.901			S5		S3		S5		S3		S4		S3
				D	→	8	→	10	→	2	→	5	→	4	→	7	→	L

** In this table, “S” stands for the word “Service”. For example, “S3” stands for “Service #3” and shows that service 3 is provided to the patient.

.

The optimal routes obtained for different experiments are also described in Figure 3. As it is obvious from Figure 3, the whole journey of the nurse is affected by changing the starting and ending points of routes by modifying the features of service #4. In the second experiment, where service #4 forces nurse #2 to start her/his path from the laboratory, giving a service to patient #6 is also included because of changing the starting point of the nurse. In addition to experiment #2, in experiment #3, owing to the attendance of the ending special feature of service #4, giving service to patient #8 is included in the route. The obtained results of the conducted sensitivity analysis on parameter R for medium- and large-sized instances are shown in

Table 9. Sensitivity analysis on parameter R for medium instances.

Sensitivity Analysis on Parameter R for Medium Instances
#	Number of Patients	Feature of Service #4	Optimal Function Value	Nurses with Starting Point at the Depot	Nurses with Starting Point at the Lab	Nurses with Ending Point at the Depot	Nurses with Ending Point at the Lab	Computational Time (Seconds)
#1	15		1050.69	Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		4.09
#2	15	Needs to start from the lab	1139.019	Nurse1, Nurse2, Nurse3	Nurse4, Nurse5	Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		4.00
#3	15	Needs to end at the lab	925.09	Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		Nurse1, Nurse2, Nurse3	Nurse4, Nurse5	3.46

and

Table 10. Sensitivity analysis on parameter R for medium instances.

Sensitivity Analysis on Parameter R for Large Instances
#	Number of Patients	Feature of Service #4	Optimal Function Value	Nurses with Starting Point at the Depot	Nurses with Starting Point at the Lab	Nurses with Ending Point at the Depot	Nurses with Ending Point at the Lab	Computational Time (Seconds)
#1	25		1139.338	Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		7.41
#2	25	Needs to start from lab	1051.981	Nurse2, Nurse3	Nurse1, Nurse4, Nurse5	Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		7.28
#3	25	Needs to end at the lab	1117.272	Nurse1, Nurse2, Nurse3, Nurse4, Nurse5		Nurse2, Nurse3	Nurse1, Nurse4, Nurse5	7.23

, respectively.

According to the obtained results of the conducted sensitivity analysis on parameter R for medium-sized instances, it can be inferred that the starting and ending needs of service #4 affect only the routes of nurses #4 and #5, which is the consequence of the existing service #4 in their planned routes.

For the large instances, the special features of service #4 affect the planned routes of nurses #1, #4, and #5.

6. Managerial Insights

Some important managerial insights can be obtained from our investigations as follows:

(1) In most of the traditional HHCRSP models, the planners assume that each patient needs only one service. In their studies, they consider that if a patient requires three services, these service needs are considered as three patients who have the same health profile and home location with just one requested service. In this study, every patient is a unique entity that can have a few service needs. This point of view can prevent patient data redundancy. Decision makers can use these clean data as a valuable resource to make their complex decisions more efficient and manage their service and employee capacities.

(2) Decision makers of home health care systems can use this novel model to have a better planning for their nurses considering different service features that may force a nurse to have different starting and ending points. This consideration can omit changes in the planning at the day of the execution. These probable changes may happen, since some special service features may be ignored at the moment of planning by the planners in this area.

7. Study Limitations, Conclusions, and Future Studies

In the real world of home health care context, there are a lot of hard constraints that cannot be considered as soft constraints with some penalties. One of the limitations of this study is the high number of hard constraints that must be satisfied. Constraints, such as special patient needs in a tight and short acceptable time window, the variety of service types that need different nurse qualifications and certificates, and also some service features and instrument requirements that forced some routes to be started from a special place complicate the problem and make the feasible region smaller. Therefore, modeling the real world of this problem was difficult, and also finding a real-world optimal solution with exact algorithms in a small feasible region was complex and needed a high computational effort. On the other hand, due to the high level of complexity in this study, uncertainties were not considered.

Nowadays, an effective management of health care systems is one of the most important concerns of policy makers. These systems can constrain high costs to the communities and have an impressive impact on the public health of the societies. At present, the correct management of health system capacities has received much attention. Giving service to patients in their homes is one of the recent methods to provide suitable health care services. The most important issue that is addressed at the operational level of this problem by the researchers is the routing and scheduling of home health care. In order to improve the quality of the services and reduce the operational costs, it is important to find an optimal solution for the planning (including routing and scheduling) of the home health care problem. This problem is actually an extension of the famous vehicle routing problem (VRP) considering additional features required by health care. This study presents a mathematical model to consider flexibility in the starting and ending points of the nurses due to different real-world service features. These real-world service features can affect the whole optimal planning of the nurses. In this regard, various constraints of home health care problems were taken into account, such as patients time windows, appropriate sequence of services, necessity of responding to all patient needs, and matching the nurse skills with the required services by the patients.

In order to demonstrate the applicability of the suggested model, a small example was first run to demonstrate the validity of the model. In addition, the interpretation of the results showed the importance of the proposed model. Several sets of problems including large-, medium-, and small-sized instances were used to show the efficiency of the new model for problems of various sizes. Moreover, to analyze the effect of important parameters of the problem, a sensitivity analysis was executed on the parameter of the required features for the services. Finally, to help the decision makers handle their limited resources more effectively, some managerial insights were presented.

As a direction for future research, considering the problem in stochastic situations could be an attractive idea. Employing improved exact techniques, such as Benders Relaxation method, could be another direction to solve the suggested model. Moreover, when exact approaches cannot be applied to large-sized problems, using metaheuristic and heuristic approaches could be worthwhile. By considering various existing stakeholder proposals, the home health care problem could be viewed from various perspectives. Thus, multiobjective optimization approaches can be applied to cover different objectives simultaneously. Finally, developing the model using time-dependent traveling times and incorporating nursing education times in the planning could be other streams.