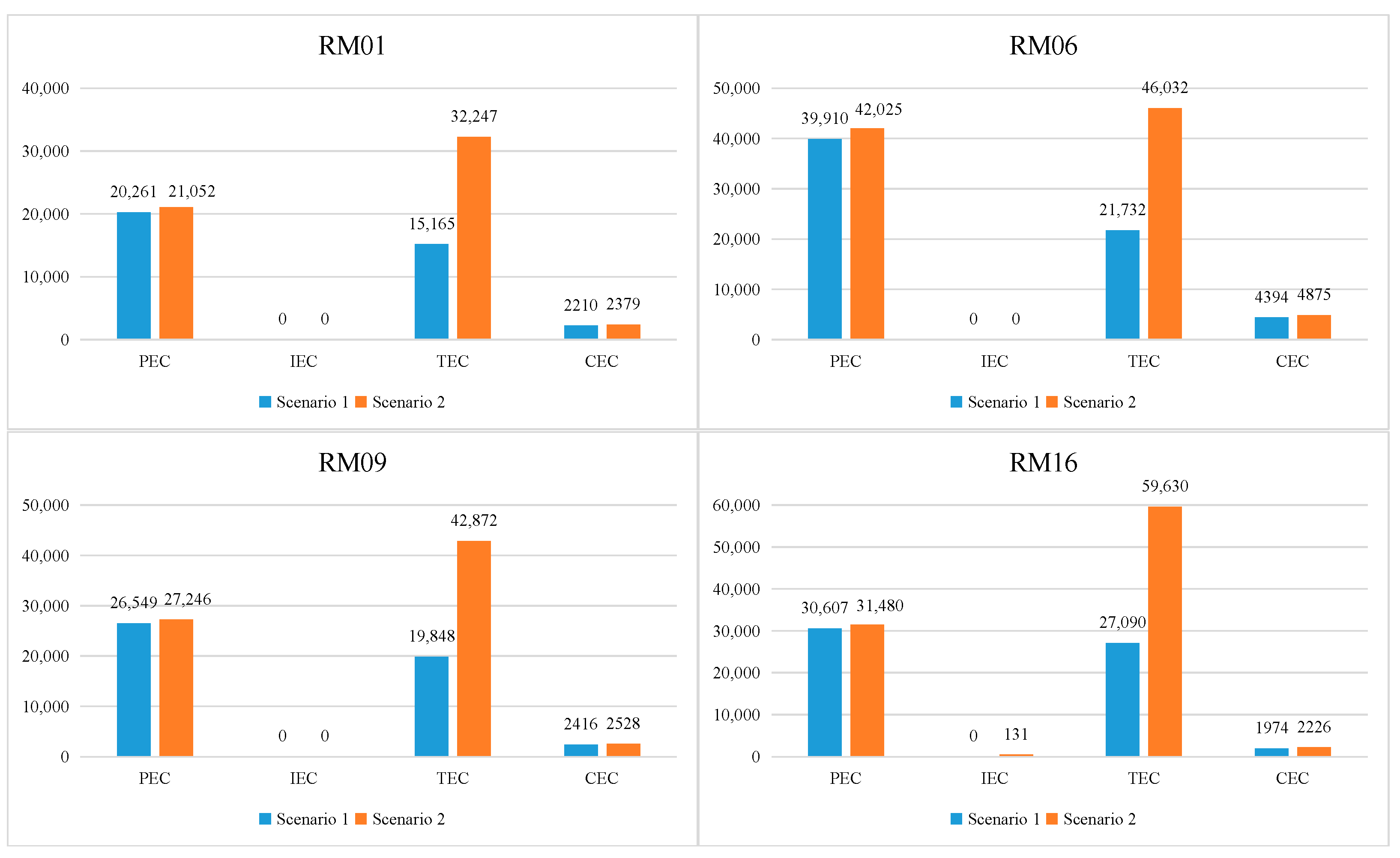1. Introduction
Suffering from growing energy costs and a worsening ecological environment, it is quite necessary to adopt some measures to achieve energy saving and consumption reduction. Reviewing this situation, some managers try to purchase more energy-efficient equipment, others attempt to redesign the products. However, these previous attempts inevitably impose substantial capital investment, which is impossible for some small and medium companies to afford such extra financial burden. In view of this fact, many researchers have turned their attention to reasonable operational management for the reduction of energy consumption. Energy-saving scheduling has been viewed as one of the most effective manners by researchers all around the world. A number of research achievements have been yielded for various manufacturing workshops, such as single machine [
1,
2,
3,
4,
5], parallel machines [
6,
7,
8,
9,
10,
11], flow shop [
12,
13,
14,
15,
16,
17,
18], and job shop [
19,
20,
21,
22,
23,
24,
25].
In recent years, considering the high theoretical complexity and strong application background, the energy-saving flexible job shop scheduling problem (ESFJSP) has become a new research hotspot in the manufacturing field. Wu et al. [
26] investigated the ESFJSP with the consideration of a deterioration effect. A multi-objective mathematical model was established to minimize total energy consumption and makespan. Then, pigeon-inspired optimization and simulated annealing algorithm are hybridized for the problem. Caldeira et al. [
27] addressed an ESFJSP with new job arrivals and turning on/off of the mechanism. A mathematical model was built to optimize the makespan, energy consumption, and instability simultaneously. An improved backtracking search algorithm was proposed to obtain the trade-off among the objectives. Dai et al. [
28] formulated an ESFJSP with transportation constraints to optimize energy consumption and makespan. Then, an improved genetic algorithm was presented to solve the problem. Yin et al. [
29] proposed a mathematical model with the consideration of flexible machining speed. A multi-objective genetic algorithm was developed to optimize productivity, energy efficiency, and noise reduction simultaneously. Liu et al. [
30] addressed an ESFJSP with crane transportation. A mixed-integer programming model was built to get the trade-off between energy consumption and makespan. Then, an integrated algorithm, consisting of a genetic algorithm, glowworm swarm optimization, and green transport heuristic strategy, was presented for the proposed model. Jiang et al. [
31] investigated an ESFJSP considering the sequence-dependent setup times and proposed an improved African buffalo optimization to get the minimum total energy consumption. Li and Lei [
32] reported an ESFJSP with transportation and sequence-dependent setup times and proposed an imperialist competitive algorithm with feedback to minimize the makespan, total tardiness and total energy consumption simultaneously. Zhang et al. [
33] studied an ESFJSP aiming to minimize makespan and total energy consumption. A multi-objective model was formulated with the consideration of sequence-dependent setup and transportation times. Then, an effective novel heuristic method was proposed to solve the problem. Gong et al. [
34] proposed a multi-objective mathematical model of a double flexible job shop scheduling problem considering the indicators of processing time, green production and human factor. Then, a hybrid genetic algorithm was presented for the model. Peng et al. [
35] addressed a multi-objective ESFJSP with job transportation and learning effect. A hybrid discrete multi-objective imperial competition algorithm was developed to solve the problem. Zhu et al. [
36] considered an ESFJSP considering worker learning effect and proposed a memetic algorithm to minimize the makespan, total carbon emission and total cost of workers. Wei et al. [
37] addressed an energy-efficient FJSP with the consideration of variable machine speed. Then some hybrid energy-efficient scheduling measures are developed to minimize the makespan and total energy consumption. Jiang et al. [
38] established a mathematical model of an ESFJSP considering job transportation and deterioration. The animal migration optimization algorithm was modified to minimize the total energy consumption. Jiang et al. [
39] considered a dual-resource constrained ESFJSP and proposed a discrete animal migration optimization algorithm to get the minimum total energy consumption.
Regarding the above literature, the ESFJSP problems have attracted considerable attention from scholars. Some research endeavors have been undertaken to narrow the gap between the scheduling problem and production application. Various practical factors have been investigated in the previous work, e.g., job deterioration effect [
26,
38], new job arrivals and turning on/off strategy [
27], job transportation constraints [
28,
30,
32,
33,
35,
38], flexible machining speed [
29,
37], machine setup times [
31,
32,
33] and double-resource constraint [
34,
35,
36,
39]. However, the above previous ESFJSP problems usually assume that the processing of the successful operation of a job cannot be started until its predecessor is finished completely. That is, the processing of any two consecutive operations of the same job is not permitted to be overlapped. In some real-life industries, e.g., metal or automobile industries, a job (lot) can always be divided into several similar parts (sublots), each of which can be dealt with individually. For such a job, it does not need to be transferred to the next step until all sublots are completed. In this situation, consecutive operations of a job can be overlapped for processing. The overlapping in operations are illustrated in
Figure 1. This strategy is often reported as lot streaming in the existing literature [
40]. One of the most important advantages of this strategy is the improvement of production efficiency. Demir and İşleyen [
41] formulated the FJSP with the consideration of overlapping operations. A genetic algorithm was proposed for solving the problem. Meng et al. [
42] designed a hybrid artificial bee colony for the FJSP with overlapping operations to minimize the total flow time. However, they only focus on improving the production efficiency and neglect the energy consumption generated in the manufacturing process. As far as we know, up to now, an ESFJSP with overlapping operations is seldom studied in the published literature. Furthermore, according to the above review, job transportation has been frequently considered in the ESFJSP [
28,
30,
32,
33,
35,
38]. The main reason for this situation is that there exist some strong interactions between production and transportation tasks in practical manufacturing. On the one hand, the machine selection of two consecutive operations in a job determines the transportation time. On the other hand, the transportation tasks could affect the idle times of machines in terms of different operation sequences. Furthermore, the energy consumption that occurs in the transportation process is nonnegligible. Based on the above review, in this study, the overlapping of operations and transportation times between machines are simultaneously considered in the ESFJSP problem.
Observed from the reviewed literature, the general solution process is to first establish a mathematical model with the expected objectives and the related constraints. Afterward, an effective algorithm is designed to solve the problem. For the ESFJSPs models, some were built as standard mathematical program models, e.g., mixed-integer linear programming [
27,
28,
33], mixed-integer programming [
29,
30]; others were not converted to standard forms or the authors did not state the model type clearly [
26,
31,
32,
34,
35,
36,
37,
38,
39]. In general, the solution methods for workshop scheduling problems fall into two main categories: exact and approximate methods [
43]. However, the ESFJSP is essentially an extended version of the traditional FJSP, consisting of many jobs, machines and objectives, which is inefficient to solve exactly and more suitable to be solved by approximate methods [
43]. In recent years, many meta-heuristics have been developed to deal with the ESFJSPs, e.g., pigeon-inspired optimization [
26], genetic algorithm [
28,
29,
30,
34], glowworm swarm optimization [
30], African buffalo optimization [
31], imperialist competitive algorithm [
32,
35], memetic algorithm [
36], animal migration optimization [
38,
39]. Nevertheless, none of them can be guaranteed to outperform other algorithms in all types of ESFJSPs. This fact is in line with the famous No Free Lunch Theorem [
44], which inspires scholars to continuously present new algorithms or modify existing ones.
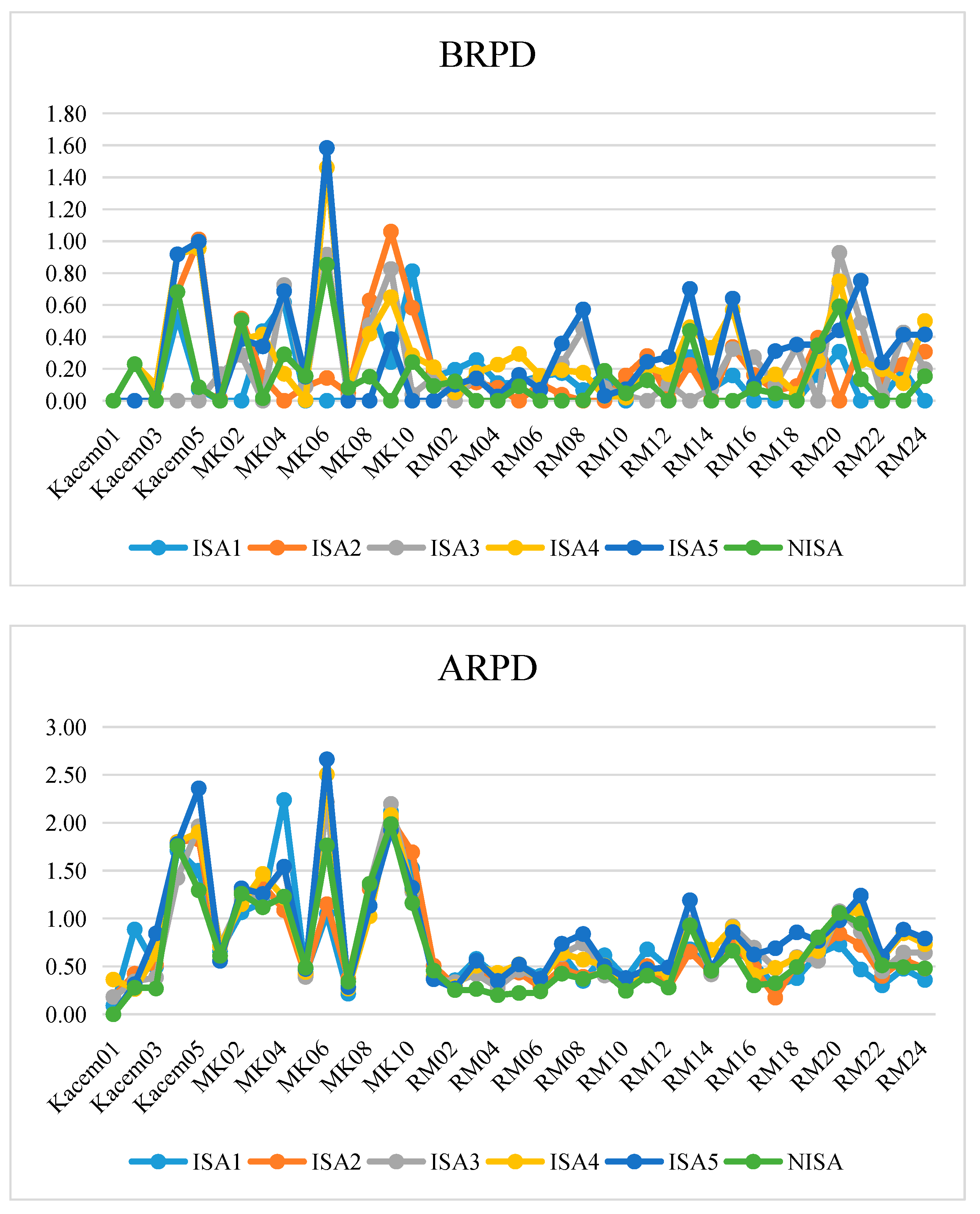
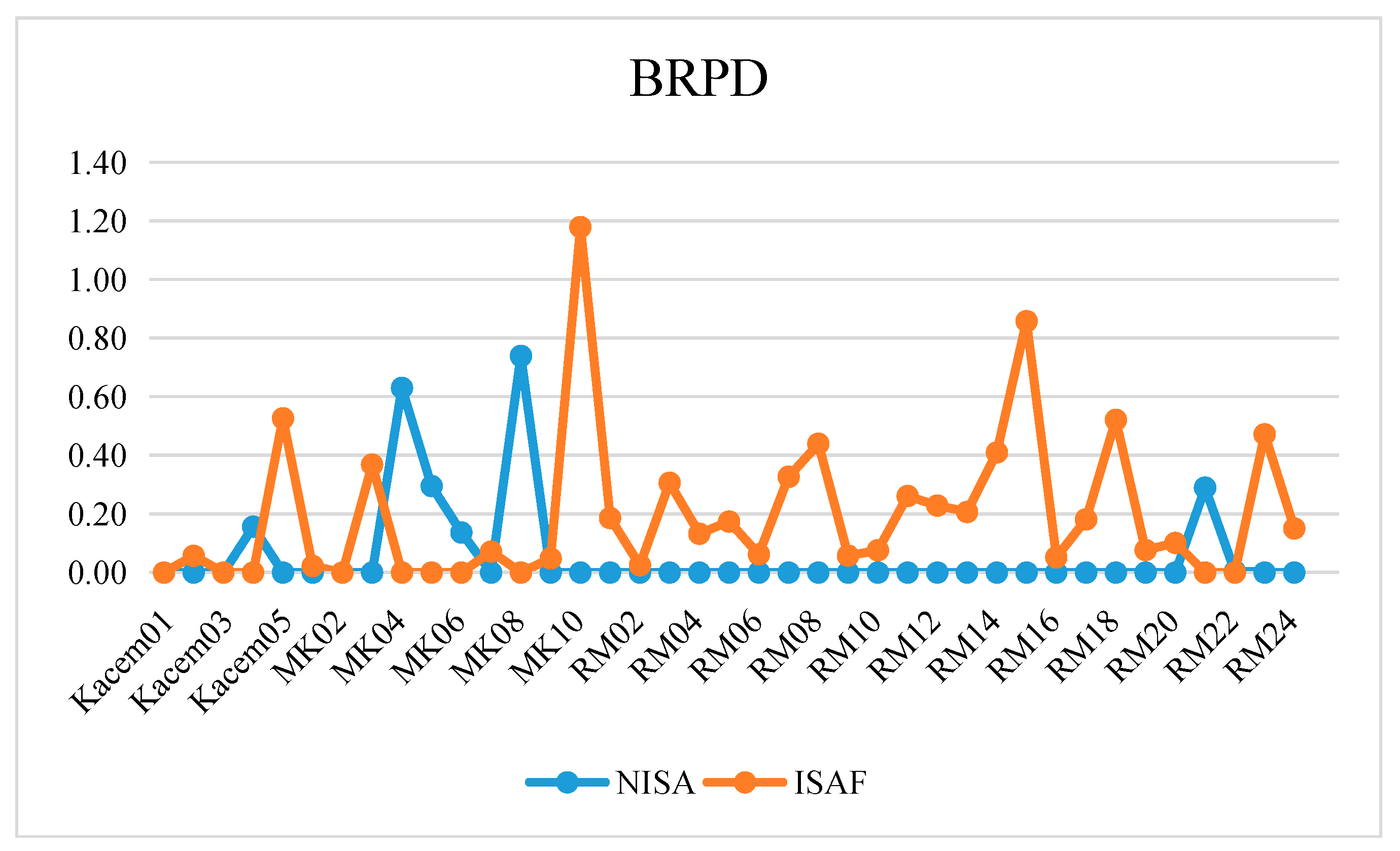
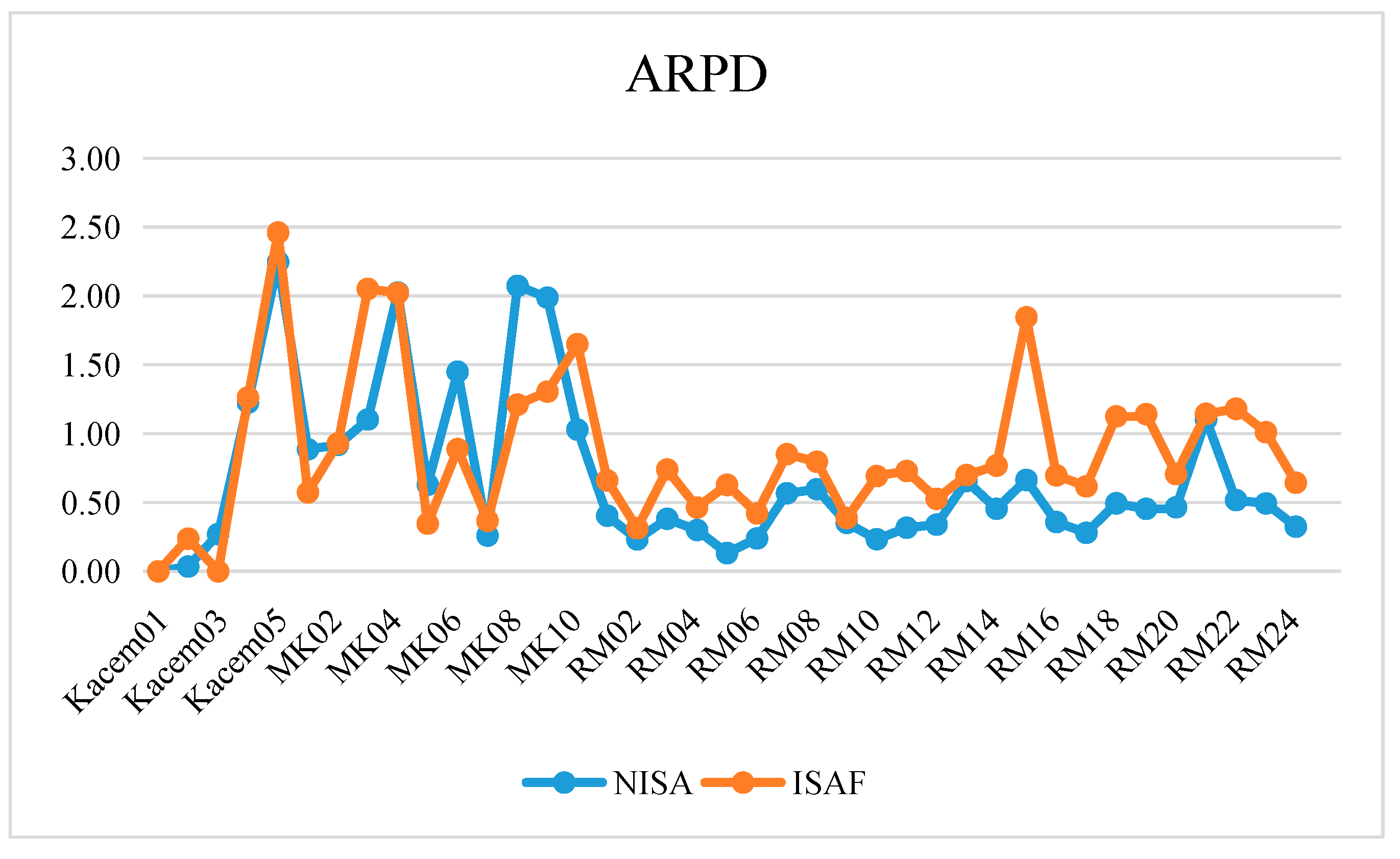
Interior search algorithms (ISA) are a novel meta-heuristic algorithm that originated from aesthetic behaviors of interior design and decoration [
45]. Since it was proposed, ISA has attracted increasing interest in dealing with various complex optimization problems [
46,
47,
48,
49,
50]. In the ISA algorithm, individuals are split into two groups with the exception of the fittest one, namely the composition group and the mirror group. These two groups are in charge of global exploration and local exploitation, respectively. A specific controlling parameter
is employed to select the group for each individual. This search mechanism gives a fine opportunity for the implementation of the cooperation between exploration and exploitation, which motivates us to select the ISA for the considered problem. Our main work is summarized as follows: (1) A mathematical model is built for the ESFJSP with the consideration of overlapping operations and transportation times simultaneously. (2) To solve the model, a NISA algorithm is elaborately designed based on the characteristics of the problem. The design work mainly includes encoding/decoding, population initialization, discrete composition optimization, discrete mirror search, tuning of parameter
and random walk. (3) Extensive experiments are performed to validate the competitive performance of the NISA algorithm and analyze the effect of transportation time and sublot number.
The remainder of this paper is organized as follows.
Section 2 reports the mathematical model of the ESFJSP with overlapping operations and transportation times.
Section 3 implements the NISA algorithm.
Section 4 assesses the performance of the NISA algorithm.
Section 5 reports the conclusion and next work.
2. Problem Description and Mathematical Model
2.1. Problem Description
In the considered problem, jobs are expected to be processed on machines. For each job, operations are sequentially processed in a certain order. For processing an operation, any machine can be selected from the operation’s compatible machine set. The capacity of the selected machine determines the processing time of each operation on the machine. In this work, each job is split into sublots with equal size. Once the processing of each sublot is finished, it will be transferred to another machine. It assumes that there are enough transporters equipped in the workshop. Meanwhile, the transporter can convey one sublot at a time, and the transportation times are known in advance. In the considered ESFJSP, the optimization objective is to get the minimum of the total energy consumption (TTEC), which contains processing energy consumption (PEC), idle energy consumption (IEC), transportation energy consumption (TEC) and common energy consumption (CEC). PEC is generated by machines when processing operations, IEC occurs when a machine is waiting for processing, TEC is consumed by transporters and CEC is consumed by accessory equipment.
Some assumptions are necessary as follows: jobs are released and machines are available at time 0; the setup times of machines are contained in the processing times; machine breakdowns are not considered; each machine cannot process two or more sublots at a given time; the number of sublots in each job is known in advance and fixed; for each operation, all sublots must be performed on the same machine; for each operation, no preemption is permitted; each machine cannot be shut down unless all jobs assigned to it are finished.
2.2. Mathematical Model
: Index of jobs, ;
: Index of machines, ;
: Number of operations contained in job , ;
: Total number of sublots of job , ;
: The th operation of job ;
: The th sublot of ;
: Processing time of on machine ;
: Total energy consumption;
: The PEC coefficient of on machine ;
: The IEC coefficient of machine in idle state;
: The CEC coefficient;
: The TEC coefficient;
: Completion time of machine ;
: Start time of machine ;
: Workload of machine , the total processing times of jobs assigned to machine ;
: Makespan;
: Transportation time between machine and for and ;
: Starting time of ;
: Completion time of ;
: A large positive number;
: 0–1 variable, if is assigned to machine , = 1; otherwise, = 0;
: 0–1 variable, if is assigned to machine , = 1; otherwise, = 0;
: 0–1 variable, if precedes on machine , = 1; otherwise, = 0.
Jiang et al. [
38] established the mathematical model of the energy-saving flexible job shop scheduling problem with the transportation time and deterioration effect. However, the overlapping in operations is not considered in their model. Here, we refer to their works to define the energy consumption and deal with the transportation constraints. The mathematical model of the ESFJSP with overlapping operations and transportation times is built as Equations (1)–(15).
Equation (1) calculates the total energy consumption; Constraint (2) defines that no interruption is allowed during the processing of each sublot; Constraint (3) denotes that any operation must be assigned to only one machine; Constraint (4) guarantees that the number of sublots processing on machine equals the total sublot number of . Constraint (5) gives the precedence relationships between the sublots of each operation, i.e., the th sublot of must be started after the th sublot is completed; Constraint (6) defines the precedence relationships between the operations belonging to the same job, i.e., the th sublot of must be started after the th sublot of is completed and transported to the next machine. Constraints (7) and (8) are disjunctive constraints where only one constraint can be met. That is, and assigned to machine cannot be processed simultaneously; Constraint (9) denotes the machine workload; Constraints (10) and (11) define the machine’s completion time and start time; Constraint (12) means that the start time of each operation is not smaller than zero; Constraints (13)–(15) state 0–1 variables.
4. Implementation of the NISA
4.1. Encoding and Decoding Approach
Similar to other meta-heuristics, one of the key issues is to design an encoding approach to implement the conversion between the solution space and the search space. In this paper, the problem is contained by machine assignment (MA) and operation permutation (OP). To represent the scheduling solutions, an encoding scheme with two vectors is employed to indicate the information of MA and OP. In the MA vector, a machine is chosen from the compatible machine set of each operation. In the OP vector, operations are sequenced to represent the precedence relationships on machines.
To illustrate the encoding approach, an instance with three jobs and three machines is given in
Figure 2. Each job contains three operations. In the MA vector, each integer number corresponds to the index of the machine for an operation. In the OP vector, each integer number corresponds to the job code. The appearance times of a job code represent the number of operations contained in the job.
Figure 1 gives the scheduling solution as follows:
.
Following the above scheduling scheme, the start times and completion times of all sublots in each operation can be determined in the decoding process. For each sublot , it cannot be processed until some necessary conditions must be satisfied: (1) The assigned machine of must be available, and the available time is represented by ; (2) If , can be immediately started once the assigned machine is available, i.e., ; (3) If , must be started after is finished and then transported from machine to , i.e., . The completion time of can be measured by .
4.2. Population Initialization
For a meta-heuristic algorithm, generating the initial population is vital for the convergence speed and solution quality. Based on the above encoding structure, the initial solutions will be created separately for the two vectors.
To obtain a machine assignment scheme, three heuristic rules [
51] are randomly adopted to choose a machine from each operation’s compatible machine set, i.e., Global Selection (GS), Local Selection (LS) and Random Rule (RR).
For a given machine assignment, three dispatching rules [
52] are randomly applied to sequence operations on machines, i.e., Most Work Remaining (MWR), Most Number of Operations Remaining (MOR) and Random Rule.
4.3. Discrete Composition Optimization
As can be seen from Equation (17), each individual updates its position randomly within a limited search space, which is derived from the individuals in the composition group. In the ISA algorithm, the composition optimization operator plays the role of global search. However, as observed from Equation (17), it cannot be applied to solving the discrete scheduling problem in this paper. Thus, the original composition optimization operator should be amended to adapt to the considered problem. It is well-known that the crossover operation is used to explore the search space and finding the global optimal solution. In view of this consideration, we develop a crossover-based component optimization operator to acquire new individuals. In order to implement it, an individual is randomly selected from the composition group at first. Then, crossover operations are carried out between the current individual and the selected one.
Based on the characteristics of the problem, two types of crossover operators [
53] are employed for the two vectors of a scheduling solution. One type is used for the OP vector, i.e., precedence preserving order-based crossover (POX) and job-based crossover (JBX), while the other is employed for the MA vector, i.e., two-point crossover (TPX) and multi-point crossover (MPX). When performing the component optimization operator, one crossover operator is randomly selected from each of the two types to act on the two vectors. It is notable that two offspring individuals will be generated by the crossover operation. After evaluating their fitness, the better offspring will be judged on whether to join the composition group or not. If the offspring is superior to the current individual, it will be accepted to replace the current individual. Otherwise, the current individual will remain unchanged.
4.4. Discrete Mirror Search
For each individual in the mirror group, a mirror is first randomly placed near the global best individual, and then the current individual is updated by absorbing the information from the mirror. However, according to Equations (18) and (19), the original mirror search operator is also unsuitable for the considered problem. Therefore, some modifications need to be conducted following the characteristics of the problem. Here, we present a neighborhood-crossover-based mirror search operator, which can be implemented below.
For each individual, two types of neighborhood structures are first randomly performed on the global best individual to generate a mirror. After the mirror generation, a crossover operation is performed between the current individual and the mirror to obtain a new individual. Herein, we employ
to represent the execution times of neighborhood operation. If
is large, the mirror may drop into the remote area of the global best; otherwise the mirror locates near the global best. Therefore,
determines the degree of exploitation of the mirror search operator. In this paper, the value of
is dynamically adjusted along with the iteration process. In the early iteration of the algorithm, individuals are updated by learning from the mirrors that are far away from the global best individual, and in the later iteration, individuals are updated by learning from the mirrors close to the global best individual. This adjustment process of
can be formulated by Equation (20), where
is the current iteration number;
represents the maximum iteration number;
and
represent the minimum and maximum values of
, which are set to be 1 and 5, respectively.
When performing the crossover operations, the POX and JBX are randomly selected for the OP vector, and the TPX and MPX are randomly selected for the MA vector. In addition, the neighborhood structures mentioned above are described below.
- (1)
Type 1 for machine assignment
TMA1: Randomly choose a position in the MA vector and randomly choose a different machine from the compatible machine set of the selected operation to take the place of the original machine.
TMA2: Randomly choose a position in the MA vector and choose the machine with the shortest processing time from the compatible machine set of the selected operation to replace the original machine.
TMA3: Randomly choose a position in the MA vector and choose the machine with the smallest PEC coefficient from the compatible machine set of the selected operation to replace the original machine.
- (2)
Type 2 for operation permutation
TOP1: Randomly select two positions with different values in the OP vector and swap their values.
TOP2: Randomly select two positions in the OP vector and insert the second position in front of the first one.
TOP3: Randomly select two positions in the OP vector and invert the values between the two positions.
4.5. Tuning of Parameter
In the basic ISA, individuals are divided into two groups controlled by parameter
, which determines the degree of emphasis on exploration and exploitation during the iteration search process. That is, if parameter
has a small value, more individuals join the composition group, and the algorithm has a stronger exploration capacity. Otherwise, the algorithm emphasizes the exploitation capacity. To acquire a balance between exploration and exploitation, Gandomi and Roke [
54] proposed a linear adjustment approach of
in Equation (21), which indicates that the search focuses on exploration by using composition optimization at the early stage, and then it is gradually switched to mirror search to emphasize exploitation at the latter stage.
4.6. Random Walk
In the ISA algorithm, a random walk acts as a local search to boost the local search capacity of the algorithm around the global best individual. To this end, a local search algorithm is constructed on the basis of the neighborhood structures in
Section 4.4. The steps of the local search algorithm are stated below.
- Step 1.
Set the current global best solution as the initial solution.
- Step 2.
Set .
- Step 3.
Perform two neighborhood structures on the MA and the OP vectors, respectively. For the two neighborhood structures, one is randomly selected from TMA1-TMA3, the other from TOP1-TOP3.
- Step 4.
Conduct the comparison between the new individual and the original one. If the new individual outperforms the original one, update the current best solution.
- Step 5.
Set , if , go to Step 6; otherwise, go to Step 2.
- Step 6.
Terminate the algorithm.
4.7. Steps of the NISA
- Step 1.
Initialize the parameters, i.e., the population size , the maximum iteration of NISA and the maximum iteration of local search algorithm .
- Step 2.
Create the initial population by using the approach in
Section 4.2.
- Step 3.
Find out the current global best solution .
- Step 4.
Calculate the value of parameter , and divide the population into the composition group and the mirror group.
- Step 5.
Perform the local search algorithm on .
- Step 6.
Perform the crossover-based composition optimization operator on the individuals in the composition group.
- Step 7.
Perform the neighborhood-crossover mirror search operator on the individuals in the mirror group.
- Step 8.
Evaluate each new individual. If it is superior to the original one, accept it; otherwise, keep the original solution unchanged.
- Step 9.
Determine whether the stop condition is met. If yes, go to Step 10; otherwise, go to Step 3.
- Step 10.
Terminate the NISA algorithm.
6. Conclusions and Future Work
In this paper, an ESFJSP is considered with overlapping operations and transportation times simultaneously. First, a mathematical model is constructed with the objective of minimizing the total energy consumption. Secondly, a new interior search algorithm (NISA) is presented according to the characteristics of the problem. To implement the algorithm, the design work mainly includes encoding/decoding, population initialization, discrete composition optimization, discrete mirror search, tuning of parameter and random walk. Thirdly, extensive experiments are conducted to test the NISA’s performance. The comparison results demonstrate that NISA is very competitive in solving the ESFJSP with overlapping operations and transportation times. In addition, the computational results indicate that the increase in transportation time and sublot number will incur an increase in transportation energy consumption, which is largely responsible for the increase in TTEC.
The model of the considered problem is abstracted and assumed in this work. In the next work, more practical constraints need to be integrated to be close to the real production, such as the dynamic/uncertain manufacturing environment, limited manufacturing resources (transporter, worker, etc.), job deterioration effect, time-of-use electricity strategy and so on. Moreover, we will extract some more efficient search rules from the problem, by which the computational efficiency of the algorithm will be further improved.