Frame-Related Sequences in Chains and Scales of Hilbert Spaces

Abstract

Frames for Hilbert spaces are interesting for mathematicians but also important for applications in, e.g., signal analysis and physics. In both mathematics and physics, it is natural to consider a full scale of spaces, and not only a single one. In this paper, we study how certain frame-related properties of a certain sequence in one of the spaces, such as completeness or the property of being a (semi-) frame, propagate to the other ones in a scale of Hilbert spaces. We link that to the properties of the respective frame-related operators, such as analysis or synthesis. We start with a detailed survey of the theory of Hilbert chains. Using a canonical isomorphism, the properties of frame sequences are naturally preserved between different spaces. We also show that some results can be transferred if the original sequence is considered—in particular, that the upper semi-frame property is kept in larger spaces, while the lower one is kept in smaller ones. This leads to a negative result: a sequence can never be a frame for two Hilbert spaces of the scale if the scale is non-trivial, i.e., if the spaces are not equal.

1. Introduction

Frames have been used as a powerful alternative to Hilbert space bases, and they allow for a deep theory (for an overview, see [1,2,3]). They are also very important for applications, e.g., in physics [4,5], signal processing [6,7], numerical treatments of operator equations [8,9], and acoustics [10].

There have been numerous generalizations of the concept of frames; see, e.g., [4,11,12,13,14,15], among others.

The basic idea in the work by Duffin and Schaeffer [16] was to have a sequence of elements in a Hilbert space that allows for redundant and stable representations. It is often more natural to not only consider a single Hilbert space, but a whole chain or scale of spaces [17,18,19,20]. Therefore, aiming at an extension of the concept of frames to such a setting is very natural. Several approaches have already been established; see Gelfand frames [8], or Riesz-like bases in rigged Hilbert spaces [21], Riesz–Fischer Maps, semi-frames, and distribution frames in rigged Hilbert spaces [22,23]. Those concepts “only” deal with a triplet of spaces, while here we will work on the concept of frames and related objects on a full scale.

In many settings, it is more natural to investigate a full scale of spaces, instead of just a single one. Examples include modulation spaces [24], which are naturally connected to Gabor analysis. One could, e.g., consider elements in the smallest modulation space, the Feichtinger algebra, to be optimal choices for Gabor windows. They allow for the representation of operators by kernels [25], in a more general way than for Schwartz classes [26,27]. Those spaces form a scale of spaces, where only the central space is a Hilbert space.

For Sobolev spaces [28], one has a scale of spaces; here, one can consider Hilbert spaces as being of a different order. Those spaces are naturally linked to the wavelet transform [29]. They are particularly important for the solution of PDEs [30], as demonstrated in [31,32].

On a more abstract level, for localized frames [33,34], a natural scale of (Banach) spaces is associated to a frame in a central Hilbert space. For all those concepts, the spaces are defined by taking an element in some distribution space and checking if the frame transformation is in a certain sequence or Lebesque space. For this concept, the frame-related properties are naturally shared on all spaces. In this manuscript, we investigate how frame-related properties are transferred in a general scale of Hilbert space.

Applications of frames for scales of Hilbert spaces can be found in the discretization of operators (as in [9,33,35,36]).

Let the increasing chain of Hilbert spaces be given [17]:

$$\dots \subseteq {\mathcal{H}}_2\subseteq {\mathcal{H}}_1\subseteq {\mathcal{H}}_0\subseteq {\mathcal{H}}_{-1}\subseteq {\mathcal{H}}_{-2}\subseteq \dots ,$$

with dense inclusions and ${\mathcal{H}}_{-n}={\mathcal{H}}_n^{\times }$, where ${\mathcal{H}}_n^{\times }$ is the antidual/conjugate dual of ${\mathcal{H}}_n$, with respect to the inner product of ${\mathcal{H}}_0$ [37], i.e., the space of continuous conjugate linear functionals on the Hilbert space ${\mathcal{H}}_n$ [38].

If such a chain is generated by the domain of an operator [39], we call this a scale of Hilbert spaces. Note that a chain of three Hilbert spaces generates always a scale of Hilbert spaces; see Section 3.3.2. For a similar definition, see the one of nested Hilbert space [40], where only a partial order is assumed. See also the similar concept of Gelfand chains [41].

In this paper, we will introduce some frame-related operators in a classical way, and study, by them, the frame-like sequences for a scale of Hilbert spaces, focusing on how the properties of those sequence are transferred between spaces. All the properties of a sequence $\psi$ in a Hilbert space of a scale of Hilbert spaces are preserved by its image through an unitary operator. However, what we have found is that not every property of a sequence in a Hilbert space of a scale is preserved if we look at it as a sequence in another space of the scale; in particular, if a sequence is a frame for two different spaces in a Hilbert scale, then they must coincide.

This paper is organized as follows: in Section 2 we collect results from the literature and fix the notation. In Section 3, we give a survey for chains of Hilbert spaces, following the literature to some extent but describing it from a new point of view, focusing on the so-called Berezanskii isomorphisms between two arbitrary spaces of the scale. In Section 4, we study how certain frame-related properties of a certain sequence in a space of a scale of Hilbert spaces and of operators directly linked to it propagate in the whole scale.

2. Known Facts, Definitions, and Notation

Before going forth, let us introduce some notations and recall the main definitions in the literature that we are going to use.

Let $\mathcal{H},\mathcal{K}$ be two separable infinite dimensional Hilbert spaces, with inner products ${〈·\left|·\right.〉}_{\mathcal{H}}$ with respect to ${〈·\left|·\right.〉}_{\mathcal{K}}$, chosen to be linear in the first entry, and the induced norms ${\parallel ·\parallel }_{\mathcal{H}}$ with respect to ${\parallel ·\parallel }_{\mathcal{K}}$. A bounded operator $A\in \mathcal{B}(\mathcal{H},\mathcal{K})$ is said to be unitary if it is isometric, i.e., ${\parallel Af\parallel }_{\mathcal{K}}={\parallel f\parallel }_{\mathcal{H}}$ for every $f\in \mathcal{H}$, and is adjacent, i.e., its range is $\mathsf{Ran}(A)=\mathcal{K}$. If we refer to a full sequence, we will denote it by a letter without an index, i.e., $c=\left(c_k\right)$.

2.1. Frames in Hilbert Spaces

Now, let $\mathcal{H}$ be a separable Hilbert space with inner product $〈·\left|·\right.〉$ and norm $\parallel ·\parallel$. A sequence $({\psi }_k)\subset \mathcal{H}$ is said to be:

• complete (or total) if $\mathsf{span}({\psi }_k)$, the linear span of $({\psi }_k)$, is dense in $\mathcal{H}$;
• a frame for $\mathcal{H}$ if there exist $A>0$ and $B<\infty$, such that:

  $${A\parallel f\parallel }^2\le \sum _{k\in \mathbb{N}}|〈f\left|{\psi }_k\right.〉{|}^2\le B{\parallel f\parallel }^2,\forall f\in \mathcal{H};$$

  (1)
• a Bessel sequence in $\mathcal{H}$ if there exists $B>0$, such that the upper inequality in (1) holds true. It is called an upper semi-frame [42] if the Bessel sequence is also complete (this is equivalent to $0<\sum _{k\in \mathbb{N}}|〈f\left|{\psi }_k\right.〉{|}^2\le {B||f||}^2,\forall f\ne 0$);
• a lower semi-frame for $\mathcal{H}$ if it satisfies the lower frame inequality in (1);
• a Riesz basis for $\mathcal{H}$ if there exist an orthonormal basis $(e_k)$ for $\mathcal{H}$ and a bounded bijective operator $T:\mathcal{H}\to \mathcal{H}$, such that ${\psi }_k=T{e}_k$ for all $k\in \mathbb{N}$.

There are several operators canonically associated to a sequence $\psi =({\psi }_k)$ of elements of a Hilbert space $\mathcal{H}$. The analysis operator $C_{\psi }:\mathsf{Dom}(C_{\psi })\subseteq \mathcal{H}\to {\ell }^2$ of $({\psi }_k)$ is defined by:

$$C_{\psi }f=(〈f\left|{\psi }_k\right.〉),\forall f\in \mathsf{Dom}(C_{\psi }),\mathrm{where}$$

$$\mathsf{Dom}(C_{\psi })=\left\{f\in \mathcal{H}:\sum _{k\in \mathbb{N}}{|〈f\left|{\psi }_k\right.〉|}^2<\infty \right\}.$$

The synthesis operator $D_{\psi }:\mathsf{Dom}(D_{\psi })\subseteq {\ell }^2\to \mathcal{H}$ of $({\psi }_k)$ is defined on the dense domain:

$$\mathsf{Dom}(D_{\psi }):=\left\{c\in {\ell }^2:\sum _{k\in \mathbb{N}}{c}_k{\psi }_k\mathrm{is}\mathrm{convergent}\mathrm{in}\mathcal{H}\right\}$$

by:

$$D_{\psi }(c_k)=\sum _{k\in \mathbb{N}}{c}_k{\psi }_k,\forall (c_k)\in \mathsf{Dom}(D_{\psi }).$$

It is known [43] that we have, for any sequence, $C_{\psi }=D_{\psi }^{*}$, where, as usual, $D_{\psi }^{*}$ indicates the adjoint of the operator $D_{\psi }$. The other two operators associated to a sequence $\psi =({\psi }_k)\subset \mathcal{H}$ are the frame operator (note that, for the definition of the frame operator as a potentially unbounded operator, the sequence does not have to be a frame) $S_{\psi }:\mathsf{Dom}(S_{\psi })\subseteq \mathcal{H}\to \mathcal{H}$ of $\psi$:

$$S_{\psi }f:=\sum _{k\in \mathbb{N}}〈f\left|{\psi }_k\right.〉{\psi }_k$$

where:

$$\mathsf{Dom}(S_{\psi })=\{f\in \mathcal{H}:\sum _{k\in \mathbb{N}}〈f\left|{\psi }_k\right.〉{\psi }_{k}convergesin\mathcal{H}\};$$

and the Gram operator $G_{\psi }:\mathsf{Dom}(G_{\psi })\subseteq {\ell }^2\to {\ell }^2,$ with:

$${\left(G_{\psi }c\right)}_k:=\sum _{l\in \mathbb{N}}{(G_{\psi })}_{k,l}·c_l,$$

where:

$$\mathsf{Dom}(G_{\psi })=\{c\in {\ell }^2:\sum _{l\in \mathbb{N}}{(G_{\psi })}_{k,l}{c}_{l}converges\forall k\in \mathbb{N}andisin{\ell }^2\}$$

and the Gram matrix ${({(G_{\psi })}_{k,l})}_{k,l}$ is defined by ${(G_{\psi })}_{k,l}=〈{\psi }_l\left|{\psi }_k\right.〉$, $k,l\in \mathbb{N}$.

If we combine those operators, we end up at the following definition: let $\psi =({\psi }_k)$ and $\varphi =({\varphi }_k)$ be two sequences in $\mathcal{H}$. The pair $\left(\psi ,\varphi \right)$ is called:

• a reproducing pair if the cross-frame operator, defined by:

  $$〈S_{\psi ,\varphi }f,g〉=\sum _k〈f,{\psi }_k〉〈{\varphi }_k,g〉$$

  is an invertible, bounded operator [44];
• a weakly dual pair [45] if it is a reproducing pair and $S_{\psi ,\varphi }={\mathsf{id}}_{}$.

Clearly, for every reproducing pair, the pair $\left(\psi ,S_{\psi ,\varphi }^{-1}\varphi \right)$ is weakly dual.

2.2. Rigged Hilbert Spaces

In a formulation using a topology viewpoint, where not all involved spaces have to be normed (see, e.g., [21]), a rigged Hilbert space (RHS) consists of a triplet $(\mathcal{D},\mathcal{H},{\mathcal{D}}^{\times })$, where $\mathcal{D}$ is a dense subspace of $\mathcal{H}$ endowed with a locally convex topology t, finer than that induced by the Hilbert norm of $\mathcal{H}$, and ${\mathcal{D}}^{\times }$ is the conjugate dual of $\mathcal{D}\left[t\right]$, endowed with the strong topology $t^{\times }:=\beta ({\mathcal{D}}^{\times },\mathcal{D})$. We have:

$$\mathcal{D}\left[t\right]\hookrightarrow \mathcal{H}\hookrightarrow {\mathcal{D}}^{\times }\left[t^{\times }\right],$$

where ↪ denotes a continuous embedding, and since ${\mathcal{D}}^{\times }$ contains a subspace that can be identified with $\mathcal{H}$, we will read (2.2) as a chain of topological inclusions: $\mathcal{D}\left[t\right]\subset \mathcal{H}\subset {\mathcal{D}}^{\times }\left[t^{\times }\right]$. These identifications imply that the sesquilinear form $B(·,·)$ that puts $\mathcal{D}$ and ${\mathcal{D}}^{\times }$ in duality is an extension of the inner product of $\mathcal{D}$: $B(f,g)=〈f\left|g\right.〉$, for every $f,g\in \mathcal{D}$ (as usual, to simplify notations, we adopt the symbol $〈·\left|·\right.〉$ for both of them).

Now, let $\mathcal{D}\left[t\right]\subset \mathcal{H}\subset {\mathcal{D}}^{\times }\left[t^{\times }\right]$ be a rigged Hilbert space, and let $\mathfrak{L}(\mathcal{D},{\mathcal{D}}^{\times })$ denote the vector space of all continuous linear maps from $\mathcal{D}\left[t\right]$ into ${\mathcal{D}}^{\times }\left[t^{\times }\right]$. If $\mathcal{D}\left[t\right]$ is barreled (e.g., reflexive), an involution $X\mapsto X^{†}$ can be introduced in $\mathfrak{L}(\mathcal{D},{\mathcal{D}}^{\times })$ by the equality:

$$〈X^{†}\eta \left|\xi \right.〉=\overline{〈X\xi \left|\eta \right.〉},\forall \xi ,\eta \in \mathcal{D}$$

(2)

and $\mathfrak{L}(\mathcal{D},{\mathcal{D}}^{\times })$ becomes a ${}^{†}$-invariant vector space; see [37] for full details.

We will show, in Section 3.3.1, how this can be expressed and extended in a Hilbert space setting.

2.3. Scales of Hilbert Spaces

Let ${\mathcal{H}}_0$ be a Hilbert space with inner product ${〈.,.〉}_0$. Let A be a self-adjoint, strictly positive, unbounded operator with domain $\mathsf{Dom}(A)\subset {\mathcal{H}}_0$ and range $\mathsf{Ran}(A)\subset {\mathcal{H}}_0$; without loss of generality, let $A=A^{*}\ge 1$. By assumption, this operator has a dense domain, a dense range, and is closed. It has closed range and is, therefore, adjacent. Its inverse $A^{-1}:{\mathcal{H}}_0\to \mathsf{Dom}(A)$ is bounded and self-adjoint.

The same argument holds for any $A^k$ and $A^{-k}$, $k\in \mathbb{N}$. Define, for each $k\ge 0$, the Hilbert space ${\mathcal{H}}_{+k}=\left\{\mathsf{Dom}(A^{k/2}),{\parallel ·\parallel }_{+k}\right\}$, i.e., the domain of $A^{k/2}$ equipped with the norm ${\parallel ·\parallel }_{+k}$ induced by the inner product ${〈x\left|y\right.〉}_{+k}:={〈A^{k/2}x\left|A^{k/2}y\right.〉}_0,x,y\in \mathsf{Dom}(A^{k/2})$. Therefore, $A^k:{\mathcal{H}}_{+2k}\to {\mathcal{H}}_0$ is bounded, even unitary.

Define ${\mathcal{H}}_{-k}$ as the completion of ${\mathcal{H}}_0$ with respect to the norm ${\parallel ·\parallel }_{-k}$ induced by the inner product ${〈f\left|g\right.〉}_{-k}:={〈A^{-k/2}f\left|A^{-k/2}g\right.〉}_0,f,g\in {\mathcal{H}}_0$. Clearly, ${\mathcal{H}}_0\subset {({\mathcal{H}}_{+k})}^{\prime }$ densely (where we apply the Riesz isomorphism for ${\mathcal{H}}_0\cong {({\mathcal{H}}_0)}^{\prime }$). We have, for $f\in {\mathcal{H}}_0$:

$${\parallel f\parallel }_{{\left({\mathcal{H}}_{+k}\right)}^{\prime }}=\underset{{\parallel g\parallel }_{+k}=1}{sup}|{〈f,g〉}_0|=\underset{\parallel A^{k/2}{g\parallel }_0=1}{sup}\left|{〈f,g〉}_0\right|=$$

$$=\underset{{\parallel h\parallel }_0=1}{sup}|{〈f,A^{-k/2}h〉}_0|=\underset{{\parallel h\parallel }_0=1}{sup}|{〈A^{-k/2}f,h〉}_0|=\parallel A^{-k/2}{f\parallel }_0,$$

and so the norms are equivalent. Therefore, ${({\mathcal{H}}_{+k})}^{\prime }={\mathcal{H}}_{-k}$. For each fixed $k>0$, the triplet:

$${\mathcal{H}}_{+k}\subset {\mathcal{H}}_0\subset {\mathcal{H}}_{-k}$$

is a rigged Hilbert space with dense inclusions. The chain of Hilbert spaces, infinite on both sides:

$$\dots \subset {\mathcal{H}}_{+k}\subset \dots \subset {\mathcal{H}}_0\subset \dots \subset {\mathcal{H}}_{-k}\subset \dots$$

is called an A-scale of Hilbert spaces [46].

An important property of an A-scale is the invariance of the structure of rigged triple ${\mathcal{H}}_{+k}\subseteq {\mathcal{H}}_0\subseteq {\mathcal{H}}_{-k}$ under shift along the A-scale, i.e., the shift of the index k; this property has been called the first invariance principle of the A-scale [46]: for any fixed $k>0$ and an arbitrary n, the triple of spaces ${\mathcal{H}}_{n+k}\subseteq {\mathcal{H}}_n\subseteq {\mathcal{H}}_{n-k}$ is a new rigged Hilbert space where, in particular, the Hilbert space ${\mathcal{H}}_{n-k}$ is the dual of ${\mathcal{H}}_{n+k}$, which becomes apparent if we complete the above construction, taking ${\mathcal{H}}_n$ as the “central space”.

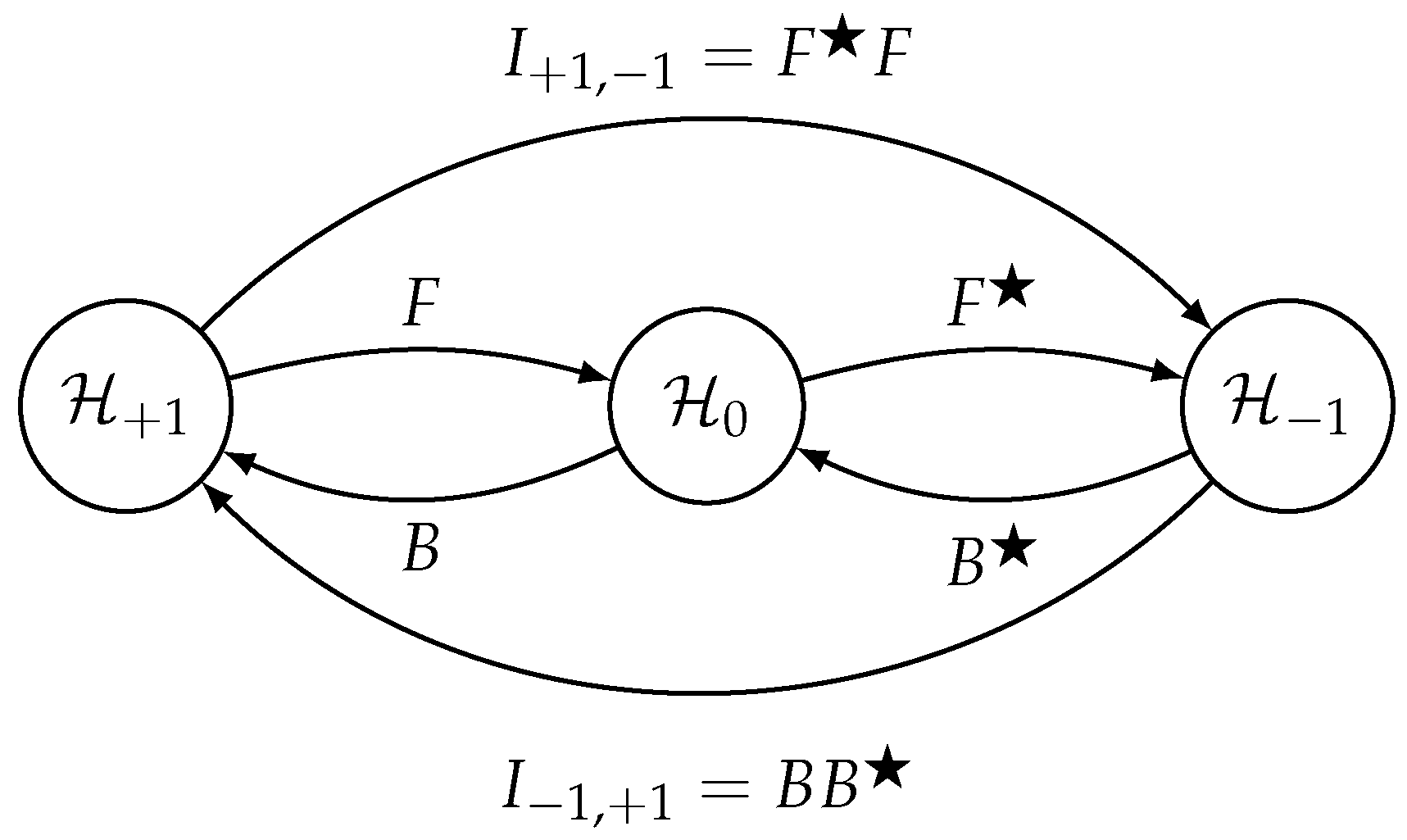
3. Hilbert Chains

In this section, we include a detailed introduction to Hilbert chains, to some extent following [47], albeit in an extended and reformulated manner, so as to make the manuscript self-contained, to stress results that are not well-known in the frame theory community, and to adapt the respective points of view. We have added details and covered new side-aspects as well.

3.1. Hilbert Triplets

This section deals with canonical Hilbert triplets, and how one can define operators between them.

Let ${\mathcal{H}}_0$ be a separable, infinite-dimensional Hilbert space with scalar product ${〈·\left|·\right.〉}_0$ and norm ${\parallel ·\parallel }_0$. Fix any $i\in \mathbb{N}\backslash \{0\}$, and let ${\mathcal{H}}_{+i}$ be a dense subspace of ${\mathcal{H}}_0$, ${\mathcal{H}}_{+i}\subseteq {\mathcal{H}}_0$, complete with respect to the norm ${\parallel ·\parallel }_{+i}$ induced by the inner product ${〈·\left|·\right.〉}_{+i}$ with:

$${\parallel x\parallel }_0\le {\parallel x\parallel }_{+i},\forall x\in {\mathcal{H}}_{+i}.$$

(3)

Let ${\iota }_{+i,0}$ be the inclusion of ${\mathcal{H}}_{+i}$ into ${\mathcal{H}}_0$, which, by (3), is bounded. We have:

$${〈f\left|x\right.〉}_0={〈f\left|{\iota }_{+i,0}x\right.〉}_0={〈{\iota }_{+i,0}^{*}f\left|x\right.〉}_{+i},\forall f\in {\mathcal{H}}_0,x\in {\mathcal{H}}_{+i}.$$

(4)

Define:

$${\iota }_{0,+i}:={\iota }_{+i,0}^{*}:{\mathcal{H}}_0\to {\mathcal{H}}_{+i},$$

(5)

where we consider the Hilbert space adjoints, i.e., apply the Riesz isomorphisms for both Hilbert spaces.

We have $\parallel {\iota }_{+i,0}\parallel \le 1$, and ${\iota }_{+i,0}$ is injective (one-to-one) and has dense range, but cannot be adjacent. Therefore, ${\iota }_{0,+i}:={\iota }_{+i,0}^{*}$ has the same properties.

On the other hand, let us note that, naturally:

$${〈x\left|y\right.〉}_{+i}\ne {〈{\iota }_{+i,0}x\left|{\iota }_{+i,0}y\right.〉}_0,x,y\in {\mathcal{H}}_{+i}$$

because, otherwise, (3) would be an equality and the two spaces would collapse into only one space.

Let us define now the scalar product:

$${〈f\left|g\right.〉}_{-i}:={〈{\iota }_{0,+i}f\left|g\right.〉}_0={〈{\iota }_{0,+i}f\left|{\iota }_{0,+i}g\right.〉}_{+i},f,g\in {\mathcal{H}}_0$$

(6)

and consider the completion ${\mathcal{H}}_{-i}$ of ${\mathcal{H}}_0$ with respect to the norm ${\parallel ·\parallel }_{-i}$ induced by the inner product defined in (6). Then, from $\parallel {\iota }_{0,+i}\parallel \le 1$, it follows that ${\parallel f\parallel }_{-i}\le {\parallel f\parallel }_0$$\forall f\in {\mathcal{H}}_0$, and we have:

$${\mathcal{H}}_{+i}\subset {\mathcal{H}}_0\subset {\mathcal{H}}_{-i},$$

with dense inclusions, and:

$${\parallel x\parallel }_{-i}\le {\parallel x\parallel }_0\le {\parallel x\parallel }_{+i},\forall x\in {\mathcal{H}}_{+i}.$$

Since ${\iota }_{0,+i}$ maps a dense subspace of ${\mathcal{H}}_{-i}$ (i.e. ${\mathcal{H}}_0$) into ${\mathcal{H}}_{+i}$, we consider the (unique) bounded extension $I_{-i,+i}=\overline{{\iota }_{0,+i}}\in \mathcal{B}({\mathcal{H}}_{-i},{\mathcal{H}}_{+i})$.

As ${\iota }_{0,+i}$ has dense range, $I_{-i,+i}$ is adjacent (surjective). By (6), $I_{-i,+i}$ is an isometry:

$${〈\alpha \left|\beta \right.〉}_{-i}={〈I_{-i,+i}\alpha \left|I_{-i,+i}\beta \right.〉}_{+i},\alpha ,\beta \in {\mathcal{H}}_{-i}.$$

Therefore, $I_{-i,+i}$ is a unitary operator; hence:

$$I_{+i,-i}:=I_{-i,+i}^{*}=I_{-i,+i}^{-1}\in \mathcal{B}({\mathcal{H}}_{+i},{\mathcal{H}}_{-i})$$

is a unitary operator too. The operators $I_{-i,+i}\in \mathcal{B}({\mathcal{H}}_{-i},{\mathcal{H}}_{+i})$ and $I_{+i,-i}\in \mathcal{B}({\mathcal{H}}_{+i},{\mathcal{H}}_{-i})$ are called Berezanskii canonical isomorphisms (see e.g., [46]). This is a particular instance of the Riesz isomorphism, if a particular duality (with the pivot space ${\mathcal{H}}_0$) is chosen.

3.2. Duality by Pivot Spaces

Now, we show that ${\mathcal{H}}_0$ can be considered a pivot space of ${\mathcal{H}}_{-i}$ and ${\mathcal{H}}_{+i}$ in the sense that the scalar product ${〈\alpha \left|x\right.〉}_0$ defines a duality relation. Consider the bilinear form $b(f,x)={〈f\left|x\right.〉}_0$ defined on ${\mathcal{H}}_0\times {\mathcal{H}}_{+i}$. Extend it by continuity to the bilinear form:

$$B_{-i,+i}:(\alpha ,x)\in {\mathcal{H}}_{-i}\times {\mathcal{H}}_{+i}\to \mathbb{C}.$$

For $f\in {\mathcal{H}}_0$ and $x\in {\mathcal{H}}_{+i}$, we have:

$$\begin{array}{ccc}\hfill |{〈f\left|x\right.〉}_0|& =& |{〈{\iota }_{0,+i}f\left|x\right.〉}_{+i}|=|{〈I_{-i,+i}f\left|x\right.〉}_{+i}|\hfill \\ \hfill & \le & \parallel I_{-i,+i}{f\parallel }_{+i}{\parallel x\parallel }_{+i}={\parallel f\parallel }_{-i}{\parallel x\parallel }_{+i}\hfill \end{array}$$

By a limit argument, we obtain:

$$|B_{-i,+i}{(\alpha ,x)|\le \parallel \alpha \parallel }_{-i}{\parallel x\parallel }_{+i},$$

(7)

for $\alpha \in {\mathcal{H}}_{-i},x\in {\mathcal{H}}_{+i}$. Therefore, $B_{-i,+i}$ is continuous.

Remark 1.

The form $B_{-i,+i}(·,·)$ that puts ${\mathcal{H}}_{+i}$ and ${\mathcal{H}}_{-i}$ in duality is an extension of the inner product ${〈·\left|·\right.〉}_0$, and we will use the latter symbol for both of them.

By a limit argument (and the conjugate symmetry of any inner product), we obtain for $\alpha ,\beta \in {\mathcal{H}}_{-i},x,y\in {\mathcal{H}}_{+i}$:

$${〈\alpha \left|x\right.〉}_0={〈I_{-i,+i}\alpha \left|x\right.〉}_{+i}\mathrm{and}{〈x\left|y\right.〉}_{+i}={〈I_{+i,-i}x\left|y\right.〉}_0$$

(8)

and:

$${〈\alpha \left|\beta \right.〉}_{-i}={〈I_{-i,+i}\alpha \left|\beta \right.〉}_0={〈\alpha \left|I_{-i,+i}\beta \right.〉}_0={〈I_{-i,+i}\alpha \left|I_{-i,+i}\beta \right.〉}_{+i}.$$

By Remark 1, we see that $\alpha \in {\mathcal{H}}_{-i}$ is in ${({\mathcal{H}}_{+i})}^{\prime }$ with the same norm. On the other hand, any functional L on ${\mathcal{H}}_{+i}$ can be represented by a $y\in {\mathcal{H}}_{+i}$, i.e.:

$$L(x)={〈y\left|x\right.〉}_{+i}={〈I_{+i,-i}y\left|x\right.〉}_0.$$

As $I_{+i,-i}$ is an isometry, we have shown:

Remark 2.

This construction corresponds to considering the dual pair $({\mathcal{H}}_{+i},{\mathcal{H}}_0)$ using ${〈·\left|·\right.〉}_0$, and choosing ${\mathcal{H}}_{-i}={\overline{{\mathcal{H}}_0}}^{\sigma ({\mathcal{H}}_{+i},{\mathcal{H}}_0)}$ using the weak dual topology [48]. ${\mathcal{H}}_{-i}$ is, therefore, a representation of the dual space of ${\mathcal{H}}_{+i}$.

Note that this is not a pure abstract baublery, but that it is important for concrete spaces. While it is true that “everything is isomorphic anyway”, these isomorphisms cannot be thought of as equal if concrete choices for ${\mathcal{H}}_{+i}$ and ${\mathcal{H}}_{-i}$ are worked with, for example, in the setting of Sobolev spaces [36]. See [33] for an application of this topology to the more general setting of co-orbit spaces of localized frames.

Remark 3.

One might expect that there is a clear link of $I_{+i,-i}$ to the inclusion ${\iota }_{+i,-i}$. However, clearly, the relation cannot be trivial, e.g., an extension, as the former operator is bijective, the latter is injective and has dense range, and both are bounded on all of ${\mathcal{H}}_{+i}$.

At the same time, it could be interesting to look at the role of the inclusion of ${\mathcal{H}}_0$ into ${\mathcal{H}}_{-i}$, i.e., ${\iota }_{0,-i}$, in this setting. Again, however, it cannot be trivially linked to $I_{-i,+i}$ as, e.g., ${\iota }_{0,-i}$ cannot be $\overline{{I_{-i,+i}}_{{|}_{{\mathcal{H}}_0}}}$ because it would otherwise be adjacent. For more on that, see Remark 7.

3.3. Hilbert Chains

Now, let us add a step more. Consider a dense subspace ${\mathcal{H}}_{+j}$ of the Hilbert space ${\mathcal{H}}_{+i}$, with $j>i$ ($i,j\in \mathbb{N}$), complete with respect to the norm ${\parallel ·\parallel }_{+j}$, induced on ${\mathcal{H}}_{+j}$ by the inner product ${〈·\left|·\right.〉}_{+j}$, such that ${\parallel x\parallel }_{+i}\le {\parallel x\parallel }_{+j}$ with $x\in {\mathcal{H}}_{+j}$. Then, ${\mathcal{H}}_{+j}$ is a dense subspace of ${\mathcal{H}}_0$, too, and ${\parallel x\parallel }_0\le {\parallel x\parallel }_{+j}$ with $x\in {\mathcal{H}}_{+j}$. If we consider the completion ${\mathcal{H}}_{-j}$ of ${\mathcal{H}}_0$, with respect to the norm ${\parallel ·\parallel }_{-j}$ defined, such as in (6) (with $i=j$ and ${\iota }_{0,+j}:{\mathcal{H}}_0\to {\mathcal{H}}_{+j}\subset {\mathcal{H}}_{+i}$, defined, as in (5), as the adjoint of the inclusion), we have, for every $x\in {\mathcal{H}}_{+j}$ and every $j>i$, $i\in \mathbb{N}$:

$${\mathcal{H}}_{+j}\subset {\mathcal{H}}_{+i}\subset {\mathcal{H}}_0\subset {\mathcal{H}}_{-i}\subset {\mathcal{H}}_{-j},$$

where every inclusion is dense. Indeed, let us prove that ${\mathcal{H}}_{-i}\subset {\mathcal{H}}_{-j}$ with $j>i$. For $f\in {\mathcal{H}}_0$, we have, from (6) and (7):

$${\parallel f\parallel }_{-j}^2={〈{\iota }_{0,+j}f\left|f\right.〉}_0\le \parallel {\iota }_{0,+j}{f\parallel }_{+i}{\parallel f\parallel }_{-i}=\parallel I_{-j,+j}{f\parallel }_{+i}{\parallel f\parallel }_{-i}\le$$

$$\le \parallel I_{-j,+j}{f\parallel }_{+j}{\parallel f\parallel }_{-i}={\parallel f\parallel }_{-j}{\parallel f\parallel }_{-i},$$

for every $f\in {\mathcal{H}}_0$.

Because ${\mathcal{H}}_{-i}\subset {\mathcal{H}}_{-j}$ are the closures of ${\mathcal{H}}_0$, with respect to those norms, we have the dense inclusions and:

$${\parallel x\parallel }_{-j}\le {\parallel x\parallel }_{-i}\le {\parallel x\parallel }_0\le {\parallel x\parallel }_{+i}\le {\parallel x\parallel }_{+j},\forall x\in {\mathcal{H}}_{+j}.$$

Since we have ${\iota }_{+j,0}={\iota }_{+i,0}{\iota }_{+j,+i}$, we also have ${\iota }_{0,+j}={\iota }_{+i,+j}{\iota }_{0,+i}$. Again, note that (in the non-trivial case) we have that ${\iota }_{-i,-j}{I}_{+i,-i}{\iota }_{+j,+i}\ne I_{+j,-j}$. However, naturally, we have ${\iota }_{k,i}={{\iota }_{j,i}}_{{}_{{|}_{{\mathcal{H}}_k}}}$ for $k\ge j\ge i$.

Note that we can change the role of the central pivot space: for every $r<p$, let:

$${\iota }_{r,p}:{\mathcal{H}}_r\to {\mathcal{H}}_p$$

(9)

be the adjoint of the inclusion of the Hilbert space ${\mathcal{H}}_p$ into the space ${\mathcal{H}}_r$, as it is known that:

$${\parallel x\parallel }_r\le {\parallel x\parallel }_p,\forall x\in {\mathcal{H}}_p.$$

(10)

Consider the bilinear form:

$$B_{r,p}:(f,x)\in {\mathcal{H}}_r\times {\mathcal{H}}_p\to {〈f\left|x\right.〉}_r\in \mathbb{C};$$

then, by (10), it is continuous for $f\in {\mathcal{H}}_r$ and for $x\in {\mathcal{H}}_p$; hence, it can be represented as a scalar product both in ${\mathcal{H}}_r$ and in ${\mathcal{H}}_p$:

$${〈f\left|x\right.〉}_r=B_{r,p}(f,x)={〈{\iota }_{r,p}f\left|x\right.〉}_p,f\in {\mathcal{H}}_r,x\in {\mathcal{H}}_p$$

where ${\iota }_{r,p}:{\mathcal{H}}_r\to {\mathcal{H}}_p$ is a bounded operator in $\mathcal{B}({\mathcal{H}}_r,{\mathcal{H}}_p)$.

Remark 4.

Let $\{{\mathcal{H}}_r;r\in \mathbb{Z}\}$ be the family of the Hilbert spaces of a Hilbert chain. For every $r,p\in \mathbb{Z}$, with $p\ge r$, the maps ${\iota }_{r,p}:{\mathcal{H}}_r\to {\mathcal{H}}_p$ are injective, such that $\parallel {\iota }_{r,p}{x\parallel }_p\le {\parallel x\parallel }_r$, $\forall x\in {\mathcal{H}}_r$, ${\iota }_{r,r}$ are the identities of ${\mathcal{H}}_r$ and ${\iota }_{r,n}={\iota }_{p,n}{\iota }_{r,p}$, $r\le p\le n$. Hence, the family $\{{\mathcal{H}}_r,{\iota }_{r,p},r,p\in \mathbb{Z},$$p\ge r\}$ is a directed contractive system of Hilbert spaces, a notion introduced and studied by one of us (GB) and Trapani in 2011. It produces a space ${\mathcal{D}}^{\times }$ obtained as the inductive limit of the system, and the algebraic inductive limit of the family gives rise to a nested Hilbert space. Because of the order-reversing involution of the set of the indices, the existence of a smaller space $\mathcal{D}$, contained as a dense subspace in every Hilbert space of the family, is not guaranteed.

We will use this in the A-scale framework and extend the notion of Berezanskii canonical isomorphism for each ordered pair of spaces ${\mathcal{H}}_k$ and ${\mathcal{H}}_l$, both $k,l\ne 0$ by defining unitary operators as $I_{k,l}:{\mathcal{H}}_k\to {\mathcal{H}}_l$ by means of fractional powers of the operator A, its closure, and their inverses.

3.3.1. Different Adjoints

Before going forth, we provide some thoughts about the adjoints, as we consider different spaces here, and “the adjoint” depends on which spaces are considered.

Consider a chain of Hilbert spaces as before. Fix any $j,i\in \mathbb{N}\backslash \{0\}$. For $A:{\mathcal{H}}_{+i}\to {\mathcal{H}}_{+j}$, we have already indicated, by $A^{*}$, the Hilbertian adjoint $A^{*}:{\mathcal{H}}_{+j}\to {\mathcal{H}}_{+i}$, i.e.,

$${〈Ax\left|y\right.〉}_{+j}={〈x\left|A^{*}y\right.〉}_{+i},\forall x\in {\mathcal{H}}_{+i},\forall y\in {\mathcal{H}}_{+j}.$$

This adjoint is not always useful, as two Riesz isomorphisms are applied, which is not compatible with a structure where we consider Hilbert spaces included in each other, i.e., ${\mathcal{H}}_{+j}\subseteq {\mathcal{H}}_{+i}\subseteq {\mathcal{H}}_0\subseteq {\mathcal{H}}_{-i}\subseteq {\mathcal{H}}_{-j}$, but distinguished from each other. (Note that even though all Hilbert spaces are isomorphic to each other, it still makes the most sense to treat them differently, e.g., $L^2(\mathbb{R})$ and ${\ell }^2(\mathbb{N})$.) By identifying the dual of ${\mathcal{H}}_{-j}$ with ${\mathcal{H}}_{+j}$, the whole scale would collapse. Therefore, taking $i,j\ge 0$, we now consider another adjoint $A^{★}\in \mathcal{B}({\mathcal{H}}_{-j},{\mathcal{H}}_{-i})$ for $A\in \mathcal{B}({\mathcal{H}}_{+i},{\mathcal{H}}_{+j})$, the “pivot adjoint”, defined as follows:

$${〈\alpha \left|Ax\right.〉}_0={〈A^{★}\alpha \left|x\right.〉}_0\forall \alpha \in {\mathcal{H}}_{-j},x\in {\mathcal{H}}_{+i}.$$

(11)

Here, the number in the circle indicates the subscript of the pivot Hilbert space ${\mathcal{H}}_0$ with respect to that from which the dual is taken. We can, very naturally, define the adjoint for any pivot space ${\mathcal{H}}_p\ne {\mathcal{H}}_0$.

The same construction is possible for $A\in \mathcal{B}({\mathcal{H}}_{-j},{\mathcal{H}}_{-i})$, $\mathcal{B}({\mathcal{H}}_{-j},{\mathcal{H}}_{+i})$ or $\mathcal{B}({\mathcal{H}}_{+i},{\mathcal{H}}_{-j})$.

We highlight that the notion of a pivot adjoint is a generalization of the involuted $A^{†}$ recalled in (2).

Moreover, similar to (4), if $A\in \mathcal{B}({\mathcal{H}}_{+i},{\mathcal{H}}_{+j})$, we have, for $\alpha \in {\mathcal{H}}_{-j},x\in {\mathcal{H}}_{+i}$:

$$\begin{array}{ccc}\hfill {〈\alpha \left|Ax\right.〉}_0& =& {〈I_{-j,+j}\alpha \left|Ax\right.〉}_{+j}={〈A^{*}{I}_{-j,+j}\alpha \left|x\right.〉}_{+i}\hfill \\ & =& ={〈I_{+i,-i}{A}^{*}{I}_{-j,+j}\alpha \left|x\right.〉}_0=\hfill \\ & =& {〈A^{★}\alpha \left|x\right.〉}_0.\hfill \end{array}$$

Therefore, we deduce that:

$$A^{★}={(I_{-i,+i})}^{-1}{A}^{*}{I}_{-j,+j}=I_{+i,-i}{A}^{*}{I}_{-j,+j}$$

(12)

and:

$$\parallel A^{★}\parallel =\parallel A^{*}\parallel =\parallel A\parallel .$$

Remark 5.

In general, if $p,q\in \mathbb{Z}$ and $A\in \mathcal{B}({\mathcal{H}}_p,{\mathcal{H}}_q)$, then $A^{*}\in \mathcal{B}({\mathcal{H}}_q,{\mathcal{H}}_p)$ and:

$$A^{★}=I_{p,-p}{A}^{*}{I}_{-q,q}\in \mathcal{B}({\mathcal{H}}_{-q},{\mathcal{H}}_{-p}).$$

(13)

Remark 6.

Because $A^{★}$ is an adjoint, two properties follow immediately:

1. 

The double pivot adjoint of an operator $A\in \mathcal{B}({\mathcal{H}}_p,{\mathcal{H}}_q)$, $p,q\in \mathbb{Z}$, is:

$$A^{★★}={(A^{★})}^{★}=Aand\parallel A^{★★}\parallel =\parallel A\parallel ;$$

2. 

Let $A\in \mathcal{B}({\mathcal{H}}_0,{\mathcal{H}}_p)$ and $B\in \mathcal{B}({\mathcal{H}}_m,{\mathcal{H}}_0)$, $p,m\in \mathbb{N}$; then ${(AB)}^{★}=B^{★}{A}^{★}.$ Indeed, if $x\in {\mathcal{H}}_m$ and $y\in {\mathcal{H}}_p$, by (11):

$${〈ABx\left|y\right.〉}_0={〈Bx\left|A^{★}y\right.〉}_0={〈x\left|B^{★}{A}^{★}y\right.〉}_0.$$

As a side remark to (12), note that $I_{+i,-i}$ is a unitary operator with respect to the pair $({\mathcal{H}}_{+i},{\mathcal{H}}_{-i})$, but is selfadjoint with respect to ${\mathcal{H}}_0$.

Note that $A^{★}$ also corresponds to the Banach space adjoint of $A:{\mathcal{H}}_{+i}\to {\mathcal{H}}_{+j}$, where the Riesz isomorphism at the pivot space level is considered to be an equality, i.e., ${\mathcal{H}}_0={\mathcal{H}}_0^{\times }$. It maps ${\mathcal{H}}_{-j}$ onto ${\mathcal{H}}_{-i}$.

Remark 7.

Define:

$${\iota }_{0,-i}:={\iota }_{+i,0}^{★}:{\mathcal{H}}_0\to {\mathcal{H}}_{-i};$$

we have $\parallel {\iota }_{0,-i}\parallel \le 1$. As we have seen in (13):

$${\iota }_{0,-i}={(I_{-i,+i})}^{-1}{\iota }_{+i,0}^{*}{I}_{0,0}=I_{+i,-i}{\iota }_{0,+i}.$$

The operator ${\iota }_{0,-i}$ is effectively the inclusion of ${\mathcal{H}}_0$ in ${\mathcal{H}}_{-i}$; indeed, by (8):

$${〈f\left|x\right.〉}_0={〈{\iota }_{0,+i}f\left|x\right.〉}_{+i}={〈I_{+i,-i}{\iota }_{0,+i}f\left|x\right.〉}_0,f\in {\mathcal{H}}_0,x\in {\mathcal{H}}_{+i}.$$

3.3.2. Putting It All Together

Let us go back to the operator ${\iota }_{0,+1}$; it acts continuously from ${\mathcal{H}}_0$ to ${\mathcal{H}}_{+1}$. Since ${\mathcal{H}}_{+1}\subseteq {\mathcal{H}}_0$, this operator may be considered as acting in ${\mathcal{H}}_0$; denote it as the operator $\widehat{I}:{\mathcal{H}}_0\to {\mathcal{H}}_0$. We have:

$$\widehat{I}={\iota }_{+1,0}{\iota }_{0,+1}.$$

(14)

The operator $\widehat{I}$ is continuous with bounds less than or equal to 1, positive and invertible onto $\mathsf{Ran}(\widehat{I})$, with $\mathsf{Ran}(\widehat{I})=\mathsf{Dom}({\widehat{I}}^{-1})$, dense in ${\mathcal{H}}_0$.

It is easy to see that ${\widehat{I}}^{-1}$ is also self-adjoint and positive in ${\mathcal{H}}_0$, (later, it will be clear that $\mathsf{Ran}(\widehat{I})=\mathsf{Dom}({\widehat{I}}^{-1})={\mathcal{H}}_{+2}$, and ${\widehat{I}}^{-1}=I_{+2,0}:{\mathcal{H}}_{+2}\to {\mathcal{H}}_0$; see (15)).

The operator ${\widehat{I}}^{-1}$ is densely defined as an operator in ${\mathcal{H}}_0$, has a closed range, and is one-to-one. Because it has a bounded inverse, it is closed. It is positive and self-adjoint, and we have ${\left({\widehat{I}}^{-1}\right)}^{1/2}={\left({\widehat{I}}^{1/2}\right)}^{-1}=:{\widehat{I}}^{-1/2}$. The properties of this operator can be summarized by:

Theorem 1.

([47], Theorem I.1.1) Consider the operator $F={({\widehat{I}}^{-1})}^{1/2}$ in the space ${\mathcal{H}}_0$. It is a positive self-adjoint operator for which $\mathsf{Dom}(F)={\mathcal{H}}_{+1}$ and $\mathsf{Ran}(F)={\mathcal{H}}_0$. This operator acts isometrically from ${\mathcal{H}}_{+1}$ onto ${\mathcal{H}}_0$:

$${〈x\left|y\right.〉}_{+1}={〈Fx\left|Fy\right.〉}_0(x,y\in {\mathcal{H}}_{+1}).$$

Consider F as an operator acting from ${\mathcal{H}}_0$ to ${\mathcal{H}}_{-1}$ and that forms the closure by continuity; denote this operator by $\mathbf{F}$. $\mathbf{F}$ acts isometrically from the whole ${\mathcal{H}}_0$ onto ${\mathcal{H}}_{-1}$:

$${〈f\left|g\right.〉}_0={〈\mathbf{F}f\left|\mathbf{F}g\right.〉}_{-1}(f,g\in {\mathcal{H}}_0),$$

and, moreover, $I_{+1,-1}=I_{-1,+1}^{-1}=\mathbf{F}F$. The relation:

$${〈f\left|Fx\right.〉}_0={〈\mathbf{F}f\left|x\right.〉}_0(f\in {\mathcal{H}}_0,x\in {\mathcal{H}}_{+1}),$$

holds; therefore, $\mathbf{F}=F^{★}$.

Let us write $B=F^{-1}$ and $\mathbf{B}={\mathbf{F}}^{-1}$.

From the factorization of $I_{-1,+1}$, it follows immediately that:

$$I_{+1,-1}=I_{-1,+1}^{-1}={\mathbf{B}}^{-1}{B}^{-1}=\mathbf{F}F=F^{★}F.$$

Thus, a factorization of $I_{-1,+1}$ is obtained in terms of isometric operators.

Using the Hilbert adjoint, we can write:

$$B=F^{*}\mathrm{and}\mathbf{B}={\mathbf{F}}^{*}.$$

We have the diagram in Figure 1.

There is a well-known connection between infinite chains of Hilbert spaces and positive self-adjoint operators in ${\mathcal{H}}_0$, if ${\mathcal{H}}_0$ is the central space; see Section 2.3.

Remark 8.

Not every infinite chain of Hilbert spaces is a scale; see ([39], p. 161). However (see, e.g., ([47], Theorem I.1.1)), given a chain of Hilbert spaces, there exists a positive self-adjoint operator $A=A^{*}$ on ${\mathcal{H}}_0$, such that the triple ${\mathcal{H}}_{+i}\subset {\mathcal{H}}_0\subset {\mathcal{H}}_{-i}$ of the chain coincides with the “central” part of the A-scale of Hilbert spaces generated by A.

We now proceed as in Section 2.3.

Consider the A-scale of Hilbert spaces where $A=F^2={\widehat{I}}^{-1}$. Since F is self-adjoint, then all its powers $F^n$, $n>0$ exist. For every $n>0$, the domain $\mathsf{Dom}(F^n)$ can be made into a Hilbert space by setting:

$${〈x\left|y\right.〉}_{+n}={〈F^{n}x\left|F^{n}y\right.〉}_0,x,y\in \mathsf{Dom}(F^n).$$

(15)

F is injective; hence, the following norm is induced:

$${\parallel x\parallel }_{+n}={({〈x\left|x\right.〉}_{+n})}^{1/2}={({〈F^{n}x\left|F^{n}x\right.〉}_0)}^{1/2}={\parallel F^{n}x\parallel }_0,x\in \mathsf{Dom}(F^n).$$

Put ${\mathcal{H}}_{+n}=\mathsf{Dom}(F^n)$, $n\ge 0$. As usual, for every $n>0$, we can consider the Hilbert spaces ${\mathcal{H}}_{-n}$ as the conjugate dual of ${\mathcal{H}}_{+n}$, with respect to the inner product of ${\mathcal{H}}_0$. We obtain, like, e.g., in ([37], Example 10.1.1), an A-scale of Hilbert spaces.

We have also that, for $B=F^{-1}$:

$${〈f\left|g\right.〉}_0={〈B^{n}f\left|B^{n}g\right.〉}_{+n},f,g\in {\mathcal{H}}_0.$$

(16)

By:

$${〈f\left|g\right.〉}_0={〈F^{★}f\left|F^{★}g\right.〉}_{-1},f,g\in {\mathcal{H}}_0,$$

we deduce:

$${〈\alpha \left|\beta \right.〉}_{-1}={〈B^{★}\alpha \left|B^{★}\beta \right.〉}_0,\alpha ,\beta \in {\mathcal{H}}_{-1},$$

$${〈x\left|y\right.〉}_{+1}={〈Fx\left|Fy\right.〉}_0={〈F^{★}Fx\left|F^{★}Fy\right.〉}_{-1},\forall x,y\in {\mathcal{H}}_{+1},$$

and:

$${〈\alpha \left|\beta \right.〉}_{-n}={〈{(B^{★})}^n\alpha \left|{(B^{★})}^n\beta \right.〉}_0,\alpha ,\beta \in {\mathcal{H}}_{-n},n>0.$$

Remark 9.

We already know that $I_{+1,-1}=F^{★}F={(B^{★})}^{-1}F$. For $0\le r\le p$, put $I_{p,r}=B^r{F}^p$. Let $p,r<0$, and put $F^p:={(F^{★})}^p={(B^{★})}^{-p}$ and $B^r:={(B^{★})}^r={(F^{★})}^{-r}$. With this convention, whatever $p,r$ are in $\mathbb{Z}$, we can decompose:

$$I_{p,r}=B^r{F}^p:{\mathcal{H}}_p\to {\mathcal{H}}_r.$$

All these operators are unitary because they are products of unitary operators. We highlight, however, that they are not Berezanskii isomorphisms unless $(p-r)/2\in \mathbb{Z}$; in fact, only in this case are ${\mathcal{H}}_p$ and ${\mathcal{H}}_r$ extreme spaces of a rigged Hilbert space. Furthermore, being ${(B^r{F}^p)}^{*}={(F^p)}^{*}{(B^r)}^{*}=B^p{F}^r$, for $0\le r\le p$, by (15) and (16), we have:

$${〈f\left|g\right.〉}_p={〈F^{p}f\left|F^{p}g\right.〉}_0={〈B^r{F}^{p}f\left|B^r{F}^{p}g\right.〉}_r={〈I_{p,r}f\left|I_{p,r}g\right.〉}_r,withf,g\in {\mathcal{H}}_p.$$

Similarly:

$${〈f\left|g\right.〉}_r={〈B^p{F}^{r}f\left|B^p{F}^{r}g\right.〉}_p={〈I_{r,p}f\left|I_{r,p}g\right.〉}_p,withf,g\in {\mathcal{H}}_r.$$

If now $f\in {\mathcal{H}}_p,g\in {\mathcal{H}}_r$:

$$\begin{array}{cc}\hfill {〈I_{p,r}f\left|g\right.〉}_r& ={〈B^r{F}^{p}f\left|g\right.〉}_r={〈F^{p}f\left|F^{r}g\right.〉}_0={〈B^p{F}^{p}f\left|B^p{F}^{r}g\right.〉}_p\hfill \\ & ={〈f\left|B^p{F}^{r}g\right.〉}_p={〈f\left|I_{r,p}g\right.〉}_p\hfill \end{array}.$$

Hence, predictably, $I_{r,p}=I_{p,r}^{*}$.

With the due changes, the same results are obtained for any $p,r\in \mathbb{Z}$.

3.4. Generator of a Scale and Shifting of the Central Space

Can we shift the central space? That is, how does the dual of ${\mathcal{H}}_{n_0+n}$ look, with respect to ${\mathcal{H}}_{n_0}$?

Corollary 1.

Let $r<p$ and let ${{\mathcal{H}}_p^{\times }}^{(r)}$ be the dual of ${\mathcal{H}}_p$ with respect to the topology of ${\mathcal{H}}_r$ (i.e., consider the triplet ${\mathcal{H}}_p\subseteq {\mathcal{H}}_r\subseteq {{\mathcal{H}}_p^{\times }}^{(r)}$).

Then, ${{\mathcal{H}}_p^{\times }}^{(r)}={\mathcal{H}}_{2r-p}$.

Proof. 

Let us consider an A-scale Hilbert space with $A=({\widehat{I}}^{-1})$, and with $\widehat{I}$ defined as in (14), so that, by the first invariant principle of A-scales (see Section 3.1), for $k=p-r$, the triple:

$${\mathcal{H}}_{r+k}={\mathcal{H}}_p\subseteq {\mathcal{H}}_r\subseteq {\mathcal{H}}_{2r-p}={\mathcal{H}}_{r-k},$$

forms a chain of Hilbert scale. □

In other words: the dual of ${\mathcal{H}}_{n_0+n}$, with respect to ${\mathcal{H}}_{n_0}$, is ${\mathcal{H}}_{n_0-n}$.

Remark 10.

Clearly, if $r<p$, then the space ${\mathcal{H}}_r$ can be considered the dual space of ${\mathcal{H}}_p$ with respect to some space ${\mathcal{H}}_{n_0}$ with ${\mathcal{H}}_p\subseteq {\mathcal{H}}_{n_0}\subseteq {\mathcal{H}}_r$, if and only if $p+r$ is an even number. If this is the case, $n_0=\frac{p+r}{2}$.

Now, for a fixed A-scale, we wonder how the operator A changes if we fix another Hilbert space of the scale as the “central” space, for example, ${\mathcal{H}}_k$, $k\in \mathbb{Z}$. Following [46], the answer to this question is given by using what has been called the second invariance principle of the A-scale. Indeed, it results that A is unitarily equivalent to its image under any “shift” along the A-scale.

Just to fix some ideas, let $k\ge 2$, and consider the A-scale:

$$\dots \subseteq {\mathcal{H}}_{2+k}\subseteq \dots \subseteq {\mathcal{H}}_{+k}\subseteq \dots \subseteq {\mathcal{H}}_2\subseteq \dots \subseteq {\mathcal{H}}_{2-k}\subseteq \dots \subseteq {\mathcal{H}}_{-k}\subseteq \dots ,$$

and the operators:

$$A_{+k}:=I_{2+k,k}:{\mathcal{H}}_{2+k}\to {\mathcal{H}}_{+k}and{A}_{-k}:=I_{2-k,-k}:{\mathcal{H}}_{2-k}\to {\mathcal{H}}_{-k},$$

with $I_{p,r}$ defined as before (in particular, $A=A_0=I_{+2,0}$). Then, it is easy to see that [46]$A_{+k}=A_{{}_{{|}_{{\mathcal{H}}_{2+k}}}}$, i.e., it is the restriction of A to ${\mathcal{H}}_{2+k}$; hence, $A_{+k}$ is self-adjoint in ${\mathcal{H}}_{2+k}$. The operator $A_{-k}$ is self-adjoint in ${\mathcal{H}}_{2-k}$, and it results in $A_{-k}={\overline{A}}^{{\parallel ·\parallel }_{-k}}$, the closure of A in ${\mathcal{H}}_{-k}$. Both operators $A_{\pm k}$ and $k\in \mathbb{N}$ are unitary images of the original operator A on ${\mathcal{H}}_0$; in fact:

$$A_{+k}=I_{0,k}A{I}_{2+k,2}=B^k{F}^0{B}^0{F}^2{B}^2{F}^{2+k}=B^k{F}^{2+k}$$

and:

$$A_{-k}=I_{0,-k}A{I}_{2-k,2}=B^{-k}{F}^0{B}^0{F}^2{B}^2{F}^{2-k}=B^{-k}{F}^{2-k},$$

i.e., for the sake of brevity, for $p\in \mathbb{Z}$:

$$A_p=B^p{F}^{2+p}=I_{2+p,p}.$$

We remark that the operator A is essentially self-adjoint in each space ${\mathcal{H}}_{-k}$, $k\ge 1$.

4. Main Results: Frame-Related Properties on Hilbert Scales

In this section, we will introduce our considerations and results on how certain frame-related properties of a certain sequence in one of the spaces propagate to other spaces in a scale. Some new results are merged to known ones (or to simply considerations deriving from known results in different frameworks) to gain a full picture about each property we have considered.

We will look at a scale of Hilbert space; let us fix:

$${\mathcal{H}}_m\subseteq {\mathcal{H}}_p\subseteq {\mathcal{H}}_r,$$

i.e., $r\le p\le m$.

We look at a sequence $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$, which has a property in some of the other spaces, and investigate how these properties “spread” to the other spaces: if it is complete, forms a Bessel sequence, a frame, a basis, has a Riesz property, etc., for a ${\mathcal{H}}_r$ (or ${\mathcal{H}}_p$), what can we say about this sequence in the other spaces?

If we allow the sequences to be changed, the results are trivial consequences of the following straightforward generalization of ([2], Cor. 5.3.4):

Corollary 2.

Given two Hilbert spaces, $\mathcal{H}$ and $\mathcal{K}$, if $\psi =({\psi }_k)$ is a frame for $\mathcal{H}$ with frame bounds $A,B$, and if $U:\mathcal{H}\to \mathcal{K}$ is a unitary operator, then $(U{\psi }_k)$ is a frame for $\mathcal{K}$ with the same frame bounds.

Remark 11.

If we have a unitary operator between two Hilbert spaces, all the frame properties naturally transfer from one Hilbert space to the other.

In the sequel, we will use the unitary operators $I_{r,p}$, defined as in Remark 9, and obtain easy results for $\left(I_{r,p}{\psi }_k\right)$. See Corollary 3.

Therefore, the results in the following subsections regarding the properties of a sequence $\psi$ in a space of the scale that is transferred to sequences as $I_{r,p}\psi$, with $I_{r,p}$ being a unitary operator, are easily obtained by Remark 11.

We need some preparation before that.

4.1. Completeness

Lemma 1.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$. Then, the following statements hold:

(i) 

If $({\psi }_k)$ is complete in ${\mathcal{H}}_p$, then it is also complete in ${\mathcal{H}}_r$ for $r\le p\le m$;

(ii) 

If $({\psi }_k)$ is complete in ${\mathcal{H}}_r$$r\le m$, then $(I_{r,p}{\psi }_k)$ is a complete sequence in ${\mathcal{H}}_p$ for any p.

Proof. 

(i) Since ${\mathcal{H}}_p\subseteq {\mathcal{H}}_r$ densely, then for each $f\in {\mathcal{H}}_r$ and $ϵ>0$, there is an element $x\in {\mathcal{H}}_p$ with ${\parallel f-x\parallel }_r<ϵ/2$. Now, let $({\psi }_k)\subseteq {\mathcal{H}}_m$ be a complete sequence in ${\mathcal{H}}_p$. Then, there exists $y\in \mathsf{span}({\psi }_k)$, such that ${\parallel x-y\parallel }_p<ϵ/2$. So:

$${\parallel f-y\parallel }_r\le {\parallel f-x\parallel }_r{+\parallel x-y\parallel }_r\le {\parallel f-x\parallel }_r+{\parallel x-y\parallel }_p<ϵ.$$

It follows that $\psi =({\psi }_k)$ is a complete sequence in ${\mathcal{H}}_r$ for $r\le p\le m$.

(ii) Trivial by Remark 11. □

Later, in Lemma 9, we will see that the converse of Lemma 1 $(i)$ is also true.

4.2. Unbounded Frame-Related Operators on Hilbert Chains

Here, we fix the notation for some frame-related operators for a sequence $\psi \subset {\mathcal{H}}_p$. In Section 4.3 and Section 4.4, we study how to write the correspondent operators, respectively, for the sequence $I_{p,r}\psi \subset {\mathcal{H}}_r$$r,p\in \mathbb{Z}$ and, much more interestingly, simply for $\psi$, considered as a sequence in ${\mathcal{H}}_r$. These results will let us reach our goal to understand (if and) how some frame-related properties of a sequence $\psi$ in a Hilbert space spread on the whole scale of Hilbert spaces.

Let us consider an arbitrary sequence $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m\subseteq {\mathcal{H}}_p$ and, as in [43], define the analysis operator $C_{\psi }^p:\mathsf{Dom}(C_{\psi }^p)\subseteq {\mathcal{H}}_p\to {\ell }^2$ of $({\psi }_k)$ by:

$$\mathsf{Dom}(C_{\psi }^p)=\left\{f\in {\mathcal{H}}_p:\sum _k{|{〈f\left|{\psi }_k\right.〉}_p|}^2<\infty \right\}$$

$$C_{\psi }^{p}f:=({〈f\left|{\psi }_k\right.〉}_p),\forall f\in \mathsf{Dom}(C_{\psi }^p).$$

In an analogous way, we can define the synthesis operator:

$$D_{\psi }^p:\mathsf{Dom}(D_{\psi }^p)\subseteq {\ell }^2\to {\mathcal{H}}_p$$

associated with the sequence $\psi$ by:

$$\mathsf{Dom}(D_{\psi }^p)=\left\{c=(c_k)\in {\ell }^2:\sum _k{c}_k{\psi }_{k}convergesin{\mathcal{H}}_p\right\}$$

$$D_{\psi }^{p}c=\sum _k{c}_k{\psi }_k,\forall c\in \mathsf{Dom}(D_{\psi }^p).$$

As it is known, $\mathsf{Dom}(D_{\psi }^p)$ is dense in ${\ell }^2$, since it contains the finite sequences which form a dense subset of ${\ell }^2$ and $C_{\psi }^p={(D_{\psi }^p)}^{*}$; hence, $C_{\psi }^p$ is closed.

Clearly, we have, for $r\le p$, that:

$$\mathsf{Dom}{D}_{\psi }^p\subseteq \mathsf{Dom}{D}_{\psi }^r,\mathsf{Ran}{D}_{\psi }^p\subseteq \mathsf{Ran}{D}_{\psi }^r$$

(17)

$$ker{D}_{\psi }^p\subseteq ker{D}_{\psi }^r\mathrm{all}\mathrm{inclusions}\mathrm{are}\mathrm{dense}.$$

Clearly, $D_{\psi }^p\subset D_{\psi }^r$, since their domains are such that $\mathsf{Dom}{D}_{\psi }^p\subseteq \mathsf{Dom}{D}_{\psi }^r$ and $D_{\psi }^{p}c=D_{\psi }^{r}c$ for every $c\in \mathsf{Dom}{D}_{\psi }^p$. Then, if we look at $D_{\psi }^p$ as an operator into a subspace of ${\mathcal{H}}_r$, we can say that $C_{\psi }^r\subset {(D_{\psi }^p)}_r^{*}$, where ${(D_{\psi }^p)}_r^{*}$ is the adjoint of $D_{\psi }^p$ as an operator from ${\ell }^2$ into ${\mathcal{H}}_r$.

Furthermore, let us consider $D_{\psi }^{00}$, defined as an operator on $c_{00}$ the space of finite sequences. By the above definition, we have that $D_{\psi }^p$ is the closure of $D_{\psi }^{00}$ for any $p\ge m$. So, $D_{\psi }^p={\overline{D_{\psi }^{00}}}^{{\mathcal{H}}_p}$. Let us now use that $r\le p$, and so ${\parallel ·\parallel }_r\le {\parallel ·\parallel }_p$, and, therefore, $D_{\psi }^r={\overline{D_{\psi }^{00}}}^{{\mathcal{H}}_r}={\overline{\left({\overline{D_{\psi }^{00}}}^{{\mathcal{H}}_p}\right)}}^{{\mathcal{H}}_r}={\overline{D_{\psi }^p}}^{{\mathcal{H}}_r}$. So, in summary:

$$D_{\psi }^r={\overline{D_{\psi }^p}}^{{\mathcal{H}}_r},forr\le p.$$

Let us also introduce the combination of those operators. Consider the “frame operator” $S_{\psi }^p\mathsf{Dom}(S_{\psi }^p)\subseteq {\mathcal{H}}_p\to {\mathcal{H}}_p$ of $\psi$:

$$S_{\psi }^{p}f:=\sum _{k\in \mathbb{N}}{〈f\left|{\psi }_k\right.〉}_p{\psi }_k$$

where

$$\mathsf{Dom}(S_{\psi }^p)=\{f\in {\mathcal{H}}_p:\sum _{k\in \mathbb{N}}{〈f\left|{\psi }_k\right.〉}_p{\psi }_k \mathrm{converges} \mathrm{in} {\mathcal{H}}_p\};$$

and the Gram operator $G_{\psi }^p:\mathsf{Dom}(G_{\psi }^p)\subseteq {\ell }^2\to {\ell }^2,$ withL

$$G_{\psi }^p{(c_k)}_k:={\left(\sum _{l\in \mathbb{N}}{(G_{\psi }^p)}_{k,l}{c}_l\right)}_k,$$

where:

$$\begin{array}{ccc}\hfill \mathsf{Dom}(G_{\psi }^p)=\{{(c_k)}_k\in {\ell }^2:& & \sum _{l\in \mathbb{N}}{(G_{\psi }^p)}_{k,l}{c}_l \mathrm{converges} \forall k\in \mathbb{N} \mathrm{and}\hfill \\ & & {\left(\sum _{l\in \mathbb{N}}{(G_{\psi }^p)}_{k,l}{c}_l\right)}_k\in {\ell }^2\}\hfill \end{array}$$

and the Gram matrix ${({(G_{\psi }^p)}_{k,l})}_{k,l}$ is defined by ${(G_{\psi }^p)}_{k,l}={〈{\psi }_l\left|{\psi }_k\right.〉}_p$, $k,l\in \mathbb{N}$.

4.3. Frame Properties of $I_{r,p}$$\psi$

Once fixed, a sequence $\psi$ with some property in a certain Hilbert space ${\mathcal{H}}_p$ of a scale of Hilbert spaces, we can use the frame-related operators just defined to study the properties of its image by unitary operators $I_{p,r}$ introduced in Remark 9.

Lemma 2.

For a given $p\in \mathbb{Z}$, let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_p$ be an arbitrary sequence. Then, for every $r\in \mathbb{Z}$, $C_{I_{p,r}(\psi )}^r=C_{\psi }^p{I}_{r,p}$ and $C_{\psi }^p=C_{I_{p,r}(\psi )}^r{I}_{p,r}$.

Proof. 

We have:

$$\begin{array}{cc}\hfill \mathsf{Dom}(C_{\psi }^p{I}_{r,p})& =\{f\in \mathsf{Dom}(I_{r,p}):I_{r,p}f\in \mathsf{Dom}{C}_{\psi }^p\}\hfill \\ \hfill & =\{f\in {\mathcal{H}}_r:({\langle I_{r,p}f,{\psi }_k\rangle }_p)\in {\ell }^2\}\hfill \\ \hfill & =\{f\in {\mathcal{H}}_r:({\langle f,I_{p,r}{\psi }_k\rangle }_r)\in {\ell }^2\}\hfill \\ \hfill & =\mathsf{Dom}(C_{I_{p,r}(\psi )}^r).\hfill \end{array}$$

By the same argument, the operators also are the same.

The other result is obtained by multiplying the operator $I_{p,r}$, the inverse of $I_{r,p}$, on the right in the equality $C_{I_{p,r}(\psi )}^r=C_{\psi }^p{I}_{r,p}$. □

An analoguous result is true for the other frame-related operators. We start with a result for the synthesis operator:

Lemma 3.

For a given $p\in \mathbb{Z}$, let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_p$ be an arbitrary sequence. Then, for every $r\in \mathbb{Z}$, $D_{I_{p,r}(\psi )}^r=I_{p,r}{D}_{\psi }^p$ and $D_{\psi }^p=I_{r,p}{D}_{I_{p,r}(\psi )}^r$.

Proof. 

If $c\in \mathsf{Dom}(D_{I_{p,r}(\psi )}^r)\subseteq {\ell }^2$, then there exists $f\in {\mathcal{H}}_r$ such that $D_{I_{p,r}(\psi )}^{r}c=f$, i.e., for every $\epsilon >0$, there exists $n_{\epsilon }\in \mathbb{N}$ such that for every $n\ge n_{\epsilon }$:

$$\begin{array}{ccc}\hfill {∥\sum _{k=1}^n{c}_k{I}_{p,r}{\psi }_k-f∥}_r& =& {∥I_{r,p}\sum _{k=1}^n{c}_k{I}_{p,r}{\psi }_k-I_{r,p}f∥}_p\hfill \\ & =& {∥\sum _{k=1}^n{c}_k{\psi }_k-I_{r,p}f∥}_p<\epsilon .\hfill \end{array}$$

Hence, $D_{\psi }^{p}c=I_{r,p}f$, $\mathsf{Dom}(D_{I_{p,r}(\psi )}^r)=\mathsf{Dom}(I_{p,r}{D}_{\psi }^p)$, and $D_{I_{p,r}(\psi )}^r=I_{p,r}{D}_{\psi }^p$. The other result is obtained by multiplying the operator $I_{r,p}$, the inverse of $I_{p,r}$, on the left in the equality $D_{I_{p,r}(\psi )}^r=I_{p,r}{D}_{\psi }^p$. □

Lemma 4.

For a given $p\in \mathbb{Z}$, let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_p$ be an arbitrary sequence. Then, for every $r\in \mathbb{Z}$, $S_{I_{r,p}(\psi )}^p=I_{r,p}{S}_{\psi }^r{I}_{p,r}$.

Proof. 

It is a consequence of the previous Lemmata 2 and 3, and of $(iii)$ in ([43], Proposition 3.3). □

Lemma 5.

For a given $p\in \mathbb{Z}$, let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_p$ be an arbitrary sequence. Then, $C_{\psi }^p{D}_{\psi }^p\subseteq G_{\psi }^p$ and $G_{\psi }^p=G_{I_{p,r}(\psi )}^r$ for every $r\in \mathbb{Z}$.

Proof. 

By $(iv)$ in ([43] Proposition 3.3) we have that $C_{\psi }^p{D}_{\psi }^p\subseteq G_{\psi }^p$, for every $p\le n$. Now, recall that ${〈{\psi }_l\left|{\psi }_k\right.〉}_p={〈I_{p,r}{\psi }_l\left|I_{p,r}{\psi }_k\right.〉}_r$; we have:

$$\begin{array}{ccc}\hfill \mathsf{Dom}(G_{\psi }^p)& =& \left\{c\in {\ell }^2:\sum _{l\in \mathbb{N}}{〈{\psi }_l\left|{\psi }_k\right.〉}_p{c}_l \mathrm{converges} \forall k\in \mathbb{N} \mathrm{and}\right.\hfill \\ & & \left.\sum _k{\left|\sum _{l\in \mathbb{N}}{〈{\psi }_l\left|{\psi }_k\right.〉}_p{c}_l\right|}^2<\infty \right\}\hfill \\ & =& \left\{c\in {\ell }^2:\sum _{l\in \mathbb{N}}{〈I_{p,r}{\psi }_l\left|I_{p,r}{\psi }_k\right.〉}_r{c}_l \mathrm{converges} \forall k\in \mathbb{N} \mathrm{and}\right.\hfill \\ & & \left.\sum _k{\left|\sum _{l\in \mathbb{N}}{〈I_{p,r}{\psi }_l\left|I_{p,r}{\psi }_k\right.〉}_r{c}_l\right|}^2<\infty \right\}=\mathsf{Dom}(G_{I_{p,r}(\psi )}^r).\hfill \end{array}$$

□

Note that all the above results lead to statements saying that if $\psi$ is a frame (Bessel sequence, Riesz basis, …) for some Hilbert space ${\mathcal{H}}_r$, $I_{r,p}\psi$ is one for ${\mathcal{H}}_p$. They all are trivial consequences of Remark 11.

Corollary 3.

For a given $p\in \mathbb{Z}$, let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_p$ be an arbitrary sequence. Then, for any $r\in \mathbb{Z}$ the following is true:

1. 

If $({\psi }_k)$ is a Bessel sequence in ${\mathcal{H}}_p$, then $(I_{p,r}{\psi }_k)$ is a Bessel sequence in ${\mathcal{H}}_r$;

2. 

If $({\psi }_k)$ is a semi-frame in ${\mathcal{H}}_p$, then $(I_{p,r}{\psi }_k)$ is a semi-frame in ${\mathcal{H}}_r$ with the same bounds;

3. 

If $({\psi }_k)$ is a frame in ${\mathcal{H}}_p$, then $(I_{p,r}{\psi }_k)$ is a frame in ${\mathcal{H}}_r$ with the same bounds;

4. 

If $({\psi }_k)$ and $({\varphi }_k)\subset {\mathcal{H}}_p$ are a reproducing pair, then $(I_{p,r}{\varphi }_k)$ and $(I_{p,r}{\psi }_k)$ are a reproducing pair in ${\mathcal{H}}_r$ with the same bounds;

5. 

If $({\varphi }_k)\subset {\mathcal{H}}_p$ is a dual sequence of $({\psi }_k)$ in ${\mathcal{H}}_p$, then $(I_{p,r}{\varphi }_k)$ is a dual sequence of $(I_{p,r}{\psi }_k)$ in ${\mathcal{H}}_r$;

6. 

If $({\psi }_k)$ is an orthonormal basis of ${\mathcal{H}}_p$, then $(I_{p,r}{\psi }_k)$ is an orthonormal basis of ${\mathcal{H}}_r$;

7. 

If $({\psi }_k)$ is a Riesz basis of ${\mathcal{H}}_p$ and $T\in \mathcal{B}({\mathcal{H}}_p)$ is the bijective operator such that $T{e}_k={\psi }_k$, for every k with $\{e_k\}$, is an orthonormal basis of ${\mathcal{H}}_p$, then $(I_{p,r}{T}^{-1}{\psi }_k)$ is an orthonormal basis of ${\mathcal{H}}_r$;

8. 

If $({\psi }_k)$ is a Riesz basis of ${\mathcal{H}}_p$, then $(I_{p,r}{\psi }_k)$ is a Riesz basis of ${\mathcal{H}}_r$ with the same bounds.

On the other hand, if $p<r$, then $\psi$ is also a sequence in ${\mathcal{H}}_p$. So, in addition to looking at ${〈f,I_{r,p}{\psi }_k〉}_p$, we can also look at ${〈f,{\psi }_k〉}_p$. This is carried out in the next section.

4.4. Frame-Related Operators for the Original Sequence $\psi$

Now, we study the properties which are preserved if we look at a sequence $\psi \subset {\mathcal{H}}_p$, with certain properties, as a sequence in another space of the scale, i.e., what happens if we do not apply the unitary operators $I_{p,r}$ to $\psi$; we still make use of frame-related operators defined before.

Lemma 6.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ be an arbitrary sequence. Then, for every $r\le p\le m$:

$$C_{\psi }^r=C_{\psi }^p{\iota }_{r,p}.$$

(18)

where ${\iota }_{r,p}$ is defined, as in (9).

Proof. 

We have:

$${〈f,{\psi }_k〉}_r={〈f,{\iota }_{p,r}{\psi }_k〉}_r={〈{\iota }_{r,p}f,{\psi }_k〉}_p$$

and:

$$\begin{array}{cc}\hfill \mathsf{Dom}(C_{\psi }^p{\iota }_{r,p})& =\{f\in \mathsf{Dom}({\iota }_{r,p});{\iota }_{r,p}f\in \mathsf{Dom}{C}_{\psi }^p\}\hfill \\ \hfill & =\{f\in {\mathcal{H}}_r;({\langle {\iota }_{r,p}f,{\psi }_k\rangle }_p)\in {\ell }^2\}\hfill \\ \hfill & =\{f\in {\mathcal{H}}_r;({\langle f,{\psi }_k\rangle }_r)\in {\ell }^2\}\hfill \\ \hfill & =\mathsf{Dom}(C_{\psi }^r).\hfill \end{array}$$

□

In consequence, we have:

Lemma 7.

If $\psi \subset {\mathcal{H}}_m$ and ψ is a Bessel sequence for ${\mathcal{H}}_p$, then, for $r\le p\le m$, ψ is a Bessel sequence for ${\mathcal{H}}_r$ with the same bound.

Proof. 

By ([2], Cor. 3.2.4 and Theor. 3.2.3), $\psi$ is a Bessel sequence in ${\mathcal{H}}_p$ if and only if $\mathsf{Dom}{D}_{\psi }^p={\ell }^2$. By (17), $\mathsf{Dom}{D}_{\psi }^p\subseteq \mathsf{Dom}{D}_{\psi }^r$; this is true if and only if $\psi$ is also a Bessel sequence for ${\mathcal{H}}_r$.

Furthermore, we have that $\parallel C_{\psi }^r\parallel \le \parallel C_{\psi }^p\parallel$ by (18). □

By ([42], Lemma 3.2), $\psi \subset {\mathcal{H}}_m$ is an upper semi-frame for ${\mathcal{H}}_p$, $p<m$, if and only if it is a total Bessel sequence for ${\mathcal{H}}_p$. Then, putting together Lemma 7 and Lemma 1$(i)$, we obtain:

Lemma 8.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ and $r\le p\le m$. If ψ is an upper semi-frame for ${\mathcal{H}}_p$, then ψ is an upper semi-frame for ${\mathcal{H}}_r$ with the same bound.

Let us now note that ${\iota }_{r,p}^{-1}$ is a densely defined, bijective operator which is not bounded. It is “never” bounded, in the sense that if it were bounded, the involved norms would be equivalent and the whole scale of Hilbert spaces would collapse; however, we can use it to show:

Lemma 9.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ be an arbitrary sequence. Then, for every $r\le p\le m$:

$$C_{\psi }^p=C_{\psi }^r{\iota }_{r,p}^{-1}\mathrm{on}\mathsf{Dom}(C_{\psi }^p)$$

(19)

Therefore, ${{\iota }_{r,p}}_{{}_{{|}_{\mathsf{Dom}(C_{\psi }^r)}}}$ is a bijective operator from $\mathsf{Dom}(C_{\psi }^r)$ onto $\mathsf{Dom}(C_{\psi }^p)$.

Furthermore, if $\psi \subset {\mathcal{H}}_m$ and ψ is complete for ${\mathcal{H}}_r$, then if $r\le p\le m$, then ψ is complete for ${\mathcal{H}}_p$.

Proof. 

The first statement is a direct consequence of (18).

For the converse of Lemma 1 (i), we use ([43], Prop.4.1(g)): $\psi$ is complete in ${\mathcal{H}}_r$ if and only if $C_{\psi }^r$ is injective, and since ${\iota }_{r,p}^{-1}$ is injective, this implies that $C_{\psi }^p$ is injective too, which is equivalent to $\psi$ being complete in ${\mathcal{H}}_p$. □

By Lemma 7, we know that a Bessel sequence in ${\mathcal{H}}_p$ is also one in ${\mathcal{H}}_r$ for $r\le p$. We can show an opposite direction for lower semi-frames.

Lemma 10.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ be a lower semi-frame for ${\mathcal{H}}_r$; then, it is also a lower semi-frame for ${\mathcal{H}}_p$ for every $r\le p\le m$ with the same lower bound.

Proof. 

A sequence is a lower semi-frame if and only if the analysis operator is boundedly invertible. By (19), we have that ${C_{\psi }^p}^{-1}={\iota }_{r,p}{C_{\psi }^r}^{-1}$.

Moreover, $\parallel {C_{\psi }^p}^{-1}\parallel \le \parallel {C_{\psi }^r}^{-1}\parallel$. □

4.4.1. Frames

If we have a frame $\psi \subset {\mathcal{H}}_p$ at hand, by combining Lemmata 8 and 10, we obtain:

Corollary 4.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ be a frame for ${\mathcal{H}}_r$; then, it is an upper semi-frame for ${\mathcal{H}}_p$, for every $r\le p\le m$, and a lower semi-frame for ${\mathcal{H}}_q$, for every $q\le r\le m$.

4.4.2. Duality

The sequence $\psi =({\psi }_k)\subset {\mathcal{H}}_p$ is a lower semi-frame for ${\mathcal{H}}_p$ if and only if [49] there exists a Bessel sequence $\varphi =({\varphi }_k)\subset {\mathcal{H}}_p$, such that:

$$f=\sum _k{〈f\left|{\psi }_k\right.〉}_p{\varphi }_k=D_{\varphi }^p{C}_{\psi }^p(f),\forall f\in \mathsf{Dom}(C_{\psi }^p).$$

(20)

Let $\psi \subseteq {\mathcal{H}}_m$ be a lower semi-frame for ${\mathcal{H}}_r$, $r\le m$; then, by Lemma 10, it is one in ${\mathcal{H}}_m$. Hence, there exists a dual sequence $\varphi \subset {\mathcal{H}}_m$, which is Bessel in ${\mathcal{H}}_m$ and, therefore, also in all spaces ${\mathcal{H}}_r$, $r\le m$. By Assumption (20), it is valid on $\mathsf{Dom}(C_{\psi }^m)$.

Now, let $f\in \mathsf{Dom}(C_{\psi }^p)$; then, by Lemma 10, (20) converges for all p, with $r\le p\le m$. Consider $g={\iota }_{p,m}f$; then, $g\in \mathsf{Dom}(C_{\psi }^m)$:

$$g=\sum _k{〈g\left|{\psi }_k\right.〉}_m{\varphi }_k=\sum _k{〈{\iota }_{p,m}{\iota }_{p,m}^{-1}g\left|{\psi }_k\right.〉}_m{\varphi }_k=\sum _k{〈{\iota }_{p,m}^{-1}g\left|{\iota }_{m,p}{\psi }_k\right.〉}_p{\varphi }_k=$$

$$=\sum _k{〈{\iota }_{p,m}^{-1}g\left|{\psi }_k\right.〉}_p{\varphi }_k=\sum _k{〈f\left|{\psi }_k\right.〉}_p{\varphi }_k.$$

Furthermore:

$$f={\iota }_{p,m}^{-1}g={\iota }_{p,m}^{-1}\sum _k{〈f\left|{\psi }_k\right.〉}_p{\varphi }_k.$$

So, in summary, this shows:

Proposition 1.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ be a lower semi-frame for ${\mathcal{H}}_r$; then, there exists a Bessel sequence $\varphi \subseteq {\mathcal{H}}_m$ such that:

$$f={\iota }_{p,m}^{-1}\sum _k{〈f\left|{\psi }_k\right.〉}_p{\varphi }_k,\forall f\in \mathsf{Dom}(C_{\psi }^p)\subseteq {\mathcal{H}}_p.$$

for all $r\le p\le m$.

4.4.3. A Negative Result

In Corollary 4, we have proved that if $\psi \subset {\mathcal{H}}_p$, then only a part of its properties propagates if we consider it as a sequence in another space of the scale. In fact, here we prove that a sequence can never be a frame for both of the different Hilbert spaces in a scale.

Proposition 2.

Let $\psi =({\psi }_k)\subseteq {\mathcal{H}}_m$ be a frame for ${\mathcal{H}}_p$, and one for ${\mathcal{H}}_q$, for every $q\le p\le m$. Then, the norms are equivalent, and so ${\mathcal{H}}_q={\mathcal{H}}_r={\mathcal{H}}_p$ for $q\le r\le p$.

Proof. 

By (19), $C_{\psi }^p=C_{\psi }^q{\iota }_{q,p}^{-1}$. As $\psi$ is a frame for ${\mathcal{H}}_q$, we have that ${\iota }_{q,p}^{-1}={(S_{\psi }^q)}^{-1}{D}_{\psi }^q{C}_{\psi }^p$, and it is, therefore, bounded. □

Remark 12.

In particular, this means that if two Hilbert spaces, one contained within the other one, do not coincide, a sequence canneverbe a frame for both of them.

Remark 13.

For this statement, it is important that we have considered Hilbert spaces and (standard) frames with the sequence space ${\ell }^2$. If we consider Banach spaces, associated to a weighted ${\ell }^p$ space [24] or Hilbert spaces with weighted ${\ell }^2$ sequence spaces [8,28], this result does not hold. Quite the opposite, e.g., for localized frames ([33], Theorem 1), one can show that a frame on the pivot space ${\mathcal{H}}_0$ is also a frame for the other (Banach) spaces ${\mathcal{H}}_q$.

5. Conclusions and Outlook

In conclusion, we have seen that, if we use a canonical isomorphism between two spaces of a scale of Hilbert spaces, all the frame-like properties of a sequence in a space are preserved by the image of the sequence in the other space of the scale. In contrast, not all the properties of a sequence in a space are maintained if we consider it as a sequence in another Hilbert space of a fixed scale. Studying the relationships between the frame-related operators for the same sequence as a sequence in different Hilbert spaces of the scale, we have observed that some properties are kept only in the spaces of the scale where other ones are, and not anywhere else. For example, the upper semi-frame property is preserved in larger spaces, unlike the lower one, which is maintained in smaller ones; on the contrary, a sequence can not be a frame for both of the different Hilbert spaces of a certain scale of Hilbert spaces.

As mentioned already in the Introduction, frames for scales of spaces find applications in the discretization of operators (as in [35,36]). This connection could be further investigated, similar to the approach in [9,50], but this time for a completely unstructured scale of spaces. A next planned step is to generalize the concept of Gelfand frames [8] to our setting. Furthermore, we will work on generalizing the concept of operator quantization from the Gabor setting [51] to our very general approach.