A Comparative Study of Models for Heat Transfer in Bidisperse Gas–Solid Systems via CFD–DEM Simulations
Abstract
:1. Introduction
2. Numerical Method
2.1. Gas-Phase Modeling
2.2. Discrete Particle Phase
3. Results and Discussion
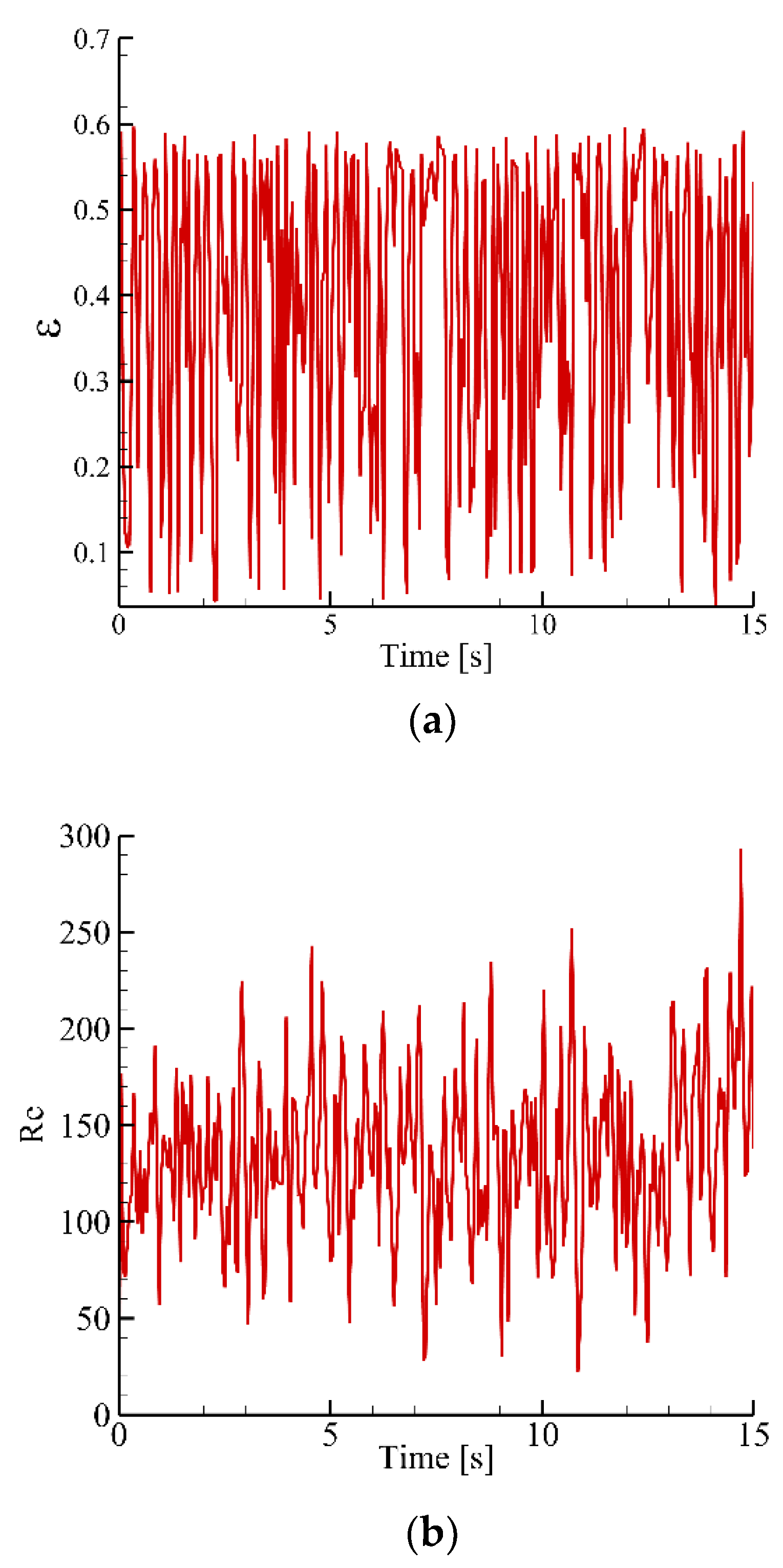
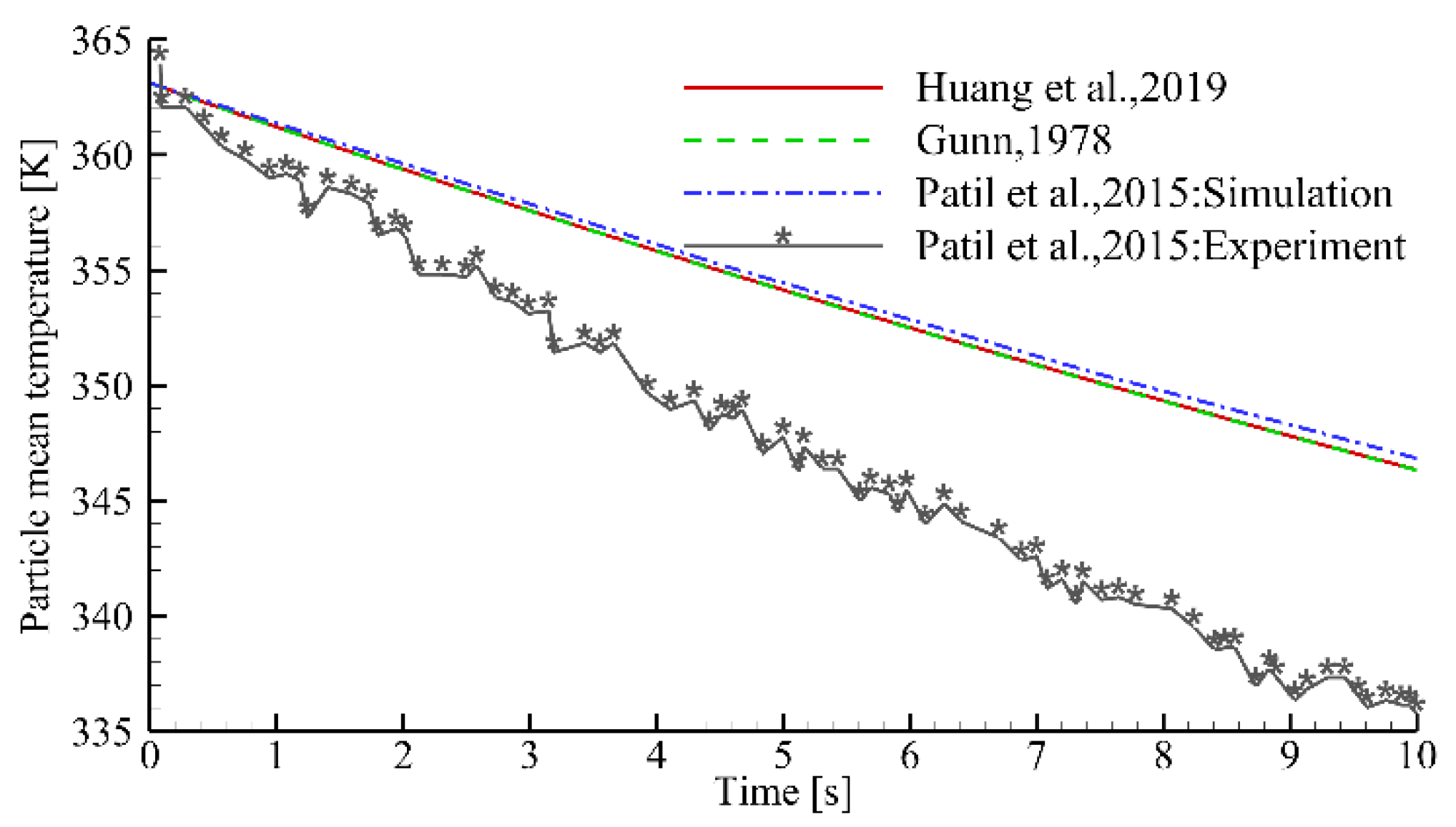
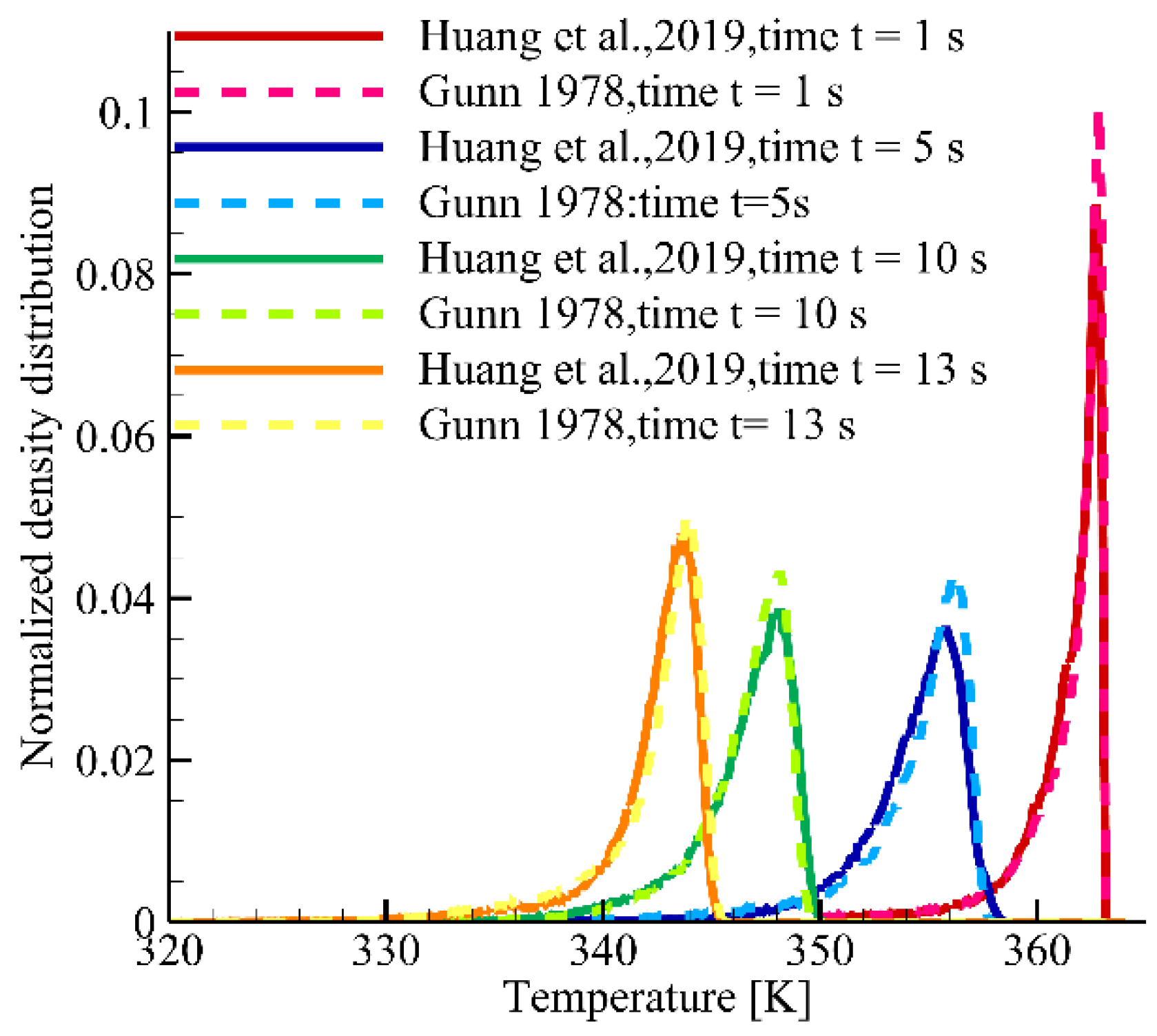
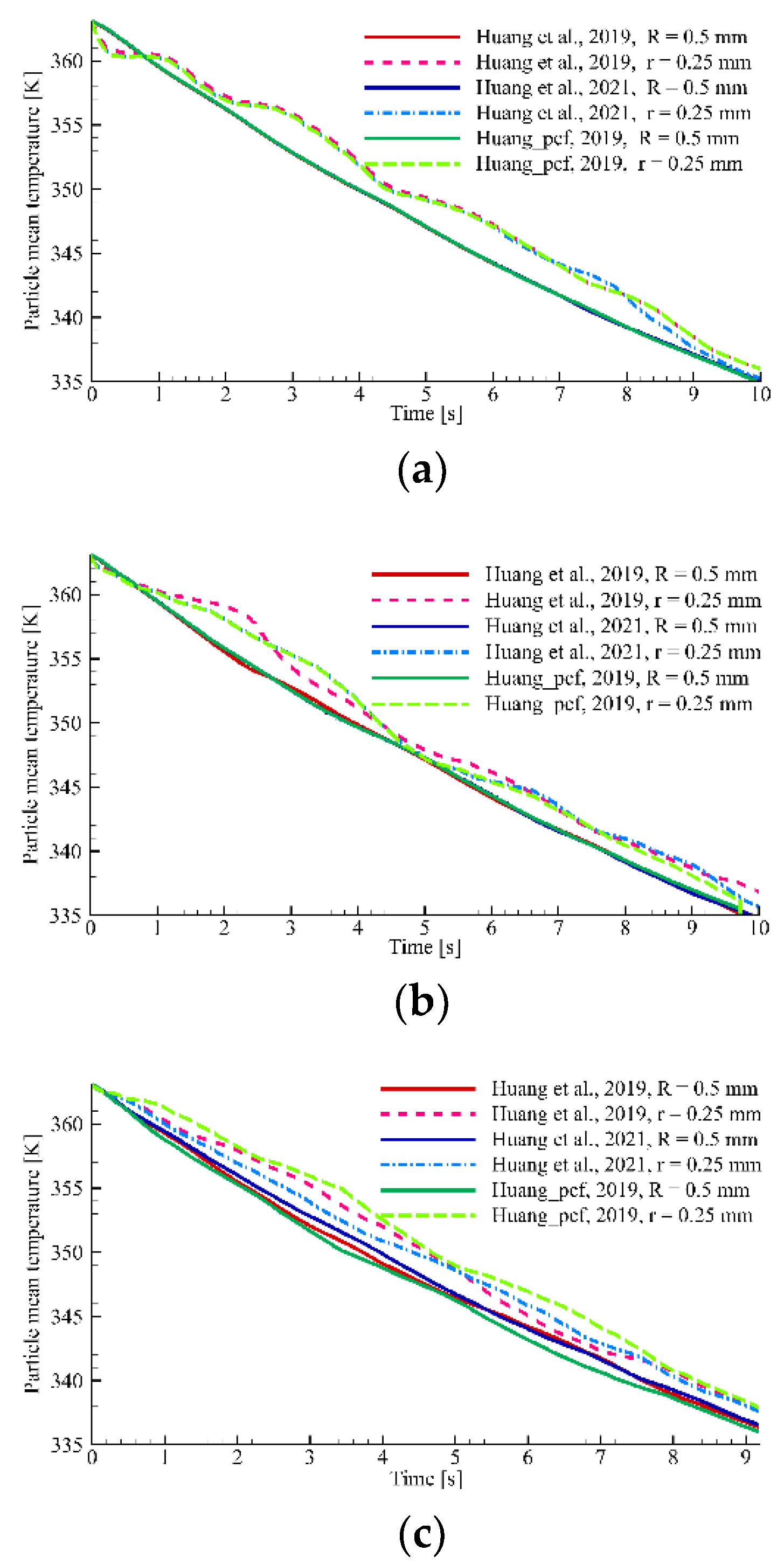
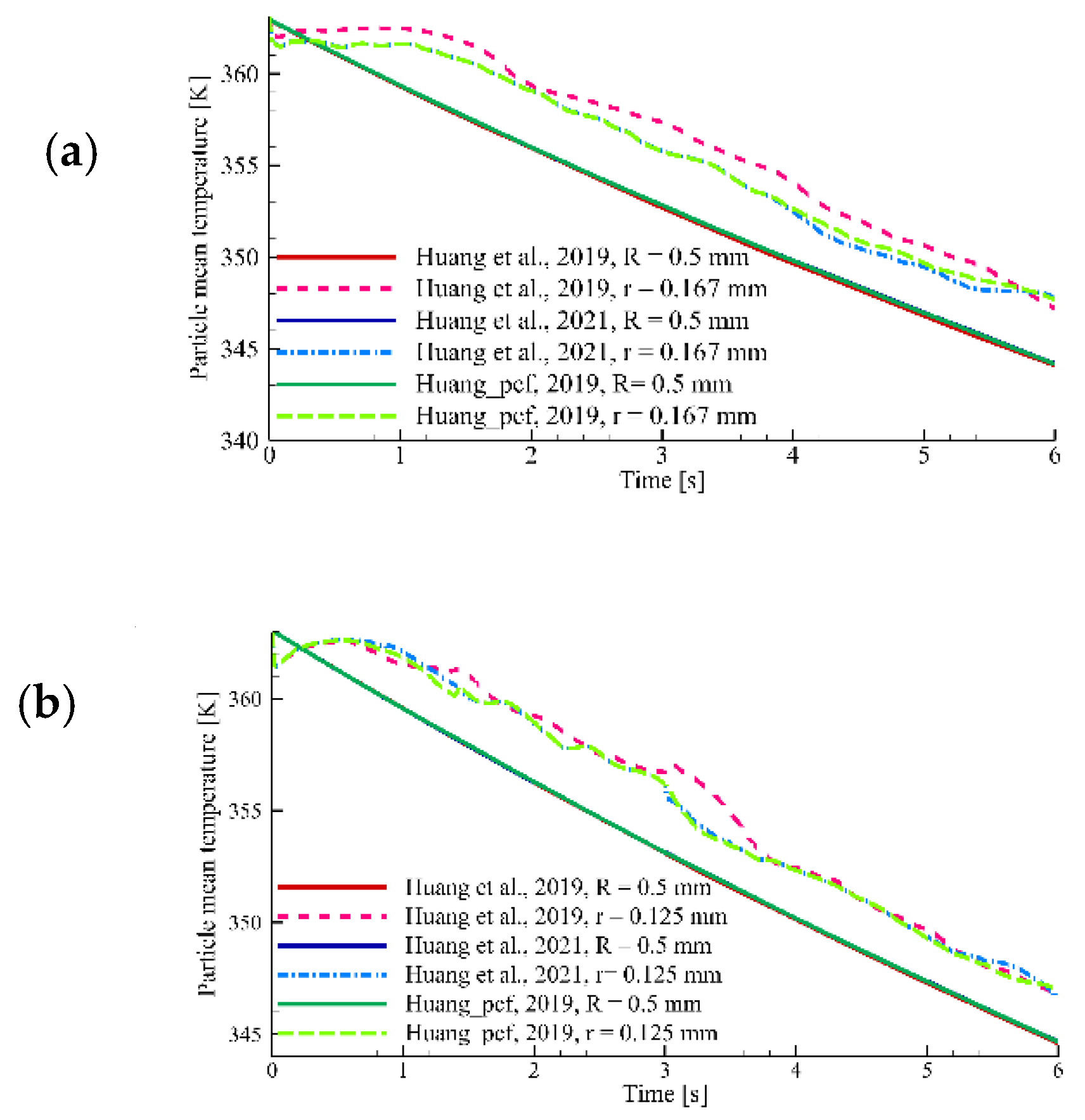
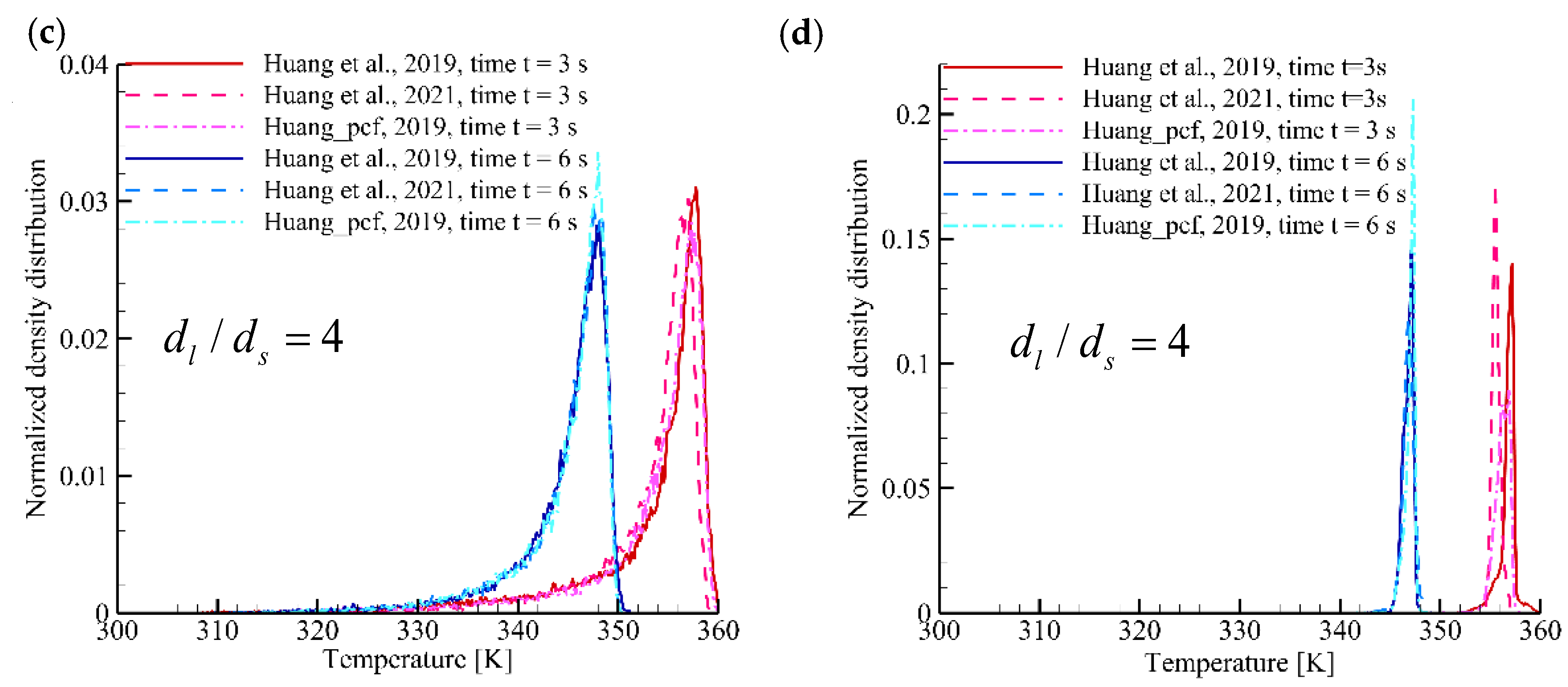
3.1. Validation
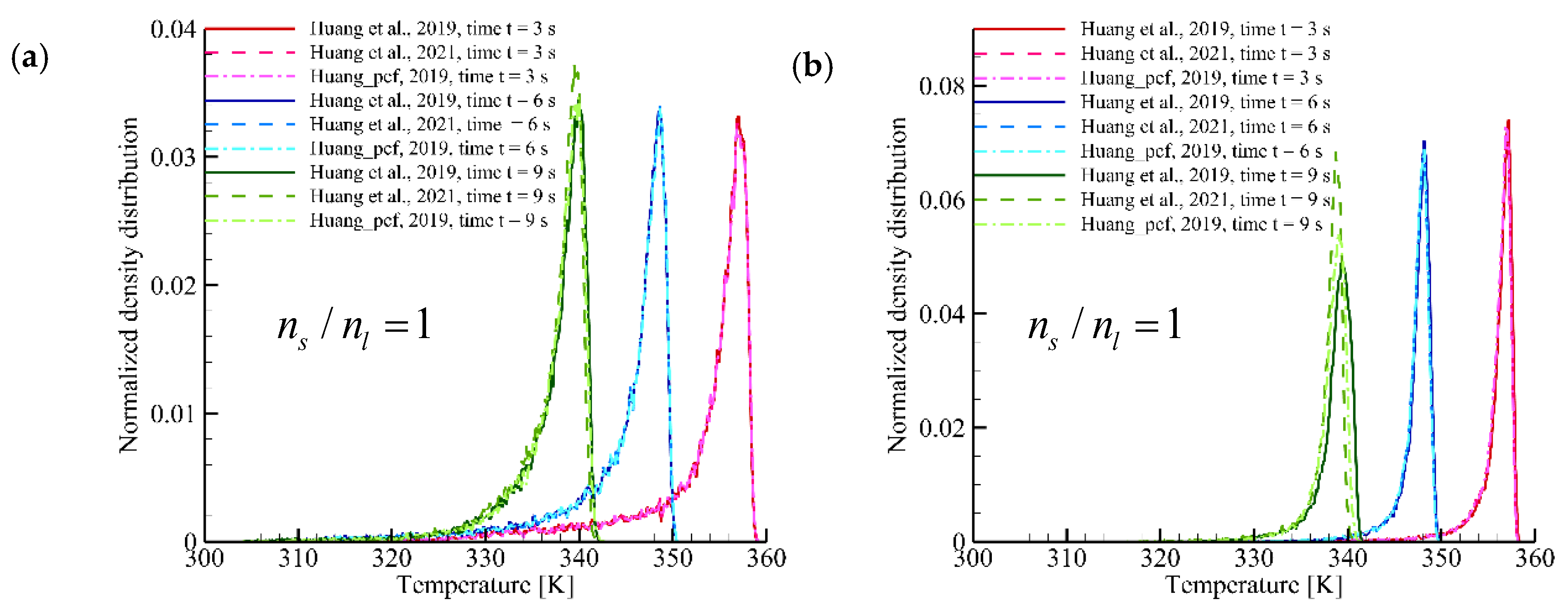
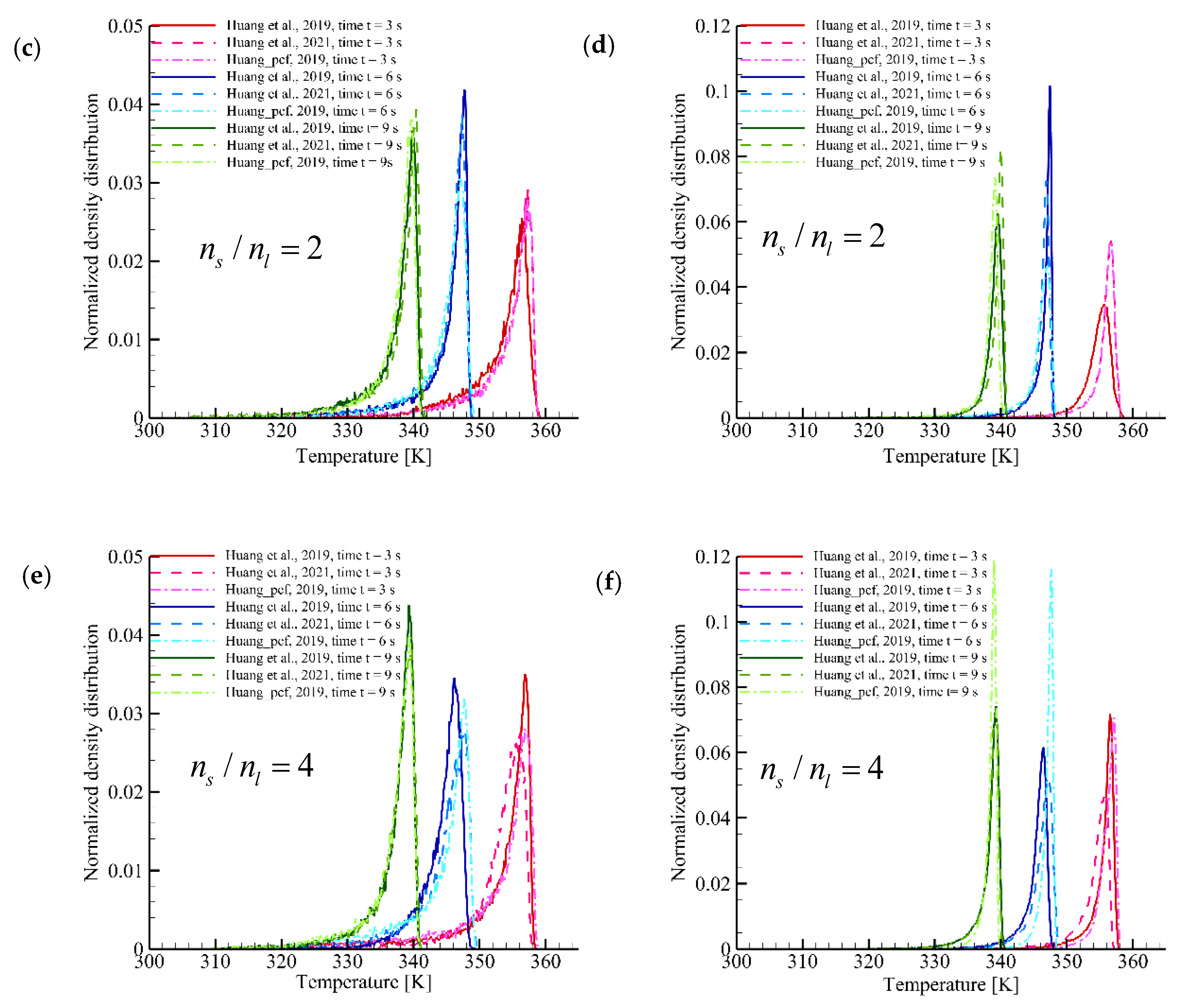
3.2. Effect of the Particle Number Ratio
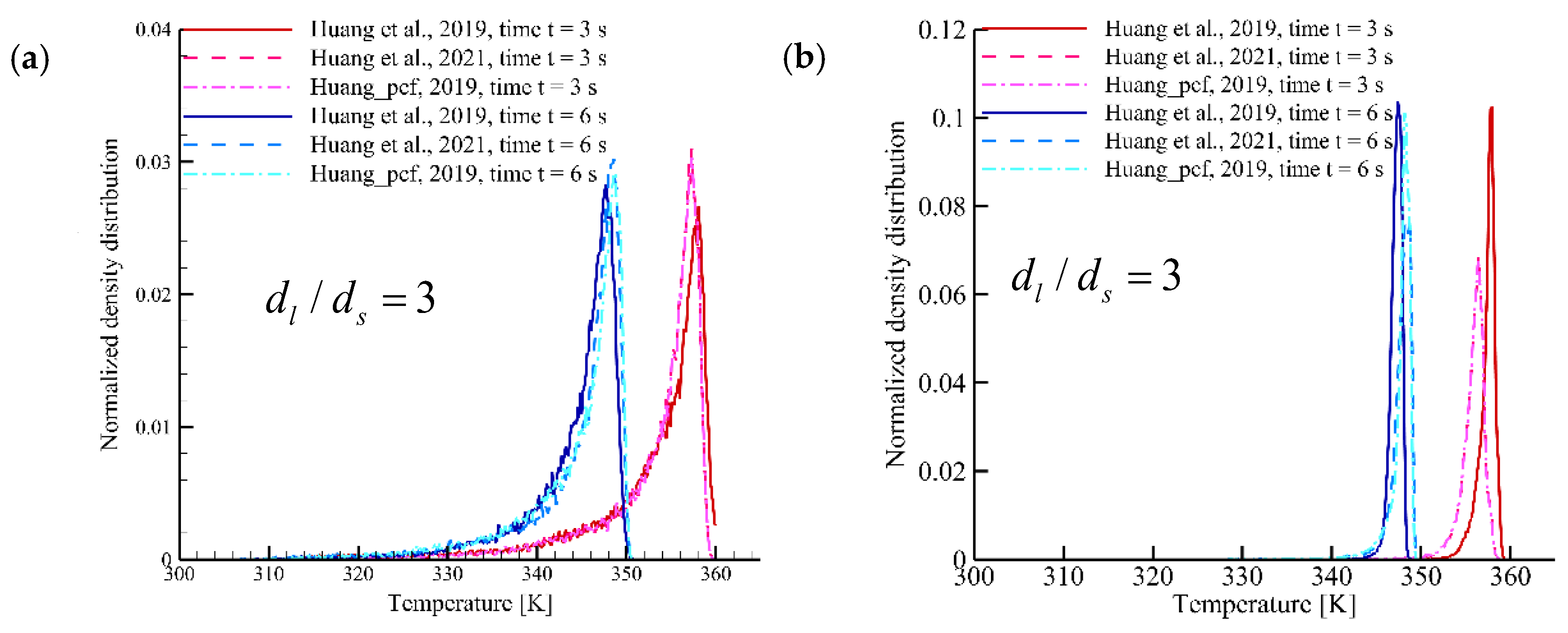
3.3. Effect of the Particle Diameter Ratio
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Particle surface area, m2 | |
| Specific heat capacity of the gas phase, J/kg /K | |
| Specific capacity of particle phase, J/kg /K | |
| Particle diameter, m | |
| Sauter mean diameter, m | |
| Contact forces, N | |
| Gravitational acceleration, m/s2 | |
| Interphase heat transfer coefficient, W/ m2/K | |
| Moment of inertia, kg × m2 | |
| Effective conductivity of the gas phase, W/m/K | |
| Conductivity of the gas phase, W/m/K | |
| Particle mass, kg | |
| Nusselt number | |
| Pressure of the gas phase, Pa | |
| Prandtl number | |
| Source term of the interphase heat transfer, W/m3 | |
| Reynolds number | |
| Momentum source term of the gas phase, kg/m/s2 | |
| Temperature of the gas phase, K | |
| Torque of the particle, N × m | |
| Particle temperature, K | |
| Velocity of the gas phase, m/s | |
| Grid volume, m3 | |
| Velocity of particle, m/s | |
| Volume of particle, m3 | |
| Particle position | |
| Scaled particle diameter | |
| Greek letters | |
| Interphase drag coefficient on the individual particle | |
| Volume fraction of the gas phase | |
| Solid volume fraction | |
| Viscosity of the gas phase, kg/m/s | |
| Density of the gas phase, kg/m3 | |
| Density of particle phase, kg/m3 | |
| Stress tensor of the gas phase, kg/m2/s2 | |
| Angular velocity of the particle, rad/s |
References
- Baltussen, M.W.; Buist, K.A.; Peters, E.A.J.F.; Kuipers, J.A.M. Multiscale modelling of dense gas-particle flows. In Advances in Chemical Engineering; Academic Press: Cambridge, MA, USA, 2018; pp. 1–52. [Google Scholar]
- Hill, R.J.; Koch, D.L.; Ladd, A.J.C. The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 2001, 448, 213–241. [Google Scholar] [CrossRef]
- Hill, R.J.; Koch, D.L.; Ladd, A.J.C. Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 2001, 448, 243–278. [Google Scholar] [CrossRef]
- Zhou, Q.; Fan, L.-S. Direct numerical simulation of low-Reynolds-number flow past arrays of rotating spheres. J. Fluid Mech. 2015, 765, 396–423. [Google Scholar] [CrossRef]
- Tang, Y.; Peters, E.A.J.F.; Kuipers, J.A.M. Direct numerical simulations of dynamic gas-solid suspensions. AIChE J. 2016, 62, 1958–1969. [Google Scholar] [CrossRef] [Green Version]
- Tenneti, S.; Garg, R.; Subramaniam, S. Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Int. J. Multiph. Flow 2011, 37, 1072–1092. [Google Scholar] [CrossRef]
- Deen, N.G.; Kriebitzsch, S.H.; van der Hoef, M.A.; Kuipers, J.A.M. Direct numerical simulation of flow and heat transfer in dense fluid–particle systems. Chem. Eng. Sci. 2012, 81, 329–344. [Google Scholar] [CrossRef]
- Feng, Z.-G.; Musong, S.G. Direct numerical simulation of heat and mass transfer of spheres in a fluidized bed. Powder Technol. 2014, 262, 62–70. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, C.; Jiang, M.; Wang, H.; Zhou, Q. Effects of particle velocity fluctuations on inter-phase heat transfer in gas-solid flows. Chem. Eng. Sci. 2019, 206, 375–386. [Google Scholar] [CrossRef]
- Municchi, F.; Radl, S. Momentum, heat and mass transfer simulations of bounded dense mono-dispersed gas-particle systems. Int. J. Heat Mass Transf. 2018, 120, 1146–1161. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Tenneti, S.; Subramaniam, S. Modeling average gas–solid heat transfer using particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2015, 86, 898–913. [Google Scholar] [CrossRef] [Green Version]
- Tavassoli, H.; Kriebitzsch, S.; van der Hoef, M.; Peters, E.; Kuipers, H. Direct numerical simulation of particulate flow with heat transfer. Int. J. Multiph. Flow 2013, 57, 29–37. [Google Scholar] [CrossRef]
- Tenneti, S.; Sun, B.; Garg, R.; Subramaniam, S. Role of fluid heating in dense gas–solid flow as revealed by particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2013, 58, 471–479. [Google Scholar] [CrossRef]
- Gunn, D.J. Transfer of heat or mass to particles in fixed and fluidized beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Beetstra, R.; van der Hoef, M.A.; Kuipers, J.A.M. Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 2007, 53, 489–501. [Google Scholar] [CrossRef]
- Cello, F.; Di Renzo, A.; Di Maio, F.P. A semi-empirical model for the drag force and fluid–particle interaction in polydisperse suspensions. Chem. Eng. Sci. 2010, 65, 3128–3139. [Google Scholar] [CrossRef]
- Holloway, W.; Yin, X.; Sundaresan, S. Fluid-particle drag in inertial polydisperse gas–solid suspensions. AIChE J. 2010, 56, 1995–2004. [Google Scholar] [CrossRef]
- Rong, L.W.; Dong, K.J.; Yu, A.B. Lattice-Boltzmann simulation of fluid flow through packed beds of spheres: Effect of particle size distribution. Chem. Eng. Sci. 2014, 116, 508–523. [Google Scholar] [CrossRef]
- Sarkar, S.; van der Hoef, M.A.; Kuipers, J.A.M. Fluid–particle interaction from lattice Boltzmann simulations for flow through polydisperse random arrays of spheres. Chem. Eng. Sci. 2009, 64, 2683–2691. [Google Scholar] [CrossRef]
- Yin, X.; Sundaresan, S. Fluid-particle drag in low-Reynolds-number polydisperse gas-solid suspensions. AIChE J. 2009, 55, 1352–1368. [Google Scholar] [CrossRef]
- Duan, F.; Zhao, L.; Chen, X.; Zhou, Q. Fluid-particle drag and particle-particle drag in low-Reynolds-number bidisperse gas-solid suspensions. Phys. Fluids 2020, 32, 113311. [Google Scholar] [CrossRef]
- Tavassoli, H.; Peters, E.; Kuipers, J.A.M. Direct numerical simulation of non-isothermal flow through dense bidisperse random arrays of spheres. Powder Technol. 2017, 314, 291–298. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Peters, E.A.; Kuipers, J.A. Direct numerical simulation of mass transfer in bidisperse arrays of spheres. AIChE J. 2020, 66, e16786. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Wang, L.; Li, Y.; Zhou, Q. Direct numerical simulation of flow and heat transfer in bidisperse gas-solid systems. Chem. Eng. Sci. 2021, 239, 116645. [Google Scholar] [CrossRef]
- Benyahia, S.; Syamlal, M.; O’Brien, T.J. Summary of MFIX Equations 2005–4; National Energy Technology Laboratory: Morgantown, WV, USA, 2008.
- Syamlal, M. MFIX Documentation: Numerical Techniques; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1998.
- Syamlal, M.; Rogers, W.; O’Brien, T.J. MFIX Documentation: Theory Guide; U.S. Department of Energy (DOE) Energy Technology Center: Morgantown, WV, USA, 1993.
- Garg, R.; Galvin, J.; Li, T.; Pannala, S. Open-source MFIX-DEM software for gas-solids flows: Part I—Verification studies. Powder Technol. 2012, 220, 122–137. [Google Scholar] [CrossRef]
- Guo, L.; Capecelatro, J. The role of clusters on heat transfer in sedimenting gas-solid flows. Int. J. Heat Mass Transf. 2019, 132, 1217–1230. [Google Scholar] [CrossRef]
- Patil, A.V.; Peters, E.; Kuipers, J.A.M. Comparison of CFD–DEM heat transfer simulations with infrared/visual measurements. Chem. Eng. J. 2015, 277, 388–401. [Google Scholar] [CrossRef]


| Simulation Parameters | Value | Simulation Parameters | Value |
|---|---|---|---|
| Particle diameter, dp | 1.0 × 10−3 m | Gas viscosity | 1.8 × 10−5 Pa·s |
| Particle heat capacity | 840 J/(kg·K) | Gas density | 1.3 kg/m3 |
| Particle density | 2500 kg/m3 | Gas heat capacity | 1010 J/(kg·K) |
| Initial particle temperature | 363.15 K | Gas conductivity | 0.02552 W/(m·K) |
| Particle conductivity | 1.4 W/(m·K) | Normal spring constant | 500 N/m |
| Particle–particle and particle–wall friction coefficient | 0.3 | Restitution coefficient for inter-particle collisions and particle–wall collisions | 0.97 |
| Ratio of the tangential spring constant to normal spring constant for inter-particle collisions and particle–wall collisions | 0.286 | Ratio of the tangential damping factor to the normal damping factor for inter-particle collisions and particle–wall collisions | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Huang, Q.; Yu, Y.; Li, Y.; Zhou, Q. A Comparative Study of Models for Heat Transfer in Bidisperse Gas–Solid Systems via CFD–DEM Simulations. Axioms 2022, 11, 179. https://doi.org/10.3390/axioms11040179
Huang Z, Huang Q, Yu Y, Li Y, Zhou Q. A Comparative Study of Models for Heat Transfer in Bidisperse Gas–Solid Systems via CFD–DEM Simulations. Axioms. 2022; 11(4):179. https://doi.org/10.3390/axioms11040179
Chicago/Turabian StyleHuang, Zheqing, Qi Huang, Yaxiong Yu, Yu Li, and Qiang Zhou. 2022. "A Comparative Study of Models for Heat Transfer in Bidisperse Gas–Solid Systems via CFD–DEM Simulations" Axioms 11, no. 4: 179. https://doi.org/10.3390/axioms11040179
APA StyleHuang, Z., Huang, Q., Yu, Y., Li, Y., & Zhou, Q. (2022). A Comparative Study of Models for Heat Transfer in Bidisperse Gas–Solid Systems via CFD–DEM Simulations. Axioms, 11(4), 179. https://doi.org/10.3390/axioms11040179







