Abstract
In this paper, a retrial queueing system of the M/M/1 type with Poisson flows of arrivals, impatient customers, collisions, and an unreliable service device is considered. To make the problem more realistic and, hence, more complicated, we include the breakdowns and repairs of the service in this research study. The retrial times of customers in the orbit, service time, impatience time of customers in the orbit, server’s lifetime (depending on whether it is idle or busy), and server recovery time are supposed to be exponentially distributed. The problem of finding the stationary probability distribution of the number of customers in orbit is solved by using the method of asymptotic diffusion analyses under the condition of a heavy load of the system and the patience of customers in orbit. Numerical results are presented that demonstrate the effectiveness of the obtained theoretical conclusions, and a comparative analysis of the method of asymptotic analysis and the method of asymptotic diffusion analysis for the considered problem is given.
Keywords:
retrial queue; impatient customers; collisions; unreliable server; asymptotic diffusion analysis MSC:
60K25; 90B22
1. Introduction
This paper is a continuation of [1], and it provides a new solution method and comparisons for the solution obtained in the cited paper. Let us briefly indicate the place of this work among the studies of queueing systems. To build real telecommunication systems and optimize their characteristics, queueing systems are widely studied as mathematical models. It is possible to single out a large class of queueing systems that are occupied by systems with repeated calls.
In the present study, a basic retrial queueing system (RQ-system) with an incoming Poisson flow, one server, and an infinite orbit are complicated by the presence of impatient customers in the orbit, conflicting customers in the system, and the fact that the server can fail. There is no service discipline for the customers in the orbit and customers may retry for service independently. Impatient calls in the orbit are understood as the case when a customer in the orbit can leave the orbit after a random time without service. Conflicts in the system occur in the following case: The device is busy with servicing and a customer comes into the system from outside or a customer from the orbit re-applies to the device for servicing. When a collision occurs, both calls (in service and requesting service) immediately proceed into orbit.
In many situations involving the transmission of data from different sources, uncoordinated attempts by multiple sources to use the same server can lead to a “collision” (data loss or corruption). In papers [2,3], a type of queueing system with repeated calls with collisions, called queues with double connections, was analyzed for the first time. In such models, an arriving client detects that the server (service device) is busy, aborts the service of the client being served at the moment, and both the arriving client and the served client join the orbit and the server immediately becomes idle. Furthermore, in [4], a CSMA/CD (Carrier Sense Multiple Access with Collision Detection) protocol model in the form of RQ with collisions and a constant reversal rate was proposed. The development of these results has been proposed for various models, which are reviewed in [5,6,7]. In all of the above works, the authors consider collision as the only cause of unsuccessful transmission and retransmission, which is not true in the case of real communication systems. This paper discusses other aspects that cause transmission failure and retransmission.
In many real-world situations, the server is prone to unpredictable breakdowns. Therefore, queueing systems assuming server failures can provide a realistic representation of such situations. This type of system can be found in communication networks and industrial and computer networks. RQ-systems with unreliable servers were first considered in works [8,9,10,11,12]. More details about the results can be viewed in [7]. In the present paper, the unreliability of the service device lies in the fact that it can fail after a random period of time. In this case, it takes time to repair the device, and if, at the time of the device’s failure, it was under service, the call from the device proceeds into orbit.
The main aim of this work is to develop a new solution with the help of asymptotic diffusion analysis and to find the area of its applicability.
2. Description of the System and Solution Method
A detailed description of the system under consideration is presented in [1], but we present it here for the sake of completely understanding the problem.
We consider a single-server RQ-system with the Poisson arrival process with parameter for the primary calls. A customer that finds the server to be idle takes it for service for an exponentially distributed random time with parameter . If the server is busy, an arriving customer (either from the source or from the orbit) enters into a collision [1,7,13,14,15] and both proceeds into orbit.
In the orbit, each customer, called secondary call, independently of the others retries for services after a random time. The retrial time is exponentially distributed with parameter . If the server is busy again, the request tries to occupy the device to obtain servicing as soon as possible. If the server is idle, the secondary customer occupies it for service for an exponentially distributed random time with parameter ; that is, no difference between the service of primary and secondary calls is observed.
In addition, we assume that a customer in the orbit leaves the system without service after a random time, which has an exponential distribution with the rate , demonstrating the impatience property. This behaviour was investigated, for example, in papers [1,13,14,15,16,17,18,19,20,21].
We also assume that the server is unreliable; that is, the lifetime is supposed to be exponentially distributed with rate if the server is idle and with parameter if it is busy. When the server breaks down, it is immediately sent for repair and the recovery time is assumed to be exponentially distributed with rate . When the server is down, the primary sources continue the generation of customers and send them to the server. Similarly, customers may retry from the orbit relative to the server, but all arriving customers immediately proceed into the orbit. Furthermore, in this unreliable model, we suppose that interrupted requests proceed to the orbit immediately and its next service is independent of the interrupted one. Queueing systems with unreliable servers were investigated, e.g., in [1,7,15,19,22,23,24,25].
All random variables mentioned in the model’s description are assumed to be independent of each other.
Figure 1 shows the model of the RQ-system, , with impatient customers, collisions, and an unreliable server.
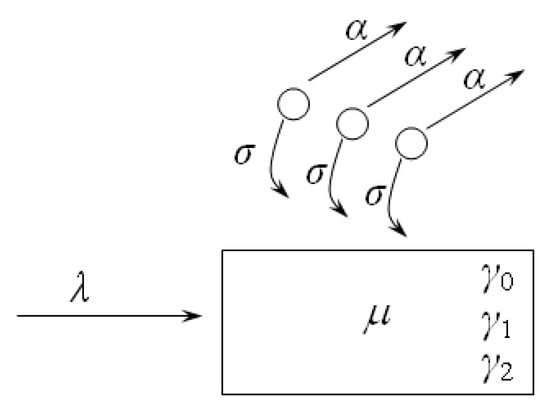
Figure 1.
Retrial queue with impatient customers in the orbit, collisions, and unreliable server.
The problem is to find the stationary distribution of the number of customers in the orbit for the described system by using the method of asymptotic diffusion analyses.
The diffusion approximation is the subject of works [26,27,28,29]. The asymptotic diffusion analysis method has already been actively developed by the Tomsk school of scientists in the field of queueing theory; see, for example, [21,30,31,32,33]. This method makes obtaining a discrete diffusion approximation possible for the probability of the distribution of the number of customers in orbit under a given asymptotic condition. In addition to the distribution of the number of customers in orbit, it is interesting to find additional characteristics of the system, for example, the ratio of calls that are in collision with the flow of primary calls or the ratio of calls leaving the orbit without service in the total flow. It should be noted that adding collisions to the model does not allow one to solve the problem analytically (or, for example, to build a recurrent algorithm for finding the desired probabilities). Therefore, we use asymptotic methods. Moreover, as our studies show (this one, and [1]), for problems with collisions of calls, the asymptotic diffusion method behaves stably in terms of the Kolmogorov distance compared to the asymptotic analysis method. We believe that this is due to the fact that by investigating models with collisions with the method of asymptotic analysis, we can obtain an asymptotic approximation of the distribution of the number of claims in orbit consisting of three parts, each of which has the form of a Gaussian distribution but with different values of the mean (see, for example, [34]).
To find the area of the applicability of the resulting approximation, we find the Kolmogorov distance as a measure of the proximity of the diffusion approximation and the distribution of the number of customers in orbit, which is the solution of a system of truncated dimensions describing the state of the system. Despite the complexity of the method, the available works, and the present study show that the method is more accurate than the method of asymptotic analysis in terms of the Kolmogorov distance.
For the numerical implementation of the theoretical results, a program code in the Mathcad 14.0 package was developed. In this work, the program code is not given, as it is in the patenting stage.
3. Investigations and Results
3.1. Theoretical Results
3.1.1. System of Kolmogorov Differential Equations
Let us introduce Markovian process where is the number of calls in the orbit at the moment t, , and defines the device’s state at moment t and takes one of the following values.
Denote by the probability that, at the moment t, there are i calls in the orbit, , and the service device is in state k.
To obtain the probability distribution , , for the states of the retrial queue M/M/1 with impatient customers, collisions, and unreliable service device, as usual, we derive a system of Kolmogorov differential equations (1), which is the same as described in [1] but its solution method will be different.
.
Introduce the partial characteristic functions
3.1.2. Obtaining the Drift Coefficient
In the system of Equations (3) and (4), we make substitutions , , , , , and , where is an infinitesimal value, and we obtain (5)
3.1.3. Centering the Process and Obtaining the Diffusion Coefficient
The solution of equations system (9) has the following form
where and are defined above, and are constants, and is a determined function.
3.1.4. Diffusion Approximation
From (9), (10) with (8), and (10)–(12), we obtain
where the diffusion coefficient is obtained as follows.
The Fokker–Plank equation for the probability density of a diffusion process with drift coefficient and diffusion coefficient has the following form.
Here, is the solution of stochastic differential Equation (15):
where is the Wiener process.
We introduce diffusion process .
The Fokker–Plank equation for has the following form.
The solution of Equation (16) is
Finally, we can obtain diffusion approximation for stationary distribution of the number of calls in the orbit:
where is determined in (17).
3.2. Numerical Results
To compare the pre-limit probability distribution of the number of calls in the orbit of the considered queueing system, , calculated via the matrix method and its approximation , and (18), constructed by using the asymptotic analysis method published in [1] and asymptotic diffusion analysis method for different values of the system’s parameters, we use Kolmogorov distance between the respective distribution functions.
Table 1 shows the results of calculating the Kolmogorov distances for various values of delay parameter and parameter when , , , , and .

Table 1.
Kolmogorov distance.
The values of the Kolmogorov distance from Table 1 and Figure 2, Figure 3, Figure 4 and Figure 5, which show the comparison of the pre-limit, asymptotic and asymptotic diffusion distributions for various values of the delay parameter , and parameter , allow us to draw the following conclusions:
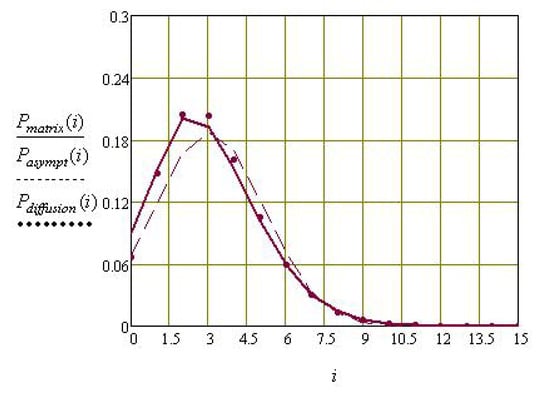
Figure 2.
Comparison of the pre-limit (solid line), asymptotic (dashed line), and diffusion (dotted line) distributions for and ( and ).
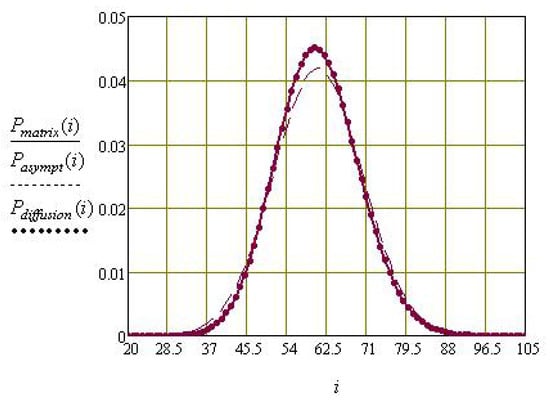
Figure 3.
Comparison of the pre-limit (solid line), asymptotic (dashed line), and diffusion (dotted line) distributions for and ( and ).
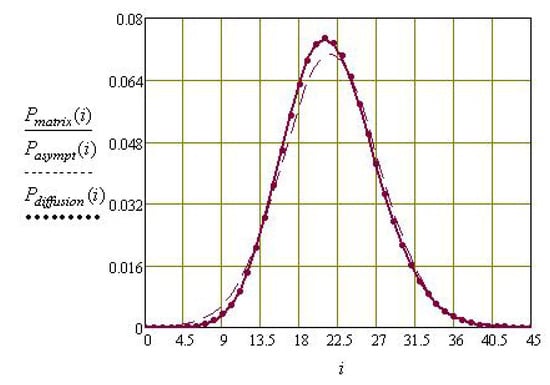
Figure 4.
Comparison of the pre-limit (solid line), asymptotic (dashed line), and diffusion (dotted line) distributions for and ( and ).
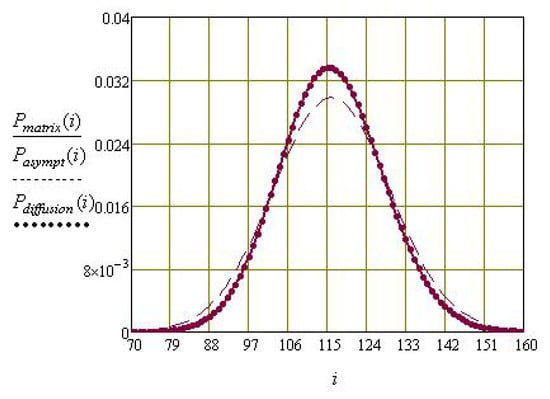
Figure 5.
Comparison of the pre-limit (solid line), asymptotic (dashed line), and diffusion (dotted line) distributions for and ( and ).
- For a fixed system load , as decreases, the Kolmogorov distance decreases;
- At a fixed value of the delay time parameter of the call in orbit and , with an increase in the value of system load , the Kolmogorov distance decreases for and increases for (this behavior of is typical for systems with collisions), and the Kolmogorov distance decreases.
Knowing the probability distribution of the number of calls in orbit (18), we can find some other characteristics of the system, such as the following:
- is the intensity of the total flow;
- is the average number of the customer’s repeating request;
- is the ratio of repeated calls in the primary flow;
- is the ratio of repeated calls in the total flow;
- is the ratio of calls leaving the orbit without service in the total flow;
- is the ratio of calls that are in collision in the flow of primary calls.
As an example, Table 2 shows the values of these characteristics for .

Table 2.
Characteristics of the system ().
4. Discussion and Conclusions
The retrial queueing system of the type with impatient customers, collisions, and the unreliable server was investigated with the following methods:
- The asymptotic analysis method: see [1];
- The numerical method: see [1];
- The asymptotic diffusion analysis method: a new contribution.
As an asymptotic condition for both methods, the system was taken as a condition for a long delay of calls in orbit and a long period of patience with respect to calls in orbit. Both methods resulted in the conclusion that the number of calls in the orbit is asymptotically normal. The asymptotic diffusion analysis method is more accurate than the asymptotic analysis method under the same asymptotic condition in terms of the Kolmogorov distance.
In the future, we plan to find the sensitivity of the diffusion approximation relative to the exogenous parameters of the system and supplement this study with a simulation model for calculating the temporal characteristics of the system.
Author Contributions
Conceptualization, E.D. and S.M.; methodology, E.D. and A.P.; software, E.D.; validation, E.D., S.M. and J.S.; formal analysis, E.D. and S.M.; writing—original draft preparation, E.D.; writing—review and editing, E.D., S.M. and J.S.; visualization, E.D.; supervision, S.M.; project administration, E.D. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Tomsk State University Development Programme (Priority-2030).
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the reviewers for their valuable comments and suggestions that improved the quality and presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Danilyuk, E.Y.; Moiseeva, S.P.; Sztrik, J. Asymptotic Analysis of Retrial Queueing System M/M/1 with Impatient Customers, Collisions and Unreliable Server. J. Sib. Fed. Univ. Math. Phys. 2020, 13, 218–230. [Google Scholar] [CrossRef]
- Jonin, G.L. Determination of probabilistic characteristics of single-line queues with double connections and repeated calls. In Models of Systems of Distribution of Information and Its Analysis; Nauka: Moscow, Russia, 1982. [Google Scholar]
- Falin, G.I.; Sukharev, Y.I. On Single-Line Queues with Double Connections; All-Union Institute for Scientific and Technical Information: Moscow, Russia, 1985; pp. 6582–6585. [Google Scholar]
- Choi, B.D.; Shin, Y.W.; Ahn, W.C. Retrial queues with collision arising from unslotted CSMA/CD protocol. Queueing Syst. 1992, 11, 335–356. [Google Scholar] [CrossRef]
- Artajelo, J.R.; Gomez-Corral, A. Retrial Queueing Systems: A Computational Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Falin, G.I.; Templeton, J.G.C. Retrial Queues; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Lakaour, L.; Aissani, D.; Adel-Aissanou, K.; Barkaoui, K.; Ziani, S. An unreliable single server retrial queue with collisions and transmission errors. Commun. Stat.-Theory Methods 2020, 51, 1085–1109. [Google Scholar] [CrossRef]
- Aissani, A. On the M/G/1 queueing system with repeated orders and unreliable server. J. Technol. 1988, 6, 93–123. (In French) [Google Scholar]
- Aissani, A. Unreliable queueing with repeated orders. Microelectron. Reliab. 1993, 33, 2093–2106. [Google Scholar] [CrossRef]
- Aissani, A. A retrial queue with redundancy and unreliable server. Queueuing Syst. 1994, 17, 431–449. [Google Scholar] [CrossRef]
- Kulkarni, V.G.; Choi, B.D. Retrial queues with server subject to breakdowns and repairs. Queueing Syst. 1990, 7, 191–208. [Google Scholar] [CrossRef]
- Anisimov, V.V.; Atadzhanov, K.L. Diffusion approximation of systems with repeated calls and an unreliable server. J. Math. Sci. 1994, 72, 3032–3034. [Google Scholar] [CrossRef]
- Danilyuk, E.; Fedorova, E.; Moiseeva, S. Asymptotic Analysis of an Retrial Queueing System M/M/1 with Collisions and Impatient Calls. Autom. Remote Control 2018, 79, 2136–2146. [Google Scholar] [CrossRef]
- Nazarov, A.; Lizyura, O. Stability Analysis for Retrial Queue with Collisions and r-Persistent Customers. Commun. Comput. Inf. Sci. 2022, 1605, 330–342. [Google Scholar]
- Sztrik, J.; Tóth, Á. Some Special Features of Finite-Source Retrial Queues with Collisions, an Unreliable Server and Impatient Customers in the Orbit. Commun. Comput. Inf. Sci. 2021, 1391, 1–15. [Google Scholar]
- Adan, I.; Hathaway, B.; Kulkarni, V. On first-come, first-served queues with two classes of impatient customers. Queueing Syst. 2019, 91, 113–142. [Google Scholar] [CrossRef]
- Artalejo, J.R.; Pla, V. On the impact of customer balking, impatience and retrials in telecommunication systems. Comput. Math. Appl. 2009, 57, 217–229. [Google Scholar]
- Kim, C.; Dudin, A.; Dudina, O.; Klimenok, V. Analysis of queueing system with non-preemptive time limited service and impatient customers. Methodol. Comput. Appl. Probab. 2020, 22, 401–432. [Google Scholar] [CrossRef]
- Chang, F.-M.; Liu, T.-H.; Ke, J.-C. On an unreliable-server retrial queue with customer feedback and impatience. Appl. Math. Model. 2018, 55, 171–182. [Google Scholar] [CrossRef]
- Phung-Duc, T. Multiserver Retrial Queues with Two Types of Nonpersistent Customers. Asia-Pac. J. Oper. Res. 2014, 31, 1440009. [Google Scholar] [CrossRef]
- Danilyuk, E.; Moiseeva, S.; Nazarov, A. Asymptotic Diffusion Analysis of an Retrial Queueing System M/M/1 with Impatient Calls. Commun. Comput. Inf. Sci. 2022, 1552, 233–246. [Google Scholar]
- Choudhury, G.; Goswami, A.; Begum, A.; Sarmah, H. Stochastic Decomposition Result of an Unreliable Queue with Two Types of Services. Math. Stat. 2020, 8, 225–232. [Google Scholar] [CrossRef]
- Singh, C.; Kaur, S. Unreliable Server Retrial Queue with Optional Service and Multi-Phase Repair. Int. J. Oper. Res. 2017, 14, 35–51. [Google Scholar]
- Kerobyan, R.; Kerobyan, K. Virtual Waiting Time in Single-Server Queueing Model M|G|1 with Unreliable Server and Catastrophes. Commun. Comput. Inf. Sci. 2021, 1391, 319–336. [Google Scholar]
- Seenivasan, M.; Ramesh, R.; Patricia, F. Markovian queueing model with catastrophe, unreliable and backup server. Int. J. Health Sci. 2022, 6, 9136–9150. [Google Scholar] [CrossRef]
- Whitt, W. A Diffusion Approximation for the G/GI/n/m Queue. Oper. Res. 2003, 52, 922–941. [Google Scholar] [CrossRef]
- Ward, A.R.; Glynn, P.W. A Diffusion Approximation for a GI/GI/1 Queue with Balking or Reneging. Queueing Syst. 2005, 50, 371–400. [Google Scholar] [CrossRef]
- Gromoll, H.C. Diffusion approximation for a processor sharing queue in heavy traffic. Ann. Appl. Probab. 2004, 14, 555–611. [Google Scholar] [CrossRef]
- Williams, R.J. Diffusion approximations for open multiclass queueing networks: Sufficient conditions involving state space collapse. Queueing Syst. Theory Appl. 1998, 30, 27–88. [Google Scholar] [CrossRef]
- Moiseev, A.; Nazarov, A.; Paul, S. Asymptotic diffusion analysis of multi-server retrial queue with hyper-exponential service. Mathematics 2020, 8, 531. [Google Scholar] [CrossRef]
- Nazarov, A.; Phung-Duc, T.; Paul, S.; Lizyura, O. Asymptotic-Diffusion Analysis of Retrial Queue with Two-Way Communication and Renewal Input. In Proceedings of the 5th International Conference on Stochastic Methods, Moscow, Russia, 23–27 November 2020; pp. 339–345. [Google Scholar]
- Nazarov, A.; Phung-Duc, T.; Paul, S.; Lizyura, O. Diffusion Limit for Single-Server Retrial Queues with Renewal Input and Outgoing Calls. Mathematics 2022, 10, 948. [Google Scholar] [CrossRef]
- Nazarov, A.; Phung-Duc, T.; Izmailova, Y. Asymptotic-Diffusion Analysis of Multi-server Retrial Queueing System with Priority Customers. In Information Technologies and Mathematical Modelling. Queueing Theory and Applications. ITMM 2020; Communications in Computer and Information Science; Springer: Cham, Switzerland, 2021; pp. 88–98. [Google Scholar]
- Danilyuk, E.; Moiseeva, S.; Nazarov, A. Asymptotic Analysis of Retrial Queueing System M/GI/1 with Collisions and Impatient Calls. Commun. Comput. Inf. Sci. 2019, 1109, 230–242. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).