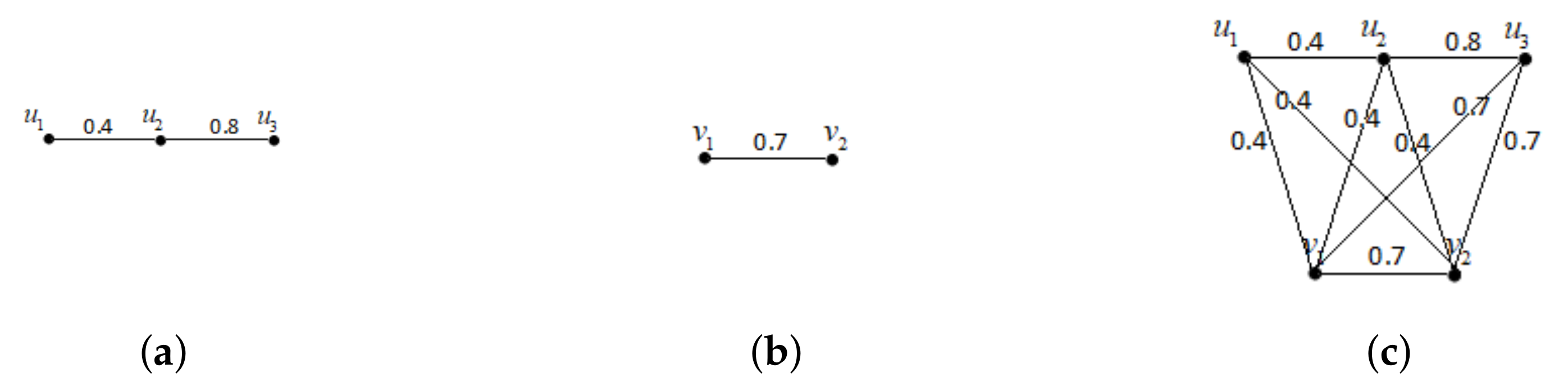1. Introduction
Many real-world problems, such as those in information theory, telecommunications, medical diagnosis, transportation, cluster analysis, traffic networks, and so on, have been mathematically modelled by using graphs since Euler’s introduction of graph theory in 1735. Although classical graph theory has been widely used in various aspects, it still has some limitations in dealing with incomplete data and uncertain information. For instance, the traffic congestion at an intersection is due to multiple uncertain factors that include the number of vehicles, cycle length of the traffic light, road conditions, and so on. Therefore, a more appropriate tool is needed to handle these vague phenomena in real-life situations.
Many researchers have studied various types of fuzzy graphs since Zadeh [
1] introduced the fuzzy theory in 1965. The fuzzy graphs with crisp vertex sets and fuzzy edge sets, also known as type 1 fuzzy graphs, were originally proposed by Kaufmann [
2] in 1973. Furthermore, Rosenfeld [
3] introduced type 2 fuzzy graphs with fuzzy vertex sets and fuzzy edge sets. Subsequently, many scholars have made a lot of generalizations about fuzzy graphs. For instance, Mordeson and Peng [
4] defined the concept of complementariness in fuzzy graphs and studied some operations on fuzzy graphs in 1994. In the same year, Craine [
5] investigated the characteristics of fuzzy interval graphs. With the development of fuzzy graph theory, R.H. Goetschel [
6] first described the concept of fuzzy hypergraphs in 1995 and gave an
-cut of a fuzzy hypergraph. It was Gong and Wang who investigated the operations of fuzzy and strong fuzzy
r-uniform hypergraphs, such as Cartesian products, strong products, normal products, lexicographic products, unions, and joining in [
7]. Notably, in [
8,
9], they analyzed the equivalence relationship between fuzzy hypergraphs and fuzzy formal concept analysis and fuzzy information systems so as to use fuzzy hypergraphs to process fuzzy information. Thereafter, Gong and Wang proposed a hesitant fuzzy hypergraph model and investigated some operations and the equivalence relationship of hesitant fuzzy hypergraphs in [
10]. In order to better analyze fuzzy graphs, Blue et al. [
11] discussed the classification of fuzzy graphs based on the various types of “fuzziness” in graphs, then provided algorithmic solutions to the problems of shortest paths and minimum cuts in fuzzy graphs with examples. The concept of bipolar fuzzy graphs and strong bipolar fuzzy graphs was initiated by Akram [
12], who then investigated some important properties of these fuzzy graphs. Recently, Talal Alhawary [
13] defined the direct product, semistrong product, and strong product on type 2 fuzzy graphs. Mathew et al. [
14] introduced transitive blocks together with their applications in fuzzy interconnection networks. Furthermore, Binu et al. [
15] proposed a connectivity index for a fuzzy graph and its application to human trafficking. For more information on fuzzy graphs, readers can refer to [
16,
17,
18,
19,
20,
21].
Graph coloring is one of the most studied problems in combinatorial optimization. The classical graph-coloring problem is to group objects into as few groups as possible, subject to the constraint that no incompatible objects end up in the same group. The smallest number of groups that is needed to color a graph is called the chromatic number. Many problems in practical situations can be modeled as coloring problems, which are known to be NP-hard [
22]. The applications of the graph-coloring problem include wiring problems [
23], printed circuits [
24], frequency assignment problems [
25], resource allocation [
26], a wide variety of scheduling problems [
27,
28,
29,
30], computer register allocation [
31], and so on.
Many researchers have experimented with various graph colorings. In some cases, ambiguity is used in coloring problems of fuzzy graphs when dealing with uncertainties such as vagueness. In the year 2005, the process of coloring the fuzzy graphs was implemented by Mu
oz [
32], who initiated two methods by which to color the vertices of the fuzzy graphs with a crisp vertex set and a fuzzy edge set (the type 1 fuzzy graphs) by means of
-cut coloring of the graphs with
and an extension of distance defined between colors. In that paper, Mu
oz et al. also discussed the application of
-cut chromatic numbers in arranging traffic flows at an intersection and the application of the second coloring method in timetabling problems. Furthermore, Eslahchi and Onagh [
33] constructed this method for fuzzy graphs with fuzzy vertex sets and fuzzy edge sets (the type 2 fuzzy graphs) based on strong adjacencies between vertices. In a similar way, Kishore and Sunitha [
34] investigated the strong coloring and chromatic number of type 2 fuzzy graphs based on strong adjacencies between vertices. They also demonstrated how to use strong coloring on fuzzy graphs to solve traffic light problems. Cioban [
35] then proposed a method for vertex coloring of type 2 fuzzy graphs by using delta-fuzzy independent vertex sets with
, and the chromatic number was dubbed the
-chromatic number. Recently, an application of vertex coloring on these graphs to solve a cell site assignment problem in a telecommunications network was given by Keshavarz [
36]. Moreover, Anjaly Kishore et al. [
37] discussed the chromatic number of the resultant type 2 fuzzy graphs in 2016. In the same year, a new concept of coloring fuzzy graphs was introduced by Sovan Samanta et al. in [
38]. Sovan Samanta also described some concepts, such as the strength cut graph and the chromatic number of fuzzy graphs.
Even though type 2 fuzzy graphs have been widely used in many research fields, it is more adaptable and perfect to use type 1 fuzzy graphs for some real-life problems. Susana Mu
oz et al. [
32], for example, used the chromatic number of a type 1 fuzzy graph to analyze traffic lights and a timing problem. Rosyida et al. [
39] proposed a new approach to determining the fuzzy chromatic set of fuzzy graphs and verified that the fuzzy chromatic number of fuzzy graphs is a discrete fuzzy number. In that paper, an application of the fuzzy chromatic number of fuzzy graphs to the problem of medical virus infection at some locations was given. Subsequently, Rosyida offered an application of the fuzzy chromatic number to determine the number of phases of an integrated traffic light system in 2020 [
40]. Due to the practicability of the type 1 fuzzy graph in real-life situations, we will continue to study this type of fuzzy graph. To the best of our knowledge, the operations on type 1 fuzzy graphs and the relationship between the chromatic numbers of fuzzy graphs and the resultant fuzzy graphs obtained by performing various operations on fuzzy graphs have not been investigated until now.
The structure of this article is as follows.
Section 2 discusses some basic concepts in fuzzy set theory and the operations on fuzzy graphs, and a new definition of the chromatic number of fuzzy graphs is given. In
Section 3, we investigate the relationship between the chromatic numbers of fuzzy graphs and that of the resultant fuzzy graphs obtained by performing various operations on fuzzy graphs such as union, cap, join, difference, ring sum, and different types of products. In
Section 4, an application example based on the coloring of fuzzy graphs with crisp vertex sets and fuzzy edge sets is provided. Finally, conclusions are given in
Section 5. We discuss some terminologies in fuzzy graphs and fuzzy graph coloring, as cited in [
32,
39,
40].
2. Preliminaries
In this section, we first recall some definitions in graph theory, fuzzy set theory, and fuzzy graph coloring that will be used in constructing chromatic numbers of fuzzy graphs. Then the definitions of operations on fuzzy graphs are introduced.
2.1. K-Coloring of Crisp Graph
A classical graph consists of a nonempty vertex set and an edge set . An edge is said to be incident to the vertices u and v. Two vertices linked by an edge are called adjacent. Furthermore, we call classical graph as a crisp graph.
For a crisp graph , there are two approaches to defining the k-coloring. In the first approach, a proper k-coloring of a graph with vertex set and edge set is a mapping f from V to the set such that whenever is an edge in E. The chromatic number of G is the smallest k for which G admits a proper k-coloring, written by . In the second approach, a k-coloring of graph is viewed as a partition of of V, where denotes the (possibly empty) set of vertices assigned colour i , for , and . A graph is k-colourable if it has a k-coloring. The minimum k for which a graph G is k-colourable is called its chromatic number.
In the year 2007, Cioban [
35] generalized the concept of
k-coloring of crisp graph
G in fuzzy graphs by partitioning of the vertex set of
G into independent vertex sets. A vertex subset
is described as an independent vertex set of
if
for all
.
2.2. Basic Concepts in Fuzzy Sets
Definition 1 ([
1]).
Let X be a nonempty universal set. A fuzzy set on X is defined as a mapping , where is the membership degree of x to the fuzzy set . We denote by the collection of all fuzzy subsets of X. Fuzzy sets are generalizations of the classical sets represented by their characteristic functions . In our case means full membership of x in , whereas expresses nonmembership, but in contrary to the classical case other membership degrees are allowed. A set is called a height of fuzzy set . Moreover, a fuzzy set is said to be a normal fuzzy set if .
Definition 2 ([
1]).
Let be a fuzzy set. The level sets of are defined as the classical sets.is called the core of the fuzzy set , andis called the support of the fuzzy set. Definition 3 ([
1]).
Let σ be a fuzzy subset of a set S and μ be a fuzzy relation on S. Then μ is called a fuzzy relation on σ ifA fuzzy relation μ is symmetric if for all .
Definition 4 ([
1]).
Let . We say that the fuzzy set is included in ifWe denote .
Definition 5 ([
1]).
Let . The intersection of and is the fuzzy set withWe denote .
Definition 6 ([
1]).
Let . The union of and is the fuzzy set , whereWe denote .
Definition 7 ([
1]).
Let be a fuzzy set. The complement of is the fuzzy set whereWe denote .
2.3. Basic Concepts of Fuzzy Graph Coloring
Kaufmann proposed the concept of fuzzy graphs . Meanwhile, Rosyida initiated the concept of fuzzy graphs based on the fuzzy relation.
In this paper, we consider fuzzy graphs , which denote the incompatibility graph. Every fuzzy graph is assumed to be finite, with no loops and an undirected graph.
Definition 8 ([
2]).
Let be a fuzzy graph, where V is the vertex set, the fuzzy edge set is characterized by the matrix : such that , and is the membership function. This type of fuzzy graph is also called a type 1 fuzzy graph.
For the sake of brevity, we declare that in this paper, each element represents the incompatible level of the edge for all with . , which is chosen suitably in all the examples, is symmetric (i.e., ). In addition, we denote the underlying crisp graph of by , where .
Assume
, where
is the fundamental set (level set) of
. In fact, a fuzzy graph
can be regarded as a generalization of an incompatibility graph
. Taking
,
becomes a crisp graph if matrix
is defined as
for any
.
Definition 9 ([
2]).
Let be a fuzzy graph having a crisp vertex set and fuzzy edge set with membership function . The fuzzy graph is called a fuzzy subgraph of , if and . Similarly, the fuzzy graph is called a fuzzy subgraph of induced by P if and for . We write to denote the fuzzy subgraph induced by P. The concept of chromatic number of fuzzy graphs (Definition 10) was introduced by Mu
oz et al. [
32]. The authors considered fuzzy graphs with a crisp vertex set, and edges with membership degree in
; moreover, they showed that the fuzzy chromatic number of a fuzzy graph is a normalized fuzzy number whose modal value is associated with the empty edge-set graph. Its meaning depends on the sense of index
, and it can be interpreted in the following way. For lower values of
there are many incompatible links between vertices and, consequently, more colors are needed in order to consider these incompatibilities. On the other hand, for higher values of
there are fewer incompatible links between vertices and fewer colors are needed (see [
32]). In order to deal with the ambiguity problem, the chromatic number summarizes all this information.
Given a fuzzy graph
, which can be characterized by the family of its
-cut graphs, and the membership function of
is
. In order to obtain more information about it, a natural approach is to analyze the family of the
-cut graphs. Let
be the family of
-cut sets of
, and the
-cut of a fuzzy graph be a crisp graph
with
. Hence, any (crisp)
k-coloring can be defined on
. The
k-coloring function of
is defined through this sequence. For each
, let
denote the chromatic number of
. The chromatic number of
is defined through a monotone family of sets [
32].
Definition 10 ([
32]).
If is such a fuzzy graph, where and μ is a fuzzy number on the set of all subsets of . Assume , where is the fundamental set (level set) of . For each , denotes the crisp graph , where and denotes the chromatic number of crisp graph . Based on Definition 10, we extend the chromatic number of fuzzy graph as the max number of as follows.
Definition 11. Let be a fuzzy graph, μ be a fuzzy number on the set of all subsets of , and be the fundamental set of . For any , denotes the crisp graph with , and denotes the chromatic number of the crisp graph . The chromatic number of fuzzy graph is the number .
Definition 12 ([
40]).
(Union) Let and be finite nonempty sets, and be two fuzzy graphs where the membership functions of and are and , respectively. A union of and is a fuzzy graph which has a vertex set and a fuzzy edge set with , for all . If , then is called a disjointed union of fuzzy graphs and . 2.4. Operations on Fuzzy Graphs
Definition 13. (Isomorphic) Let and be two fuzzy graphs, and be the membership functions of and , respectively. We will say that and are isomorphic, written by , if there exists a bijection such that for all .
Definition 14. (Complement) Let be a fuzzy graph, μ be the membership functions of . The complement graph of is a fuzzy graph with , for any . Moreover, if , then is called self-complementary.
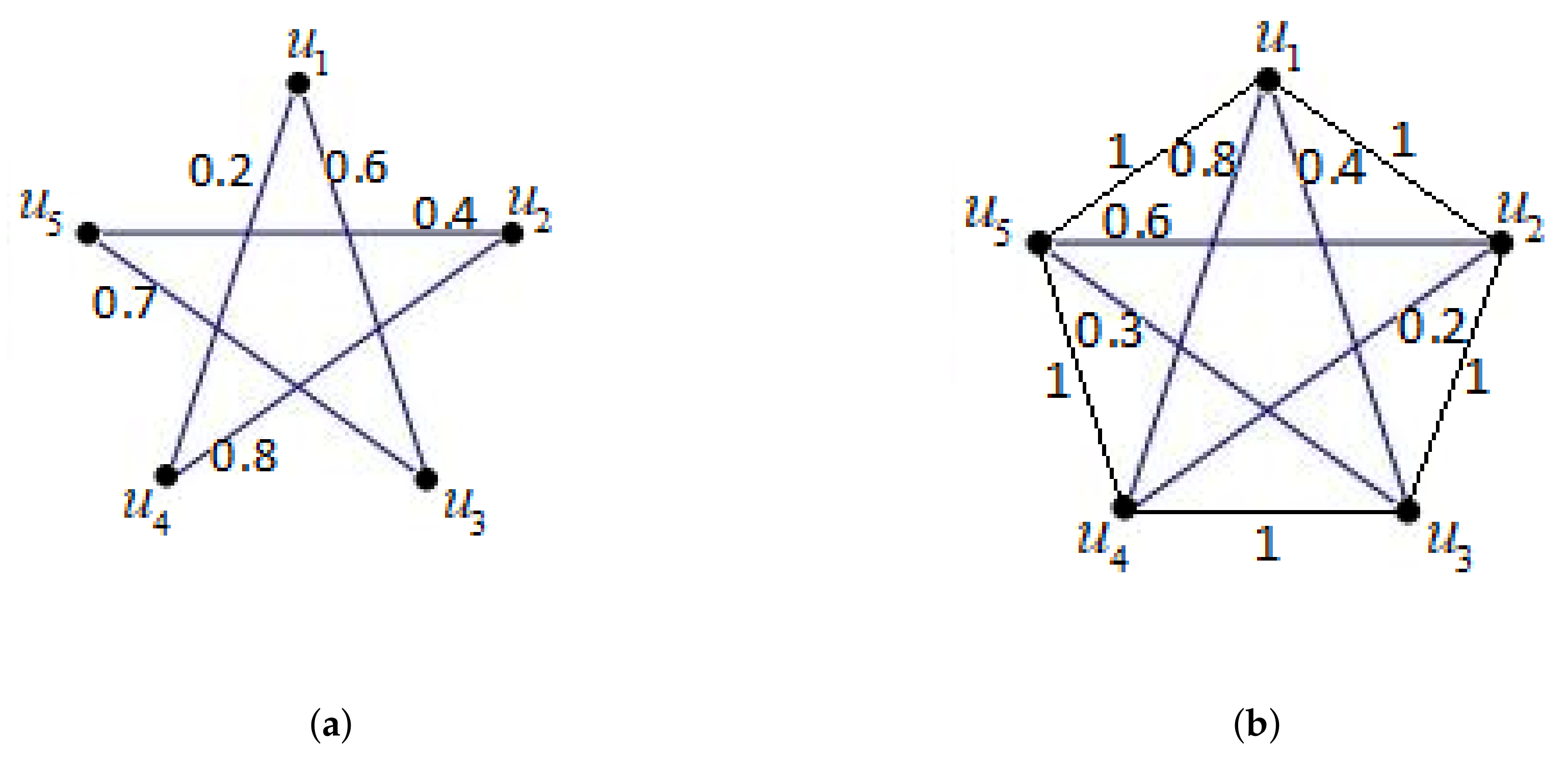
Example 1. Let be a fuzzy graph, , the membership function of be is shown as (a) in Figure 1. For simplicity, we show only the computing of and . By Definition 14, we have , . The position of in matrix is the first row and the third column, the position of in matrix μ is the first row and the fourth column. By computing, it is easy to obtain , as shown as (b) in Figure 1, , and the membership function of is Definition 15. (Fuzzy neighbour edge set) Let be a fuzzy graph. For a given vertex u in vertex set V, the fuzzy edge set is called the fuzzy neighbour edge set of vertex u, denoted by .
Definition 16. (Fuzzy complete graph) A fuzzy graph is a fuzzy complete graph, if , for all .
Definition 17 ((Clique) [
41]).
A clique of simple crisp graphs is a subset S of V, such that the graph induced by S is complete. Remark 1. Let be a fuzzy graph with the underlying graph . A clique with maximum number of vertices in is a maximal clique of the graph .
Definition 18. (Cap) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The cap of and is a fuzzy graph which has a fuzzy edge set , and , for all .
Definition 19. (Difference) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The difference of and is a fuzzy graph which has a fuzzy edge set , and , for all .
Definition 20. (Ring sum) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The ring sum of and is a fuzzy graph Remark 2. The ring sum of two fuzzy graphs satisfies commutative law and associative law, i.e., Definition 21. (Join) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The join of two disjoint fuzzy graphs and is a fuzzy graph , where , , is the set of all edges joining and , and the membership function of is , is calculated as follows: Example 2. Given two fuzzy graphs and , where and , the membership functions of and are and , respectively: By Definition 21, we can obtain the join of fuzzy graphs and , denoted by , where and the membership function of is μ as follows. For simplicity, we show only the computing of and . By Definition 21, we have The position of in matrix μ is the fourth row and the first column, the position of in matrix μ is the fourth row and the third column.
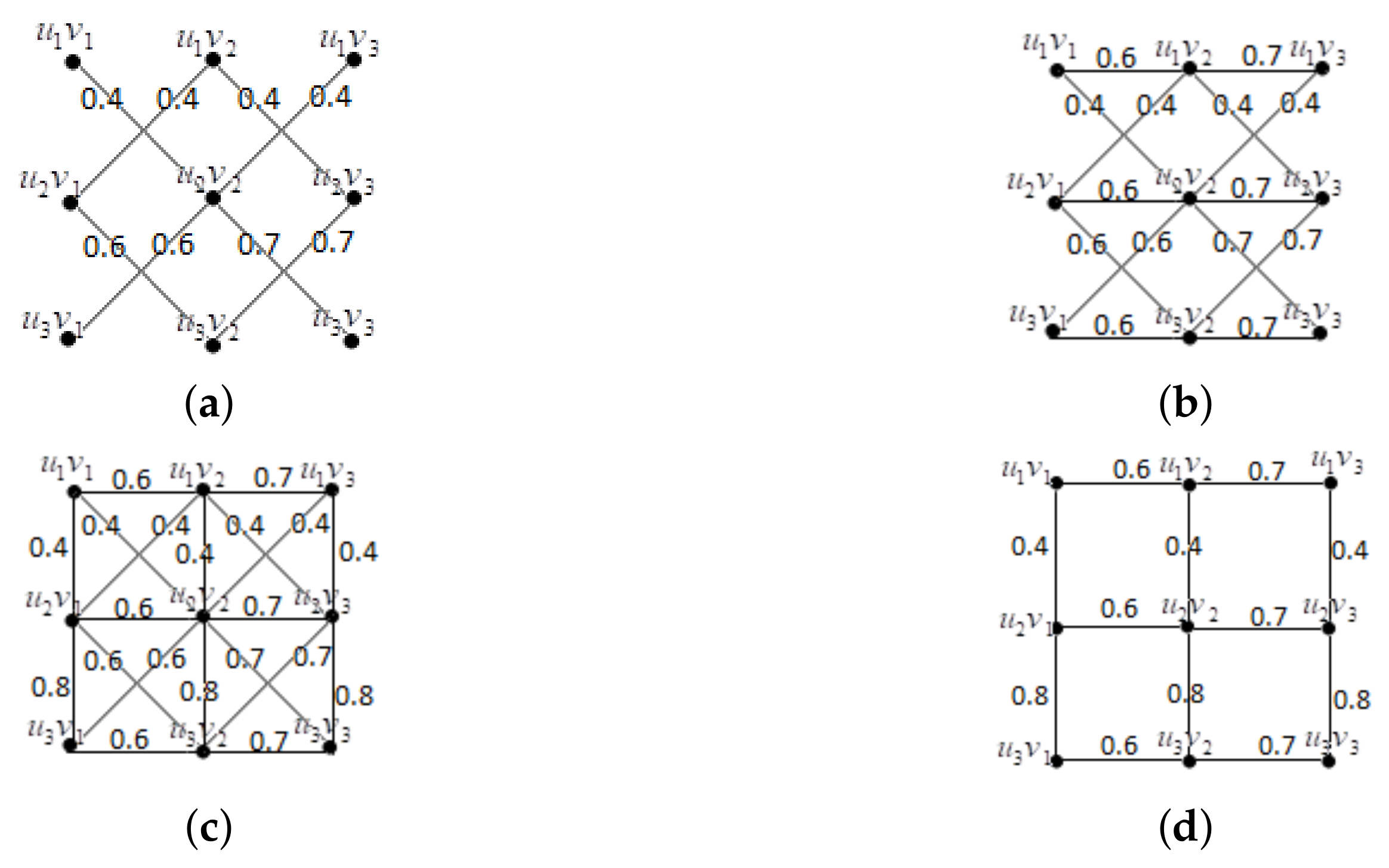
Fuzzy graphs , and are shown as (a), (b), and (c) in Figure 2, respectively. Definition 22. (Direct product) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The direct product of two fuzzy graphs and is a fuzzy graph , where , and , Definition 23. (Semiproduct) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The semiproduct of two fuzzy graphs and is a fuzzy graph , where , and , Definition 24. (Strong product) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The strong product of two fuzzy graphs and is a fuzzy graph , where , and , Definition 25. (Cartesian product) Let and be two fuzzy graphs, and be the membership functions of and , respectively. The Cartesian product of two fuzzy graphs and is a fuzzy graph , where , and , Example 3. Consider two fuzzy graphs and with the underlying graph and , respectively, such that , and , , the corresponding to and are shown as follows: Then the direct product , the semiproduct , the strong product and the Cartesian product of above two fuzzy graphs and as shown in Figure 3a–d, respectively. 3. Chromatic Number of Fuzzy Graphs
Lemma 1. Let and be two fuzzy graphs, and be the underlying graphs of and , respectively. If then .
Proof. Suppose that , and then there exists a bijection such that for all . It is obvious that there exists a bijection such that for all , i.e., . □
Lemma 2. For two fuzzy graphs and , if then .
Proof. Obviously, this lemma can be obtained from Lemma 1, and the definition of the chromatic number of fuzzy graphs. □
Theorem 1. Let be a self-complementary fuzzy graph, and the chromatic number of fuzzy graph is the same with the fuzzy graph .
Proof. By the definition of the self-complementary fuzzy graph, it is obvious that . Furthermore, based on Lemma 2, it is obvious that . □
Lemma 3. Let and be two fuzzy graphs. If then .
Proof. It is clear that if . □
Corollary 1. For two fuzzy graphs and . If , then .
Theorem 2. Let be a fuzzy graph. If is the fundamental set of , then for such that , we have .
Proof. For the fuzzy graph , if , then is a crisp graph, where . Meanwhile, is a crisp graph, where .
Let , then , i.e., . Therefore, , and by Lemma 3, . □
Theorem 3. Let and be two fuzzy graphs, the chromatic numbers of and be and , respectively. If fuzzy graph is the union of two fuzzy graphs and , then the chromatic number of satisfies .
Proof. We will construct the union of fuzzy graphs and . We consider the following two cases.
Case 1. . Assume that , and are the membership functions of , and , respectively. Because , it is clear that with for all if and only if or . For each in the fundamental set of , either belongs to the fundamental set of or to the fundamental set of . Hence, the minimum value of in the fundamental set of is the minimum among that in the fundamental sets of and . Let it be , the minimum value of in the fundamental set of . Then has all the adjacencies of and . By Definition 4, .
Case 2. .
In this case, there are two possibilities as follows.
- (i)
There do not form new cycles in fuzzy graphs . It is obvious that .
- (ii)
There are new cycles formed in the fuzzy graph . In order to satisfy , new colors may be required in . It is obvious that .
Combining the above results, we obtain that . □
Corollary 2. For two fuzzy graphs and . If , then .
Theorem 4. Let and be two fuzzy graphs, the chromatic numbers of and be and , respectively. If is the difference of two fuzzy graphs and , then the chromatic number of satisfies .
Proof. By the definition of the difference between fuzzy graphs, we have . Moreover, based on Lemma 3, it is obvious that . □
Theorem 5. Let and be two fuzzy graphs, the chromatic numbers of and be and , respectively. If is the cap of two fuzzy graphs and , then the chromatic number of satisfies .
Proof. By the definition of the cap of two fuzzy graphs, , . Also, and . By Lemma 3, it is clear that . □
Theorem 6. Let and be two fuzzy graphs, the chromatic numbers of and be and , respectively. If is the ring sum of two fuzzy graphs and , then the chromatic number of satisfies .
Proof. By the definition of the ring sum in fuzzy graphs, we know . Based on the proof of Theorem 3 and Lemma 3, there are . □
Theorem 7. Let and be two fuzzy graphs, the chromatic numbers of and be and , respectively. If is the join of two fuzzy graphs and , then the chromatic number of satisfies where . Equality holds if and are complete graphs, where and are the underlying graphs of and , respectively.
Proof. By the definition of join in fuzzy graphs, the underlying graph of join graph becomes a complete graph if and only if both and are complete graphs. □
Remark 3. Let and be two fuzzy graphs, the fuzzy graph is the join of and , then is a fuzzy complete graph if and are both fuzzy complete graphs.
Theorem 8. For two fuzzy graphs and , the chromatic number of the direct product .
Proof. By the definition of direct product of fuzzy graphs, any two vertices are adjacent if and only if the corresponding vertices in and are adjacent. Because the chromatic number depends on adjacency, the number of colors required to color the vertices of is the minimum of and . □
Theorem 9. For two fuzzy graphs and , the chromatic number of the semiproduct . Where C is a maximal clique of .
Proof. By the definition of semiproduct, the largest complete subgraph of is the graph with corresponding adjacent vertices and , where and , i.e., the largest complete subgraph is the graph with edges of the form with as a vertex of maximum degree in and edges of the form , where and . Hence the chromatic number of the semiproduct is the chromatic number corresponding to this largest complete subgraph. □
Theorem 10. For two fuzzy graphs with the membership function and with the membership function . If and , for all and , the chromatic number of the strong product , where and .
Proof. By the definition of strong product, if and , for all and , then is a complete graph with vertices. Hence, . □
Theorem 11. For two fuzzy graphs and , the chromatic number of the Cartesian product , where and .
Proof. The Cartesian product graph
decomposes into
copies of
and
copies of
, where
and
. By the definition of Cartesian product,
has two types of edges: those with vertices that have the same first coordinate, and those with vertices that have the same second coordinate. The edges joining vertices with a given value of the first coordinate form a copy of
, so the edges of the first type form
. Similarly, the edges of the second type form
, and the union is as follows:
Based on the proof of Theorem 3, it is obvious that . □
4. Application of Chromatic Number of Fuzzy Graphs
In this section, we describe a couple of example applications of the chromatic number of fuzzy graphs.
4.1. The Examination Problem
The examination scheduling problem consists of assigning a number of exams to a number of slots within the examination period, taking into account that students cannot take more than one exam at the same time. This problem can be modeled as a classical coloring problem. Each exam is a vertex of the graph, and the edges link those incompatible exams in the sense that at least one student shares both of them. Each color represents a slot, and all equally colored vertices are assigned to the same slot. The minimum chromatic number has the same property of minimizing the overall exam period.
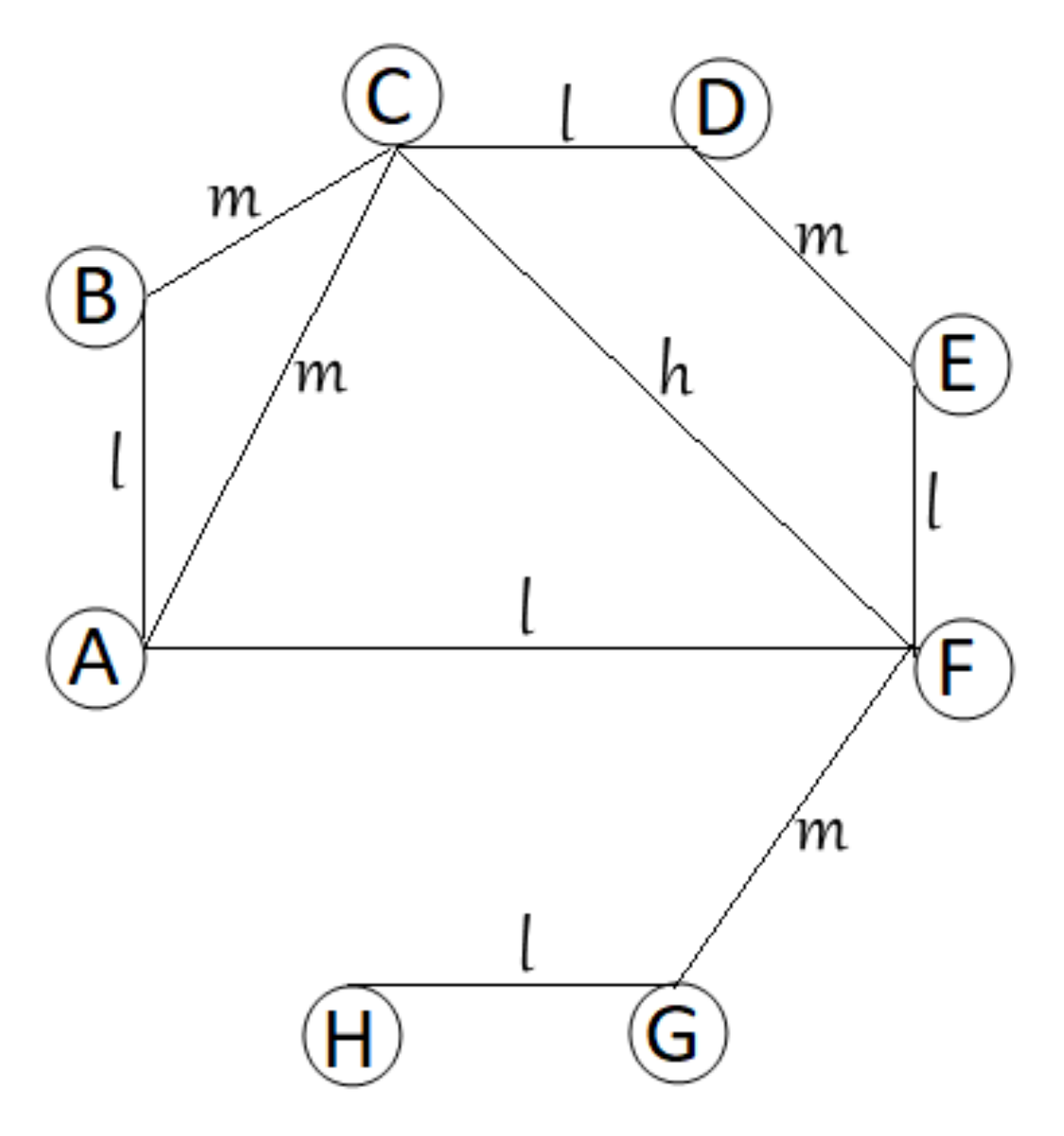
Now, we take into account the difficulty and the implied specialties or profiles and other factors of the examination subjects. The incompatibility between the exams is valued in the following way: n if they are compatible, and l, m and h if the incompatibility degree is, respectively, low, medium, and high. The incompatibility degree can be interpreted in the following way: any compatible exams can share the same slot; if the incompatibility degree between exams i and j is l, m, or h, then both exams must be scheduled, leaving at least 1, 2, or 3 slots between them, respectively (to ensure that students have relatively sufficient review time). Then, this problem can be modeled by means of fuzzy graphs.
Example 4. Suppose there are eight exams . The model of this examination scheduling problem is a fuzzy graph , where , The corresponding fuzzy graphs is depicted in Figure 4. The problem is to schedule the eight exams with these constraints and minimizing the overall exam period. For the above data, the minimum number of slots is four and an optimum schedule (in other words we need 4 colours to dye the vertices in this fuzzy graph) by
Table 1.
4.2. The Traffic Light System Problem
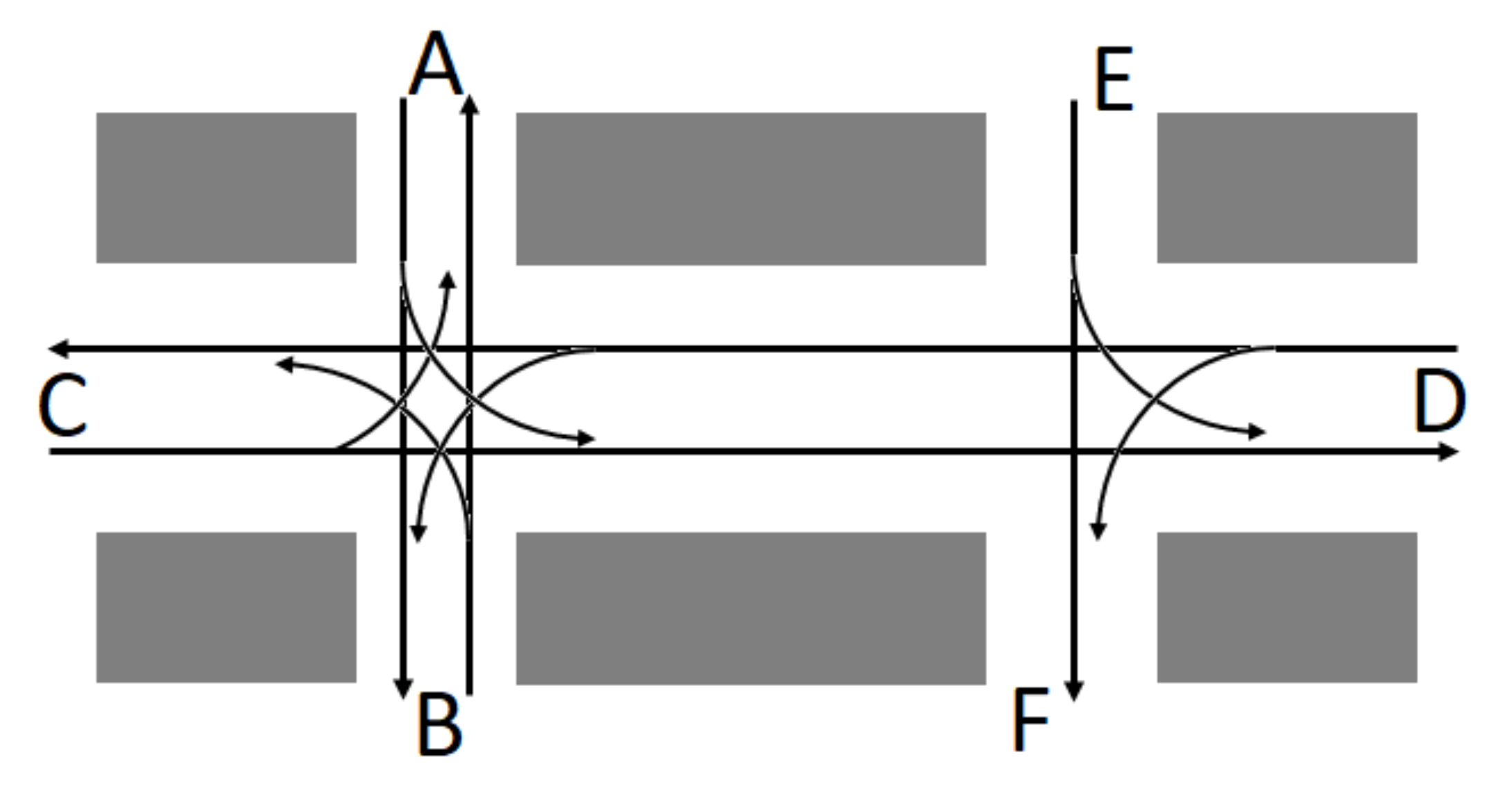
Let us consider a four-way crossroad at two intersections, as illustrated in
Figure 5. There are four directions on the left side intersection, i.e.,
A on the north,
B on the south,
C on the west, and
D on the east. Moreover, there are four directions at the right side of the intersection, i.e.,
E,
F,
C, and
D. Thus, there are traffic movements in different directions, i.e.,
,
,
,
,
,
,
,
,
,
, and
. Certain routes, such as
and
,
and
, and
and
, are compatible with one another, whereas others, such as
and
,
and
, are not.
A vertex represents the movement of traffic from one direction to another. Two vertices that represent incompatible traffic movements should be connected with an edge. The traffic light system will be modified by the vertex coloring of fuzzy graphs. The minimum chromatic number has the same property of minimizing the traffic light phases.
One can represent the two signaled intersections through the union of two fuzzy graphs. A membership degree of a fuzzy edge represents the incompatibility of two vertices, which is a possibility for traffic incidents to occur between vehicles from both traffic movements.
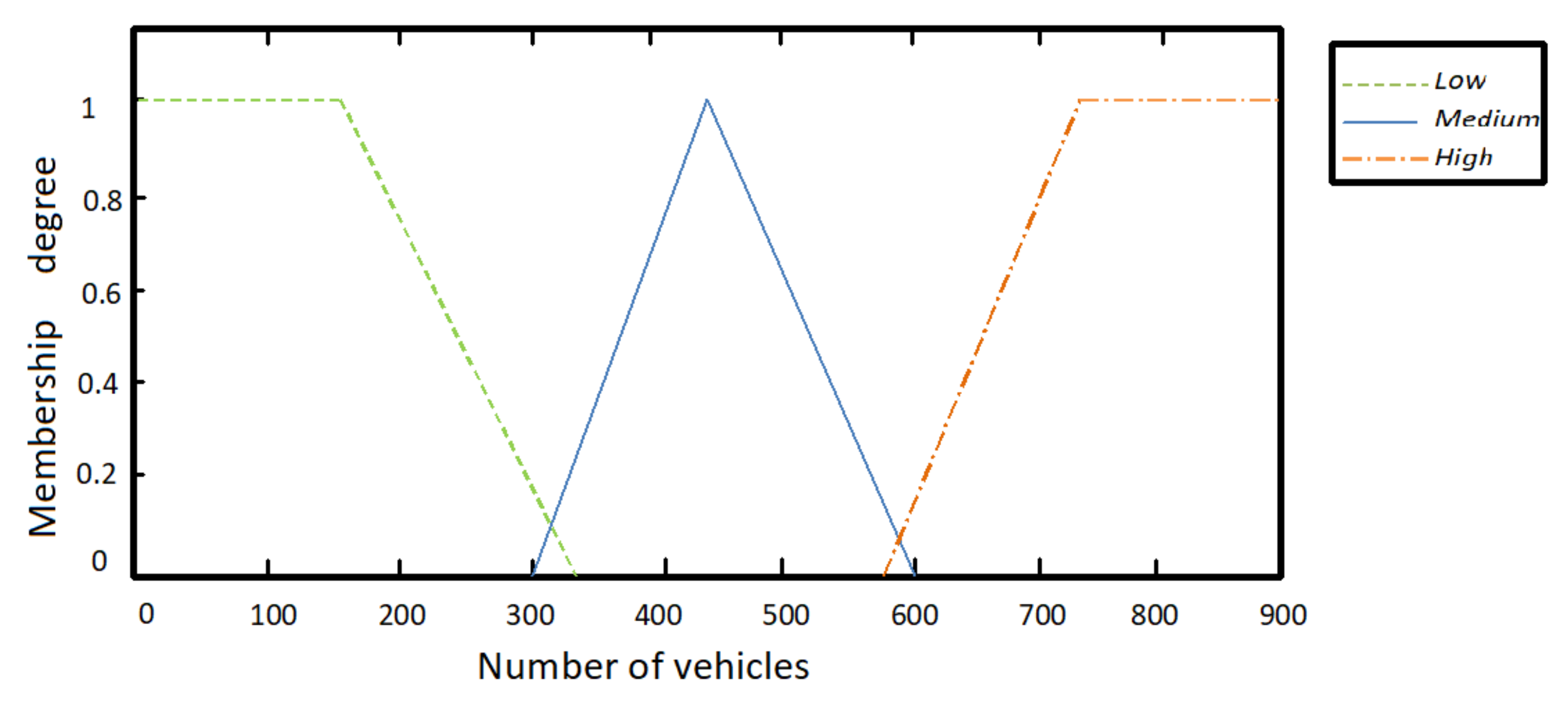
The first stage in research is to divide the data on traffic flows into three groups of fuzzy sets, i.e., low, medium, or high flows, as shown in
Table 2.
The symbols
l,
m, and
h mean low, medium, and high, respectively. The notation
n denotes the number of vehicles per hour (vehicles/h) involved in a traffic movement. A trapezoidal membership function at intervals of
is used to present the fuzzy set of low traffic flow, a triangular membership function at intervals of
is used to present the fuzzy set of medium traffic flow, and a trapezoidal membership function at intervals of
is used to present the fuzzy set of high traffic flow.
Figure 6 depicts the fuzzification of traffic flow data in
Table 2. Displaying the membership degree of an edge is helpful in order to understand the incompatibility of two traffic flows.
The second step is to determine the degrees of membership of all edges by using a rule as follows.
- (i)
If traffic movements and are incompatible, then there is an edge . In addition, we choose a maximum value of membership degree of and to determine the membership degree of the fuzzy edge .
- (ii)
If the traffic movements and are compatible, which means they can move at the same time, then there is no edge. This indicates that the fuzzy edge’s membership degree is 0.
Therefore, traffic flows on the left and right intersection in
Figure 5 can be modelled as two fuzzy graphs
and
based on the given rules, respectively, where the vertex sets are
and
.
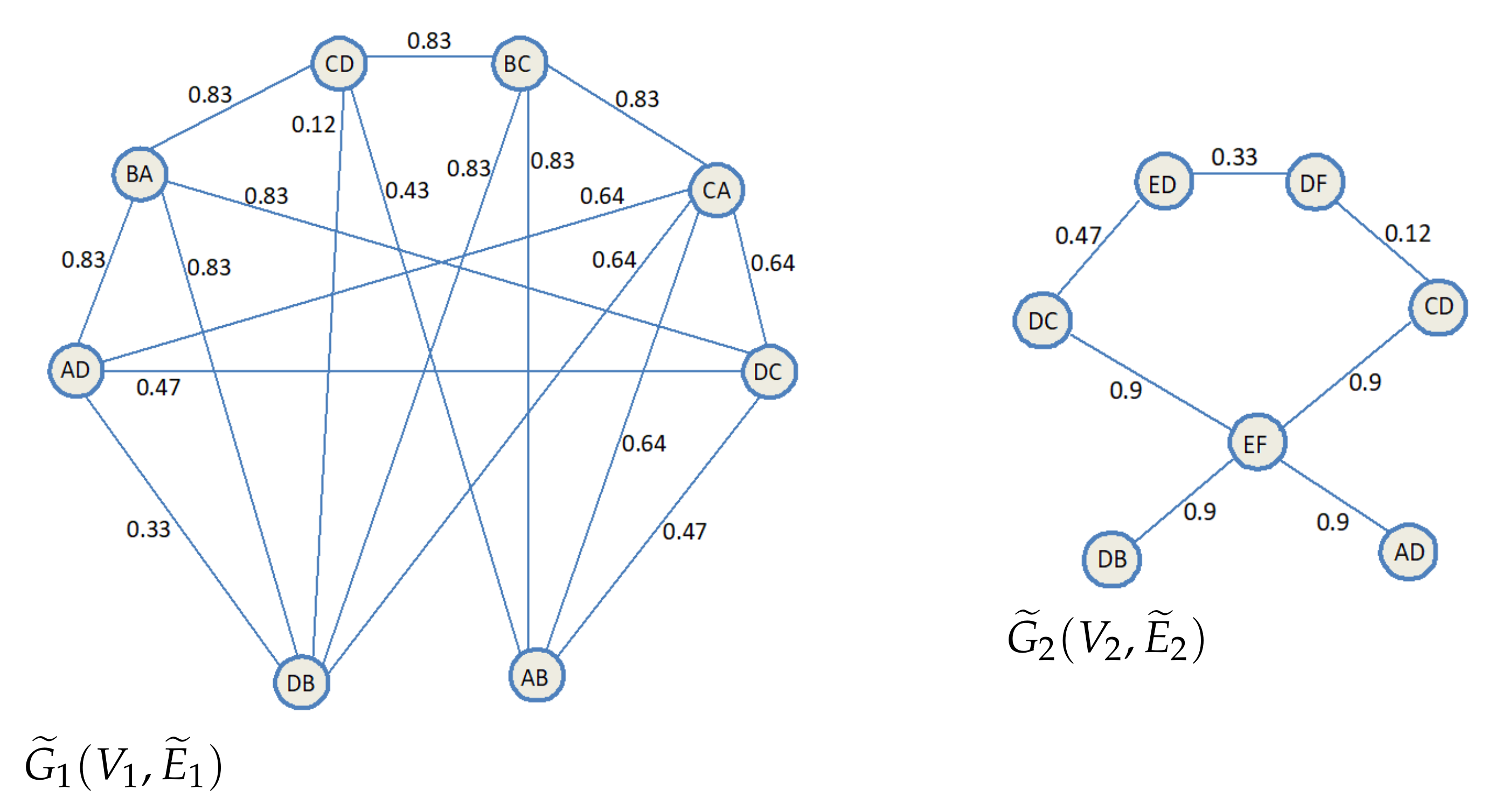
The membership degrees of edges in fuzzy edge set
is presented in
Table 3. One can obtain the fundamental set
of fuzzy graph
from
Table 3. It can be known that routes
and
are more incompatible than routes
and
. The fuzzy graphs
and
are shown as
Figure 7.
There exist some methods of colouring in fuzzy graphs. It is not difficult to get chromatic numbers of fuzzy graphs and by using any chromatic algorithm. The chromatic numbers of and are as follows: and .
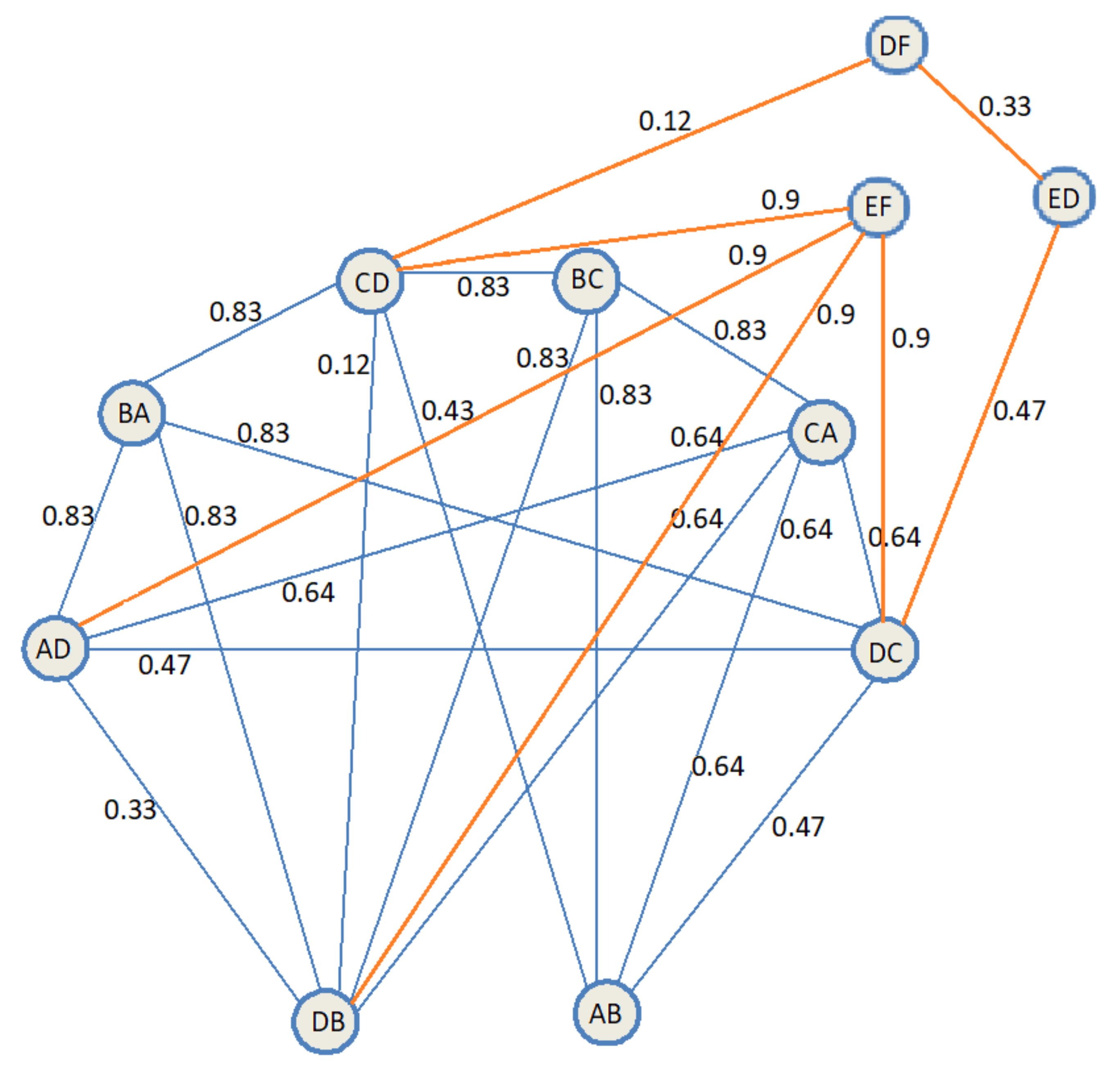
Furthermore, two intersections in
Figure 5 can be modelled into an integrated traffic light system by using a union of fuzzy graphs
as illustrated in
Figure 8. According to Definition 11 and Theorem 3, we get chromatic number of union in
Figure 7 as follows:
.
The chromatic number of crisp graphs can be interpreted as follows: the number k represents the number of phases needed on the integrated system and degree of membership represents the possibility that there may occur traffic incidents when we use k phases.
Based on chromatic number
k of
-cut graph of fuzzy graph
, traffic flows in
Figure 5 could be arranged in particular patterns as shown in
Table 4. For higher values of
(i.e., the higher degree of incompatibility), there are fewer colors needed and less safety. For example, when we make use of
phases, then 0.64 degree of incompatibility is reached. Traffic flows allowed to move simultaneously (i.e., get the green light) on the first phase are
,
,
,
and
,
,
,
on the second phase,
,
and
on the third phase.
Finally, one can obtain an optimal arrangement. The optimality is reached when maximum safety level is attained (i.e., the minimum degree of incompatibility) whereas the number of phases is minimum (i.e., minimum cycle time of traffic light). When , the objective is reached, traffic flows allowed to move simultaneously on the first phase are , and , , , , and on the second phase, and on the third phase, and and on the fourth phase. Only in this way can the maximum avoid traffic incidents.