Latent Multi-View Semi-Nonnegative Matrix Factorization with Block Diagonal Constraint
Abstract
1. Introduction
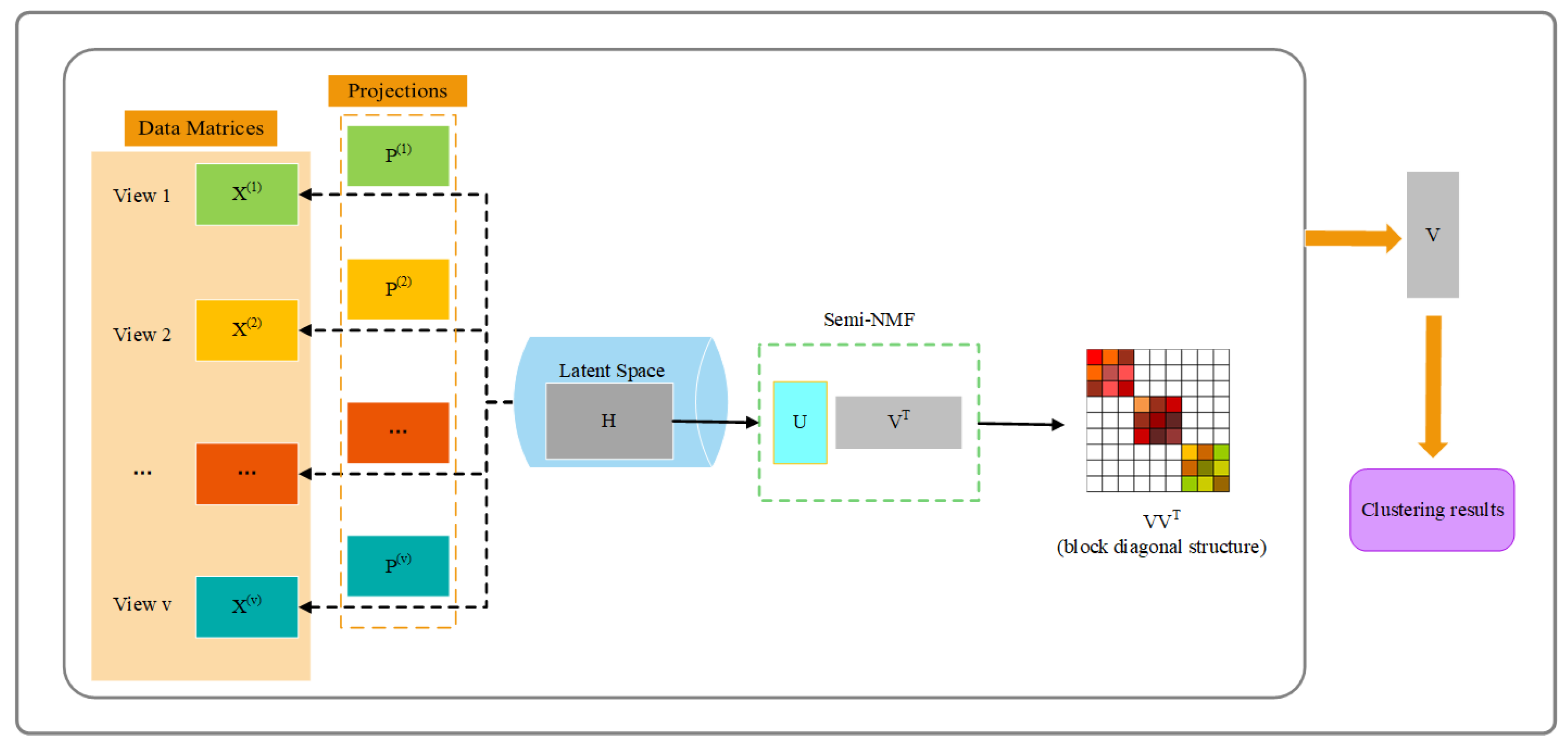
- Benefited from the latent representation and Semi-NMF, our algorithm can get a robust low-dimensional representation that fused the consistent information of the multiple views.
- Deploying the graph regularization, our model is able to keep the local geometry consistency between the new low-dimensional representation and original multi-view data.
- By adding the k-block diagonal constraint, not only our model sufficiently utilizes the prior information, but the new low-dimensional representation captures the global structure.
2. Notations and Related Works
2.1. Notations
2.2. NMF and Semi-NMF
2.3. Block Diagonal Constraint
3. Proposed Method
3.1. Latent Representation Learning
3.2. Lower Dimensional Representation Learning
3.3. Local Geometry Preserving
3.4. Our Proposed Model
4. Optimization
| Algorithm 1:LMSNB |
Input: Multi-view data X, , , , the dimension K of latent representation H. Initialize:, , , , , , , , . Initialize H, U, V with random values. Generating a weight matrix S of Multi-view data X by Equation (7). whilenot convergeddo 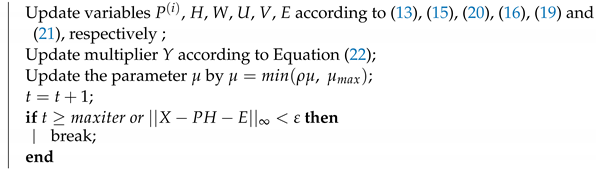 end Output:P, H, E, U, V. |
5. Experiment
5.1. Compared Algorithms
5.2. Evaluation Metrics
5.3. Datasets
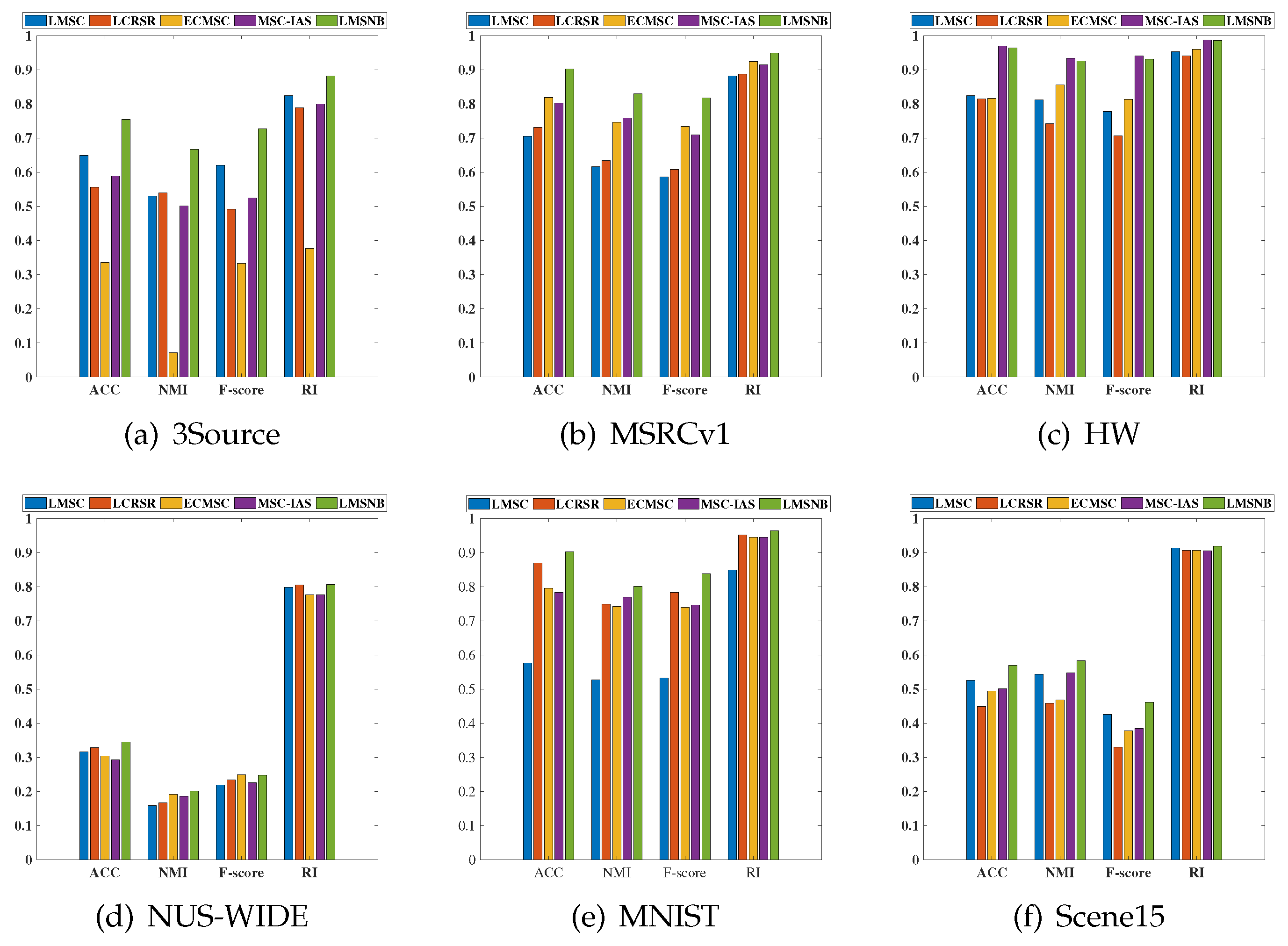
5.4. Clustering Results
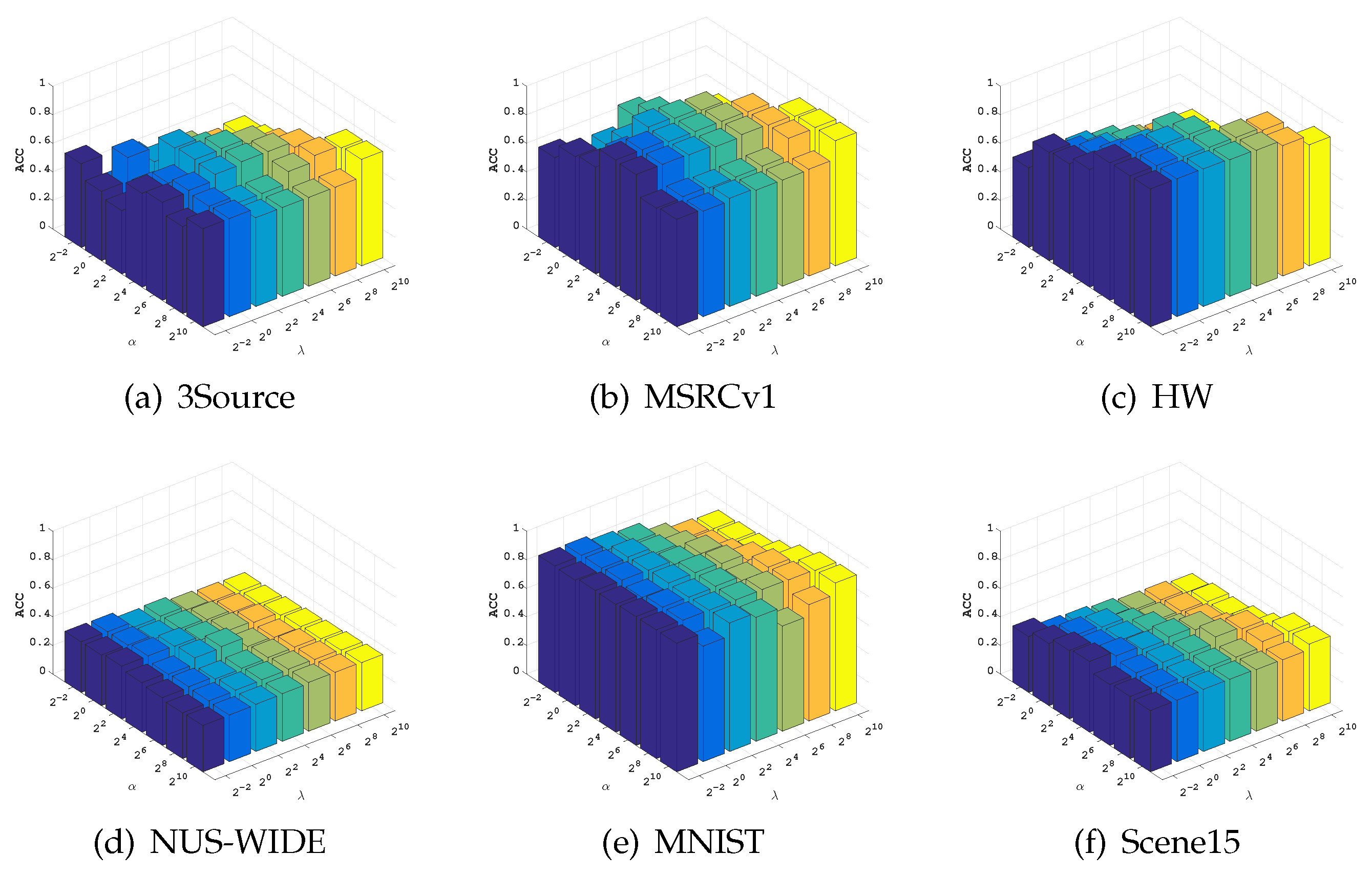
5.5. Parameter Sensitivity Analysis
5.6. Ablation Study
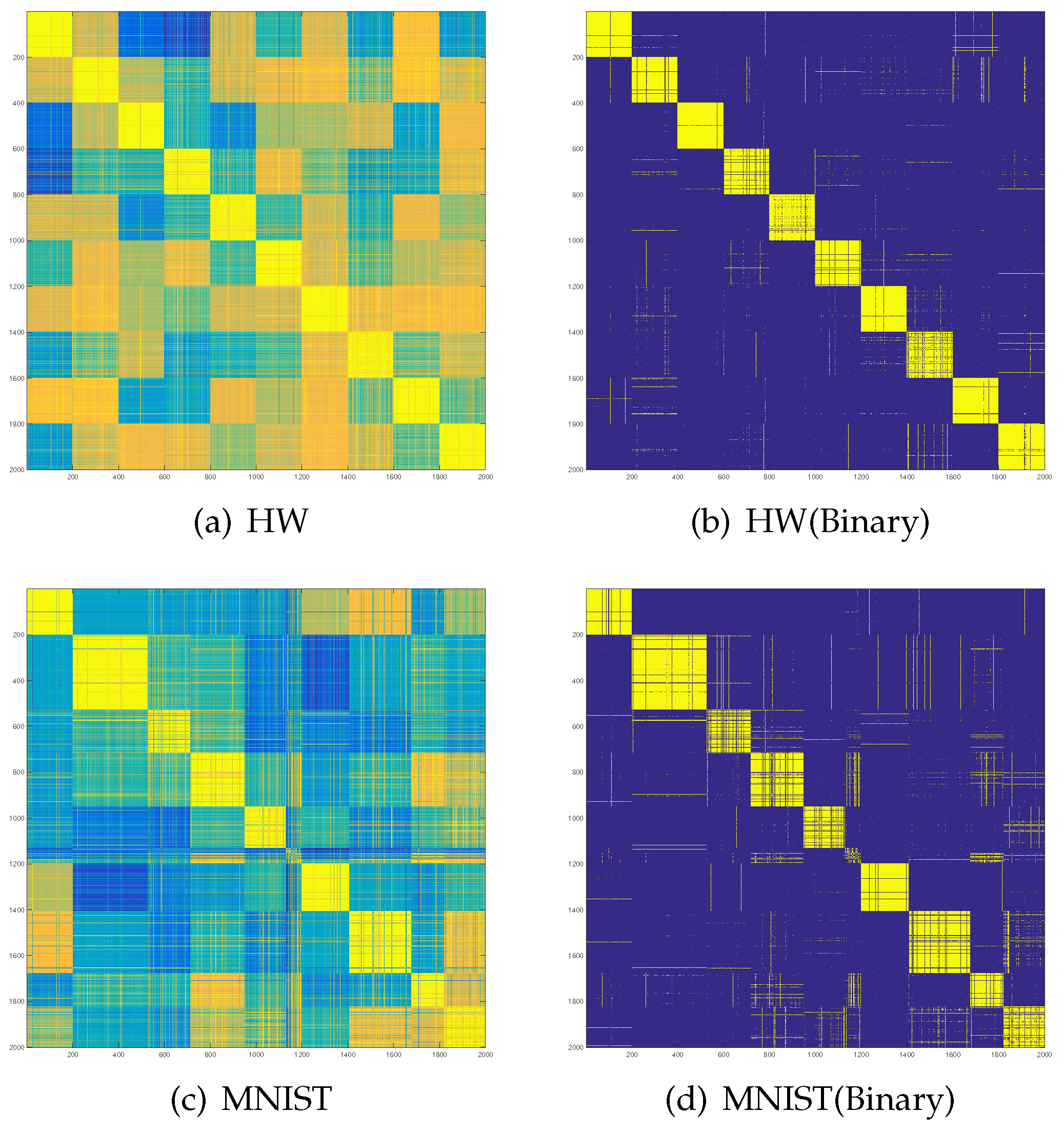
5.7. Visualization of
5.8. Time Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MVC | multi-view clustering |
| SSC | Sparse Subspace Clustering |
| LRR | Low Rank Representation |
| NMF | Nonnegative Matrix Factorization |
| SVD | Singular Value Decomposition |
| KKT | Karush–Kuhn–Tucker |
Appendix A. The Proof of Theorem 4
References
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Ehsan Elhamifar, R.V. Sparse subspace clustering. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; Volume 6, pp. 2790–2797. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 171–184. [Google Scholar] [CrossRef]
- Saberi-Movahed, F.; Rostami, M.; Berahmand, K.; Karami, S.; Tiwari, P.; Oussalah, M.; Band, S.S. Dual Regularized Unsupervised Feature Selection Based on Matrix Factorization and Minimum Redundancy with application in gene selection. Knowl.-Based Syst. 2022, 256, 109884. [Google Scholar] [CrossRef]
- Rostami, M.; Oussalah, M.; Farrahi, V. A Novel Time-Aware Food Recommender-System Based on Deep Learning and Graph Clustering. IEEE Access 2022, 10, 52508–52524. [Google Scholar] [CrossRef]
- Caruso, G.; Gattone, S.A.; Balzanella, A.; Di Battista, T. Cluster Analysis: An Application to a Real Mixed-Type Data Set. In Models and Theories in Social Systems; Springer International Publishing: Cham, Switerland, 2019; pp. 525–533. [Google Scholar] [CrossRef]
- Eisen, M.B.; Spellman, P.T.; Brown, P.O.; Botstein, D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 1998, 95, 14863–14868. [Google Scholar] [CrossRef]
- Takita, M.; Matsumoto, S.; Noguchi, H.; Shimoda, M.; Chujo, D.; Itoh, T.; Sugimoto, K.; SoRelle, J.A.; Onaca, N.; Naziruddin, B.; et al. Cluster analysis of self-monitoring blood glucose assessments in clinical islet cell transplantation for type 1 diabetes. Diabetes Care 2011, 34, 1799–1803. [Google Scholar] [CrossRef]
- Azadifar, S.; Rostami, M.; Berahmand, K.; Moradi, P.; Oussalah, M. Graph-based relevancy-redundancy gene selection method for cancer diagnosis. Comput. Biol. Med. 2022, 147, 105766. [Google Scholar] [CrossRef]
- Bickel, S.; Scheffer, T. Multi-View Clustering. In Proceedings of the Fourth IEEE International Conference on Data Mining (ICDM’04), Brighton, UK, 1–4 November 2004; pp. 19–26. [Google Scholar]
- Chao, G.; Sun, S.; Bi, J. A survey on multi-view clustering. IEEE Trans. Artif. Intell. 2021, 2, 146–168. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Xia, L.; Yan, F.; Wan, Z.; Shi, F.; Yuan, H.; Jiang, H.; Wu, D.; Sui, H.; Zhang, C.; et al. Diagnosis of coronavirus disease 2019 (COVID-19) with structured latent multi-view representation learning. IEEE Trans. Med. Imaging 2020, 39, 2606–2614. [Google Scholar] [CrossRef]
- Fu, L.; Lin, P.; Vasilakos, A.V.; Wang, S. An overview of recent multi-view clustering. Neurocomputing 2020, 402, 148–161. [Google Scholar] [CrossRef]
- Wang, R.; Nie, F.; Wang, Z.; Hu, H.; Li, X. Parameter-free weighted multi-view projected clustering with structured graph learning. IEEE Trans. Knowl. Data Eng. 2019, 32, 2014–2025. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Zhu, E.; Tang, C.; Liu, J.; Hu, J.; Xia, J.; Yin, J. Multi-view Clustering via Late Fusion Alignment Maximization. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019; pp. 3778–3784. [Google Scholar]
- Peng, X.; Huang, Z.; Lv, J.; Zhu, H.; Zhou, J.T. COMIC: Multi-view clustering without parameter selection. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 5092–5101. [Google Scholar]
- Nie, F.; Shi, S.; Li, X. Auto-weighted multi-view co-clustering via fast matrix factorization. Pattern Recognit. 2020, 102, 107207. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Wang, R.; Nie, F. Multi-view clustering: A scalable and parameter-free bipartite graph fusion method. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 330–344. [Google Scholar] [CrossRef]
- Kumar, A.; Daumé, H. A co-training approach for multi-view spectral clustering. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 393–400. [Google Scholar]
- Lee, C.; Liu, T. Guided co-training for multi-view spectral clustering. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 4042–4046. [Google Scholar]
- Lu, R.; Liu, J.; Wang, Y.; Xie, H.; Zuo, X. Auto-encoder based co-training multi-view representation learning. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 23rd Pacific-Asia Conference, PAKDD 2019, Macau, China, 14–17 April 2019; Springer: Cham, Switerland, 2019; pp. 119–130. [Google Scholar]
- Zhao, B.; Kwok, J.T.; Zhang, C. Multiple kernel clustering. In Proceedings of the 2009 SIAM International Conference on Data Mining, Sparks, NV, USA, 30 April–2 May 2009; pp. 638–649. [Google Scholar]
- Sun, M.; Wang, S.; Zhang, P.; Liu, X.; Guo, X.; Zhou, S.; Zhu, E. Projective Multiple Kernel Subspace Clustering. IEEE Trans. Multimed. 2021, 24, 2567–2579. [Google Scholar] [CrossRef]
- Nie, F.; Li, J.; Li, X. Parameter-free auto-weighted multiple graph learning: A framework for multiview clustering and semi-supervised classification. In Proceedings of the IJCAI, New York, NY, USA, 9–15 July 2016; pp. 1881–1887. [Google Scholar]
- Hussain, S.F.; Mushtaq, M.; Halim, Z. Multi-view document clustering via ensemble method. J. Intell. Inf. Syst. 2014, 43, 81–99. [Google Scholar] [CrossRef]
- Nie, F.; Li, J.; Li, X. Self-weighted Multiview Clustering with Multiple Graphs. In Proceedings of the IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 2564–2570. [Google Scholar]
- Zhang, C.; Fu, H.; Hu, Q.; Cao, X.; Xie, Y.; Tao, D.; Xu, D. Generalized latent multi-view subspace clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 86–99. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, X.; Xiong, J.; Zhou, S.; Zhao, W.; Zhu, E.; Cai, Z. Consensus one-step multi-view subspace clustering. IEEE Trans. Knowl. Data Eng. 2020, 34, 4676–4689. [Google Scholar] [CrossRef]
- Gao, H.; Nie, F.; Li, X.; Huang, H. Multi-view subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4238–4246. [Google Scholar]
- Brbić, M.; Kopriva, I. Multi-view low-rank sparse subspace clustering. Pattern Recognit. 2018, 73, 247–258. [Google Scholar] [CrossRef]
- Wang, X.; Guo, X.; Lei, Z.; Zhang, C.; Li, S.Z. Exclusivity-consistency regularized multi-view subspace clustering. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 923–931. [Google Scholar]
- Xu, C.; Tao, D.; Xu, C. Multi-view intact space learning. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2531–2544. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Q.; Fu, H.; Zhu, P.; Cao, X. Latent multi-view subspace clustering. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4279–4287. [Google Scholar]
- Lin, K.; Wang, C.; Meng, Y.; Zhao, Z. Multi-view unit intact space learning. In Knowledge Science, Engineering and Management, Proceedings of the 10th International Conference, KSEM 2017, Melbourne, VIC, Australia, 19–20 August 2017; Springer: Cham, Switzerland, 2017; pp. 211–223. [Google Scholar]
- Huang, L.; Chao, H.Y.; Wang, C.D. Multi-view intact space clustering. Pattern Recognit. 2019, 86, 344–353. [Google Scholar] [CrossRef]
- Tao, H.; Hou, C.; Qian, Y.; Zhu, J.; Yi, D. Latent complete row space recovery for multi-view subspace clustering. IEEE Trans. Image Process. 2020, 29, 8083–8096. [Google Scholar] [CrossRef]
- Chen, M.; Huang, L.; Wang, C.; Huang, D. Multi-view clustering in latent embedding space. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3513–3520. [Google Scholar]
- Xie, D.; Gao, Q.; Wang, Q.; Zhang, X.; Gao, X. Adaptive latent similarity learning for multi-view clustering. Neural Netw. 2020, 121, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Lei, Z.; Guo, X.; Zhang, C.; Shi, H.; Li, S.Z. Multi-view subspace clustering with intactness-aware similarity. Pattern Recognit. 2019, 88, 50–63. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T. Graph regularized non-negative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar]
- Ding, C.H.; Li, T.; Jordan, M.I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 45–55. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.; Gao, J.; Han, J. Multi-view clustering via joint nonnegative matrix factorization. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 252–260. [Google Scholar]
- Hidru, D.; Goldenberg, A. EquiNMF: Graph Regularized Multiview Nonnegative Matrix Factorization. arXiv 2014, arXiv:1409.4018. [Google Scholar]
- Rai, N.; Negi, S.; Chaudhury, S.; Deshmukh, O. Partial multi-view clustering using graph regularized NMF. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2192–2197. [Google Scholar]
- Zhao, H.; Ding, Z.; Fu, Y. Multi-view clustering via deep matrix factorization. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2921–2927. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Cichocki, A.; Lee, H.; Kim, Y.; Choi, S. Non-negative matrix factorization with α-divergence. Pattern Recognit. Lett. 2008, 29, 1433–1440. [Google Scholar] [CrossRef]
- Févotte, C.; Idier, J. Algorithms for nonnegative matrix factorization with the β-divergence. Neural Comput. 2011, 23, 2421–2456. [Google Scholar] [CrossRef]
- Feng, J.; Lin, Z.; Xu, H.; Yan, S. Robust subspace segmentation with block-diagonal prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3818–3825. [Google Scholar]
- Lu, C.; Feng, J.; Lin, Z.; Mei, T.; Yan, S. Subspace clustering by block diagonal representation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 487–501. [Google Scholar] [CrossRef] [PubMed]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 585–591. [Google Scholar]
- Dattorro, J. Convex Optimization & Euclidean Distance Geometry; Lulu: Durham, NC, USA, 2019. [Google Scholar]
- Huang, J.; Nie, F.; Huang, H. Spectral rotation versus k-means in spectral clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013; Volume 27. [Google Scholar]
- Yang, J.; Yin, W.; Zhang, Y.; Wang, Y. A fast algorithm for edge-preserving variational multichannel image restoration. SIAM J. Imaging Sci. 2009, 2, 569–592. [Google Scholar] [CrossRef]
- Chua, T.; Tang, J.; Hong, R.; Li, H.; Luo, Z.; Zheng, Y. Nus-wide: A real-world web image database from National University of Singapore. In Proceedings of the ACM International Conference on Image and Video Retrieval, Santorini Island, Greece, 8–10 July 2009; pp. 1–9. [Google Scholar]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2169–2178. [Google Scholar]
- Dai, D.; Van Gool, L. Ensemble projection for semi-supervised image classification. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2072–2079. [Google Scholar]
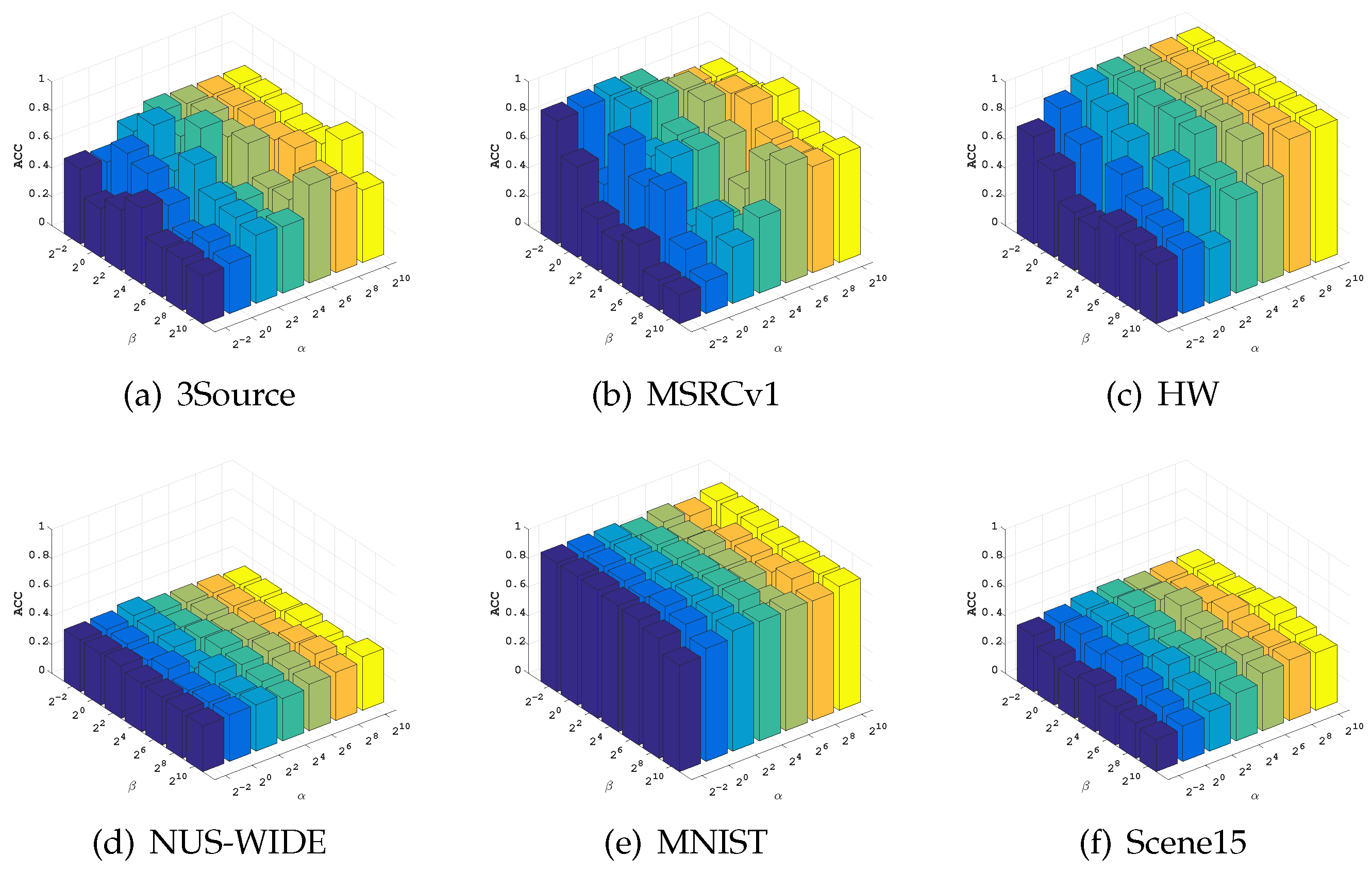
| Datasets | Samples | Views | Clusters |
|---|---|---|---|
| 3Source | 169 | 3 | 6 |
| MSRCv1 | 210 | 5 | 7 |
| HW | 2000 | 6 | 10 |
| NUS-WIDE | 1600 | 6 | 8 |
| MNIST | 2000 | 3 | 10 |
| Scene15 | 4485 | 3 | 15 |
| Parameter | 3Source | MSRCv1 | HW | NUS-WIDE | MNIST | Scene15 |
|---|---|---|---|---|---|---|
| Datasets | Methods | ACC | NMI | F-Score | RI |
|---|---|---|---|---|---|
| 3Sourse | LMSC | ||||
| LCRSR | |||||
| ECMSC | |||||
| MSC_IAS | |||||
| LMSNB | |||||
| MSRCv1 | LMSC | ||||
| LCRSR | |||||
| ECMSC | |||||
| MSC_IAS | |||||
| LMSNB | |||||
| HW | LMSC | ||||
| LCRSR | |||||
| ECMSC | |||||
| MSC_IAS | |||||
| LMSNB | |||||
| NUS-WIDE | LMSC | ||||
| LCRSR | |||||
| ECMSC | |||||
| MSC_IAS | |||||
| LMSNB | |||||
| MNIST | LMSC | ||||
| LCRSR | |||||
| ECMSC | |||||
| MSC_IAS | |||||
| LMSNB | |||||
| Scene15 | LMSC | ||||
| LCRSR | |||||
| ECMSC | |||||
| MSC_IAS | |||||
| LMSNB |
| Datasets | LMSNB | LMSN | t-Test |
|---|---|---|---|
| 3Sourse | Yes | ||
| MSRCv1 | Yes | ||
| HW | Yes | ||
| NUS-WIDE | Yes | ||
| MNIST | Yes | ||
| Scene15 | Yes |
| Methods | 3Source | MSRCv1 | HW | NUS-WIDE | MNIST | Scene15 |
|---|---|---|---|---|---|---|
| LMSC | 9.41 | 3.00 | 552.98 | 278.37 | 620.81 | 6253.14 |
| LCRSR | 2.93 | 1.30 | 13.79 | 14.56 | 4.98 | 465.73 |
| ECMSC | 183.04 | 2.21 | 158.14 | 97.06 | 53.43 | 1476.50 |
| MSC_IAS | 11.02 | 1.02 | 14.93 | 14.72 | 16.32 | 80.34 |
| LMSNB | 69.40 | 1.12 | 27.15 | 17.58 | 30.60 | 306.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Yang, X.; Xing, Z.; Ma, Y. Latent Multi-View Semi-Nonnegative Matrix Factorization with Block Diagonal Constraint. Axioms 2022, 11, 722. https://doi.org/10.3390/axioms11120722
Yuan L, Yang X, Xing Z, Ma Y. Latent Multi-View Semi-Nonnegative Matrix Factorization with Block Diagonal Constraint. Axioms. 2022; 11(12):722. https://doi.org/10.3390/axioms11120722
Chicago/Turabian StyleYuan, Lin, Xiaofei Yang, Zhiwei Xing, and Yingcang Ma. 2022. "Latent Multi-View Semi-Nonnegative Matrix Factorization with Block Diagonal Constraint" Axioms 11, no. 12: 722. https://doi.org/10.3390/axioms11120722
APA StyleYuan, L., Yang, X., Xing, Z., & Ma, Y. (2022). Latent Multi-View Semi-Nonnegative Matrix Factorization with Block Diagonal Constraint. Axioms, 11(12), 722. https://doi.org/10.3390/axioms11120722






