Abstract
Brain tumors are most common in children and the elderly. It is a serious form of cancer caused by uncontrollable brain cell growth inside the skull. Tumor cells are notoriously difficult to classify due to their heterogeneity. Convolutional neural networks (CNNs) are the most widely used machine learning algorithm for visual learning and brain tumor recognition. This study proposed a CNN-based dense EfficientNet using min-max normalization to classify 3260 T1-weighted contrast-enhanced brain magnetic resonance images into four categories (glioma, meningioma, pituitary, and no tumor). The developed network is a variant of EfficientNet with dense and drop-out layers added. Similarly, the authors combined data augmentation with min-max normalization to increase the contrast of tumor cells. The benefit of the dense CNN model is that it can accurately categorize a limited database of pictures. As a result, the proposed approach provides exceptional overall performance. The experimental results indicate that the proposed model was 99.97% accurate during training and 98.78% accurate during testing. With high accuracy and a favorable F1 score, the newly designed EfficientNet CNN architecture can be a useful decision-making tool in the study of brain tumor diagnostic tests.
1. Introduction
The brain has billions of active cells, making analysis very difficult. Today, one of the leading causes of childhood and adult death is brain tumors. Primary brain tumors affect about 250,000 individuals worldwide each year and account for less than 2% of all malignancies. In total, 150 different kinds of brain tumors may be seen in humans. Among them are: (i) benign tumors; and (ii) malignant tumors. Benign tumors spread within the brain. Typically, malignant tumors are referred to as brain cancer since they may spread outside of the brain [1]. Early diagnosis and true grading of brain tumors are vital to save the life of human beings. The manual technique is very difficult because of the significant density of brain tumors. Thus, an automated computer-based method is very beneficial for tumor detection [2]. Today, things are very different. Using machine learning and deep learning to improve brain tumor detection algorithms [3] enables radiologists to quickly locate tumors without requiring surgical intervention. Recent advances in deep neural network modeling have resulted in the emergence of a novel technology for the study, segmentation, and classification of brain tumors [4,5].
Brain tumor classification is possible with the help of the fully automated CNN model to make fast and accurate decisions by researchers. However, achieving high accuracy is still an endless challenge in brain image classification due to vagueness. The objective of this paper is to designate fully automatic CNN models with min-max normalization for multi-classification of the brain tumors using publicly available datasets. We have proposed a dense EfficientNet network for three-class brain tumor classification to obtain better accuracy. It is focused on data augmentation with min-max normalization combined with dense EfficientNet to enhance the quicker training accuracy with higher depth of the network. It contains separable convolution layers in-depth to reduce to a smaller extent the parameters and computation. However, to segment brain tumors, the EfficientNet model must be further expanded via the use of dense chain blocks. Thus, dense EfficientNet can also achieve excellent classification accuracy. It obtains deep image information and reconstructs dense segmentation masks for brain tumor classification of three tumor kinds. It was evaluated on T1-weighted contrast-enhanced magnetic resonance imaging. The performance of the network was tested using pre-processing, augmentation, and classification. A novel dense depth classifier is presented based on a deep convolutional neural network. The suggested approach has higher classification accuracy compared to existing deep learning methods. The suggested approach provides excellent performance with a smaller number of training samples as is demonstrated in the confusion matrix. The issue of overfitting is minimized with reduced classification error owing to dropout layers.
This paper is split into several sections: the next part deals with the various related work about tumor segmentation; suggested methodology is described in Section 3; additionally, Section 4 emphasizes the findings using confusion matrix analysis; and finally, Section 5 provides the conclusion derived from the study output and the scope of the potential development.
2. Related Work
Medical image segmentation for detection and classification of brain tumor from the magnetic resonance (MR) images is a very important process for deciding the right therapy at the right time. Many techniques have been proposed for classification of brain tumors in MRI. Shelhamer et al. [6] proposed a dual path CNN skipping architecture that combines deep, coarse layer with fine layer to find accurate and detailed segmentation of brain cancer. Brain tumor cells have soaring baleful fluid which has very high vigor and is vague. Therefore, min-max normalization is a better pre-processing tool to classify tumors into different grades [7]. Today, there are several image processing methodologies used for classifying MR images [8,9]. Karunakaran created a technique for detecting meningioma brain tumors utilizing fuzzy-logic-based enhancement and a co-active adaptive neuro-fuzzy inference system, as well as U-Net convolutional neural network classification algorithms. The suggested method for detecting meningioma tumors includes the following stages: enhancement, feature extraction, and classification. Fuzzy logic is used to improve the original brain picture, and then a dual tree-complex wavelet transform is performed on the augmented image at various scale levels. The deconstructed sub-band pictures are used to calculate the features, which are then categorized using the CAN FIS classification technique to distinguish meningioma brain images from non-meningioma brain images. The projected meningioma brain’s performance sensitivity, specificity, segmentation accuracy, and dice coefficient index with detection rate are all evaluated for the tumor detection and segmentation system [10]. Recent advances in deep learning ideas have increased the accuracy of computer-aided brain tumor analysis on tumors with significant fluctuation in form, size, and intensity. Cheng et al. [11] used T1-MRI data to investigate the three-class brain tumor classification issue. This method employs image dilation to enlarge the tumor area, which is then divided into progressively fine ring-form sub-regions. Badza and Barjaktarovic [12] presented a novel CNN architecture based on the modification of an existing pre-trained network for the categorization of brain tumors using T1-weighted contrast-enhanced magnetic resonance images. The model’s performance is 96.56 percent, and it is composed of two 10-fold cross-validation techniques using augmented pictures. Mzough et al. [13] used a pre-processing method based on intensity normalization and adaptive contrast enhancement to propose a completely automated 3D CNN model for glioma brain tumor categorization into low-grade and high-grade glioma. They obtained validation accuracy of 96.49 percent overall when utilizing the Brats-2018 dataset. A hybrid technique: Hashemzehi et al. [14] evaluated the detection of brain cancers from MRI images using a hybrid model CNN and NADE. They used 3064 T1-weighted contrast-enhanced images. They evaluated in order to identify three distinct kinds of brain cancers with a 96 percent accuracy rate. Diaz-Pernas et al. [15] presented a completely automated brain tumor segmentation and classification algorithm based on MRI scans of meningioma, glioma, and pituitary tumors. They utilized CNN to implement the idea of a multi-scale approach inherent in human functioning. They achieved 97 percent accuracy on a 3064-slice imaging collection from 233 patients. Sultan et al. [16] utilized a CNN structure comprising 16 convolution layers, pooling and normalizing, and a dropout layer before the fully linked layer. They discovered a 96 percent accuracy rate when 68 percent of the pictures were used for training and the remaining images were used for validation and testing. Abd et al. [17] conducted their experiment on 25,000 brain magnetic resonance imaging (MRI) pictures using a differential deep-CNN to identify various kinds of brain tumor. They achieved outstanding total performance with an accuracy of 99.25 percent in training. Sajja et al. [18] conducted their research on Brat’s dataset which includes 577 T1-weighted brain tumors for classifying malignant and benign tumors using the VGG16 network. They performed their performance with 96.70 inaccuracy. Das et al. [19] identified various kinds of brain cancers, such as glioma tumor, meningioma tumor, and pituitary tumor using a convolutional neural network which includes 3064 T1-weighted contrast-enhanced MRI pictures. The CNN model was trained to utilize several convolutional and pooling procedures. They obtained 94 percent accuracy by resizing the convolutional network based on convolutional filters/kernels of variable size.
3. Proposed Methodology
In this paper, the authors have applied min-max normalization and data augmentation techniques on a large dataset of 3260 different types of brain MRI images [20]. The image database includes 3064 T1-weighted contrast-enhanced MRI images collected from Kaggle.com. These are mainly three kinds of brain tumors: one is meningioma which contains 708 pictures; the second is glioma which contains 1426 pictures; and lastly there is pituitary tumor which contains 930 pictures. All pictures were collected from 233 patients in three planes: sagittal (1025 photos), axial (994 photos), and coronal (1045 photos). The authors divided the dataset into three distinct parts for training, validation, and testing. The suggested model is composed of different stages which are illustrated in Figure 1.
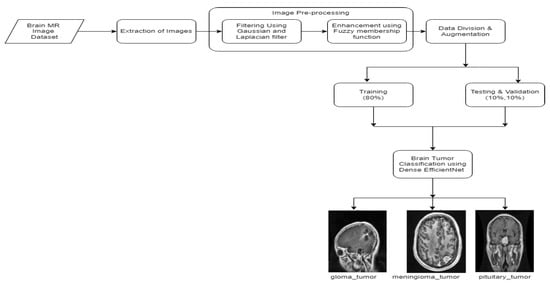
Figure 1.
Overview of proposed dense EfficientNet methodology.
3.1. Image Pre-Processing
The brain tumor images have low quality due to noises and low illumination. The proposed method converts the low pixel value images to brighter ones using data normalization and using the min-max normalization function method followed by Gaussian and Laplacian filter. Initially, the authors added Gaussian blur to the original images and then subtracted the blurred image by adding a weighted portion of the mask to obtain the de-blurred image. Then they used a Laplacian filter with kernel size 3 × 3 for smoothing the images which are shown in Figure 2.
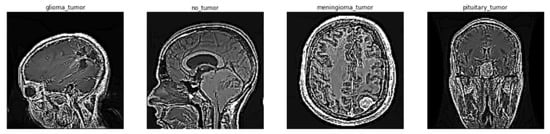
Figure 2.
T1- contrast MR images of each label after filtration.
The MRI image as obtained from the patient’s database is unclear. These images also contain a certain amount of uncertainty. Therefore, brain images need to be normalized before further processing. Usually, MRI images look like grey scale images. Hence, the images are easily normalized to improve the image quality and reduce miscalculation. Nayak et al. [21] applied L membership function with the morphology concept to detect brain tumors. The membership function used in the study is as follows:
where d = double (image), mn = min (min (image)), mx = max (max (image)), and r = normalized image.
This membership function is mainly used to normalize the image for enhancement with the range 0 to 1. Thus, it is also called the max-min normalization method.
The resultant image after applying the normalization is shown in Figure 3.
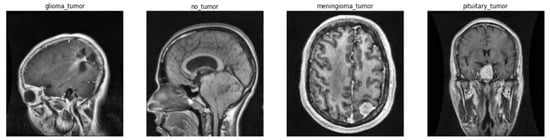
Figure 3.
T1-contrast MR images of each label after fuzzification.
3.2. Data Division and Augmentation
The deep neural network needs large datasets for better results but our dataset is limited. Our dataset contains 3260 brain images, further divided into 80% for training, which remains for testing and validation purposes. So, data augmentation is needed to change in the minor. The authors have applied rotation, width-shift, height-shift, and the zoom—range for the data requirement. They augmented the original data 21 times for better training. This will enhance the amount of training data, allowing the model to learn more effectively. This may assist in increasing the quantity of relevant data. It contributes to the reduction of overfitting and enhances generalization. Data augmentation (DA) is the process of creating additional samples to supplement an existing dataset via transformation. Dropout through augmentation, practical solutions such as dropout regularization, and batch normalization are performed on the original dataset. By data warping or oversampling, this augmentation exaggerated the size of the training dataset.
3.3. Dense EfficientNet CNN Model
A novel dense CNN model is presented in this article, which is a mix of pre-trained EfficientNetB0 with dense layers. EfficientB0 has 230 layers and 7 MBConv blocks [22,23]. It features a thick block structure consisting of four tightly linked layers with a development rate of 4. Each layer in this structure uses the output feature maps of the preceding levels as the input feature maps. The dense block concept is composed of convolution layers of the same size as the input feature maps in EfficientNet. Dense block takes advantage of the preceding convolution layers’ output feature maps to generate more feature maps with fewer convolution kernels. This CNN model retrieved 150 × 150 enhanced MRI image data. The dense EfficientNet network has an alternate dense and drop-out layer. A dense layer is the basic layer which feeds all outputs from the previous layer to all its neurons, each neuron providing one output to the next layer. The drop-out layer is used to reduce the capacity or thin the network during training and avoids the overfitting. We begin by adding a pooling layer, followed by four dense layers and three drop-out layers to ensure the model runs smoothly. The numbers of neurons in the dense units are 720, 360, 360, and 180, respectively. The drop-out values are 0.25, 0.25, and 0.5, respectively. Finally, the authors have used a dense layer composed of four fully connected neurons in conjunction with a Softmax output layer to compute and classify the probability score for each class. Figure 4 illustrates the structure of the proposed EfficientNet in detail.
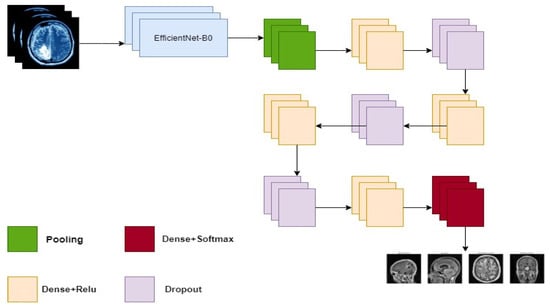
Figure 4.
Proposed dense EfficientNet CNN model architecture.
4. Results and Discussion
Numerous experimental assessments have been conducted to determine the suggested dense CNN model’s validity. All the experimental evaluations have been conducted using a Python programming environment with GPU support. First, pre-processing is performed to enhance the contrast in MRI images using max-min normalization and then the images are augmented for training. The proposed dense-CNN model activated the augmented tumors for better accuracy. The proposed model showed 99.97% accuracy on training data and 98.78% accuracy on the testing dataset which is plotted in Figure 5.
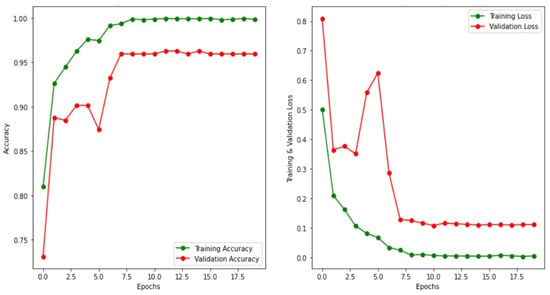
Figure 5.
Graph representing model accuracy and model loss for training and validation set using the dense EfficientNet approach.
The experiment has been performed in 20 epochs. A batch size of 32, image size 150, and verbose 1 have been considered for the experiment. In the accuracy model, initial validation accuracy is below 0.75 but after one epoch the validation accuracy suddenly increases to nearly 0.88. In the same manner, the initial validation loss is above 0.8 but after one epoch the loss decreases below 0.4. As shown in Figure 5, there is a positive trend toward improving accuracy and reducing loss. At first, validation accuracy is low, but it progressively improves to almost 97.5 percent. The succeeding part of the measure was accomplished on the ResNet50 model, MobileNet, and the MobileNetV2 model, which are shown in Figure 6, Figure 7, and Figure 8, respectively.
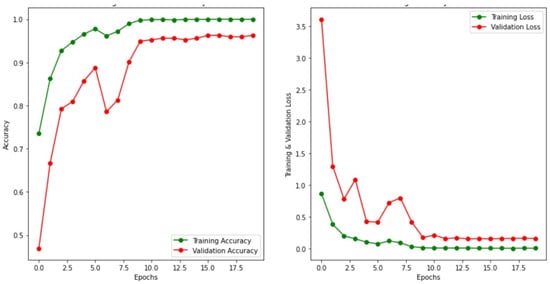
Figure 6.
Graph representing model accuracy and model loss for training and validation set using the ResNet50 approach.
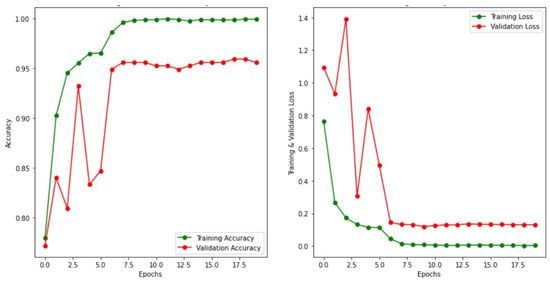
Figure 7.
Graph representing model accuracy and model loss for training and validation set using the MobileNet approach.
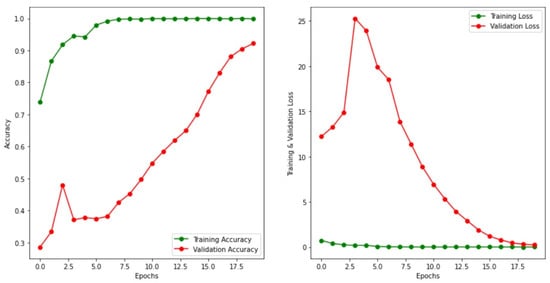
Figure 8.
Graph representing model accuracy and model loss for training and validation set using the MobileNetV2 approach.
From the above model accuracy and model loss graphs, the authors concluded that in the case of the mobile net case, the graph is disordered, and the difference between loss and accuracy is very high. So, the accuracy value of MobileNetV2 is lower than the others. The accuracy and loss graphs of dense EfficientNet, ResNet, and MobileNet are almost nearly equal. The testing accuracy and testing loss of dense EfficientNet is 98.78% and 0.0645, respectively, whereas the accuracy and loss in the case of MobileNetV2 is 96.94% and 0.2452, respectively. The testing accuracy acquired using the MobileNet model is 96.94% and the test loss is 0.1339 whereas the accuracy and loss value of ResNet is just less than MobileNet. The detailed comparison of test accuracy, as well as loss of different models, is shown in Table 1, and performance analysis is shown in Figure 9.

Table 1.
Comparison of accuracy and loss among different pre-trained deep-learning-based techniques.
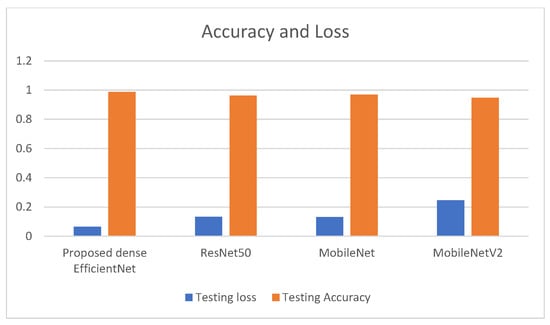
Figure 9.
Comparison of accuracy and loss among different pre-trained deep-learning-based techniques.
Different performance measures, such as accuracy, precision, recall, and F1-score, were utilized to compare the suggested model’s performance. These parameters are evaluated using the confusion matrix. The details were also examined using the confusion matrix which is shown in Figure 10. The confusion matrix presents misclassifications as a consequence of overfitting using 10% of testing data obtained from the original dataset of 3260. From the matrix it is observed that the misclassified tumors in the proposed dense EfficientNet model have 04, the ResNet50 model has 12, MobileNet has 10, and MobileNetV2 has 15 out of 326 testing images/ Due to lesser amounts of misclassified data, the accuracy of the proposed model is higher than the others. The confidence level of the pituitary in the case of MobileNetV2 is the worst in comparison to other tumors. All CNN models perform the classification of meningioma tumor very well. The majority of the misclassified samples belong to the “glioma” class which cannot learn as effectively as the other three.
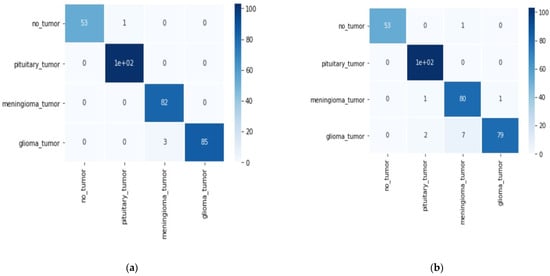
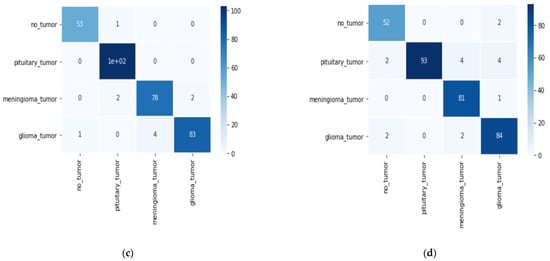
Figure 10.
Confusion matrix of: (a) proposed dense EfficientNet model; (b) ResNet50 model; (c) MobileNet model; (d) MobileNetV2 model.
For comparison of different techniques, three important measures have been considered: precision, recall, and F1-score. All the assessment metrics for all the CNN models were evaluated from Table 2 and are displayed in Figure 11. All these measures are based on the following parameters:

Table 2.
Class-specific evaluation of brain tumors using different CNN.
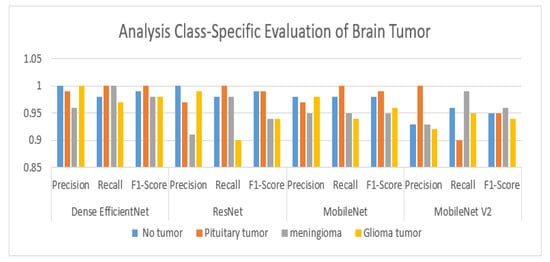
Figure 11.
Analysis: class-specific evaluation of brain tumor using different CNN.
- True positive (TP) = classified as +ve and sample belongs to the tumor;
- True negative (TN) = classified as −ve and sample belongs to healthy;
- False positive (FP) = classified as +ve and sample belongs to healthy;
- False negative (FN) = classified as −ve and sample belongs to a tumor.
These parameters are calculated from the confusion matrix, which is shown in Figure 10.
Hence, the different measures can be defined as follows:
where Recall is the same as Sensitivity as shown in Equation (2).
It is observed from Table 2 and the analysis graph in Figure 11 that dense EfficientNet has the highest precision, recall, and F1-score when compared to the other three models. The pituitary tumor has the best performance in all measurements when compared to other types of tumors. All the values of precision, recall, and F1-score of pituitary tumors are quite good. The overall results of dense EfficientNet are excellent. For comparison purposes, the authors have also considered the recent performance of modified CNN structure by the different researchers, which is shown in Table 3 analysis and is displayed in Figure 12. The accuracy, precision, and F1-score of the proposed method are 98.78%, 98.75%, and 98.75%, respectively, which is better than other comparison methods. As shown in Table 3, the proposed deep learning segmentation algorithm outperforms state-of-the-art techniques. Based on Table 3, the authors conclude that dense EfficientNet outperforms other techniques because deep-learning-based approaches are more efficient and capable of handling large amounts of data for classification.

Table 3.
Comparison of performance among different deep-learning-based techniques.
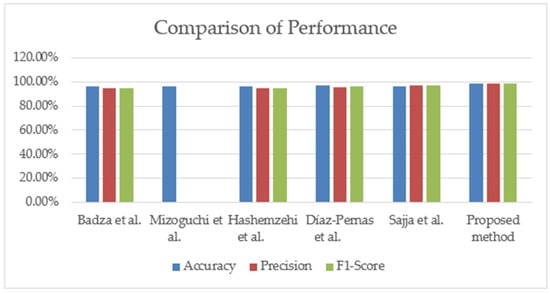
Figure 12.
Comparison of performance among different deep-learning-based techniques. Data from [12,13,14,15,18].
Figure 12 illustrates that all mentioned authors used contrast brain tumors for their experiments. The proposed dense EfficientNet method has higher accuracy, at nearly 99%, than the others do.
5. Conclusions
In this paper, the authors have used dense EfficientNet with min-max normalization that is suitable to classify the different types of brain tumors with 98.78% accuracy, which is better than other related work using the same dataset. The suggested technique outperforms existing deep learning methods in terms of accuracy, precision, and F1-score. This proposed idea can play a prognostic role in detecting tumors in the brain. It has been observed that glioma has the lowest detection rate with an F1-score of 98% and pituitary has the highest rate with an F1-score of 100%. Among deep learning methods, dense CNN has performed more rapidly, with higher classification accuracy. This method is suitable to locate and detect tumors easily.
Further, a better pre-processing technique can be applied with fuzzy thresholding concept or nature-based algorithms for early diagnosis of dangerous medical imaging disease by adapting more layers to segment the different medical image segmentation. Our future research will concentrate on minimizing the number of parameters and computing time required to run the suggested model without sacrificing performance.
Author Contributions
Writing—original draft preparation, D.R.N., N.P., P.K.M., M.Z. and S.K. Writing—review and editing, D.R.N., N.P., P.K.M., M.Z. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Acknowledgments
This work is supported by the Ministry of Science and Higher Education of the Russian Federation (Government Order FENU-2020-0022).
Conflicts of Interest
There is no such conflict of interest disclosed by the authors in relation to the content of the work.
References
- Pradhan, A.; Mishra, D.; Das, K.; Panda, G.; Kumar, S.; Zymbler, M. On the Classification of MR Images Using “ELM-SSA” Coated Hybrid Model. Mathematics 2021, 9, 2095. [Google Scholar] [CrossRef]
- Reddy, A.V.N.; Krishna, C.P.; Mallick, P.K.; Satapathy, S.K.; Tiwari, P.; Zymbler, M.; Kumar, S. Analyzing MRI scans to detect glioblastoma tu-mor using hybrid deep belief networks. J. Big Data 2020, 7, 35. [Google Scholar] [CrossRef]
- Nayak, D.R.; Padhy, N.; Mallick, P.K.; Bagal, D.K.; Kumar, S. Brain Tumour Classification Using Noble Deep Learning Approach with Parametric Optimization through Metaheuristics Approaches. Computers 2022, 11, 10. [Google Scholar] [CrossRef]
- Mansour, R.F.; Escorcia-Gutierrez, J.; Gamarra, M.; Díaz, V.G.; Gupta, D.; Kumar, S. Ar-tificial intelligence with big data analytics-based brain intracranial hemorrhage e-diagnosis us-ing CT images. Neural Comput. Appl. 2021. [Google Scholar] [CrossRef]
- Rehman, A.; Naz, S.; Razzak, M.I.; Akram, F.; Imran, M.A. Deep learning-based framework for automatic brain tumors classification using transfer learning. Circuits Syst. Signal Processing 2020, 39, 757–775. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ozyurt, F.; Sert, E.; Avci, D. An expert system for brain tumor detection, Fuzzy C-means with super-resolution and convolutional neural network with extreme learning machine. Med. Hypotheses 2020, 134, 109433. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Zhong, Y.; Xie, S.; Lv, H.; Lv, Z. Fuzzy System Based Medical Image Processing for Brain Disease Prediction. Front. Neurosci. 2021, 15, 714318. [Google Scholar] [CrossRef] [PubMed]
- Maqsood, S.; Damasevicius, R.; Shah, F.M. An Efficient Approach for the Detection of Brain Tumor Using Fuzzy Logic and U-Net CNN Classification. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2021; Volume 12953. [Google Scholar]
- Ragupathy, B.; Karunakaran, M. A fuzzy logic-based meningioma tumor detection in magnetic resonance brain images using CANFIS and U-Net CNN classification. Int. J. Imaging Syst. Technol. 2021, 31, 379–390. [Google Scholar] [CrossRef]
- Cheng, J.; Huang, W.; Cao, S.; Yang, R.; Yang, W.; Yun, Z.; Wang, Z.; Feng, Q. Correction, enhanced performance of brain tumor classification via tumor region augmentation and partition. PLoS ONE 2015, 10, e0144479. [Google Scholar] [CrossRef] [PubMed]
- Badža, M.M.; Barjaktarović, M.Č. Classification of brain tumors from MRI images using a convolutional neural network. Appl. Sci. 2020, 10, 1999. [Google Scholar] [CrossRef] [Green Version]
- Mzoughi, H.; Njeh, I.; Wali, A.; Slima, M.B.; BenHamida, A.; Mhiri, C.; Mahfoudhe, K.B. Deep multi-scale 3D convolutional neural network (CNN) for MRI gliomas brain tumor classification. J. Digit. Imaging 2020, 33, 903–915. [Google Scholar] [CrossRef] [PubMed]
- Hashemzehi, R.; Mahdavi, S.J.S.; Kheirabadi, M.; Kamel, S.R. Detection of brain tumors from MRI images base on deep learning using hybrid model CNN and NADE. Biocybern. Biomed. Eng. 2020, 40, 1225–1232. [Google Scholar] [CrossRef]
- Díaz-Pernas, F.J.; Martínez-Zarzuela, M.; Antón-Rodríguez, M.; González-Ortega, D. A deep learning approach for brain tumor classification and segmentation using a multiscale convolutional neural network. Healthcare 2021, 9, 153. [Google Scholar] [CrossRef] [PubMed]
- Sultan, H.H.; Salem, N.M.; Al-Atabany, W. Multi-classification of brain tumor images using deep neural network. IEEE Access 2019, 7, 69215–69225. [Google Scholar] [CrossRef]
- Abd El Kader, I.; Xu, G.; Shuai, Z.; Saminu, S.; Javaid, I.; Salim Ahmad, I. Differential deep convolutional neural network model for brain tumor classification. Brain Sci. 2021, 11, 352. [Google Scholar] [CrossRef] [PubMed]
- Sajja, V.R. Classification of Brain tumors using Fuzzy C-means and VGG16. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 2103–2113. [Google Scholar]
- Das, S.; Aranya, O.R.; Labiba, N.N. Brain tumor classification using a convolutional neural network. In Proceedings of the 2019 1st International Conference on Advances in Science, Engineering and Robotics Technology (ICASERT), Dhaka, Bangladesh, 3 May 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Cheng, J. Brain tumor dataset. Figshare. Dataset. 2017, 1512427/5. Available online: https://figshare.com/articles/dataset/brain_tumor_dataset/1512427 (accessed on 12 October 2021).
- Nayak, D.R.; Padhy, N.; Swain, B.K. Brain Tumor Detection and Extraction using Type-2 Fuzzy with Morphology. Int. J. Emerg. Technol. 2020, 11, 840–844. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet, Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Available online: https://towardsdatascience.com/complete-architectural-details-of-all-efficientnet-models-5fd5b736142 (accessed on 16 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).