A New Hybrid Triple Bottom Line Metrics and Fuzzy MCDM Model: Sustainable Supplier Selection in the Food-Processing Industry
Abstract
:1. Introduction
- Developing a new composite model for supplier selection for a sustainable food-processing supply chain.
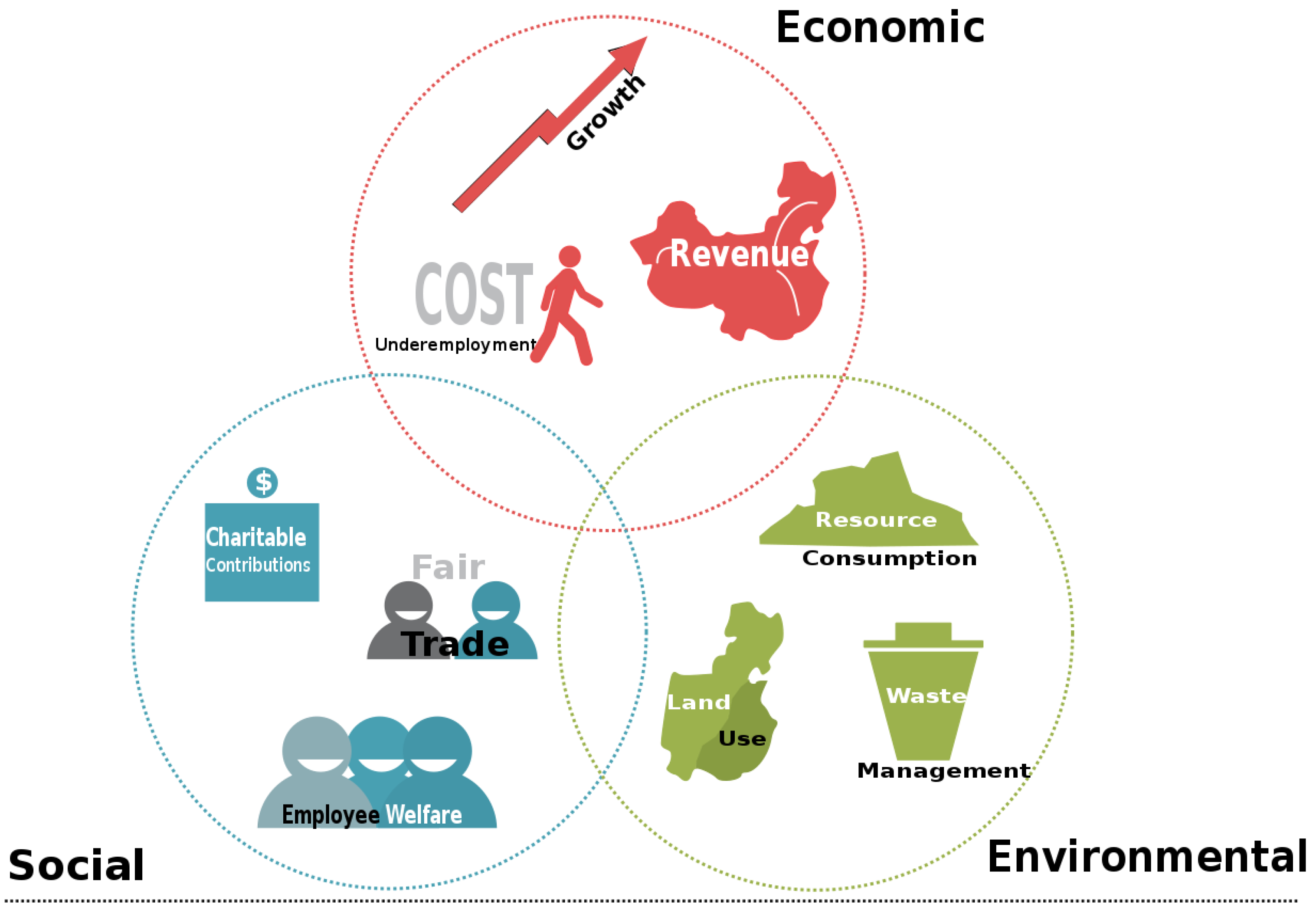
- Achieving sustainable goals, the author used the Triple Bottom Line (TPL) for defining criteria that affect the decision-making process. Then, a Fuzzy Analytical Hierarchy Process (FAHP) method and the Combined Compromise Solution (CoCoSo) model was used to select an optimal supplier (Xanthan gum (β-glucopyranose (C35H49O29)n) supplier).
- Evaluating the fuzzy multi-criteria decision model for a case study.
2. Literature Review
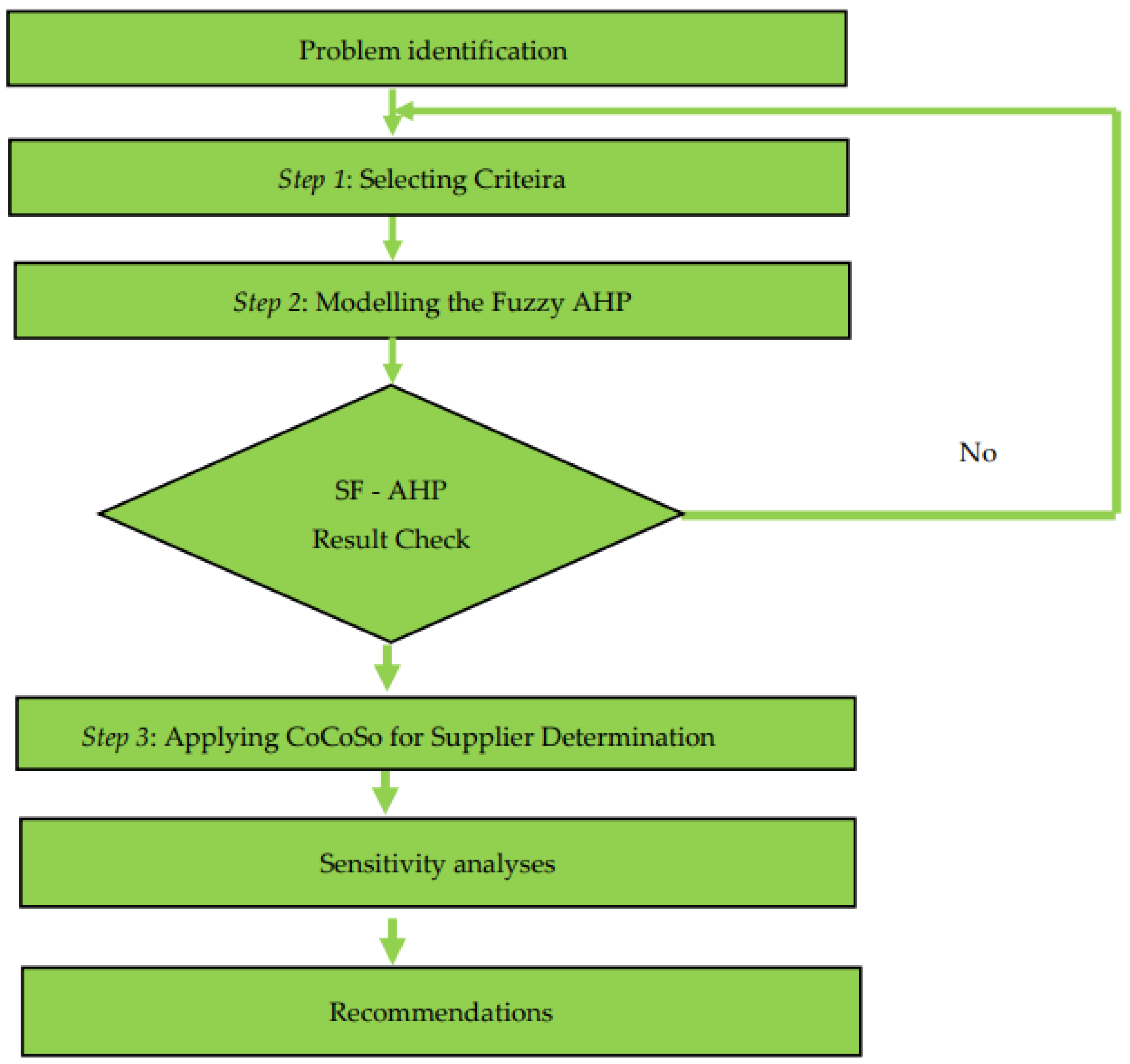
3. Methodology
3.1. Fuzzy Analytical Hierarchy Process (FAHP) Method
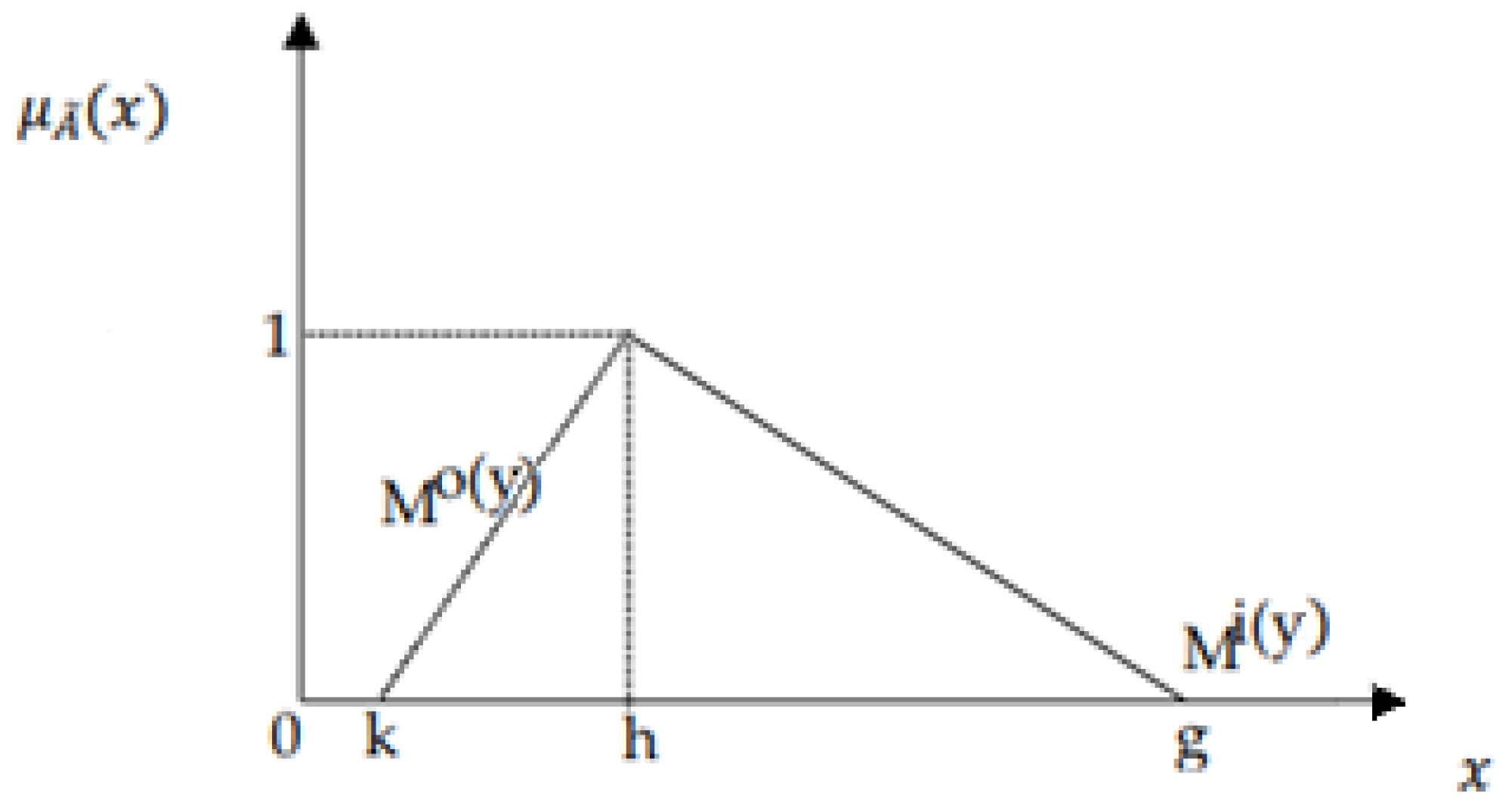
3.1.1. Theoretical Fuzziness
3.1.2. Fuzzy Analytical Hierarchy Process (FAHP)
3.2. Combined Compromise Solution (CoCoSo)
4. Case Study
5. Sensitivity Analysis
6. Conclusions
- ⮚
- The proposed FMCDM model is the first Xanthan-gum (β-glucopyranose (C35H49O29)n) supplier evaluation and selection model in Vietnam by interviewing experts and reviewing the literature.
- ⮚
- Second, this is the first study to provide a case study on evaluating suppliers for the food-processing industry utilizing the model proposed by the combination of FAHP and CoCoSo models.
- ⮚
- The proposed model can also address different complex problems in supplier selection in other industries.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sức Hút Của Ngành Công Nghiệp Chế Biến Thực Phẩm Việt Nam. Available online: https://thanguy.com/tin-thi-truong-4/ (accessed on 18 October 2021).
- Làm gì để Phát Triển Bền Vững Công Nghiệp Chế Biến Thực Phẩm? Available online: https://dantocmiennui.vn/lam-gi-de-phat-trien-ben-vung-cong-nghiep-che-bien-thuc-pham/180544.html (accessed on 18 October 2021).
- Beske-Janssen, P.; Johnson, M.P.; Schaltegger, S. 20 years of performance measurement in sustainable supply chain management—What has been achieved? Supply Chain. Manag. Int. J. 2015, 20, 664–680. [Google Scholar] [CrossRef]
- What Is Sustainable Sourcing? Available online: https://ecovadis.com/glossary/sustainable-sourcing/#:~:text=Sustainable%20sourcing%20is%20the%20integration,the%20process%20of%20selecting%20suppliers.&text=The%20ultimate%20goal%20of%20sustainable,long%2Dterm%20relationships%20with%20suppliers (accessed on 18 October 2021).
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Đạt, L.Q.; Phượng, B.H.; Thu, N.T.P.; Anh, T.T.L. Xây dựng mô hình ra quyết định đa tiêu chuẩn tích hợp để lựa chọn và phân nhóm nhà cung cấp xanh. Tạp Chí Khoa Học Đhqghn Kinh Tế Và Kinh Doanh Tập 2017, 33, 43–54. [Google Scholar]
- Slaper, T.F.; Hall, T.J. The triple bottom line: What is it and how does it work. Indiana Bus. Rev. 2011, 86, 4–8. [Google Scholar]
- Schramm, V.B.; Cabral, L.P.B.; Schramm, F. Approaches for supporting sustainable supplier selection—A literature review. J. Clean. Prod. 2020, 273, 123089. [Google Scholar] [CrossRef]
- Stojčić, M.; Zavadskas, E.K.; Pamučar, D.; Stević, Ž.; Mardani, A. Application of MCDM methods in sustainability engineering: A literature review 2008–2018. Symmetry 2019, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Matić, B.; Jovanović, S.; Das, D.K.; Zavadskas, E.K.; Stević, Ž.; Sremac, S.; Marinković, M. A new hybrid MCDM model: Sustainable supplier selection in a construction company. Symmetry 2019, 11, 353. [Google Scholar] [CrossRef] [Green Version]
- Önüt, S.; Kara, S.S.; Işik, E. Long term supplier selection using a combined fuzzy MCDM approach: A case study for a telecommunication company. Expert Syst. Appl. 2009, 36, 3887–3895. [Google Scholar] [CrossRef]
- Nallusamy, S.; Sri Lakshmana Kumar, D.; Balakannan, K.; Chakraborty, P.S. MCDM tools application for selection of suppliers in manufacturing industries using AHP, Fuzzy Logic and ANN. Int. J. Eng. Res. Afr. 2016, 19, 130–137. [Google Scholar] [CrossRef]
- Yazdani, M. An integrated MCDM approach to green supplier selection. Int. J. Ind. Eng. Comput. 2014, 5, 443–458. [Google Scholar] [CrossRef]
- Sarkis, J.; Dhavale, D.G. Supplier selection for sustainable operations: A triple-bottom-line approach using a Bayesian framework. Int. J. Prod. Econ. 2015, 166, 177–191. [Google Scholar] [CrossRef]
- Govindan, K.; Khodaverdi, R.; Jafarian, A. A fuzzy multi criteria approach for measuring sustainability performance of a supplier based on triple bottom line approach. J. Clean. Prod. 2013, 47, 345–354. [Google Scholar] [CrossRef]
- Nikolaou, I.E.; Evangelinos, K.I.; Allan, S. A reverse logistics social responsibility evaluation framework based on the triple bottom line approach. J. Clean. Prod. 2013, 56, 173–184. [Google Scholar] [CrossRef]
- Rezaeisaray, M.; Ebrahimnejad, S.; Khalili-Damghani, K. A novel hybrid MCDM approach for outsourcing supplier selection: A case study in pipe and fittings manufacturing. J. Model. Manag. 2016, 11, 536–559. [Google Scholar] [CrossRef]
- Fallahpour, A.; Nayeri, S.; Sheikhalishahi, M.; Wong, K.Y.; Tian, G.; Fathollahi-Fard, A.M. A hyper-hybrid fuzzy decision-making framework for the sustainable-resilient supplier selection problem: A case study of Malaysian Palm oil industry. Environ. Sci. Pollut. Res. 2021, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.Y.; Lee, A.H.; Yang, C.Y. A fuzzy ANP model for supplier selection as applied to IC packaging. J. Intell. Manuf. 2012, 23, 1477–1488. [Google Scholar] [CrossRef]
- Hadian, H.; Chahardoli, S.; Golmohammadi, A.M.; Mostafaeipour, A. A practical framework for supplier selection decisions with an application to the automotive sector. Int. J. Prod. Res. 2020, 58, 2997–3014. [Google Scholar] [CrossRef]
- Wang, C.N.; Tsai, H.T.; Nguyen, V.T.; Nguyen, V.T.; Huang, Y.F. A hybrid fuzzy analytic hierarchy process and the technique for order of preference by similarity to ideal solution supplier evaluation and selection in the food processing industry. Symmetry 2020, 12, 211. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-N.; Nguyen, V.T.; Thai, H.T.N.; Tran, N.N.; Tran, T.L.A. Sustainable Supplier Selection Process in Edible Oil Production by a Hybrid Fuzzy Analytical Hierarchy Process and Green Data Envelopment Analysis for the SMEs Food Processing Industry. Mathematics 2018, 6, 302. [Google Scholar] [CrossRef] [Green Version]
- Milovanović, V.R.; Aleksić, A.V.; Sokolović, V.S.; Milenkov, M.A. Uncertainty modeling using intuitionistic fuzzy numbers. Vojnotehnički Glasnik/Mil. Tech. Cour. 2021, 69, 905–929. [Google Scholar] [CrossRef]
- Fazlollahtabar, H.; Kazemitash, N. Green supplier selection based on the information system performance evaluation using the integrated best-worst method. Facta Univ. Ser. Mech. Eng. 2021, 19, 345–360. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Ullah, K.; Khan, Q. Einstein Geometric Aggregation Operators using a Novel Complex Interval-valued Pythagorean Fuzzy Setting with Application in Green Supplier Chain Management. Rep. Mech. Eng. 2021, 2, 105–134. [Google Scholar] [CrossRef]
- Radovanovic, M.; Ranđelović, A.; Jokić, Ž. Application of hybrid model fuzzy AHP-VIKOR in selection of the most efficient procedure for rectification of the optical sight of the long-range rifle. Decis. Mak. Appl. Manag. Eng. 2020, 3, 131–148. [Google Scholar] [CrossRef]
- Biswas, T.; Chatterjee, P.; Choudhuri, B. Selection of commercially available alternative passenger vehicle in automotive environment. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 16–27. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Kizielewicz, B.; Shekhovtsov, A.; Wątróbski, J.; Sałabun, W. Methodical Aspects of MCDM Based E-Commerce Recommender System. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2192–2229. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are mcda methods benchmarkable? A comparative study of topsis, vikor, copras, and promethee ii methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Wang, H. Models for MADM with hesitant interval-valued fuzzy information under uncertain environment. Int. J. Knowl.-Based Intell. Eng. Syst. 2021, 25, 315–322. [Google Scholar] [CrossRef]
- Pamučar, D.S.; Savin, L.M. Multiple-criteria model for optimal off-road vehicle selection for passenger transportation: BWM-COPRAS model. Vojnoteh. Glas. 2020, 68, 28–64. [Google Scholar] [CrossRef]
- Durmić, E.; Stević, Ž.; Chatterjee, P.; Vasiljević, M.; Tomašević, M. Sustainable supplier selection using combined FUCOM–Rough SAW model. Rep. Mech. Eng. 2020, 1, 34–43. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. Sustainable supplier selection: A novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. J. Clean. Prod. 2020, 266, 121981. [Google Scholar] [CrossRef]
- Tavana, M.; Shaabani, A.; Di Caprio, D.; Bonyani, A. An integrated group fuzzy best-worst method and combined compromise solution with Bonferroni functions for supplier selection in reverse supply chains. Clean. Logist. Supply Chain. 2021, 2, 100009. [Google Scholar] [CrossRef]
- Yazdani, M.; Pamucar, D.; Chatterjee, P.; Torkayesh, A.E. A multi-tier sustainable food supplier selection model under uncertainty. Oper. Manag. Res. 2021, 1–30. [Google Scholar] [CrossRef]
- Hoseini, S.A.; Fallahpour, A.; Wong, K.Y.; Mahdiyar, A.; Saberi, M.; Durdyev, S. Sustainable Supplier Selection in Construction Industry through Hybrid Fuzzy-Based Approaches. Sustainability 2021, 13, 1413. [Google Scholar] [CrossRef]
- Gogus, O.; Boucher, T.O. Strong transitivity, rationality and weak monotonicity in fuzzy pairwise comparisons. Fuzzy Sets Syst. 1998, 94, 133–144. [Google Scholar] [CrossRef]
- Chang, D.-Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Công nghiệp thực phẩm Việt Nam có tiềm năng lớn trong thu hút đầu tư. Available online: https://tapchitaichinh.vn/nghien-cuu-trao-doi/cong-nghiep-thuc-pham-viet-nam-co-tiem-nang-lon-trong-thu-hut-dau-tu-315296.html (accessed on 18 October 2021).
- Thách Thức và cơ hội cho ngành chế biến thực phẩm ở Việt Nam năm. 2021. Available online: https://fbsp.ftu.edu.vn/thach-thuc-va-co-hoi-cho-nganh-che-bien-thuc-pham-o-viet-nam-nam-2021/ (accessed on 18 October 2021).
- 4 Ways to Make Food Processing More Sustainable. Available online: https://certification.bureauveritas.com/magazine/4-ways-make-food-processing-more-sustainable (accessed on 18 October 2021).
- Smarandache, F. α-Discounting Method for Multi-Criteria Decision Making. 2016. Available online: https://digitalrepository.unm.edu/math_fsp/243/ (accessed on 18 October 2021).
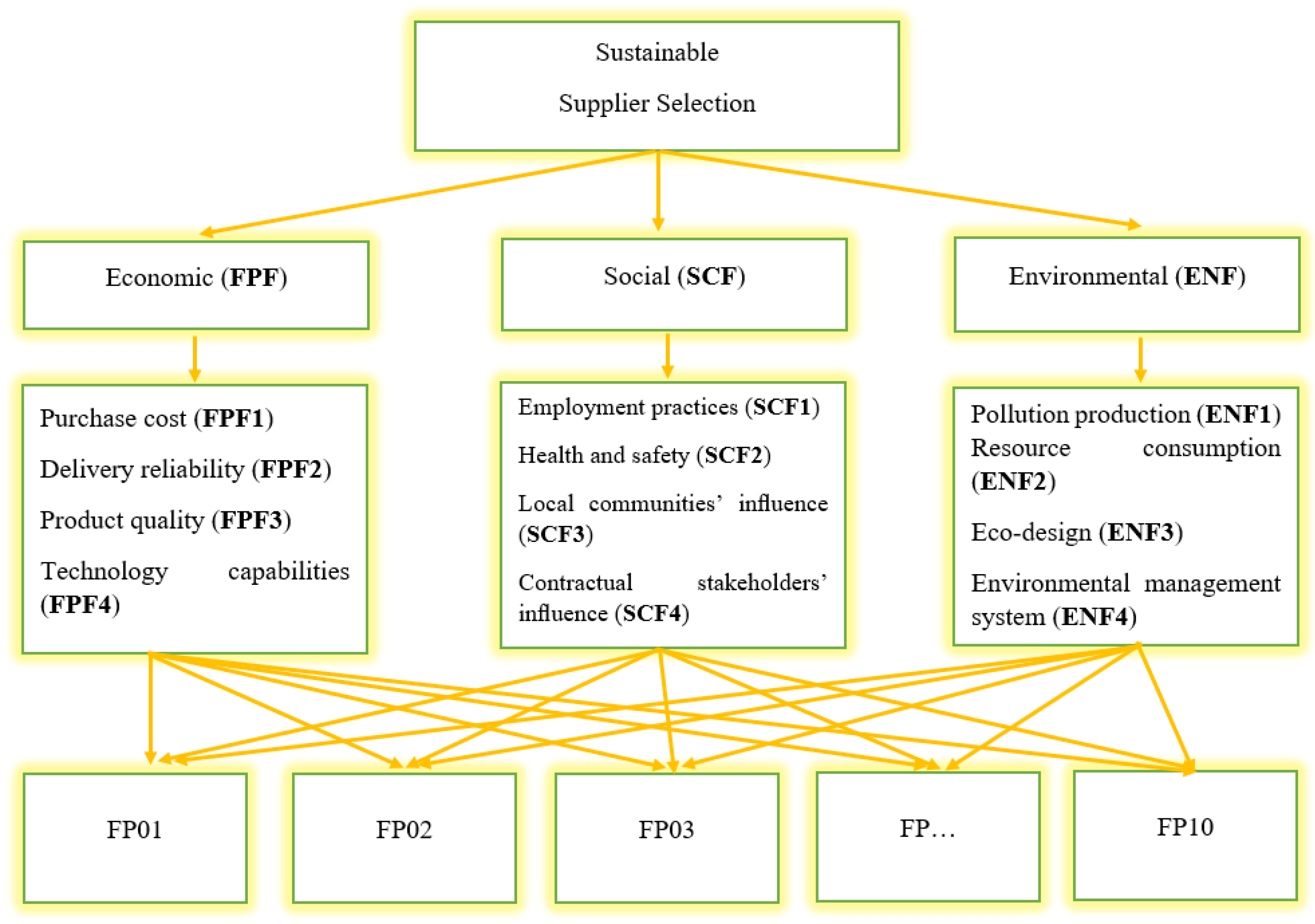
| Criteria | Fuzzy Geometric Mean of Each Row | Fuzzy Weights | BNP | Normalization | ||||
|---|---|---|---|---|---|---|---|---|
| FPF1 | 0.7826 | 1.0928 | 1.5255 | 0.0471 | 0.0895 | 0.1704 | 0.102 | 0.0905 |
| FPF2 | 0.7423 | 1.0208 | 1.3842 | 0.0447 | 0.0836 | 0.1546 | 0.094 | 0.0834 |
| FPF3 | 1.0156 | 1.4132 | 1.8999 | 0.0612 | 0.1157 | 0.2122 | 0.130 | 0.1147 |
| FPF4 | 0.7778 | 1.0613 | 1.4265 | 0.0469 | 0.0869 | 0.1593 | 0.098 | 0.0864 |
| SCF1 | 0.9556 | 1.3108 | 1.7732 | 0.0576 | 0.1073 | 0.1981 | 0.121 | 0.1069 |
| SCF2 | 0.6177 | 0.8340 | 1.1373 | 0.0372 | 0.0683 | 0.1270 | 0.078 | 0.0685 |
| SCF3 | 0.5958 | 0.8236 | 1.1620 | 0.0359 | 0.0674 | 0.1298 | 0.078 | 0.0687 |
| SCF4 | 0.7313 | 0.9981 | 1.3208 | 0.0440 | 0.0817 | 0.1475 | 0.091 | 0.0805 |
| ENF1 | 0.7376 | 0.9978 | 1.3213 | 0.0444 | 0.0817 | 0.1476 | 0.091 | 0.0807 |
| ENF2 | 0.6489 | 0.8768 | 1.2198 | 0.0391 | 0.0718 | 0.1363 | 0.082 | 0.0728 |
| ENF3 | 0.5461 | 0.7051 | 0.9682 | 0.0329 | 0.0577 | 0.1081 | 0.066 | 0.0586 |
| ENF4 | 0.8013 | 1.0781 | 1.4638 | 0.0483 | 0.0883 | 0.1635 | 0.100 | 0.0884 |
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| FPF1 | 0.04523 | 0.04523 | 0.00000 | 0.04523 | 0.00000 | 0.09047 | 0.09047 | 0.04523 | 0.00000 | 0.00000 |
| FPF2 | 0.08336 | 0.04168 | 0.00000 | 0.04168 | 0.00000 | 0.08336 | 0.00000 | 0.04168 | 0.08336 | 0.04168 |
| FPF3 | 0.00000 | 0.05733 | 0.00000 | 0.05733 | 0.05733 | 0.00000 | 0.05733 | 0.00000 | 0.11465 | 0.05733 |
| FPF4 | 0.08636 | 0.00000 | 0.04318 | 0.04318 | 0.00000 | 0.08636 | 0.00000 | 0.08636 | 0.04318 | 0.00000 |
| SCF1 | 0.10695 | 0.05347 | 0.00000 | 0.05347 | 0.00000 | 0.00000 | 0.05347 | 0.10695 | 0.05347 | 0.00000 |
| SCF2 | 0.06852 | 0.03426 | 0.03426 | 0.06852 | 0.03426 | 0.03426 | 0.03426 | 0.00000 | 0.03426 | 0.06852 |
| SCF3 | 0.06869 | 0.00000 | 0.06869 | 0.00000 | 0.06869 | 0.00000 | 0.06869 | 0.00000 | 0.00000 | 0.00000 |
| SCF4 | 0.08054 | 0.04027 | 0.08054 | 0.00000 | 0.04027 | 0.04027 | 0.08054 | 0.04027 | 0.04027 | 0.08054 |
| ENF1 | 0.04033 | 0.04033 | 0.00000 | 0.08065 | 0.04033 | 0.04033 | 0.08065 | 0.08065 | 0.04033 | 0.08065 |
| ENF2 | 0.07282 | 0.05462 | 0.07282 | 0.05462 | 0.05462 | 0.01821 | 0.05462 | 0.00000 | 0.07282 | 0.05462 |
| ENF3 | 0.05857 | 0.04393 | 0.04393 | 0.02929 | 0.01464 | 0.02929 | 0.01464 | 0.02929 | 0.00000 | 0.04393 |
| ENF4 | 0.08842 | 0.05894 | 0.02947 | 0.05894 | 0.02947 | 0.05894 | 0.05894 | 0.00000 | 0.02947 | 0.05894 |
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| FPF1 | 0.93922 | 0.93922 | 0.00000 | 0.93922 | 0.00000 | 1.00000 | 1.00000 | 0.93922 | 0.00000 | 0.00000 |
| FPF2 | 1.00000 | 0.94386 | 0.00000 | 0.94386 | 0.00000 | 1.00000 | 0.00000 | 0.94386 | 1.00000 | 0.94386 |
| FPF3 | 0.00000 | 0.92360 | 0.00000 | 0.92360 | 0.92360 | 0.00000 | 0.92360 | 0.00000 | 1.00000 | 0.92360 |
| FPF4 | 1.00000 | 0.00000 | 0.94189 | 0.94189 | 0.00000 | 1.00000 | 0.00000 | 1.00000 | 0.94189 | 0.00000 |
| SCF1 | 1.00000 | 0.92855 | 0.00000 | 0.92855 | 0.00000 | 0.00000 | 0.92855 | 1.00000 | 0.92855 | 0.00000 |
| SCF2 | 1.00000 | 0.95362 | 0.95362 | 1.00000 | 0.95362 | 0.95362 | 0.95362 | 0.00000 | 0.95362 | 1.00000 |
| SCF3 | 1.00000 | 0.00000 | 1.00000 | 0.00000 | 1.00000 | 0.00000 | 1.00000 | 0.00000 | 0.00000 | 0.00000 |
| SCF4 | 1.00000 | 0.94571 | 1.00000 | 0.00000 | 0.94571 | 0.94571 | 1.00000 | 0.94571 | 0.94571 | 1.00000 |
| ENF1 | 0.94563 | 0.94563 | 0.00000 | 1.00000 | 0.94563 | 0.94563 | 1.00000 | 1.00000 | 0.94563 | 1.00000 |
| ENF2 | 1.00000 | 0.97927 | 1.00000 | 0.97927 | 0.97927 | 0.90398 | 0.97927 | 0.00000 | 1.00000 | 0.97927 |
| ENF3 | 1.00000 | 0.98329 | 0.98329 | 0.96021 | 0.92201 | 0.96021 | 0.92201 | 0.96021 | 0.00000 | 0.98329 |
| ENF4 | 1.00000 | 0.96479 | 0.90743 | 0.96479 | 0.90743 | 0.96479 | 0.96479 | 0.00000 | 0.90743 | 0.96479 |
| Alternatives | Ka | Ranking | Kb | Ranking | Kc | Ranking | K |
|---|---|---|---|---|---|---|---|
| A1 | 0.1285 | 1 | 3.9590 | 1 | 1.0000 | 1 | 2.4942 |
| A2 | 0.1098 | 4 | 2.7852 | 4 | 0.8539 | 4 | 1.8887 |
| A3 | 0.0788 | 10 | 2.0980 | 10 | 0.6127 | 10 | 1.3959 |
| A4 | 0.1113 | 3 | 2.9811 | 3 | 0.8656 | 3 | 1.9790 |
| A5 | 0.0871 | 8 | 2.1166 | 9 | 0.6775 | 8 | 1.4602 |
| A6 | 0.1007 | 5 | 2.6960 | 6 | 0.7835 | 5 | 1.7904 |
| A7 | 0.1129 | 2 | 3.1732 | 2 | 0.8785 | 2 | 2.0685 |
| A8 | 0.0794 | 9 | 2.2679 | 8 | 0.6179 | 9 | 1.4694 |
| A9 | 0.1005 | 6 | 2.7778 | 5 | 0.7818 | 6 | 1.8220 |
| A10 | 0.0911 | 7 | 2.5803 | 7 | 0.7087 | 7 | 1.6769 |
| λ = 0.1 | λ = 0.2 | λ = 0.3 | λ = 0.4 | λ = 0.5 | λ = 0.6 | λ = 0.7 | λ = 0.8 | λ = 0.9 | λ = 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 2.4952 | 2.3842 | 2.4002 | 2.5042 | 2.3972 | 2.4350 | 2.5142 | 2.4768 | 2.4979 | 2.4904 |
| A2 | 1.8987 | 1.8971 | 1.8950 | 1.8923 | 1.8887 | 1.8836 | 1.8757 | 1.8621 | 1.8329 | 1.7251 |
| A3 | 1.4014 | 1.4005 | 1.3994 | 1.3979 | 1.3959 | 1.3930 | 1.3887 | 1.3811 | 1.3651 | 1.3065 |
| A4 | 1.9866 | 1.9854 | 1.9838 | 1.9818 | 1.9790 | 1.9751 | 1.9692 | 1.9590 | 1.9371 | 1.8575 |
| A5 | 1.4697 | 1.4682 | 1.4662 | 1.4637 | 1.4602 | 1.4554 | 1.4479 | 1.4351 | 1.4074 | 1.3038 |
| A6 | 1.7973 | 1.7961 | 1.7947 | 1.7929 | 1.7904 | 1.7868 | 1.7814 | 1.7721 | 1.7522 | 1.6797 |
| A7 | 2.0737 | 2.0728 | 2.0718 | 2.0704 | 2.0685 | 2.0658 | 2.0617 | 2.0547 | 2.0397 | 1.9858 |
| A8 | 1.4724 | 1.4719 | 1.4713 | 1.4705 | 1.4694 | 1.4678 | 1.4654 | 1.4613 | 1.4525 | 1.4212 |
| A9 | 1.8274 | 1.8266 | 1.8254 | 1.8240 | 1.8220 | 1.8193 | 1.8150 | 1.8077 | 1.7921 | 1.7359 |
| A10 | 1.6808 | 1.6802 | 1.6794 | 1.6783 | 1.6769 | 1.6750 | 1.6719 | 1.6667 | 1.6557 | 1.6159 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thanh, N.V.; Lan, N.T.K. A New Hybrid Triple Bottom Line Metrics and Fuzzy MCDM Model: Sustainable Supplier Selection in the Food-Processing Industry. Axioms 2022, 11, 57. https://doi.org/10.3390/axioms11020057
Thanh NV, Lan NTK. A New Hybrid Triple Bottom Line Metrics and Fuzzy MCDM Model: Sustainable Supplier Selection in the Food-Processing Industry. Axioms. 2022; 11(2):57. https://doi.org/10.3390/axioms11020057
Chicago/Turabian StyleThanh, Nguyen Van, and Nguyen Thi Kim Lan. 2022. "A New Hybrid Triple Bottom Line Metrics and Fuzzy MCDM Model: Sustainable Supplier Selection in the Food-Processing Industry" Axioms 11, no. 2: 57. https://doi.org/10.3390/axioms11020057
APA StyleThanh, N. V., & Lan, N. T. K. (2022). A New Hybrid Triple Bottom Line Metrics and Fuzzy MCDM Model: Sustainable Supplier Selection in the Food-Processing Industry. Axioms, 11(2), 57. https://doi.org/10.3390/axioms11020057






