Limits to the Validity of Thermal-Pressure Equations of State

Abstract

Thermal-pressure Equations of State (EoS) such as the Mie-Grüneisen-Debye (MGD) model depend on several assumptions, including the quasi-harmonic approximation (QHA) and a simplified phonon density of states. We show how the QHA is violated by materials exhibiting anisotropic thermal pressure. We also show that at pressures lower than those of the isochor of the reference volume, the static pressure may become sufficiently negative to make the compressional part of the EoS invalid. This limit is sensitive to the combined effects of the EoS parameters K’₀, q and the Grüneisen parameter γ₀. Large values of q, which correspond to a rapid decrease in phonon mode frequencies with increasing volume, can also lead to the bulk modulus becoming zero at high pressures and temperatures that are not particularly extreme for planetary geotherms. The MGD EoS therefore has an extremely limited P and T regime over which it is both valid and has physically-meaningful properties. Outside of this range, additional terms should be included in the thermal pressure that represents the physical properties of the solid. Or, alternatively, ‘isothermal’ EoS in which the temperature variation of the elastic properties is explicitly modeled without reference to a physical model can be used.

1. Introduction

The text book written by Orson Anderson titled “Equations of State of Solids for Geophysics and Ceramic Science” [1] is a masterful summary of the principles, theory, and practical application of Equations of State (EoS). In particular, it is emphasized that “By physicists’ standards, the materials of planets are not well characterized……The corresponding physical theories applied to these planetary materials are also necessarily simplified...” [1] (p. 113). Therefore, Orson Anderson took great care in laying out the assumptions and simplifications underlying each EoS discussed, and in explaining the consequent limitations on the P, T, and V regimes in which they are valid. The presentation of this material was based on the deep knowledge and insights that Orson Anderson and his contemporaries and co-workers developed over their research careers. Unfortunately, as research into planetary interiors moves into new regimes of P and T, and science “frees itself from the tyranny of Earth’s geotherm” [2], these limitations on EoS are often forgotten and EoS are blindly used in pressure and temperature regimes where they are unphysical and have no validity. In this contribution, we build on the work of Orson Anderson by first reviewing the properties and behavior of thermal-pressure type EoS, and then indicate further limits to their physical validity, in particular at high-temperature and low-pressure conditions not found on the terrestrial geotherm. These conditions are more likely to occur on the smaller terrestrial planets (i.e., Mars, Mercury) in the solar system. Furthermore, advances in the field of extrasolar planet exploration have led to the discovery of planets with a wide variability in their characteristics from Earth-like planets with different masses and radii, to planets that have no solar system analogues (e.g., [3,4]). As equations of state are the link between astrophysical observations and the interpretation of the interiors of exoplanets [5], knowing the limitations of PVT EoS is fundamental for the study of exoplanets.

2. Methods

All numerical calculations were performed with v7.5 of the EosFit7c software [6], which was released in summer 2019. The code has been validated [6] against a wide variety of other software and algebraic solutions, as documented in the help system for the software. Most recently, the calculated properties of the Mie-Grüneisen-Debye thermal pressure EoS have been validated against a Matlab code independently written by Eleanor Berryman.

3. Thermal-Pressure EoS

In thermal-pressure EoS, the pressure at a given volume V and temperature T is treated as the sum of two contributions:

P(V,T) = P_ref(V,T₀) + ΔP_th(V,T)

(1)

The pressure P_ref is the pressure required to compress the material from its volume V₀ at reference conditions (T₀ and P = 0) to the volume V at the same temperature T₀. The second term is the change in thermal pressure ΔP_th. This is the pressure change at constant volume due to the temperature difference between T₀ and T. It is thus the pressure change along an isochor of the material (Figure 1). If the volume V of the material at P and T is equal to its volume V₀ at the reference conditions, then no compression at the reference conditions is required to attain the final volume V, so P_ref = 0. In this case, the total pressure is equal to ΔP_th (black line and symbols in Figure 1).

At pressures above the isochor of V₀ the volume V is smaller than V₀ and this is obtained with a positive pressure P_ref (blue in Figure 1). On the other hand, for P, T conditions below the isochor of V₀ the V is greater than V₀, and the material must be expanded at T₀ to obtain the required V. This means that P_ref < 0 (red in Figure 1). The isochor passing through the reference conditions therefore divides P–T space into two regions: at P above this reference isochor the P_ref is positive, but at pressures below the reference isochor the P_ref is negative.

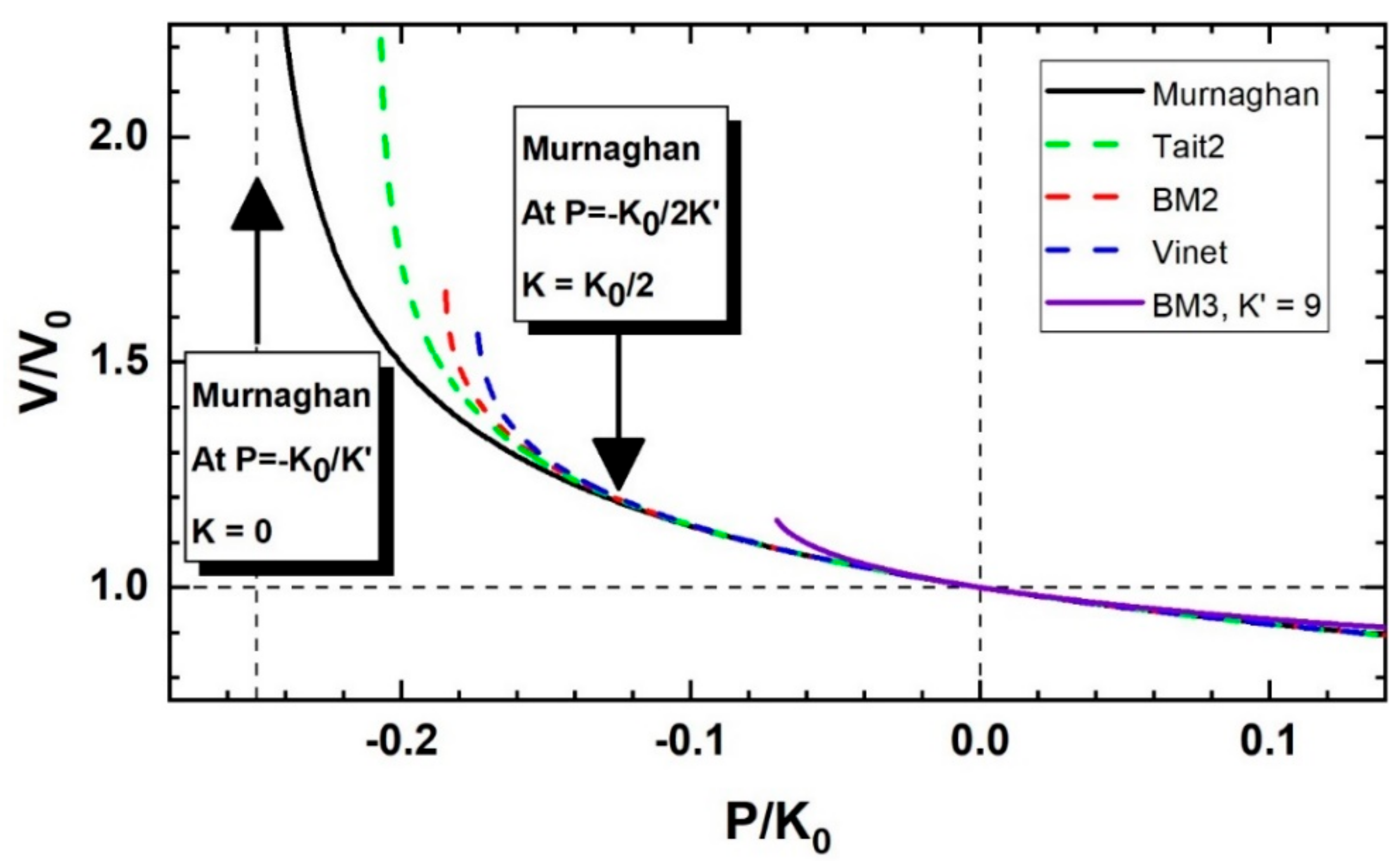
3.1. Limitations to Isothermal EoS in Expansion

The volume variation of a material with pressure at T₀ is described by its isothermal equation of state. Such EoS for solids are developed explicitly for describing their behavior under compression, and their validity for negative pressures and volume expansion relative to the reference conditions is limited. This limit should be considered when working with thermal pressure EoS at volumes greater than V₀. The limit is illustrated in Figure 2 which shows that all common isothermal EoS show a divergence of V (and thus V/V₀) to very large values at negative pressures that are a small fraction (typically <25%) of the value of the bulk modulus K₀ at the reference conditions.

This divergence can be most easily understood by reference to the Murnaghan EoS [10] which has the property that the bulk modulus is linear in pressure:

K = K₀ + K’₀P

(2)

with K’₀ being the pressure derivative of the bulk modulus. It is clear that with K’₀ > 0, there is a pressure P = −K₀/K’₀ at which the bulk modulus K becomes zero and thus the volume diverges to infinity (Figure 2). The pressure at which this divergence occurs depends on the EoS. It is generally less-negative than for the Murnaghan EoS because other EoS include a variation in K’ = (dK/dP)_T which is expressed as K’’ = (dK’/dP)_T. The value of K’’ is zero in the Murnaghan EoS (Equation (2)) but for most materials it is actually negative [1], and the implied value of K’’ for the 2nd-order EoS shown in Figure 2 is also negative (e.g., [1,6,11,12]). Therefore, K’ becomes more positive at negative pressures in other EoS than in the Murnaghan, and thus the bulk modulus becomes zero at smaller negative pressures. If the value of K’₀ is larger, then the decrease of K is faster, and the limit to the validity of the EoS is at less-negative pressures (deep purple line in Figure 2). This pressure limit becomes even less-negative in 4th-order EoS with K’’ more negative than the implied value of the 3rd-order EoS. It follows that there is no simple dependence upon the reference parameters of the EoS of the pressure at which the divergence of volume occurs. Further, before the volume curves show strong divergence, the bulk modulus and its pressure derivatives show values that would be considered anomalous for solid materials. Therefore, rather than just considering the algebraic limit (e.g., K = 0) to the validity of EoS in expansion, it is necessary to find a practical limit to their physical reasonableness or validity. Figure 2 also shows that the difference between the various EoS only becomes significant at pressures more negative than where the bulk modulus of the Murnaghan EoS becomes one-half of K₀, which suggests that K > K₀/2 is a reasonable criterium to use for a limit to the validity of EoS. For the Murnaghan EoS this gives a limiting pressure P_lim = −K₀/2K’₀. For other EoS the expressions for P_lim are more complex, but the values of P_lim are typically 5–10% less negative than for a Murnaghan EoS with the same values of the parameters K₀ and K’₀. For the example of an olivine-like EoS used in Figure 2, P_lim ranges from −14.0 to −15.6 GPa for different types of isothermal EoS. The influence of K’₀ on this limit is significant. For an orthopyroxene-like EoS with K’₀ = 9 and the same value of K₀, the EoS is restricted in expansion to only P_lim ~ 6–7 GPa (deep purple line, Figure 2).

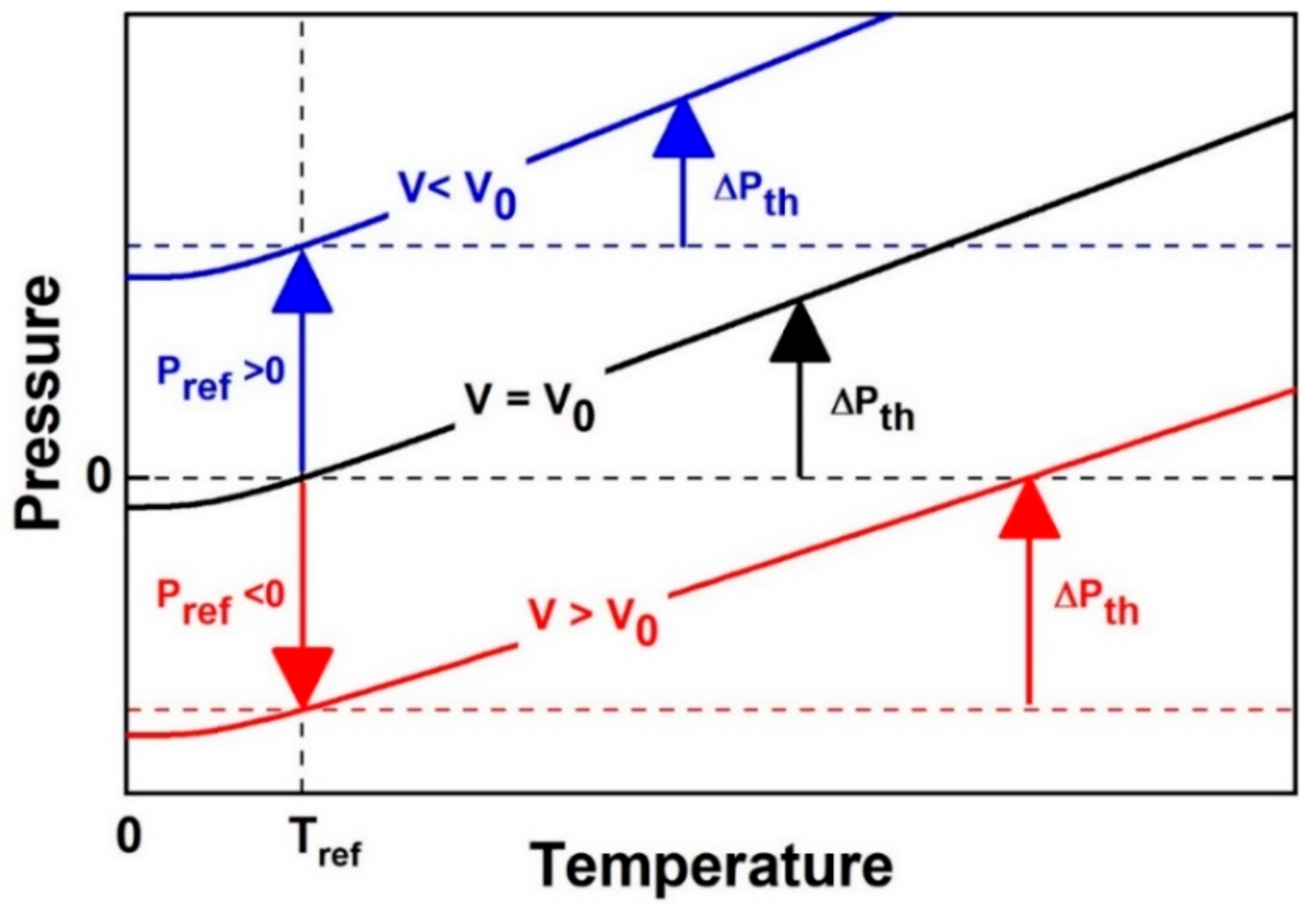
3.2. Limitations to Thermal-Pressure EoS

Thus, at sufficiently high temperatures, thermal-pressure EoS will have large enough ΔP_th that P_ref is more negative than P_lim, thus making the EoS physically invalid. Given that in planetary science we are only interested in positive total pressures, the largest negative value of P_ref will occur for calculations of volume at ambient pressure, for which P_ref = −ΔP_th. The corresponding temperature limit, T_lim, to the validity of the thermal-pressure EoS at room pressure then follows from requiring −ΔP_th > P_lim. For isochors that are approximately linear and parallel, we can estimate T_lim by using the slope of the isochor (dP/dT)_V = αK ~ α₀K₀ and equating it to the slope of the isochor from P_lim and T_ref to P = 0 and T_lim, thus:

$${\left(\frac{dP}{dT}\right)}_V\approx {\alpha }_0{K}_0\approx \frac{-P_{lim}}{\left(T_{lim}-T_0\right)}$$

(3)

If we further take the value of P_lim = −K₀/2K’₀ from the Murnaghan EoS, one can obtain an estimate of the limiting temperature in terms of the EoS parameters at the reference conditions:

$$T_{lim}\approx T_0+ \frac{1}{\left(2{\alpha }_0{K^{\prime }}_0\right)}$$

(4)

For our olivine-like EoS parameters, one obtains a T_lim ~ 5000 K, but for orthopyroxene-like EoS parameters, the larger K’₀ reduces T_lim to the range 1900–2400 K (depending on the value of the thermal expansion coefficient). If the isochors are not quasi-parallel, a better estimate of T_lim can be obtained if one does not equate αK = α₀K₀, thereby obtaining:

$$T_{lim}\approx T_0+ \frac{K_0}{\left(2{K^{\prime }}_0{\alpha }_{Plim}{K}_{Plim}\right)}$$

(5)

where the subscript “Plim” indicates the parameter values at the pressure P_lim and T₀. One can imagine that low-pressure conditions that exceed these temperature limits to the validity of the thermal-pressure EoS may occur in several planetary environments. Certainly, they could occur in the later stages of post-impact recovery from shock, when temperatures remain high but the shock wave-induced pressure has decayed. Alternatively they could occur in the early stages of the evolution of hot small planets.

The thermal pressure in a crystal arises from the excitation of its collective vibrational modes, the phonons. Different thermal-pressure EoS are distinguished by the method used to calculate the thermal pressure and hence the change in thermal pressure, ΔP_th, from the reference temperature. It can be modeled either in an ad-hoc thermodynamic approach by fitting parameters such as the thermal expansion coefficient and the bulk modulus and their derivatives to experimental data, or it can be calculated from an analysis of the properties of the phonon modes themselves via statistical mechanics [13]. In the thermodynamic approach there are no further assumptions, and the temperature limit T_lim is a direct constraint on the physical meaningfulness of the EoS. On the other hand, for thermal-pressure EoS based on statistical mechanics, T_lim may not be of practical relevance if the assumptions behind the derivation of the EoS are already violated at lower temperatures. Therefore, each EoS formulism of this type needs to be examined individually, as we do for the Mie-Grüneisen-Debye EoS in Section 4. Nonetheless, in order to prevent EoS software from crashing in the large V regime, it is certainly necessary to impose a limit to how negative P_ref can become. In the latest release of EosFit software suite [6,14], this limit is now set as the requirement that K > K₀/2 for all steps of all EoS calculations.

4. Mie-Grüneisen-Debye EoS

The Mie-Grüneisen-Debye (MGD) EoS is based on the quasi-harmonic approximation (QHA) to the statistical mechanics of the collective vibrational modes (phonons) of crystalline materials [1] (chapter 2). Under the QHA it is assumed that the vibrational modes do not interact and are completely independent of one another, and that their wavenumbers (and thus frequencies) are only dependent upon the molar volume; the effects of P and T on the wavenumbers of the phonon modes are thus indirect in the sense that they change the volume, which then changes the wavenumbers. The volume dependence of the phonon frequencies ω_ι is defined by the phonon-mode Grüneisen parameters ${\gamma }_i=\frac{V}{{\omega }_i}\frac{\partial \omega }{\partial V}$. In order to derive the Mie-Grüneisen-Debye EoS, further assumptions are necessary. The first is that the volume dependence of all of the phonon frequencies is the same, and can be represented by a single Grüneisen parameter γ. Then the thermal pressure becomes $P_{th}=\frac{\gamma }{V}{E}_{th}$, where V is explicitly the molar volume and E_th is the thermal energy that is the energy of the vibrational modes. E_th is further assumed to derive from a simplified phonon density of states, which can be characterized by a single Debye frequency, or alternatively the Debye temperature θ_D, whose energy is represented by the Debye function [1] which is a function of only T and θ_D and is an integral from T = 0 to T. Therefore, if a finite temperature is chosen for T₀, the change in thermal pressure from T₀ becomes:

$$∆P_{th}= \frac{3nR\gamma }{V}\left[TD\left(\frac{{\theta }_D}{T}\right)-T_{ref}D\left(\frac{{\theta }_D}{T_0}\right)\right]$$

(6)

In which $D\left(\frac{{\theta }_D}{T}\right)$ represents the Debye function, R is the gas constant and n is the number of atoms in the formula unit corresponding to the molar volume V.

4.1. Limitations to MGD EoS from Expansion

As demonstrated in [1] (Figure 10.1 therein), the temperature range in which the QHA is valid and the material properties are dominated by harmonic effects is bounded by regions of invalidity at both low and high temperatures. At ambient pressure and low temperatures, below T ~ 0.8θ_D, quantum effects start to become significant, whereas above T ~ 1.2θ_D there can be significant contributions from anharmonicity. Given that Debye temperatures for minerals are typically in the range 500–800 K, this is a significant restriction, but the range of temperatures in which the QHA remains valid is significantly expanded under high pressures [1] (Figure 10.2 therein) and [15]. If the non-validity of the compressional part of the EoS discussed in Section 3 is to be significant for a MGD EoS, T_lim must therefore be of the order of 1 – 2θ_D. Figure 3 shows isochors (in black) calculated for a range of values of γ for the BM2 EoS representative of olivine minerals. All of the isochors are drawn from the same pressure close to P_lim and therefore all represent the same volume, and the same value of K at T_ref. For low values of γ, the thermal expansion coefficients are reasonable (α₀ ~ 2.6 × 10⁻⁵ K⁻¹), and the T_lim where the isochors cut the temperature axis are far in excess of T = 2θ_D. Extreme values of γ = 5, which lead to unrealistic values of the volume thermal expansion coefficient at reference conditions (α₀ ~ 1.3 × 10⁻⁴ K⁻¹), are required to reduce T_lim to the vicinity of 2θ_D. In contrast, the orthopyroxene-like EoS has a much larger value of K’₀ and thus a smaller P_lim. Thus, although the slopes of the isochors through P_lim are very similar to those of the olivine-like EoS, the T_lim is in the vicinity of 2θ_D for γ = 2.

The isochors shown as solid lines in Figure 3 are each calculated with a constant value of γ, although it would be expected to increase with increasing volume. The variation in γ with volume is usually modeled in the MGD EoS by $\gamma ={\gamma }_0{\left(\frac{V}{V_0}\right)}^q$. The effect of q > 0 is to increase the value of γ at high temperatures, increasing the volume thermal expansion coefficient and thus steepening the isochors, as shown by the dashed lines in Figure 3, which both have γ₀ = 1 and an extreme value of q = 5 so as to clearly demonstrate the effects. The influence of large positive values of q is clearly stronger on isochors of the EoS with the smaller K’₀, but they are not expected to bring T_lim within the range of temperature for which the QHA will be valid. Therefore, the temperature limit T_lim appears to only be relevant for materials with large values of K’₀ for which it is possible for T_lim to be in the vicinity of 2θ_D (purple lines in Figure 3).

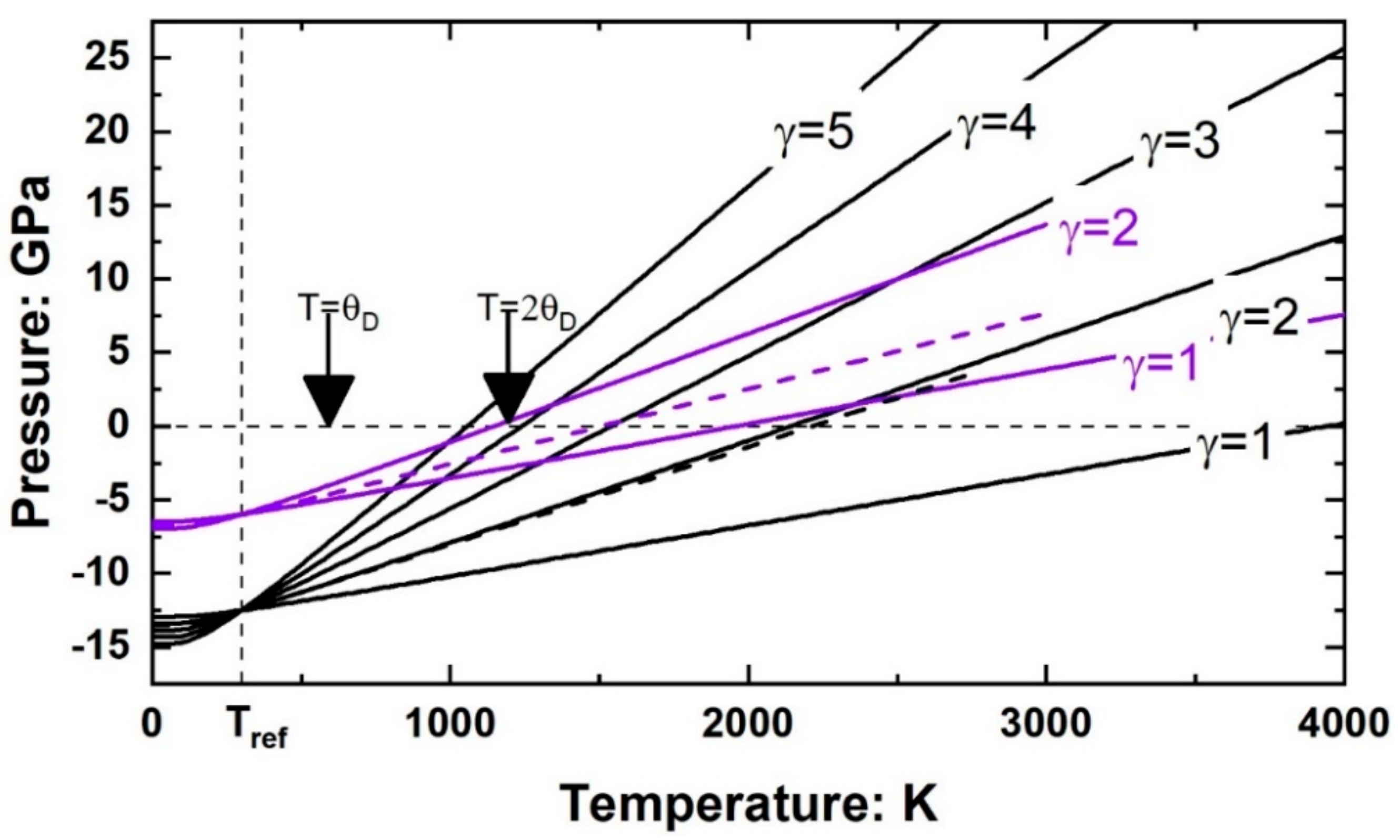
4.2. The Consequences of q

We have already noted how the value of the γ parameter influences the volume thermal expansion coefficient at room conditions, and that the value of q controls how the value of γ changes, especially at large volumes corresponding to high temperatures. More generally, both γ₀ and q affect the value of both the thermal expansion coefficient and the bulk modulus at all P, T conditions. In this section we take the results of Anderson [1] and show how extreme values of these variables place additional constraints on the validity of the MGD EoS.

Taking the volume differential of Equation (1) and multiplying by the volume V, one obtains an expression for the bulk modulus of a thermal-pressure EoS at any P, T:

$$\begin{array}{c}-V{\left(\frac{\partial P}{\partial V}\right)}_{}=-V{\left(\frac{\partial P_{ref}}{\partial V}\right)}_{}-V{\left(\frac{\partial P_{th}}{\partial V}\right)}_{}\\ K_{}=K_{Pref}-V{\left(\frac{\partial P_{th}}{\partial V}\right)}_{}\end{array}$$

(7)

Thus, the bulk modulus is the sum of two terms. The first is the bulk modulus, $K_{Pref}$, on the isochor at T₀, which is at the pressure P_ref. The second term is the volume derivative of the thermal pressure. At high temperatures the Debye function $D\left(\frac{{\theta }_D}{T}\right)$ approaches the value of 1, allowing Equation (6) to be used to obtain an approximation for the P_th of the MGD EoS at high temperatures (see Equation (2.39) in [1]):

$$P_{th}\approx \frac{3nR\gamma T}{V}$$

(8)

By substituting ${\gamma }_0{\left(\frac{V}{V_0}\right)}^q$ for γ, taking the derivative of this expression with respect to V and then multiplying by V, one obtains an expression for the last term in Equation (7):

$$-V{\left(\frac{\partial P_{th}}{\partial V}\right)}_{}\approx \frac{-3nR{\gamma }_{0}T{V}^{\left(q-1\right)}}{V_0^q}\left(q-1\right)$$

(9)

This term appears in Equation (2.42) in reference [1]. Along an isochor the terms in V remain constant, as do the constants n, R, and γ₀. Therefore, the sign of this contribution to the bulk modulus variation along an isochor depends on (q − 1). For q = 1, the derivative (Equation (9)) is zero, and therefore from Equation (7) $K= K_{Pref}$. This means that the bulk modulus remains constant and equal to K_Pref along an isochor. The Holland-Powell thermal-pressure EoS has this same property [7,13,16]. In the MGD EoS when q < 1, the expression for $-V{\left(\frac{\partial P_{th}}{\partial V}\right)}_{}$ is positive and the bulk modulus increases with increasing temperature along an isochor. This is also a property of the MGD EoS with q = 0, or constant γ = γ₀, that are shown as solid lines in Figure 3. Conversely, for q > 1, the bulk modulus decreases as temperature increases along an isochor. It is believed that most minerals and planetary materials exhibit values of q in the range 1 to 2 [1] providing that there are no phase transitions. However, for all values of q > 1, there will be a temperature at which the bulk modulus becomes zero, and the EoS again becomes physically invalid. This limit is reached at lower temperatures with larger values of q. For example, along the isochor shown as a purple dashed line in Figure 3 for the orthopyroxene-like EoS with γ₀ = 1 and q = 5, the bulk modulus becomes zero just above 3000 K and 7.6 GPa. At the same time, the volume thermal expansion coefficient becomes infinite, because the product αK_T has to remain equal to the slope ${\left(\frac{\partial P}{\partial T}\right)}_V$ of the isochor.

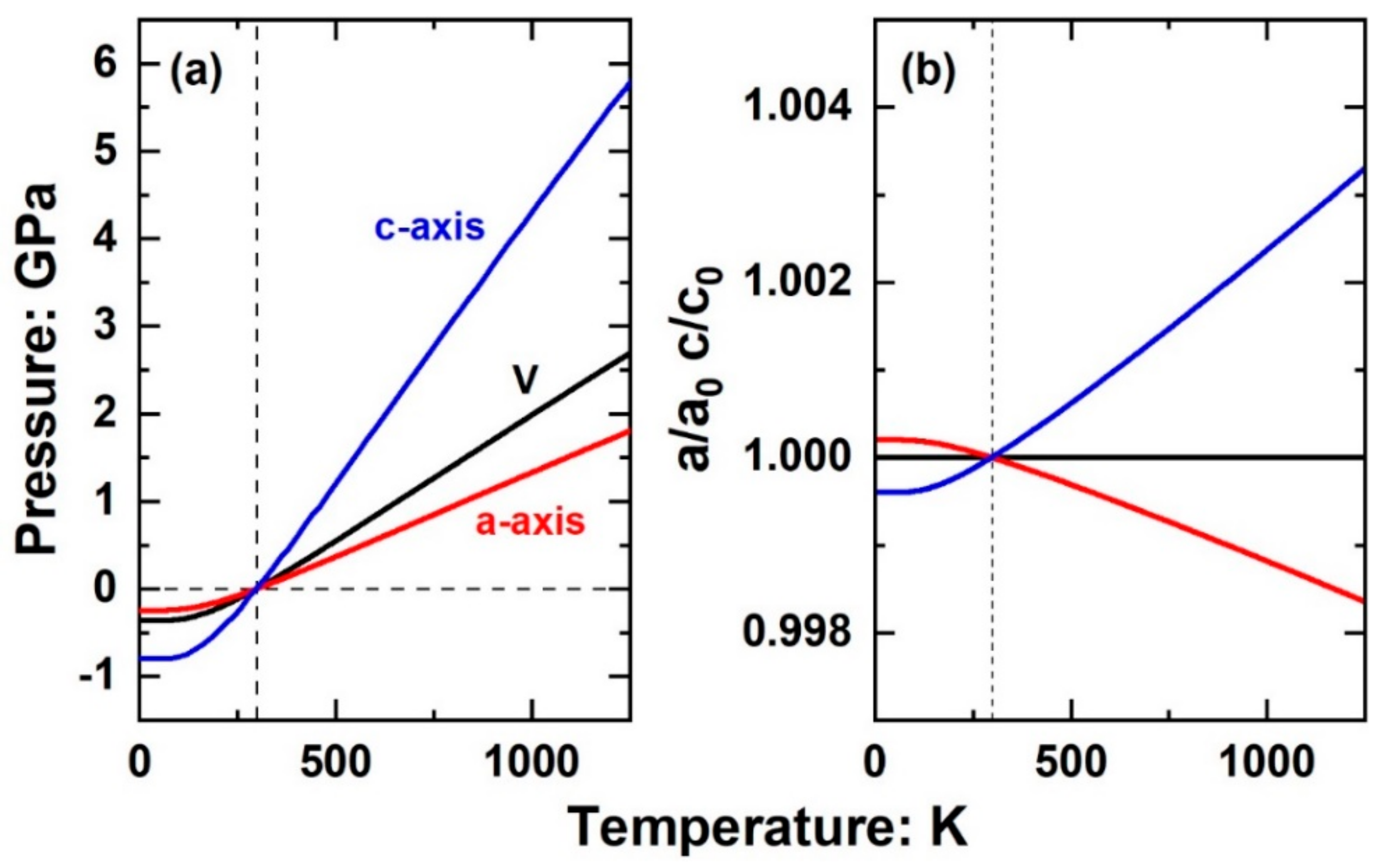
4.3. The Consequences of Anisotropic Pth

The basis of the MGD EoS are the concepts of thermal pressure and isochors, with the thermal pressure being the increase in pressure along an isochor. However, the thermal expansion and compressibility which describe the response of a crystal to respectively temperature and hydrostatic pressure are only isotropic for cubic crystals. Therefore, for lower-symmetry crystals, the cell parameters vary by different amounts for a given change in P or T. From the definitions of the thermal expansion tensor α_ij and the compressibility tensor β_ij [17], the combined effect of a change in P and T is described by the strain tensor ε_ij:

$${\epsilon }_{ij}={\alpha }_{ij}dT-{\beta }_{ij}dP$$

(10)

It is therefore not possible to maintain all of the cell parameters or the lengths of all directions in the crystal constant when P and T are changed. However, along a line defined by

$${\left(\frac{\partial P}{\partial T}\right)}_{}=\frac{{\alpha }_{ij}}{{\beta }_{ij}}$$

(11)

the strain ε_ij will remain constant. The property $\frac{{\alpha }_{ij}}{{\beta }_{ij}}$ of a crystal varies with direction in the crystal, but it is not a tensor property. It defines lines in P–T space along which there is no strain in one chosen direction within the crystal. By analogy with the conventional definition of thermal pressure, ${\left(\frac{\partial P}{\partial T}\right)}_V$, Equation (11) defines the anisotropic thermal pressure of a crystal.

In particular, for uniaxial crystals (in which a = b) and orthorhombic crystals, one can calculate from the values of the axial thermal expansion coefficients and axial compressibilities lines in P–T space along which the individual cell parameters a, b and c remain constant. It has long-been recognized [18] that many minerals exhibit the property that directions with large thermal expansion tend to compress more under pressure, which is equivalent to saying that the anisotropic thermal pressure defined by Equation (11) tends to be close to isotropic in many crystal structures. However, for crystals in which the structural response to P and T appears to be dominated by cation-cation repulsion along one axis, this axis tends to be relatively incompressible (small β) and at the same time exhibits a large thermal expansion coefficient α. These compounds then exhibit significantly anisotropic thermal pressure (Equation (11)). Figure 4 illustrates one way in which the anisotropy of the thermal pressure of a material may be evaluated, directly from the thermal expansion and compressibility tensors measured at room conditions. Figure 4a shows lines of constant a (=b) and c cell parameters calculated from the well-constrained elastic properties of zircon at room conditions [19,20]. These two lines deviate significantly from the isochor, with the consequence that there are significant linear strains along isochors (Figure 4b). Because phonon-mode frequencies change linearly with small strains [21,22,23,24,25], this implies that the phonon-mode frequencies of materials with anisotropic thermal pressure change along the isochors, in violation of the assumptions of the QHA.

Whether the resulting strains along the isochors are sufficiently large to constitute a significant violation of the QHA and invalidate the MGD EoS depends on the magnitudes of the components of the phonon-mode Grüneisen tensors which relate the phonon frequencies to the strains [19,22,23,25]. One direct test is to compare the measured changes in the phonon-mode frequencies (e.g., the frequencies of Raman bands) with pressure and with temperature. If the isobaric and isothermal change in phonon wavenumbers obey the relationship ${\left(\frac{\partial \omega }{\partial P}\right)}_T=-\left(\frac{{\beta }_V}{{\alpha }_V}\right){\left(\frac{\partial \omega }{\partial T}\right)}_P$, then the thermal pressure is effectively isotropic [19]. The isobaric variation of the bulk modulus with temperature is also a sensitive indicator of the validity of the QHA because it is sensitive to the parameter K’₀. If fitting the temperature variation of the bulk modulus requires a value of K’₀ that is inconsistent with that required to fit either the volume variation with pressure or the measured change in the elastic moduli with pressure this may indicate that the anisotropic thermal pressure is significant. EoS such as the MGD which rely on the QHA should not be used for materials in which the thermal pressure is significantly anisotropic.

5. Conclusions

In his book, Orson Anderson [1] took great pains to explain the assumptions behind various EoS formula and to explore the limits of these assumptions. For the MGD EoS, he emphasized the point that the temperature range within which the QHA is valid is extremely limited at ambient pressures, although it expands at higher pressures as both quantum-mechanical and anharmonic effects are suppressed [15]. Further, in his chapter 5 [1] he demonstrated that only ‘close-packed’ structures have phonon densities of state that are ‘Debye-like’, meaning that MGD EoS should not be applied to open-framework materials whose structural response to changing pressure and temperature is dominated by tilting of relatively rigid polyhedral structural units such as SiO₄ tetrahedra, (e.g., [18,26]). In this contribution we have identified further limitations on thermal-pressure type EoS. First, that structures that respond by polyhedral tilting [26] and even densely-packed structures such as rutile and zircon can exhibit strong anisotropy in their thermal pressure. This leads to changes of their phonon-mode frequencies along the isochors, and thus invalidates a fundamental assumption behind thermal-pressure EoS including the MGD and the Holland-Powell EoS [16] widely used for petrological and planetary thermodynamics. Fits of a thermal-pressure EoS to volume and elastic data of such materials are often poor, and at the same time can lead to extreme values of EoS parameters [27]. Second, at low pressures below the isochor of the reference volume V₀ (and thus at high temperatures), the static pressure P_ref may become sufficiently negative to make the compressional part of the EoS invalid. This limit to the validity of the MGD EoS is sensitive to the combined effects of the EoS parameters K’₀, q, and γ (Figure 3). Third, large values of q which correspond to a rapid decrease in phonon mode frequencies with volume can lead to the bulk modulus becoming zero at pressures and temperatures that are not particularly extreme for planetary geotherms. If one obtains extreme values of especially K’₀, q, and γ through fitting of P–V–T data, it is worthwhile to explore the physical reason for the values and consider whether or not one or more of the assumptions behind the derivation of thermal-pressure EoS are violated by the known structure, properties, or phonon density of states of the material. Possible causes could include the presence of phase transitions, anisotropic thermal pressure, or significant anharmonic contributions (both phonon and electronic) to the thermal pressure. There are at least two possible types of approaches to obtaining more accurate and valid EoS in these cases. One is to include additional terms in the thermal pressure that represent the physical properties of the solid, for example by using additional oscillators to better represent the phonon density of state [28] and explicitly adding terms to describe the anharmonic contributions of the phonons [1,29,30] or electrons, (e.g., [31]), or by determining the anisotropy of the thermal Grüneisen parameter from the variation of the unit-cell parameters with temperature [29,30,32]. The alternative approach is not to use thermal-pressure EoS, but to employ “isothermal” EoS in which the temperature variation of the elastic properties such as K and K’ is explicitly modeled [7]. Which approach is tractable and appropriate depends on the data available for the material.