Modeling the Liberation of Comminuted Scheelite Using Mineralogical Properties
Abstract
1. Introduction
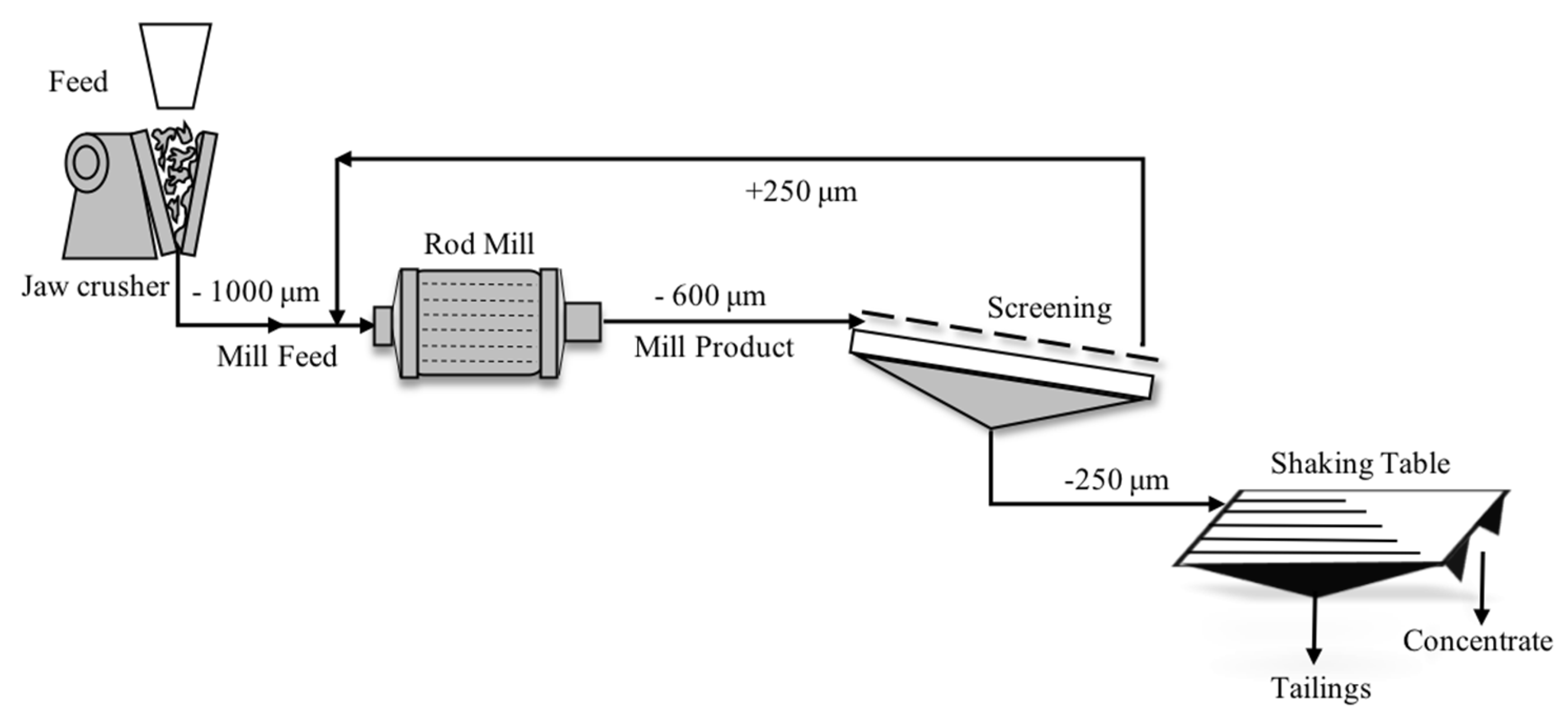
2. Materials and Methods
2.1. Materials
2.2. Work Index Test
2.3. Analytical Methods
3. Results and Discussion
3.1. Chemical Composition
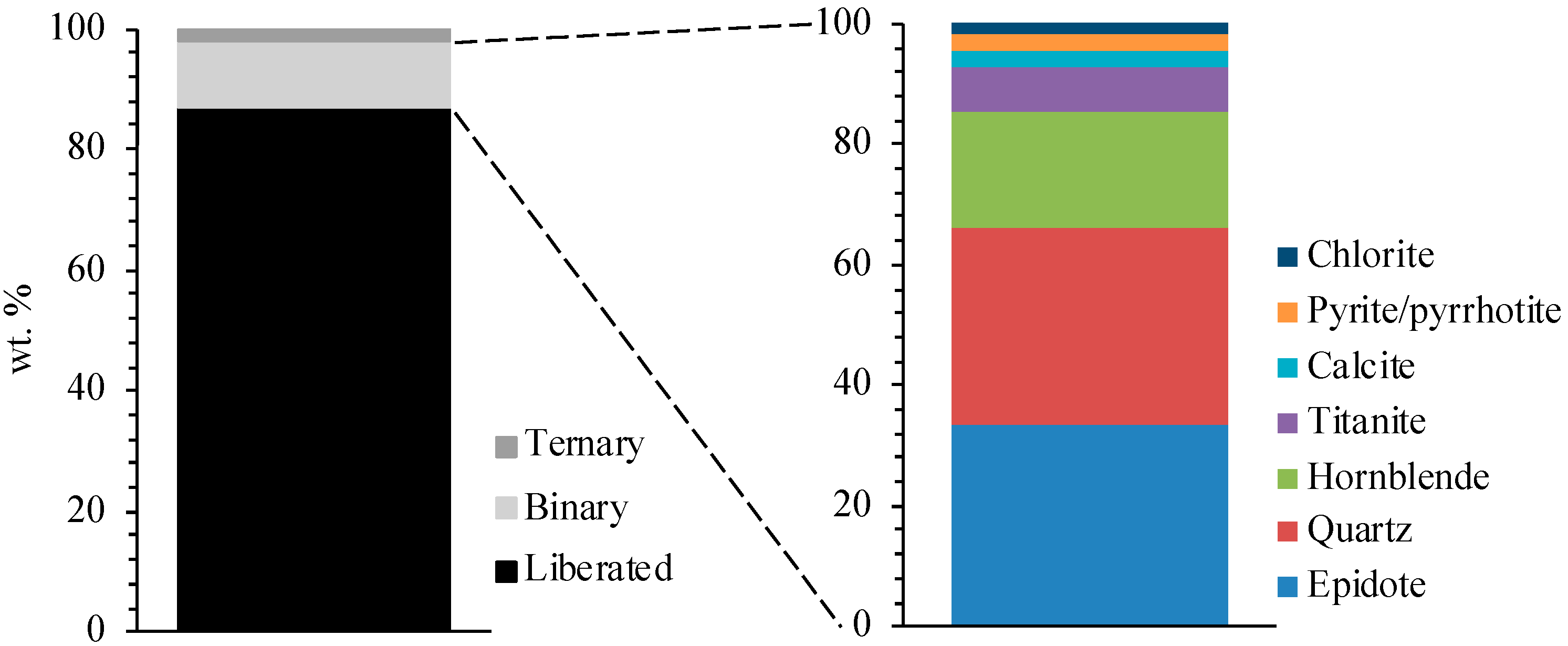
3.2. Mineral Association
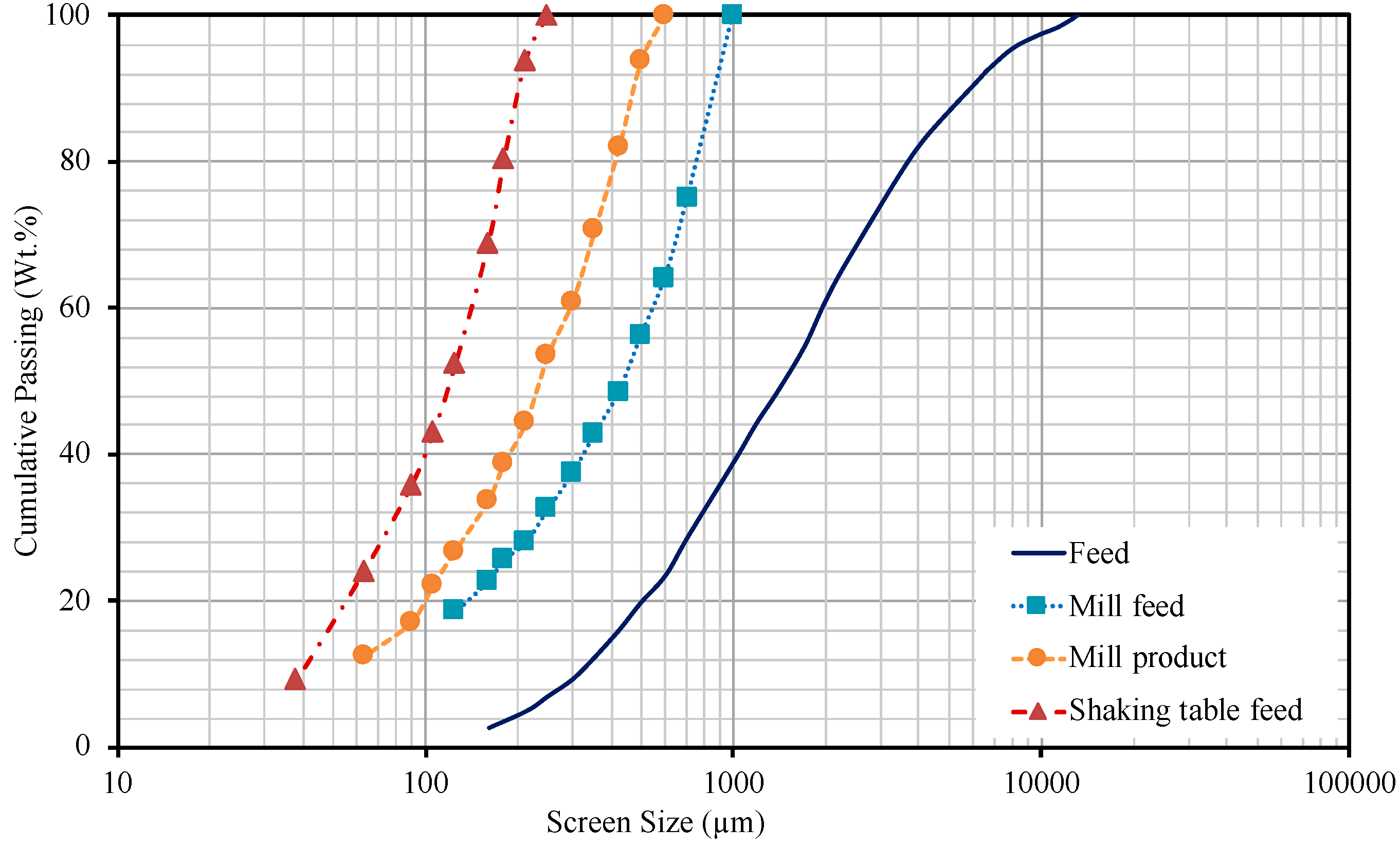
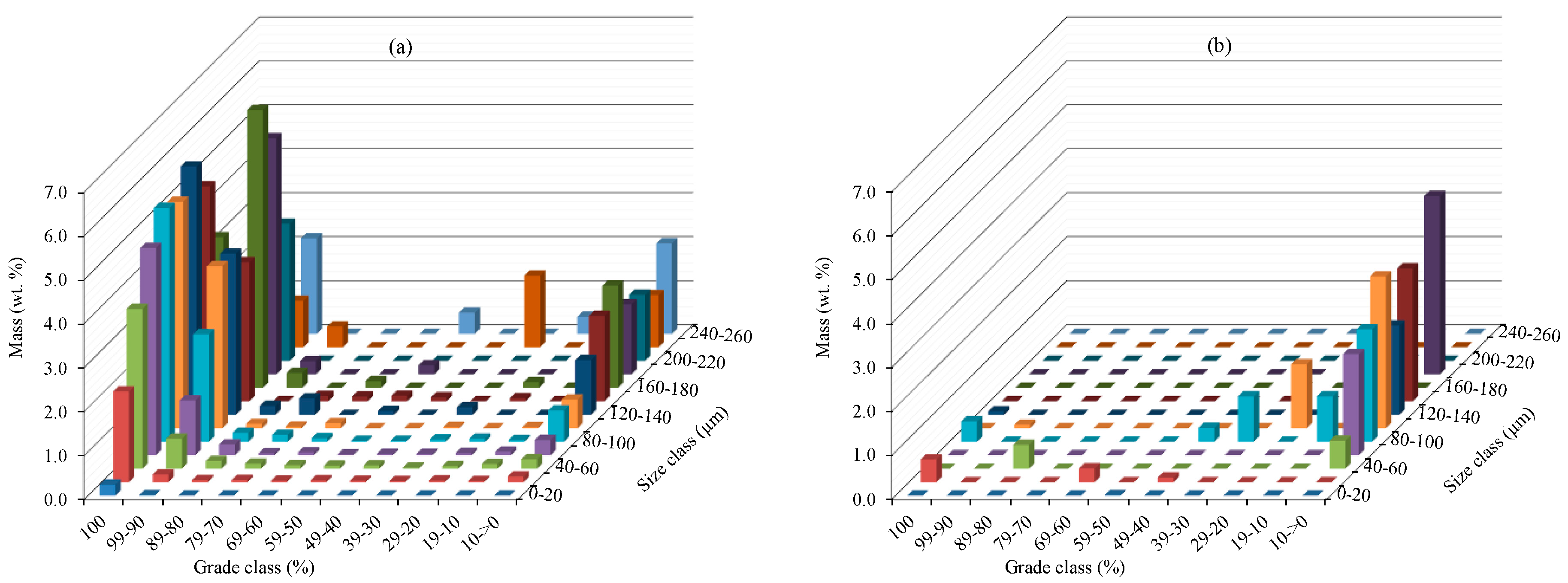
3.3. Particle Size Distribution
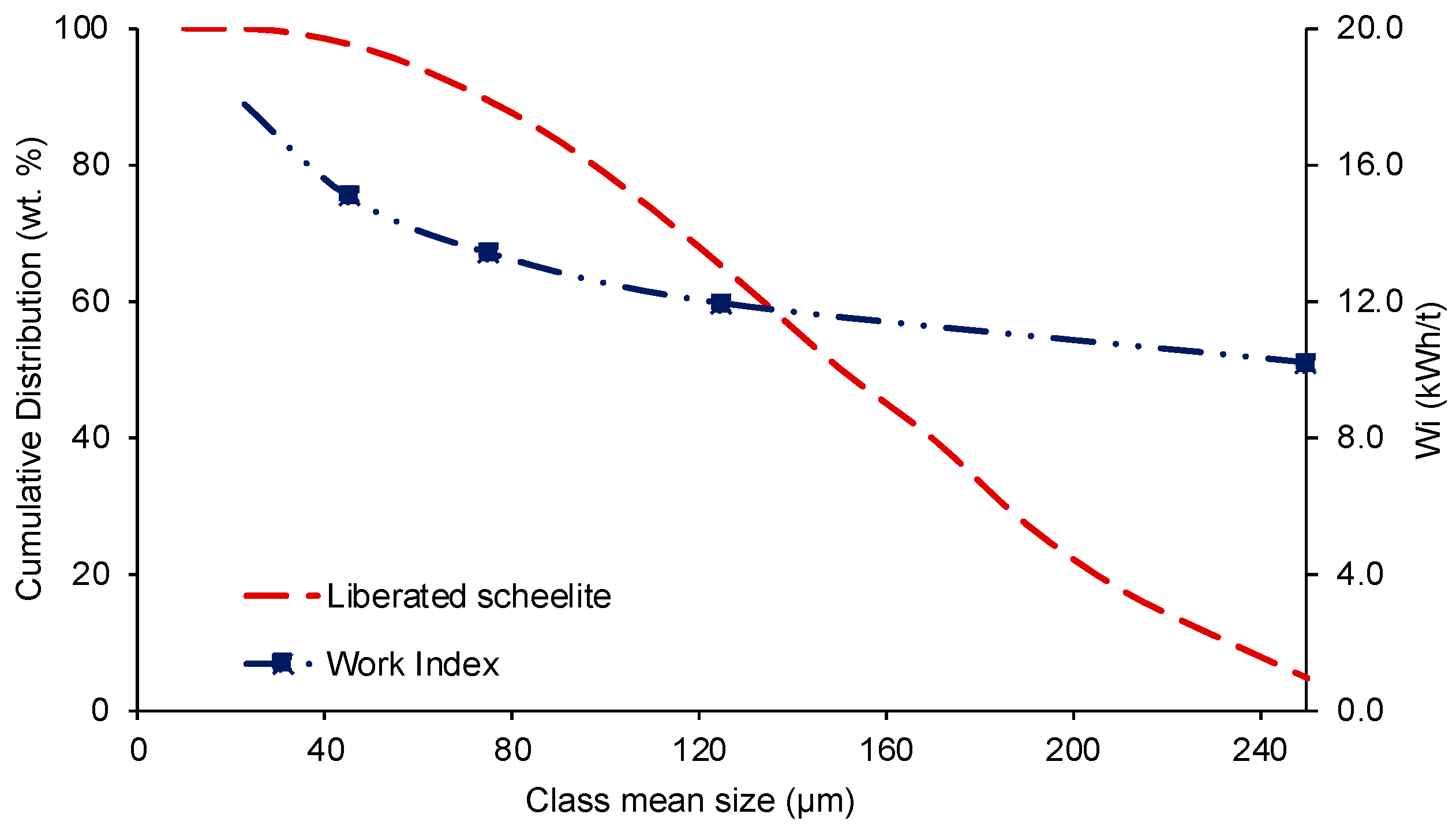
3.4. Work Index and Energy Consumption
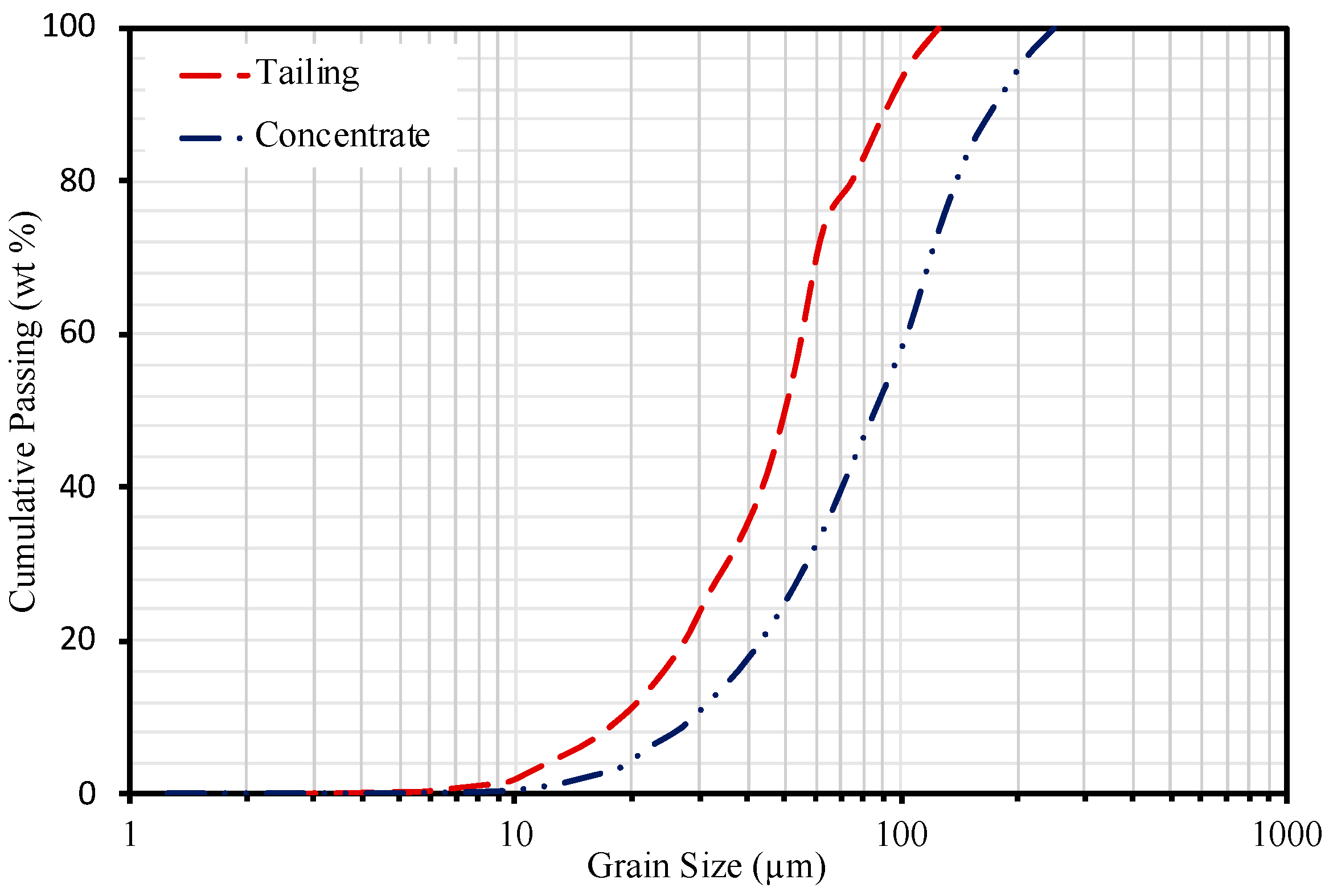
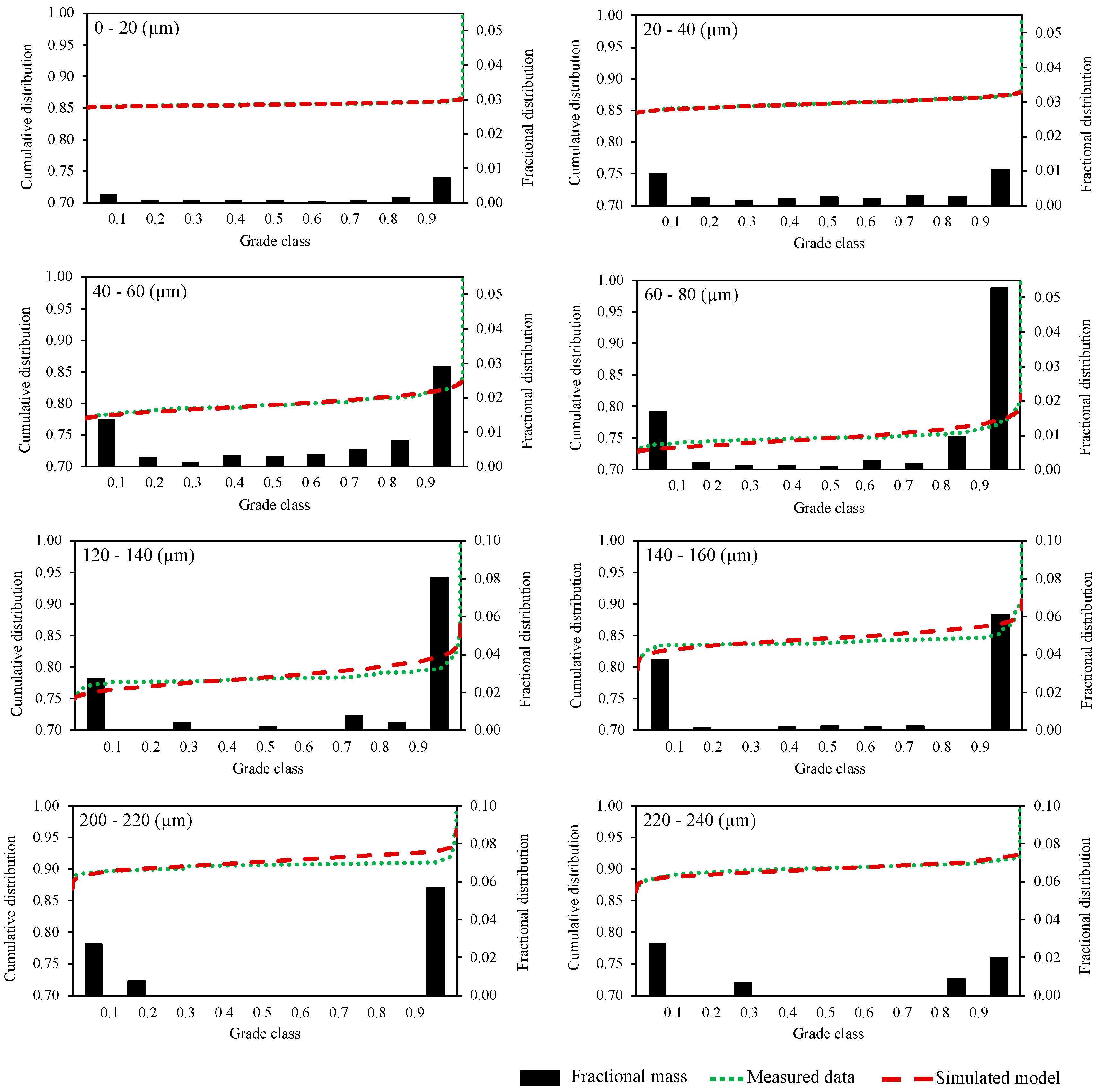
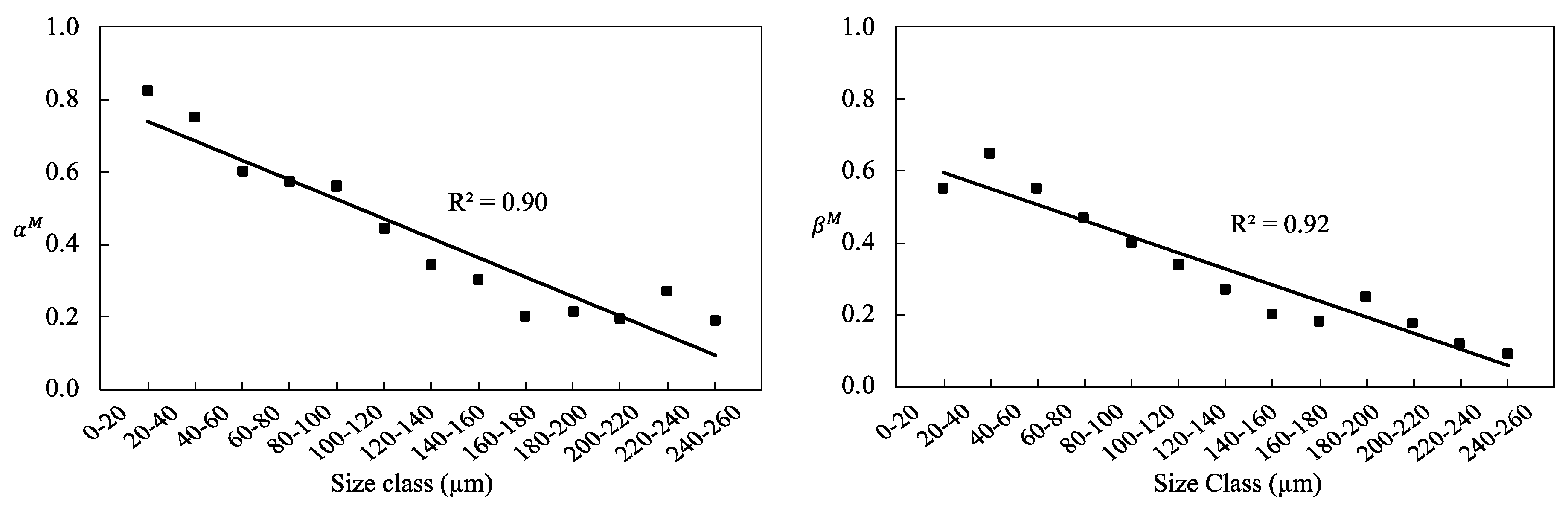
3.5. Mineral Liberation Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. Study on the Review of the List of Critical Raw Materials; European Commission: Brussels, Belgium, 2017; p. 515. Available online: https://publications.europa.eu/en/publication-detail/-/publication/08fdab5f-9766-11e7-b92d-01aa75ed71a1/language-en (accessed on 21 April 2018).
- Mohammadnejad, S.; Noaparast, M.; Hosseini, S.; Aghazadeh, S.; Mousavinezhad, S.; Hosseini, F. Physical methods and flotation practice in the beneficiation of a low grade tungsten-bearing scheelite ore. Russ. J. Non-Ferr. Met. 2018, 59, 6–15. [Google Scholar] [CrossRef]
- Rieck, G.D. Tungsten and Its Compounds; Pergamon Press: Norwich, UK, 1967. [Google Scholar]
- Ilhan, S.; Kalpakli, A.O.; Kahruman, C.; Yusufoglu, I. The investigation of dissolution behavior of gangue materials during the dissolution of scheelite concentrate in oxalic acid solution. Hydrometallurgy 2013, 136, 15–26. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Mineral Commodity Summaries; U.S. Geological Survey: Reston, VA, USA, 2019. [CrossRef]
- Chakhmouradian, A.R.; Smith, M.P.; Kynicky, J. From “strategic” tungsten to “green” neodymium: A century of critical metals at a glance. Ore Geol. Rev. 2015, 64, 455–458. [Google Scholar] [CrossRef]
- Suárez Sánchez, A.; Krzemień, A.; Riesgo Fernández, P.; Iglesias Rodríguez, F.J.; Sánchez Lasheras, F.; de Cos Juez, F.J. Investment in new tungsten mining projects. Resour. Policy 2015, 46, 177–190. [Google Scholar] [CrossRef]
- Zhang, J.; Subasinghe, N. Prediction of mineral liberation characteristics of comminuted particles of high-grade ores. Miner. Eng. 2013, 49, 68–76. [Google Scholar] [CrossRef]
- Foucaud, Y.; Dehaine, Q.; Filippov, L.O.; Filippova, I.V. Application of falcon centrifuge as a cleaner alternative for complex tungsten ore processing. Minerals 2019, 9, 448. [Google Scholar] [CrossRef]
- Lastra, R. Seven practical application cases of liberation analysis. Int. J. Miner. Process. 2007, 84, 337–347. [Google Scholar] [CrossRef]
- Fandrich, R.; Gu, Y.; Burrows, D.; Moeller, K. Modern SEM-based mineral liberation analysis. Int. J. Miner. Process. 2007, 84, 310–320. [Google Scholar] [CrossRef]
- Fandrich, R.G.; Bearman, R.A.; Boland, J.; Lim, W. Mineral liberation by particle bed breakage. Miner. Eng. 1997, 10, 175–187. [Google Scholar] [CrossRef]
- King, R.P.; Schneider, C.L. Mineral liberation and the batch comminution equation. Miner. Eng. 1998, 11, 1143–1160. [Google Scholar] [CrossRef]
- Gu, Y. Automated scanning electron microscope based mineral liberation analysis. An introduction to JKMRC/FEI Mineral Liberation Analyser. J. Miner. Mater. Charact. Eng. 2003, 2, 33–41. [Google Scholar] [CrossRef]
- Gu, Y.; Schouwstra, R.P.; Rule, C. The value of automated mineralogy. Miner. Eng. 2014, 58, 100–103. [Google Scholar] [CrossRef]
- Lassner, E.; Schubert, W. Tungsten: Properties, Chemistry, Technology of the Element, Alloys, and Chemical Compounds; Springer: New York, NY, USA, 1999. [Google Scholar]
- Hu, Y.; Gao, Z.; Sun, W.; Liu, X. Anisotropic surface energies and adsorption behaviors of scheelite crystal. Colloid. Surface A 2012, 415, 439–448. [Google Scholar] [CrossRef]
- Shepeta, E.D.; Samatova, L.A.; Kondrat’ev, S.A. Kinetics of calcium minerals flotation from scheelite–carbonate ores. J. Min. Sci. 2012, 48, 746–753. [Google Scholar] [CrossRef]
- King, R.P. A quantitative model for mineral liberation. J. S. Afr. Inst. Min. Metall. 1975, 76, 170–172. [Google Scholar]
- King, R.P. A model for the quantitative estimation of mineral liberation by grinding. Int. J. Miner. Process. 1979, 6, 207–220. [Google Scholar] [CrossRef]
- Schaap, W. Illustrated liberation-flotation recovery model for a disseminated mineral in low-grade ore. Trans. Inst. Min. Metall. Section C-Miner. Process. Extr. Metall. 1979, 88, C220–C228. [Google Scholar]
- Barbery, G. Mineral Liberation-Measurement, Simulation and Practical Use in Mineral Processing; Quebec Éditions: Montreal, QC, Canada, 1991. [Google Scholar]
- Barbery, G.; Leroux, D. Prediction of particle composition distribution after fragmentation of heterogeneous materials. Int. J. Miner. Process. 1988, 22, 9–24. [Google Scholar] [CrossRef]
- Subasinghe, G.K.N. The prediction of flotation characteristics of a disseminated ore using ore texture data. In Proceedings of the XXIV International Mineral Processing Congress, Beijing, China, 24–28 September 2008; Wang, D.Z., Sun, C.Y., Wang, F.L., Zhang, L.C., Han, L., Eds.; Science Press: Beijing, China, 2008; pp. 2339–2349. [Google Scholar]
- King, R.P. Modelling and Simulation of Mineral Processing Systems; Society for Mining, Metallurgy, and Exploration, Inc. (SME): Englewood, CO, USA, 2012; pp. 55–96. [Google Scholar]
- Zhang, J. Prediction and Influence of Mineral Liberation on Froth Flotation Performance. Ph.D. Thesis, Curtin University, Perth, Australia, 2012; p. 222. [Google Scholar]
- Zhang, J.; Subasinghe, N. Development of a flotation model incorporating liberation characteristics. Miner. Eng. 2016, 98, 1–8. [Google Scholar] [CrossRef]
- Anticoi, H.; Guasch, E.; Hamid, S.A.; Oliva, J.; Alfonso, P.; Garcia-Valles, M.; Bascompta, M.; Sanmiquel, L.; Escobet, T.; Argelaguet, R.; et al. Breakage Function for HPGR: Mineral and Mechanical Characterization of Tantalum and Tungsten Ores. Minerals 2018, 8, 170. [Google Scholar] [CrossRef]
- Gupta, A.; Yan, D.S. Introduction to Mineral Processing Design and Operation; Elsevier: Amsterdam, The Netherlands, 2006; pp. 683–685. [Google Scholar]
- Bond, F.C.; Maxson, W.L. Standard grindability tests and calculations. Transactions 1943, 153, 362–373. [Google Scholar]
- Magdalinović, N. A procedure for rapid determination of the Bond work index. Int. J. Miner. Process. 1989, 27, 125–132. [Google Scholar] [CrossRef]
- Man, Y.T. Why is the Bond Ball Mill Grindability Test done the way it is done? Eur. J. Miner. Process. Environ. Prot. 2002, 2, 34–39. [Google Scholar]
- Wikedzi, A.; Arinanda, M.A.; Leißner, T.; Peuker, U.A.; Mütze, T. Breakage and liberation characteristics of low grade sulphide gold ore blends. Miner. Eng. 2018, 115, 33–40. [Google Scholar] [CrossRef]
- Bond, F.C. The third theory of comminution. Trans. AIME Min. Eng. 1952, 193, 484–494. [Google Scholar]
- Rietveld, H. Line profiles of neutron powder-diffraction peaks for structure refinement. Acta Crystallogr. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Hill, R.J.; Howard, C.J. Quantitative phase analysis from neutron powder diffraction data using the Rietveld method. Appl. Crystallogr. 1987, 20, 467–474. [Google Scholar] [CrossRef]
- König, U.; Spicer, E. X-ray diffraction (XRD) as a fast industrial analysis method for heavy mineral sands in process control and automation—Rietveld refinement and data clustering. In The 6th International Heavy Minerals Conference ‘Back to Basics’; The Southern African Institute of mining and Metallurgy, Nyala Game Lodge: Natal, South Africa, 2007. [Google Scholar]
- Parian, M.; Lamberg, P.; Möckel, R.; Rosenkranz, J. Analysis of mineral grades for geometallurgy: Combined element-to-mineral conversion and quantitative X-ray diffraction. Miner. Eng. 2015, 82, 25–35. [Google Scholar] [CrossRef]
- Filippova, I.V.; Filippov, L.O.; Duverger, A.; Severov, V.V. Synergetic effect of a mixture of anionic and nonionic reagents: Ca mineral contrast separation by flotation at neutral pH. Miner. Eng. 2014, 66–68, 135–144. [Google Scholar] [CrossRef]
- Rozendaal, A.; le Roux, S.G.; du Plessis, A. Application of microCT scanning in the recovery of endo-skarn associated scheelite from the Riviera Deposit, South Africa. Miner. Eng. 2018, 116, 163–178. [Google Scholar] [CrossRef]


| Specification | Unit | Test |
|---|---|---|
| Feed graded charge | mm | 13.2 |
| Total media mass | kg | 9530 |
| Mass of ore sample | kg | 2.680 |
| Dried bulk density | g/cm3 | 1.90 |
| Mill speed | rpm | 46 |
| Mill length | mm | 610 |
| Mill diameter | mm | 305 |
| Power drawn | W | 255 |
| Unload power | W | 201 |
| Net power | W | 54 |
| Milling time | m | 18 |
| Specific energy intensity (−600 μm) | kWh/t | 1.46 |
| Specific energy intensity (−250 μm) | kWh/t | 3.94 |
| Oxides | SiO2 | Al2O3 | MnO | TiO2 | FeO | MgO | CaO | Na2O | K2O | MnO | P2O5 | LOI | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Content (wt.%) | 59.30 | 12.25 | 0.14 | 0.74 | 6.96 | 5.94 | 7.17 | 2.77 | 1.30 | 0.79 | 0.09 | 1.55 | 99.00 |
| Mineral (wt.%) | Density | XRD | MLA | |||
|---|---|---|---|---|---|---|
| Ore | Tailings | Concentrate | Tailings | Concentrate | ||
| Scheelite | 6.01 | 0.35 | 0.20 | 17.01 | 0.85 | 17.82 |
| Quartz | 2.62 | 15.30 | 15.37 | 6.74 | 17.13 | 7.50 |
| Plagioclase | 2.68 | 22.30 | 22.42 | 7.90 | 28.27 | 8.39 |
| K-feldspar | 2.56 | 4.50 | 4.54 | 0.51 | 2.87 | 0.49 |
| Hornblende | 3.23 | 33.00 | 27.95 | 20.79 | 28.47 | 20.18 |
| Actinolite | 3.04 | 6.40 | 6.24 | 1.00 | - | - |
| Pyroxene | 3.40 | 1.00 | 8.02 | 3.20 | 9.08 | 2.91 |
| Vesuvianite | 3.40 | - | 0.98 | 0.27 | - | 0.22 |
| Epidote | 3.45 | 4.30 | 1.00 | 15.47 | 0.42 | 14.88 |
| Biotite | 3.09 | 7.70 | 5.90 | 2.92 | 6.22 | 1.80 |
| Muscovite | 2.82 | - | 2.15 | 0.30 | 1.76 | 0.28 |
| Chlorite | 2.65 | 4.90 | - | 0.29 | - | 0.41 |
| Titanite | 6.01 | - | 1.63 | 3.50 | 1.51 | 3.64 |
| Fe oxide | 2.62 | - | 0.02 | 0.31 | 0.04 | 0.17 |
| Apatite | 2.68 | - | 0.18 | 0.45 | 0.22 | 0.60 |
| Calcite | 2.56 | - | 1.50 | 0.63 | 1.45 | 0.70 |
| Fluorite | 3.23 | - | 0.02 | 0.04 | 0.02 | 0.04 |
| Fe sulfide | 3.04 | - | 1.10 | 17.35 | 1.06 | 18.20 |
| Chalcopyrite | 3.40 | - | 0.02 | 0.75 | 0.03 | 0.83 |
| Arsenopyrite | 3.40 | - | - | 0.11 | - | 0.13 |
| Total | - | 99.75 | 99.24 | 99.54 | 99.40 | 99.19 |
| Differential Mass | Liberation Class (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size Class (µm) | 100 | 100–90 | 90–80 | 80–70 | 70–60 | 60–50 | 50–40 | 40–30 | 30–20 | 20–10 | 10–>0 | Total |
| −20 | 0.2523 | 0.0132 | 0.0029 | 0.0013 | 0.0008 | 0.0011 | 0.0016 | 0.0012 | 0.0013 | 0.0018 | 0.0028 | 0.280 |
| 20–40 | 2.0663 | 0.1761 | 0.0478 | 0.0510 | 0.0357 | 0.0431 | 0.0343 | 0.0262 | 0.0397 | 0.0282 | 0.1312 | 2.680 |
| 40–60 | 3.6404 | 0.6841 | 0.1784 | 0.1164 | 0.0806 | 0.0723 | 0.0781 | 0.0251 | 0.0610 | 0.1095 | 0.2165 | 5.262 |
| 60–80 | 4.7151 | 1.2482 | 0.2450 | 0.0466 | 0.0672 | 0.0200 | 0.0327 | 0.0332 | 0.0520 | 0.0808 | 0.3477 | 6.888 |
| 80–100 | 5.3194 | 2.4475 | 0.2051 | 0.1582 | 0.0802 | 0.0207 | 0.0194 | 0.0536 | 0.0708 | 0.0389 | 0.7146 | 9.129 |
| 100–120 | 5.1505 | 3.6864 | 0.0985 | 0.0369 | 0.1160 | 0.0000 | 0.0000 | 0.0290 | 0.0000 | 0.0252 | 0.6531 | 9.795 |
| 120–140 | 5.6492 | 3.6631 | 0.2026 | 0.3713 | 0.0000 | 0.0879 | 0.0000 | 0.1721 | 0.0000 | 0.0000 | 1.2448 | 11.391 |
| 140–160 | 4.8906 | 3.1626 | 0.0000 | 0.1214 | 0.1076 | 0.1263 | 0.0901 | 0.0000 | 0.0708 | 0.0000 | 1.9450 | 10.514 |
| 160–180 | 3.4226 | 6.3199 | 0.3390 | 0.0000 | 0.1530 | 0.0000 | 0.0000 | 0.0000 | 0.1289 | 0.0000 | 2.3243 | 12.688 |
| 180–200 | 2.0142 | 5.3722 | 0.3014 | 0.0000 | 0.0000 | 0.2080 | 0.0000 | 0.0000 | 0.0000 | 0.1427 | 1.5944 | 9.633 |
| 200–220 | 2.1339 | 3.1198 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.5034 | 6.757 |
| 220–240 | 3.8020 | 1.0597 | 0.4747 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.6339 | 0.0000 | 0.2655 | 1.1875 | 8.423 |
| 240–260 | 1.4555 | 2.1710 | 0.0000 | 0.0000 | 0.0000 | 0.4848 | 0.0000 | 0.0000 | 0.3913 | 0.0000 | 2.0561 | 6.559 |
| Total | 44.512 | 33.124 | 2.095 | 0.903 | 0.641 | 1.064 | 0.256 | 1.974 | 0.816 | 0.693 | 13.921 | 100.00 |
| Liberation Size Class (µm) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | −20 | 20–40 | 40–60 | 60–80 | 80–100 | 100–120 | 120–140 | 140–160 | 160–180 | 180–200 | 200–220 | 220–240 | 240–260 |
| n | 217 | 605 | 356 | 180 | 137 | 94 | 67 | 51 | 50 | 32 | 18 | 10 | 13 |
| αM | 0.82 | 0.75 | 0.60 | 0.57 | 0.56 | 0.44 | 0.34 | 0.30 | 0.20 | 0.21 | 0.19 | 0.27 | 0.19 |
| βM | 0.55 | 0.65 | 0.55 | 0.47 | 0.40 | 0.34 | 0.27 | 0.20 | 0.18 | 0.25 | 0.18 | 0.12 | 0.09 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad Hamid, S.; Alfonso, P.; Oliva, J.; Anticoi, H.; Guasch, E.; Hoffmann Sampaio, C.; Garcia-Vallès, M.; Escobet, T. Modeling the Liberation of Comminuted Scheelite Using Mineralogical Properties. Minerals 2019, 9, 536. https://doi.org/10.3390/min9090536
Ahmad Hamid S, Alfonso P, Oliva J, Anticoi H, Guasch E, Hoffmann Sampaio C, Garcia-Vallès M, Escobet T. Modeling the Liberation of Comminuted Scheelite Using Mineralogical Properties. Minerals. 2019; 9(9):536. https://doi.org/10.3390/min9090536
Chicago/Turabian StyleAhmad Hamid, Sarbast, Pura Alfonso, Josep Oliva, Hernan Anticoi, Eduard Guasch, Carlos Hoffmann Sampaio, Maite Garcia-Vallès, and Teresa Escobet. 2019. "Modeling the Liberation of Comminuted Scheelite Using Mineralogical Properties" Minerals 9, no. 9: 536. https://doi.org/10.3390/min9090536
APA StyleAhmad Hamid, S., Alfonso, P., Oliva, J., Anticoi, H., Guasch, E., Hoffmann Sampaio, C., Garcia-Vallès, M., & Escobet, T. (2019). Modeling the Liberation of Comminuted Scheelite Using Mineralogical Properties. Minerals, 9(9), 536. https://doi.org/10.3390/min9090536











