Obtaining Hyperspectral Signatures for Seafloor Massive Sulphide Exploration
Abstract
1. Introduction
1.1. Seafloor Massive Sulphides
1.2. Related Work
1.3. Underwater Light Propagation
2. Materials and Methods
2.1. Samples
2.2. Equipment
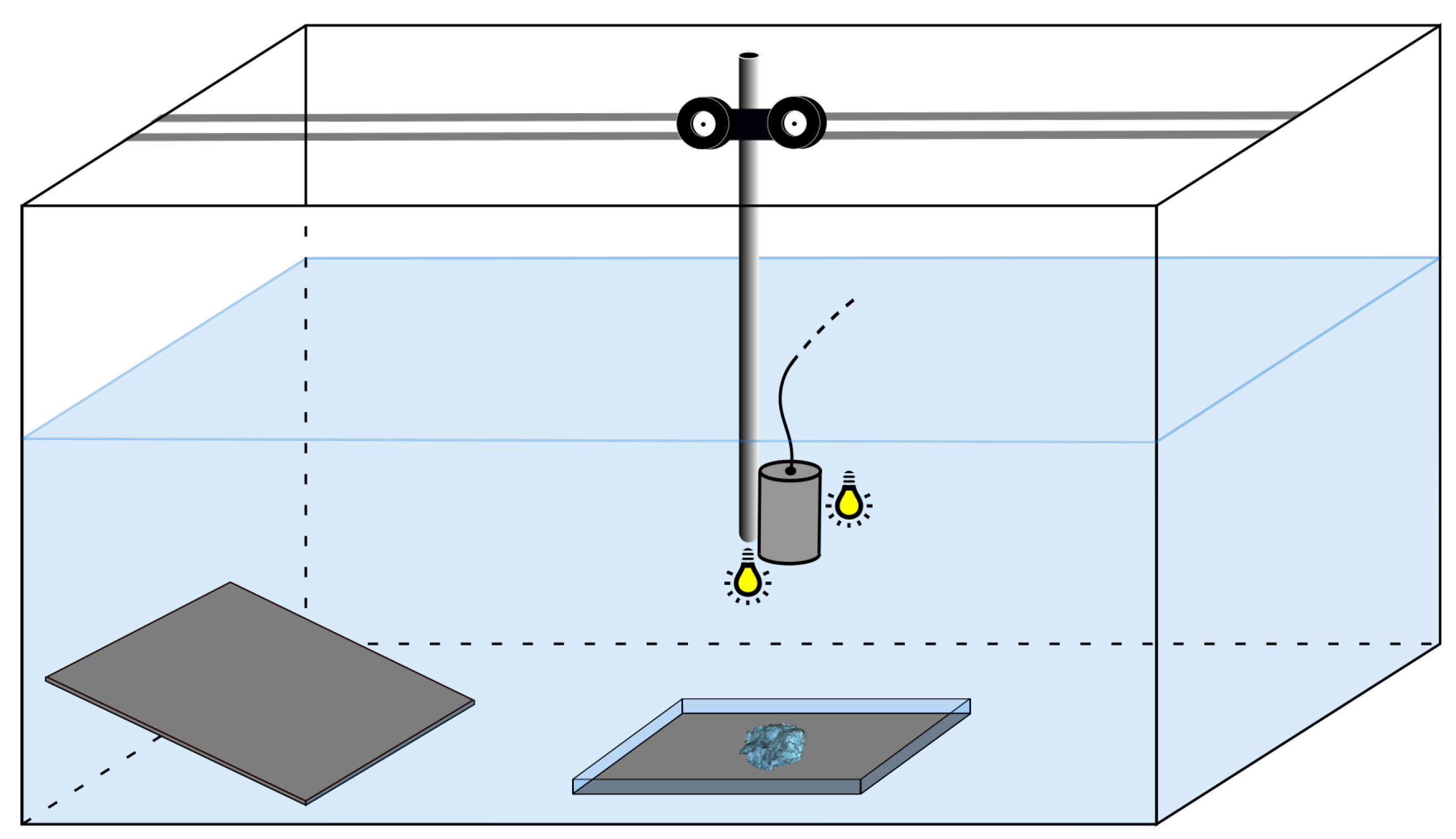
2.3. Laboratory Setup
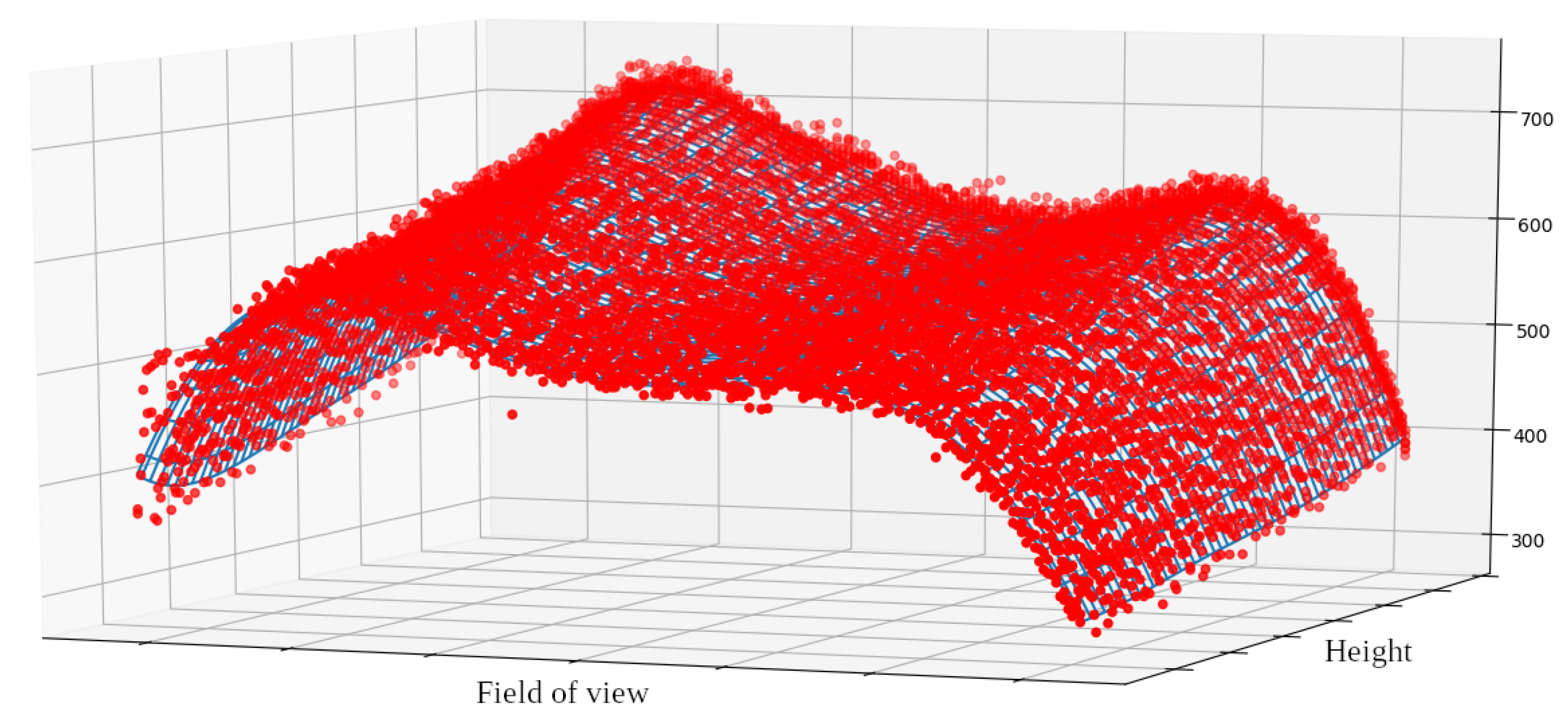
2.4. Inclined Reference Plate
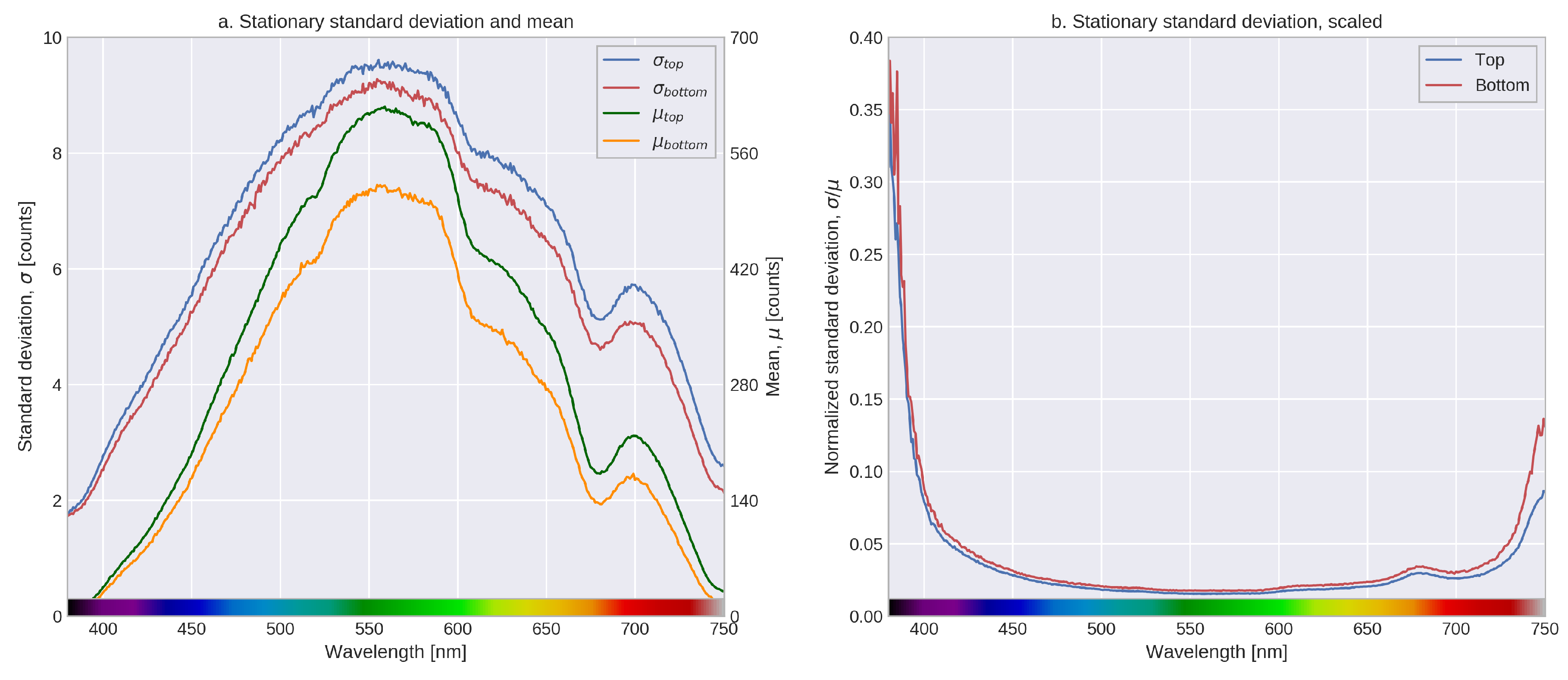
2.5. Noise Properties
2.6. Non-Parametric Regression
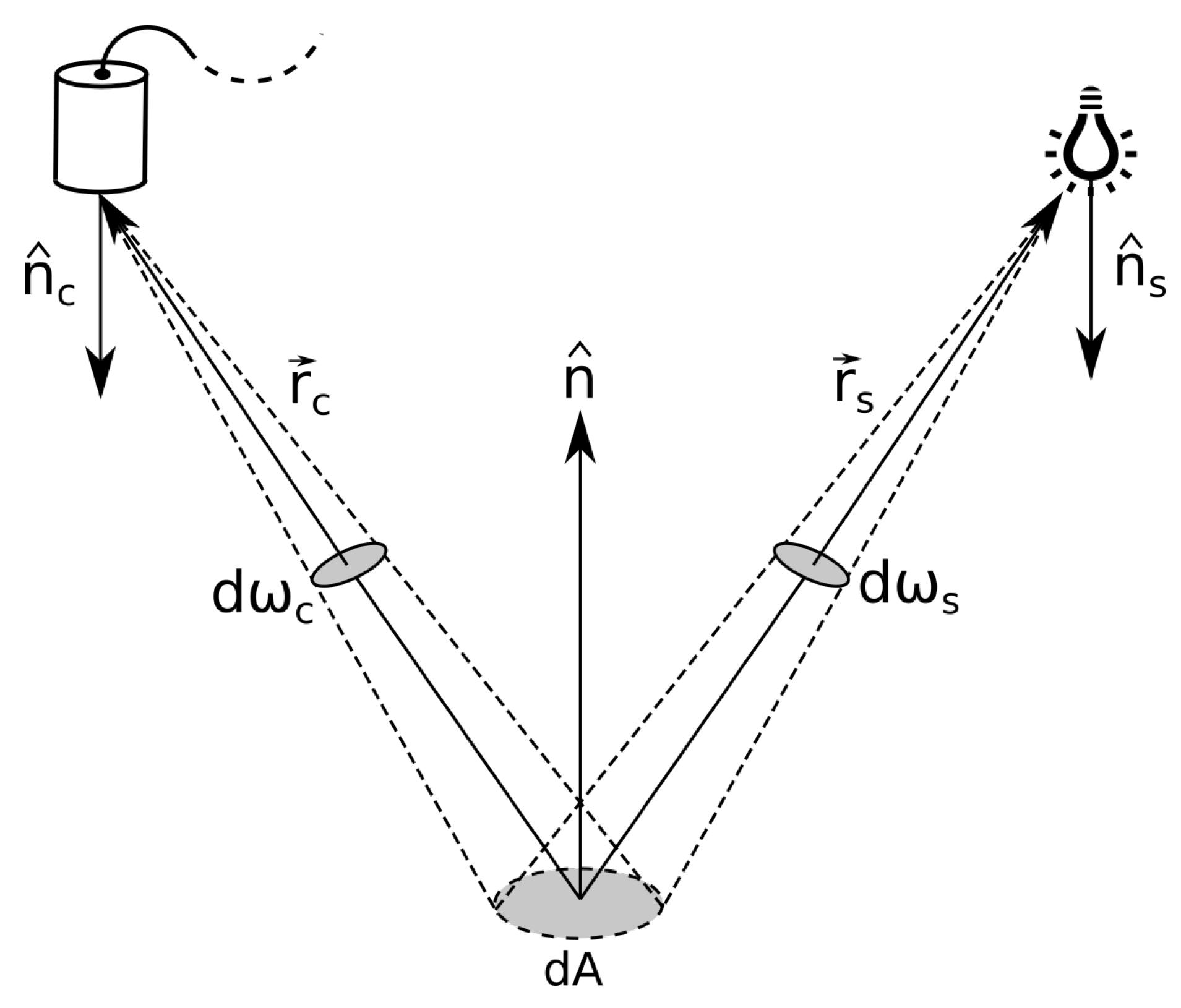
2.7. Reflectance Calculation
2.8. Signal-to-Noise Threshold
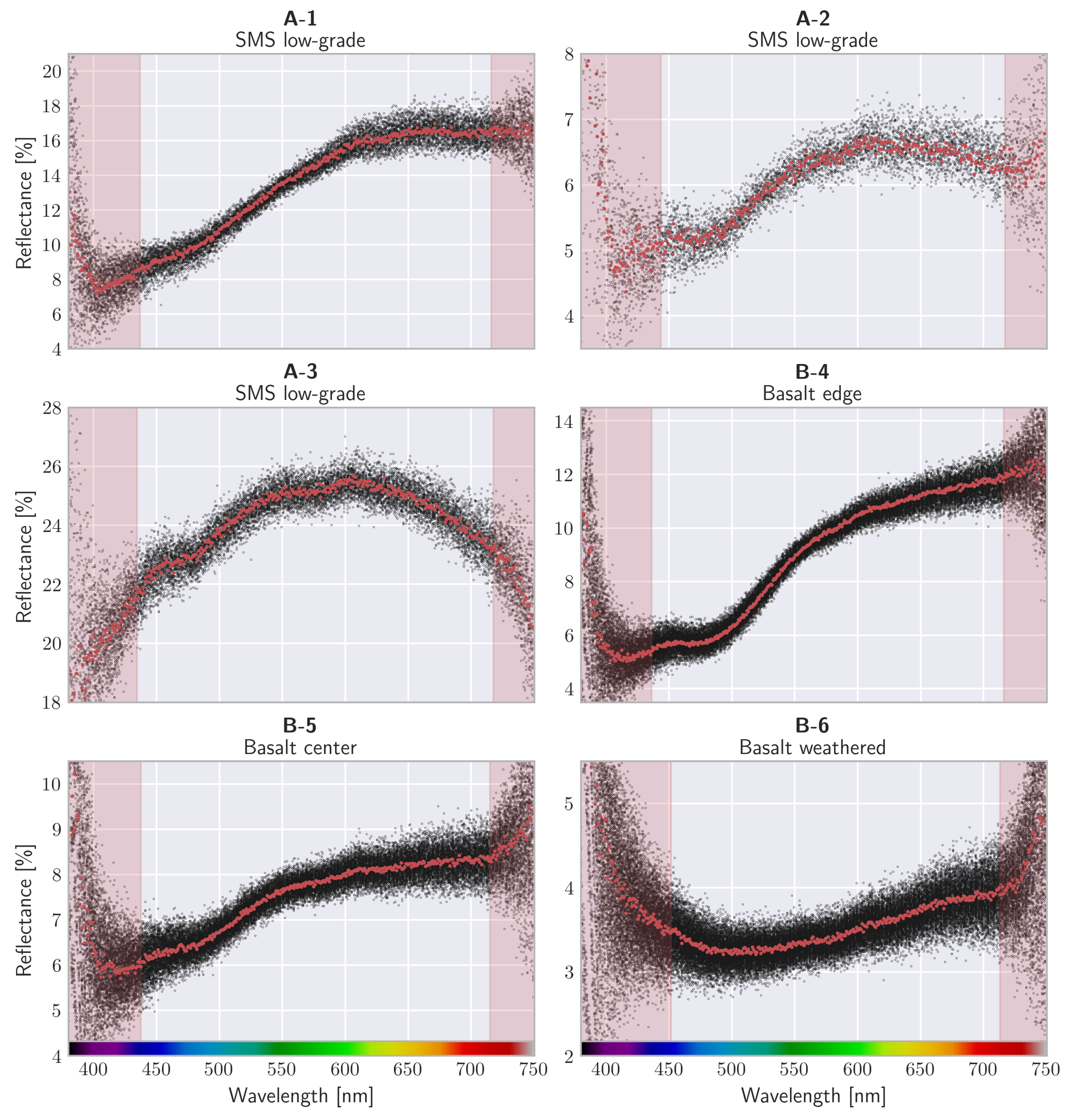
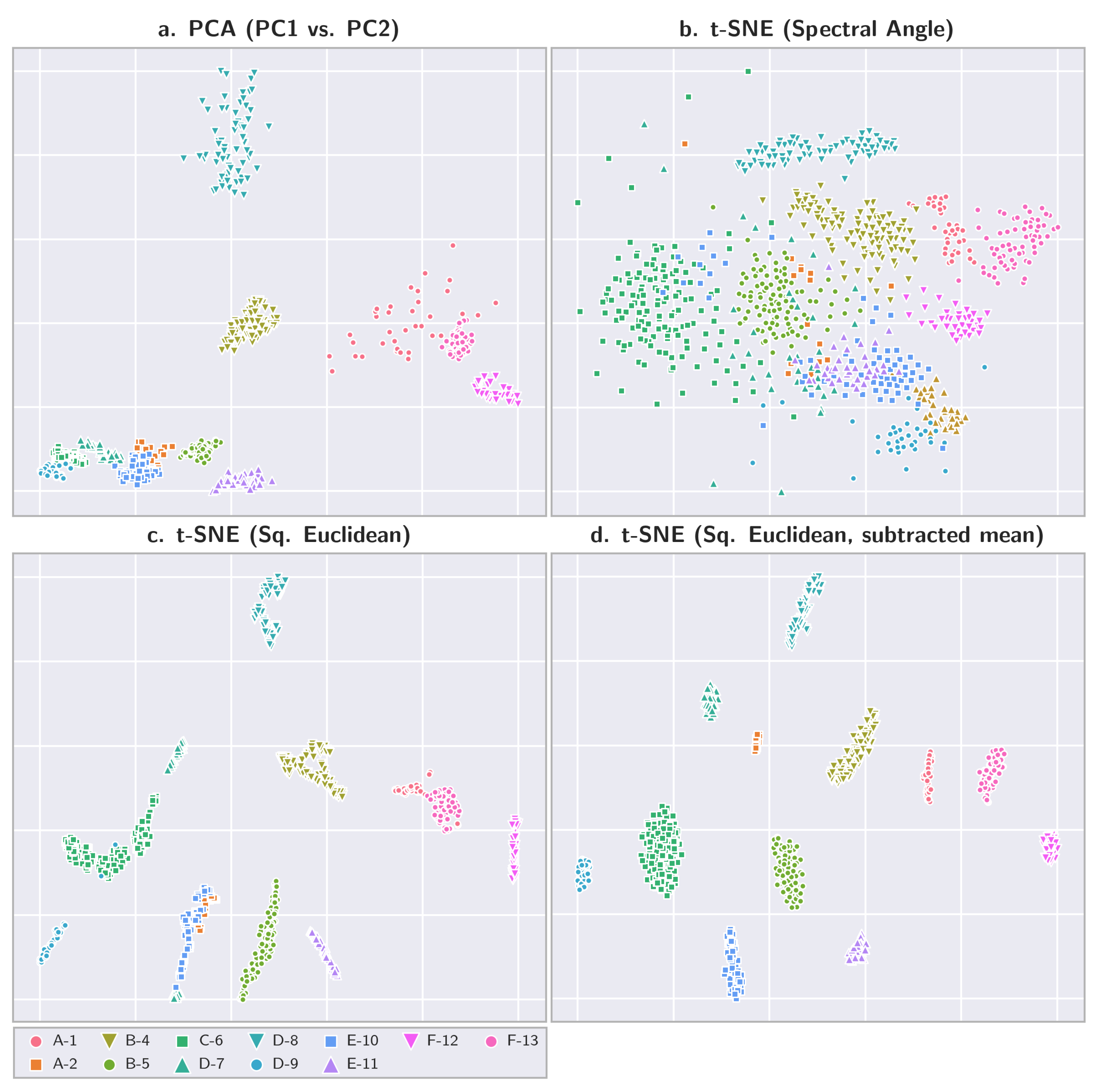
3. Results
4. Discussion
4.1. Experimental Setup
4.2. Field Applicability
4.3. Spectral Separability
4.4. Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Whole-Rock Geochemistry
| Analyte | Au | Mo | Cu | Pb | Zn | Ag | Ni | Co | Mn | Fe | As | U | Th | Sr | Cd | Sb | Bi | V | Ca | P | La | Cr | Mg | Ba | Ti | |
| Unit | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | % | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | % | % | PPM | PPM | % | PPM | % | |
| MDL | 0.01 | 0.5 | 0.5 | 0.5 | 5 | 0.5 | 0.5 | 1 | 5 | 0.01 | 5 | 0.5 | 0.5 | 5 | 0.5 | 0.5 | 0.5 | 10 | 0.01 | 0.01 | 0.5 | 1 | 0.01 | 5 | 0.001 | |
| Basalt interior | Rock Pulp | n/a | 0.5 | 152.1 | 3.8 | 90 | <0.5 | 528.5 | 52 | 2441 | 8.01 | <5 | <0.5 | <0.5 | 95 | <0.5 | <0.5 | <0.5 | 308 | 6.9 | 0.06 | 3.7 | 216 | 4.39 | 68 | 0.91 |
| Basalt edge | Rock Pulp | n/a | 1.8 | 261.9 | 6.9 | 119 | <0.5 | 264.3 | 69 | 3271 | 8.03 | 12 | <0.5 | 0.8 | 93 | <0.5 | <0.5 | <0.5 | 319 | 4.65 | 0.06 | 4.9 | 177 | 5.08 | 30 | 0.931 |
| Mudstone | Rock Pulp | n/a | 1.5 | 60 | 7.3 | 128 | <0.5 | 281.8 | 19 | 337 | 4.83 | 28 | 2.8 | 9 | 90 | <0.5 | 0.7 | <0.5 | 223 | 0.27 | 0.1 | 31 | 153 | 2.64 | 725 | 0.53 |
| SMS low-grade white | Rock Pulp | 5.328 | 3.9 | 56.1 | 122 | 846.8 | 16 | 0.39 | 221 | 0.9 | <0.5 | 630 | <0.5 | 8.3 | <5 | <0.5 | 0.08 | <0.5 | <10 | 76 | 0.02 | 8124 | <1 | 0.02 | <5 | 0.01 |
| SMS low-grade black | Rock Pulp | 4.031 | 13.2 | 7647.8 | 13376 | 1818.1 | 341 | 3.6 | 1387 | 2.6 | <0.5 | 321 | 29.5 | 84.2 | 8.3 | <0.5 | 0.05 | <0.5 | <10 | 186 | 0.07 | 252 | <1 | 0.12 | <5 | 0.06 |
| SMS high-grade | Rock Pulp | 0.048 | 6.1 | 20457.3 | 37418.1 | 73830 | 18.2 | 469.9 | <1 | 777 | 21.27 | 5 | <0.5 | <0.5 | 5 | 186.4 | 3.1 | 32.1 | <10 | 0.02 | <0.01 | <0.5 | 62 | 0.04 | 91 | <0.001 |
| Analyte | Al | Na | K | W | Zr | Ce | Sn | Y | Nb | Ta | Be | Sc | Li | S | Rb | Hf | Se | Ba | Be | Co | Cs | Ga | Hf | Nb | Rb | |
| Unit | % | % | % | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | % | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | |
| MDL | 0.01 | 0.01 | 0.01 | 0.5 | 0.5 | 5 | 0.5 | 0.5 | 0.5 | 0.5 | 5 | 1 | 0.5 | 0.05 | 0.5 | 0.5 | 5 | 1 | 1 | 0.2 | 0.1 | 0.5 | 0.1 | 0.1 | 0.1 | |
| Basalt interior | Rock Pulp | 7.62 | 2.27 | 0.04 | 0.6 | 69 | 10 | 1.4 | 32.2 | 2.3 | <0.5 | <5 | 38 | 5.3 | 1.17 | 0.6 | 3.4 | <5 | 73 | 2 | 43.5 | <0.1 | 15.6 | 2.5 | 1.7 | <0.1 |
| Basalt edge | Rock Pulp | 6.91 | 2.83 | 0.09 | 1.1 | 56.7 | 14 | 2.3 | 32.7 | 2.5 | <0.5 | <5 | 40 | 17.1 | <0.05 | 1.1 | 2 | <5 | 39 | 5 | 62.6 | <0.1 | 15.1 | 2.7 | 2.1 | 0.8 |
| Mudstone | Rock Pulp | 8.58 | 1.45 | 1.97 | 1.7 | 24.3 | 64 | 2 | 9.2 | 15 | 1 | <5 | 15 | 25.3 | 0.14 | 51.9 | 0.5 | <5 | 739 | 2 | 17 | 3.6 | 19.9 | 4.8 | 14.3 | 82.1 |
| SMS low-grade white | Rock Pulp | <0.01 | <0.01 | <0.01 | 6.8 | <0.5 | <5 | <0.5 | <0.5 | <0.5 | <0.5 | 0.31 | 0.6 | <0.5 | <0.05 | <0.5 | <0.5 | <5 | <1 | <1 | 0.7 | <0.1 | 0.5 | 6 | 3399.2 | 1.7 |
| SMS low-grade black | Rock Pulp | 0.8 | <0.01 | <0.01 | 28.7 | <0.5 | <5 | <0.5 | <0.5 | <0.5 | 0.9 | 5.42 | 2.8 | <0.5 | 91 | 1.8 | <0.5 | <5 | 1.1 | 4.9 | 0.2 | <0.1 | 2.5 | 28 | 874.3 | 0.6 |
| SMS high-grade | Rock Pulp | 0.03 | 0.22 | 0.02 | <0.5 | <0.5 | <5 | 10 | <0.5 | <0.5 | <0.5 | <5 | <1 | 12.4 | 18.43 | 1.2 | <0.5 | 633 | 153 | <1 | <0.2 | 0.3 | <0.5 | <0.1 | <0.1 | 0.6 |
| Analyte | Sn | Sr | Ta | Th | U | V | W | Zr | Y | La | Ce | Pr | Nd | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu | |||
| Unit | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | PPM | |||
| MDL | 1 | 0.5 | 0.1 | 0.2 | 0.1 | 8 | 0.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.02 | 0.3 | 0.05 | 0.02 | 0.05 | 0.01 | 0.05 | 0.02 | 0.03 | 0.01 | 0.05 | 0.01 | |||
| Basalt interior | Rock Pulp | <1 | 102.4 | 0.1 | <0.2 | <0.1 | 313 | 0.7 | 85.1 | 33.9 | 3.4 | 10.3 | 1.73 | 9.9 | 3.32 | 1.4 | 5.02 | 0.95 | 6.07 | 1.36 | 4.1 | 0.59 | 3.71 | 0.56 | ||
| Basalt edge | Rock Pulp | 2 | 101.6 | 0.2 | 0.7 | 0.3 | 316 | 1.5 | 88.2 | 36.1 | 5 | 15.6 | 2.07 | 11.3 | 3.85 | 1.3 | 5.38 | 0.99 | 6.46 | 1.38 | 4.07 | 0.6 | 3.76 | 0.56 | ||
| Mudstone | Rock Pulp | 2 | 102.4 | 1 | 11.6 | 5.1 | 226 | 2.3 | 169.9 | 28 | 43.8 | 90.5 | 9.65 | 35.7 | 6.82 | 1.59 | 6.45 | 0.98 | 5.6 | 1.12 | 3.25 | 0.45 | 3.16 | 0.47 | ||
| SMS low-grade white | Rock Pulp | <1 | 1 | <0.1 | <0.2 | 0.1 | <8 | 0.9 | 0.2 | <0.1 | <0.1 | <0.1 | <0.02 | 1.22 | <0.05 | 0.15 | <0.05 | <0.01 | <0.05 | <0.02 | <0.03 | <0.01 | <0.05 | <0.01 | ||
| SMS low-grade black | Rock Pulp | <1 | 2.8 | <0.1 | 0.6 | 0.2 | <8 | <0.5 | <0.1 | <0.1 | <0.1 | <0.1 | 0.14 | 0.18 | <0.05 | <0.02 | <0.05 | <0.01 | <0.05 | <0.02 | <0.03 | <0.01 | <0.05 | <0.01 | ||
| SMS high-grade | Rock Pulp | 9 | 9.5 | <0.1 | <0.2 | 0.5 | <8 | 1 | 0.1 | <0.1 | 0.2 | <0.1 | <0.02 | <0.3 | <0.05 | <0.02 | <0.05 | <0.01 | <0.05 | <0.02 | <0.03 | <0.01 | <0.05 | <0.01 |
Appendix B. Whole-Rock Mineralogy
| SMS Samples | Description | qtz | po | brt | amo | py | mrc | sp | iso | ccp | gn |
| Low grade white | White | +++ | + | ||||||||
| Low grade black | Dark rusty | + | +++ | ++ | + | + | ++ | + | ++ | + | |
| High grade | Dark rusty | +++ | + | + | + | ++ | +++ | ++ | + | + | |
| Non-SMS Samples | Description | qtz | po | ab | chl | aug | gl | ms | mc | ||
| Basalt interior, centre | Unaltered | + | +++ | ++ | +++ | ||||||
| Basalt interior, edge | Altered | + | +++ | +++ | +++ | ||||||
| Mudstone | Massive | +++ | + | ++ | +++ | + | + | ++ | + |
References
- Van der Meer, F.D.; Van der Werff, H.M.; Van Ruitenbeek, F.J.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Van Der Meijde, M.; Carranza, E.J.M.; De Smeth, J.B.; Woldai, T. Multi-and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Sabins, F.F. Remote sensing for mineral exploration. Ore Geol. Rev. 1999, 14, 157–183. [Google Scholar] [CrossRef]
- Bolin, B.J.; Moon, T.S. Sulfide detection in drill core from the Stillwater Complex using visible/near-infrared imaging spectroscopy. Geophysics 2003, 68, 1561–1568. [Google Scholar] [CrossRef]
- Johnsen, G.; Volent, Z.; Dierssen, H.; Pettersen, R.; Van Ardelan, M.; Søreide, F.; Fearns, P.; Ludvigsen, M.; Moline, M. Underwater hyperspectral imagery to create biogeochemical maps of seafloor properties. In Subsea Optics and Imaging; Elsevier: Amsterdam, The Netherlands, 2013; pp. 508–535, 536e–540e. [Google Scholar]
- Tivey, M.K. Generation of seafloor hydrothermal vent fluids and associated mineral deposits. Oceanography 2007, 20, 50–65. [Google Scholar] [CrossRef]
- Shanks, W.C.; Thurston, R. Volcanogenic Massive Sulfide Occurrence Model; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2012. [Google Scholar]
- Humphris, S.E.; Herzig, P.M.; Miller, D.J.; Alt, J.C.; Becker, K.; Brown, D.; Brügmann, G.; Chiba, H.; Fouquet, Y.; Gemmell, J.; et al. The internal structure of an active sea-floor massive sulphide deposit. Nature 1995, 377, 713–716. [Google Scholar] [CrossRef]
- German, C.R.; Petersen, S.; Hannington, M.D. Hydrothermal exploration of mid-ocean ridges: Where might the largest sulfide deposits be forming? Chem. Geol. 2016, 420, 114–126. [Google Scholar] [CrossRef]
- Herzig, P.M.; Hannington, M.D. Polymetallic massive sulfides at the modern seafloor a review. Ore Geol. Rev. 1995, 10, 95–115. [Google Scholar] [CrossRef]
- Deloitte Sustainability; British Geological Survey; Bureau de Recherches Géologiques et Minières; Netherlands Organisation for Applied Scientific Research. Study on the Review of the List of Critical Raw Materials - Criticality Assessments; European Commission: Brussels, Belgium, 2017. [Google Scholar] [CrossRef]
- Deloitte Sustainability; British Geological Survey; Bureau de Recherches Géologiques et Minières; Netherlands Organisation for Applied Scientific Research. Study on the Review of the List of Critical Raw Materials—Non-Critical Raw Materials Factsheets; European Commission: Brussels, Belgium, 2017. [Google Scholar] [CrossRef]
- Singer, D.A. Future copper resources. Ore Geol. Rev. 2017, 86, 271–279. [Google Scholar] [CrossRef]
- Marscheider-Weidemann, F.; Langkau, S.; Hummen, T.; Erdmann, L.; Tercero Espinoza, L.; Angerer, G.; Marwede, M.; Benecke, S. Summary: Raw Materials for Emerging Technologies; German Mineral Resources Agency (DERA): Berlin, Germany, 2016.
- Letnes, P.A.; Hansen, I.M.; Aas, L.M.; Eide, I.; Pettersen, R.; Tassara, L.; Receveur, J.; le Floch, S.; Guyomarch, J.; Camus, L.; et al. Underwater hyperspectral classification of deep sea corals exposed to a toxic compound. bioRxiv 2018, 150060. [Google Scholar] [CrossRef]
- Mogstad, A.A.; Johnsen, G. Spectral characteristics of coralline algae: A multi-instrumental approach, with emphasis on underwater hyperspectral imaging. Appl. Opt. 2017, 56, 9957–9975. [Google Scholar] [CrossRef]
- Ødegård, Ø.; Mogstad, A.A.; Johnsen, G.; Sørensen, A.J.; Ludvigsen, M. Underwater hyperspectral imaging: A new tool for marine archaeology. Appl. Opt. 2018, 57, 3214–3223. [Google Scholar]
- Dumke, I.; Ludvigsen, M.; Ellefmo, S.L.; Søreide, F.; Johnsen, G.; Murton, B.J. Underwater hyperspectral imaging using a stationary platform in the Trans-Atlantic Geotraverse hydrothermal field. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2947–2962. [Google Scholar] [CrossRef]
- Johnsen, G.; Ludvigsen, M.; Sørensen, A.; Aas, L.M.S. The use of underwater hyperspectral imaging deployed on remotely operated vehicles-methods and applications. IFAC-PapersOnLine 2016, 49, 476–481. [Google Scholar] [CrossRef]
- Bongiorno, D.L.; Bryson, M.; Bridge, T.C.L.; Dansereau, D.G.; Williams, S.B. Coregistered Hyperspectral and Stereo Image Seafloor Mapping from an Autonomous Underwater Vehicle. J. Field Robot. 2017, 35, 312–329. [Google Scholar] [CrossRef]
- Sture, Ø.; Ludvigsen, M.; Aas, L.M.S. Autonomous underwater vehicles as a platform for underwater hyperspectral imaging. In Proceedings of the OCEANS 2017-Aberdeen, Aberdeen, UK, 19–22 June 2017; pp. 1–8. [Google Scholar]
- Dumke, I.; Nornes, S.M.; Purser, A.; Marcon, Y.; Ludvigsen, M.; Ellefmo, S.L.; Johnsen, G.; Søreide, F. First hyperspectral imaging survey of the deep seafloor: high-resolution mapping of manganese nodules. Remote Sens. Environ. 2018, 209, 19–30. [Google Scholar] [CrossRef]
- Palmer, J.M.; Grant, B.G. The Art of Radiometry; SPIE Press: Bellingham, WA, USA, 2010; pp. 26–27. [Google Scholar]
- McGlamery, B. Computer analysis and simulation of underwater camera system performance. Scripps Inst. Oceanogr. SIO Ref. 1975, 75, 2. [Google Scholar]
- McGlamery, B. A computer model for underwater camera systems. In Ocean Optics VI; International Society for Optics and Photonics: Bellingham, WA, USA, 1980; Volume 208, pp. 221–232. [Google Scholar]
- Jaffe, J.S. Computer modeling and the design of optimal underwater imaging systems. IEEE J. Ocean. Eng. 1990, 15, 101–111. [Google Scholar] [CrossRef]
- Dick, H.J.; Lin, J.; Schouten, H. An ultraslow-spreading class of ocean ridge. Nature 2003, 426, 405. [Google Scholar] [CrossRef] [PubMed]
- Hannington, M.; Jamieson, J.; Monecke, T.; Petersen, S.; Beaulieu, S. The abundance of seafloor massive sulfide deposits. Geology 2011, 39, 1155–1158. [Google Scholar] [CrossRef]
- Hannington, M.D.; Jonasson, I.R.; Herzig, P.M.; Petersen, S. Physical and chemical processes of seafloor mineralization at mid-ocean ridges. Geophys. Monogr. Am. Geophys. Union 1995, 91, 115–157. [Google Scholar]
- Ludvigsen, M.; Aasly, K.; Ellefmo, S.L.; Hilário, A.; Ramirez-Llodra, E.; Søreide, F.X.; Falcon-Suarez, I.; Juliani, C.J.; Kieswetter, A.; Lim, A.; et al. MarMine Cruise Report-Arctic Mid-Ocean Ridge 15.08. 2016-05.09; NTNU Cruise Reports; Norwegian University of Science and Technology: Trondheim, Norway, 2016; ISSN 2535-2520. [Google Scholar]
- Pedersen, R.B.; Rapp, H.T.; Thorseth, I.H.; Lilley, M.D.; Barriga, F.J.; Baumberger, T.; Flesland, K.; Fonseca, R.; Früh-Green, G.L.; Jorgensen, S.L. Discovery of a black smoker vent field and vent fauna at the Arctic Mid-Ocean Ridge. Nat. Commun. 2010, 1, 126. [Google Scholar] [CrossRef] [PubMed]
- Snook, B.; Drivenes, K.; Rollinson, G.; Aasly, K. Characterisation of Mineralised Material from the Loki’s Castle Hydrothermal Vent on the Mohn’s Ridge. Minerals 2018, 8, 576. [Google Scholar] [CrossRef]
- Zhang, H.; Voss, K.J. Bidirectional reflectance study on dry, wet, and submerged particulate layers: Effects of pore liquid refractive index and translucent particle concentrations. Appl. Opt. 2006, 45, 8753–8763. [Google Scholar] [CrossRef] [PubMed]
- Voss, K.J.; Zhang, H. Bidirectional reflectance of dry and submerged Labsphere Spectralon plaque. Appl. Opt. 2006, 45, 7924–7927. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2, pp. 79–104. [Google Scholar]
- Liu, H.; Ong, Y.S.; Shen, X.; Cai, J. When Gaussian process meets big data: A review of scalable GPs. arXiv 2018, arXiv:1807.01065. [Google Scholar]
- Titsias, M. Variational Learning of Inducing Variables in Sparse Gaussian Processes. Proc. Mach. Learn. Res. 2009, 5, 567–574. [Google Scholar]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic variational inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Hensman, J.; Fusi, N.; Lawrence, N.D. Gaussian processes for big data. arXiv 2013, arXiv:1309.6835. [Google Scholar]
- Smith, J.; Lin, T.L.; Ranson, K. The Lambertian assumption and Landsat data. Photogramm. Eng. Remote Sens. 1980, 46, 1183–1189. [Google Scholar]
- Mark, H.; Workman, J., Jr. Chemometrics in Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Mark, H.; Workman, J., Jr. Statistics in Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2003; pp. 63–68. [Google Scholar]
- Steckner, M.C. A simple method for estimating the noise level in a signal region of an MR image. Med Phys. 2010, 37, 5072–5079. [Google Scholar] [CrossRef] [PubMed]
- Maaten, L.V.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Wirsen, C.O.; Jannasch, H.W.; Molyneaux, S.J. Chemosynthetic microbial activity at Mid-Atlantic Ridge hydrothermal vent sites. J. Geophys. Res. Solid Earth 1993, 98, 9693–9703. [Google Scholar] [CrossRef]
- GPy. GPy: A Gaussian Process Framework in Python. 2012. Available online: http://github.com/SheffieldML/GPy (accessed on 9 November 2019).
- Matthews, A.G.D.G.; van der Wilk, M.; Nickson, T.; Fujii, K.; Boukouvalas, A.; León-Villagrá, P.; Ghahramani, Z.; Hensman, J. GPflow: A Gaussian process library using TensorFlow. J. Mach. Learn. Res. 2017, 18, 1–6. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Whitney, D.L.; Evans, B.W. Abbreviations for names of rock-forming minerals. Am. Mineral. 2010, 95, 185–187. [Google Scholar] [CrossRef]


| Imager | 12 mm fore objective, spectrograph, sCMOS |
| Size (H × W) | 355 × 135 (cylindrical) |
| Weight | 11 in air, 6 in water |
| Depth rating | 3000 |
| Operating distance | 0.2 to 7 |
| Operating temp | to 30 |
| Power | 12 to 36 DC, max. 35 |
| Frame rate | 1 to 80 |
| Spectral range | 380–800 nm |
| Diff. lim. spec. res. | 5 nm |
| Spatial res. | 1920 pixels |
| Radiometric res. | 12 bits per band |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sture, Ø.; Snook, B.; Ludvigsen, M. Obtaining Hyperspectral Signatures for Seafloor Massive Sulphide Exploration. Minerals 2019, 9, 694. https://doi.org/10.3390/min9110694
Sture Ø, Snook B, Ludvigsen M. Obtaining Hyperspectral Signatures for Seafloor Massive Sulphide Exploration. Minerals. 2019; 9(11):694. https://doi.org/10.3390/min9110694
Chicago/Turabian StyleSture, Øystein, Ben Snook, and Martin Ludvigsen. 2019. "Obtaining Hyperspectral Signatures for Seafloor Massive Sulphide Exploration" Minerals 9, no. 11: 694. https://doi.org/10.3390/min9110694
APA StyleSture, Ø., Snook, B., & Ludvigsen, M. (2019). Obtaining Hyperspectral Signatures for Seafloor Massive Sulphide Exploration. Minerals, 9(11), 694. https://doi.org/10.3390/min9110694






