2.1. Validating A Digital Algorithm for Non-Porous Rocks
In view of the several approximations mentioned above, and others not mentioned here (since they are dependent on particular techniques), it is important to validate any numerical algorithm against a theoretical solution. For application to certain elastic problems with simple geometry (e.g., a borehole in a uniform stressed medium), theoretical solutions are available. However, for a realistic rock-physics problem, the complexity of geometry precludes any general theoretical solution.
It is possible to construct a rock physics model with an idealized micro-geometry for which a theoretical solution exists (e.g., for ellipsoidal cracks [
3]). However, this is not useful for a realistic rock. The overall elasticity of a realistic rock is, in general, not theoretically calculable because the microgeometry is so complicated. Instead, theoretical upper and lower bounds on the bulk elastic moduli have been proposed. Those derived by Hill [
4] are not absolute bounds, since they depend upon a micro-geometric assumption (non-correlation of stress and strain, at the micro level), which might not be true.
However, strict bounds on the overall elasticity were derived by Hashin and Shtrikman [
5], independent of these issues, and furthermore are closer together than are the Hill “bounds”. For solid composites of two isotropic constituents (with bulk moduli
Ki and shear moduli
μi and volume fractions
fi), the lower (−) and upper (+) H–S (Hashin - Shtrikman) bounds for the bulk modulus
K and the shear modulus
μ are
In Equation (6), the combination of moduli
for each constituent appears in the bounds for the shear modulus. Here, it is assumed (following [
5]) that
and also that
; this correlation is common. If it should happen that
while
, then the roles of
and
, defined in Equation (5), are reversed. If it should happen that
while
, then the roles of
and
, defined in Equation (6), are reversed.
The bounds on the bulk modulus (Equation (5)) may be combined to show the difference:
where
and
. Hence, the bounds on
K coincide exactly in the special case where the two minerals have identical shear modulus (∆
μ = 0), in which case the bulk modulus is given exactly by
(where
μ is the common shear modulus, of the two constituents and of the aggregate) for any random microgeometry of the two isotropic constituents. (The special case of Equation (9) with
μ = 0 yields the Reuss average [
4] bulk modulus, the correct result for such a suspension.)
The generalization of Equation (5) for composites of more than two isotropic constituents was given by Hashin and Shtrikman [
5]. For such composites, the upper and lower bounds on
K coincide, yielding a unique result, if the shear moduli are equal for all constituents.
Of course, few if any physical aggregates have constituents with identical shear moduli. However, although Equation (9) is not a useful result for physical aggregates, it is a very useful result for numerical analyses, since it poses a necessary criterion for the validity of any digital rock physics numerical algorithm: any numerical algorithm which is proposed to calculate the elasticity of a realistic 3D geometry should first be validated by verifying that it satisfies Equation (9), when equal isotropic shear moduli are assigned to the grains; this may be called the “K-test”.
Similarly, the bounds on the shear modulus in Equation (6) may be combined to show the difference:
Hence, the bounds on the shear moduli coincide exactly, in the special case where
For composites of more than two isotropic constituents, the upper and lower bounds on μ coincide, yielding a unique result, if the condition of Equation (11) holds for all constituents.
The condition of Equation (11) serves as a calculation of any one of the four constituent moduli, when the other three are specified. For example, it implies that
For composites of two constituents which confirm Equation (11), the shear modulus is given exactly by
independent of the microgeometry of the two isotropic constituents.
Of course, few if any physical aggregates have constituents which confirm Equation (11). However, although Equations (12) and (13) are not a useful result for physical aggregates, they are a very useful result for numerical analyses, since they pose another necessary criterion for the validity of any digital rock physics numerical algorithm: any numerical algorithm which is proposed to calculate the elasticity of a realistic 3D geometry should first be validated by verifying that it satisfies Equation (13) when the constituent moduli are constrained by Equation (11); this may be called the “μ-test”.
2.2. Validating A Digital Algorithm for Porous, Saturated Rocks
Modeling a rock with fluid-filled porosity involves additional considerations. The theory of poro-elasticity (e.g., in [
6,
7]) requires consideration of the pore fluid properties, the frequency of excitation, and the hydraulic condition (e.g., open or closed) of the rock, all of which are outside of the present scope. However, it also requires consideration of
KS, the average solid modulus of the grains of the rock; this topic can be addressed here.
Love [
8] (see especially Sections 121 and 123 (iii, iv)) proved that, for any shape of a homogeneous isotropic solid, its elastic response to a uniform increase of pore pressure (on all of its surfaces, internal and external) is independent of that shape, with each linear dimension decreasing proportionally, so that its shape is preserved. Hence the bulk modulus of the solid shape is the intrinsic bulk modulus of that solid. The proof is valid for any homogeneous isotropic shape, if the pore space is fully connected hydraulically, so that the fluid pressure is uniform.
This theorem may be applied to a representative volume element of a porous rock in a (hydraulically open) “unjacketed compression” experiment, wherein the increase in external pressure on a rock is balanced by an equal increase in internal pore pressure. If the porosity is fully connected on the time scale of the compression, the pore pressure will be uniform throughout, regardless of the complexity of the geometry. In such a test, the solid is compressed on all sides with the same additional pressure, and Love’s theorem applies.
A straightforward extension of Love’s proof to the case of a heterogeneous isotropic solid then concludes that, in an unjacketed test on such a rock with fully connected porosity, the solid modulus is approximately the intrinsic average modulus of the grains, as calculated above.
2.3. A Particular Algorithm
The tests proposed above are the most general conclusions of the present work. Successful passage of these tests should be demonstrated for any digital rock physics project proposed in the future. A failure in any test might be due to a shortcoming in the numerical algorithm applied, or to any of the other issues mentioned in
Section 1.1, which may be different in each project. Below, we apply these tests to a particular algorithm, in a context where none of these other issues occur.
A staggered-grid finite-difference damped time-stepping algorithm has been proposed by Lin et al. [
9,
10] (“LFZ”) for this digital rock physics problem. The LFZ algorithm produces a solution to the static elastic problem by solving the corresponding elasto-dynamic wave equation, with attenuation artificially added to damp out the kinetic energy (while keeping the strain energy) so that the dynamic solution converges to the static solution. The advantage of the algorithm is its computational efficiency: the time-marching scheme does not require the inversion of a large matrix, as in the static approach. The computational effort in such an inversion can be so significant that approximations permitting a 2D inversion of a 3D model have been proposed [
11]. Therefore, the computational efficiency of the LFZ algorithm offers a significant advantage.
The method is based upon the first-order hyperbolic system of Virieux [
12]: the equation of motion for continua:
and the linear isotropic constitutive relation:
where
vi is the particle velocity vector (a function of space and time),
ρ is the density,
is the position vector, and
λ =
K − 2
μ/3 is the Lame parameter. However, LFZ augmented the equation of motion (14) with a velocity-damping term:
where the constant artificial damping coefficient
d was chosen to efficiently damp out the kinetic energy, for the study of static elastic problems. The physical realism of the damping is immaterial; it is just an artifice to attenuate the kinetic energy. With the inertial terms damped out, the resulting deformation is independent of the material density.
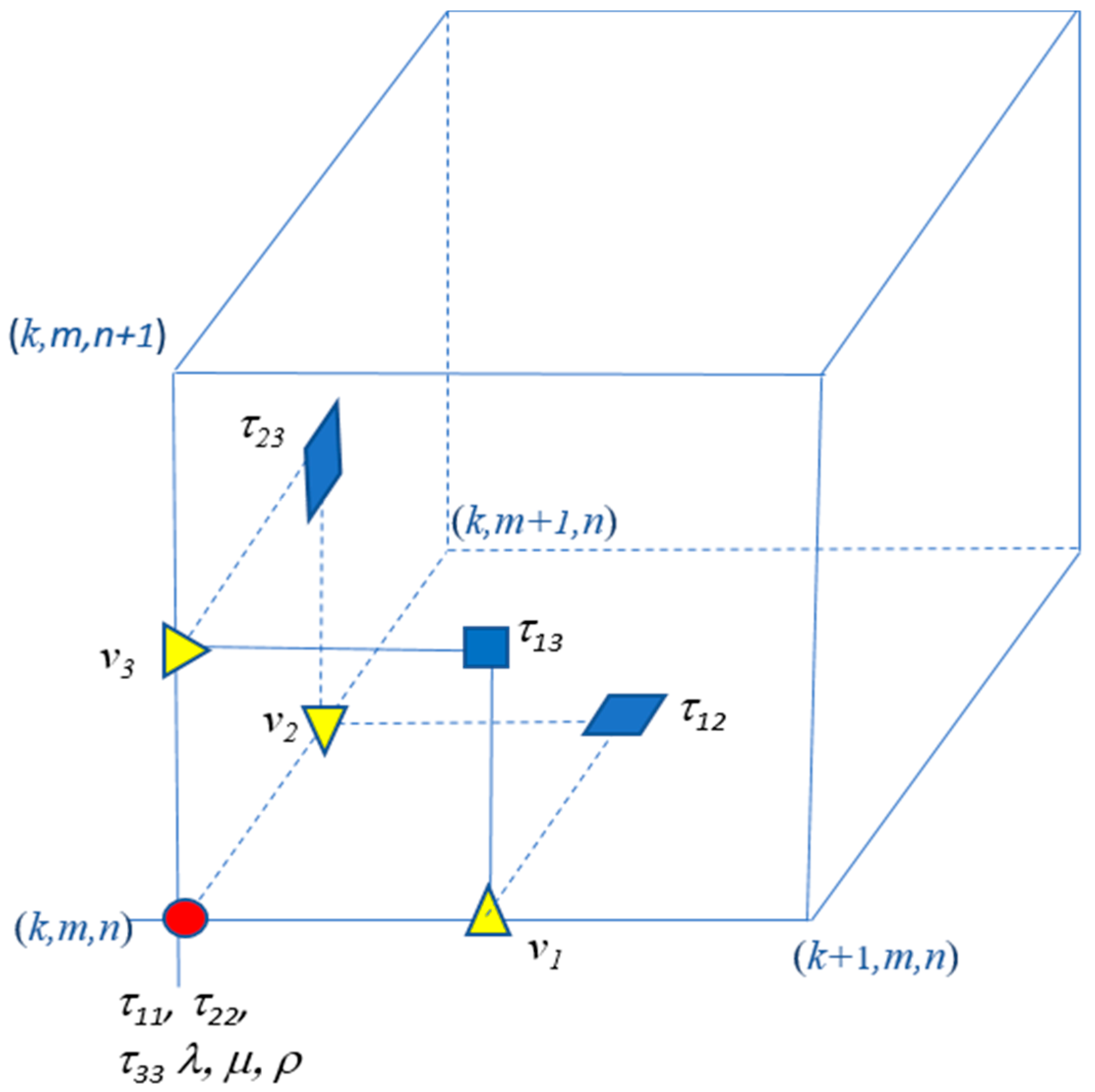
These equations incorporate local heterogeneity of the elastic moduli and density explicitly (hence no need to consider local boundary conditions), although the model analyzed herein (described below) has piecewise uniform elasticity within each numerical cell. The dynamic algorithm (Equations (15) and (16)) is implemented on a staggered Cartesian numerical grid, similar to that proposed by Virieux [
12], shown in
Figure 1.
The derivatives are discretized by centered finite differences, with the various quantities evaluated at different positions on the staggered grid, as shown in the
Figure 1. The stress components are evaluated at
t time units; the velocity components are evaluated at (
t + 1/2) time units. As the computation approaches its asymptotic (static) limit, these time differences become irrelevant. This pattern of staggering arises naturally from the centering of the finite derivatives.
Where a grid node separates domains of different elasticity, the elastic moduli and density at that node are assigned appropriate average values, depending on the properties of its eight nearest neighbors in three dimensions. This procedure partially smooths the spatial variation of physical properties, with an accuracy which depends upon the resolution of the grid.