Particle Size Distribution of Cemented Rockfill Effects on Strata Stability in Filling Mining
Abstract
1. Introduction
2. Experimental Method and Results
2.1. Experimental Materials
2.2. Experimental Specimens
2.3. Experimental Equipment and Testing Process
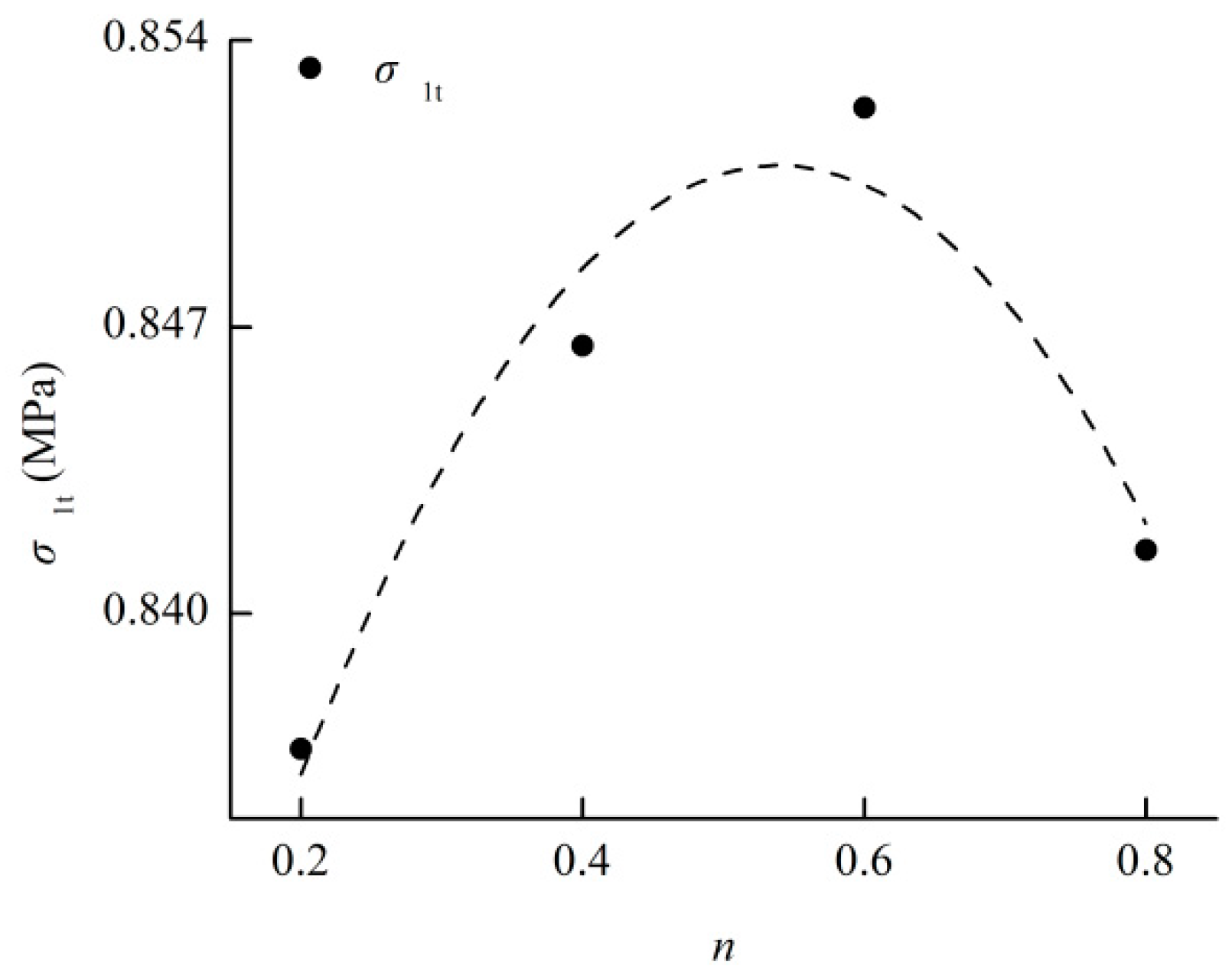
2.4. Particle Size Distribution of Aggregate Effects on the Mechanical Parameters of Cemented Rockfill
3. Numerical Simulation and Results
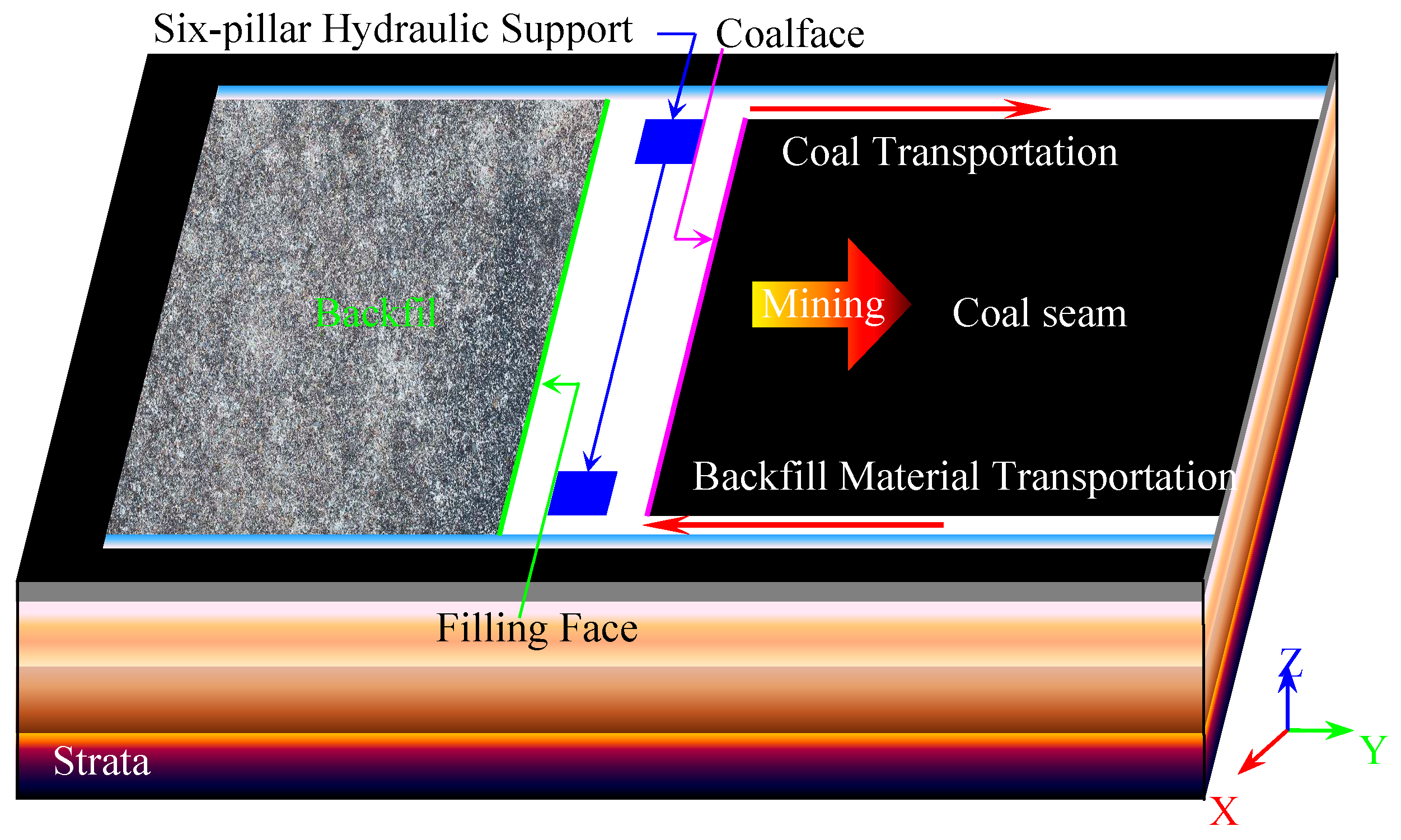
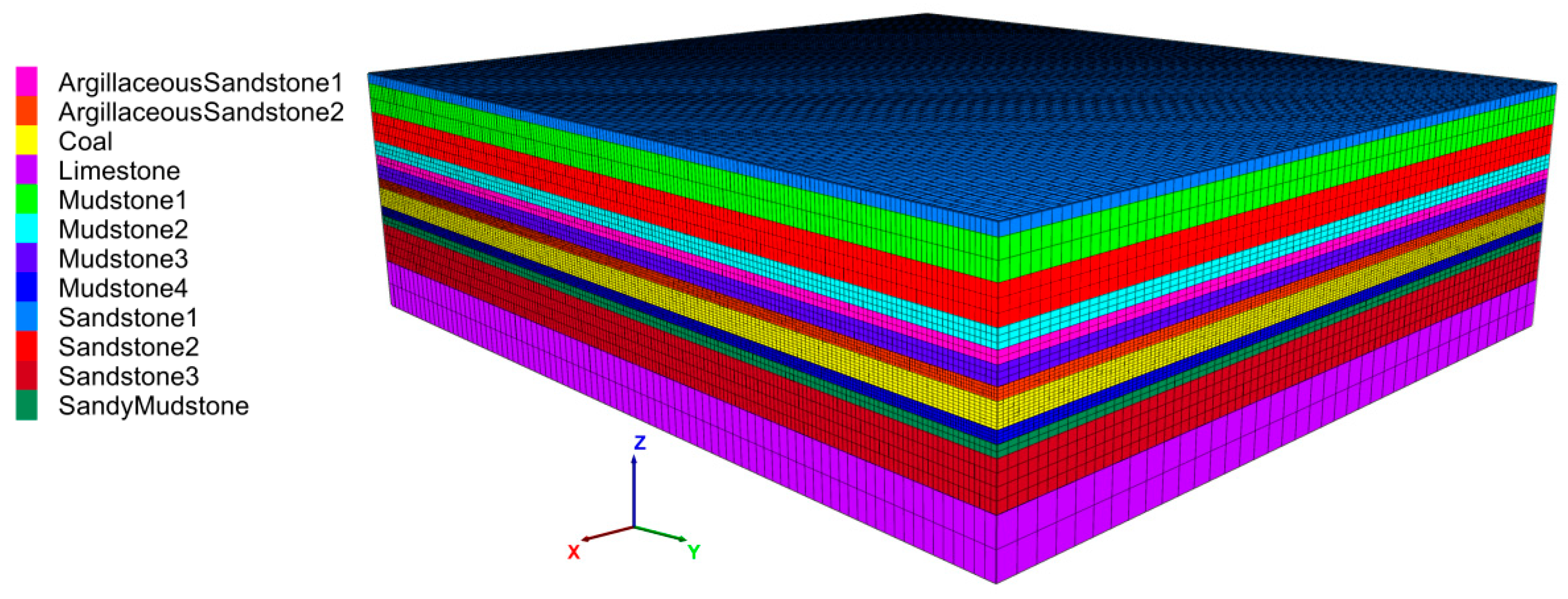
3.1. Establishment of Filling Mining Model in Coal Mine
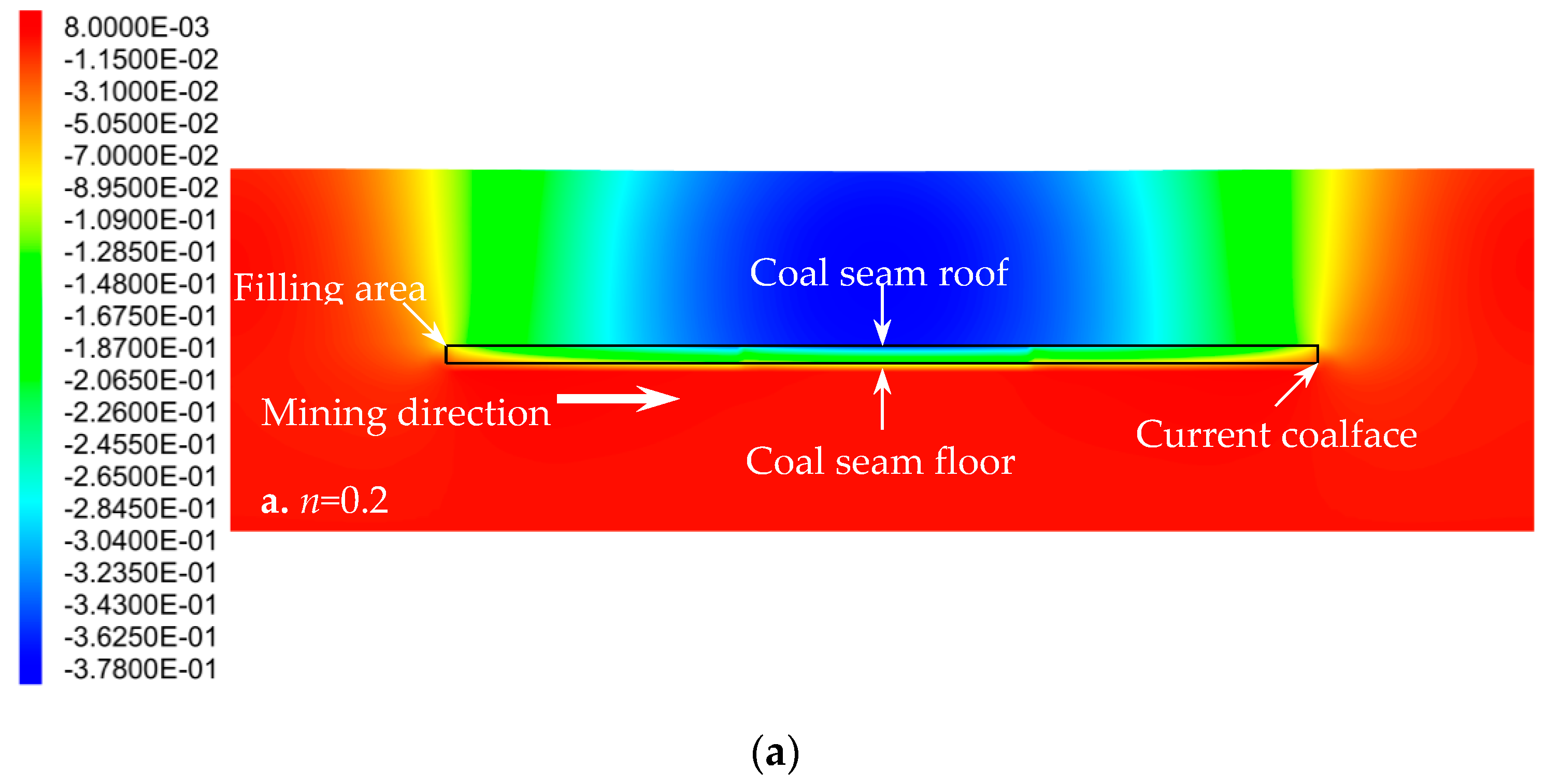
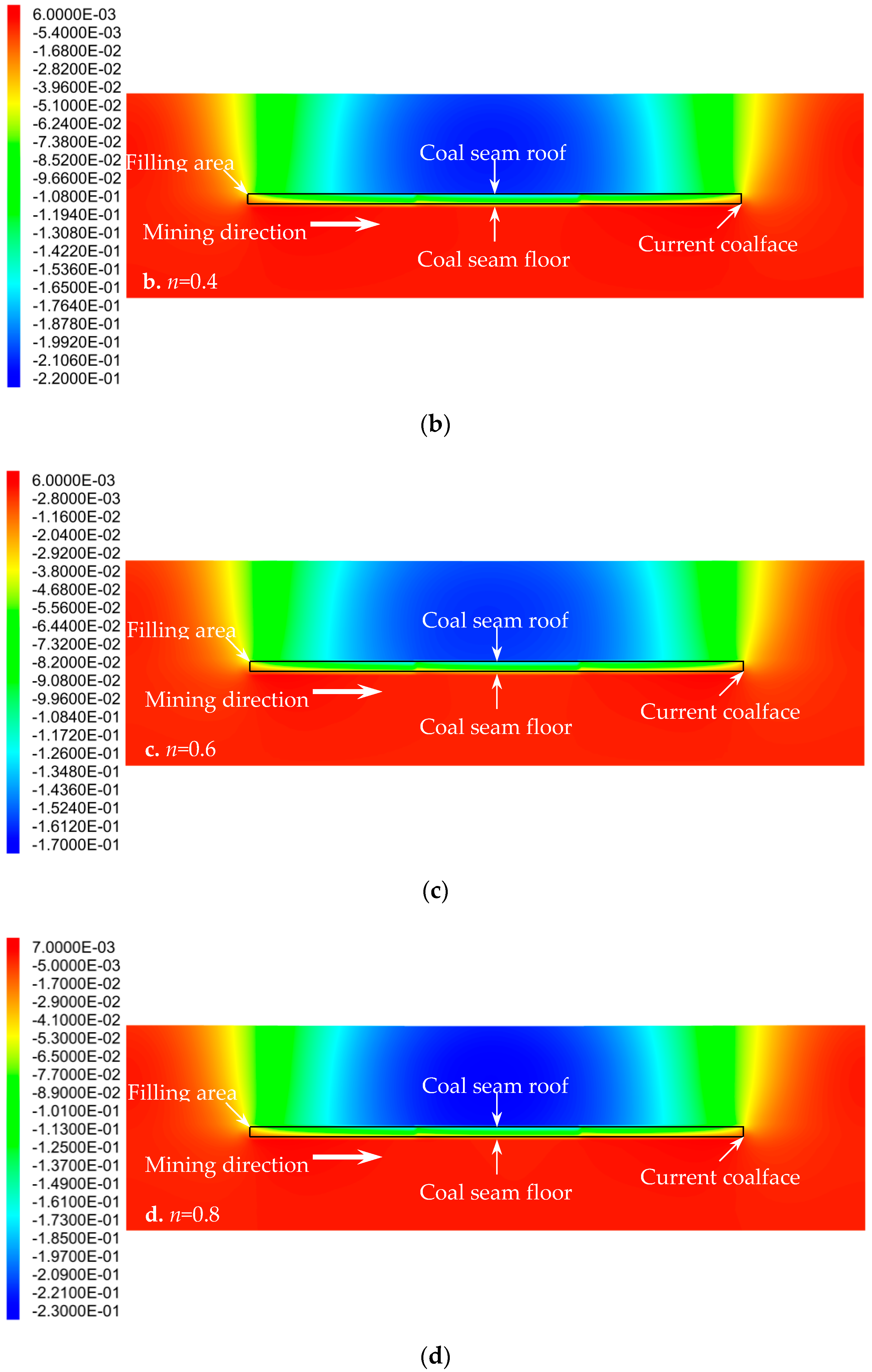
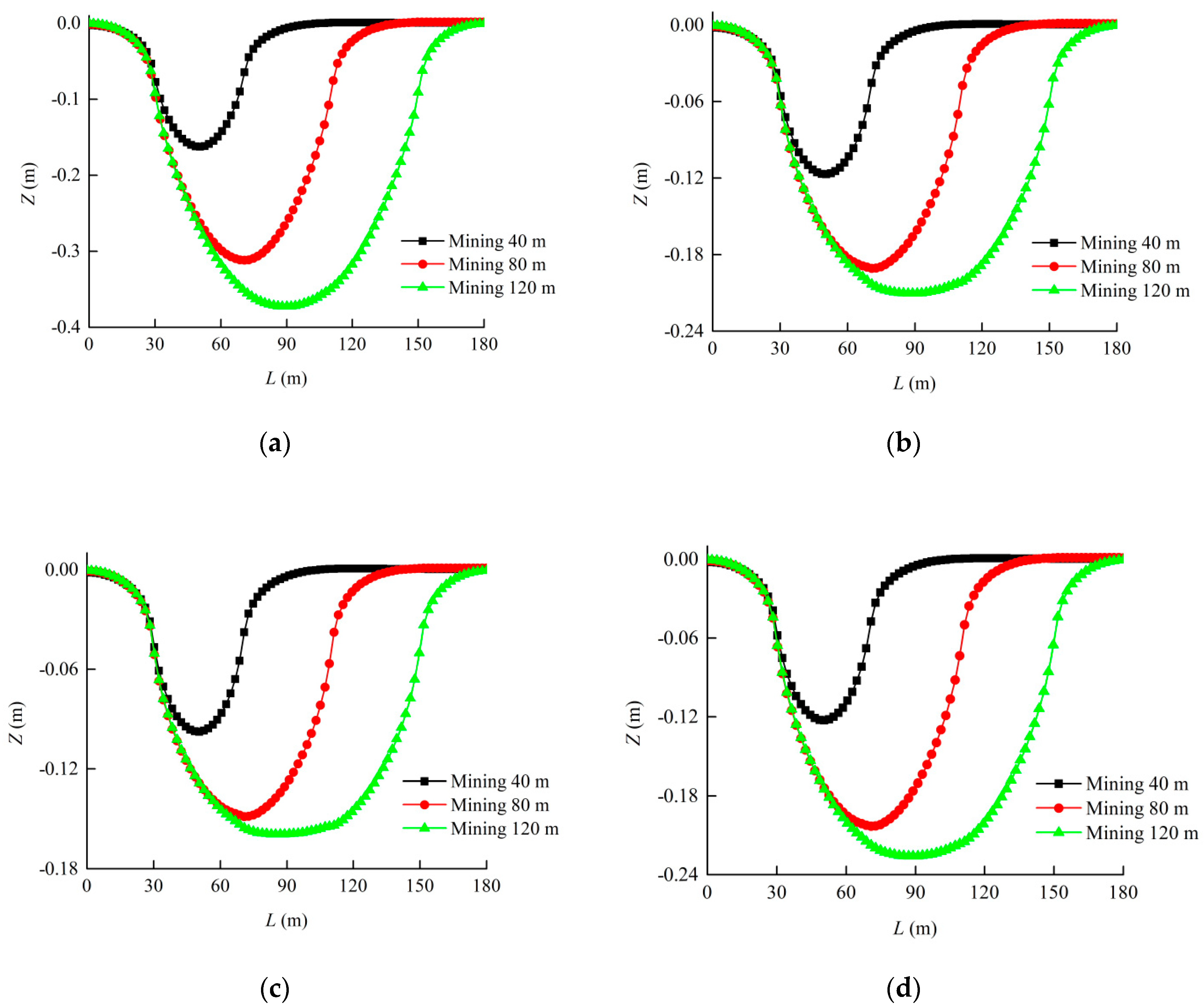
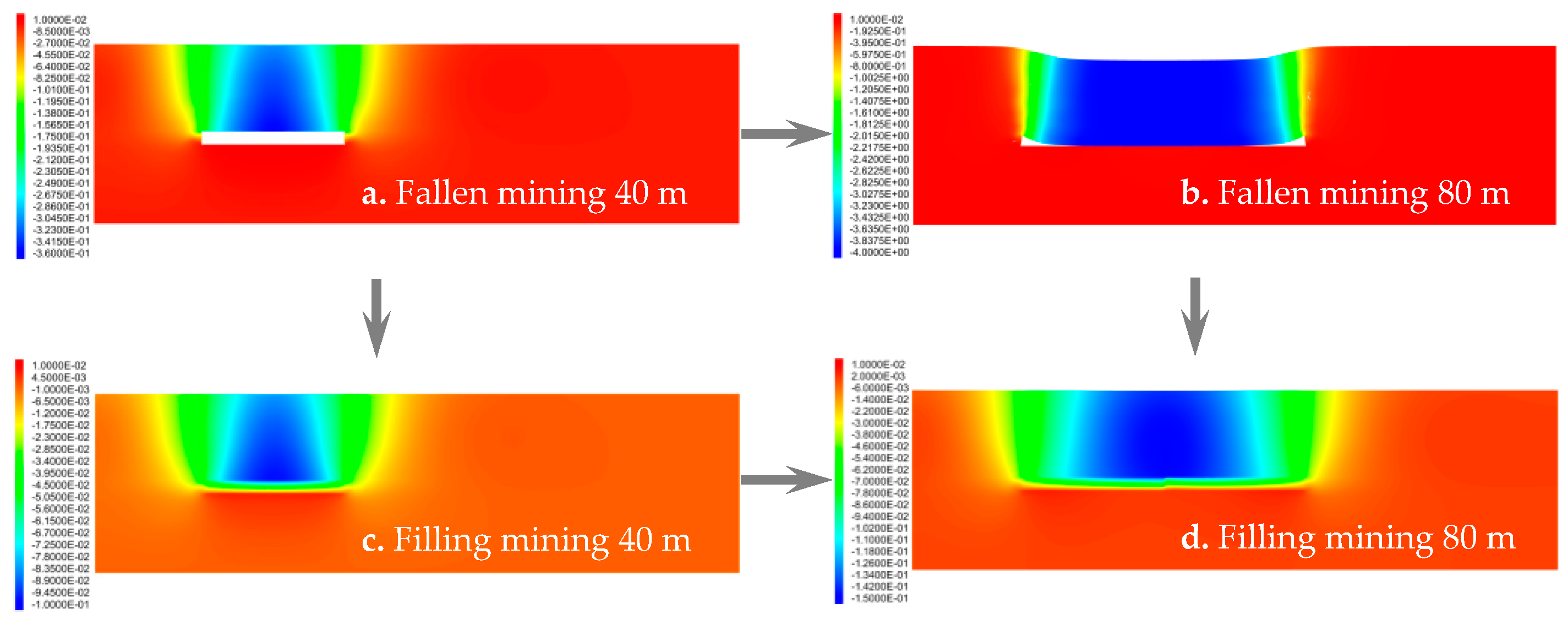
3.2. Particle Size Distribution of Aggregate in Cemented Rockfill Effects on Displacement Field of Strata
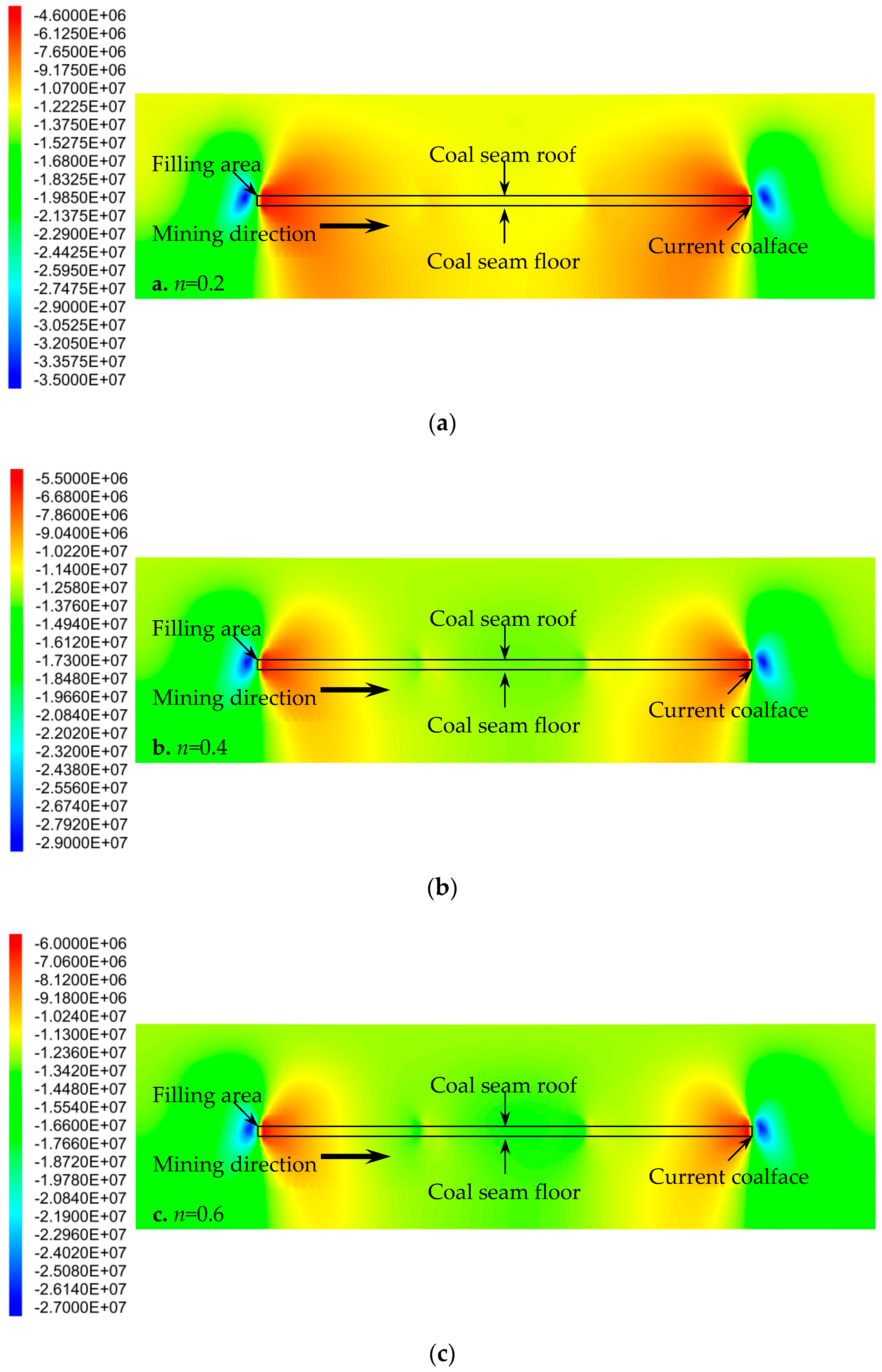
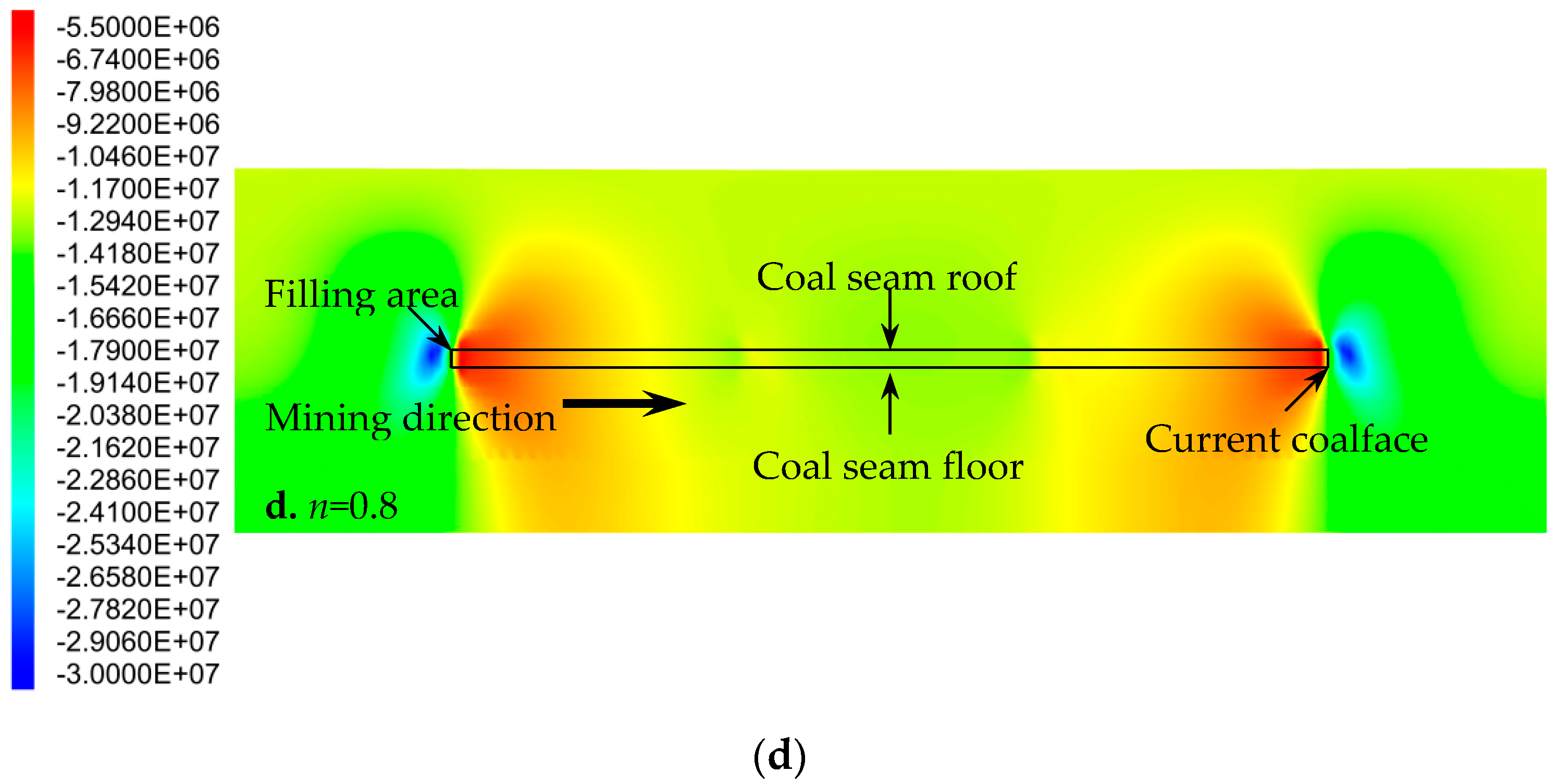
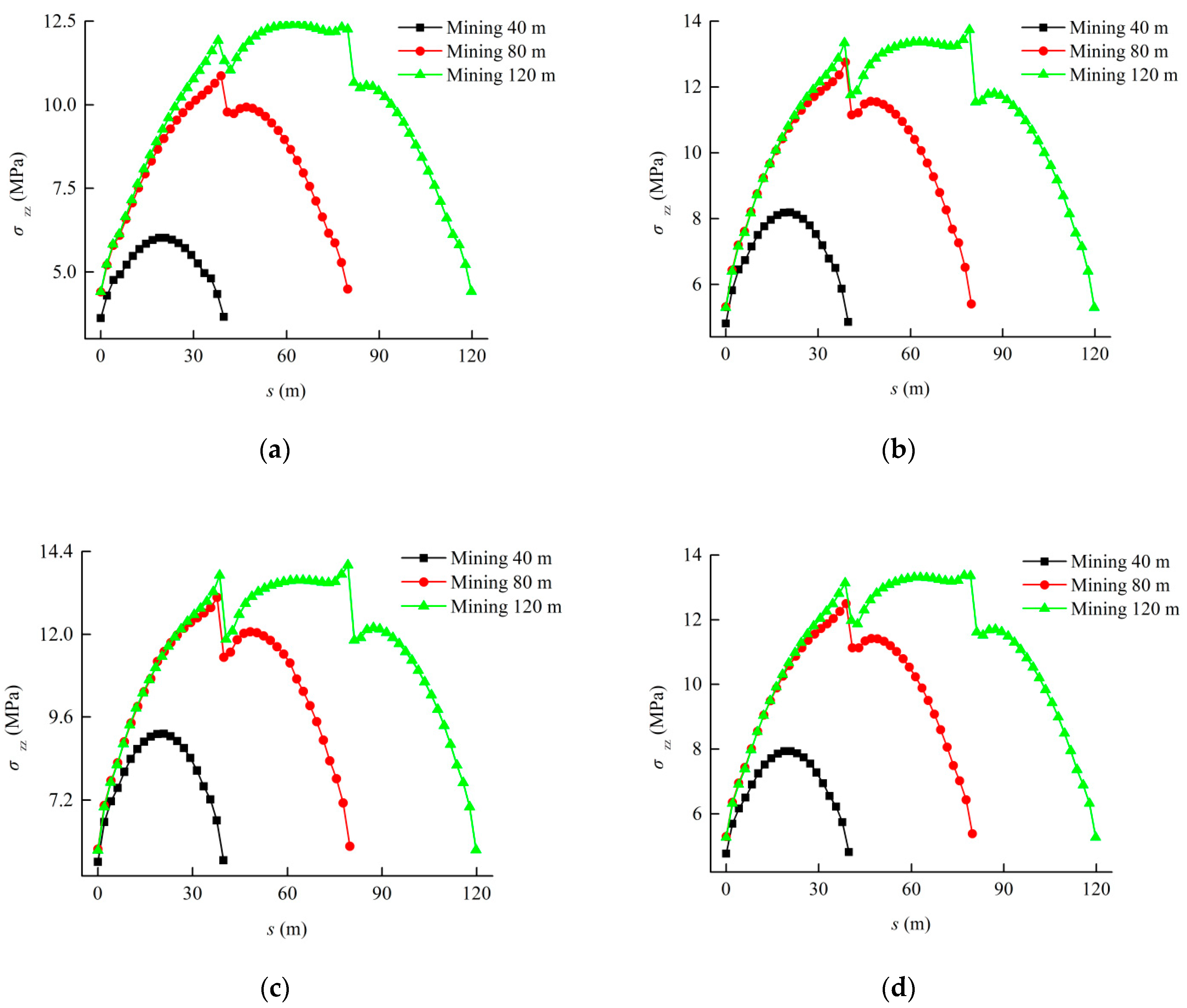
3.3. Particle Size Distribution of Aggregate in Cemented Rockfill Effects on Stress Field of Strata
4. Discussions
5. Conclusions
- (1)
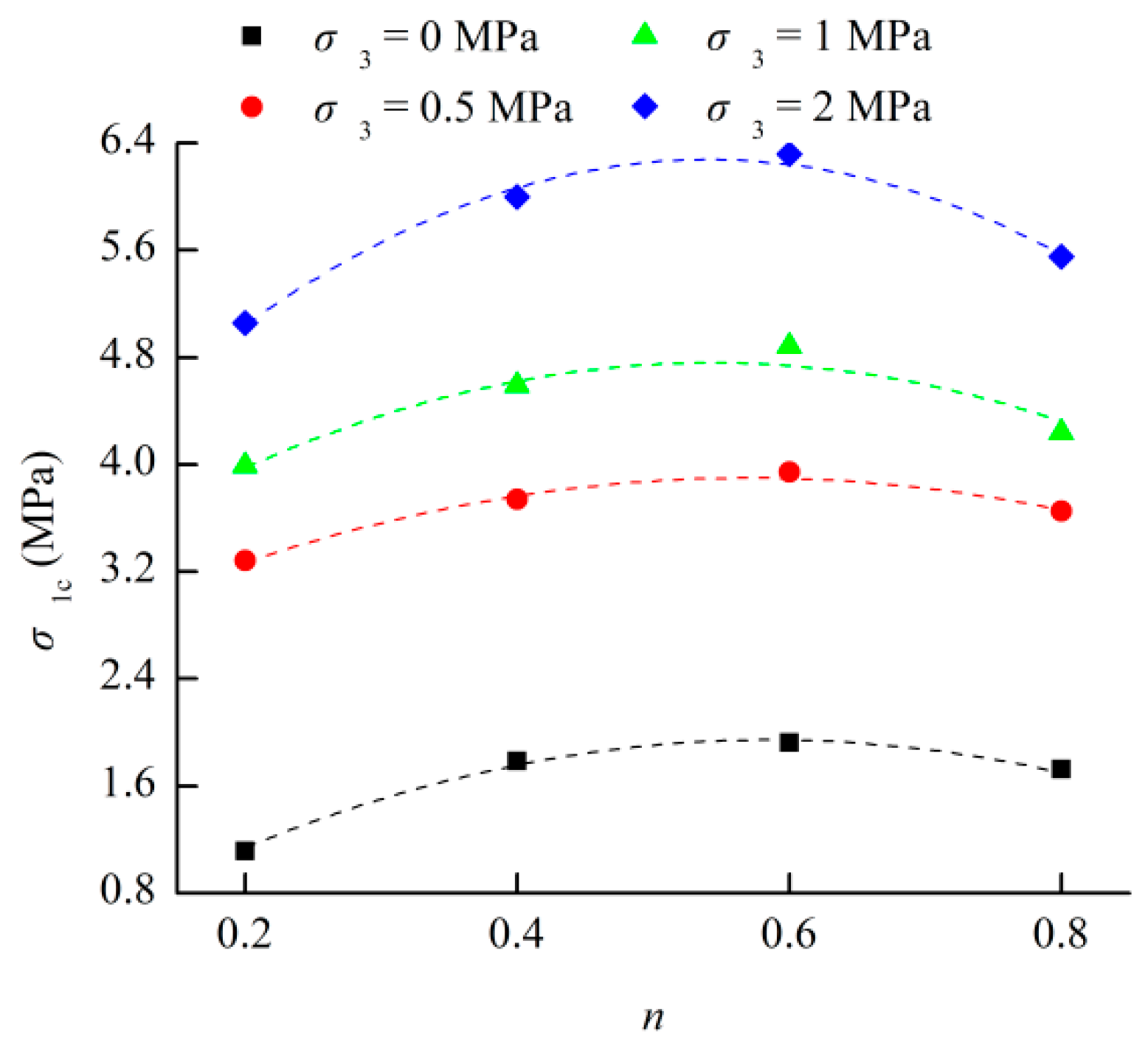
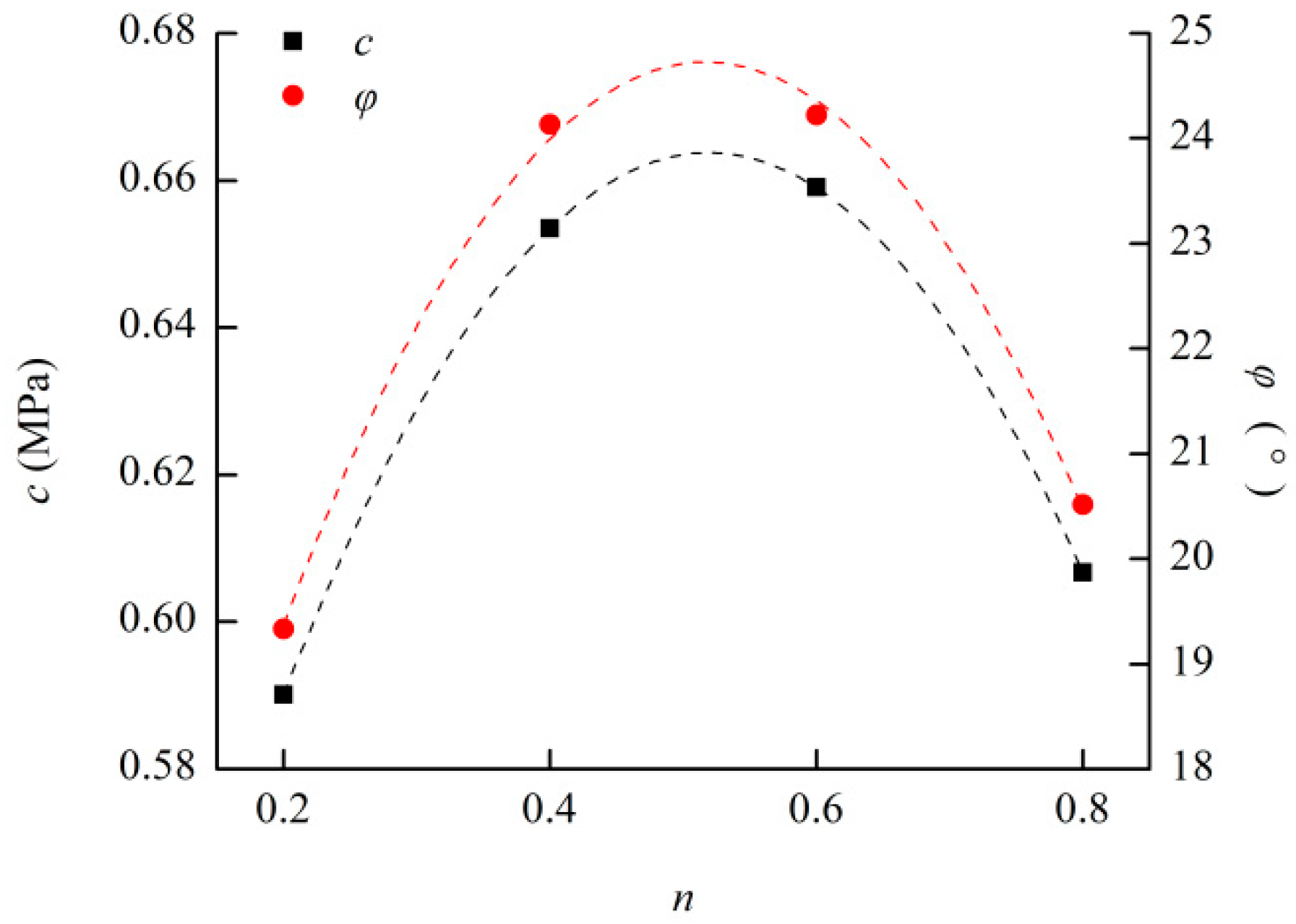
- The relationships between the mechanical parameters (Poisson ratio, elastic modulus, compressive strength, cohesive force, internal friction angle, and tensile strength) of the cemented rockfill and the Talbot index of granule gradation can be described by quadratic polynomial functions, and the extreme of the established function can be used to characterize the optimal granule gradation of the cemented rockfill material.
- (2)
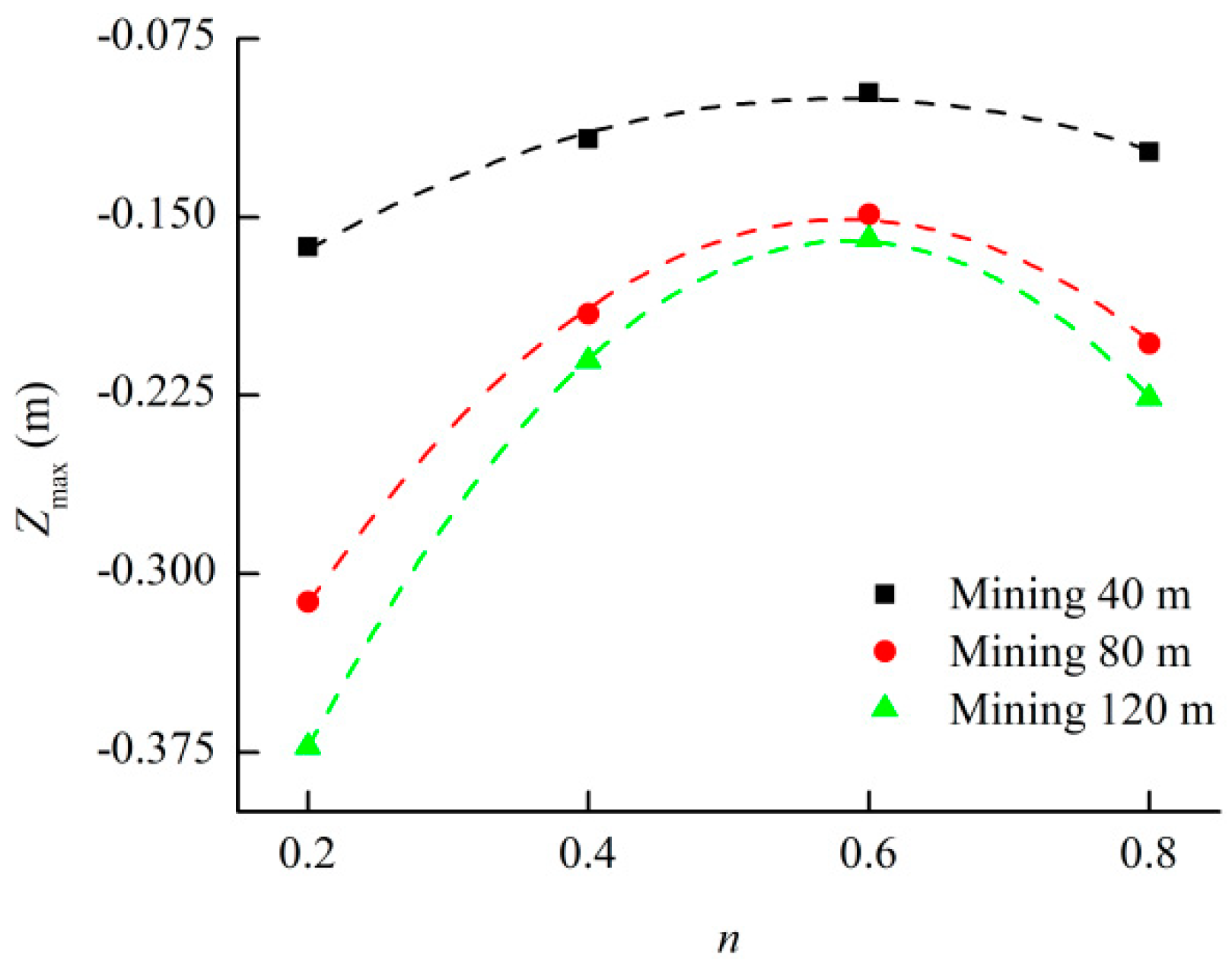
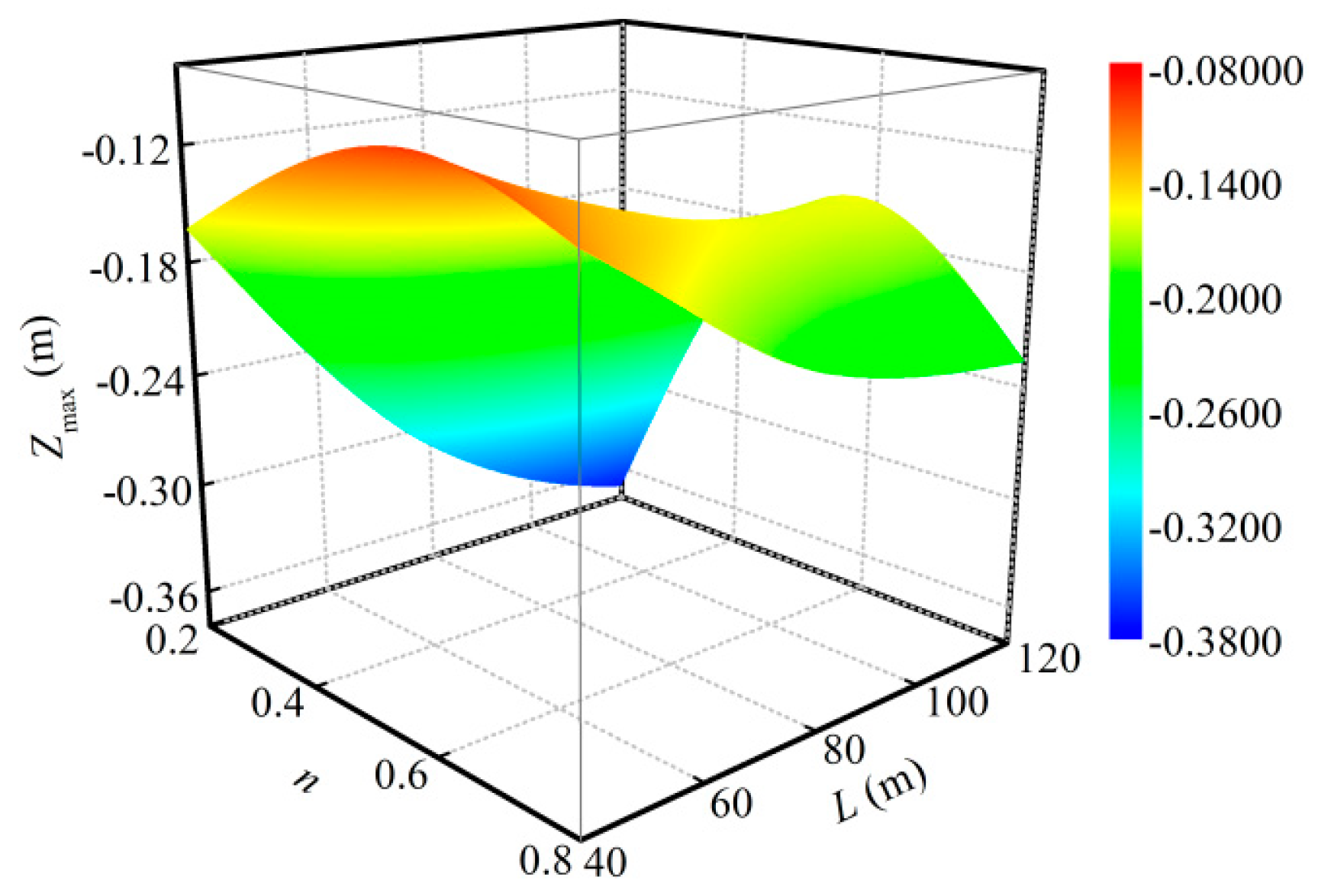
- The movement of each stratum was mainly located above the filling area. The closer to the filling area, the greater the subsidence displacement of the stratum; the subsidence displacement was concentrated in the middle of each stratum. As both ends of the filling area could still rely on the original rock mass to load, it presented a small subsidence displacement. The subsidence displacements of the overlying strata increased with the advancement of the coalface, but the fall velocity gradually slowed down. The maximum subsidence displacement always occurred above the middle of the filling area, and it had a quadratic polynomial relation with the Talbot index of the cemented rockfill. It was considered that optimizing the particle size distribution of the aggregate in the cemented rockfill could effectively control the strata movement.
- (3)
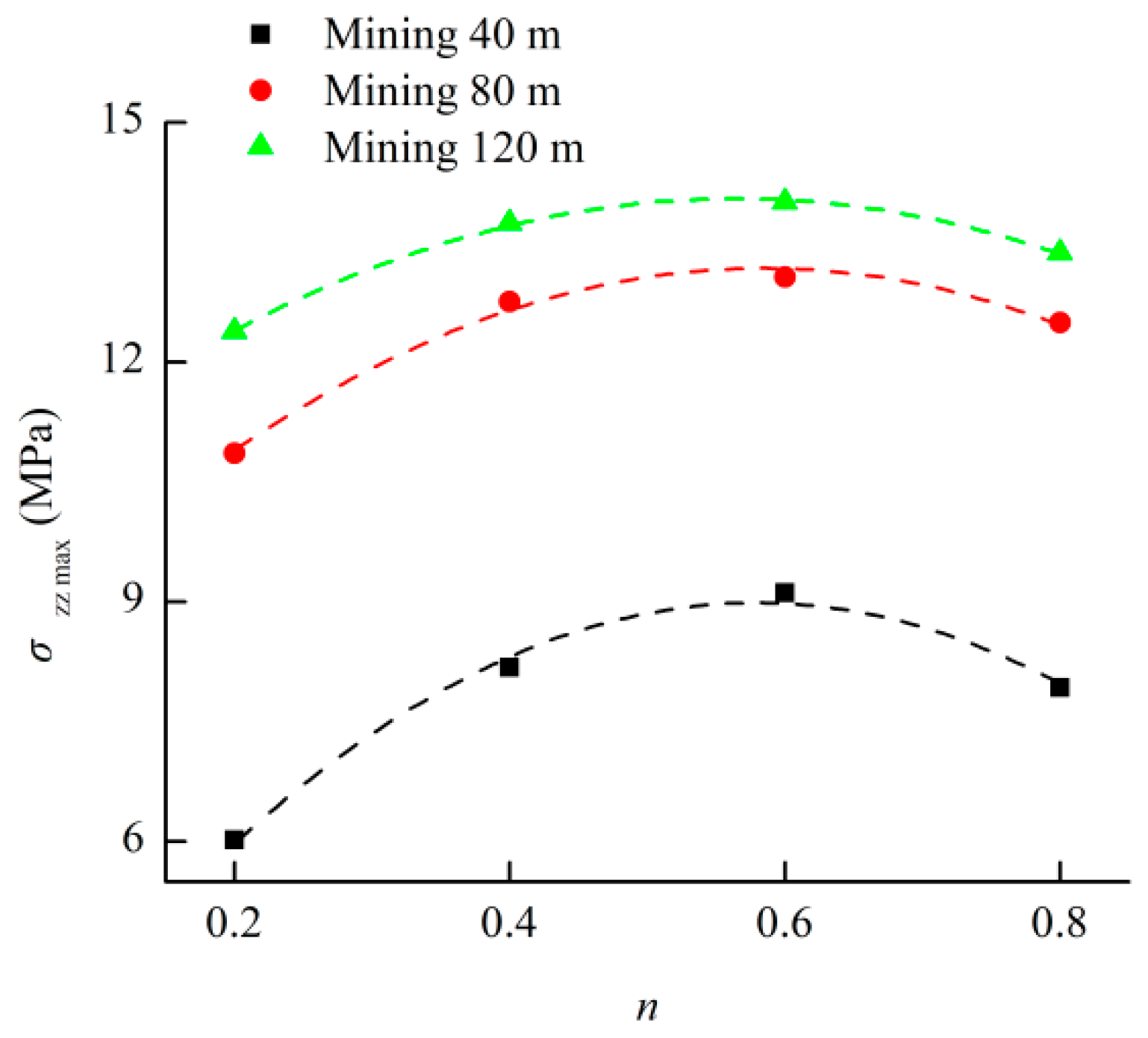
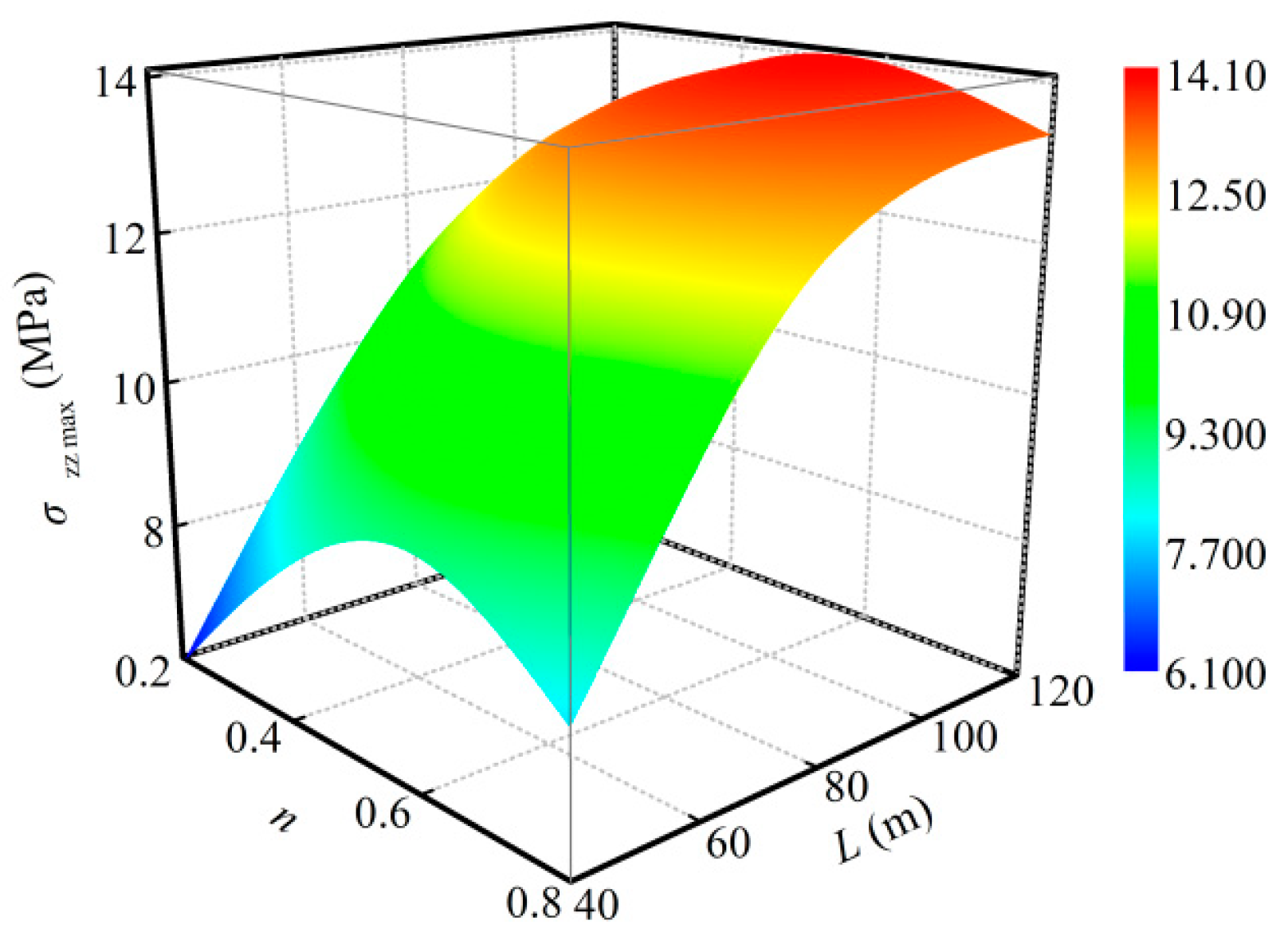
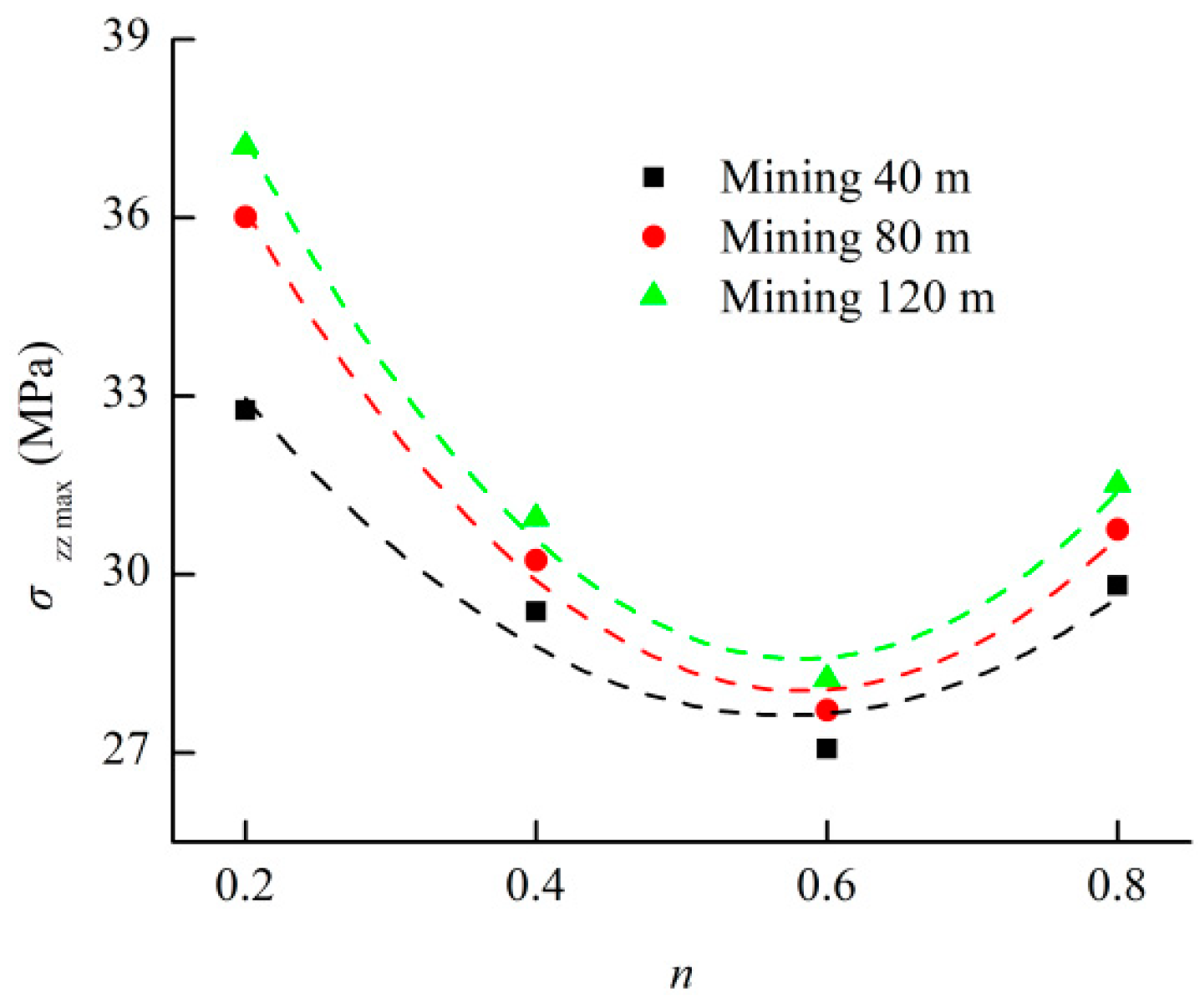
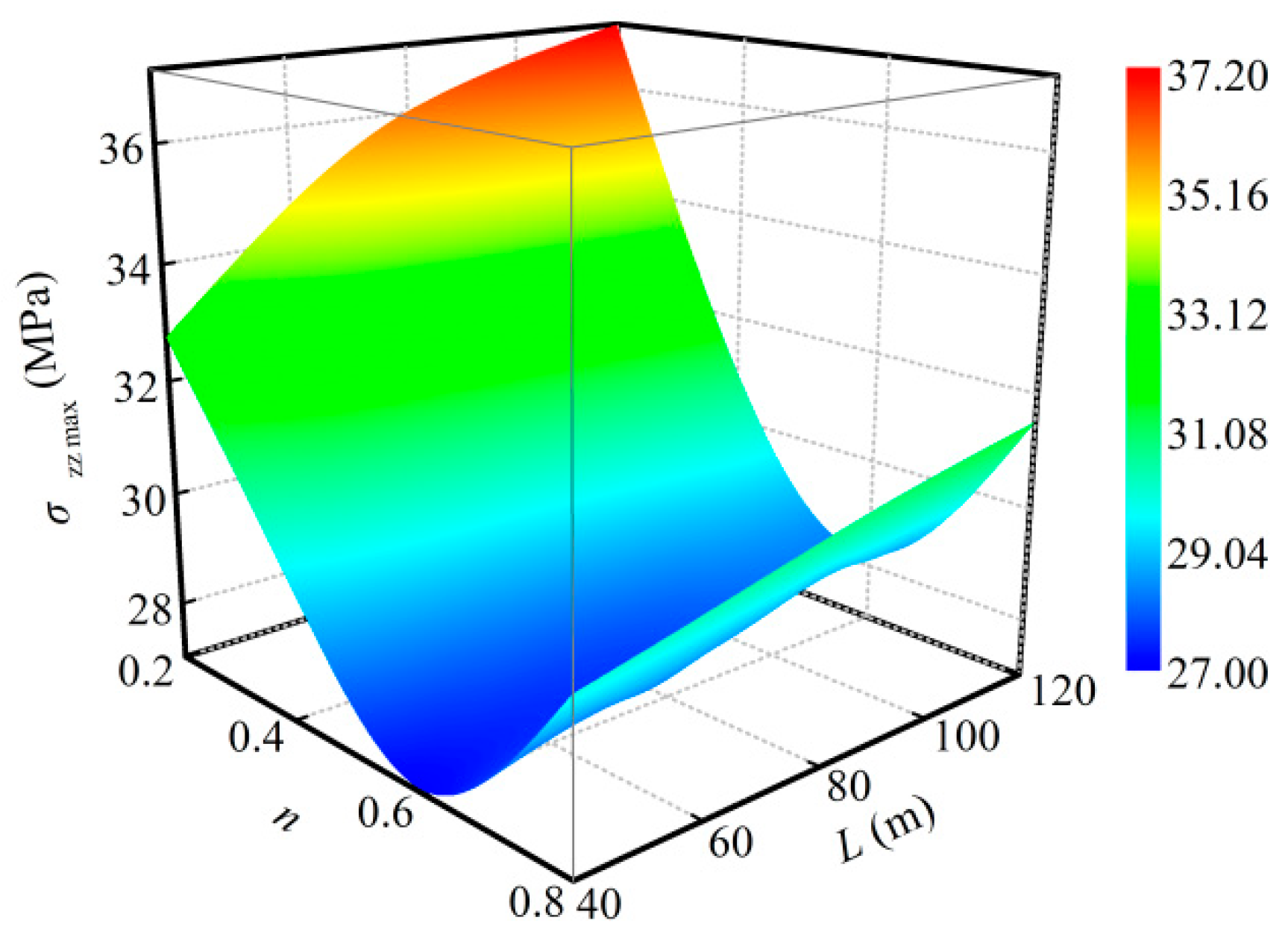
- The stress of the strata was concentrated in the rock mass in the coalface. The stress field distribution in the filling area presented a large stress in the middle part and small stress at the two ends. This distribution characteristic was also suitable for describing that of each stratum above and below the filling area. The internal stress of the backfill and the stress of the rock mass in the coalface increased with the advancement of the coalface, but the increasing rates gradually slowed down. The maximum internal stress of the backfill was always located in the middle of the filling area, where the maximum value was in a quadratic polynomial relation with the Talbot index of the cemented rockfill. This function is also suitable for describing the relationship between the stress of the rock mass in the coalface and the Talbot index of the cemented rockfill. It was considered that optimizing the particle size distribution of the aggregate in the cemented rockfill could improve the loading capacity of the backfill in order to improve the filling effect, and it could decrease the internal stress of the rock mass in the coalface to reduce the potential dangers around the coalface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Deng, D.Q.; Liu, L.; Yao, Z.L.; Song, K.; Lao, D.Z. A practice of ultra-fine tailings disposal as filling material in a gold mine. J. Environ. Manag. 2017, 196, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Li, X.B.; Li, D.Y.; Liu, Z.X.; Zhao, G.Y.; Wang, W.H. Determination of the minimum thickness of crown pillar for safe exploitation of a subsea gold mine based on numerical modelling. Int. J. Rock Mech. Min. Sci. 2013, 57, 42–56. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: The roles of aperture, surface roughness, and number of intersections. Adv. Water. Resour. 2016, 88, 53–65. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Y.; Li, B.; Yu, L. Estimating permeability of porous media based on modified Hagen–Poiseuille flow in tortuous capillaries with variable lengths. Microfluid. Nanofluid. 2016, 20, 120. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Yu, L.; Jiang, Y.; Jing, H. A discrete-fracture-network fault model revealing permeability and aperture evolutions of a fault after earthquakes. Int. J. Rock. Mech. Min. 2018, 107, 19–24. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, B.Y.; Zhou, N.; Zhang, Q. Application of solid backfilling to reduce hard-roof caving and longwall coal face burst potential. Int. J. Rock Mech. Min. Sci. 2016, 88, 197–205. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, T.H.; Bai, H.B.; Gamage, R.P. Longwall mining–induced damage and fractures: Field measurements and simulation using FDM and DEM coupled method. Int. J. Geomech. 2018, 18, 04017127. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.X.; Huang, Y.L.; Zhou, N. Effects of particle size of crushed gangue backfill materials on surface subsidence and its application under buildings. Environ. Earth Sci. 2017, 76, 603. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, M.; Liu, Z.; Zhou, N. Fractal characteristics of crushed particles of coal gangue under compaction. Powder Technol. 2017, 305, 12–18. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.X.; Quan, K.; Zhou, N. Innovative Extraction Method for a Coal Seam with a Thick Rock-Parting for Supporting Coal Mine Sustainability. Sustainability 2017, 9, 1982. [Google Scholar] [CrossRef]
- Sivakugan, N.; Rankine, R.M.; Rankine, K.J.; Rankine, K.S. Geotechnical considerations in mine backfilling in Australia. J. Clean. Prod. 2006, 14, 1168–1175. [Google Scholar] [CrossRef]
- Benzaazoua, M.; Belem, T.; Bussière, B. Chemical factors that influence the performance of mine sulphidic paste backfill. Cem. Concr. Res. 2002, 32, 1133–1144. [Google Scholar] [CrossRef]
- Belem, T.; Benzaazoua, M. Design and application of underground mine paste backfill technology. Geotech. Geol. Eng. 2008, 26, 147–174. [Google Scholar] [CrossRef]
- Abdul-Hussain, N.; Fall, M. Thermo-hydro-mechanical behaviour of sodium silicate-cemented paste tailings in column experiments. Tunn. Undergr. Space Technol. 2012, 29, 85–93. [Google Scholar] [CrossRef]
- Holt, E.; Leivo, M. Cracking risks associated with early age shrinkage. Cem. Concr. Compos. 2004, 26, 521–530. [Google Scholar] [CrossRef]
- Ouellet, S.; Bussière, B.; Aubertin, M.; Benzaazoua, M. Characterization of cemented paste backfill pore structure using SEM and IA analysis. Bull. Eng. Geol. Environ. 2008, 67, 139–152. [Google Scholar] [CrossRef]
- Wu, A.X.; Wang, Y.; Wang, H.J.; Yin, S.H.; Miao, X.X. Coupled effects of cement type and water quality on the properties of cemented paste backfill. Int. J. Min. Process. 2015, 143, 65–71. [Google Scholar] [CrossRef]
- Ouellet, S.; Bussière, B.; Mbonimpa, M.; Benzaazoua, M.; Aubertin, M. Reactivity and mineralogical evolution of an underground mine sulphidic cemented paste backfill. Miner. Eng. 2006, 19, 407–419. [Google Scholar] [CrossRef]
- Fall, M.; Benzaazoua, M.; Saa, E.G. Mix proportioning of underground cemented tailings backfill. Tunn. Undergr. Space Technol. 2008, 23, 80–90. [Google Scholar] [CrossRef]
- Liu, Z.X.; Dang, W.G.; Liu, Q.L.; Chen, G.H.; Peng, K. Optimization of clay material mixture ratio and filling process in gypsum mine goaf. Int. J. Min. Sci. Technol. 2013, 23, 337–342. [Google Scholar] [CrossRef]
- Fall, M.; Benzaazoua, M. Modeling the effect of sulphate on strength development of paste backfill and binder mixture optimization. Cem. Concr. Res. 2005, 35, 301–314. [Google Scholar] [CrossRef]
- Yin, S.H.; Wu, A.X.; Hu, K.J.; Wang, Y.; Zhang, Y.K. The effect of solid components on the rheological and mechanical properties of cemented paste backfill. Miner. Eng. 2012, 35, 61–66. [Google Scholar] [CrossRef]
- Ke, X.; Hou, H.; Zhou, M.; Wang, Y.; Zhou, X. Effect of particle gradation on properties of fresh and hardened cemented paste backfill. Constr. Build. Mater. 2015, 96, 378–382. [Google Scholar] [CrossRef]
- Fall, M.; Benzaazoua, M.; Ouellet, S. Experimental characterization of the influence of tailings fineness and density on the quality of cemented paste backfill. Miner. Eng. 2005, 18, 41–44. [Google Scholar] [CrossRef]
- Börgesson, L.; Johannesson, L.E.; Gunnarsson, D. Influence of soil structure heterogeneities on the behaviour of backfill materials based on mixtures of bentonite and crushed rock. Appl. Clay Sci. 2003, 23, 121–131. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Benzaazoua, M.; Kesimal, A.; Ercikdi, B. Evaluation of the strength properties of deslimed tailings paste backfill. Miner. Resour. Eng. 2013, 12, 129–144. [Google Scholar]
- Orejarena, L.; Fall, M. The use of artificial neural networks to predict the effect of sulphate attack on the strength of cemented paste backfill. Bull. Eng. Geol. Environ. 2010, 69, 659–670. [Google Scholar] [CrossRef]
- Gautam, B.P.; Panesar, D.K.; Sheikh, S.A.; Vecchio, F.J. Effect of coarse aggregate grading on the ASR expansion and damage of concrete. Cem. Concr. Res. 2017, 95, 75–83. [Google Scholar] [CrossRef]
- Yilmaz, E.; Benzaazoua, M.; Bussière, B.; Kesimal, A.; Ercikdi, B. Influence of disposal configurations on hydrogeological behaviour of sulphidic paste tailings: A field experimental study. Int. J. Miner. Process. 2014, 131, 12–25. [Google Scholar] [CrossRef]
- Ke, X.; Zhou, X.; Wang, X.; Wang, T.; Hou, H.B.; Zhou, M. Effect of tailings fineness on the pore structure development of cemented paste backfill. Constr. Build. Mater. 2016, 126, 345–350. [Google Scholar] [CrossRef]
- Kesimal, A.; Ercikdi, B.; Yilmaz, E. The effect of desliming by sedimentation on paste backfill performance. Miner. Eng. 2003, 16, 1009–1011. [Google Scholar] [CrossRef]
- Wu, J.Y.; Feng, M.M.; Chen, Z.Q.; Mao, X.B.; Han, G.S.; Wang, Y.M. Particle size distribution effects on the strength characteristic of cemented paste backfill. Minerals 2018, 8, 322. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.X.; Zhou, N.; Huang, Y.L. Effect of Particle Size on the Energy Evolution of Crushed Waste Rock in Coal Mines. Rock Mech. Rock Eng. 2017, 50, 1–8. [Google Scholar] [CrossRef]
- Koohestani, B.; Koubaa, A.; Belem, T.; Bussière, B.; Bouzahzah, H. Experimental investigation of mechanical and microstructural properties of cemented paste backfill containing maple-wood filler. Constr. Build. Mater. 2016, 121, 222–228. [Google Scholar] [CrossRef]
- Ercikdi, B.; Cihangir, F.; Kesimal, A.; Deveci, H.; Alp, İ. Utilization of water-reducing admixtures in cemented paste backfill of sulphide-rich mill tailings. J. Hazard. Mater. 2010, 179, 940–946. [Google Scholar] [CrossRef] [PubMed]
- Koohestani, B.; Darban, A.K.; Mokhtari, P. A comparison between the influence of superplasticizer and organosilanes on different properties of cemented paste backfill. Constr. Build. Mater. 2018, 173, 180–188. [Google Scholar] [CrossRef]
- Koohestani, B.; Bussière, B.; Belem, T.; Koubaa, A. Influence of polymer powder on properties of cemented paste backfill. Int. J. Min. Process. 2017, 167, 1–8. [Google Scholar] [CrossRef]
- Koohestani, B. Effect of saline admixtures on mechanical and microstructural properties of cementitious matrices containing tailings. Constr. Build. Mater. 2017, 156, 1019–1027. [Google Scholar] [CrossRef]
- Pourjavadi, A.; Fakoorpoor, S.M.; Hosseini, P.; Khaloo, A. Interactions between superabsorbent polymers and cement-based composites incorporating colloidal silica nanoparticles. Cem. Concr. Compos. 2013, 37, 196–204. [Google Scholar] [CrossRef]
- Koohestani, B.; Belem, T.; Koubaa, A.; Bussière, B. Experimental investigation into the compressive strength development of cemented paste backfill containing Nano-silica. Cem. Concr. Compos. 2016, 72, 180–189. [Google Scholar] [CrossRef]
- Jongpradist, P. Effective Void Ratio for Assessing the Mechanical Properties of Cement-Clay Admixtures at High Water Content. J. Geotech. Geoenviron. 2011, 137, 621–627. [Google Scholar] [CrossRef]
- Ercikdi, B.; Külekci, G.; Yilmaz, T. Utilization of granulated marble wastes and waste bricks as mineral admixture in cemented paste backfill of sulphide-rich tailings. Constr. Build. Mater. 2015, 93, 573–583. [Google Scholar] [CrossRef]
- Fall, M.; Célestin, J.C.; Pokharel, M.; Touré, M. A contribution to understanding the effects of curing temperature on the mechanical properties of mine cemented tailings backfill. Eng. Geol. 2010, 114, 397–413. [Google Scholar] [CrossRef]
- Wu, D.; Fall, M.; Cai, S.J. Coupling temperature, cement hydration and rheological behaviour of fresh cemented paste backfill. Miner. Eng. 2013, 42, 76–87. [Google Scholar] [CrossRef]
- Jiang, H.Q.; Fall, M.; Cui, L. Freezing behaviour of cemented paste backfill material in column experiments. Constr. Build. Mater. 2017, 30, 837–846. [Google Scholar] [CrossRef]
- Fall, M.; Pokharel, M. Coupled effects of sulphate and temperature on the strength development of cemented tailings backfills: Portland cement-paste backfill. Cem. Concr. Compos. 2010, 32, 819–828. [Google Scholar] [CrossRef]
- Cui, L.; Fall, M. Mechanical and thermal properties of cemented tailings materials at early ages: Influence of initial temperature, curing stress and drainage conditions. Constr. Build. Mater. 2016, 125, 553–563. [Google Scholar] [CrossRef]
- Fall, M.; Samb, S.S. Effect of high temperature on strength and microstructural properties of cemented paste backfill. Fire Saf. J. 2009, 44, 642–651. [Google Scholar] [CrossRef]
- Ghirian, A.; Fall, M. Coupled thermo-hydro-mechanical-chemical behaviour of cemented paste backfill in column experiments. Part II: Physical, hydraulic and thermal processes and characteristics. Eng. Geol. 2013, 164, 195–207. [Google Scholar] [CrossRef]
- Jiang, H.; Fall, M.; Liang, C. Yield stress of cemented paste backfill in sub-zero environments: Experimental results. Miner. Eng. 2016, 92, 141–150. [Google Scholar]
- Yilmaz, E.; Belem, T.; Benzaazoua, M. Effects of curing and stress conditions on hydromechanical, geotechnical and geochemical properties of cemented paste backfill. Eng. Geol. 2014, 168, 23–37. [Google Scholar] [CrossRef]
- Cihangir, F.; Ercikdi, B.; Kesimal, A.; Deveci, H.; Erdemir, F. Paste backfill of high-sulphide mill tailings using alkali-activated blast furnace slag: Effect of activator nature, concentration and slag properties. Miner. Eng. 2015, 83, 117–127. [Google Scholar] [CrossRef]
- Yilmaz, E.; Benzaazoua, M.; Belem, T.; Bussière, B. Effect of curing under pressure on compressive strength development of cemented paste backfill. Miner. Eng. 2009, 22, 772–785. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Benzaazoua, M. One-dimensional consolidation parameters of cemented paste backfills. Miner. Resour. Manag. 2012, 28, 29–45. [Google Scholar]
- Yilmaz, E.; Belem, T.; Bussière, B.; Benzaazoua, M. Relationships between microstructural properties and compressive strength of consolidated and unconsolidated cemented paste backfills. Cem. Concr. Compos. 2011, 33, 702–715. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Bussière, B.; Mbonimpa, M.; Benzaazoua, M. Curing time effect on consolidation behaviour of cemented paste backfill containing different cement types and contents. Constr. Build. Mater. 2015, 75, 99–111. [Google Scholar] [CrossRef]
- Cao, S.; Song, W.D. Effect of filling interval time on the mechanical strength and ultrasonic properties of cemented coarse tailing backfill. Int. J. Miner. Process. 2017, 166, 62–68. [Google Scholar] [CrossRef]
- Cao, S.; Yilmaz, E.; Song, W.D. Evaluation of Viscosity, Strength and Microstructural Properties of Cemented Tailings Backfill. Minerals 2018, 8, 352. [Google Scholar] [CrossRef]
- Miao, X.X.; Zhang, J.X.; Feng, M.M. Waste-filling in fully-mechanized coal mining and its application. J. China Univ. Min. Technol. 2008, 18, 479–482. [Google Scholar] [CrossRef]
- Huang, G.; Kulatilake, P.H.S.W.; Shreedharan, S.; Cai, S.J.; Song, H.Q. 3-D discontinuum numerical modeling of subsidence incorporating ore extraction and backfilling operations in an underground iron mine in China. Int. J. Min. Sci. Technol. 2017, 27, 191–201. [Google Scholar] [CrossRef]
- An, B.F.; Miao, X.X.; Zhang, J.X.; Ju, F.; Zhou, N. Overlying strata movement of recovering standing pillars with solid backfilling by physical simulation. Int. J. Min. Sci. Technol. 2016, 26, 301–307. [Google Scholar] [CrossRef]
- Sari, D.; Pasamehmetoglu, A.G. The effects of gradation and admixture on the pumice lightweight aggregate concrete. Cem. Concr. Res. 2005, 35, 936–942. [Google Scholar] [CrossRef]
- Bosiljkov, V.B. SCC mixes with poorly graded aggregate and high volume of limestone filler. Cem. Concr. Res. 2003, 33, 1279–1286. [Google Scholar] [CrossRef]
- Wu, J.Y.; Feng, M.M.; Yu, B.Y.; Chen, Z.Q.; Mao, X.B.; Han, G.S. Experimental study of strength and deformation characteristics of cemented waste rock backfills with continuous gradation. Rock Soil Mech. 2017, 38, 101–108. [Google Scholar]
- Ma, D.; Rezania, M.; Yu, H.; Bai, H. Variations of hydraulic properties of granular sandstones during water inrush: Effect of small particle migration. Eng. Geol. 2017, 217, 61–70. [Google Scholar] [CrossRef]
- Cao, S.; Song, W.D.; Yilmaz, E. Influence of structural factors on uniaxial compressive strength of cemented tailings backfill. Constr. Build. Mater. 2018, 174, 190–201. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Benzaazoua, M. Specimen size effect on strength behavior of cemented paste backfills subjected to different placement conditions. Eng. Geol. 2015, 185, 52–62. [Google Scholar] [CrossRef]
- ASTM C192/C192M-13a, Standard Practice for Making and Curing Concrete Test Specimens in the Laboratory; ASTM International: West Conshohocken, PA, USA, 2013; Available online: http://dx.doi.org/10.1520/C0192_C0192M-13A (accessed on 19 September 2016).
- Ulusay, R. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Darlignton, W.J.; Ranjith, P.G.; Choi, S.K. The effect of specimen size on strength and other properties in lab testing of rock and rock-like cementitious brittle materials. Rock Mech. Rock Eng. 2011, 44, 513–529. [Google Scholar] [CrossRef]
- Ma, D.; Zhou, Z.; Wu, J.; Li, Q.; Bai, H. Grain Size Distribution Effect on the Hydraulic Properties of Disintegrated Coal Mixtures. Energies 2017, 10, 612. [Google Scholar]
- Feng, M.M.; Wu, J.Y.; Ma, D.; Ni, X.Y.; Yu, B.Y.; Chen, Z.Q. Experimental investigation on seepage property of saturated broken red sandstone of continuous gradation. Bull. Eng. Geol. Environ. 2018, 77, 1167–1178. [Google Scholar] [CrossRef]
- Talbot, A.N.; Richart, F.E. The Strength of Concrete and Its Relation to the Cement, Aggregate and Water; University of Illinois Engineering Experiment Station: Urbana, IL, USA, 1923; Volume 137, pp. 1–118. [Google Scholar]
- Diamond, S. The patch microstructure in concrete: Effect of mixing time. Cement. Concr. Res. 2005, 35, 1014–1016. [Google Scholar] [CrossRef]
- Dollimore, D.; Mangabhai, R.J. Effect of mixing time on heat evolution pattern of cement pastes. Thermochim. Acta 1985, 85, 223–226. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Taheri, A.; Deng, J.; Ke, B. Effects of superplasticizer on the hydration, consistency, and strength development of cemented paste backfill. Minerals 2018, 8, 381. [Google Scholar] [CrossRef]
- Ghirian, A.; Fall, M. Coupled behavior of cemented paste backfill at early ages. Geotech. Geol. Eng. 2015, 33, 1141–1166. [Google Scholar] [CrossRef]
- Ghirian, A.; Fall, M. Strength evolution and deformation behaviour of cemented paste backfill at early ages: Effect of curing stress, filling strategy and drainage. Int. J. Min. Sci. Technol. 2016, 26, 809–817. [Google Scholar] [CrossRef]
- Wu, J.Y.; Feng, M.M.; Yu, B.Y.; Han, G.S. The length of pre-existing fissures effects on the mechanical properties of cracked red sandstone and strength design in engineering. Ultrasonics 2018, 82, 188–199. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.Y.; Chen, Z.Q.; Feng, M.M.; Wang, Y.M.; Han, G.S. The length of pre-existing fissure effects on the dilatancy behavior, acoustic emission, and strength characteristics of cracked sandstone under different confining pressures. Environ. Earth. Sci. 2018, 77, 430. [Google Scholar] [CrossRef]
- Hoek, E. Estimating Mohr-Coulomb friction and cohesion values from the Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 227–229. [Google Scholar] [CrossRef]
- Zhang, J.X.; Jiang, H.Q.; Deng, X.J.; Ju, F. Prediction of the height of the water-conducting zone above the mined panel in solid backfill mining. Mine Water Environ. 2014, 33, 317–326. [Google Scholar] [CrossRef]
- Zhang, J.X.; Miao, X.X.; Guo, G.L. Consolidated Solid Backfill Mining Method and Its Applications; Science Press: Beijing, China, 2015. [Google Scholar]
- Zhang, J.X.; Ju, F.; Zhou, N. Extract Room Mining Pillars Using Solid Backfill Mining Technology: Theories and Methods; Science Press: Beijing, China, 2015. [Google Scholar]
- Ju, F.; Zhang, J.X.; Zhang, Q. Vertical transportation system of solid material for backfilling coal mining technology. Int. J. Min. Sci. Technol. 2012, 22, 41–45. [Google Scholar] [CrossRef]


| Varieties (%) | Al2O3 | CaO | Fe | Fe2O3 | K2O | MgO | Na2O | SiO2 | SO3 | TiO2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Waste rock | 13.21 | 3.91 | 3.69 | - | 0.02 | 2.87 | - | 67.75 | - | - |
| P.C. 32.5R | 4.67 | 62.19 | - | 3.69 | 0.68 | 2.87 | 0.21 | 21.56 | 1.91 | 0.16 |
| n | Mass (g) of Particles in Different Sizes (mm) | Mass Percent (%) of Particles in Different Sizes (mm) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–0.5 | 0.5–1.0 | 1.0–1.5 | 1.5–2.5 | 2.5–5.0 | 5.0–8.0 | 8.0–10.0 | 0–0.5 | 0.5–1.0 | 1.0–1.5 | 1.5–2.5 | 2.5–5 | 5.0–8.0 | 8.0–10.0 | |
| 0.2 | 164.78 | 24.51 | 15.99 | 22.08 | 33.81 | 25.74 | 13.09 | 54.93 | 8.17 | 5.33 | 7.36 | 11.27 | 8.58 | 4.36 |
| 0.4 | 90.51 | 28.92 | 21.03 | 31.84 | 55.05 | 47.03 | 25.62 | 30.17 | 9.64 | 7.01 | 10.61 | 18.35 | 15.68 | 8.54 |
| 0.6 | 49.72 | 25.64 | 20.76 | 34.47 | 67.34 | 64.48 | 37.59 | 16.57 | 8.55 | 6.92 | 11.49 | 22.45 | 21.49 | 12.53 |
| 0.8 | 27.31 | 20.23 | 18.22 | 33.20 | 73.34 | 78.65 | 49.05 | 9.10 | 6.74 | 6.07 | 11.07 | 24.45 | 26.22 | 16.35 |
| Talbot Index | Type of Cementing Material | Content of Cementing Material m/g | Content of Distilled Water v/mL |
|---|---|---|---|
| 0.2 | Cement | 30 | 22.5 |
| 0.4 | Cement | 30 | 22.5 |
| 0.6 | Cement | 30 | 22.5 |
| 0.8 | Cement | 30 | 22.5 |
| n | Relationship | Correlation Coefficient |
|---|---|---|
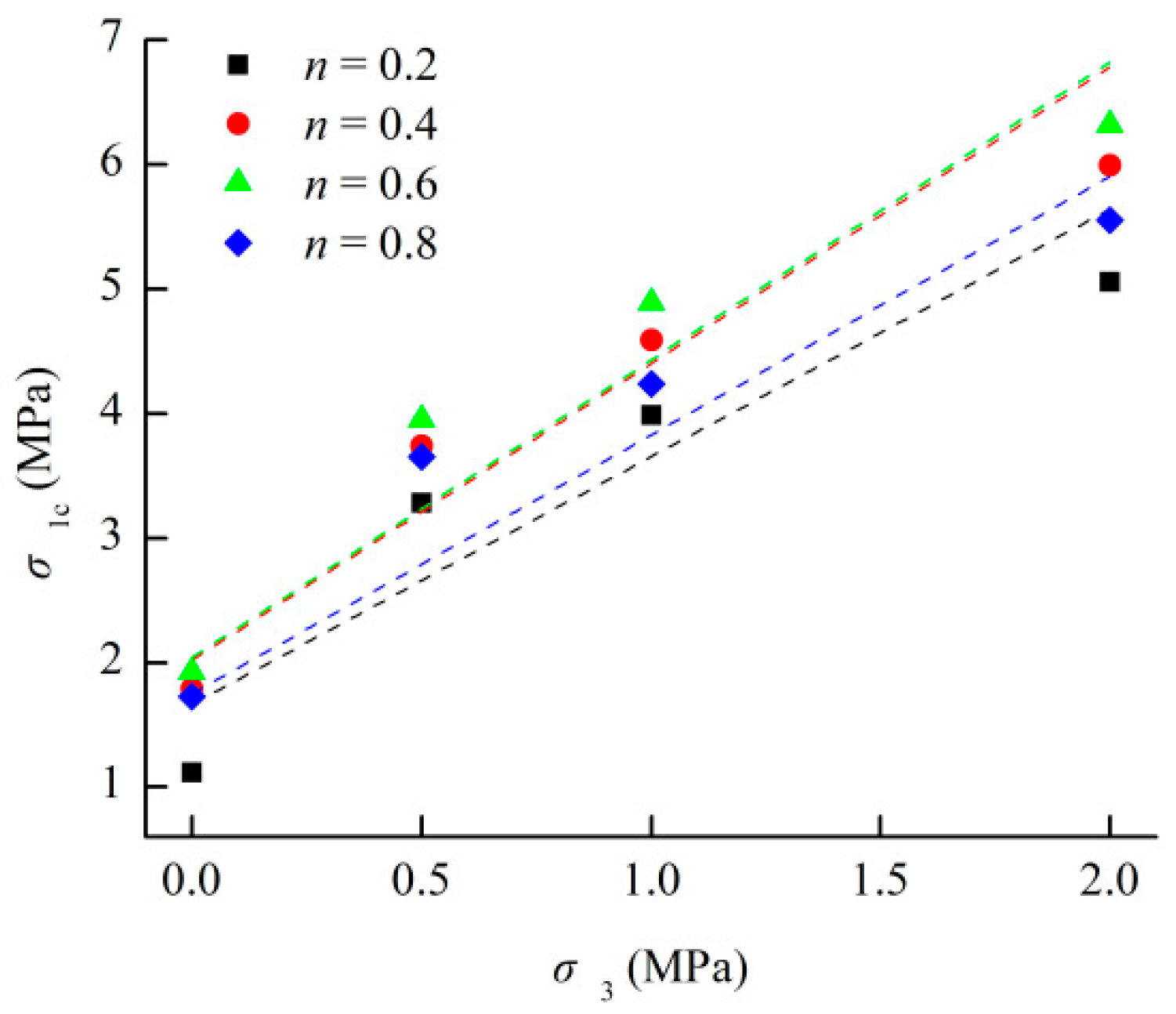
| 0.2 | σ1c = 1.9897σ3 + 1.6648 | 0.9043 |
| 0.4 | σ1c = 2.3832σ3 + 2.0175 | 0.8981 |
| 0.6 | σ1c = 2.3916σ3 + 2.0385 | 0.9461 |
| 0.8 | σ1c = 2.0791σ3 + 1.7497 | 0.9160 |
| Mechanical Parameter | Relationship | Correlation Coefficient |
|---|---|---|
| 0.9999 | ||
| 0.8232 | ||
| 0.9689 | ||
| 0.9577 | ||
| 0.9160 | ||
| 0.9719 | ||
| 0.9999 | ||
| 0.9934 | ||
| 0.8247 |
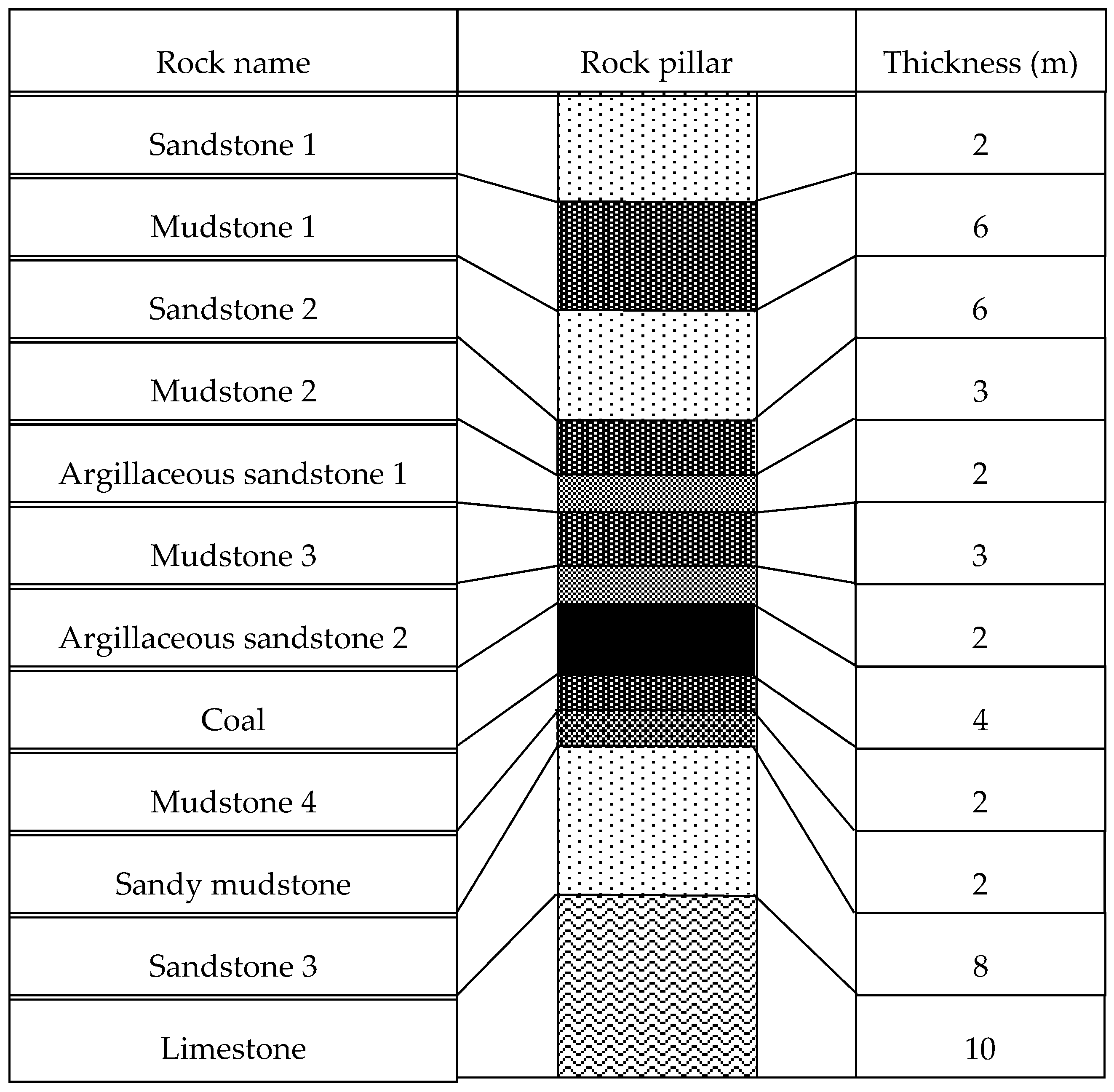
| Strata | Height (m) | Density (kg/m−3) | Es (MPa) | μ | φ (°) | c (MPa) | σt (MPa) |
|---|---|---|---|---|---|---|---|
| Sandstone 1 | 2 | 2590 | 5300 | 0.28 | 34 | 9.5 | 6.1 |
| Mudstone 1 | 6 | 2460 | 3100 | 0.32 | 28 | 5.9 | 2.2 |
| Sandstone 2 | 6 | 2660 | 4600 | 0.27 | 37 | 9.7 | 6.6 |
| Mudstone 2 | 3 | 2470 | 3700 | 0.31 | 27 | 5.9 | 2.7 |
| Argillaceous sandstone 1 | 2 | 2550 | 4500 | 0.27 | 29 | 7.0 | 3.9 |
| Mudstone 3 | 3 | 2450 | 3800 | 0.30 | 28 | 5.9 | 2.8 |
| Argillaceous sandstone 2 | 2 | 2650 | 4900 | 0.27 | 32 | 13.8 | 7.7 |
| Coal | 4 | 1600 | 1910 | 0.33 | 22 | 2.5 | 1.5 |
| Mudstone 4 | 2 | 2500 | 3300 | 0.31 | 31 | 5.3 | 3.2 |
| Sandy mudstone | 2 | 2600 | 8900 | 0.28 | 33 | 6.9 | 4.3 |
| Sandstone 3 | 8 | 2700 | 13,200 | 0.25 | 36 | 12.8 | 7.5 |
| Limestone | 10 | 2750 | 27,900 | 0.22 | 47 | 15.9 | 9.5 |
| Cemented Rockfill | Height (m) | Density (kg/m−3) | Es (MPa) | μ | φ (°) | c (MPa) | σt (MPa) |
|---|---|---|---|---|---|---|---|
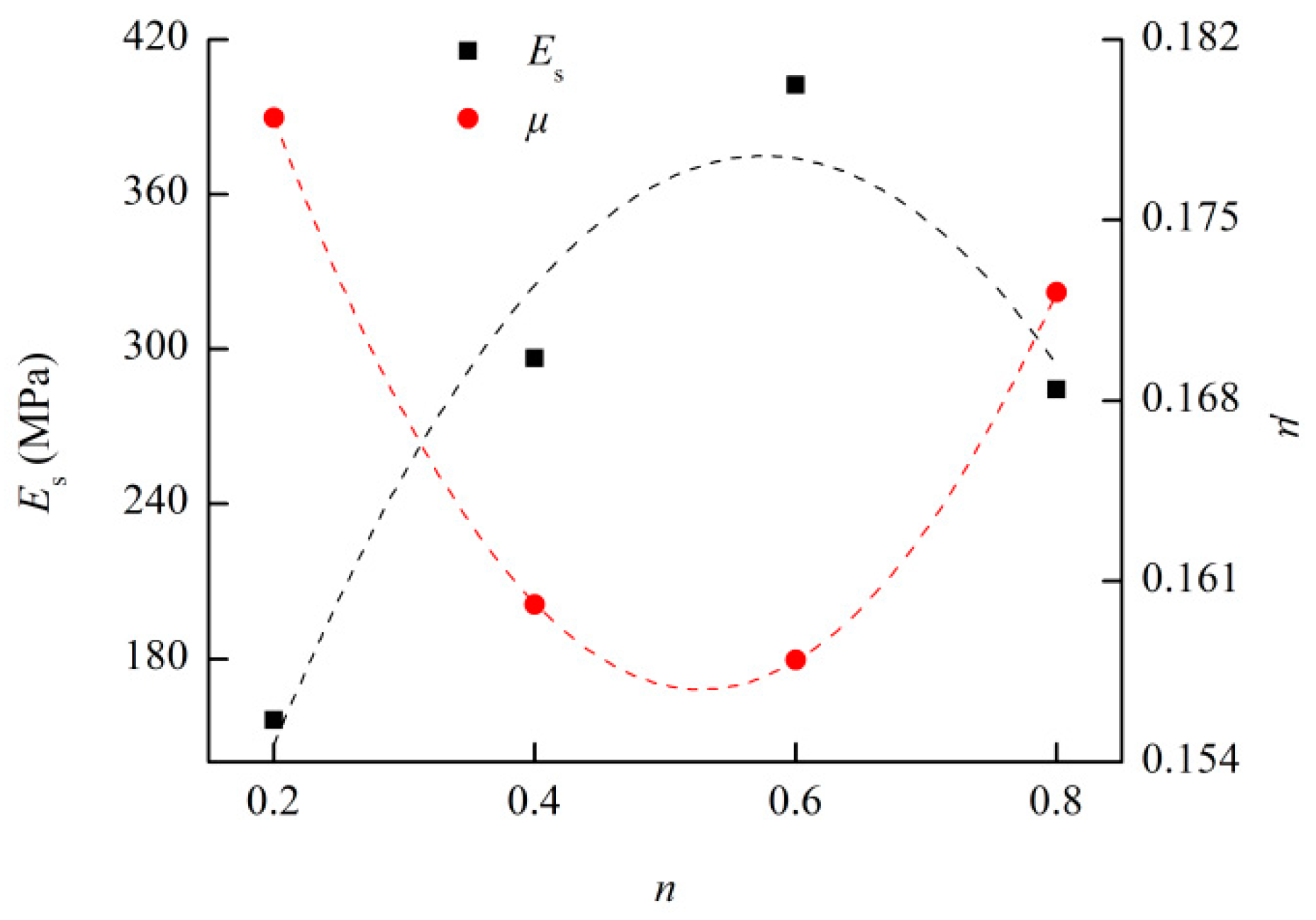
| n = 0.2 | 4 | 1795 | 156.1705 | 0.1790 | 19.3317 | 0.5901 | 0.8367 |
| n = 0.4 | 4 | 1795 | 296.4508 | 0.1601 | 24.1322 | 0.6534 | 0.8466 |
| n = 0.6 | 4 | 1795 | 402.4365 | 0.1580 | 24.2242 | 0.6591 | 0.8524 |
| n = 0.8 | 4 | 1795 | 284.4737 | 0.1722 | 20.5154 | 0.6067 | 0.8416 |
| Mining Distance (MPa) | Relationship | Correlation Coefficient |
|---|---|---|
| 40 | Zmax = −0.4403n2 + 0.5100n − 0.2480 | 0.9770 |
| 80 | Zmax = −1.0968n2 + 1.2809n − 0.5250 | 0.9968 |
| 120 | Zmax = −1.4309n2 + 1.6766n − 0.6512 | 0.9997 |
| Mining Distance (MPa) | Relationship | Correlation Coefficient |
|---|---|---|
| 40 | σzz max = −20.9000n2 + 24.2344n + 1.9649 | 0.9776 |
| 80 | σzz max = −15.3538n2 + 17.9621n + 7.9208 | 0.9741 |
| 120 | σzz max = −12.4038n2 + 14.0005n + 10.0938 | 0.9962 |
| Mining Distance (MPa) | Relationship | Correlation Coefficient |
|---|---|---|
| 40 | σzz max = 38.3988n2 − 43.9721n + 40.2200 | 0.8551 |
| 80 | σzz max = 55.1113n2 − 64.2664n + 46.7808 | 0.9784 |
| 120 | σzz max = 59.5725n2 − 69.4488n + 48.8251 | 0.9988 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Feng, M.; Xu, J.; Qiu, P.; Wang, Y.; Han, G. Particle Size Distribution of Cemented Rockfill Effects on Strata Stability in Filling Mining. Minerals 2018, 8, 407. https://doi.org/10.3390/min8090407
Wu J, Feng M, Xu J, Qiu P, Wang Y, Han G. Particle Size Distribution of Cemented Rockfill Effects on Strata Stability in Filling Mining. Minerals. 2018; 8(9):407. https://doi.org/10.3390/min8090407
Chicago/Turabian StyleWu, Jiangyu, Meimei Feng, Jingmin Xu, Peitao Qiu, Yiming Wang, and Guansheng Han. 2018. "Particle Size Distribution of Cemented Rockfill Effects on Strata Stability in Filling Mining" Minerals 8, no. 9: 407. https://doi.org/10.3390/min8090407
APA StyleWu, J., Feng, M., Xu, J., Qiu, P., Wang, Y., & Han, G. (2018). Particle Size Distribution of Cemented Rockfill Effects on Strata Stability in Filling Mining. Minerals, 8(9), 407. https://doi.org/10.3390/min8090407






