Multiscale Computational Simulation of Amorphous Silicates’ Structural, Dielectric, and Vibrational Spectroscopic Properties

Abstract

Silicates are among the most abundant and important inorganic materials, not only in the Earth’s crust, but also in the interstellar medium in the form of micro/nanoparticles or embedded in the matrices of comets, meteorites, and other asteroidal bodies. Although the crystalline phases of silicates are indeed present in nature, amorphous forms are also highly abundant. Here, we report a theoretical investigation of the structural, dielectric, and vibrational properties of the amorphous bulk for forsterite (Mg₂SiO₄) as a silicate test case by a combined approach of classical molecular dynamics (MD) simulations for structure evolution and periodic quantum mechanical Density Functional Theory (DFT) calculations for electronic structure analysis. Using classical MD based on an empirical partial charge rigid ionic model within a melt-quenching scheme at different temperatures performed with the GULP 4.0 code, amorphous bulk structures for Mg₂SiO₄ were generated using the crystalline phase as the initial guess. This has been done for bulk structures with three different unit cell sizes, adopting a super-cell approach; that is, 1 × 1 × 2, 2 × 1 × 2, and 2 × 2 × 2. The radial distribution functions indicated a good degree of amorphization of the structures. Periodic B3LYP-geometry optimizations performed with the CRYSTAL14 code on the generated amorphous systems were used to analyze their structure; to calculate their high-frequency dielectric constants (ε_∞); and to simulate their IR, Raman, and reflectance spectra, which were compared with the experimental and theoretical crystalline Mg₂SiO₄. The most significant changes of the physicochemical properties of the amorphous systems compared to the crystalline ones are presented and discussed (e.g., larger deviations in the bond distances and angles, broadening of the IR bands, etc.), which are consistent with their disordered nature. It is also shown that by increasing the unit cell size, the bulk structures present a larger degree of amorphization.

1. Introduction

Amorphous materials are disordered solid-state systems that present a lack of long-range order, and from a thermodynamic standpoint, they are less stable than the corresponding crystalline structures. As a consequence of this long-range structural disorganization, amorphous materials usually exhibit different properties with respect to their crystalline counterparts. This is the case, for instance, for silica [1]. Whereas crystalline silica presents cytotoxicity when in contact with cellular systems [2,3,4,5], amorphous silica particles show high levels of biocompatibility [6], thus allowing them to be used in bioglass-based implants [7] and as drug delivery systems [8]. In other cases, because of the different physicochemical properties between the crystalline and the amorphous partners, the amorphous phases are preferable to be used in semiconductor devices, such as the case of HfO₂ and ZrO₂ and their alloys [9,10,11].

The understanding and the prediction of the physicochemical properties of noncrystalline solids rely on the proper description of their structure at the atomic level. Experimental techniques with this purpose are X-ray and neutron diffraction, which are directly sensitive to the structure, and also vibrational-related spectroscopies such as infrared (IR) and Raman, in which detailed structural information can be achieved. However, an atomic-level understanding of amorphous materials derived from these experimental methods has so far remained elusive, in part because of the limited capabilities of the instrumentation for direct characterization. For instance, crystalline silicates exhibit a wealth of narrow IR bands [12,13], whereas for amorphous silicates, these bands result in a significant broadening and blending due to the wide range of bond lengths and angles characteristic of the amorphous nature [14,15,16]. Thus, deriving detailed structural information by means of these experimental techniques is a daunting task. A complimentary tool with which to obtain atomistic details of the structure of amorphous systems and their relationships with their physicochemical features such as spectral signatures is the theoretical modeling approach. However, in contrast to crystalline systems, theoretical studies of the structure of amorphous materials are quite limited, probably because of the difficulty in generating realistic and reliable structural models with the available theoretical methods [17,18]. Among the different strategies to generate bulk amorphous structures, the melt-and-quench scheme has successfully been used to simulate different amorphous oxides [10,18,19,20,21,22,23,24,25,26]. This scheme consists of performing molecular dynamics (MD) simulations, taking the crystalline bulks as the initial guess and submitting them to a series of heating/cooling cycles. The heating at high temperatures followed by rapid cooling allows the sampling of the large configurational spaces and ensures a good degree of amorphization of the initial crystalline systems. However, the simulation of amorphous structures typically requires systems with more than 100 atoms per unit cell. Accordingly, despite the enormous growth in computational power, generating highly disordered materials adopting the melt-and-quench scheme approach by means of first-principles MD simulations are often prohibitively expensive, so the simulation timescales are limited to several picoseconds, which are relatively short in terms of the time frame for evolution into the amorphous structures. As an alternative, classical force field MD simulations are computationally less expensive, thus allowing larger timescales of up to several hundred picoseconds. By contrast, these classical MD simulations require accurate and reliable interatomic potentials, since the results are biased by the employed force fields. Proceeding this way, first-principles calculations onto the generated structural models are subsequently mandatory if the electronic structure and spectroscopic properties are desired.

Silicate-based materials constitute ca. 95 percent of the rocks of the Earth’s crust [27]. Silicates are inorganic materials whose main feature is the orthosilicate [SiO₄]⁴⁻ building block. The negative net electrical charge is compensated by metal cations. The ways how the different tetrahedral [SiO₄]⁴⁻ units are linked (i.e., sharing corners, edges, and faces) and the nature of the countercations give rise to the wide class of silicate structures. The wide presence of silicates is not only limited to the Earth’s crust; they are also major components of the solid matter present in the universe, comprising a part of interstellar, circumstellar, and interplanetary dust particles; comets; and meteorites [28,29,30]. The most astrophysically important silicate groups are olivines and pyroxenes, with the preponderance of Mg²⁺ and Fe²⁺ as countercations, since they appear with the highest cosmic abundance. Olivines are characterized to have the [SiO₄]⁴⁻ tetrahedra linked by Mg²⁺ and Fe²⁺ and the general formula Mg_2xFe_(2−2x)SiO₄ (x = 0–1), with the two end members named forsterite (Mg₂SiO₄) and fayalite (Fe₂SiO₄); whereas pyroxenes are formed by single chains of [SiO₄]⁴⁻ intercalated by the divalent cations and have the general formula Mg_xFe_(1−x)SiO₃ (x = 0–1), with the two end members named enstatite (MgSiO₃) and ferrosilite (FeSiO₃). In contrast to the terrestrial silicates, cosmic silicates are mainly found in an amorphous state [28,31], probably due to their exposure with various processes during their life cycle such as incident cosmic rays and UV radiation, thermal shocks, or sputtering/shattering effects. Cosmic silicates play a significant role in the chemical evolution occurring in space as they provide the surfaces where important chemical reactions can take place, such as the formation of H₂ [32] and H₂O [33,34]. On the other hand, both crystalline and amorphous silicates can be synthesized, with special efforts regarding forsterite. Synthetic crystalline forsterite was achieved for the first time by Shankland and coworkers [35] using the Verneuil flame fusion method for the solid-state reaction between powders of MgO and SiO₂. However, the crystals contained inclusions of unreacted MgO. Accordingly, this procedure has been improved (e.g., [36,37]) or modified (e.g., by mixing bauxite with MgCO₃ [38]), and alternative methods with enhanced qualities of the synthesized crystals have appeared, such as various sol–gel methods [39,40,41] and the application of modified Czochralski-pulling procedures; the latter providing large high-quality forsterite single nanocrystals [42,43,44]. Amorphous phases of forsterite can be synthesized by a variety of techniques: standard melt-and-quench methods [45,46,47], sol–gel reactions [48], sputtering techniques [49], and via energetic processing of the starting materials such as shocks [50] or collisions [51,52]. To produce amorphous silicate interstellar dust analogues, the processing of crystalline forsterite is usually performed [53,54,55]. The synthesized materials are characterized by standard solid-state techniques. X-ray diffraction (XRD) is useful to assess the degree of crystallinity and to analyze the phase pureness in crystalline samples [56,57,58]. X-ray absorption spectroscopy (XAS), including extended X-ray absorption fine structure (EXAFS) and X-ray absorption near edge structure (XANES), is an analytical technique to determine short- and medium-range order in partially amorphous forsterite samples. This technique has been useful to determine that bond lengths and angles within the SiO₄ tetrahedra are not affected by the structural state [48]. Infrared-based spectroscopy is also useful to characterize the structural state, since crystalline forsterite presents a group of sharp bands in the 200–1000 cm⁻¹ range [59,60], while amorphous phases present essentially two broad bands centered at about 1000 and 500 cm⁻¹ [61]. Scanning electronic microscopy (SEM) is used to analyze the surface morphology of forsterite powders, which can be diverse (e.g., spherical, chain-like, porous, dendritic, etc.) depending on the experimental preparation [56,62], while transmission electron microscopy (TEM) provides direct imaging of parts of the forsterite nanoparticle samples, thus allowing the measuring of their composition, shape, size, and the atomic arrangement [63,64,65]. Synthesized forsterite nanoparticles have potential applications in enhanced weathering, namely sequestering CO₂ by mineral reactions [66,67,68,69,70], and as a biomaterial for implants [71,72,73,74,75]. Moreover, doping the forsterite nanomaterials with Eu³⁺, Tb³⁺, or Er³⁺ induces enhancement of their photoluminescence properties [76,77,78], rendering them to have applications in optoelectronic devices.

The present work focuses on the theoretical modelling and electronic structure study of amorphous Mg₂SiO₄. Here, we combine classical MD simulations adopting the melt-and-quench scheme, for structural model generation, and DFT-based quantum mechanical (QM) calculations, for electronic structure analysis, to theoretically characterize the structural, dielectric, and spectroscopic properties of different amorphous silicate systems. Detailed analysis of the amorphous structures is carried out, including the coordination number and the radial distribution function of the systems. Geometry relaxations followed by calculation of the vibrational modes of the amorphous structural models serve to simulate the corresponding IR, Raman, and reflectance spectra at the B3LYP density functional level of theory by means of the periodic CRYSTAL14 ab initio code [79], which in turn are compared with the corresponding crystalline systems and the available experimental data. The presented results will be of great significance in the field of silicate chemistry. First, by matching the ab initio results with the experimental data, relationships between silicate spectral signatures and their atomistic structural details can be elucidated, which will be particularly useful for current and future astronomical archives (i.e., ALMA and the James Webb Space Telescope) and for the analysis of forthcoming results. Results will also be of importance for those studies devoted to the characterization of the spectroscopic properties of doped and/or modified forsterite nanomaterials, since we provide the reference spectroscopic properties of pure forsterite in both the crystalline and amorphous structural state. Finally, the work can also have repercussions from a computational point of view. Generating the bulk structure of forsterite in an amorphous state is the first step towards obtaining the surface slab models for the same material. Having reliable slab models is of great importance since it is the basis upon which to subsequently carry out surface chemical studies, such as adsorption phenomena and heterogeneous catalytic reactivity. Finally, our results will be very useful to improve the force field parameters devoted to simulating the structure of silicates in an amorphous state. Only reliable parameters for crystalline silicates are available hitherto, so the present results can be used as a benchmark for the parametrization and to assess the accuracy of the force field, both in the simulation of the structure as well as in the prediction of the solid-state properties.

2. Computational Methods

2.1. Classical Molecular Dynamics (MD) Simulations

The procedure to generate the amorphous silicate models is inspired by that done for simulated bioglasses [18,19,21]. All models were generated by means of classical molecular dynamics simulations using the atomistic Born model of solids [80] implemented in the General Utility Lattice program (GULP) [81]. This model represents all ions as point charges interacting through Coulomb forces. Pairwise Buckingham potentials were used to represent Pauli repulsion and dispersion interactions, and the polarization of oxygen was represented by the shell model. All the interatomic potential parameters used in this work are shown in

Table 1. Classical potential parameters used in this study. Sub-index c and s have been used to refer to the core and shell of the atoms.

Charges
Ions	Core	Shell	Core–shell interactions (eV Å−2)
Mg	+2.00000
Si	+4.00000
O	+0.84819	−2.84819	74.92
Buckingham Potential	A (eV)	ρ (Å)	C (eV Å6)
Mgc–Os	1428.500	0.31813	0.00000
Sic–Os	1283.907	0.32052	10.66158
Oc–Os	22,764.300	0.14900	27.88000
Three-Body Potential	k (eV rad−2)	Θ0 (degree)
Os–Sic–Os	2.097240	109.47000

, which were derived from these references [82,83,84]. Moreover, the bulk structure of the crystalline Mg₂SiO₄ system calculated with GULP using these parameters is in very good agreement with the experimental one (see Figure S1 and Table S1, Supplementary Materials). The classical molecular dynamics (MD) simulations were carried out within the (N,V,T) canonical ensemble. The leapfrog Verlet algorithm was adopted using an integration time-step of 1 fs. The velocity rescaling scheme was used to control the temperature. Although the pressure was not directly equilibrated, we controlled the pressure of the system along all the simulations and we did not detect any dramatic change in the pressure that could cause a warning alert or stop the execution of the simulations.

(1)

Nose–Hoover thermostat. A total of 17 different final temperatures were considered, between 400 K and 2000 K, separated by 100 K each. It is worth mentioning that higher temperatures than the melting point of Mg₂SiO₄ (at about 1800 K) would have been desirable to accelerate the dynamics of the melting. However, we found that with MD simulations at these temperatures (e.g., 2500 K), the system was unstable because the interatomic potential parameters fail. After the heating process, classical MD simulations at the (N,V,T) ensemble at the given temperature were performed, which consisted of a 100 ps equilibration phase and a 200 ps production phase.

(2)

Cooling phase: After the production phase of the previous step, the resulting systems were subjected to MD simulations where the temperature was decreased by 0.005 K every time-step to reach the temperature of 300 K. At this temperature, the systems were equilibrated for 50 ps.

(3)

Second thermal/production phase: The structures obtained after the cooling simulations were then heated again to the temperature chosen in the first step. Then, MD simulations with an equilibration phase of 100 ps and a production phase of 200 ps production were performed.

2.2. Quantum Mechanical (QM) Calculations

The resulting amorphous structures generated by the classical MD simulations were then optimized by means of periodic quantum mechanical calculations. To this end, simulations carried out with the CRYSTAL14 code [79] were performed, in which the crystalline orbitals representing the multielectron wave function are expressed by localized Gaussian-type orbitals (GTO). The following GTO basis set contractions were used: oxygen, (8s)–(411sp)–(1d); magnesium, (8s)–(511sp)–(1d); and silicon, (8s)–(6311sp)–(1d).

Self-Consistent Field (SCF) calculations and geometry optimizations were carried out using the hybrid B3LYP [85,86] DFT-based method. No symmetry was imposed during the geometry optimizations (i.e., P1 group symmetry), to enforce the maximum degrees of freedom in the optimization process. Both internal coordinates and lattice constants were optimized, using the Broyden−Fletcher−Goldfarb−Shanno (BFGS) algorithm [87]. All these technical details have already been used for the simulation of crystalline forsterite [88,89,90] and fayalite [91] bulk properties. Additional calculations have been done at B3LYP-D2, adopting the scheme proposed by Grimme [92] to include dispersion interactions and to check if they are of significance in the geometry optimization. Results (shown in Tables S1 and S2, Supplementary Materials) indicate that the inclusion of dispersion is, in practice, negligible; it systematically slightly reduces the internal bond lengths and the lattice distances compared to the pure B3LYP values, which in some cases (e.g., Mg–O distances), are shorter than the experimental values.

For the tolerances controlling the Coulomb and exchange series, the default values have been adopted; namely, (6 6) and (6 6 16), respectively. Accordingly, when the overlap between two atomic orbitals is smaller than 10⁻⁶ (for Coulomb) and 10⁻¹⁶ (for exchange), the integral is disregarded. The Brillouin zone is sampled by diagonalizing the Hamiltonian matrix in 63 reciprocal lattice points (k points), which corresponds to a shrinking factor of 5 [93]. The unrestricted formalism was adopted for the open-shell calculations.

Vibrational frequencies of the systems under study have been obtained as the eigenvalues of the diagonalized mass-weighted Hessian matrix considering the Γ point (i.e., the central zone, point k = 0 in the first Brillouin zone). The mass-weighted Hessian matrix was calculated via numerical differentiation of the analytical first energy derivatives, in which each 3N equilibrium nuclear coordinate was displaced by 0.003 Å. More details of the computational conditions and other numerical aspects concerning the calculation of the vibrational frequencies can be found in [94]. The infrared intensities were computed with the variation of the dipole moment along each normal mode, using, in this case, localized Wannier functions [95,96,97], whereas Raman intensities were calculated analytically through the coupled-perturbed Hartree-Fock (CPHF) scheme implemented in CRYSTAL [98,99] and successfully performed for different crystalline minerals [100,101,102,103,104,105,106,107,108]. The reflectance spectra (R(ν)) were simulated by first calculating different properties: (i) the vibrational frequencies, the corresponding intensities, and separation of the longitudinal and transverse optical modes [94,109]; (ii) the high-frequency dielectric tensor (ε_∞) [101,103,105,108], which contributes to the frequency-dependent complex dielectric function (ε(ν)) [98,99,110,111]; and (iii) the mass-weighted effective mode Born charges [112,113,114]. By combining all these ingredients, the reflectance spectra of several crystalline mineral systems have successfully been simulated [88,89,91,115,116,117].

3. Results and Discussion

This section is organized as follows. The first part addresses the generation of an amorphous bulk structure of forsterite (Mg₂SiO₄) by means of classical MD simulations and subsequent optimization at a quantum chemical level. A structural analysis of the optimized structure is presented, and investigations on its dielectric and vibrational properties by calculating the high-frequency dielectric constants and simulating the infrared, Raman, and reflectance spectra are shown, which in turn are compared with the experimental and theoretical crystalline Mg₂SiO₄ data. The second part is focused on the influence of the unit cell size of the amorphous Mg₂SiO₄ bulk on the structural, dielectric, and vibrational properties.

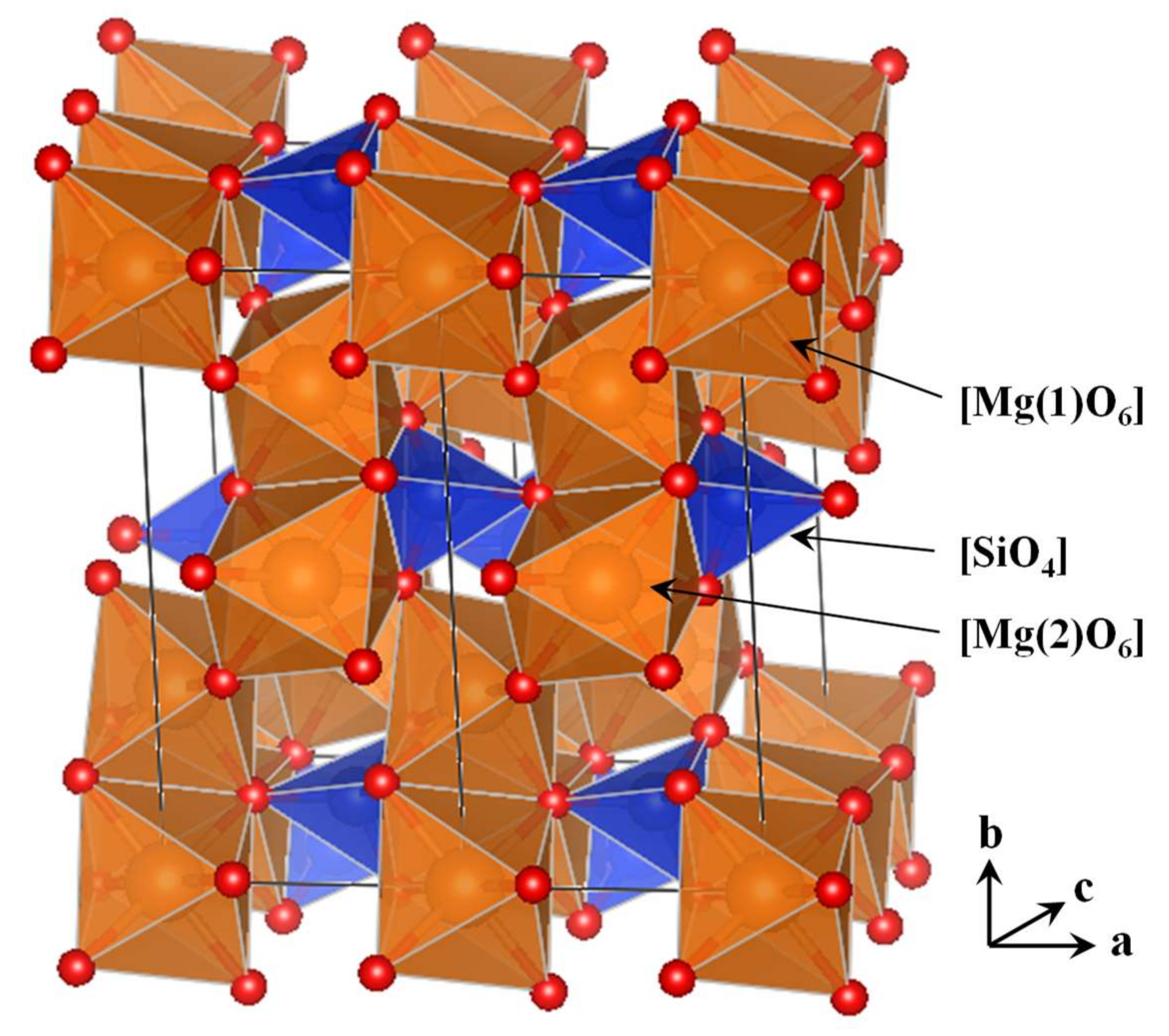
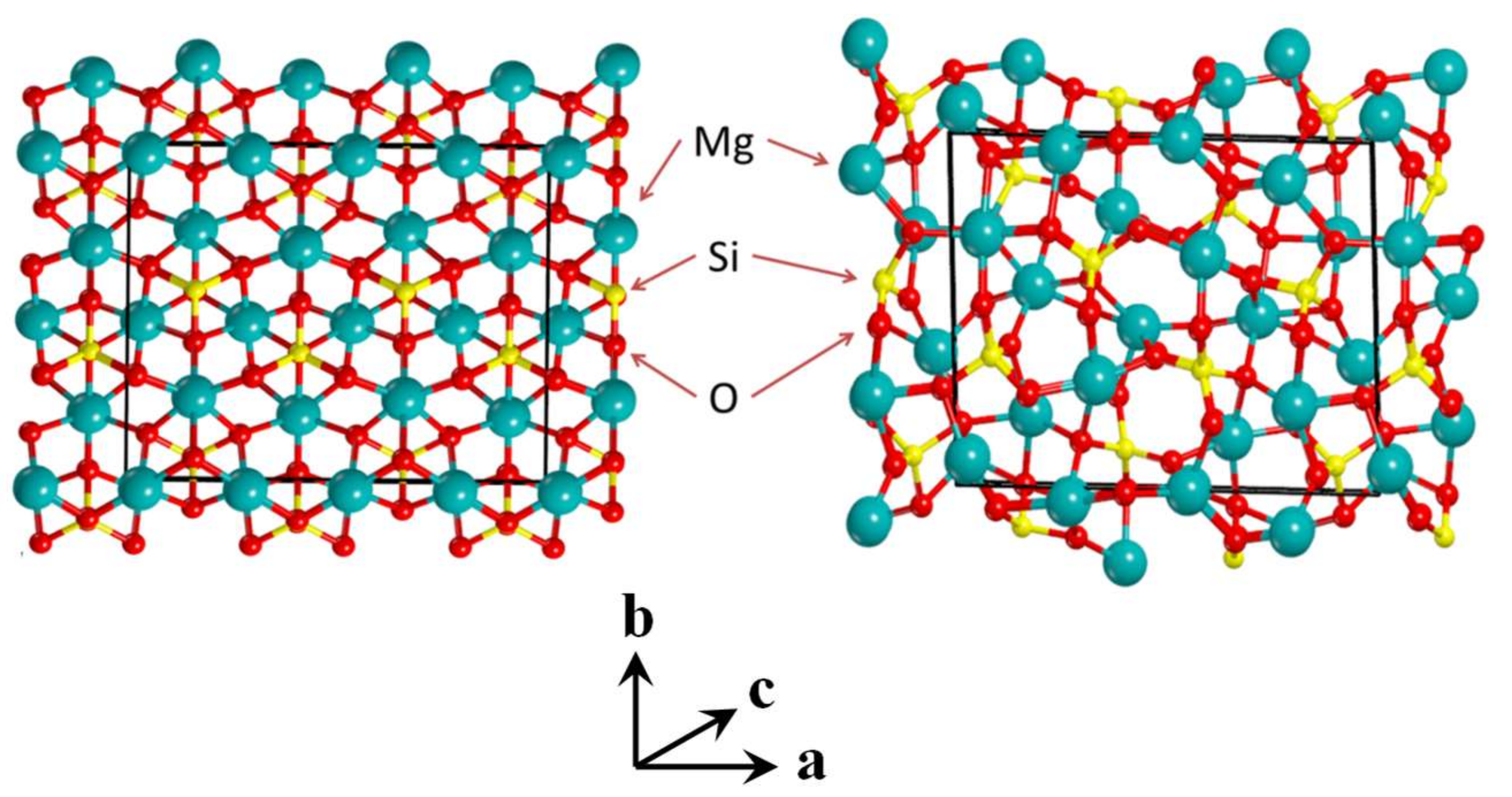
3.1. The Amorphous 1 × 1 × 2 Super-Cell Mg₂SiO₄ System

As mentioned in Computational Methods, the initial guess used to generate the amorphous Mg₂SiO₄ bulk structure (hereafter referred to as Fo) was the Mg₂SiO₄ crystalline system. The bulk crystal structure of Mg₂SiO₄ consists of distorted SiO₄ and MgO₆ units that share their vertices (see Figure 1). Two symmetry-independent Mg atoms (referred to as Mg1 and Mg2 in Figure 1) are present in the crystal system. The Mg1-centered octahedra share edges, forming rods parallel to the crystallographic c axis, while the Mg2-centered octahedra link these rods through their edges (see Figure 1).

Classical MD simulations at different temperatures adopting the procedure described in Computational Methods were executed to amorphize the structure of crystalline Mg₂SiO₄. As the primitive unit cell is small (Pbnm space symmetry with lattice parameters of a = 4.79 Å, b = 10.19 Å, and c = 5.85 Å), in this part, a larger unit cell has been adopted by doubling the c lattice parameter to favor an easier amorphization of the structure (hereafter referred to as 1 × 1 × 2). In the next section, a detailed analysis of the effect of the unit cell size on the physicochemical properties of the amorphous structures is presented. Figure 2 shows the resulting structures at the end of the simulations run at the different temperatures. As one can see, the initial crystallinity becomes lost when increasing the temperatures. Figure 3 shows the pair correlation functions, g(r), for the Mg atoms with either the neighboring Mg atoms (a, Mg–Mg) or the O atoms (b, Mg–O), derived from the simulations at T = 300, 700, 900, 1200, 1500, and 1800 K. It is worth mentioning that the g(r) curves should tend to 1 at long ranges. However, due to the relatively small size of the unit cell, if we account for the periodic boundary conditions (PBC), g(r) curves are limited to ca. 3.5 Å, hampering us in providing significant information. These g(r) curves are shown in Figure S2 (Supplementary Materials). Therefore, in order to extend the g(r) curves beyond the limits of the unit cell, we did not consider the PBC and hence, the g(r) curves are not forced to tend to 1. In our particular case, they tend to 0 as a consequence of the absence of replica images (i.e., equivalent atomic positions) when the pair correlation functions were calculated. At 300 K, the g(r) functions first present a sharp peak, followed by a subset of lower well-defined peaks, in agreement with the crystalline nature of Fo at this temperature. The first peak is representative of the Mg–Mg and Mg–O lengths of the first shell, while the others represent the distribution of the Mg–Mg and Mg–O distances of the outer shells. An increase of the temperature produces a broader profile of g(r), in which the first peak significantly loses intensity, while the others overlap each other up to a point where at high temperatures, only two broad peaks are appreciable. These changes clearly indicate that a progressive loss of crystallinity occurs upon temperature increase.

As the structure generated at T = 1800 K is the most disordered one, this was chosen for study of the structural and vibrational properties at the DFT level. Figure 4 shows the initial (crystalline) and the final (amorphous) structures optimized at the B3LYP theory level. It is also worth mentioning that those structures generated between 400 and 1600 K collapsed onto the crystal system upon optimization, whereas those between 1700 and 2000 K remained as amorphous structures.

Table 2. Bond distance ranges and cell parameters of the Mg₂SiO₄ bulk structures: experimental values of the crystal system as well as B3LYP-optimized values of the crystal and amorphous systems. The calculated volume and densities derived from the B3LYP-optimized geometries are also shown.

	Experimental	Crystal	Amorphous
Si–O (Å)	1.616–1.649	1.628–1.673	1.618–1.693
Mg1–O (Å)	2.069–2.126	2.073–2.131	1.929–2.226
Mg2–O (Å)	2.040–2.166	2.062–2.222
a (Å)	4.746	4.789	4.93
b (Å)	10.18	10.25	9.37
c (Å)	5.976	6.009	5.97 (11.94) 1
α (degrees)	90.0	90.0	87.4
β (degrees)	90.0	90.0	90.6
γ (degrees)	90.0	90.0	88.6
Volume (Å3)	288.73	295.10	275.78 (551.00) 1
Density (g·cm−3)	3.22	3.34	3.37

¹ Because of the enlargement of the unit cell along the c axis (see text), for a proper comparison, bare values were derived from the actual calculated values (values in parenthesis).

shows the B3LYP-optimized lattice parameters and the range of the calculated Mg–O and Si–O bond lengths of amorphous Fo, as well as the volume and the density. For comparison, Table 2 also presents the same parameters for Fo crystal (experimental and calculated). In addition to the systematic larger values obtained by the calculated values for the crystal system, results indicate that the range of values of the amorphous system is larger than the crystal ones. This is indicative that the B3LYP-optimized amorphous Fo presents a larger distribution of bond lengths characteristic of the amorphous materials. It is worth mentioning that due to the disorganization of the internal atomic positions in the amorphous Fo, classifying the Mg atoms as Mg1 and Mg2 is not possible. The cell parameters of the amorphous Fo experiencing more variation compared to the crystalline values are a and b; that is, a is about 0.2 Å larger, while b is 0.8 Å shorter. Calculated lattice angles are also somewhat different, and essentially deviate from the ideal 90 degrees. Because of the significant shortening of the b cell parameter, the volume of the amorphous Fo is smaller than the crystal volumes. The fact that the density of the crystalline systems is lower than the amorphous one is also indicative of the amorphization of the system. Bearing in mind that amorphous materials are characterized by a random structure and poor order, giving rise to the presence of porosity.

In order to understand the nature of the amorphization of the silicate material, the deviation of the internal O–Si–O and O–Mg–O angles of the optimized system with respect to the ideal values is examined (reported in

Table 3. Mean values and the corresponding average deviations (with respect to the ideal value) of the O–Si–O and O–Mg–O angles of the optimized amorphous 1 × 1 × 2, 2 × 1 × 2, and 2 × 2 × 2 Mg₂SiO₄ systems.

Angle (Degrees)	Ideal Value	Mean Value ± Standard Deviation (Average Deviation)
		1 × 1 × 2	2 × 1 × 2	2 × 2 × 2
O–Si–O	110.0	109.5 ± 7.2(6.53%)	108.9 ± 12.4(11.3%)	104.9 ± 12.8(11.6%)
O–Mg–O	90.0	94.7 ± 13.8(15.3%)	100.9 ± 22.1(24.6%)	104.1 ± 16.5(18.3%)

). These values reveal that the O–Mg–O angle presents the largest deviation (≈15.3%), and therefore, the distortion of these angles contributes significantly to the amorphous nature. However, the deviation of the O–Si–O angle is not insubstantial (≈6.5%), although the distortion of these angles also contributes by some amount to the internal atomic disorder.

The high-frequency dielectric constants (ε_∞) were also calculated using the CPKS scheme implemented in the CRYSTAL code. Results are shown in

Table 4. High-frequency dielectric constants (ε_∞) for the Mg₂SiO₄ bulk structures along the x, y, and z directions: experimental values of the crystal system and B3LYP-optimized values of the crystal and amorphous systems.

	Experimental 1	Crystal	Amorphous
ε∞,x	2.789	2.571	2.284
ε∞,y	2.673	2.424	2.247
ε∞,z	2.726	2.475	2.218

¹ From reference [118].

, in which the ε_∞ values along the x, y, and z directions of the amorphous Fo are compared with the experimental and calculated ones for Fo crystal. For the crystal systems, ε_∞ is notably symmetrical, the values slightly differing as a function of the direction; that is, both the experimental [118] and calculated values give ε_∞,x as the largest value, yet ε_∞,y as the smallest, with a difference of 0.12–0.15 units. In contrast, for amorphous Fo, the difference between the largest and the smallest ε_∞ values, which now correspond to ε_∞,x and ε_∞,z, respectively, is a meager 0.07 units. This is consistent with the disordered nature of amorphous Fo, since the direction dependency of ε_∞ typical of crystalline systems is partially lost.

Crystalline Fo has an orthorhombic structure. It presents 28 atoms in the unit cell (six symmetry-independent atoms), which give rise to four formula units per cell. Its symmetry decomposition corresponds to Г_total = 11A_g + 11B_1g + 7B_2g + 7B_3g + 10A_u + 10B_1u + 14B_2u + 14B_3u, in which the three B_1u, B_2u, and B_3u correspond to rigid transitions and the remaining modes are the vibrational and rotational modes that can be classified as: 35 IR-active modes (9B_1u + 13B_2u + 13B_3u), 36 Raman-active modes (11A_g + 11B_1g + 7B_2g + 7B_3g), and 10A_u inactive modes. In previous works, mode classification and band assignments of crystalline Fo have exhaustively been discussed by means of infrared, Raman, and reflectance spectroscopic measurements [12,59,60,119,120,121,122,123,124]. In this part, we focus our attention on the most important changes due to the amorphization of the crystal system. Figure 5 shows the B3LYP-simulated IR spectrum of amorphous Fo, where for comparison, the B3LYP-simulated and the experimental IR spectra for the crystal systems are also shown. The simulated spectra were broadened by Lorentzian functions with a typical width of δν = 20 cm⁻¹, which is comparable with the bandwidth of experimental IR spectrum. For crystal Fo, the experimental and theoretical vibrational IR and Raman spectra compare fairly well. In the IR case, both spectra present a wealth of narrow bands in agreement with their crystalline nature. As already described by some of us and by other colleagues, B3LYP frequencies reproduce the experimental IR values very well (for more details, see [90,125]). Figure 6 shows the B3LYP-simulated Raman spectrum of amorphous and crystal Fo, and

Table 5. Active Raman frequencies (ν, in cm⁻¹) calculated in this work and their comparison with the experimental data. The shifts between the calculated and the experimental values (Δν) are also provided.

	N	This Work		[121]		[119]		[60]		[59]
		ν	I (%)	ν	Δν	ν	Δν	ν	Δν	ν	Δν
Ag	1	212	0.05	184	28	183	29	183	29	183	29
	2	261	0.08	227	34	226	35	227	34	227	34
	3	351	0.11	304	47	304	47	305	46	305	46
	4	367	1.20	329	38	329	38	329	38	329	38
	5	391	0.78	339	52	332	59	340	51	340	51
	6	474	0.62	421	53	422	52	424	50	424	50
	7	608	12.4	544	64	545	63	546	62	545	63
	8	675	22.2	608	67	608	67	609	66	609	66
	9	848	81.1	824	24	824	24	826	22	826	22
	10	883	100	856	27	856	27	856	27	856	27
	11	999	20.6	966	33	965	34	966	33	966	33
B1g	12	253	0.00	-	-	220	33	224	29	197	56
	13	294	0.06	-	-	274	20	260	34	265	29
	14	361	1.05	316	45	318	43	318	43	317	44
	15	417	1.68	-	-	351	66	-	-	-	-
	16	420	0.38	-	-	383	37	418	2	418	2
	17	489	2.21	434	55	434	55	434	55	434	55
	18	658	1.39	588	70	582	76	585	73	583	75
	19	713	0.43	-	-	632	81	632	81	632	81
	20	869	1.28	838	31	838	31	839	30	839	30
	21	897	3.37	866	31	866	31	866	31	866	31
	22	1012	0.37	-	-	975	37	976	36	976	36
B2g	23	-		-	-	175	-	142	-	-	-
	24	229	0.01	243	−14	242	−13	244	−15	244	−15
	25	343	0.17	-	-	323	20	324	19	324	19
	26	365	0.08	-	-	365	0	368	−3	365	0
	27	431	2.93	-	-	-	-	-	-	407	24
	28	463	0.69	434	29	439	24	441	22	438	25
	29	665	14.3	588	77	586	79	588	77	585	80
	30	956	6.98	882	74	881	75	884	72	881	75
B3g	31	203	0.00	243	−40	-	-	226	−23	-	-
	32	296	0.00	-	-	286	10	272	24	-	-
	33	-		316	-	315	-	318	-	314	-
	34	369	0.31	373	−4	374	−5	376	−7	374	−5
	35	413	1.35	409	4	410	3	412	1	406	7
	36	-		-	-	435	-	-	-	466	-
	37	514	3.34	-	-	-	-	-	-	484	30
	38	670	2.82	588	82	592	78	595	75	591	79
	39	908	5.14	920	−12	920	−12	922	−14	920	−12

reports the calculated Raman-active frequencies (classified by their symmetries) with the corresponding intensity of the crystalline system, which are compared with those measured experimentally (including frequency deviations). In the Raman case, B3LYP reproduces the experimental Raman data quite well, with a mean average deviation of 24.9–34.6 cm⁻¹ and a largest deviation of 81–82 cm⁻¹. Remarkably, for the calculated two most intense Raman peaks (i.e., at 848 and 883 cm⁻¹), the deviations compared to the corresponding experimental values are 27 and 22–24 cm⁻¹, respectively.

More interesting are the differences between the B3LYP-simulated crystalline and amorphous IR and Raman spectra. Crystal Fo presents a set of well-defined bands, in which the total active vibrations are not fully visualized in the form of bands because some are either overlapped with contiguous bands or present at very low intensities. The spectra of amorphous Fo are clearly different; that is, they are based on single broad bands. In particular, the IR and Raman spectra of amorphous Fo present three and two well-defined zones, respectively: for IR, one band between 1000–800 cm⁻¹, a peak at about 600 cm⁻¹, and another band between 500–300 cm⁻¹; for Raman, bands between 1000–800 cm⁻¹ and between 700–400 cm⁻¹. These regions correspond essentially to the Si–O stretching and O–Si–O bending vibrations, respectively. However, vibrations associated with rotations of the SiO₄ tetrahedra and translations of Mg²⁺ also contribute in the low region of the lower bands. The significant broadening and blending of the IR bands presented by amorphous Fo compared to the crystal systems is due to the wider and more diverse distribution of bond lengths and angles given in the former system, which is typical in amorphous materials. In fact, the hyperfine structure of the IR spectra of amorphous Fo (built by bands consisting of single lines) presents a great number of active vibrational bands that, upon imposing band width, overlap each other, rendering squat-shaped bands. The presence of more active vibrational bands compared to the crystal system is mainly due to the lack of symmetry in amorphous Fo. This means that some vibrations that are inactive in the crystal system, according to selection rules, are active in the amorphous one. Moreover, the cell enlargement means that equivalent vibrations by the translational symmetry in the minimal unit cell are different in the super-cell, giving rise to the apparition of new vibrational bands. Astronomical IR and Raman measurements of cosmic silicates revealed that they are mainly in an amorphous state. The recorded spectra generally present two single broad bands at about 1000 cm⁻¹ and 550 cm⁻¹, associated with the Si–O stretching and O–Si–O bending vibrations, respectively [28]. Our simulated vibrational results of the amorphous Fo are thus in line with the astronomical IR and Raman spectral features.

As anticipated in Computational Methods, the reflectance spectrum of a given 3D-periodic system can be simulated with the CRYSTAL code. An important ingredient for the construction of the reflectance curves is ε_∞, whose values are discussed above. The B3LYP-simulated reflectance spectra of Fo, both crystalline and amorphous, are shown in Figure 7. The reflectivity is separated according to the three crystallographic axes (a, b, and c), which for the crystal system, are coincident with the vibration symmetry (B_3u, B_2u, and B_1u, respectively). The topology of the simulated reflection curves of crystalline Fo perfectly matches with the experimental ones. A detailed analysis of the effect of different fitting procedures to properly reproduce the experimental reflectance spectra is provided in [88]. The B3LYP-simulated reflectance spectra of amorphous Fo is significantly different. The broad reflectance curves of the crystalline system are sharper and present more bands. This is, in line to what is mentioned above, due to the higher number of active vibrational modes in the amorphous systems.

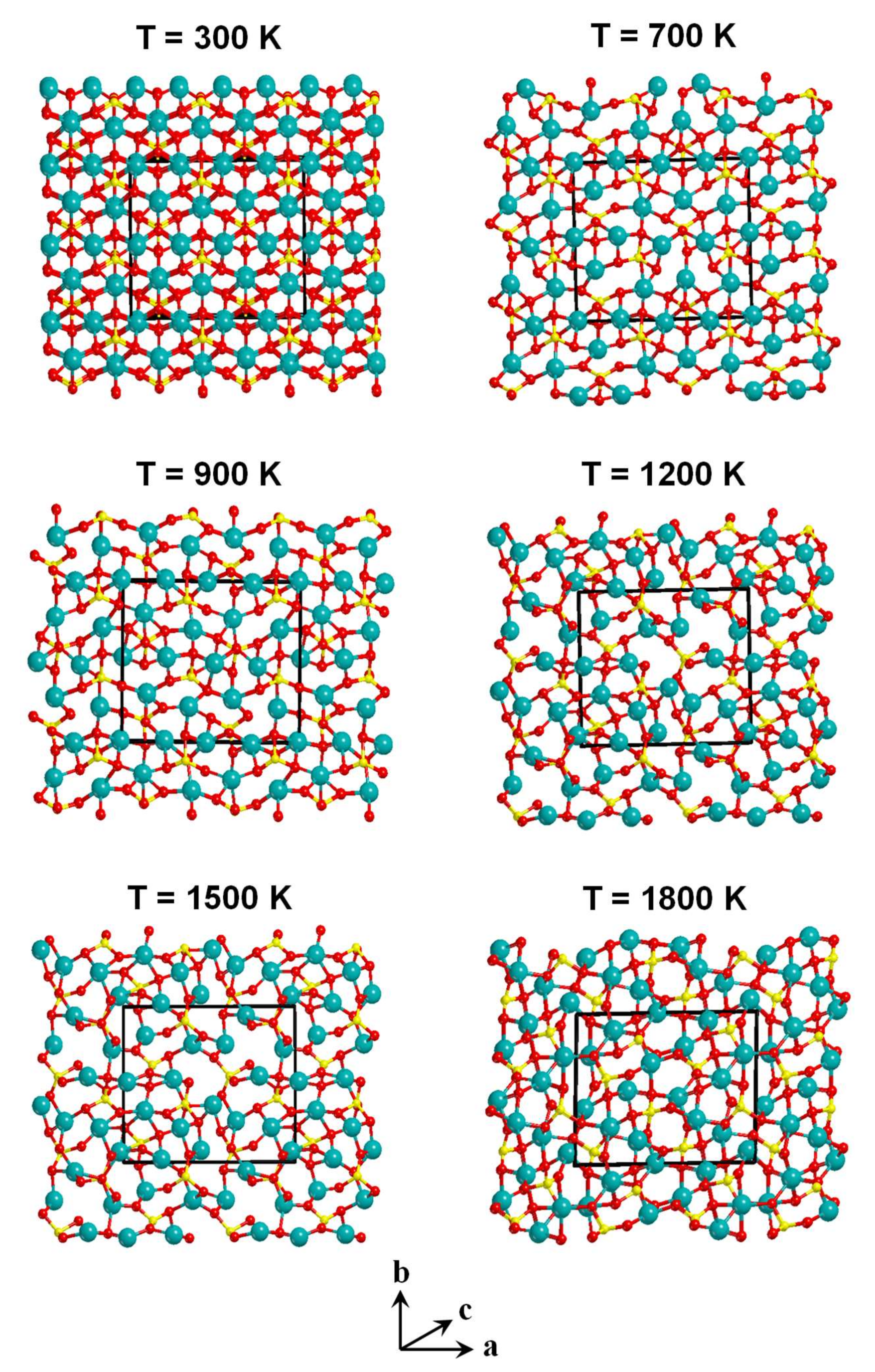
3.2. Unit Cell Size Effects in the Amorphisation of the Mg₂SiO₄ System

In the previous section, a comprehensive comparison of the bulk physicochemical properties between crystalline and amorphous Mg₂SiO₄ is presented for a given unit cell. In this section, we aim to explore if the degree of amorphization is affected by the unit cell size. Our initial hypothesis is: the larger the unit cell, the more internal structural parameters to be randomly disordered, and accordingly, the larger the degree of amorphization. To demonstrate the validity (or not) of our hypothesis, different unit cell sizes have been considered, they have been amorphized, and an analysis of their structural, dielectric, and vibrational properties has been carried out by comparing these physicochemical properties between them. It is worth mentioning that the possible differences are associated with the different degree of amorphization, since, rigorously speaking, these physicochemical properties are not strictly size-dependent. However, we anticipate that the degree of amorphization is, in our systems, linked to the size of the unit cell and accordingly, these physicochemical properties are indeed ultimately related to the size of the unit cells.

To carry out these investigations, the following different super-cell sizes have been adopted: 1 × 1 × 2, 2 × 1 × 2, and 2 × 2 × 2. The procedure to amorphize the corresponding crystalline systems was the same as that presented in the previous section; that is, classical MD simulations at 1800 K followed by B3LYP optimization of the resulting geometry to carry out the theoretical analysis. For all super-cell systems, the Mg–Mg and Mg–O g(r) pair correlation functions are similar, showing several broad but distinguishable bands representing the different Mg–Mg and Mg–O shells (see Figure S3, Supplementary Materials). The similarity between the band widths of the different super-cell systems indicates that for all cases, the amorphization was definitely achieved.

The B3LYP-optimized structures of the different super-cell systems are shown in Figure 8, both in their atomistic and polyhedral forms.

Table 6. B3LYP-optimized bond distance ranges and cell parameters of the 1 × 1 × 2, 2 × 1 × 2, and 2 × 2 × 2 Mg₂SiO₄ bulk structures. Volumes and densities are also shown.

	1 × 1 × 2	2 × 1 × 2	2 × 2 × 2
Si–O (Å)	1.618–1.693	1.592–1.906	1.579–1.983
Mg–O (Å)	1.929–2.226	1.860–2.211	1.800–2.209
a (Å)	4.93	10.168	9.589
b (Å)	9.37	10.177	20.574
c (Å)	11.9	11.329	11.937
α (degrees)	87.4	89.6	85.7
β (degrees)	90.6	83.6	93.4
γ (degrees)	88.6	97.1	91.7
Volume (Å3)	551.00	1156.77	2343.91
Density (g·cm−3)	3.373	3.214	3.172

presents the B3LYP-calculated lattice parameters, the range of the calculated Mg–O and Si–O bond lengths, and the volume and the density of the bulk materials. In Table 3, the mean values and the associated deviations of the internal O–Si–O and O–Mg–O angles compared to the ideal values are also reported for the 2 × 1 × 2 and 2 × 2 × 2 systems. By visual inspection of the images of Figure 8, one can identify that the larger the super-cell size, the more distorted the tetrahedral SiO₄ and octahedral MgO₆ building blocks. This larger distortion is also reflected by the mean values and the average deviations of the internal angles. In the 2 × 1 × 2 and 2 × 2 × 2 super-cell systems, they are larger than in the 1 × 1 × 2 one. In addition to this, from a careful visual inspection of the atomistic structure of the amorphous systems, we realized that some unusual structural motifs are present in the 2 × 1 × 2 and 2 × 2 × 2 systems, which are absent in the 1 × 1 × 2 one; in particular: (i) pentacoordinated Si atoms (SiO₅ adopting a trigonal pyramid-like geometry), (ii) pentacoordinated Mg atoms (MgO₅ adopting either square-pyramid-like or trigonal pyramid-like geometries), and (iii) tetracoordinated Mg atoms (MgO₄ adopting highly distorted tetrahedral geometries). The presence of these structural motifs is indicative of the high degree of amorphization of these systems. In addition to this visual inspection, we also calculated the area under the g(r) curves to measure the coordination numbers. For Si–O, they are 4.06, 4.12 (2 × 1 × 2), and 4.23 for the 1 × 1 × 2, 2 × 1 × 2, and 2 × 2 × 2 systems, respectively, clearly indicating an increase of the Si–O coordination number for larger unit cells, due to the presence of these highly-coordinated motifs. It is worth mentioning that Si atoms with coordination numbers larger than 4 have been reported in a couple of synthesized minerals; namely, a high-pressure phase of MgSi(OH)₆ [126] and a dense phase (so-called phase D) of MgSi(OH)₂O₄ [127,128], predicted by means of theoretical calculations to occur in thaumasite [129], a naturally-occurring mineral present in the Earth’s crust. For Mg–O, the coordination numbers are kept at 5.82 for all unit cell systems, probably due to compensation effects in the different Mg coordination spheres.

The calculated densities are reported in

Table 7. Calculated high-frequency dielectric constants (ε_∞) for the B3LYP-optimized 1 × 1 × 2, 2 × 1 × 2, and 2 × 2 × 2 Mg₂SiO₄ bulk structures along the x, y, and z directions.

	1 × 1 × 2	2 × 1 × 2	2 × 2 × 2
ε∞,x	2.284	2.153	2.148
ε∞,y	2.247	2.161	2.135
ε∞,z	2.218	2.168	2.132

and indicate that they decrease when the sizes of the super-cell increase; that is, 3.373 g·cm⁻³ (1 × 1 × 2) > 3.214 g·cm⁻³ (2 × 1 × 2) > 3.172 g·cm⁻³ (2 × 2 × 2). This is consistent with the fact that the larger the super-cell size, the larger the amorphous nature of the system. Indeed, by increasing the size of the super-cell, the structures can sport more defects and porosity, and consequently, the density is lower. The calculated ε_∞ constants along the x, y, and z directions (reported in Table 7) show the same pattern. An incremental increase of the super-cell size leads to a reduced dependency along the direction of the ε_∞ values as a consequence of the larger degree of disorder, which is equal along the three directions.

In relation to the vibrational properties, Figure 9 shows the simulated IR, Raman, and reflectance spectra. As mentioned above, the 1 × 1 × 2 system presents three and two well-defined broad IR and Raman bands, respectively. In contrast, the IR spectrum of the 2 × 2 × 2 system presents two largely broad bands; that is, the two bands in the low-frequency region of the 1 × 1 × 2 system overlap in the 2 × 2 × 2 system. Similar changes occur in the Raman spectrum: the two regions present in the 1 × 1 × 2 system become fused in the 2 × 2 × 2 system. The IR and Raman spectra of the 2 × 1 × 2 system present intermediate profiles between those of the 1 × 1 × 2 and the 2 × 2 × 2 systems; that is, the different frequency regions clearly identified in the 1 × 1 × 2 system are still identifiable, but are more diffuse. A similar transition in the topology of the reflectance spectra can be observed from the 1 × 1 × 2 and 2 × 1 × 2 to the 2 × 2 × 2 systems. In this case, an increase of the unit cell size leads to spectra that present sharper and more bands due to the major number of independent active bands. All these changes in the topology of the vibrational-related spectra clearly indicate that there is a progressive increase of the amorphous nature from the 1 × 1 × 2 to the 2 × 2 × 2 super-cell systems.

4. Conclusions

By combining classical MD simulations with periodic DFT calculations, a detailed theoretical study on the structural, dielectric, and vibrational properties of Mg₂SiO₄ as a silicate test case has been presented. The amorphous structures for Mg₂SiO₄ have been generated using classical MD simulations at different temperatures within a melt-and-quench scheme, taking the crystalline phase as the initial guess structure. Periodic B3LYP calculations have been carried out to optimize the geometries of the generated structure and calculate their high-frequency dielectric constants and simulate the IR, Raman, and reflectance spectra. The most interesting points emerging from this work are:

• The combined approach of classical MD for structure evolution and quantum chemical DFT for electronic structure analysis is a reliable technique to investigate the physicochemical properties of silicates.
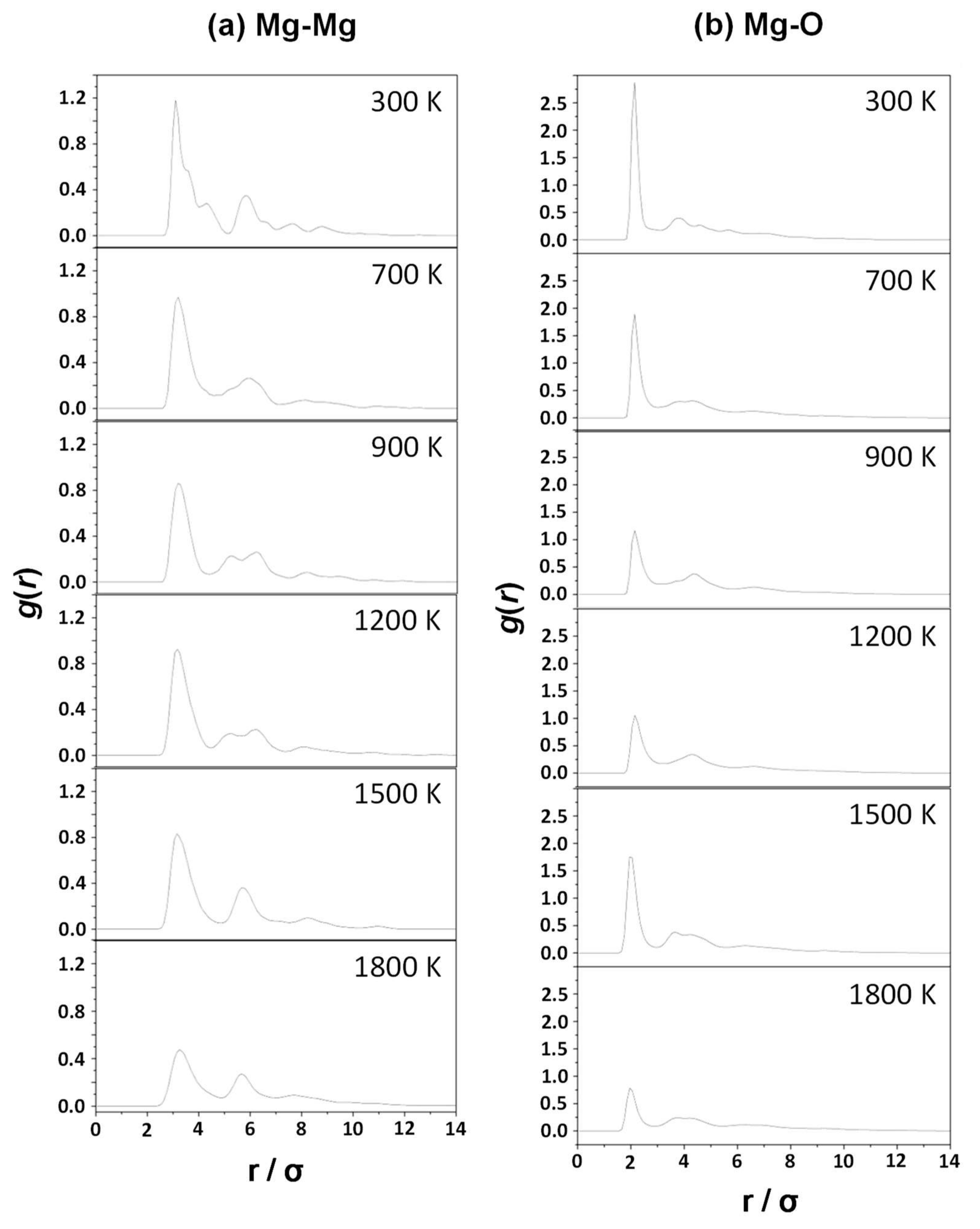
• The Mg–Mg and Mg–O pair correlation functions, g(r), derived from the classical MD simulations indicate that an increase of the temperature produces broader profiles of g(r), indicating a progressive loss of crystallinity with temperature.
• B3LYP-optimized geometries of the amorphous bulk systems present larger distributions of bond lengths and angles than the crystal analogues (for instance, the Si–O distance ranges, 1.618–1.693 Å vs 1.628–1.673 Å) due to the significant disorganization of the internal atomic positions. Consequently, the tetrahedral SiO₄ and octahedral MgO₆ motifs become largely distorted, which is characteristic of amorphous materials. Calculated densities of the amorphous bulks are lower than the crystalline ones; that is, 3.373 (1 × 1 × 2), 3.214 (2 × 1 × 2), 3.172 (2 × 2 × 2) versus 3.34 (crystalline), due to the presence of internal cavities produced during the amorphization process.
• Related to the high-frequency dielectric constants along the x, y, and z directions (ε_∞,x, ε_∞,y, and ε_∞,z), while in the crystalline Mg₂SiO₄ they are clearly different (2.571, 2.424, and 2.475, respectively), in agreement with the direction dependency caused by the inherently crystallinity of the system, in the amorphous phases, they are more similar (e.g., for the 2 × 2 × 2 system, 2.148, 2.135, and 2.132, respectively), showing a convergence between the calculated ε_∞,x, ε_∞,y, and ε_∞,z values. Accordingly, ε_∞ values do not depend on a particular direction because the system is likewise disordered in all the directions.
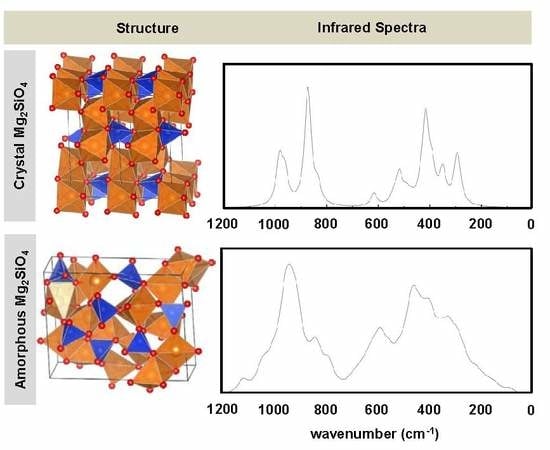
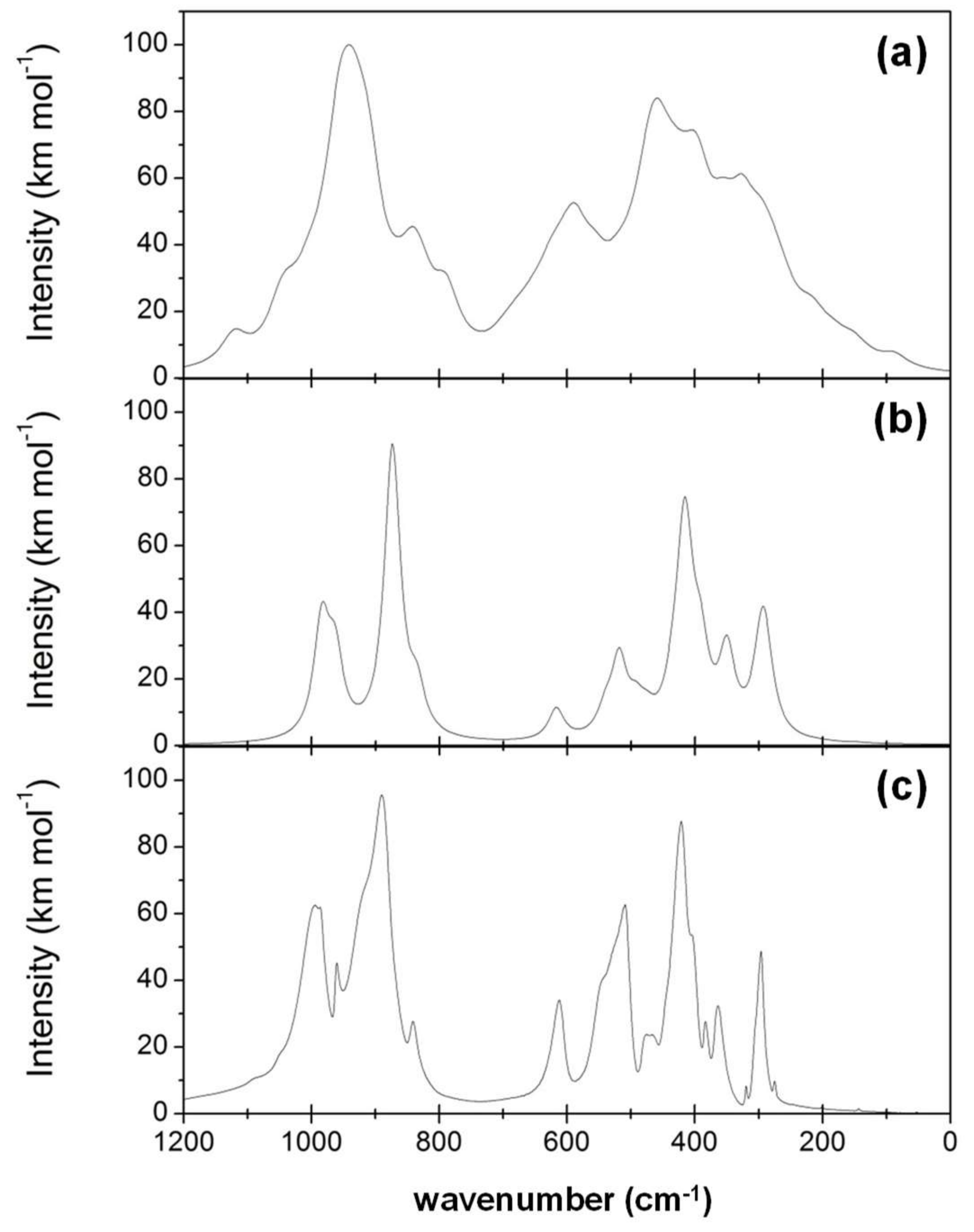
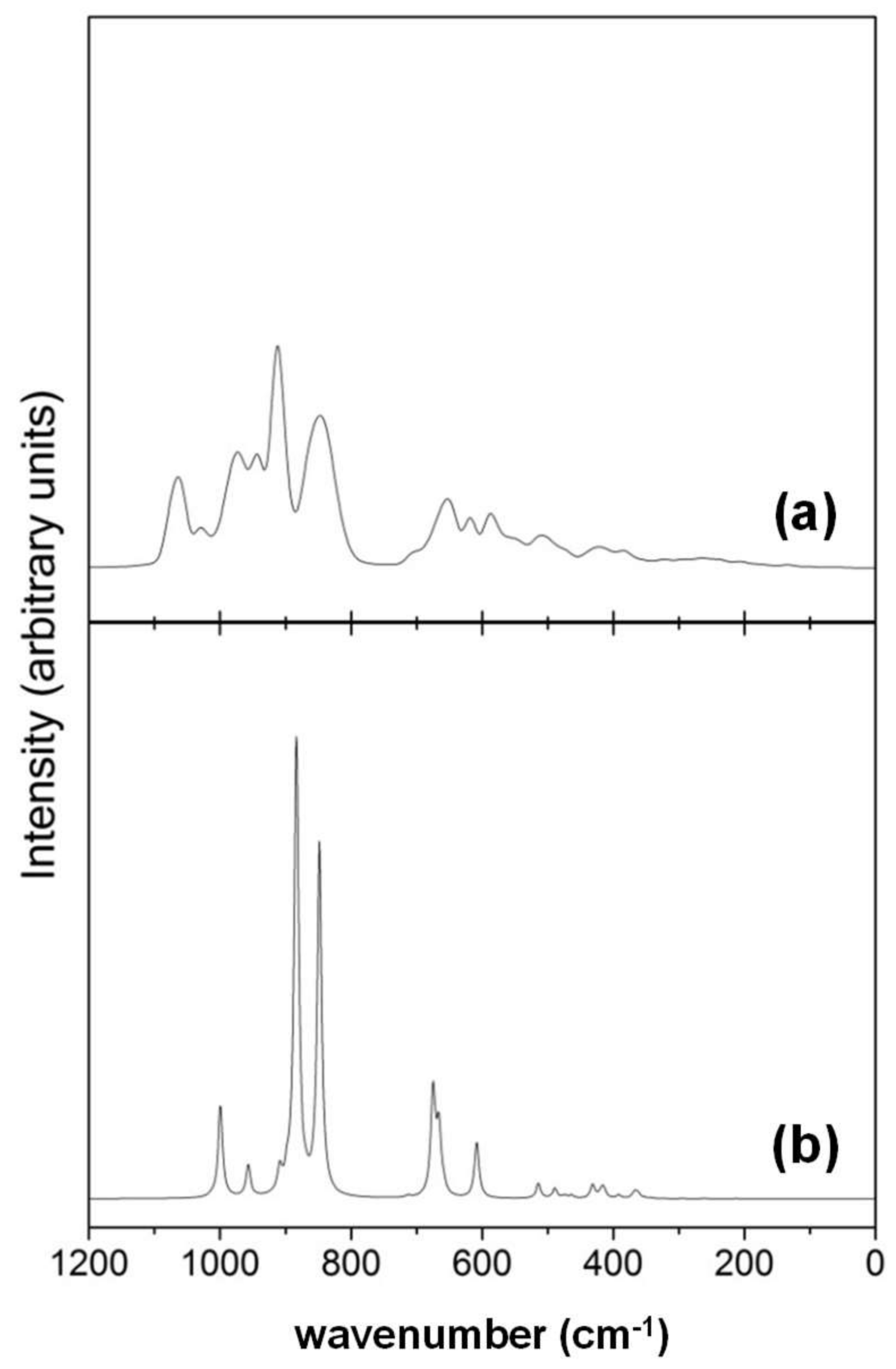
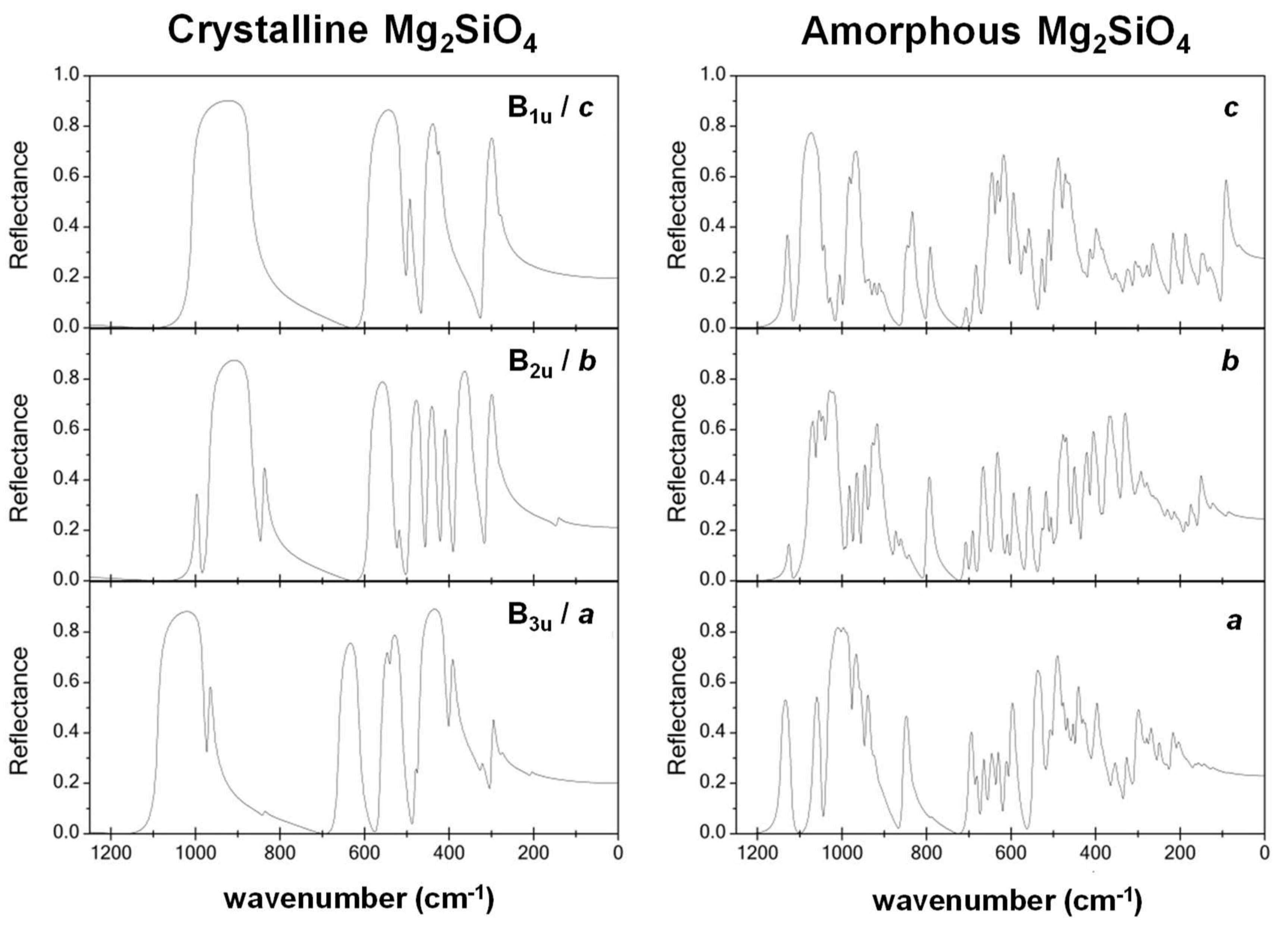
• While the IR and Raman spectra of the crystalline phase present well-defined narrow bands covering the 1000–200 cm⁻¹ region, the spectra of the amorphous analogues, due to the wider and more diverse distribution of lengths and angles, are dominated by broader bands caused by multiple bands overlapping; namely, for IR, three broad bands are observed (between 1000–800 cm⁻¹, a peak at 600 cm⁻¹, and between 500–300 cm⁻¹), while for Raman, two broad bands are observed (between 1000–800 cm⁻¹ and between 700–400 cm⁻¹). The simulated spectra agree fairly well with those recorded for Mg₂SiO₄ in astrophysical environments, with the IR broad bands being centered at 1000 cm⁻¹ and 500 cm⁻¹. In the case of reflectance spectra, the broad reflectance curves of the crystalline system change with bands increasing in sharpness and number for the amorphous systems, due to the presence of more active modes.
• Regarding the unit cell size effects, results clearly provide evidence that an increase of the unit cell size infers a larger degree of amorphization due to the presence of more internal degrees of freedom to be disordered.

The presented results can be useful in several aspects. From a computational point of view, from these amorphous bulk systems, one can generate slab surface models in the same amorphous state to carry out surface chemical studies (for instance, to study a given heterogeneous catalytic process). Additionally, results can be used as a benchmark for the development of force fields devoted to simulating amorphous/glassy silicates. The characterized spectroscopic properties can be stored in current astronomical databases and archives devoted to measuring spectroscopic properties of astrophysical silicate-based dust particles, to be compared with forthcoming results. Finally, they can stimulate future experimental work in the synthesis and physicochemical characterization of amorphous forsterite under highly controllable conditions, whose results can be compared with the present ones.