(10.4) Face of Ordered and Disordered Dolomite, MgCa(CO₃)₂: A Computational Study to Reveal the Growth Mechanism

Abstract

In this study, the stability of the (10.4) face of dolomite was systematically investigated. The surface energies at 0 K of the different (10.4) surfaces resulting from the cut of both ordered and disordered bulk structures were determined and compared, to establish how different atomic configurations (surface terminations) can affect the stability of the investigated face. To study the thermodynamic behavior of a surface, a 2D periodic slab model and the ab initio CRYSTAL code were adopted. The surface energies of the (10.4) faces of calcite and magnesite were also calculated in order to compare them with those of the different terminations of the (10.4) face of dolomite. Our calculations showed that the bulk of the dolomite crystal must have an ordered structure to reach the minimum of the energy, whereas the (10.4) surface is more stable when its structure is disordered. A growth model of the (10.4) face has been proposed: the peculiarity of this model consists in the existence of some disordered layers forming at the interface crystal/solution, which arrange in an ordered structure once covered by others disordered layers resulting by the spiral steps propagation.

1. Introduction

Dolomite, CaMg(CO₃)₂, is one of the most abundant carbonate minerals in the Earth [1,2]. The study and the analysis of the stability of carbonate mineral phases, in general, are significant in several research fields of Earth Science and industrial applications. For instance, the role of dolomite in CO₂-H₂O systems [3]; the study of trace elements and isotopes in sedimentary carbonates [4]; the characterization of magmatic process [5], devolatilization of the subducted oceanic crust [6], the fault weakening [7] and the implications of ordering in double carbonates in subduction zones [8].

Several studies concerning the distribution of calcium and magnesium cations into dolomite crystallographic sites have been carried out. The results show that the temperature influenced the ordered distribution of cations introducing defects in the crystal lattice interpreted as an intra-layer cations disorder [9,10,11,12]. In particular, the intra-layer cations disorder was observed approximately between 1150 K and 1350 K [8,11,12]. Therefore, the degree of disordering is significant to completely describe dolomite.

Some studies have been carried out on phase relations of binary carbonate solid solutions [13,14,15]. Furthermore, many works focus on the computational chemistry of dolomite: simulation of defects and phase stabilities as a function of temperature and pressure were carried out [16,17,18,19]. In particular, Zucchini et al. [16] performed ab initio calculations at the athermal limit (T = 0 K) to study the effect of cation order/disorder on the stability of dolomite. They carried out the calculations by means of the CRYSTAL code [20,21] and using the WC1LYP Hamiltonian [22]. They took into account nine different bulk structures of dolomite (named in their work as SC1, SC8, SC278, SC279, SC4341, SC4895, SC5505, CC2 and CC3) having space group $R\overline{3}$ or $R3$, and different degrees of cation disorder. The comparison between total static energies allowed them to observe that the configuration SC1 is the most stable one at 0 K. They also estimated that at T of ~300 K, SC8 is the most stable configuration, whereas at T ~750 K the most stable one is SC4895. The bulk structures SC1, SC8 and SC4895 will be described below.

Starting from these interesting results, we decided to study the stability of the (10.4) face of dolomite when the bulk structures SC1 and SC4895 are considered. Then, the surface energies at 0 K of the different (10.4) surfaces resulting from the cut of the bulk structures were determined and compared, to establish how different atomic configurations (i.e., surface terminations) can affect the stability of the (10.4) face. The stability of a crystal face is governed by its surface energy, which is the energy needed per unit area to form a surface (γ; J/m²). To establish whether one surface termination is more stable with respect to another one, it is necessary to calculate their surface energies; the more stable surface termination is that with the lower surface energy. In this work, the optimized surface structures and surface energies were determined at quantum-mechanical level by using the CRYSTAL code [20,21]. Unfortunately, as explained in the following, it was not possible to calculate the surface energy of the (10.4) face obtained by the bulk structure SC8. Nevertheless, an unexpected behavior of the (10.4) surface emerged from our calculations, and a new growth model for dolomite is proposed.

The paper is structured as follows: (i) explanation of the computational method used to study the (10.4) surfaces of dolomite; (ii) description of the bulk configurations SC1, SC8 and SC4895; (iii) characterization of the different (10.4) surface terminations resulting by the cut of the bulk structures; (iv) description of a new growth model for dolomite.

2. Computational Details

To investigate the thermodynamic behavior of a surface, a 2D periodic slab model [23] and the ab initio CRYSTAL code [20,21] were adopted. The ab initio CRYSTAL code implements the Hartree-Fock and Kohn-Sham self-consistent field (SCF) method for the study of periodic systems [24]. The bulk structures (i.e., calcite, magnesite, and dolomite SC1, SC8 and SC4895) and their energies were also investigated by using the CRYSTAL code.

The calculations were performed at the DFT (Density Functional Theory) level by using the B3LYP Hamiltonian [25,26,27], which provided accurate results for the surface properties of calcite [28].

In CRYSTAL, the multi-electronic wave function is constructed as an anti-symmetrized product (Slater determinant) of mono-electronic crystalline orbitals (COs), which are linear combinations of local functions (i.e., atomic orbitals, AOs) centered on each atom of the crystal. In turn, AOs are linear combinations of Gaussian-type functions (GTF, the product of a Gaussian times a real solid spherical harmonic to give s-, p- and d-type AOs). We used the all Gaussian-type basis sets recently developed by Peintinger et al. [29] for O, C, Mg and Ca. It consists of a TZVP contraction that has been systematically derived for solid-state systems starting from def2-TZVP [30,31] basis sets devised for molecular cases.

The thresholds controlling the accuracy in the evaluation of Coulomb and exchange integrals (ITOL1, ITOL2, ITOL3, ITOL4 and ITOL5, see Dovesi et al. [21]) were set to 10⁻⁸ (ITOL1 to ITOL4) and 10⁻¹⁸ (ITOL5). The threshold on the SCF energy was set to 10⁻¹⁰ Hartree.

In the adopted package, the DFT exchange and correlation contributions are evaluated by numerically integrating functions of the electron density and of its gradient over the cell volume. The choice of the integration grid is based on an atomic partition method, originally developed by Becke [32]. In the present study, a pruned (75, 974) p grid was adopted (XLGRID in the code [21]), which ensured a satisfactory accuracy in the numerically integrated electron charge density.

The reciprocal space was sampled according to a Monkhorst-Pack mesh [33] with shrinking factor 6, corresponding to 20k points in the first irreducible Brillouin zone.

Bulk and surfaces structures were optimized by using the analytical energy gradients with respect to atomic coordinates and lattice parameters within a quasi-Newton scheme, combined with the Broyden-Fletcher-Goldfarb-Shanno scheme for Hessian updating [34,35,36]. Convergence was checked on energy, gradient components and nuclear displacements. The threshold on energy between two subsequent optimization steps was set to 10⁻⁷ Hartree; the thresholds on the root-mean-square of the gradient components and of the nuclear displacements were set to 3.0 × 10⁻⁴ Hartree bohr⁻¹ and 1.2 × 10⁻³ bohr, respectively; those on the maximum components of the gradients and displacements were set to 4.5 × 10⁻⁴ Hartree bohr⁻¹ and 1.8 × 10⁻³ bohr, respectively.

The slabs of a given thickness were made by cutting their respective bulk structures parallel to the hkl planes of interest (i.e., 10.4). Then, the slab geometry (atomic coordinates and 2D cell parameters) was optimized by considering all the atoms free to move. The slab was generated preserving the center of inversion to ensure the vanishing of the dipole moment perpendicular to the slab. The CRYSTAL output files, listing the optimized fractional coordinates and optimized 2D cell parameters of the slabs, are freely available at [37]. The calculations were done by considering slabs with a thickness sufficient to obtain an accurate description of the surfaces. The slab thickness is considered appropriate when the bulk-like properties are reproduced at the center of the slab. In the present work, a slab of five layers was used for all the phases: calcite, magnesite and dolomite.

The specific surface energy γ (J/m²) at T = 0 K was calculated by means of the relation [20,23]:

$$\mathsf{\gamma }=\underset{\mathrm{n}\to \infty }{\lim }{\mathrm{E}}_{\mathrm{S}}\left(\mathrm{n}\right)=\underset{\mathrm{n}\to \infty }{\lim }\frac{\mathrm{E}{\left(\mathrm{n}\right)}_{\mathrm{slab}}-{\mathrm{nE}}_{\mathrm{bulk}}}{2\mathrm{A}}$$

(1)

where $\mathrm{E}{\left(\mathrm{n}\right)}_{\mathrm{slab}}$ and ${\mathrm{E}}_{\mathrm{bulk}}$ are the energy of a n-layer slab and of the bulk, respectively; A is the area of the primitive unit cell of the surface; the factor 2 in the denominator accounts for both the upper and lower surfaces of the slab. ${\mathrm{E}}_{\mathrm{S}}\left(\mathrm{n}\right)$ is thus the energy (per unit area) required for the formation of the surface from the bulk. When $\mathrm{n}\to \infty$, ${\mathrm{E}}_{\mathrm{S}}\left(\mathrm{n}\right)$ will converge to the surface energy per unit area (γ). We verified that five layers are sufficient to reach convergence on the surface energy value of the (10.4) face for all the phases; no variations of surface energy values are observed by increasing the number of layers.

3. Results and Discussion

3.1. Bulk Structures of Dolomite

In this paragraph, we briefly describe the bulk structures SC1, SC8 and SC4895 studied by Zucchini et al. [16]. In the present study, we used these configurations as references to carry out the (10.4) surfaces analysis. We optimized the bulk structures (SC1, SC8 and SC4895) by using the B3LYP Hamiltonian and the all Gaussian-type basis sets recently developed by Peintinger et al. [29]. In

Table 1. Optimized hexagonal cell parameters (Å) of calcite, magnesite and dolomite (SC1, SC8 and SC4895).

		This Work		Zucchini et al. [16]
	Space Group	a (Å)	c (Å)	a (Å)	c (Å)
calcite	$R\overline{3}c$	5.062	17.351	-	-
SC1	$R\overline{3}$	4.855	16.210	4.825	15.971
SC8	$R3$	4.857	16.227	4.827	16.000
SC4895	$R\overline{3}$	4.866	16.249	4.838	15.992
magnesite	$R\overline{3}c$	4.668	15.108	-	-

, our results (cell parameters) are listed and compared with those obtained by Zucchini et al. [16], who used the WC1LYP Hamiltonian and a different basis sets. Our calculations were performed by considering a hexagonal cell. Drawings of the bulk structures are in the paper by Zucchini et al. [16].

SC1 consists of a layered structure, with $R\overline{3}$ symmetry, in which Ca²⁺ and Mg²⁺ fill alternated planes separated by planar carbonate groups normal to the c axis of the hexagonal cell; this is the structure of a totally ordered dolomite. The repetition unit is then formed by two cationic planes: [Ca] [Mg].

SC8 is a not center-symmetric disordered structure, with $R3$ symmetry, in which four planes normal to the c axis of the hexagonal cell containing the cations are individuated: (i) one filled by only Mg²⁺, (ii) one filled by only Ca²⁺, (iii) one filled by 3/4 Mg²⁺ and 1/4 Ca²⁺ and (iv) one filled by 3/4 Ca²⁺ and 1/4 Mg²⁺. These four planes build the repetition unit: [Mg] [Ca] [Mg_3/4 Ca_1/4] [Mg_1/4 Ca_3/4].

SC4895 is a disordered structure, with $R\overline{3}$ symmetry, in which Ca²⁺ and Mg²⁺ are simultaneously present in each plane that separates the planar carbonate groups normal to the c axis of the hexagonal cell. The repetition unit, in this structure, is composed by two planes: [Ca_3/4 Mg_1/4] [Ca_1/4 Mg_3/4].

According to our calculations, the stability order of the structures at 0 K is SC1 < SC8 < SC4895. Indeed, the static energy per mole of CaMg(CO₃)₂ of the structure SC1 is lower by 11.15 and 19.60 kJ/mol than that of the structures SC8 and SC4895, respectively. Such differences are very close to those determined by Zucchini et al. [16]: 10.05 and 17.90 kJ/mol. When the configurational entropy is not present (i.e., at 0 K the Gibbs free energy coincides with the static energy, if the zero-point energy is neglected), the more stable structure results to be the ordered one. This is no longer true when the configurational entropy is taken into account, as demonstrated by Zucchini et al. [16]. At room temperature (300 K) the structures SC1 and SC8 have the same probability to exist, whereas SC4895 has a very low probability to be observed. At ~750 K the panorama is completely different: SC8 and SC4895 have the same probability to exist, whereas the probability of finding SC1 is almost zero. Unfortunately, such results are not in agreement with literature data which point out the first appearance of disorder at approximately 1200 K [8]. Zucchini et al. [16] ascribe such discrepancies to the fact that their calculations do not take into account both (i) the kinetics of the disordering process and (ii) the vibrational contributions (i.e., vibrational energy and entropy) to the energy of the system. This might explain the observed underestimation of the disordering temperatures. Then, it is licit to expect that the SC1 structure is stable at temperature well above 300 K.

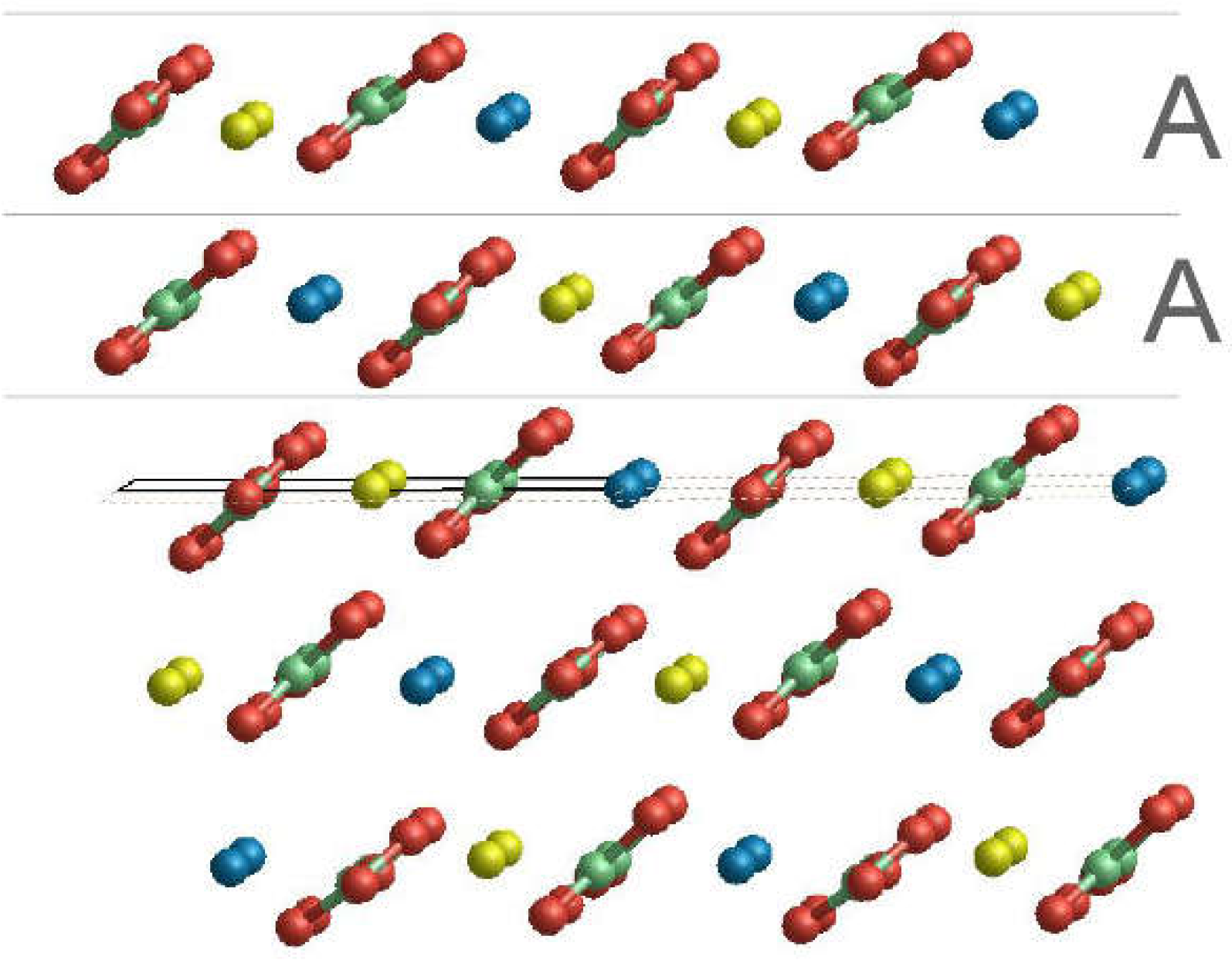
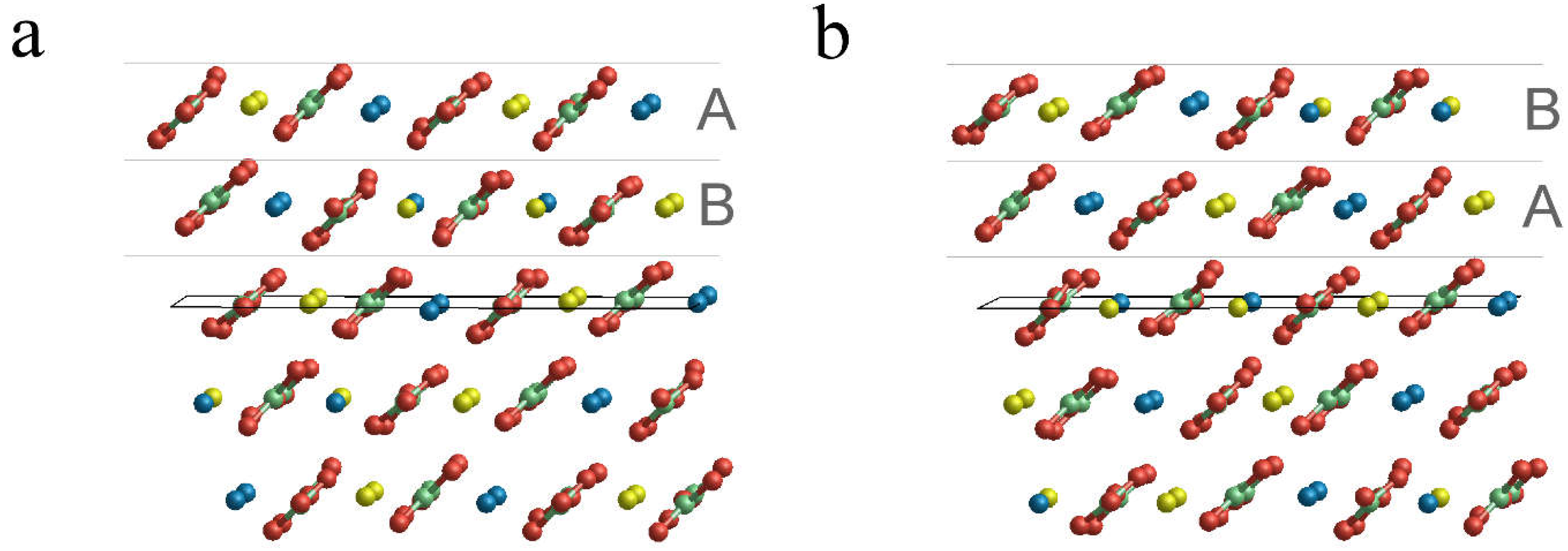
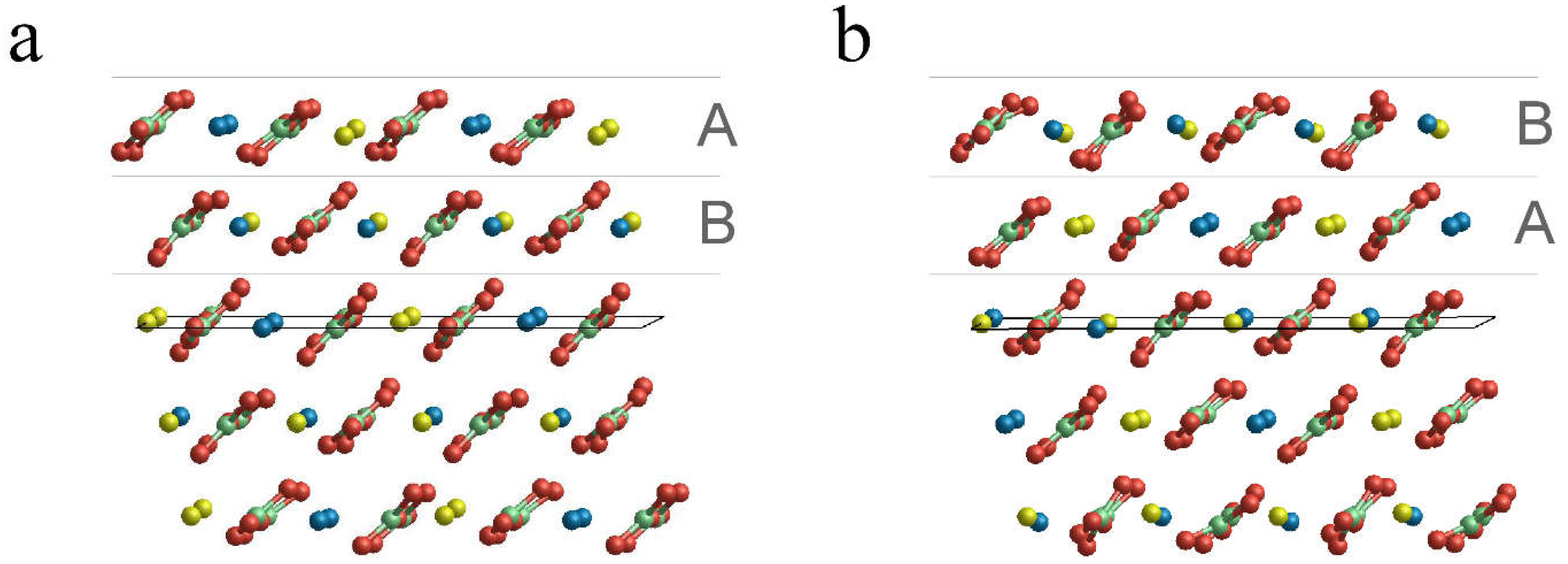
3.2. Surface Terminations and Surface Energies of the (10.4) Faces of Dolomite

All the possible surface terminations obtained by cutting the bulk structures SC1, SC8 and SC4895 are illustrated and their surface energies discussed.

When cutting the bulk structure SC1 along the 10.4 plane, only a surface termination is possible (Figure 1), with all of the layers forming the slab being equal (i.e., … AAA …). Whereas, it is possible to generate two (10.4) surface terminations from both the bulk structures SC8 and SC4895 (Figure 2 and Figure 3 respectively), since in these cases there is a stacking of two different cationic layers forming the slab (… ABABA …). In the following, both for SC8 and SC4895, the two surface terminations are named with A and B, according to the outer layer forming the slab. Moreover, to indicate the different (10.4) slabs resulting by the cut of the structures SC1 and SC4895, we used the notations: ${\left(10.4\right)}_{\mathrm{SC}1}$, ${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{A}}$ and ${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{B}}$. Instead, for calcite (Cal) and magnesite (Mgs): ${\left(10.4\right)}_{\mathrm{Cal}}$ and ${\left(10.4\right)}_{\mathrm{Mgs}}$, respectively.

The (10.4) slabs obtained by SC1 and SC4895 preserve the center of inversion, with $R\overline{3}$ being the space group of the bulk structures. This made it possible to calculate their surface energies because the dipole moment perpendicular to the surfaces is null. On the contrary, SC8 is a not a center-symmetric structure (space group: $R3$); in this case, the surface energy of the (10.4) face diverges ($\mathsf{\gamma }\to \infty$) when increasing the thickness of the slab, hindering in this way the comparison with the others surface terminations. Additional and detailed remark on the dipolar surfaces are reported in Bruno [38].

The surface energies of the (10.4) faces of calcite and magnesite were also calculated in the present work, in order to compare them with those of the different terminations of the (10.4) face of dolomite. The surface energies are listed in

Table 2. Optimized 2D cell parameters (a, b, a^b) and surface energies (γ) of the (10.4) slabs of calcite, magnesite and dolomite.

Slab	Space Group	a (Å)	b (Å)	a^b (°)	γ (J/m2)
${\left(10.4\right)}_{\mathrm{Cal}}$	$R\overline{3}c$	5.0426	8.1526	90.0	0.507
${\left(10.4\right)}_{\mathrm{SC}1}$	$R\overline{3}$	4.8551	7.7862	90.0	0.489
${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{A}}$	$R\overline{3}$	9.6602	15.4230	90.0	0.437
${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{B}}$	$R\overline{3}$	9.6743	15.3506	89.8	0.450
${\left(10.4\right)}_{\mathrm{Mgs}}$	$R\overline{3}c$	4.6682	7.3769	90.0	0.493

, along with the optimized 2D cell parameters of the slabs.

From the analysis of the surface energy values, some interesting considerations about the stability of the (10.4) faces can be made:

• The surface energy of the (10.4) face of calcite (0.507 J/m²) is slightly higher than that of magnesite (0.493 J/m²). Previous surface energy calculations on the (10.4) face of calcite and magnesite were performed by our research group, always using the B3LYP Hamiltonian but considering a poorer basis sets: 0.508 and 0.501 J/m² for calcite and magnesite, respectively [39]. These small variations in the surface energy values suggest that our estimates are barely affected by the Basis Set Superposition Error (BSSE) [23]. Indeed, if the use of richer basis sets does not produce significant variations in the surface energy value, then it is licit to suppose that our estimates are reliable.
• The surface energies of the ${\left(10.4\right)}_{\mathrm{SC}1}$, ${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{A}}$ and ${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{B}}$ faces are lower than those of calcite and magnesite: 0.489, 0.437 and 0.450 J/m². This clearly highlights that the (10.4) face is strongly stabilized when there is a mixing of Ca²⁺ and Mg²⁺. Furthermore, such stabilization is also a function of the ordering degree of Ca²⁺ and Mg²⁺. Indeed, the surface energies of the ${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{A}}$ and ${\left(10.4\right)}_{\mathrm{SC}4895}^{\mathrm{B}}$ faces are decreased by 10.6% and 8.0%, respectively, compared to that of the ${\left(10.4\right)}_{\mathrm{SC}1}$ face. Our calculations suggest that a disordered surface is more stable of an ordered one, in contrast with the findings on the bulk of the crystal [16], where the more stable structure is the ordered one (SC1).
• The two surface terminations obtained by cutting SC4895 have very similar surface energy. This implies an analogous probability to be observed when a crystal grows.

It is important to specify that our calculations were performed by considering a dry surface (i.e., a (10.4) face in contact with vacuum), the effect of the mother solution (e.g., water supersaturated in dolomite) from which the crystal grows is not taken into account. Therefore, we are not able to evaluate how the surface energy is modified when solvent and/or impurities are present. In order to evaluate these effects on the surfaces stability, empirical or ab initio molecular dynamic simulations should be performed.

In addition, it is noteworthy to highlight that our calculations were performed at 0 K, and the vibrational energy and entropy of the slabs were not evaluated. However, according to the ab initio calculations performed by Bruno et al. [39], the surface energies at 298 K of the (10.4) face of calcite (0.459 J/m²) and magnesite (0.452 J/m²) are reduced by the same percentage (~10%) with respect to the values at 0 K. Then, we can suppose that the surface energies of the (10.4) faces of dolomite are also reduced by the same percentage, and that the temperature does not affect their ratio.

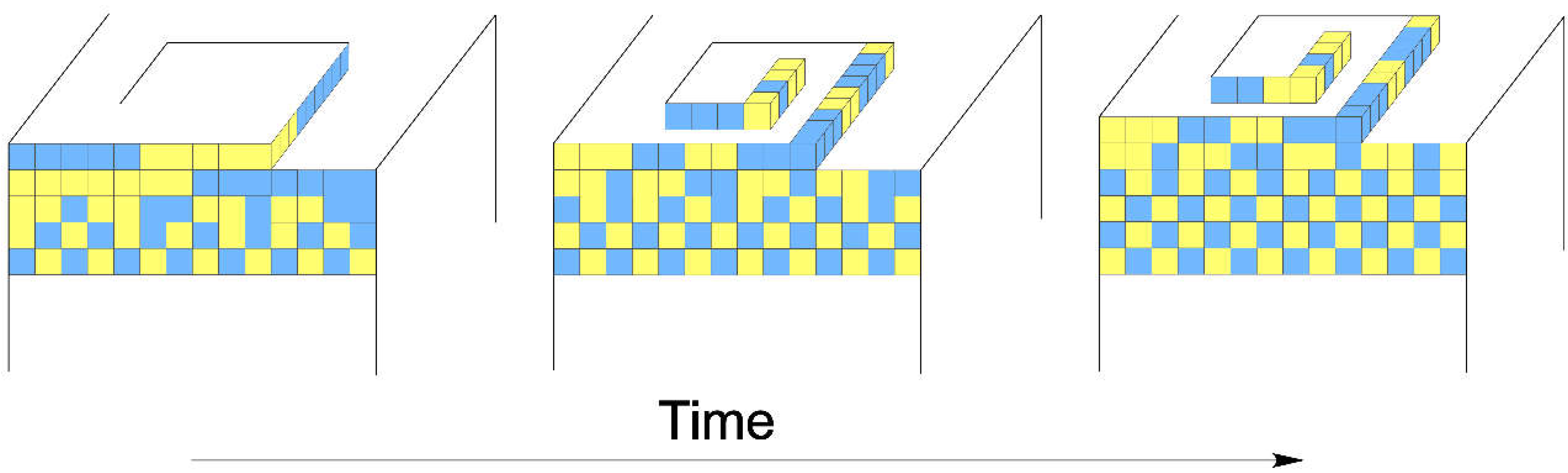
3.3. A Growth Model for Dolomite

Our calculations, along with those of Zucchini et al. [16], showed that the bulk of the dolomite crystal must have an ordered structure to reach the minimum of the energy, whereas the (10.4) surface is more stable when its structure is disordered. There is an extremely different structural behavior between the inner portion (bulk) and the outer one (surface) of the same crystal. To reconcile these structural differences in a crystal growing from a supersaturated aqueous solution, we conceived the growth model detailed below.

According to the Hartman and Perdock [40] classification, the (10.4) face of dolomite is a flat one. This implies that its advancement is mainly due to the spiral growth mechanism: the steps of the spiral advance and cover the (10.4) face by overlapping successive d_10.4 layers. At this point, we supposed that the d_10.4 layers forming in contact with the mother solution are structurally disordered, being energetically favored according to our estimations of the surface energies. Successively, when these disordered layers are buried by other ones, the ordering process begins by means of the intra-crystalline diffusion, until reaching the complete order represented by the structure SC1. The growth mechanism just described is sketched in Figure 4.

The peculiarity of this growth model consists in the existence of some disordered layers forming at the interface crystal/solution, which are arranged in an ordered structure once covered by other disordered layers resulting from the spiral step propagation. We are not able to define the thickness (i.e., number of d_10.4 layers) of this disordered interface, but we can suppose that it is a function of the crystal growth rate and temperature: (i) the higher the growth rate the greater the thickness of the disordered interface; (ii) the higher the temperature the smaller the disordered interface, with the intra-crystalline diffusion being more effective. Therefore, the thickness of the disordered zone is determined by the competition of two processes: the growth kinetics of the (10.4) face and the cations diffusion inside the crystal. It is obvious that the cations diffusion will be more effective at higher temperature (i.e., T > 200 °C), being the diffusion coefficient an exponential function of T. It is important to underline that the intra-crystalline diffusion should start only when the disordered layers are far away enough from the interface to be considered bulk layers, that is, when the influence of the interface is negligible and, as a consequence, the minimum of the energy is reached by imposing the ordered structure SC1. However, according to our ab initio calculations performed on calcite and magnesite (10.4) slabs [39], the number of layers influenced by the presence of a surface is approximately four. It is then predictable that the layers below these ones can be considered bulk layers and, as a consequence, they will be ordered to reproduce the structure SC1.

In our model, we supposed that the disordered layers at the interface have the same composition of the layers in the bulk crystal. This could be untrue. Indeed, a chemical-physics phenomenon named segregation at the crystal surface is well known and has been widely described, which implies the deviation of the surface composition from that of the bulk. The creation of a surface always requires a positive free energy change. In order to minimize this positive surface free energy, the surface will be enriched (by segregation) by the constituent with the lowest surface free energy; see the recent paper by Bruno [41] and references therein for an exhaustive description of surface segregation. Therefore, it is possible that the disordered layers forming the interface have a different composition (i.e., a different Ca²⁺/Mg²⁺ ratio) with respect to that of the bulk layers.

4. Conclusions

We performed ab initio calculations to study the stability of ordered and disordered (10.4) surfaces of dolomite. The surface energies at 0 K of the different (10.4) surfaces resulting by the cut of both ordered and disordered bulk structures were determined and compared. Interestingly, we observed that the surface energy of a disordered surface is lower than that of an ordered one, suggesting that the layers forming at the crystal/solution interfaces are disordered. Such behavior is in contrast with the findings concerning the bulk structure of dolomite, where the more stable structure is ordered. Then, in order to reconcile these structural differences between surface and bulk, we conceived a new crystal growth model: some disordered layers grow at the interface crystal/solution, which arrange in an ordered structure once covered by others disordered layers resulting by the spiral steps propagation; the ordering takes place by means of intra-crystalline diffusion.

It is important to highlight that this model was developed for the (10.4) face, the growth of others crystal faces can be governed by a different mechanism. It should be interesting, in the near future, to perform ab initio calculations on other important faces of dolomite, to verify whether for them, too, the surface energy of a disordered structure is lower than that of an ordered one. Moreover, it should be interesting to perform molecular dynamic calculations on the (10.4) face of dolomite growing in aqueous solution, to verify the reliability of our growth model.

We also highlight that our results are not in contrast with the re-precipitation model of dolomite [42,43,44], i.e., ordering in dolomite progresses by dissolution of disordered dolomite and re-precipitation of more ordered dolomite. Indeed, also in the case of a re-precipitation, according to our calculations, the surface should be disordered, whereas the bulk of the crystal should be ordered. This should guarantee a dolomite crystal with the lowest energy.

In conclusion, it is important to specify that we determined the surface energy of a crystal face cut by a particular disordered bulk structure. We cannot exclude that another more disordered bulk structure gives a surface energy value lower than that estimated in this work. A systematic computational work should be undertaken to find the structure of the (10.4) surface with the lowest surface energy.