Trace Element Partitioning Dualism under Mineral–Fluid Interaction: Origin and Geochemical Significance
Abstract
:1. Introduction
2. Background
3. Methods
3.1. Experimental Procedure
3.2. Analytical Methods
3.2.1. Analysis of Precious Metals
3.2.2. Analytical Data Selections for Single Crystals (ADSSC)
3.2.3. Analysis of Rare Earth Elements
3.2.4. X-ray Photoelectron Spectroscopy (XPS)
4. Natural Materials
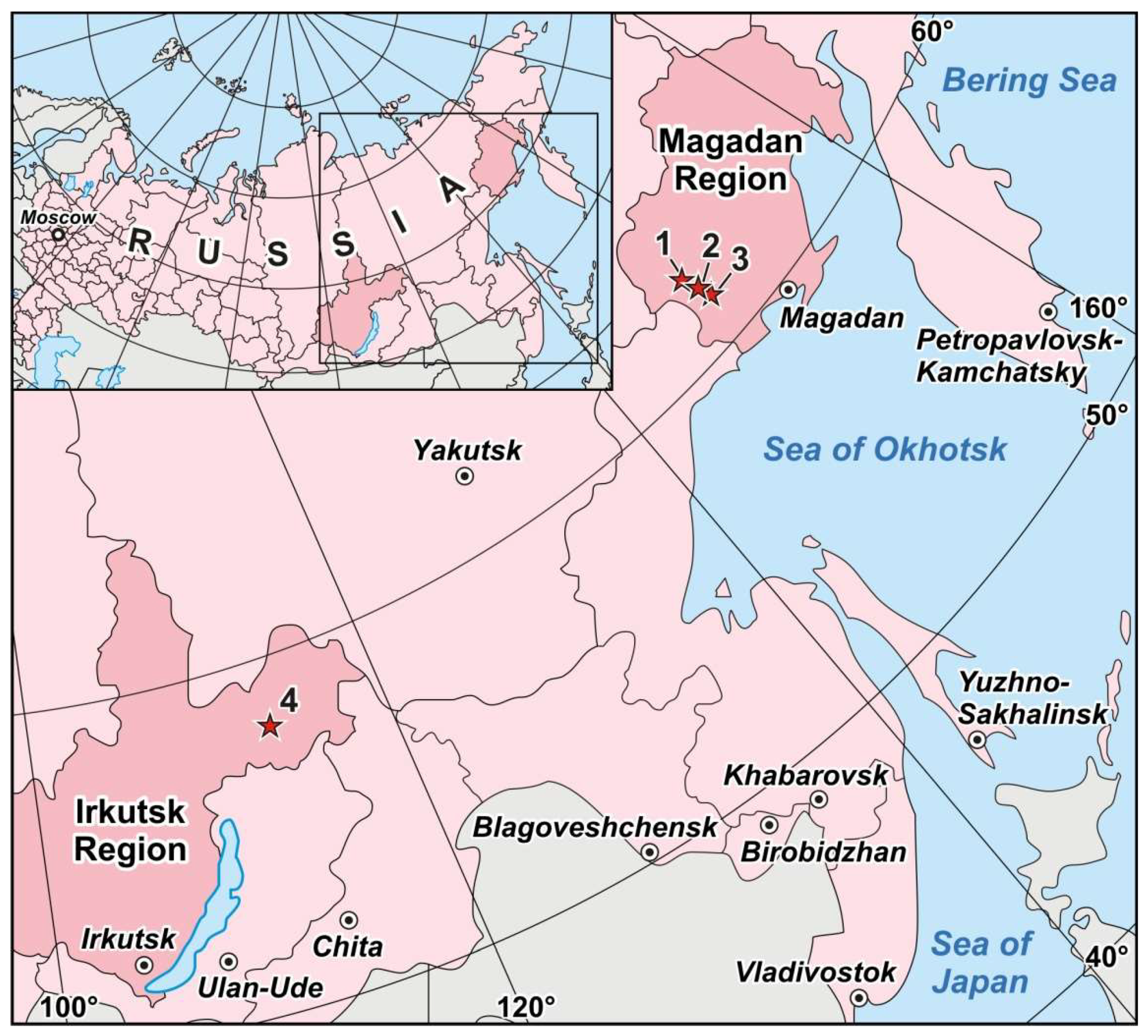
4.1. Degdekan, Natalkinskoe and Zolotaya Rechka Deposits
4.1.1. Degdekan Deposit
4.1.2. Natalkinskoe Deposit
4.1.3. Zolotaya Rechka Deposit
4.2. Krasnoye Deposit
4.3. Analysis Procedure
5. Results
5.1. Distribution of Precious Metals
5.2. Distribution of REE
5.3. Gold and PGE in Natural Pyrite and Ore-Forming Fluids
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Navrotsky, A. Thermodynamics of element partitioning: (1) Systematics of transition metals in crystalline and molten silicates and (2) Defect chemistry and the Henry’s law problem. Geochim. Cosmochim. Acta 1978, 42, 887–902. [Google Scholar] [CrossRef]
- Abramovich, M.G.; Shmakin, B.M.; Tauson, V.L.; Akimov, V.V. Mineral typochemistry: Anomalous trace-element concentrations in solid solutions with defect structures. Int. Geol. Rev. 1990, 32, 608–615. [Google Scholar] [CrossRef]
- Urusov, V.S.; Dudnikova, V.B. The trace-component trapping effect: Experimental evidence, theoretical interpretation, and geochemical applications. Geochim. Cosmochim. Acta 1998, 62, 1233–1240. [Google Scholar] [CrossRef]
- Tauson, V.L.; Akimov, V.V. Introduction to the theory of forced equilibria: General principles, basic concepts, and definitions. Geochim. Cosmochim. Acta 1997, 61, 4935–4943. [Google Scholar] [CrossRef]
- Jones, J.H. Thoughts and reminiscences on experimental trace element partitioning. Geochem. Perspect. 2016, 5, 147–251. [Google Scholar] [CrossRef]
- Hiraga, T.; Anderson, I.M.; Kohlstedt, D.L. Chemistry of grain boundaries in mantle rocks. Am. Mineral. 2003, 88, 1015–1019. [Google Scholar] [CrossRef]
- Toulhoat, H.; Digne, M.; Arrouvel, C.; Raybaud, P. DFT studies of fluid-mineral interactions at the molecular level: Examples and perspectives. Oil Gas Sci. Technol. Rev. IFP 2005, 60, 417–433. [Google Scholar] [CrossRef]
- Tauson, V.L.; Babkin, D.N.; Parkhomenko, I.Y.; Men’shikov, V.I.; Lipko, S.V.; Pastushkova, T.M. Distribution of heavy-metal (Hg, Cd, and Pb) chemical species between pyrite and hydrothermal solution. Geochem. Int. 2010, 48, 611–616. [Google Scholar] [CrossRef]
- Tauson, V.L.; Parkhomenko, I.Y.; Babkin, D.N.; Men’shikov, V.I.; Lustenberg, E.E. Cadmium and mercury uptake by galena crystals under hydrothermal growth: A spectroscopic and element thermo-release atomic absorption study. Eur. J. Mineral. 2005, 17, 599–610. [Google Scholar] [CrossRef]
- Tauson, V.L.; Babkin, D.N.; Lustenberg, E.E.; Lipko, S.V.; Parkhomenko, I.Y. Surface typochemistry of hydrothermal pyrite: Electron spectroscopic and scanning probe microscopic data. I. Synthetic pyrite. Geochem. Int. 2008, 46, 565–577. [Google Scholar] [CrossRef]
- Tauson, V.L.; Kravtsova, R.G.; Grebenshchikova, V.I.; Lustenberg, E.E.; Lipko, S.V. Surface typochemistry of hydrothermal pyrite: Electron spectroscopic and scanning probe microscopic data. II. Natural pyrite. Geochem. Int. 2009, 47, 231–243. [Google Scholar] [CrossRef]
- Tauson, V.L.; Kravtsova, R.G.; Smagunov, N.V.; Spiridonov, A.M.; Grebenshchikova, V.I.; Budyak, A.E. Structurally and superficially bound gold in pyrite from deposits of different genetic types. Russ. Geol. Geophys. 2014, 55, 273–289. [Google Scholar] [CrossRef]
- Bancroft, G.M.; Jean, G. Gold deposition at low temperature on sulfide minerals. Nature 1982, 298, 730–731. [Google Scholar] [CrossRef]
- Hyland, M.M.; Bancroft, G.M. An XPS study of gold deposition at low temperatures on sulphide minerals: Reducing agents. Geochim. Cosmochim. Acta 1989, 53, 367–372. [Google Scholar] [CrossRef]
- Scaini, M.J.; Bancroft, G.M.; Knipe, S.W. An XPS, AES, and SEM study of the interactions of gold and silver chloride species with PbS and FeS2: Comparison to natural samples. Geochim. Cosmochim. Acta 1997, 61, 1223–1231. [Google Scholar] [CrossRef]
- Tauson, V.L. Isomorphism and endocrypty: New approaches to study the behavior of trace elements in mineral systems. Russ. Geol. Geophys. 1999, 40, 1468–1474. [Google Scholar]
- Guevremont, J.M.; Strongin, D.R.; Schoonen, M.A.A. Thermal chemistry of H2S and H2O on the (100) plane of pyrite: Unique reactivity of defect sites. Am. Mineral. 1998, 83, 1246–1255. [Google Scholar] [CrossRef]
- Tauson, V.L.; Ovchinnikova, O.V.; Bessarabova, O.I.; Smagunov, N.V.; Pastushkova, T.M. Distribution of gold deposited under reducing adsorption from HAuCl4 solution on magnetite, sphalerite, and galena crystals. Russ. Geol. Geophys. 2000, 41, 1427–1430. [Google Scholar]
- Koneev, R.I.; Knalmatov, R.A.; Mun, Y.S. Nanomineralogy and nanogeochemistry of ores of Uzbekistan gold deposits. Zapiski Russ. Mineral. Obshchestva 2010, 139, 1–14. (In Russian) [Google Scholar] [CrossRef]
- Rusanov, A.I. Phase Equilibria and Surface Phenomena; Khimia: Leningrad, Russia, 1967. (In Russian) [Google Scholar]
- Tauson, V.L.; Babkin, D.N.; Pastushkova, T.M.; Krasnoshchekova, T.S.; Lustenberg, E.E.; Belozerova, O.Y. Dualistic distribution coefficients of elements in the system Mineral-Hydrothermal solution. I. Gold accumulation in pyrite. Geochem. Int. 2011, 49, 568–577. [Google Scholar] [CrossRef]
- Tauson, V.L.; Lipko, S.V.; Smagunov, N.V.; Arsent’ev, K.Y.; Loginov, B.A. Influence of surface nanophases on the processes of crystal formation in multiphase mineral systems. Dokl. Earth Sci. 2014, 455, 317–322. [Google Scholar] [CrossRef]
- Tauson, V.L.; Babkin, D.N.; Pastushkova, T.M.; Akimov, V.V.; Krasnoshchekova, T.S.; Lipko, S.V.; Belozerova, O.Y. Dualistic distribution coefficients of elements in the system Mineral-Hydrothermal solution. II. Gold in magnetite. Geochem. Int. 2012, 50, 227–245. [Google Scholar] [CrossRef]
- Tauson, V.L.; Babkin, D.N.; Pastushkova, T.M.; Smagunov, N.V.; Lipko, S.V.; Voronova, I.Y.; Men’shikov, V.I.; Bryanskii, N.V.; Arsent’ev, K.Y. Dualistic distribution coefficients of trace elements in the system Mineral-Hydrothermal solution. III. Precious metals (Au and Pd) in magnetite and manganmagnetite. Geochem. Int. 2016, 54, 149–166. [Google Scholar] [CrossRef]
- Tauson, V.L.; Lipko, S.V.; Arsent’ev, K.Y.; Mikhlin, Y.L.; Babkin, D.N.; Smagunov, N.V.; Pastushkova, T.M.; Voronova, I.Y.; Belozerova, O.Y. Dualistic distribution coefficients of trace elements in the system Mineral-Hydrothermal solution. IV. Platinum and silver in pyrite. Geochem. Int. 2017, 55, 753–774. [Google Scholar] [CrossRef]
- Tauson, V.L. Gold solubility in the common gold-bearing minerals: Experimental evaluation and application to pyrite. Eur. J. Mineral. 1999, 11, 937–947. [Google Scholar] [CrossRef]
- Goldfarb, R.J.; Groves, D.I. Orogenic gold: Common or evolving fluid and metal sources through time. Lithos 2015, 233, 2–26. [Google Scholar] [CrossRef]
- Gaboury, D. Does gold in orogenic deposits come from pyrite in deeply buried carbon-rich sediments? Insight from volatiles in fluid inclusions. Geology 2013, 41, 1207–1210. [Google Scholar] [CrossRef]
- Tauson, V.L.; Akimov, V.V.; Lipko, S.V.; Spiridonov, A.M.; Budyak, A.E.; Belozerova, O.Y.; Smagunov, N.V. Typomorphism of pyrite of the Sukhoi Log deposit (East Siberia). Russ. Geol. Geophys. 2015, 56, 1394–1413. [Google Scholar] [CrossRef]
- Arifulov, C.H.; Arsentieva, I.V.; Shchegolkov, Y.V. About the long-prism pyrite in gold-bearing black shale deposits of the Kirovsko-Kvarkenskiy ore district, East Orenburg region. Rudy I Met. 2011, 5, 78–84. (In Russian) [Google Scholar]
- Bloomstein, E.L.; Kydd, R.A.; Levinson, A.A. Development of ammonium geochemistry as a new technique in precious and base metals exploration. J. Geochem. Explor. 1987, 29, 386. [Google Scholar] [CrossRef]
- Men’shikov, V.I.; Voronova, I.Y.; Proidakova, O.A.; Malysheva, S.F.; Ivanova, N.I.; Belogorlova, N.A.; Gusarova, N.K.; Trofimov, B.A. Preconcentration of gold, silver, palladium, platinum, and ruthenium with organophosphorus extractants. Russ. J. Appl. Chem. 2009, 82, 183–189. [Google Scholar] [CrossRef]
- Tauson, V.L.; Lipko, S.V. Pyrite as a concentrator of gold in laboratory and natural systems: A surface-related effect. In Pyrite: Synthesis, Characterization and Uses; Whitley, N., Vinsen, P.T., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2013; Chapter 1; pp. 1–40. [Google Scholar]
- Palenik, C.S.; Utsunomiya, S.; Reich, M.; Kesler, S.E.; Wang, L.; Ewing, R.C. Invisible gold revealed: Direct imaging of gold nanoparticles in a Carlin-type deposit. Am. Mineral. 2004, 89, 1359–1366. [Google Scholar] [CrossRef]
- Tauson, V.L.; Lustenberg, E.E. Quantitative determination of modes of gold occurrence in minerals by the statistical analysis of analytical data samplings. Geochem. Int. 2008, 46, 423–428. [Google Scholar] [CrossRef]
- Tauson, V.L.; Babkin, D.N.; Akimov, V.V.; Lipko, S.V.; Smagunov, N.V.; Parkhomenko, I.Y. Trace elements as indicators of the physicochemical conditions of mineral formation in hydrothermal sulfide systems. Russ. Geol. Geophys. 2013, 54, 526–543. [Google Scholar] [CrossRef]
- Bolanz, R.M.; Kiefer, S.; Göttlicher, J.; Steininger, R. Hematite (α-Fe2O3)—A potential Ce4+ carrier in red mud. Sci. Total Envirn. 2018, 622–623, 849–860. [Google Scholar] [CrossRef] [PubMed]
- Naumkin, A.V.; Kraut-Vass, A.; Gaarenstroom, S.W.; Powell, C.J. NIST X-ray Photoelectron Spectroscopy Database. 2012. Available online: https://srdata.nist.gov/xps/EnergyTypeValSrch.aspx (accessed on 25 June 2018).
- Moulder, J.E.; Sticle, W.F.; Sobol, P.E.; Bomben, K.D. Handbook of X-ray Photoelectron Spectroscopy; Perkin-Elmer Corp.: Eden Prairie, MN, USA, 1992. [Google Scholar]
- Grosvenor, A.P.; Kobe, B.A.; Biesinger, M.C.; McIntyre, N.S. Investigation of multiplet splitting of Fe 2p XPS spectra and bonding in iron compounds. Surf. Interface Anal. 2004, 36, 1564–1574. [Google Scholar] [CrossRef]
- Groves, D.I.; Goldfarb, R.J.; Gebre-Mariam, M.; Hagemann, S.G.; Robert, F. Orogenic gold deposits: A proposed classification in the context of their crustul distributoin and relationship to other gold deposit types. Ore Geol. Rev. 1998, 13, 7–27. [Google Scholar] [CrossRef]
- Goncharov, V.I.; Voroshin, S.V.; Sidorov, V.A. Natalkinskoe Gold-Ore Deposit; North-East Complex Research Institute, Far-East Branch of RAS: Magadan, Russia, 2002. (In Russian) [Google Scholar]
- Goryachev, N.A.; Vikent’eva, O.V.; Bortnikov, N.S.; Prokof’ev, V.Y.; Alpatov, V.A.; Golub, V.V. The world-class Natalka gold deposit, Northeast Russia: REE patterns, fluid inclusions, stable oxygen isotopes, and formation conditions of ore. Geol. Ore Depos. 2008, 50, 362–390. [Google Scholar] [CrossRef]
- Mikhailov, B.K.; Struzhkov, S.F.; Natalenko, M.V.; Cimbalyuk, N.V. Multifactor model of large-volume gold-ore deposit Degdekan (Magadan region). Otechestvennaya Geol. 2010, 2, 20–31. [Google Scholar]
- Khanchuk, A.I.; Plyusnina, L.P.; Nikitenko, E.M.; Kuzmina, T.V.; Barinov, N.N. The noble metal distribution in the black shales of the Degdekan gold deposit in Northeast Russia. Russ. J. Pacif. Geol. 2011, 5, 89–96. [Google Scholar] [CrossRef]
- Palenova, E.E.; Belogub, E.V.; Novoselov, K.A.; Zabotina, M.V. Mineralogical and geochemical characteristics of gold-ore hosting carbonaceous series of Artemovskyi ore cluster (Bodaibo region). Izv. SO RAEN. Geol. Prosp. Explor. Ore Depos. 2013, 43, 29–36. (In Russian) [Google Scholar]
- Palenova, E.E.; Kotliarov, V.A.; Belogub, E.V.; Yuminov, A.M.; Zateeva, P.A. Formation conditions of gold-ore objects of Artemovskyi ore cluster (Bodaibo region). Vopr. Estestvoznaniya 2015, 3, 53–56. (In Russian) [Google Scholar]
- Smythe, D.J.; Brenan, J.M. Magmatic oxygen fugacity estimated using zircon-melt partitioning of cerium. Earth Planet. Sci. Lett. 2016, 453, 260–266. [Google Scholar] [CrossRef]
- Smythe, D.J.; Brenan, J.M. Cerium oxidation state in silicate melts: Combined fO2, temperature and compositional effect. Geochim. Cosmochim. Acta 2015, 170, 173–187. [Google Scholar] [CrossRef]
- Nishimura, K. A trace-element geochemistry model for imperfect fractional crystallization associated with the development of crystal zoning. Geochim. Cosmochim. Acta 2009, 73, 2142–2149. [Google Scholar] [CrossRef]
- Tauson, V.L. The principle of continuity of phase formation at mineral surfaces. Dokl. Earth Sci. 2009, 425, 471–475. [Google Scholar] [CrossRef]
- Bochkarev, A.V.; Trefilova, A.N.; Bobrov, M.F.; Tsurkov, N.A. Isotope separation during ionic crystal growth from solution. Russ. J. Phys. Chem. 2003, 77, 1868–1872. [Google Scholar]
- Burton, J.A.; Prim, R.C.; Slichter, W.P. The distribution of solute in crystals grown from the melt. Part I. Theoretical. J. Chem. Phys. 1953, 21, 1987–1991. [Google Scholar] [CrossRef]
- Watson, E.B. Surface enrichment and trace-element uptake during crystal growth. Geochim. Cosmochim. Acta 1996, 60, 5013–5020. [Google Scholar] [CrossRef]
- Graham, U.M.; Ohmoto, H. Experimental study of formation mechanisms of hydrothermal pyrite. Geochim. Cosmochim. Acta 1994, 58, 2187–2202. [Google Scholar] [CrossRef]
- Chen, J.H.; Harvey, W.W. Cation self-diffusion in chalcopyrite and pyrite. Met. Trans. B 1975, 6, 331–339. [Google Scholar] [CrossRef]
- Watson, E.B.; Cherniak, D.J.; Frank, E.A. Retention of biosignatures and mass-independent fractionations in pyrite: Self-diffusion of sulfur. Geochim. Cosmochim. Acta 2009, 73, 4792–4802. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Law, M.; Wu, R.Q. Atomic modeling of sulfur vacancy diffusion near iron pyrite surfaces. J. Phys. Chem. C 2015, 119, 24859–24864. [Google Scholar] [CrossRef]
- Hallström, S.; Höglund, L.; Ågren, J. Modeling of iron diffusion in the iron oxides magnetite and hematite with variable stoichiometry. Acta Mater. 2011, 59, 53–60. [Google Scholar] [CrossRef]
- Alibert, C. Rare earth elements in Hamersley BIF minerals. Geochim. Cosmochim. Acta 2016, 184, 311–328. [Google Scholar] [CrossRef]

| Number of Cryst. (Starting-Final Sample) | Characteristics of the Final Sample | TE Contents (ppm) * | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Num. of Cryst. | Range of Mass. (mg) | (mg) | (mm) | (mm2/mg) | (ppm) | |||||
| Gold | ||||||||||
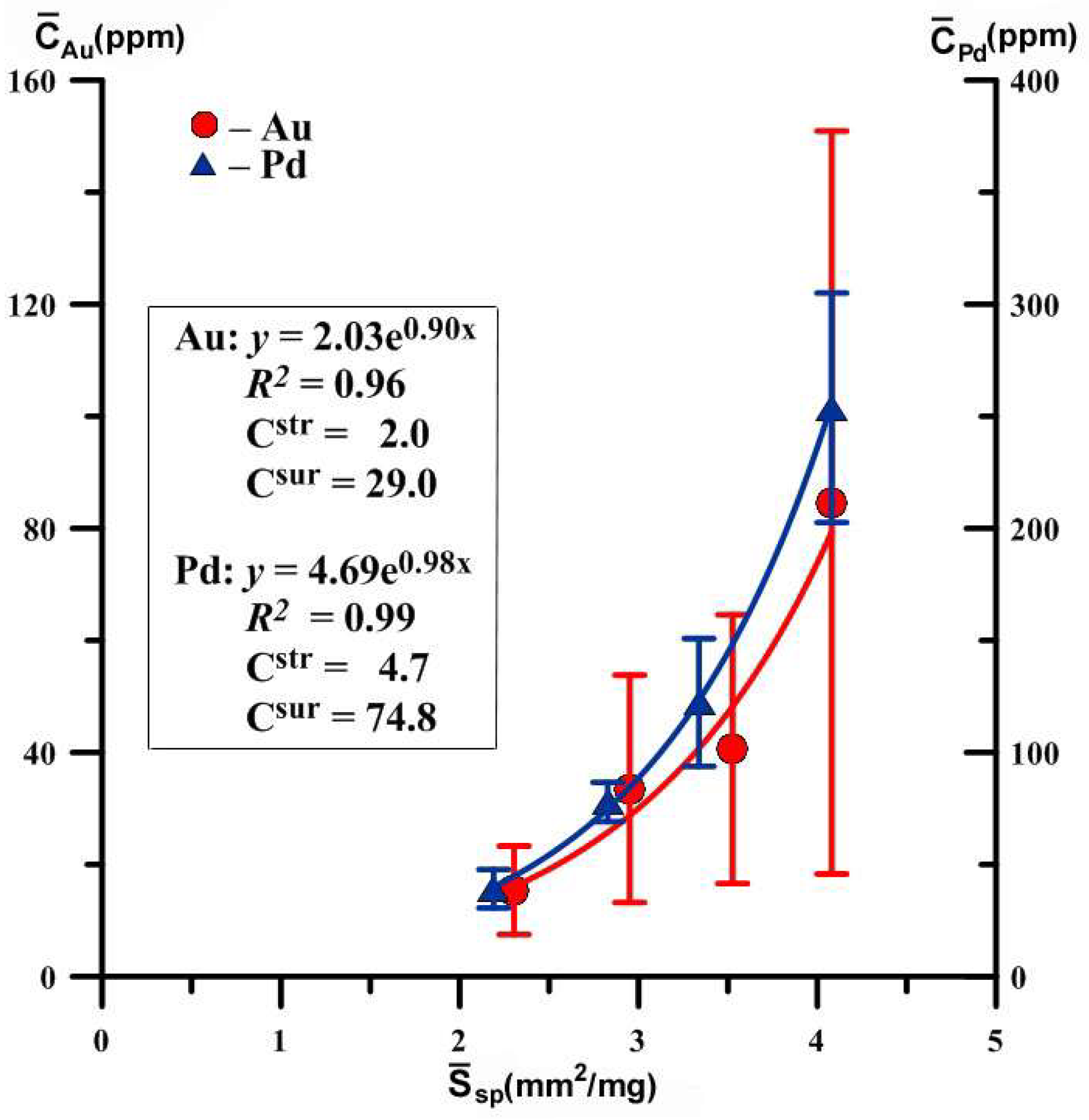
| 43–26 | 7 7 6 6 | 0.09–0.12 0.14–0.20 0.21–0.38 0.39–0.83 | 0.11 0.17 0.29 0.61 | 0.360 0.416 0.497 0.637 | 4.081 3.526 2.951 2.303 | 85 ± 66 41 ± 24 34 ± 20 15 ± 8 | 110 | 30 | 2.0 | 29.0 |
| Palladium | ||||||||||
| 41–31 | 9 7 7 8 | 0.09–0.12 0.14–0.21 0.23–0.38 0.39–1.48 | 0.11 0.20 0.33 0.71 | 0.360 0.439 0.519 0.670 | 4.081 3.338 2.828 2.190 | 254 ± 51 122 ± 28 78 ± 9 39 ± 8 | 111 | 78 | 4.7 | 74.8 |
| Metal | Mineral | Experimental Conditions | ** | Ref. | |||
|---|---|---|---|---|---|---|---|
| T (°C) | Batch | Solution * | |||||
| Gold | Magnetite | 450 500 | Fe2O3 + Fe(FeO) Fe2O3 + FeO | a.c., a.c. + HCl a.c. | 1.0 ± 0.3 0.5 | 9.5 ± 5.5 10 | [21] [24] |
| Mangan-magnetite | 450 500 | Fe2O3 + Mn2O3 ± FeO FeO + Mn2O3 | a.c. + HCl a.c. | 1.6 0.8 ± 0.5 | 9.4 17 ± 9 | [24] [24] | |
| Pyrite As-pyrite | 450 450 | Fe + S Fe + S + As | a.c., a.c. + Na2S, a.c. + HCl same | 0.14 ± 0.04 0.05 ± 0.03 | 0.3 ± 0.2 0.4 ± 0.5 | [23] [23] | |
| Hematite | 450 | Fe2O3 + FeO + Cr2O3 | a.c. | 4.3 | 63 | This work | |
| Platinum | Magnetite | 500 | Fe2O3 + FeO | same | 46 | 350 | same |
| Mangan-magnetite | 500 | FeO + Mn2O3 | same | 27 | 394 | same | |
| Pyrite | 500 | Fe + S ± As | a.c., a.c. + Na2S, a.c. + HCl | 21 ± 7 | 210 ± 80 | [25] | |
| Palladium | Magnetite | 450 500 | Fe2O3 + FeO + Mn2O3 Fe2O3 + FeO | a.c. + HCl a.c. | 2.6 3.4 | 53 84 | [24] [24] |
| Mangan-magnetite | 450 500 | Fe2O3 + FeO + Mn2O3 FeO + Mn2O3 | a.c. + HCl a.c. | 3.0 2.9 ± 0.7 | 71 52 ± 3 | [24] [24] | |
| Hematite | 450 | Fe2O3 + FeO + Cr2O3 | a.c. | 10.9 | 174 | This work | |
| Sample No. | Photo-Electron Peak | Lorentz a | Binding Energy (eV) | FWHM b (eV) | MPE c | MF d |
|---|---|---|---|---|---|---|
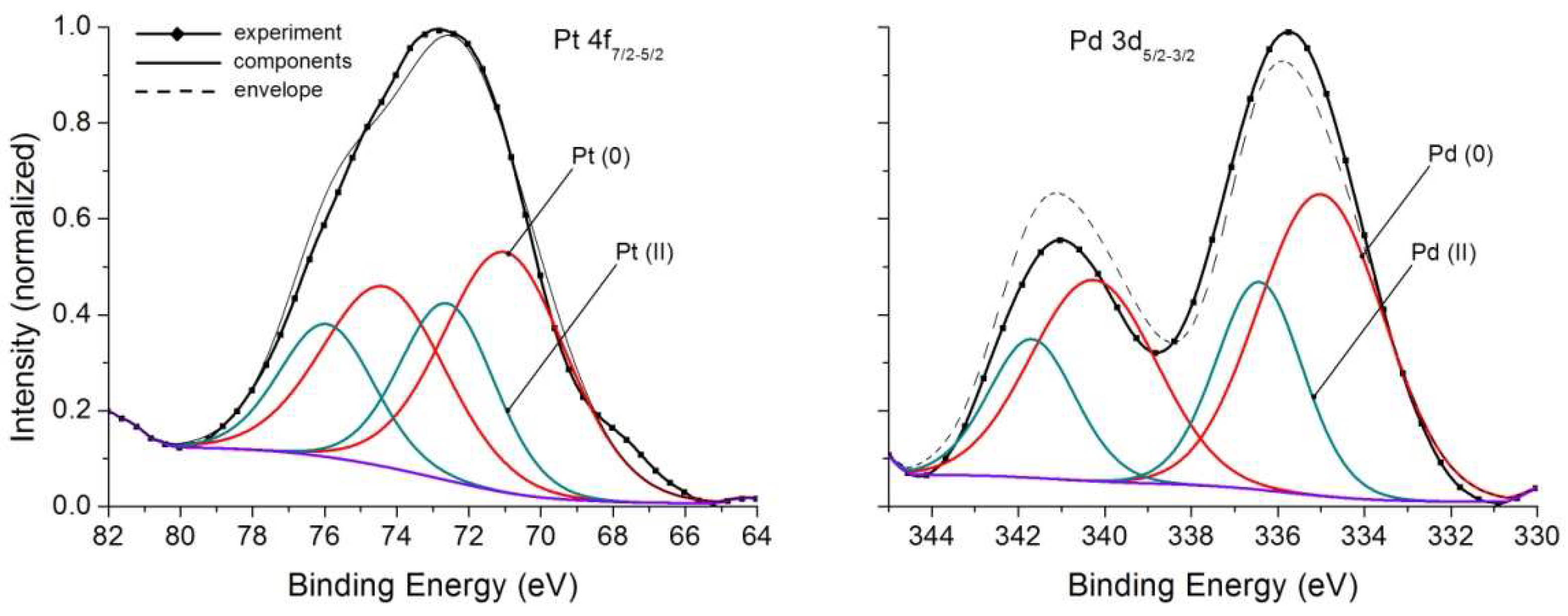
| 1 | 3d5/2 3d3/2 3d5/2 3d3/2 | 0.7 0.7 1.0 1.0 | 335.0 340.3 336.4 341.7 | 3.4 3.4 2.4 2.4 | Pd(0) Pd(II) | 0.67 0.33 |
| 2 | 4f7/2 4f5/2 4f7/2 4f5/2 | 0.7 0.7 0.7 0.7 | 71.0 74.4 72.6 75.9 | 4.0 4.0 3.1 3.1 | Pt(0) Pt(II) | 0.64 0.36 |
| Exper. No. | Mineral | Solution-Mineralizer | REE Concentrations, ppm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| In Crystals | In Solution from Sampler | ||||||||||
| Ce | Eu | Er | Yb | Ce | Eu | Er | Yb | Fe | |||
| 1 | Magnetite | 5% NH4Cl | 0.45 | 0.36 | 0.23 | 0.22 | 600 | 234 | 30.3 | 19.3 | 9880 |
| 2 | Magnetite | 10% NH4Cl | 0.26 | 0.30 | 0.83 | 1.23 | 407 | 210 | 136 | 77.7 | 11,290 |
| 3 | Hematite | 5% NH4Cl | 3.79 | 2.67 | 1.51 | 2.59 | 296 | 54.8 | 6.7 | 3.7 | 2340 |
| 4 | Hematite | 10% NH4Cl | 0.99 | 2.20 | 2.25 | 4.20 | 1190 | 135 | 11.5 | 7.3 | 9380 |
| Exper. No. * | Mineral | ||||
|---|---|---|---|---|---|
| Ce | Eu | Er | Yb | ||
| 1 | Magnetite | 10−5 | 2.1 × 10−5 | 10−4 | 1.6 × 10−4 |
| 2 | Magnetite | 10−5 | 2.2 × 10−5 | 9.5 × 10−5 | 2.5 × 10−4 |
| 3 | Hematite | 4.3 × 10−5 | 1.6 × 10−4 | 7.5 × 10−4 | 2.3 × 10−3 |
| 4 | Hematite | 1.1 × 10−5 | 2.2 × 10−4 | 2.6 × 10−3 | 7.7 × 10−3 |
| Exper. No. * | Mineral | , ppm | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ce | Eu | Er | Yb | Ce | Eu | Er | Yb | ||
| 1 | Magnetite | 24 | 26 | 55 | 44 | 5.3 × 10−4 | 1.5 × 10−3 | 2.4 × 10−2 | 3.2 × 10−2 |
| 2 | Magnetite | 33 | 64 | 93 | 74 | 1.3 × 10−3 | 4.7 × 10−3 | 1.1 × 10−2 | 1.5 × 10−2 |
| 3 | Hematite | 433 | 60 | 21 | 24 | 4.9 × 10−3 | 3.5 × 10−3 | 10−2 | 2.1 × 10−2 |
| 4 | Hematite | 412 | 64 | 43 | 55 | 4.6 × 10−3 | 6.4 × 10−3 | 4.9 × 10−2 | 10−2 |
| Sample * | Photo-Electron Peak | Binding Energy (eV) | FWHM (eV) ** | MPE ** | MF ** |
|---|---|---|---|---|---|
| 2 | 3d5/2 3d5/2 | 882.0 885.8 | 2.8 3.6 | Ce4+ Ce3+ | 28 72 |
| 2, Ar+ | 3d5/2 3d5/2 | 881.7 885.5 | 3.0 3.3 | Ce4+ Ce3+ | 38 62 |
| 3 | 3d5/2 3d3/2 | 882.0 900.6 | 3.0 3.0 | Ce4+ | 30 |
| 3d5/2 3d3/2 | 885.8 904.4 | 3.5 3.5 | Ce3+ | 70 | |
| 3, Ar+ | 3d5/2 3d3/2 | 881.2 899.8 | 3.0 3.0 | Ce4+ | 31 |
| 3d5/2 3d3/2 | 885.4 904.0 | 4.1 4.1 | Ce3+ | 69 |
| Sample * | High-Spin Multiplet Fe3+, Peak Number ** | High-Spin Multiplet Fe2+, Peak Number ** | Fe3+/Fe2+ | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | ||
| 1 | 710.6 | 711.8 | 713.0 | 714.2 | 708.3 | 709.5 | 710.7 | 1.1 |
| 2 | 710.6 | 711.8 | 713.0 | 714.2 | 708.4 | 709.6 | 710.8 | 1.2 |
| 3 | 710.0 | 711.2 | 712.4 | 713.6 | 708.5 | 709.7 | 710.9 | 1.1 |
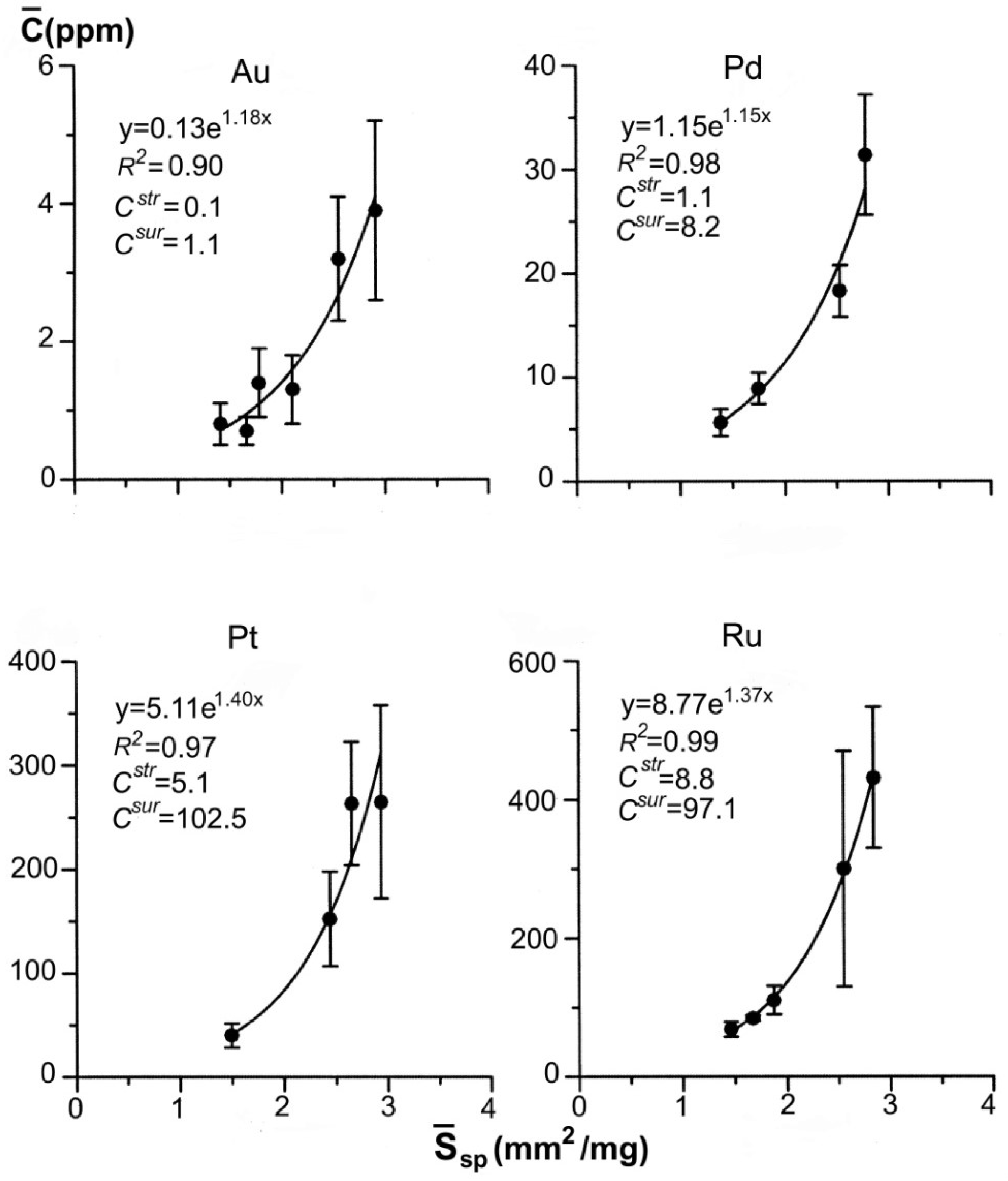
| Sample No. | Deposit | Number of Crystals (Starting–Final Sample) | Element | Element Concentration in Py (ppm) | (ppm) | (Au/Pt)aq | |
|---|---|---|---|---|---|---|---|
| Structural Mode | Surficial Mode | ||||||
| M-163/10 | Degdekan | 95–59 | Au | 0.21 | 0.53 | 2.1 | 21 |
| 92–71 | Pt | 2.0 | 7.1 | 0.1 | |||
| DG-10/14 * | same | 67–44 | Au | 0.13 | 1.1 | 1.3 | 5.4 |
| 34–22 | Pt | 5.1 | 102 | 0.24 | |||
| Kr-9 | Krasnoye | 80–56 | Au | 0.04 | 0.36 | 0.4 | 4.0 |
| 78–53 | Pt | 2.2 | 16 | 0.1 | |||
| Kr-39 | same | 86–55 | Au | 0.11 | 0.25 | 1.1 | 7.3 |
| 72–61 | Pt | 3.2 | 37 | 0.15 | |||
| UV-3/13 * | Natalkinskoe | 80–52 | Au | 0.29 | 1.37 | 2.9 | 1.6 |
| 79–52 | Pt | 37 | 189 | 1.8 | |||
| ZR-10/13 * | Zolotaya Rechka | 66–41 | Au | 3.4 | 6.3 | 34 | 56.7 |
| 65–47 | Pt | 12.0 | 259 | 0.6 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tauson, V.L.; Lipko, S.V.; Smagunov, N.V.; Kravtsova, R.G. Trace Element Partitioning Dualism under Mineral–Fluid Interaction: Origin and Geochemical Significance. Minerals 2018, 8, 282. https://doi.org/10.3390/min8070282
Tauson VL, Lipko SV, Smagunov NV, Kravtsova RG. Trace Element Partitioning Dualism under Mineral–Fluid Interaction: Origin and Geochemical Significance. Minerals. 2018; 8(7):282. https://doi.org/10.3390/min8070282
Chicago/Turabian StyleTauson, Vladimir L., Sergey V. Lipko, Nikolay V. Smagunov, and Raisa G. Kravtsova. 2018. "Trace Element Partitioning Dualism under Mineral–Fluid Interaction: Origin and Geochemical Significance" Minerals 8, no. 7: 282. https://doi.org/10.3390/min8070282
APA StyleTauson, V. L., Lipko, S. V., Smagunov, N. V., & Kravtsova, R. G. (2018). Trace Element Partitioning Dualism under Mineral–Fluid Interaction: Origin and Geochemical Significance. Minerals, 8(7), 282. https://doi.org/10.3390/min8070282






