Multi-Objective Parameter Optimisation of High-Pressure Grinding Rolls Based on Grey Relational Theory

Abstract

The roller press crushing of ore is a complex process involving the interplay of multiple factors. Roller dimensions, gap settings, and rotational speed all influence this process, which in turn affects the comprehensive crushing performance of the high-pressure grinding rolls (HPGR). Therefore, to simultaneously enhance the HPGR’s size reduction effectiveness (SRE) and throughput while controlling its energy consumption, wear, and edge effect, multi-objective parameter optimization of the HPGR is required. This study utilizes the Discrete Element Method (DEM) to simulate ore comminution within an HPGR. By first dividing the release zone into segments, the particle size distribution of the crushed product at different locations within this zone is investigated. Then, the influence of various factors on the SRE at different locations within HPGR is examined through single-factor experiments. Subsequently, the relative influence of roller diameter, roller width, roller speed, and roll gap on the comprehensive crushing performance of the HPGR is determined through signal-to-noise ratio (SNR) analysis and analysis of variance (ANOVA). Finally, multi-objective parameter optimization of the roller press crushing is conducted based on grey relational analysis (GRA), incorporating the weights assigned to different response target. The results indicate that the proportion of unbroken ore particles is relatively significant, primarily due to the edge effect. Further analysis reveals that along the horizontal diameter of the rollers, regions closer to the roller surface exhibit better SRE. Additionally, roller speed is identified as the most influential factor affecting the uniformity of SRE in the HPGR. The application of GRA to the multi-objective optimization of roller press crushing enables effective balancing of the comprehensive crushing performance in HPGR.

1. Introduction

As an efficient comminution equipment in the mineral processing industry, high-pressure grinding rolls (HPGR) are widely used in the fine and ultra-fine crushing processes of various ores, playing a critical role within the overall ore crushing circuit [1,2,3,4,5]. As ore passes through the HPGR, interparticle breakage occurs under bed compression between the two rollers. This breakage mechanism results in energy consumption reductions of 10%–50% compared to conventional grinding mills [6,7,8,9]. Studs are embedded in the roller surfaces to minimize wear, while cheek plates are fitted to both sides of the rolls to prevent material spillage.

Figure 1a shows the structural construction of HPGR. The primary components comprise the roller system, feed system, hydraulic system, main motor, and frame. Additionally, the complete unit incorporates ancillary systems including lubrication, monitoring, the main drive motor cooling station, and others [10]. The working principle of the HPGR is shown in Figure 1b. The roll assembly consists of a fixed roll and a floating roll. Driven by the main drive motor, both rolls rotate synchronously in opposite directions. The fixed roll is constrained against horizontal displacement, while the floating roll is capable of horizontal movement. This movement, actuated by the hydraulic system, applies high pressure to the material fed into the gap between the rolls [11,12].

The roller crushing process of material can be divided into three characteristic areas: acceleration zone, compression zone and release zone. The material enters from the top of HPGR feeding device and enters the acceleration zone under the action of its own gravity. Afterwards, under the combined action of the roll pressure and the frictional force between the material and the rolls, the material undergoes accelerated motion and is carried by the rolls to the compression zone. When the material enters the compression zone, squeezing force is applied to the rollers, causing the floating roll to have a tendency to move outward. However, the reverse pressure provided by the hydraulic system balances the thrust of the material and maintains the stability of the roll gap. In the stabilized roll gap, the material undergoes laminated crushing with the rotation of the rolls, and the crushed material is finally discharged from the release zone [13].

The breakage of particles in the HPGR’s compression zone constitutes a dynamic process governed by the coupled effects of multiple factors. It is collectively regulated by parameters such as roller diameter, roller width, roller speed, among others [14,15]. Therefore, to enhance the comprehensive crushing performance of the HPGR, multi-objective optimization considering the aforementioned factors must be performed. This optimization aims to ensure high comminution efficiency and throughput while simultaneously achieving low energy consumption, reduced wear, and minimized edge effect.

Mathematical methods formed the cornerstone of engineering applications, where numerical simulation and parameter optimization effectively addressed practical engineering challenges. Zhang et al. [16] employed the Discrete Element Method (DEM) to simulate the breakage process within the HPGR. The results demonstrated that roller speed had a significant influence on the HPGR’s throughput but exhibited a relatively minor effect on the particle size distribution of the crushed product. Furthermore, the ore exhibited enhanced breakage efficiency and reduced residual breakage energy after secondary grinding. Rodriguez et al. [17] employed the DEM to simulate the breakage process in HPGR equipped with flanges. The results revealed that rolls with a higher aspect ratio yielded finer product size distribution. Furthermore, HPGR equipped with flanges achieved higher throughput compared to those fitted with cheek plates and produced a more uniform particle size distribution. Barrios et al. [18] employed a coupled DEM-Multi-Body Dynamics (DEM-MBD) approach to more accurately characterize the dynamic nip zone variations in HPGR. The results showed strong agreement between the DEM-MBD simulations and phenomenological model predictions for throughput, operating gap, and roll pressure distribution. Zou et al. [19] analyzed the wear characteristics of the striped roller surface and its impact on HPGR performance using the Archard wear model. The study revealed that the wear was most severe in the central zone of the rollers, and the wear extent on the moving roller exceeded that on the fixed roller. As roller surface wear intensified, the operating power decreased significantly and the product particle size became coarser, while the effect on throughput was relatively minor. Thivierge et al. [20,21] developed a comprehensive process model framework for HPGR and validated it using 18 distinct datasets. The model demonstrated reasonably accurate predictions of HPGR mass flow rate, power consumption, and particle size distribution. Dundar et al. [22] measured the values of the selection and breakage functions in the population balance model via granular bed compression tests and predicted the product size distribution after roll crushing under different operating conditions. Torres et al. [23] investigated the influence of factors such as ore properties and HPGR operating parameters on SRE. Based on this, they developed a phenomenological and steady-state model for roller press comminution. This model could predict the SRE of the roller press under various comminution processes. Yang et al. [24] optimized the operating parameters of the HPGR using the entropy weight method and the response surface methodology (RSM), respectively, and analyzed roll surface pressure, throughput, and particle diameter ratio. Consequently, the response surface methodology demonstrated its ability to capture the interaction effects among factors, leading to superior global optimization. Gu et al. [25] characterized the edge effect of the HPGR by the pressure difference across different zones in the compression area and optimized it using the response surface methodology. The results showed that the optimized set of process parameters effectively reduced the variance in force distribution across different zones, thereby improving the HPGR’s edge effect.

Numerous scholars conducted extensive research on various aspects of HPGR through numerical simulation. However, studies on the particle size distribution of its crushed products and the variation patterns of SRE at different locations within HPGR remain limited. Furthermore, research concerning the optimization of HPGR crushing parameters generally focused on single-objective optimization, while paying less attention to multi-objective parameter optimization problems under complex conditions.

In summary, this study conducted multi-objective parameter optimization for ore roll crushing based on grey relational theory. As the fine particle mass fraction in the crushed product (reflecting size reduction effectiveness) is a common indicator of HPGR crushing performance, it was investigated first in this study. Subsequently, the Taguchi method was employed for experimental design. SNR analysis and ANOVA were then utilized to determine the significance of the influence exerted by different parameters on each response target. Finally, multi-objective parameter optimization for roll crushing was performed based on grey relational theory. This resulted in obtaining the optimal parameter combination that satisfied the assigned weights for each response target.

2. Materials and Methods

2.1. DEM Model and Particle Breakage

The discrete element method (DEM) was proposed by Prof. Cundall in 1971 based on the principles of molecular dynamics [26]. DEM is a numerical simulation method that addresses discontinuous media problems by calculating the movement and collision data of particles. This method has unique advantages and is widely used in the fields of mineral processing, geotechnical engineering, pharmaceuticals [27,28,29].

The ore breakage process in the HPGR was simulated using the DEM software EDEM 2023 in this study. The Tavares UFRJ Breakage model (Tavares model) was employed as the breakage model. The Tavares model demonstrated high computational accuracy and efficiency. Furthermore, it facilitated the convenient quantification of the granulometric distribution of the crushed products. The Tavares model is a model that describes the law of particle damage accumulation and weakening, the principle of the model is shown in Figure 2 [30,31].

The relationship between the initial fracture energy of each particle at generation and its fracture probability conforms to the variation in the upper-truncated lognormal distribution, given by [32,33].

$$P(E)=0.5\left\{1+erf\left[(\ln E^{*}-\ln E_{50})/\sqrt{2}\sigma \right]\right\}$$

(1)

$$E^{*}={Emax}_{max}$$

(2)

where E is the particle fracture energy distribution corresponding to the maximum stressing energy that it can sustain in a collision, E_max is the upper truncation value of the distribution, E₅₀, σ are the median and standard deviation of the distribution, respectively. The median specific fracture energy of a particle is defined as [32,33]

$$E_{50}=\left[E_{\infty }/(1+k_p/k_s)\right]\left[1+{(d_0/d_p)}^{\phi }\right]$$

(3)

where E_∞ is the limiting value of particle crushing energy, d₀ is the transition particle size from crack emergence to extension, φ can be fitted by crushing tests, d_p is a representative size; k_p and k_s are the stiffnesses of the particles and the steel, respectively.

If the energy applied to the particle is less than its residual fracture energy, the model will be updated based on continuum damage mechanics. The updated fracture energy is considered as an intrinsic property of the particle and is given by [34,35]

$$E_f^{\prime }=E_f(1-D)$$

(4)

$$D={\left\{\left[2\gamma /(2\gamma -5D+5)\right](e{E}_k/e_f)\right\}}^{2\gamma /5}$$

(5)

where E_f is the fracture energy of the particle, D is the damage, eE_k is effective impact energy, and γ is the damage accumulation coefficient, which characterizes the amenability of a material to sustain damage before catastrophically breaking. Finally, e is the proportion of energy involved in a collision which is allocated to the particles based on their stiffness. Given by

$$e=1/(1+k_p/k_s)$$

(6)

where K_p is the particle stiffness and K_s is the stiffness of the surface in contact with the particles. If two identical particles collide then the energy is distributed equally between them, K_p = K_s in the above equation e = 0.5.

The degree of fragmentation of the particles is denoted by t₁₀, a parameter that represents the proportion of fragments in the offspring fragments that are smaller than 1/10 of the particle size of the parent particle.

$$t_{10}=A\left\{1-\exp \left[-b(e{E}_k/E_f)\right]\right\}$$

(7)

where A and b are parameters fitted from the impact test of the particle [34,35].

2.2. Archard Wear Model

During the operation of the roller press, the wear of the rollers and cheek plates is quite severe. Moreover, once worn out, they are not easy to replace, which affects the processing efficiency. Therefore, wear is equally important in evaluating the comprehensive crushing performance of the HPGR.

The Archard Wear model is based on the theory proposed by Archard in 1953. This theory posits that the wear volume of contacting surfaces is proportional to the frictional work generated by particles. Grounded in experimental observations and empirical formulations, the Archard Wear model enables reliable quantification of wear volume. In this study, the wear volume, Δv, was calculated using this model as follows [36]

$$\Delta v={\displaystyle \frac{K}{H_{\mathrm{v}}}}\left|F_{\mathrm{n}}\right|\Delta d=W\left|F_{\mathrm{n}}\right|\Delta d$$

(8)

where H_v denotes the Vickers hardness (Pa) of the contacting body, K is the dimensionless wear coefficient, F_n represents the normal contact force between particles and the wearing body, Δd signifies the sliding distance of particles on the body’s surface, and W is the wear constant. The wear depth can be expressed as [36]

$$\Delta h_w={\displaystyle \frac{\Delta v}{A}}$$

(9)

where A is the unit area. The wear principle of the Archard model is shown in Figure 3 [19].

Wear models in the DEM were widely used in wear studies of various types of mills [37,38,39]. Since the Archard Wear model responds to the wear depth of the HPGR, it was used in this paper to analyze the wear of the rolls and cheek plates. The wear constants for this model Ref. [40].

2.3. HPGR Crushing Process Simulation

For ensure the stability of the roller press process, it is generally necessary to screen the feed material to ensure that the feed size is within a certain size range. For industrial medium and large-scale HPGRs, the feed size generally depends on the type and dimensions of the ore. Specifically for iron ore processing, the typical feed size ranges from 20 to 40 mm. This study adopted Benxi iron ore as the research subject and conducted parameter optimization on an industrial-scale HPGR with a feed size of 32 mm. During the crushing of this iron ore particle size fraction, roller diameters were typically selected within the range of 1.5–2.5 m, while diameter-to-width ratios generally ranged from 1.33 to 2.86. Three-dimensional models of the rolls and cheek plates were created using Creo parametric modelling software 5.0 and subsequently assembled. The rolls had a diameter of 2000 mm and a width of 1000 mm, with a roll gap of 38 mm. Studs with a diameter of 30 mm and a height of 7 mm were arranged in a regular array pattern on the roll surfaces. The assembled HPGR model configured with these features is shown in Figure 4.

This study calibrated the parameters required by the Tavares breakage model using standard uniaxial compression breakage tests and drop-weight impact breakage tests. The iron ore used for the breakage tests was from a Benxi processing plant, with an iron content of 40% Fe and a particle size range of 20–60 mm. The uniaxial compression crushing test was used to determine the fracture energy of iron ore, which was fitted to the fracture probability to obtain the fracture energy-fracture probability relationship for iron ore of different grain sizes (Figure 5a). The drop hammer impact crushing test was used for iron ore crushing and screening (Figure 5b). The t₁₀ parameter was obtained and used to calculate the particle size distribution of the crushed ore. Detailed experimental procedures were described in the authors’ previous studies [41]. The parameters of the Tavares model are shown in

Table 1. Parameters of the Tavares model obtained from the tests.

γ	E Infinity	d0	Phi (Φ)	Std Deviation	Alpha Percentage	b
5	92.27	13.2	2.08	2.62	42.13	0.38

.

In practice, the ore is first screened to ensure that the feed size is within a certain range and then enter the HPGR. However, a small number of ore beyond the screening range will also enter the HPGR. Therefore, this study analyzed the feed particle size distribution of HPGR through ore sieve analysis, with the results as shown in

Table 2. The feed particle size distribution of HPGR.

Particle Size (mm)	17.6	22.4	27.2	28.8	32	33.6	35.2
Mass ratio (%)	1	2	5	10	72	5	5

.

A discrete element simulation of the ore roll crushing process was established using the above model. Figure 6 shows a simulation of the HPGR crushing process.

3. The Size Reduction Effectiveness of HPGR

3.1. Particle Size Distribution of Crushed Products

The particle size distribution (PSD) of post-compaction ore serves as a direct indicator of SRE and constitutes the primary quantitative measure for evaluating crusher performance. To investigate the PSD of HPGR-processed ore, particle monitoring sensors were installed in the discharge zone using the built-in particle monitoring feature of the EDEM. This monitor measured the dimensions of ore particles passing through the detection area while simultaneously counting their quantities. Figure 7a illustrates the positioning of the monitoring instruments. Figure 7b displays the PSD of the crushed ore, where unfragmented ore constitutes a substantial proportion (approximately 25%) of the total ore mass. This phenomenon primarily arises from inherent edge effects within the HPGR system.

Ore exhibits distinct motion and stress conditions at different positions in the compression zone; consequently, the PSD after extrusion undergoes corresponding changes. To investigate the PSD characteristics of ore fragmented at different compression zone locations, the release zone was partitioned along both the axial and radial dimensions of the rolls. The release zone was partitioned along the roller axial and radial directions: the axial direction is divided into nine equal segments, while the radial direction is segmented into five zones, as illustrated in Figure 8. By continuously monitoring particle size and quantity of ore across different zones, the PSD of crushed products in distinct regions of the HPGR was determined. The PSD of crushed products at different HPGR locations are illustrated in Figure 9. The vertical axis indicates the percentage mass of ore passing through the corresponding sieve size.

The PSD characteristics of comminution products across axial segments of the roll are illustrated in Figure 9a. In the axial direction, regions proximal to the cheek plates (roll ends) exhibited reduced SRE, resulting in a lower mass proportion of finer-sized products post-breakage. The central axial zone exhibited a diminished mass fraction of unfragmented particles. Optimal SRE occurred in regions flanking the roll centre (Levels 4 and 6). The axial pressure distribution across the HPGR roll surface exhibited a downward-opening parabolic profile. Consequently, ore particles in the central roll region were subjected to elevated pressure, whereas the roll ends demonstrated significantly reduced pressure due to insufficient lateral confinement. Concurrently, the inherent clearance between the roll periphery and cheek plates caused a fraction of ore particles to bypass effective compression while traversing the compression zone.

Figure 9b illustrates the particle size distribution of comminution products along the five radial zones established in Figure 8b. Along the radial orientation of the rolls, ore particles in direct contact with the roll surfaces underwent intense confinement pressure exerted by both the rolls and surrounding material, inducing enhanced fragmentation. Ore positioned in the central inter-roll gap region (non-contacting with roll surfaces) exhibited significantly diminished breakage intensity, resulting from the reduced density of the material bed [41].

3.2. Effect of Operating Variables on Size Reduction

The HPGR can be used for fine and ultra-fine crushing of ores, as well as in the preparation stage prior to grinding to reduce the feed particle size. Consequently, the mass percentage of HPGR product meeting the particle size specifications for grinding mill feed serves as a quantitative indicator of its size reduction efficacy. The mineral processing industry widely acknowledges that ores crushed by HPGR to particle sizes ≤ 6 mm are suitable for direct feed into grinding mills [24,41]. Therefore, the SRE of HPGR was quantified by the mass percentage of product particles below 6 mm (P₆). Ten levels were selected for each of the four parameters—roller diameter, roller width, roll gap, and roller speed—to analyze their effects on ore fragmentation at different locations within HPGR. The division of the release zone is illustrated in Figure 8, while parameter values at different experimental levels are tabulated in

Table 3. Parameters of simulation models at different levels.

Level	1	2	3	4	5	6	7	8	9	10
roll diameter (mm)	1600	1700	1800	1900	2000	2100	2200	2300	2400	2500
roll width (mm)	742	806.5	871	935.5	1000	1064.5	1129	1193.5	1258	1322.5
roll gap (mm)	34	35	36	37	38	39	40	41	42	43
roll speed (m/s)	1.26	1.51	1.76	2.01	2.26	2.52	2.77	3.02	3.27	3.52

. Using EDEM, simulations of the HPGR comminution process employing distinct parameter sets were conducted, and the resultant PSD of crushed products was analyzed.

Variations in SRE across axial roll regions due to different factors appear in Figure 10a–d, while the corresponding standard deviation is presented in Figure 10e [25]. The standard deviation effectively captured the uniformity of SRE across regions, corresponding to the edge effects in HPGR operation. Roller diameter significantly influenced SRE and edge effects (Figure 10a,e). As roller diameter primarily governed the HPGR’s nip zone angle and material layer thickness, it substantially influenced stress distribution within the particle bed. This consequently affected SRE and edge effects. In addition, the SRE of the HPGR gradually diminished with increasing roll gap, while it was minimally affected by roll width and roll speed (Figure 10b–d).

Increasing roll diameter enhanced the SRE of the HPGR but simultaneously induced more pronounced edge effects. This compromised the overall comminution performance, indicating that practical operations require balancing these counteracting factors. An increase in both roll gap resulted in reduced SRE across all axial zones of the rolls but simultaneously mitigated the edge effect in HPGRs. HPGR edge effects were minimally influenced by roller width but exhibited progressive reduction with increasing rotational speed.

Variations in SRE across radial roll regions resulting from different factors are illustrated in Figure 11a–d, while the standard deviation of this effectiveness metric is presented in Figure 11e. The influence trends of the investigated factors on SRE across radial direction of the rolls were similar to those observed along the axial direction. Roller diameter emerged as the most influential factor on SRE (Figure 11a). When the roll diameter was increased from 1600 mm to 2500 mm, the SRE improved by approximately 10% across all regions along this direction. With the exception of roll speed, other factors exerted minimal effects on the uniformity of the SRE along the radial direction of the rolls (Figure 11e). When the roll speed was increased from 1.26 m/s to 3.52 m/s, the SRE of ore decreased at the roll contact zones, while a marginal improvement was observed in the inter-roll central region. However, further increases in roll speed resulted in reduced SRE across all regions. In summary, increased roller speed exerted a minor effect on the overall SRE of the HPGR, a conclusion that aligned with the findings reported by Zhang et al. [16]. While roller speed primarily influenced the uniformity of crushed products across distinct zones of the HPGR.

4. Multi-Objective Parameter Optimization

4.1. Experimental Design

The Taguchi orthogonal array design proves a highly efficient and robust experimental methodology that effectively resolves multi-objective optimization challenges under complex conditions. This approach is particularly suitable for investigating ore comminution processes involving coupling effects among multiple operational parameters in HPGR. The Taguchi orthogonal design employs orthogonal arrays with different factor levels to evaluate the effects of individual factors on the response target. This orthogonal array design enables representative experimental results with balanced dispersion and comparable characteristics to be achieved with significantly fewer experimental runs [42]. In this paper, the statistical analysis software Minitab 22 was used for experimental design and parameter optimization.

Based on the preceding analysis, a Taguchi orthogonal array design was employed with roller diameter, roller width, roller speed, and roll gap as the parameters to be optimized, each assigned five levels.

Table 4. The levels and factors in the experiment.

Factor	Level 1	Level 2	Level 3	Level 4	Level 5
Roll diameter (mm)	1600	1800	2000	2200	2400
Roll width (mm)	742	871	1000	1129	1258
Roll speed (m/s)	1.26	1.76	2.26	2.77	3.27
Roll gap (mm)	34	36	38	40	42

presents five distinct levels assigned to each of the four parameters.

Table 5. Table of Taguchi’s orthogonal experiments.

NO.	Roll Diameter (mm)	Roll Width (mm)	Roll Speed (m/s)	Roll Gap (mm)
1	1600	742	1.26	34
2	1600	871	1.76	36
3	1600	1000	2.26	38
4	1600	1129	2.77	40
5	1600	1258	3.27	42
6	1800	742	1.76	38
7	1800	871	2.26	40
8	1800	1000	2.77	42
9	1800	1129	3.27	34
10	1800	1258	1.26	36
11	2000	742	2.26	42
12	2000	871	2.77	34
13	2000	1000	3.27	36
14	2000	1129	1.26	38
15	2000	1258	1.76	40
16	2200	742	2.77	36
17	2200	871	3.27	38
18	2200	1000	1.26	40
19	2200	1129	1.76	42
20	2200	1258	2.26	34
21	2400	742	3.27	40
22	2400	871	1.26	42
23	2400	1000	1.76	34
24	2400	1129	2.26	36
25	2400	1258	2.77	38

displays the orthogonal array layout constructed following Taguchi’s methodology.

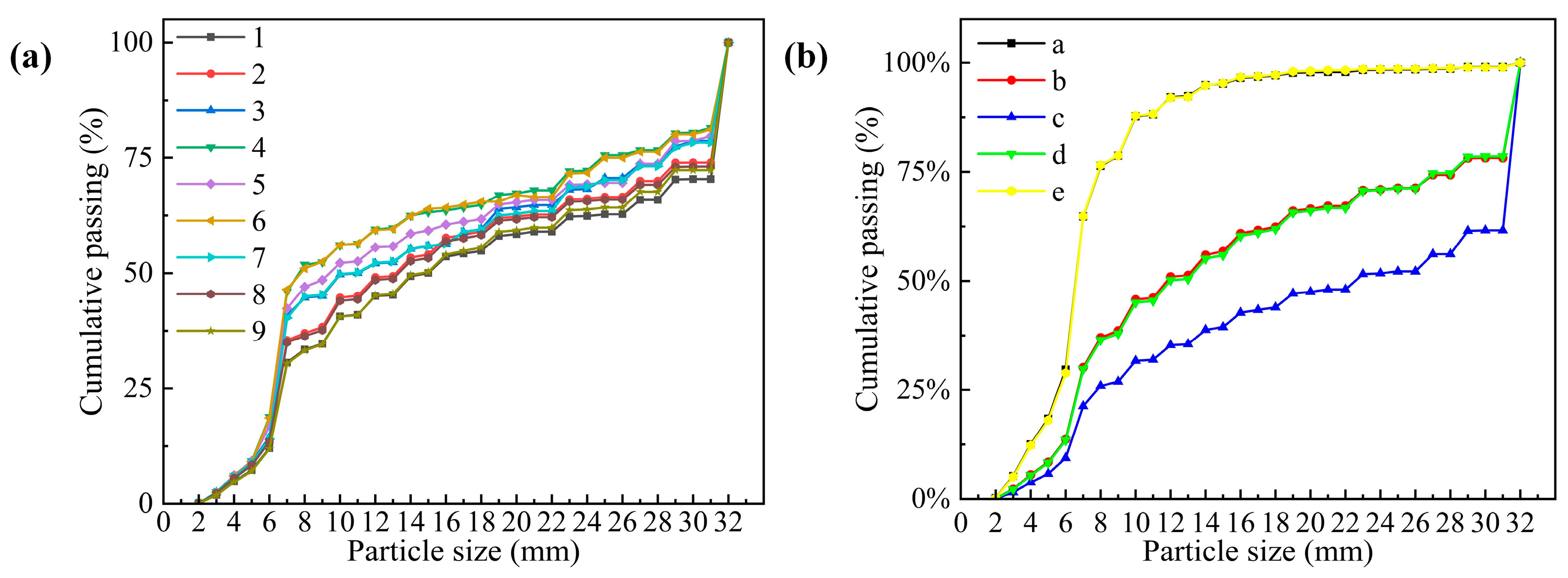
This study targeted five optimization objectives for the HPGR: SRE, throughput, average energy consumption, wear, and edge effect. The optimization objective was to maintain high SRE and throughput of the HPGR while reducing average energy consumption, wear, and edge effects. The SRE (%) of the HPGR was still quantified by the mass fraction of crushed product with particle size ≤ 6 mm. The throughput (t/h) was defined as the mass of ore passing through the release zone per hour. The energy consumption (kwh/t) of the HPGR was characterized by the average energy expended per ton of ore processed by a single roller. The wear (mm/h) of the HPGR was defined as the sum of the average hourly wear losses on both the roller and the cheek plates. The edge effect (%) of the HPGR was quantified as the standard deviation of SRE across different axial positions of the roller.

4.2. Analysis of Variance and Signal-to-Noise Ratio

The Taguchi method employs the signal-to-noise ratio (SNR) to quantify process robustness. Depending on distinct requirements for each optimization objective, the SNR is categorized into three characteristics: larger-the-better (LTB), smaller-the-better (STB), and nominal-the-best (NTB). In the optimization of HPGR, SRE (I) was set as the primary objective, with the optimization expectation that larger values indicate better outcomes. Consequently, the analysis of SRE adopted the LTB characteristic. Under the premise of ensuring SRE, the throughput (II) of the roller press was also treated with the LTB characteristic. For the optimization of HPGR, smaller values were preferred for average energy consumption (III), wear (IV), and edge effect (V). Consequently, the smaller-the-better (STB) characteristic was applied to the analysis of these corresponding objectives. The SNR for distinct characteristic types were derived through the following [43]:

$$S/N=\left\{\begin{array}{l}-10\log \left({\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\frac{1}{y_i^2}}\right)LTB\\ -10\log \left({\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{y}_i^2}\right)STB\\ -10\log \left({\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(y_i-m\right)}^2}\right)NTB\end{array}\right.$$

(10)

where y_i is the response target and n denote the total number of trials.

Table 6. ANOVA table for response targets.

Source		Roll Diameter (A)	Roll Width (B)	Roll Speed (C)	Roll Gap (D)	Residual	Total Variation
Degrees of freedom (DOF)		4	4	4	4	8	24
(I)	Seq SS	316.185	4.073	8.956	106.932	0.829	436.975
	Adj MS	79.0463	1.0181	2.2391	26.733	0.1036
	F	762.72	9.82	21.61	257.95
	p	0	0.004	0	0
(II)	Seq SS	112,134	3,337,474	3,696,765	37,502	108,576	7,292,451
	Adj MS	28,034	834,368	924,191	9376	13,572
	F	2.07	61.48	68.10	0.69
	p	0.178	0	0	0.619
(III)	Seq SS	0.000952	0.000008	0.000871	0.000211	0.000029	0.002071
	Adj MS	0.000238	0.000002	0.000218	0.000053	0.000004
	F	65.18	0.52	59.62	14.45
	p	0	0.723	0	0.001
(IV)	Seq SS	0.004932	0.000536	0.000463	0.001489	0.000204	0.007625
	Adj MS	0.001233	0.000134	0.000116	0.000372	0.000026
	F	48.29	5.25	4.53	14.58
	p	0	0.023	0.033	0.001
(V)	Seq SS	1.37501	0.01339	1.37674	0.26132	0.06677	3.09323
	Adj MS	0.343752	0.003348	0.344185	0.065329	0.008347
	F	41.18	0.40	41.24	7.83
	p	0	0.803	0	0.007

provides the analysis of variance (ANOVA) table for these response targets, where conducting ANOVA reveals the statistical significance of process parameter effects on individual response targets. The response tables of the SNR of each response target are presented in

Table 7. Response table on response target signal-to-noise ratio.

Response Target		Level					Range	Ranking
		1	2	3	4	5
(I)	A	28.47	29.15	29.86	30.48	31.27	2.80	1
	B	29.74	29.79	29.80	29.90	29.99	0.26	4
	C	29.61	29.76	29.93	29.94	29.98	0.37	3
	D	30.65	30.24	29.84	29.47	29.03	1.61	2
(II)	A	64.50	64.84	65.09	65.33	65.57	1.06	3
	B	62.44	63.92	65.21	66.36	67.39	4.95	2
	C	61.76	64.16	65.61	66.59	67.22	5.46	1
	D	64.80	64.95	65.10	65.19	65.29	0.48	4
(III)	A	34.52	32.76	31.65	30.31	28.99	5.53	1
	B	31.75	31.61	31.70	31.70	31.47	0.28	4
	C	34.55	32.68	31.48	30.29	29.22	5.32	2
	D	30.68	30.90	31.58	32.21	32.85	2.17	3
(IV)	A	39.46	36.73	33.92	30.67	26.63	12.83	1
	B	34.42	34.28	33.68	32.89	32.15	2.27	3
	C	33.75	33.33	32.39	33.66	34.29	1.90	4
	D	30.05	31.60	33.68	35.19	36.89	6.84	2
(V)	A	−3.89	−4.60	−5.09	−5.81	−7.04	3.16	2
	B	−5.44	−5.30	−4.99	−5.43	−5.27	0.45	4
	C	−6.69	−6.15	−5.47	−4.61	−3.51	3.18	1
	D	−6.12	−5.43	−5.11	−5.01	−4.77	1.36	3

.

In ANOVA, the F-distribution table serves as a statistical tool to determine the significance of experimental results. It distinguishes the significance of individual factors based on degrees of freedom and significance levels. The common values of significance level (α) are 0.1, 0.05, and 0.01, indicating the rigour of the test. In ANOVA, degrees of freedom comprise the numerator degrees of freedom (df₁) and the denominator degrees of freedom (df₂). Here, df₁ equals the number of treatment groups minus one, while df₂ equals the total degrees of freedom minus the sum of degrees of freedom for all factors in the experiment. The F-distribution table provides critical values as follows: F_0.1(4,8) = 2.81, F_0.05(4,8) = 3.84, and F_0.01(4,8) = 7.01.

Table 6 shows that all four factors exerted significant effects on SRE, as their F-values exceeded F_0.01(4,8). Among these, roller diameter demonstrated the highest F-value, indicating its extremely significant influence, followed by roll gap. In contrast, roller speed and roll width exhibited less pronounced effects. The SNR-based response ranking revealed that the statistical significance ranking of the four factors affecting SRE was: roller diameter > roller gap > roller speed > roller width (Table 7).

Based on the ANOVA for HPGR throughput, the F-values for roll width and roll speed were significantly greater than F_0.01(4,8), indicating an extremely significant impact on throughput. Conversely, the F-values for roll diameter and roll gap were lower than F_0.1(4,8), suggesting that their effects were negligible (Table 6). The SNR-based response ranking revealed that the statistical significance ranking of the four factors affecting throughput was: roller speed > roller width > roller diameter > roller gap (Table 7).

ANOVA of the HPGR’s average energy consumption, wear, and edge effect revealed the following significance rankings of influencing factors:

• Average energy consumption: roll diameter > roll speed > roll gap > roll width.
• Wear: roll diameter > roll gap > roll width > roll speed.
• Edge effect: roll speed > roll diameter > roll gap > roll width.

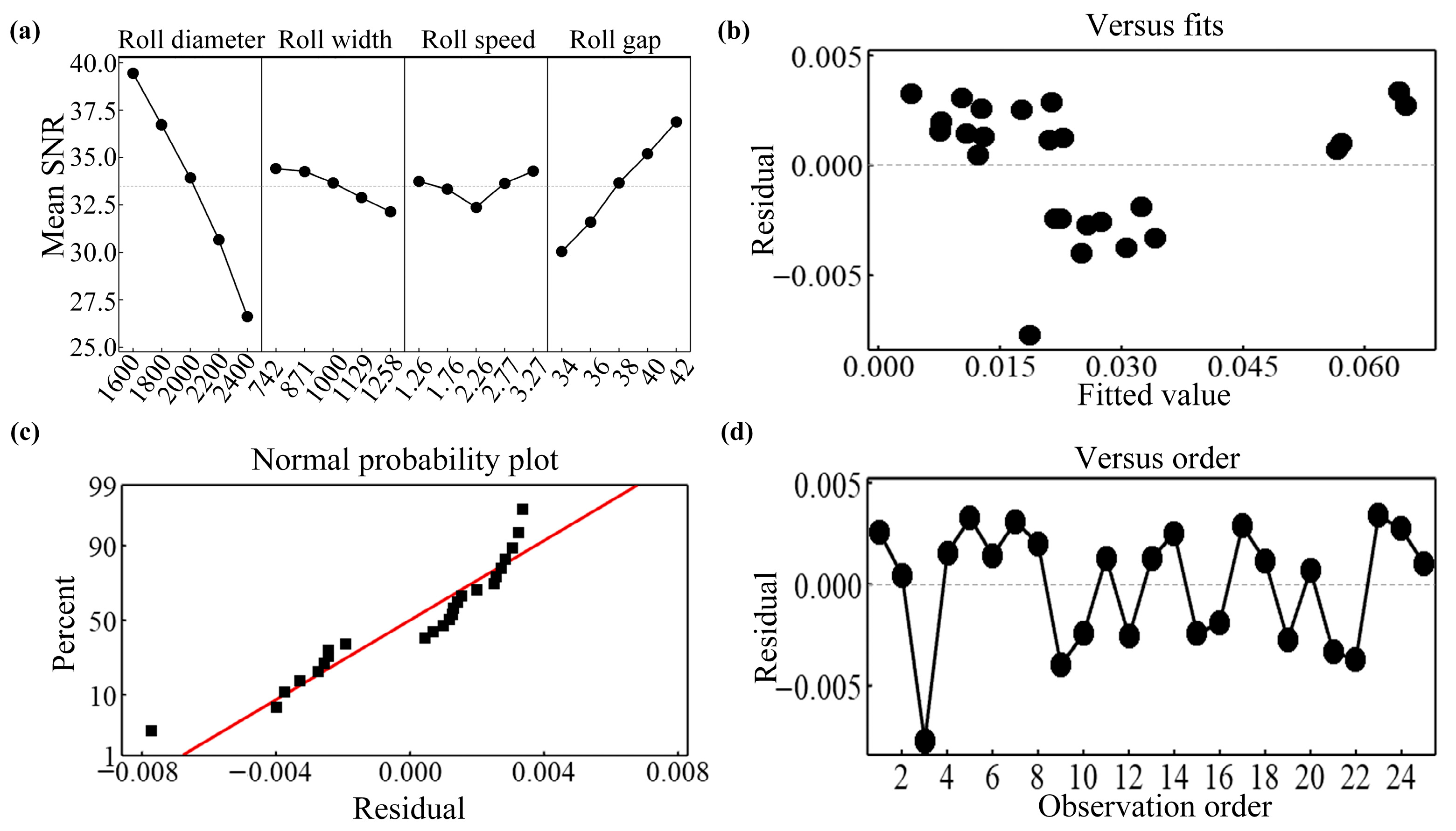
Figure 12 shows the main effect and residual plot of the SNR of the SRE. According to the variation curve of the mean SNR for each factor, the mean SNR of the SRE significantly increased with larger roller diameters (Figure 12a). As the roller diameter increased, the system stability improved and became less susceptible to noise factors. Consequently, rollers with larger diameters contributed to enhanced SRE. Consequently, larger roller diameters generated finer product fineness, which aligned with the findings reported by Rodriguez et al. [17].

Figure 12c displays the normal probability plot of the residuals, with the points densely distributed along the diagonal (red reference line) and no obvious bias. Figure 12b,d show the residuals-versus-fits plot and residuals-versus-order plot, respectively. Both plots exhibit randomly scattered residuals with no discernible patterns, while the residuals collectively sum to zero. These diagnostic graphs fully conform to established statistical standards for model validation.

Figure 13 shows the main effect and residual plot of the SNR of the throughput. Analysis of the SNR for HPGR throughput revealed that increases in roll width and roll speed enhanced the response value, reduced variability, and improved system robustness (Figure 13a). However, with continued increases, the gradient of the curve gradually declined, indicating diminished effects.

Figure 14 shows the main effect and residual plot of the SNR of the average energy consumption. As roll diameter and roll speed progressively increased, the mean SNR for the average energy consumption of HPGR gradually decreased, indicating that excessive roll diameter and speed elevated energy consumption (Figure 14a). Conversely, increases in roll gap corresponded to a rise in the mean SNR, reducing energy consumption variability. Although increased roll width elevated the drive energy consumption of the rollers, it concurrently enhanced the throughput of the HPGR, leading to a minor net effect on average energy consumption.

Figure 15 shows the main effect and residual plot of the SNR of the wear. The mean SNR for HPGR wear exhibited negative correlations with roll diameter and roll width, with roll diameter exerting greater influence (Figure 15a). Conversely, a positive correlation was observed between the roll gap and the mean SNR for wear. The mean SNR for the wear of HPGR initially decreased and subsequently increased with rising roll speed, reaching a minimum value at 2.26 m/s. This demonstrates that this specific speed level maximized the robustness of the wear of HPGR performance.

Figure 16 shows the main effect and residual plot of the SNR of the edge effect. The mean SNR for the edge effect of HPGR exhibited positive correlations with roll speed and roll gap, with roll speed exerting greater influence (Figure 16a). This occurred because roller speed predominantly governed the uniformity of comminution products across distinct HPGR zones. Conversely, a negative correlation was observed between the roll diameter and the mean SNR for edge effect. The mean SNR for the edge effect of HPGR initially increased and subsequently decreased with rising roll width, peaking at 1000 mm. This indicates that this specific width level resulted in significant fluctuations in the edge effect.

Figure 13, Figure 14, Figure 15 and Figure 16b–d likewise demonstrate that the residual plots for the throughput, average energy consumption, wear, edge effect SNR conform to established statistical criteria.

4.3. Multi-Objective Optimization of HPGR

Taguchi orthogonal experiments are generally employed for single-objective optimization. When optimization involves multiple responses, grey relational analysis (GRA) is required. This methodology converts all response into a grey relational grade (GRG) considering assigned weights prior to optimization. Yang et al. [24] employed RSM to effectively optimize the throughput, SRE, and roll surface pressure of HPGR, which demonstrated robust predictive capability and revealed significant interaction effects among variables. Whereas this study addressed a more complex multi-objective scenario involving comprehensive optimization of multiple targets including energy consumption and wear, wherein GRA proved more appropriate. In multi-objective optimization, the initial step requires defining a reference sequence and comparison sequences. The reference sequence is set as the desired values for each response target, while the comparison sequences consist of the experimental data obtained for these response targets. Subsequently, the data undergo standardization, typically employing the zero-mean normalization method, given by [44]

$$\left\{\begin{array}{l}{\mathrm{x}}_i^{\prime }(k)={\displaystyle \frac{{\mathrm{x}}_i(k)}{\mathrm{mean}({\mathrm{x}}_i)}}\\ \mathrm{mean}({\mathrm{x}}_i)={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{k=1}^n{\mathrm{x}}_i(k)}\end{array}\right.$$

(11)

where x_i′(k) denotes the standardized value, mean(x_i) represents the arithmetic mean of the i-th sequence, and n is the size of the sequence.

To quantify the pointwise similarity between comparison sequences and the reference sequence, the grey relational coefficient (GRC) must be calculated. The GRC is given by [45]

$${\xi }_i\left(k\right)={\displaystyle \frac{\underset{i}{\min }\left|x_i^0\right.-\left.x_i\left(k\right)\right|+\xi \underset{i}{\max }\left|x_i^0\right.-\left.x_i\left(k\right)\right|}{\left|x_i^0\right.-\left.x_i\left(k\right)\right|+\xi \underset{i}{\max }\left|x_i^0\right.-\left.x_i\left(k\right)\right|}}$$

(12)

where x_i(k) denotes the standardized response value, ζ(k) represents the grey relational coefficient, and x_i⁰ indicates the ideal standardized value for the i-th experimental group. The denominator terms correspond to the minimum and maximum of the absolute differences between the reference sequence and each comparison sequence. The distinguishing coefficient ζ is set to 0.4 for all calculations.

To quantify the relative importance of each response target in the comprehensive evaluation, the calculation of the GRG must incorporate weights assigned to different response targets [46].

$${\gamma }_i={\displaystyle \frac{1}{n}}{\displaystyle \sum _{k=1}^n{\xi }_i}\left(k\right)$$

(13)

Based on parameters from an iron ore plant and its actual production conditions, weights for each response targets were established (

Table 8. The weights of each response target.

Response Targets	SRE	Throughput	Average Energy Consumption	Wear	Edge Effect
Weight	0.4	0.32	0.18	0.07	0.03

).

Based on the aforementioned data, the GRG incorporating the weights of each response objective was calculated, followed by SNR and ANOVA analyses.

Table 9. ANOVA table for grey relational grade.

Source	DOF	Seq. SS	Adj. MS	F	p	Contribution Rate
A	4	0.003219	0.000805	1.82	0.218	8.540047
B	4	0.022655	0.005664	12.82	0.001	60.104
C	4	0.007138	0.001785	4.04	0.044	18.9372
D	4	0.001149	0.000287	0.65	0.643	3.048311
Range	8	0.003533	0.000442
Total Variation	24	0.037693

and

Table 10. Response table for grey relational grade.

Level	GRG
	Roll Diameter	Roll Width	Roll Speed	Roll Gap
1	0.7327	0.6843	0.694	0.7267
2	0.7116	0.6946	0.7086	0.7118
3	0.7089	0.7174	0.722	0.7269
4	0.7118	0.7346	0.7384	0.712
5	0.7348	0.7689	0.7368	0.7224
Range	0.026	0.0846	0.0444	0.0151
Ranking	3	1	2	4

present the ANOVA table and the SNR response table for GRG, respectively.

Table 9 and Table 10 indicate that roll width exerts the strongest influence on the unified GRG. The factors are ranked by impact magnitude as follows: roll width > roll speed > roll diameter > roll gap.

Figure 17 shows the main effect and residual plot of the SNR of the GRG. The mean SNR for roll width exhibited a monotonic increase with larger roll widths (Figure 17a). However, excessive width-to-diameter ratios were observed to induce HPGR vibration, potentially leading to equipment failure. Consequently, roll width should be maximized while ensuring stable HPGR operation. In addition, a specific roller speed value was identified that maximized the comprehensive crushing performance of the HPGR. The variations in roll diameter and roll gap exhibited complex nonlinear effects on the comprehensive crushing performance of the HPGR. Consequently, their optimal values should be determined based on the assigned weights of individual response targets through grey relational analysis.

The optimal parameter combination satisfying the assigned weights of all response targets was determined as follows: roll diameter of 2400 mm, roll width of 1258 mm, roll speed of 2.77 m/s, and roll gap of 38 mm (Figure 17a).

Table 11. Comparison of response objectives before and after optimization.

Response Target	I (%)	II (t/h)	III (kwh/t)	IV (mm/h)	V (%)
1	38.04	2994.82	0.043	0.058	2.05
2	39.72	1683.27	0.036	0.068	2.65
3	35.02	1824.41	0.045	0.031	1.82

displays a comparison of results before and after optimization. The experimental group (1) employs the aforementioned parameter combination, while the control groups represent configurations achieving maximized SRE (2) and maximized average energy consumption (3), respectively.

The group with optimal SRE demonstrated only a 4.4% improvement compared to the experimental group. However, it exhibited a 43.8% reduction in throughput, along with 17.2% and 29.3% increases in wear rate and edge effect, respectively. Owing to its lower throughput, average energy consumption decreased by approximately 16.3%.

The configuration maximizing average energy consumption demonstrated reductions of 7.9% in SRE and 39.1% in throughput compared to the experimental group. However, it also exhibited decreases of approximately 46.6% in wear rate and 11.2% in edge effect. This result indicates that the higher energy consumption yielded only marginal reductions in wear and edge effect at the expense of substantially compromised SRE and throughput, representing a counterproductive trade-off.

The parameter combination optimized via grey relational analysis, which incorporated the assigned weights of response targets, achieved high SRE and throughput while constraining average energy consumption, wear, and edge effect. Therefore, during engineering implementation, the weighting coefficients of parameters were determined based on operational conditions to ensure that the optimized parameters could meet practical production requirements.

5. Conclusions

(1) Roll speed demonstrates the most significant impact on the uniformity of ore fragmentation across different grinding zones. This mechanistic understanding provides valuable guidance for calibrating roller speed. By enabling precise adjustment of roller speed, it effectively mitigates edge effects in HPGR operations, thereby achieving more uniform product size distribution.

(2) The hierarchy of parameter influences across response targets is ranked as follows:

• SRE: Roll diameter > Roll gap > Roll speed > Roll width.
• Throughput: Roll speed > Roll width > Roll diameter > Roll gap.
• Average energy consumption: Roll diameter > Roll speed > Roll gap > Roll width.
• Wear: Roll diameter > Roll gap > Roll width > Roll speed.
• Edge effect: Roll speed > Roll diameter > Roll gap > Roll width.

(3) This study demonstrates that GRA offers a viable strategy for industrial HPGR optimization, effectively balancing often conflicting objectives. The optimal parameter set significantly enhances the comprehensive crushing performance of the HPGR.

The primary contribution of this work lies in establishing a systematic optimization workflow for HPGR operation, which offers significant practical implications. The quantitative optimal parameters derived in this study are specifically applicable to iron ore processing. Future applications will extend this methodology to diverse mineral ores, with the versatility undergoing rigorous validation.