Computational Approaches to Assess Flow Rate Efficiency During In Situ Recovery of Uranium: From Reactive Transport to Streamline- and Trajectory-Based Methods
Abstract
1. Introduction
- How to determine the distribution of concentration of the leaching agent inside the technological block?
- How to distribute the flow rates of the wells accounting for the effective distance between the wells to improve the efficiency of production?
2. Materials and Methods
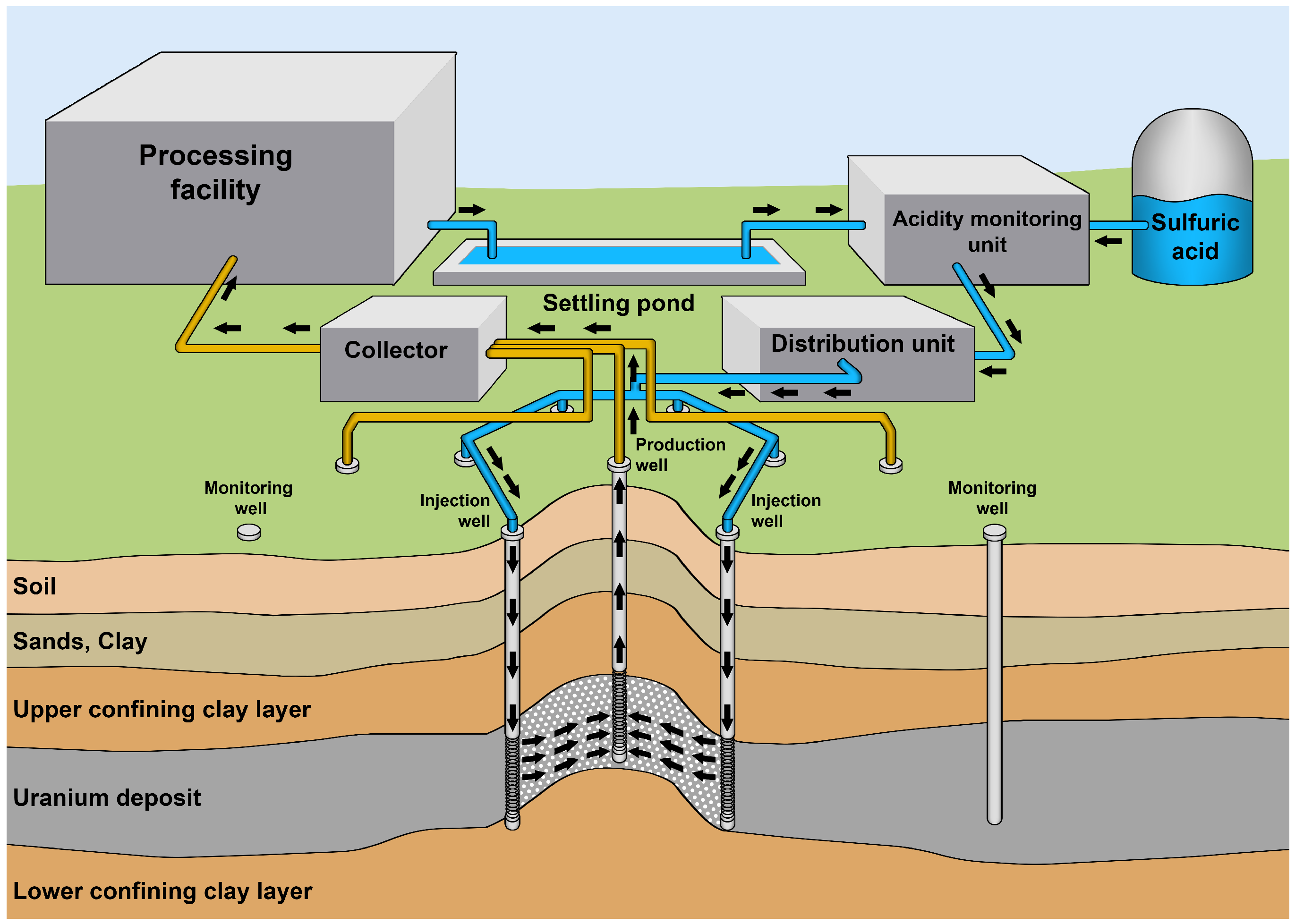
2.1. The Model of the Hydrodynamic Process
2.2. The Reactive Transport Model
3. Results and Discussion
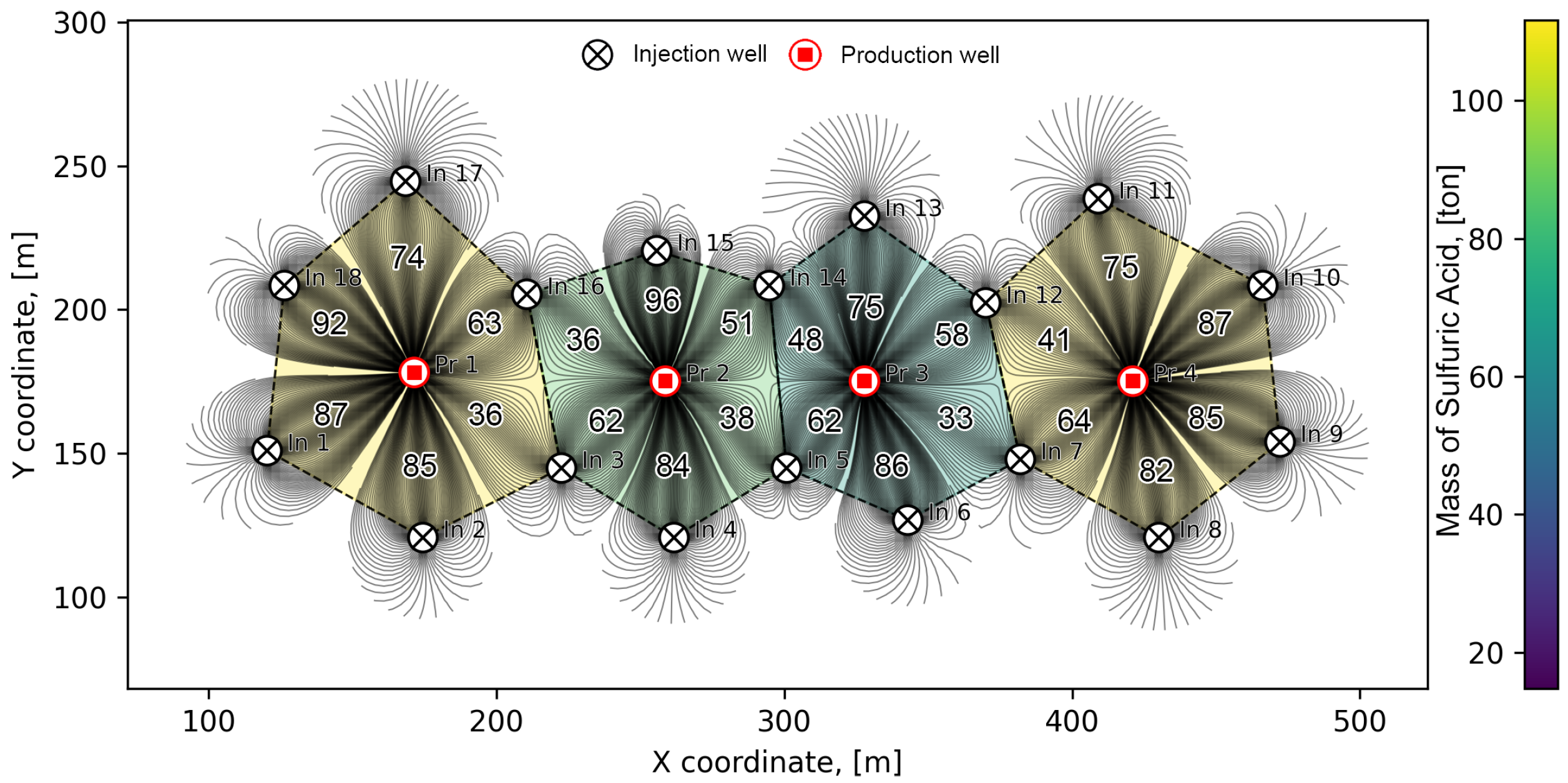
3.1. Traditional Method for Determining the Balance of Solutions
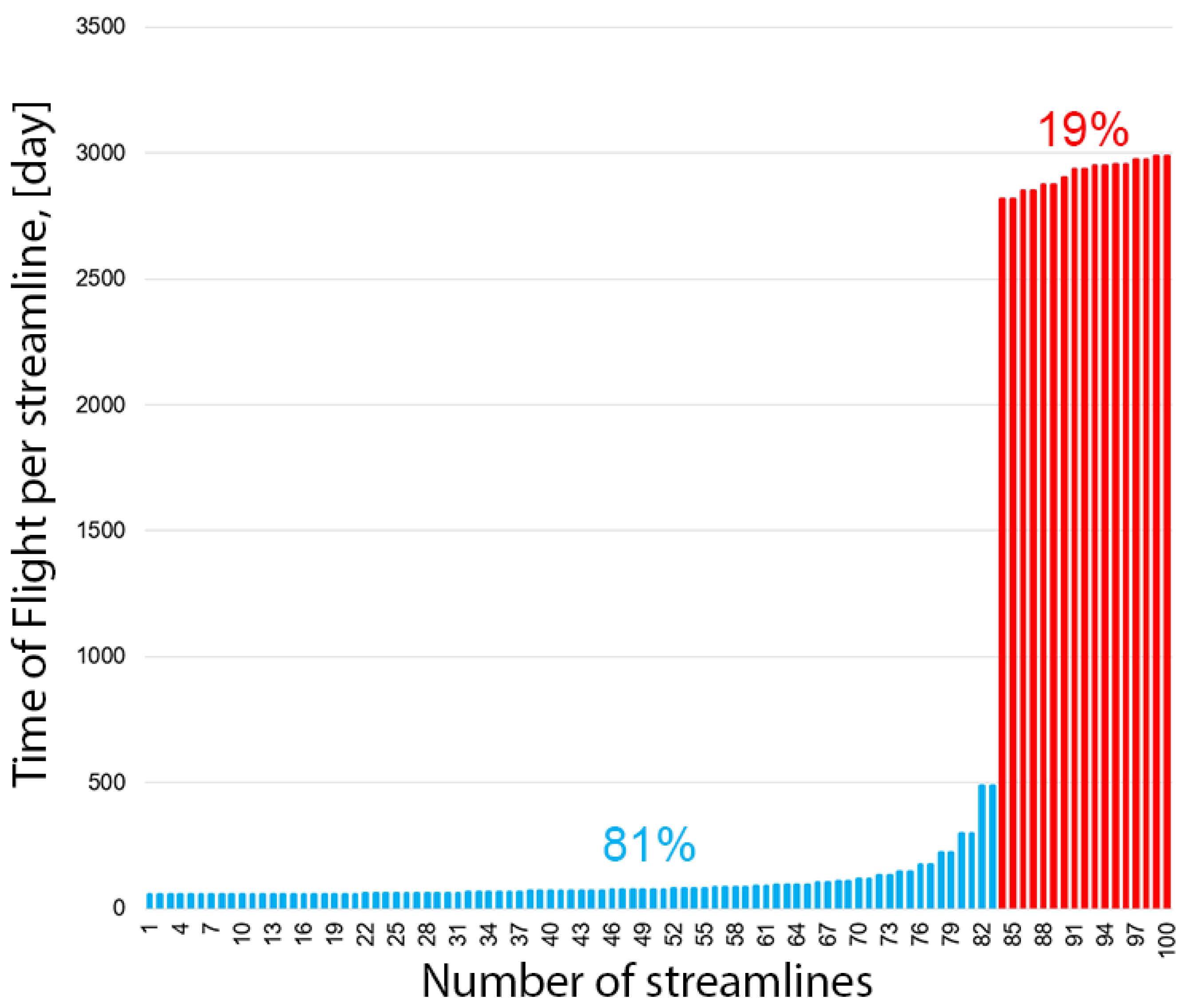
3.2. Streamline-Based Method for Determining the Balance of Solutions
3.3. Trajectory-Based Method for Determining the Balance of Solutions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abzalov, M.Z. Sandstone-Hosted Uranium Deposits Amenable for Exploitation by In Situ Leaching Technologies. Appl. Earth Sci. 2012, 121, 55–64. [Google Scholar] [CrossRef]
- Seredkin, M.; Zabolotsky, A.; Jeffress, G. In Situ Recovery, an Alternative to Conventional Methods of Mining: Exploration, Resource Estimation, Environmental Issues, Project Evaluation and Economics. Ore Geol. Rev. 2016, 79, 500–514. [Google Scholar] [CrossRef]
- Li, G.; Yao, J. A Review of In Situ Leaching (ISL) for Uranium Mining. Mining 2024, 4, 120–148. [Google Scholar] [CrossRef]
- Bhargava, S.K.; Ram, R.; Pownceby, M.; Grocott, S.; Ring, B.; Tardio, J.; Jones, L. A Review of Acid Leaching of Uraninite. Hydrometallurgy 2015, 151, 10–24. [Google Scholar] [CrossRef]
- Nuclear Energy Agency. Uranium 2024: Resources, Production and Demand; OECD Publishing: Paris, France, 2025; pp. 12–14. Available online: http://oecd-nea.org/upload/docs/application/pdf/2025-04/7683_uranium_2024_-_resources_production_and_demand_2025-04-22_14-29-2_928.pdf (accessed on 25 July 2025).
- Bruneton, P.; Cuney, M. Geology of Uranium Deposits. Uranium Nucl. Power 2016, 2, 11–52. [Google Scholar] [CrossRef]
- Poezhaev, I.P.; Polynovsky, K.D.; Gorbatenko, O.A.; Panova, E.N.; Bulenova, K.Z.; Karmanov, E.M.; Blynsky, P.A.; Bitovt, O.A. Geotechnology of Uranium [Geotehnologiya Urana]; Kazakh Universitety: Almaty, Kazakhstan, 2017; p. 319. (In Russian) [Google Scholar]
- Aizhulov, D.; Tungatarova, M.; Kaltayev, A. Streamlines Based Stochastic Methods and Reactive Transport Simulation Applied to Resource Estimation of Roll-Front Uranium Deposits Exploited by In-Situ Leaching. Minerals 2022, 12, 1209. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Kaltayev, A.; Royer, J.-J. Reactive Transport Modeling during Uranium In Situ Leaching (ISL): The Effects of Ore Composition on Mining Recovery. Minerals 2022, 12, 1340. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, T.T.; Tan, K.X.; Yao, Y.X.; Wang, Y.A.; Li, C.G.; Li, Y.M.; Zhang, Y.; Wang, H. Hydrodynamic Simulation of the Influence of Injection Flowrate Regulation on In-Situ Leaching Range. Minerals 2022, 12, 787. [Google Scholar] [CrossRef]
- Zhang, C.; Tan, K.; Xie, T.; Tan, Y.; Fu, L.; Gan, N.; Kong, L. Flow Microbalance Simulation of Pumping and Injection Unit in In Situ Leaching Uranium Mining Area. Processes 2021, 9, 1288. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Niu, Y.; Tan, K.; Xie, T.; Yao, Y.; Li, C.; Liu, Z. Quantitative determination of the leaching range of in situ leaching mining area by stagnation point. Nucl. Eng. Technol. 2024, 103204. [Google Scholar] [CrossRef]
- Li, H.; Tang, Z.; Xiang, D. Study on Numerical Simulation of Reactive-Transport of Groundwater Pollutants Caused by Acid Leaching of Uranium: A Case Study in Bayan-Uul Area, Northern China. Water 2024, 16, 500. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, G.; Xu, L.; Liu, J.; Sun, Z.; Shi, W. Uranium recovery from sandstone-type uranium deposit by acid in situ leaching—An example from the Kujieertai. Hydrometallurgy 2019, 191, 105209. [Google Scholar] [CrossRef]
- Collet, A.; Regnault, O.; Ozhogin, A.; Imantayeva, A.; Garnier, L. Three-Dimensional Reactive Transport Simulation of Uranium In Situ Recovery: Large-Scale well Field Applications in Shu Saryssu Bassin, Tortkuduk Deposit (Kazakhstan). Hydrometallurgy 2022, 211, 105873. [Google Scholar] [CrossRef]
- Escario, S.; Seigneur, N.; Collet, A.; Regnault, O.; de Boissezon, H.; Lagneau, V.; Descostes, M. A reactive transport model designed to predict the environmental footprint of an ’in situ recovery’ uranium exploitation. J. Contam. Hydrol. 2023, 254, 104106. [Google Scholar] [CrossRef] [PubMed]
- De Boissezon, H.; Levy, L.; Jakymiw, C.; Distinguin, M.; Guerin, F.; Descostes, M. Modeling uranium and 226Ra mobility during and after an acidic in situ recovery test (Dulaan Uul, Mongolia). J. Contam. Hydrol. 2020, 103711. [Google Scholar] [CrossRef] [PubMed]
- Seigneur, N.; Grozeva, N.; Purevsan, B.; Descostes, M. Reactive transport modelling as a toolbox to compare remediation strategies for aquifers impacted by uranium in situ recovery. J. Contam. Hydrol. 2024, 265, 104392. [Google Scholar] [CrossRef]
- Ushakov, A.O.; Zherin, I.I.; Muslimova, A.V.; Noskov, M.D. Research of the influence of the feed solution flow rate on the uranium refining in an extraction column cascade. At. Energy 2023, 135, 40–46. [Google Scholar] [CrossRef]
- Noskov, M.D.; Mikhailov, A.N.; Narushkin, R.S.; Rusin, R.S. “Smart field” of in situ leach uranium mining. Gorn. Zh. 2022, 4, 39–45. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Royer, J.-J.; Aizhulov, D.Y.; Shayakhmetov, N.M.; Kaltayev, A. Streamline-based reactive transport modeling of uranium mining during in situ leaching: Advantages and drawbacks. Hydrometallurgy 2023, 220, 106107. [Google Scholar] [CrossRef]
- Shayakhmetov, N.M.; Alibayeva, K.A.; Kaltayev, A.; Panfilov, I. Enhancing uranium in situ leaching efficiency through the well reverse technique: A study of the effects of reversal time on production efficiency and cost. Hydrometallurgy 2023, 219, 106086. [Google Scholar] [CrossRef]
- Imankulov, T.; Lebedev, D.; Matkerim, B.; Daribayev, B.; Kassymbek, N. Numerical Simulation of Multiphase Multicomponent Flow in Porous Media: Efficiency Analysis of Newton–Based Method. Fluids 2021, 6, 355. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Kuchin, Y.; Amirgaliyev, Y.; Yunicheva, N.; Muhamedijeva, E. Estimation of Filtration Properties of Host Rocks in Sandstone-Type Uranium Deposits Using Machine Learning Methods. IEEE Access 2022, 10, 18855–18872. [Google Scholar] [CrossRef]
- Wang, B.; Luo, Y.; Qian, J.; Liu, J.; Li, X.; Zhang, Y.; Chen, Q.; Li, L.; Liang, D.; Huang, J. Machine learning–based optimal design of the in situ leaching process parameter (ISLPP) for the acid in situ leaching of uranium. J. Hydrol. 2023, 626, 130234. [Google Scholar] [CrossRef]
- Daribayev, B.; Akhmed-Zaki, D.; Imankulov, T.; Nurakhov, Y.; Kenzhebek, Y. Using machine learning methods for oil recovery prediction. In Proceedings of the 17th European Conference on the Mathematics of Oil Recovery, Virtual-Online, 14–17 September 2020; p. 166287. [Google Scholar] [CrossRef]
- Aizhulov, D.; Tungatarova, M.; Kurmanseiit, M.; Shayakhmetov, N. Artificial Neural Networks for Mineral Production Forecasting in the In Situ Leaching Process: Uranium Case Study. Processes 2024, 12, 2285. [Google Scholar] [CrossRef]
- Kurmanseiit, M.B.; Tungatarova, M.S.; Abdullayeva, B.Z.; Aizhulov, D.Y.; Shayakhmetov, N.M. Acceleration of Numerical Modeling of Uranium In Situ Leaching: Application of IDW Interpolation and Neural Networks for Solving the Hydraulic Head Equation. Minerals 2024, 14, 1043. [Google Scholar] [CrossRef]
- Qiu, W.; Yang, Y.; Song, J.; Que, W.; Liu, Z.; Weng, H.; Wu, J.; Wu, J. A deep-learning-based multiobjective optimization for the design of in situ uranium leaching system under multiple uncertainties. J. Hydrol. 2025, 651, 132576. [Google Scholar] [CrossRef]
- Kiskira, K.; Lymperopoulou, T.; Lourentzatos, I.; Tsakanika, L.-A.; Pavlopoulos, C.; Papadopoulou, K.; Ochsenkühn, K.-M.; Tsopelas, F.; Chatzitheodoridis, E.; Lyberatos, G.; et al. Bioleaching of Scandium from Bauxite Residue using Fungus Aspergillus Niger. Waste Biomass Valor. 2023, 14, 3377–3390. [Google Scholar] [CrossRef]
- Laurent, G.; Izart, C.; Lechenard, B.; Fabrice, G.; Philippe, M.; Pauline, C.; Truche, L.; Royer, J.-J.; Fillipov, L. Numerical modelling of column experiments to investigate in situ bioleaching as an alternative mining technology. Hydrometallurgy 2019, 188, 272–290. [Google Scholar] [CrossRef]
- Abhilash; Mehta, K.D.; Kumar, V.; Pandey, B.D.; Tamrakar, P.K. Bioleaching—An Alternate Uranium Ore Processing Technology for India. Energy Procedia 2011, 7, 158–162. [Google Scholar] [CrossRef]
- DePonty Jersy, D.; Shane, R.G.; DePinto, P.; Grant Kornrumph, S.; Marvin, F.; Glotfelty, R.G. Plumbness and Alignment Standards—Analysis and Recommendations for Operational Applicability. pp. 1–7. Available online: https://inspectapedia.com/water/Water-well-plumbness-alignment-standards-DePonty.pdf (accessed on 24 June 2025).
- Patrin, A.P.; Zabaznov, V.L.; Chistilin, P.E. The main results of a full-scale field experiment on the ISL of Uranium at site №2 of the Budenovskoye deposit. In Proceedings of the V International Conference, “Actual Problems of the Uranium Industry”, Almaty, Kazakhstan, 19–20 September 2008; pp. 198–204. [Google Scholar]
- Podrezov, D.R. Development and Identification of Models for the Reserves Estimating of the URANIUM In-Situ Leaching Mine. Master’s Thesis, National Research Technological University “MISIS”, Moscow, Russia, 2021. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications Inc.: New York, NY, USA, 2014; p. 757. [Google Scholar]
- Acosta, J.L.; Camacho, A.F. Porous Media: Heat and Mass Transfer, Transport and Mechanics; Nova Science Publishers Inc.: New York, NY, USA, 2009; p. 255. [Google Scholar]
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Engineer Research and Development Center: Vicksburg, MS, USA, 1999; p. 24. [Google Scholar]
- Danayev, N.T.; Korsakova, N.K.; Penkovskiy, V.I. Mass Transfer in the Near-Wellbore Zone and Electromagnetic Formation Logging [Massoperenos vs. Priskvazhinnoy Zone i Elektromagnitnyy Karotazh Plasta]; Qazaq universiteti: Almaty, Kazakhstan, 2005; p. 180. (In Russian) [Google Scholar]
- Gromov, B.V. Introduction to Chemical Technology of Uranium [VVedenie vs. Himicheskuyu Tehnologiyu Urana]; Atomizdat: Moscow, Russia, 1978; p. 326. (In Russian) [Google Scholar]
- Steefel, C.I.; DePaolo, D.J.; Lichtner, P.C. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Pollock, D.W. Semi-analytical Computation of Path Line for Finite Difference Models. Ground Water 1988, 6, 743–750. [Google Scholar] [CrossRef]
- Kuljabekov, A. Model of Chemical Leaching with Gypsum Sedimentation in Porous Media. Ph.D. Thesis, University of Lorraine, Nancy, France, Almaty, Kazakhstan, 2014; p. 99. [Google Scholar]












| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Deposit average thickness | H | m | 11.28 |
| Average uranium mass fraction | kg.kg−1 | 0.00077 | |
| Uranium meter-percent 1 | m% | 0.8686 | |
| Hydraulic conductivity | m.day−1 | 7.0 | |
| Rock density | kg.m−3 | 1700 | |
| Rock porosity | m3.m−3 | 0.22 |
| Parameter | Cell 1 | Cell 2 | Cell 3 | Cell 4 | Outside of Cells |
|---|---|---|---|---|---|
| Well cell volume | |||||
| V, [] | 95,796.67 | 74,178.39 | 72,539.09 | 90,981.22 | |
| Mass of individual components | |||||
| , [t] | 108.87 | 130.91 | 128.96 | 109.40 | 239.12 |
| , [t] | 10.92 | 7.39 | 7.46 | 10.11 | 0.33 |
| , [t] | 76.95 | 39.35 | 37.63 | 70.46 | 0.00 |
| Mass of components per unit volume | |||||
| , [] | 1.14 | 1.76 | 1.78 | 1.20 | |
| , [] | 0.11 | 0.10 | 0.10 | 0.11 | |
| , [] | 0.80 | 0.53 | 0.52 | 0.77 | |
| Parameter | Cell 1 | Cell 2 | Cell 3 | Cell 4 | Total |
|---|---|---|---|---|---|
| [] | −0.69 | −0.69 | −0.69 | −0.69 | |
| , [] | −1199.56 | −1199.56 | −1199.56 | −1199.56 | |
| , [t] | −14.73 | −14.73 | −14.73 | −14.73 | −58.93 |
| Parameter | Cell 1 | Cell 2 | Cell 3 | Cell 4 | Outside of Cells | Total |
|---|---|---|---|---|---|---|
| [] | −6.90 | −4.57 | −2.56 | −5.97 | ||
| , [] | −11928.34 | −7895.88 | −4420.70 | −10,318.96 | ||
| , [t] | −108.33 | −72.91 | −42.53 | −93.78 | 258.22 | −59.32 |
| Parameter | Cell 1 | Cell 2 | Cell 3 | Cell 4 | Outside of Cells | Total |
|---|---|---|---|---|---|---|
| [] | −8.31 | −5.65 | −4.49 | −8.14 | ||
| , [] | −14,368.15 | −9777.74 | −7772.34 | −14,081.44 | ||
| , [t] | −126.16 | −87.31 | −70.36 | −123.73 | 348.24 | −59.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurmanseiit, M.; Shayakhmetov, N.; Aizhulov, D.; Abdullayeva, B.; Tungatarova, M. Computational Approaches to Assess Flow Rate Efficiency During In Situ Recovery of Uranium: From Reactive Transport to Streamline- and Trajectory-Based Methods. Minerals 2025, 15, 835. https://doi.org/10.3390/min15080835
Kurmanseiit M, Shayakhmetov N, Aizhulov D, Abdullayeva B, Tungatarova M. Computational Approaches to Assess Flow Rate Efficiency During In Situ Recovery of Uranium: From Reactive Transport to Streamline- and Trajectory-Based Methods. Minerals. 2025; 15(8):835. https://doi.org/10.3390/min15080835
Chicago/Turabian StyleKurmanseiit, Maksat, Nurlan Shayakhmetov, Daniar Aizhulov, Banu Abdullayeva, and Madina Tungatarova. 2025. "Computational Approaches to Assess Flow Rate Efficiency During In Situ Recovery of Uranium: From Reactive Transport to Streamline- and Trajectory-Based Methods" Minerals 15, no. 8: 835. https://doi.org/10.3390/min15080835
APA StyleKurmanseiit, M., Shayakhmetov, N., Aizhulov, D., Abdullayeva, B., & Tungatarova, M. (2025). Computational Approaches to Assess Flow Rate Efficiency During In Situ Recovery of Uranium: From Reactive Transport to Streamline- and Trajectory-Based Methods. Minerals, 15(8), 835. https://doi.org/10.3390/min15080835






