Continental Rift Driven by Asthenosphere Flow and Lithosphere Weakening by Flood Basalts: South America and Africa Cenozoic Rifting
Abstract
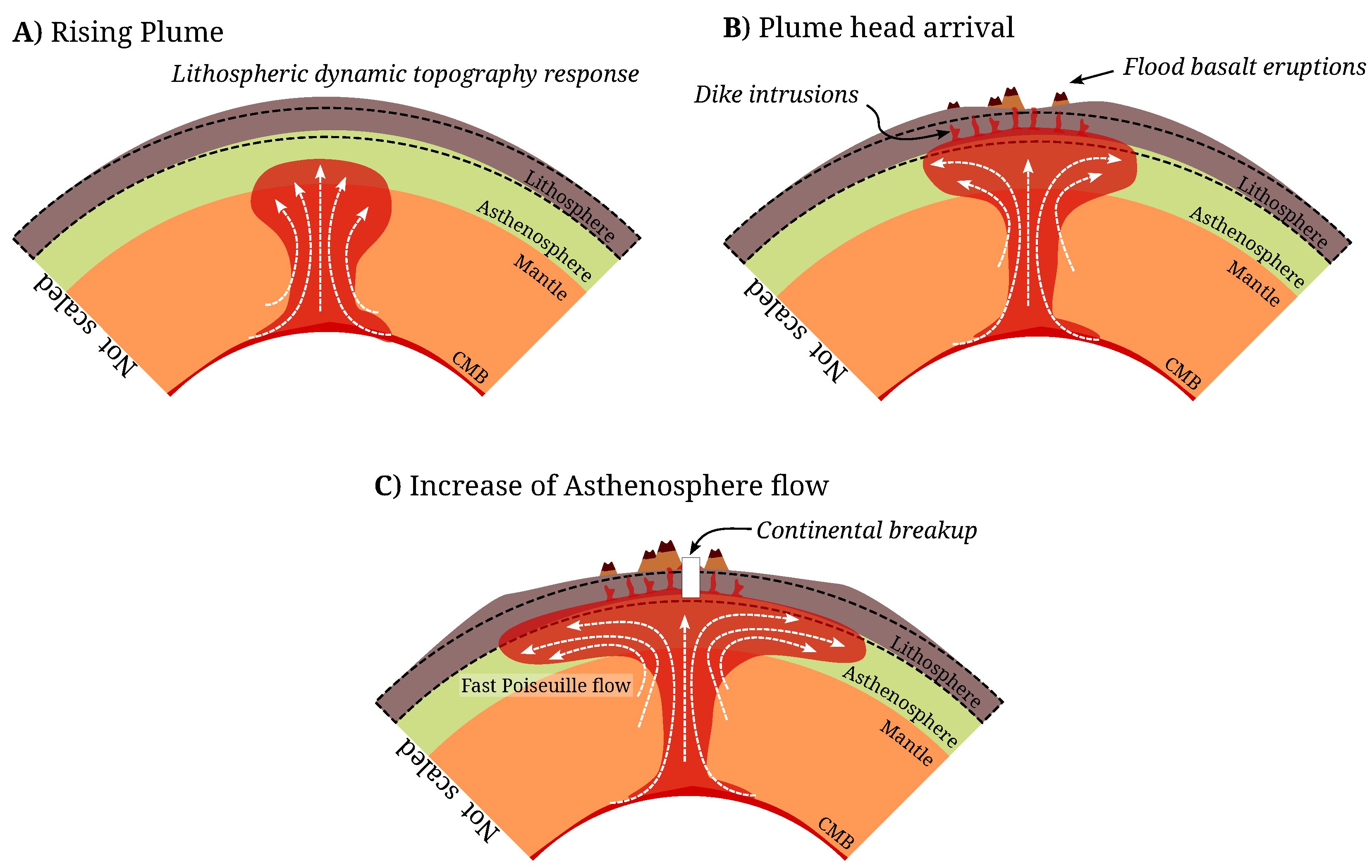
1. Introduction
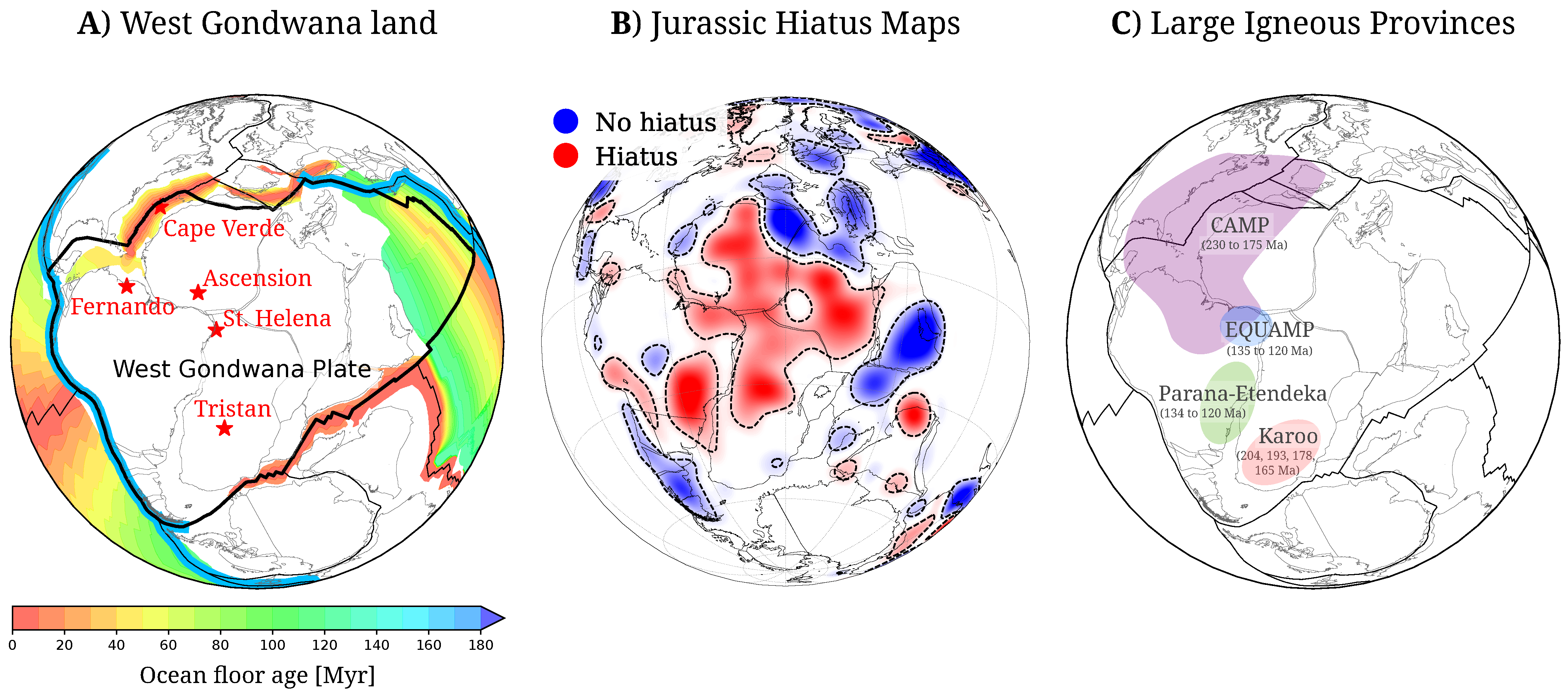
2. Plume Signal in the Stratigraphic Record
3. Large Igneous Provinces at the Time of Rifting
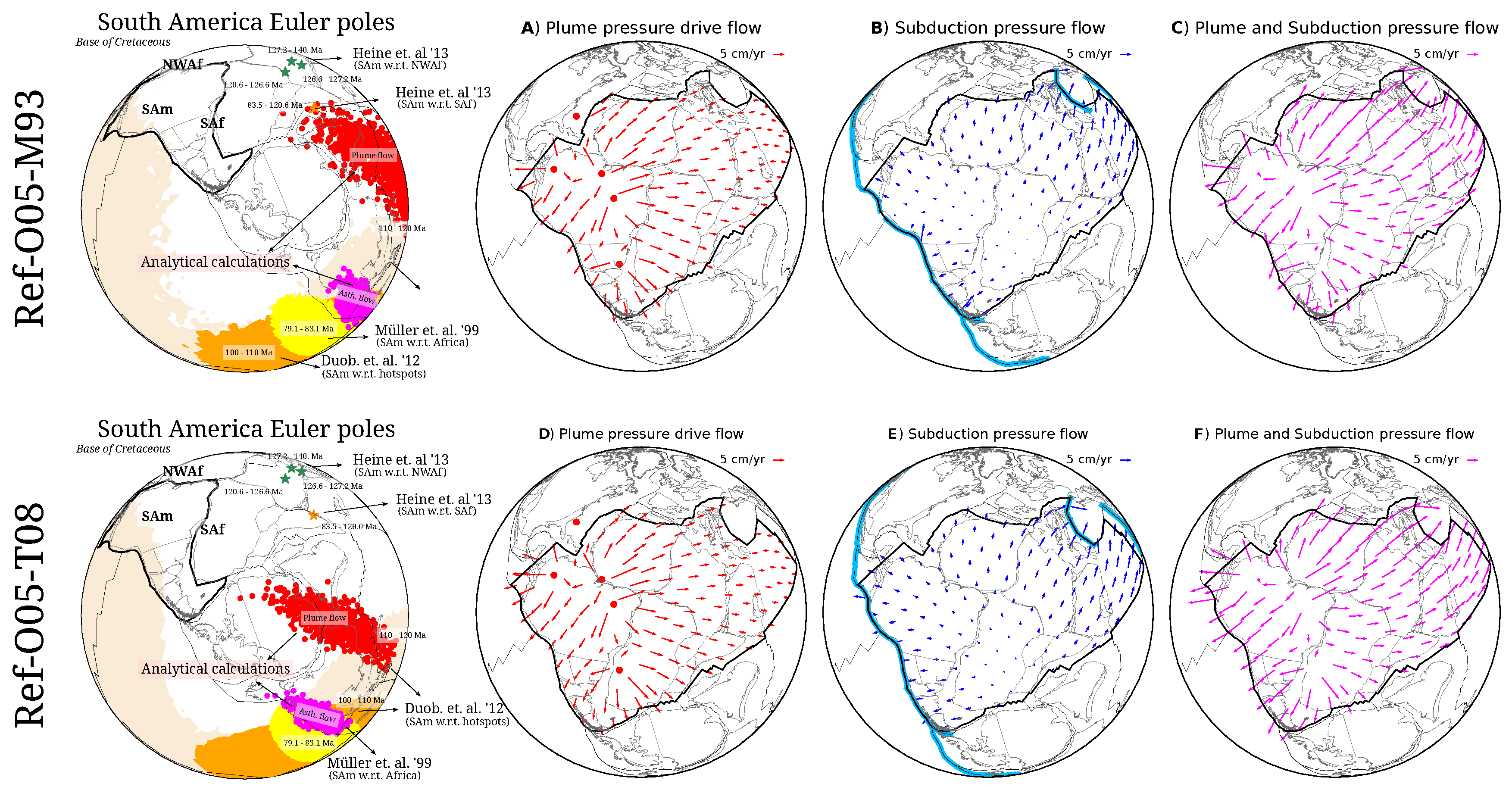
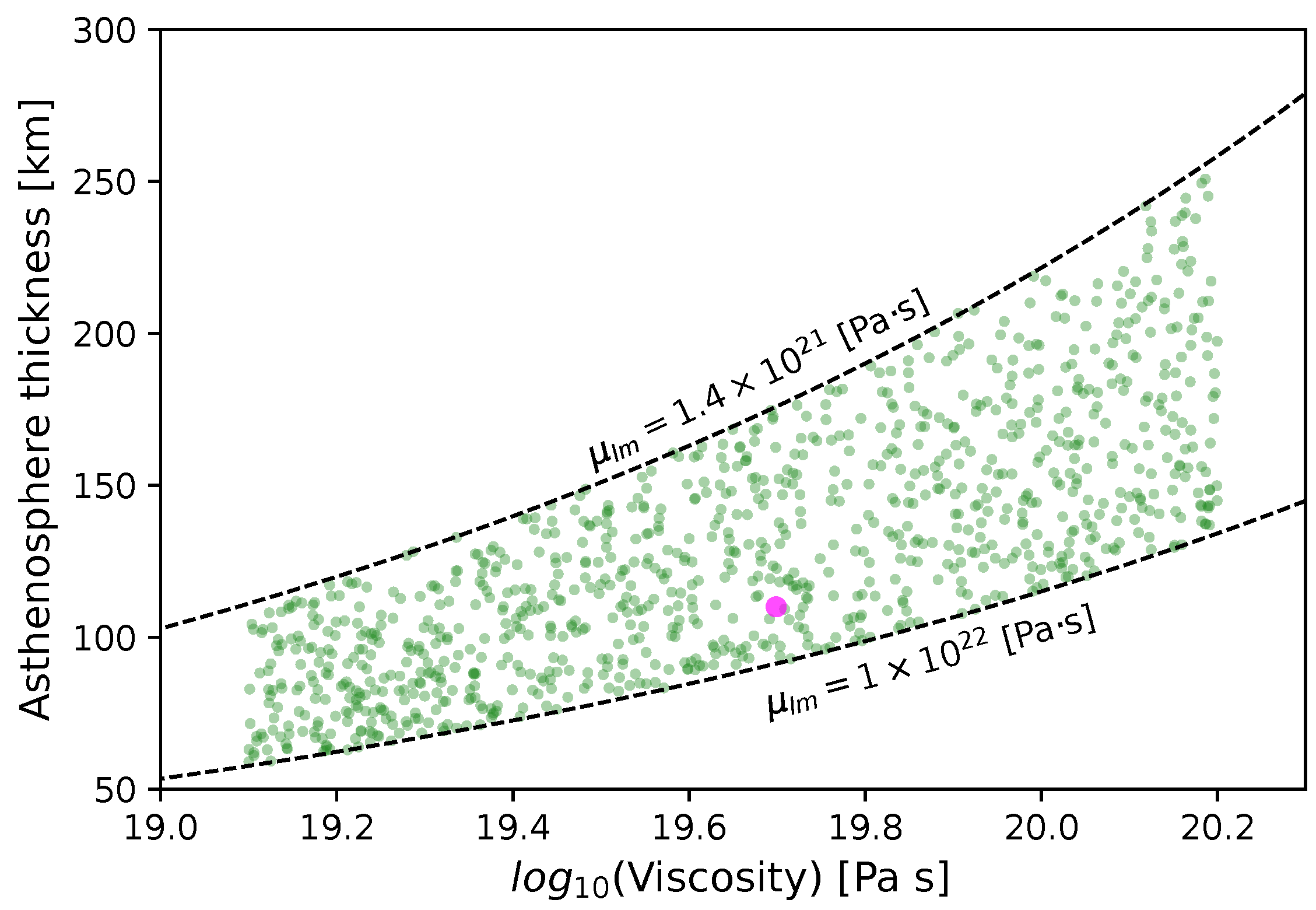
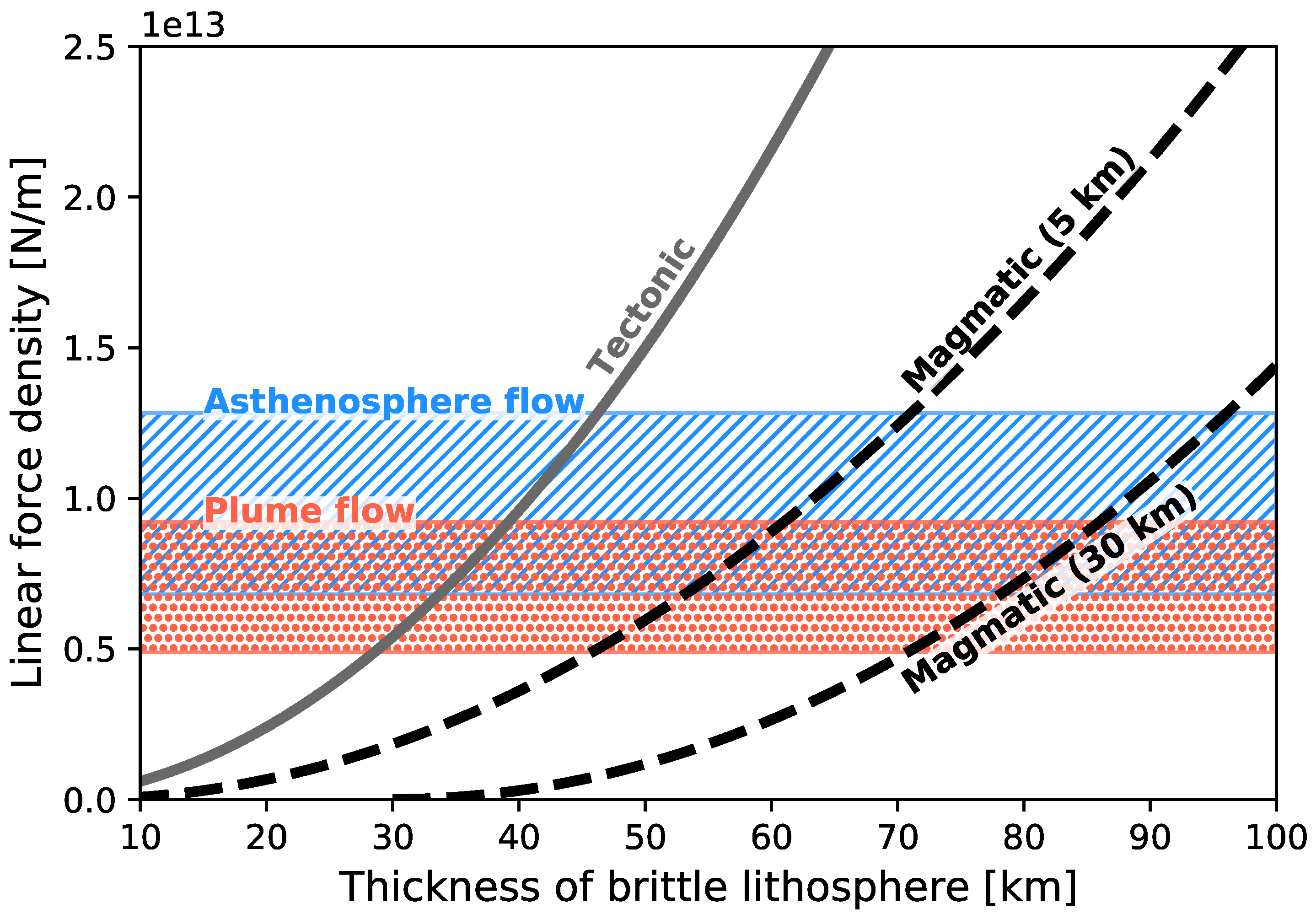
4. Poiseuille Flow Model
5. Continental Rift and Subsequent Drift
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Wegener, A. Die Entstehung der Kontinente und Ozeane, 5th ed.; Friedr. Vieweg & Sohn A.-G.: Braunschweig, Germany, 1929. [Google Scholar]
- Carey, S.W. Wegener’s South African Assembly, Fit or Misfit? Geol. Mag. 1955, 92, 196–200. [Google Scholar] [CrossRef]
- Bullard, E.; Everett, J.; Smith, A. The fit of the continents around the Atlantic. Philos. Trans. R. Soc. Lond. 1965, 258, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Sykes, L.R. Seismicity of the South Pacific Ocean. Geophys. Res. 1963, 68, 5999–6006. [Google Scholar] [CrossRef]
- Sykes, L.R. The seismicity of the Arctic. Bull. Seismol. Soc. Am. 1965, 55, 501–518. [Google Scholar]
- Cox, A.; Doell, R.R.; Dalrymple, G.B. Geomagnetic polarity epochs and Pleistocene geochronometry. Nature 1963, 198, 1049–1051. [Google Scholar] [CrossRef]
- Cox, A. Geomagnetic reversals. Science 1969, 163, 237–245. [Google Scholar] [CrossRef]
- McDougall, I.; Tarling, D.H. Dating of polarity zones in the Hawaiian islands. Nature 1963, 200, 54–56. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Von Herzen, R.P.; Hsu, K.J.; Andrews, J.E.; Saito, T.; Percival, S.F.; Milow, E.D.; Boyce, R.E. Deep sea drilling in the South Atlantic. Science 1970, 168, 1047–1059. [Google Scholar] [CrossRef] [PubMed]
- Ewing, M.; Ewing, J.; Talwan, M. Sediment distribution in the oceans: The Mid-Atlantic Ridge. Bull. Seismol. Soc. Am. 1964, 75, 17–36. [Google Scholar] [CrossRef]
- Wilson, J.T. A new class of faults and their bearing on continental drift. Nature 1965, 207, 343–347. [Google Scholar] [CrossRef]
- Davies, G.F.; Richards, M.A. Mantle convection. J. Geol. 1992, 100, 151–206. [Google Scholar] [CrossRef]
- Richards, M.A.; Lenardic, A. The Cathles Parameter (Ct): A Geodynamic Definition of the Asthenosphere and Implications for the Nature of Plate Tectonics. Geochem. Geophys. Geosyst. 2018, 19, 4858–4875. [Google Scholar] [CrossRef]
- Stotz, I.L.; Iaffaldano, G.; Davies, D.R. Pressure-Driven Poiseuille Flow: A Major Component of the Torque-Balance Governing Pacific Plate Motion. Geophys. Res. Lett. 2018, 45, 117–125. [Google Scholar] [CrossRef]
- Vilacís, B.; Hayek, J.N.; Stotz, I.L.; Bunge, H.P.; Friedrich, A.M.; Carena, S.; Clark, S. Evidence for active upper mantle flow in the Atlantic and Indo-Australian realms since the Upper Jurassic from hiatus maps and spreading rate changes. Proc. R. Soc. Math. Phys. Eng. Sci. 2022, 478, 20210764. [Google Scholar] [CrossRef]
- Hoeink, T.; Lenardic, A. Three-dimensional mantle convection simulations with a low-viscosity asthenosphere and the relationship between heat flow and the horizontal length scale of convection. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Hoeink, T.; Lenardic, A. Long wavelength convection, Poiseuille-Couette flow in the low-viscosity asthenosphere and the strength of plate margins. Geophys. J. Int. 2010, 180, 23–33. [Google Scholar] [CrossRef]
- Hoeink, T.; Lenardic, A.; Richards, M. Depth-dependent viscosity and mantle stress amplification: Implications for the role of the asthenosphere in maintaining plate tectonics. Geophys. J. Int. 2012, 191, 30–41. [Google Scholar] [CrossRef]
- Stotz, I.L.; Vilacís, B.; Hayek, J.N.; Bunge, H.P.; Friedrich, A.M. Yellowstone Plume Drives Neogene North American Plate Motion Change. Geophys. Res. Lett. 2021, 48, e2021GL095079. [Google Scholar] [CrossRef]
- Stotz, I.L.; Carena, S.; Vilacís, B.; Hayek, J.N.; Bunge, H.P. Kerguelen Plume Drives the Eocene Directional Change in Australian Plate Motion. Lithosphere 2024, 2024, lithosphere_2023_289. [Google Scholar] [CrossRef]
- Wang, Z.R.; Stotz, I.L.; Bunge, H.P.; Vilacís, B.; Hayek, J.N.; Ghelichkhan, S.; Lebedev, S. Cenozoic upper mantle flow history of the Atlantic realm based on Couette/Poiseuille models: Towards paleo-mantle-flowgraphy. Phys. Earth Planet. Inter. 2023, 340, 107045. [Google Scholar] [CrossRef]
- Colli, L.; Stotz, I.; Bunge, H.P.; Smethurst, M.; Clark, S.; Iaffaldano, G.; Tassara, A.; Guillocheau, F.; Bianchi, M.C. Rapid South Atlantic spreading changes and coeval vertical motion in surrounding continents: Evidence for temporal changes of pressure-driven upper mantle flow. Tectonics 2014, 33, 1304–1321. [Google Scholar] [CrossRef]
- Conrad, C.P.; Lithgow-Bertelloni, C. How Mantle Slabs Drive Plate Tectonics. Science 2002, 298. [Google Scholar] [CrossRef]
- Morgan, W.J. Plate motions and deep mantle convection. Mem. Geol. Soc. Am. 1972, 132, 7–22. [Google Scholar]
- Morgan, W. Convection Plumes in the Lower Mantle. Nature 1971, 230, 42–43. [Google Scholar] [CrossRef]
- Morgan, J.P.; Smith, W.H.F. Flattening of the sea-floor depth-age curve as a response to asthenospheric flow. Nature 1992, 359, 524–527. [Google Scholar] [CrossRef]
- Morgan, J.P.; Morgan, W.J.; Zhang, Y.S.; Smith, W.H.F. Observational hints for a plume-fed, suboceanic asthenosphere and its role in mantle convection. J. Geophys. Res. Solid Earth 1995, 100, 12753–12767. [Google Scholar] [CrossRef]
- Stotz, I.L.; Vilacís, B.; Hayek, J.N.; Carena, S.; Bunge, H.P. Plume driven plate motion changes: New insights from the South Atlantic realm. J. South Am. Earth Sci. 2023, 124, 104257. [Google Scholar] [CrossRef]
- Hager, B.H.; Clayton, R.W.; Clayton, R.W.; Comer, R.P.; Dziewonski, A.M. Lower mantle heterogeneity, dynamic topography and the geoid. Nature 1985, 313, 541–545. [Google Scholar] [CrossRef]
- Şengör, A.M.C. Elevation as indicator of mantle-plume activity. Mantle Plumes Their Identif. Through Time 2001, 352, 183–245. [Google Scholar] [CrossRef]
- Rainbird, R.H.; Ernst, R.E. The sedimentary record of mantle-plume uplift. Spec. Pap.-Geol. Soc. Am. 2001, 352, 227–246. [Google Scholar] [CrossRef]
- Campbell, I.H. Testing the plume theory. Chem. Geol. 2007, 241, 153–176. [Google Scholar] [CrossRef]
- Saunders, A.; Jones, S.; Morgan, L.; Pierce, K.; Widdowson, M.; Xu, Y. Regional uplift associated with continental large igneous provinces: The roles of mantle plumes and the lithosphere. Chem. Geol. 2007, 241, 282–318. [Google Scholar] [CrossRef]
- Friedrich, A.M.; Bunge, H.P.; Rieger, S.M.; Colli, L.; Ghelichkhan, S.; Nerlich, R. Stratigraphic framework for the plume mode of mantle convection and the analysis of interregional unconformities on geological maps. Gondwana Res. 2018, 53, 159–188. [Google Scholar] [CrossRef]
- Suess, E. Das Antlitz der Erde (The Face of the Earth); G. Freytag: Leipzig, Germany, 1885; Volume 1. [Google Scholar]
- Lawver, L.A.; Gahagan, L.M. Subduction Zones, Magmatism, and the Breakup of Pangea. In Flow and Creep in the Solar System: Observations, Modeling and Theory; Springer: Amsterdam, The Netherlands, 1993; pp. 225–247. [Google Scholar] [CrossRef]
- Coffin, M.; Eldholm, O. Volcanism and continental break-up: A global compilation of large igneous provinces. Geol. Soc. Lond. Spec. Publ. 1992, 68, 17–30. [Google Scholar] [CrossRef]
- Burke, K.; Gunnell, Y. The African Erosion Surface: A Continental-Scale Synthesis of Geomorphology, Tectonics, and Environmental Change over the Past 180 Million Years. Geol. Soc. Am. Mem. 2008, 201, 21–66. [Google Scholar]
- Mueller, R.D.; Seton, M.; Zahirovic, S.; Williams, S.E.; Matthews, K.J.; Wright, N.M.; Shephard, G.E.; Maloney, K.T.; Barnett-Moore, N.; Hosseinpour, M.; et al. Ocean Basin Evolution and Global-Scale Plate Reorganization Events Since Pangea Breakup. Annu. Rev. Earth Planet. Sci. 2016, 44, 107–138. [Google Scholar] [CrossRef]
- Hayek, J.N.; Vilacís, B.; Bunge, H.P.; Friedrich, A.M.; Carena, S.; Vibe, Y. Continent-scale Hiatus Maps for the Atlantic Realm and Australia since the Upper Jurassic and links to mantle flow induced dynamic topography. Proc. R. Soc. Math. Phys. Eng. Sci. 2020, 476, 20200390. [Google Scholar] [CrossRef]
- Colli, L.; Ghelichkhan, S.; Bunge, H.P. On the ratio of dynamic topography and gravity anomalies in a dynamic Earth. Geophys. Res. Lett. 2016, 43, 2510–2516. [Google Scholar] [CrossRef]
- Friedrich, A.M. Palaeogeological hiatus surface mapping: A tool to visualize vertical motion of the continents. Geol. Mag. 2019, 156, 308–319. [Google Scholar] [CrossRef]
- Vibe, Y.; Friedrich, A.M.; Bunge, H.P.; Clark, S.R. Correlations of oceanic spreading rates and hiatus surface area in the North Atlantic realm. Lithosphere 2018, 10, 677–684. [Google Scholar] [CrossRef]
- Carena, S.; Bunge, H.P.; Friedrich, A.M. Analysis of geological hiatus surfaces across Africa in the Cenozoic and implications for the timescales of convectively-maintained topography. Can. J. Earth Sci. 2019, 56, 1333–1346. [Google Scholar] [CrossRef]
- Vilacís, B.; Brown, H.; Bunge, H.P.; Carena, S.; Hayek, J.N.; Stotz, I.L.; Wang, Z.R.; Friedrich, A.M. Dynamic topography and the planform of mantle convection since the Jurassic inferred from global continental hiatus maps. Proc. R. Soc. Math. Phys. Eng. Sci. 2024, 480, 20240311. [Google Scholar] [CrossRef]
- Cohen, K.M.; Harper, D.; Gibbard, P.L. ICS International Chronostratigraphic Chart. August 2018. Available online: www.stratigraphy.org (accessed on 10 February 2025).
- Ernst, R.E.; Buchan, K.L. Maximum size and distribution in time and space of mantle plumes: Evidence from large igneous provinces. J. Geodyn. 2002, 34, 309–342. [Google Scholar] [CrossRef]
- Coffin, M.F.; Eldholm, O. Large Igneous Provinces. In Encyclopedia of Ocean Sciences, 3rd ed.; Cochran, J.K., Bokuniewicz, H.J., Yager, P.L., Eds.; Academic Press: Oxford, UK, 2019; pp. 337–345. [Google Scholar] [CrossRef]
- Ernst, R.E.; Bond, D.P.G.; Zhang, S.H.; Buchan, K.L.; Grasby, S.E.; Youbi, N.; El Bilali, H.; Bekker, A.; Doucet, L.S. Large Igneous Province Record Through Time and Implications for Secular Environmental Changes and Geological Time-Scale Boundaries. In Large Igneous Provinces; American Geophysical Union (AGU): Washington, DC, USA, 2021; Chapter 1; pp. 1–26. [Google Scholar] [CrossRef]
- Buchan, K.L.; Ernst, R.E. Plumbing systems of large igneous provinces (LIPs) on Earth and Venus: Investigating the role of giant circumferential and radiating dyke swarms, coronae and novae, and mid-crustal intrusive complexes. Gondwana Res. 2021, 100, 25–43. [Google Scholar] [CrossRef]
- Buchan, K.; Ernst, R. Giant circumferential dykes swarms: Catalogue and characteristics. In Dyke Swarms of the World: A Modern Perspective; Srivastava, R., Ernst, R., Peng, P., Eds.; Springer: Singapore, 2019; pp. 1–44. [Google Scholar]
- El Bilali, H.; Ernst, R.E. Far-travelled 3700 km lateral magma propagation just below the surface of Venus. Nat. Commun. 2024, 15, 1759. [Google Scholar] [CrossRef] [PubMed]
- Tessier, A.D.; Ernst, R.E.; El Bilali, H. Heng-o Corona, Venus: Dyke swarms record evolution of its underlying mantle plume. Icarus 2024, 417, 116090. [Google Scholar] [CrossRef]
- Frimmel, H.E. Configuration of Pan-African Orogenic Belts in Southwestern Africa. In Neoproterozoic-Cambrian Tectonics, Global Change and Evolution: A Focus on Southwestern Gondwana; Gaucher, C., Sial, A., Haverson, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 145–151. [Google Scholar]
- Heine, C.; Zoethout, J.; Müller, D. Kinematics of the South Atlantic Rift. Solid Earth 2013, 4, 215–253. [Google Scholar] [CrossRef]
- Baksi, A. Critical evaluation of 40Ar/39Ar ages for the Central Atlantic Magmatic Province: Timing, duration and possible migration of magmatic centers. In Washington DC American Geophysical Union Geophysical Monograph Series; Wiley: Hoboken, NJ, USA, 2003; Volume 136, pp. 77–90. [Google Scholar] [CrossRef]
- Whalen, L.; Gazel, E.; Vidito, C.; Puffer, J.; Bizimis, M.; Henika, W.; Caddick, M.J. Supercontinental inheritance and its influence on supercontinental breakup: The Central Atlantic Magmatic Province and the breakup of Pangea. Geochem. Geophys. Geosyst. 2015, 16, 3532–3554. [Google Scholar] [CrossRef]
- Ernst, R.E.; Buchan, K.L. Giant Radiating Dyke Swarms: Their Use in Identifying Pre-Mesozoic Large Igneous Provinces and Mantle Plumes. In Large Igneous Provinces: Continental, Oceanic, and Planetary Flood Volcanism; American Geophysical Union (AGU): Washington, DC, USA, 1997; pp. 297–333. [Google Scholar] [CrossRef]
- Marzoli, A.; Renne, P.R.; Piccirillo, E.M.; Ernesto, M.; Bellieni, G.; De Min, A. Extensive 200-million-year-old continental flood basalts of the central Atlantic magmatic province. Science 1999, 284, 616–618. [Google Scholar] [CrossRef]
- Cox, K.G. The Karoo Province. In Continental Flood Basalts; Macdougall, J.D., Ed.; Springer: Dordrecht, The Netherlands, 1988; pp. 239–271. [Google Scholar] [CrossRef]
- Segev, A. Flood basalts, continental breakup and the dispersal of Gondwana: Evidence for periodic migration of upwelling mantle flows (plumes). Egu Stephan Mueller Spec. Publ. Ser. 2002, 2, 171–191. [Google Scholar] [CrossRef]
- Burke, K.; Dewey, J.F. Plume-Generated Triple Junctions: Key Indicators in Applying Plate Tectonics to Old Rocks. J. Geol. 1973, 81, 406–433. [Google Scholar] [CrossRef]
- Piccirillo, E.M.; Melfi, A.J.; Comin-Chiaramonti, P.; Bellieni, G.; Ernesto, M.; Marques, L.S.; Nardy, A.J.R.; Pacca, I.G.; Roisenberg, A.; Stolfa, D. Continental Flood Volcanism From the Paraná Basin (Brazil). In Continental Flood Basalts; Macdougall,, J.D.,, Ed.; Springer: Dordrecht, The Netherlands, 1988; pp. 195–238. [Google Scholar] [CrossRef]
- Peate, D.W. The Paraná-Etendeka Province. In Large Igneous Provinces: Continental, Oceanic, and Planetary Flood Volcanism; American Geophysical Union (AGU): Washington, DC, USA, 1997; pp. 217–245. [Google Scholar] [CrossRef]
- Hollanda, M.H.B.M.; Archanjo, C.J.; Macedo Filho, A.A.; Fossen, H.; Ernst, R.E.; de Castro, D.L.; Melo, A.C.; Oliveira, A.L. The Mesozoic Equatorial Atlantic Magmatic Province (EQUAMP). In Dyke Swarms of the World: A Modern Perspective; Srivastava, R.K., Ernst, R.E., Peng, P., Eds.; Springer: Singapore, 2019; pp. 87–110. [Google Scholar] [CrossRef]
- Buck, R. 6.08 Dynamic Processes in Extensional and Compressional Settings: The Dynamics of Continental Breakup and Extension. Treatise Geophys. 2007, 6, 335–376. [Google Scholar] [CrossRef]
- Bird, P. Testing hypotheses on plate-driving mechanisms with global lithosphere models including topography, thermal structure, and faults. J. Geophys. Res.-Solid Earth 1998, 103, 10115–10129. [Google Scholar] [CrossRef]
- Brune, S. Forces within continental and oceanic rifts: Numerical modeling elucidates the impact of asthenospheric flow on surface stress. Geology 2018, 46, 191. [Google Scholar] [CrossRef]
- Bird, P.; Liu, Z.; Rucker, W.K. Stresses that drive the plates from below: Definitions, computational path, model optimization, and error analysis. J. Geophys. Res. 2008, 113, B11406. [Google Scholar] [CrossRef]
- Karato, S. On the origin of the asthenosphere. Earth Planet. Sci. Lett. 2012, 321–322, 95–103. [Google Scholar] [CrossRef]
- Grand, S.P.; Helmberger, D.V. Upper mantle shear structure of North America. Geophys. J. R. Astron. Soc. 1984, 76, 399–438. [Google Scholar] [CrossRef]
- Debayle, E.; Kennett, B.; Priestley, K. Global azimuthal seismic anisotropy and the unique plate-motion deformation of Australia. Nature 2005, 433, 509–512. [Google Scholar] [CrossRef]
- French, S.; Lekic, V.; Romanowicz, B. Waveform Tomography Reveals Channeled Flow at the Base of the Oceanic Asthenosphere. Science 2013, 342, 227–230. [Google Scholar] [CrossRef]
- Paulson, A.; Richards, M.A. On the resolution of radial viscosity structure in modelling long-wavelength postglacial rebound data. Geophys. J. Int. 2009, 179, 1516. [Google Scholar] [CrossRef]
- Haskell, N.A. The viscosity of the asthenoshpere. Am. J. Sci. 1937, 33, 22–28. [Google Scholar] [CrossRef]
- Mitrovica, J.X. Haskell [1935] revisited. J. Geophys. Res. Solid Earth 1996, 101, 555–569. [Google Scholar] [CrossRef]
- Freed, A.M.; Bürgmann, R.; Calais, E.; Freymueller, J.; Hreinsdóttir, S. Implications of deformation following the 2002 Denali, Alaska, earthquake for postseismic relaxation processes and lithospheric rheology. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Freed, A.M.; Hashima, A.; Becker, T.W.; Okaya, D.A.; Sato, H.; Hatanaka, Y. Resolving depth-dependent subduction zone viscosity and afterslip from postseismic displacements following the 2011 Tohoku-oki, Japan earthquake. Earth Planet. Sci. Lett. 2017, 459, 279–290. [Google Scholar] [CrossRef]
- Hu, Y.; Bürgmann, R.; Banerjee, P.; Feng, L.; Hill, E.; Ito, T.; Tabei, T.; Wang, K. Asthenosphere rheology inferred from observations of the 2012 Indian Ocean earthquake. Nature 2016, 538, 368–372. [Google Scholar] [CrossRef]
- Iaffaldano, G.; Lambeck, K. Pacific plate–motion change at the time of the Hawaiian–Emperor bend constrains the viscosity of Earth’s asthenosphere. Geophys. Res. Lett. 2014. in review. [Google Scholar] [CrossRef]
- Stixrude, L.; Lithgow-Bertelloni, C. Mineralogy and elasticity of the oceanic upper mantle: Origin of the low-velocity zone. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Patočka, V.; Čížková, H.; Pokorný, J. Dynamic Component of the Asthenosphere: Lateral Viscosity Variations Due to Dislocation Creep at the Base of Oceanic Plates. Geophys. Res. Lett. 2024, 51, e2024GL109116. [Google Scholar] [CrossRef]
- Hoggard, M.J.; Winterbourne, J.; Czarnota, K.; White, N. Oceanic residual depth measurements, the plate cooling model, and global dynamic topography. J. Geophys. Res. Solid Earth 2017, 122, 2328–2372. [Google Scholar] [CrossRef]
- Buck, W.R. The role of magma in the development of the Afro-Arabian Rift System. In The Afar Volcanic Province within the East African Rift System; Geological Society of London: London, UK, 2006. [Google Scholar] [CrossRef]
- Müller, R.D.; Royer, J.Y.; Cande, S.C.; Roest, W.R.; Maschenkov, S. Chapter 2: New constraints on the late cretaceous/tertiary plate tectonic evolution of the caribbean. In Caribbean Basins; Mann, P., Ed.; Elsevier: Amsterdam, The Netherlands, 1999; Volume 4, pp. 33–59. [Google Scholar] [CrossRef]
- Doubrovine, P.V.; Steinberger, B.; Torsvik, T.H. Absolute plate motions in a reference frame defined by moving hot spots in the Pacific, Atlantic, and Indian oceans. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Algeo, T.J. Geomagnetic polarity bias pattern through the Phanerozoic. J. Geophys. Res. 1996, 101, 2785–2814. [Google Scholar] [CrossRef]
- Yuen, D.; Fleitout, L. Thinning of the lithosphere by small-scale convective destabilization. Nature 1985, 313, 125–128. [Google Scholar] [CrossRef]
- Fleitout, L.; Froidevaux, C.; Yuen, D. Active lithospheric thinning. Tectonophysics 1986, 132, 271–278. [Google Scholar] [CrossRef]
- Sleep, N. Lithospheric Heating by Mantle Plumes. Geophys. J. R. Astron. Soc. 1987, 91, 1–11. [Google Scholar] [CrossRef]
- Gurnis, M. Large-scale mantle convection and the aggregation and dispersal of supercontinents. Nature 1988, 332, 695–699. [Google Scholar] [CrossRef]
- Segev, A. Synchronous magmatic cycles during the fragmentation of Gondwana: Radiometric ages from the Levant and other provinces. Tectonophysics 2000, 325, 257–277. [Google Scholar] [CrossRef]
- Davies, G.F. Ocean bathymetry and mantle convection large-scale flow and hotspots. J. Geophys. Res.-Solid Earth Planets 1988, 93, 10467–10480. [Google Scholar] [CrossRef]
- Marzoli, A.; Callegaro, S.; Dal Corso, J.; Davies, J.H.F.L.; Chiaradia, M.; Youbi, N.; Bertrand, H.; Reisberg, L.; Merle, R.; Jourdan, F. The Central Atlantic Magmatic Province (CAMP): A Review. In The Late Triassic World: Earth in a Time of Transition; Tanner, L.H., Ed.; Springer: Cham, Switzerland, 2018; pp. 91–125. [Google Scholar] [CrossRef]
- Westaway, R. Forces associated with mantle plumes. Earth Planet. Sci. Lett. 1993, 119, 331–348. [Google Scholar] [CrossRef]
- Hartley, R.A.; Roberts, G.G.; White, N.; Richardson, C. Transient convective uplift of an ancient buried landscape. Nat. Geosci. 2011, 4, 562–565. [Google Scholar] [CrossRef]
- Jordan, T.H. Composition and development of the continental tectosphere. Nature 1978, 274, 544–548. [Google Scholar] [CrossRef]
- Conrad, C.P.; Lithgow-Bertelloni, C. Influence of continental roots and asthenosphere on plate-mantle coupling. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Karato, S.i.; Wu, P. Rheology of the upper mantle: A synthesis. Science 1993, 260, 771–778. [Google Scholar] [CrossRef] [PubMed]
- Semple, A.G.; Lenardic, A. Plug flow in the Earth’s asthenosphere. Earth Planet. Sci. Lett. 2018, 496, 29–36. [Google Scholar] [CrossRef]
- Wilson, J.T. Did the Atlantic close and then re-open? Nature 1966, 211, 676–681. [Google Scholar] [CrossRef]
- Burke, K.; Dewey, J.F. The Wilson Cycle. In Proceedings of the Geological Society of America, Northeastern Section, 10th Annual Meeting, Abstracts with Programs, Syracuse, NY, USA, 6–8 March 1975; p. 48. [Google Scholar]
- Dunbar, J.; Sawyer, D. How pre-existing weaknesses control the style of continental breakup. J. Geophys. Res. 1989, 94, 7278–7292. [Google Scholar] [CrossRef]
- Vauchez, A.; Barruol, G.; Tommasi, A. Why do continents break-up parallel to ancient orogenic belts? Terra Nova 1997, 9, 62–66. [Google Scholar] [CrossRef]
- Audet, P.; Bürgmann, R. Dominant role of tectonic inheritance in supercontinent cycles. Nat. Geosci. 2011, 4, 184–187. [Google Scholar] [CrossRef]
- Wilson, R.; Houseman, G.; Buiter, S.; McCaffrey, K.; Dore, A. Fifty years of the Wilson Cycle Concept in Plate Tectonics: An Overview. Geol. Soc. Lond. Spec. Publ. 2019, 470, 1–17. [Google Scholar] [CrossRef]
- Carey, S.W. The tectonic approach to continental drift. In Continental Drift—A Symposium; Carey, S.W., Ed.; University of Tasmania: Hobart, Australia, 1958; pp. 177–363, Expanding Earth from p. 311 to p. 349. [Google Scholar]
- O’Neill, C.; Müller, D.; Steinberger, B. On the uncertainties in hot spot reconstructions and the significance of moving hot spot reference frames. Geochem. Geophys. Geosyst. 2005, 6, Q04003. [Google Scholar] [CrossRef]
- Steinberger, B.; Torsvik, T.H. Absolute plate motions and true polar wander in the absence of hotspot tracks. Nature 2008, 452, 620–623. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.D.; Royer, J.Y.; Lawver, L.A. Revised plate motions relative to the hotspots from combined Atlantic and Indian Ocean hotspot tracks. Geology 1993, 21, 275–278. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stotz, I.L.; Vilacís, B.; Hayek, J.N.; Bunge, H.-P. Continental Rift Driven by Asthenosphere Flow and Lithosphere Weakening by Flood Basalts: South America and Africa Cenozoic Rifting. Minerals 2025, 15, 644. https://doi.org/10.3390/min15060644
Stotz IL, Vilacís B, Hayek JN, Bunge H-P. Continental Rift Driven by Asthenosphere Flow and Lithosphere Weakening by Flood Basalts: South America and Africa Cenozoic Rifting. Minerals. 2025; 15(6):644. https://doi.org/10.3390/min15060644
Chicago/Turabian StyleStotz, Ingo L., Berta Vilacís, Jorge N. Hayek, and Hans-Peter Bunge. 2025. "Continental Rift Driven by Asthenosphere Flow and Lithosphere Weakening by Flood Basalts: South America and Africa Cenozoic Rifting" Minerals 15, no. 6: 644. https://doi.org/10.3390/min15060644
APA StyleStotz, I. L., Vilacís, B., Hayek, J. N., & Bunge, H.-P. (2025). Continental Rift Driven by Asthenosphere Flow and Lithosphere Weakening by Flood Basalts: South America and Africa Cenozoic Rifting. Minerals, 15(6), 644. https://doi.org/10.3390/min15060644





