Estimation of Copper Grade, Acid Consumption, and Moisture Content in Heap Leaching Using Extended and Unscented Kalman Filters
Abstract
1. Introduction
- The design of EKF and UKF observers for estimating copper grade, acid consumption, and moisture content in heap leaching processes.
- The automatic adjustment of parameters of interest within the heap leaching mathematical model using particle swarm optimization (PSO).
- An in-depth analysis and comparison of Kalman-based estimators within different simulated scenarios of the heap leaching process.
2. Materials and Methods
- Neglect of energy balances: The scenario is assumed to be isothermal, since the dissolution of oxide minerals does not involve significant exothermic or endothermic reactions.
- Dominant vertical axis: Mass balances are primarily considered in the vertical direction, assuming negligible lateral flow [24].
- Hydraulic relationships for unsaturated flow media: The model incorporates explicit dependencies on drainage and dynamic moisture, representing the solution content per mineral portion.
- Neglect of diffusional mass flux: The diffusional mass flux is disregarded due to its significantly lower magnitude than advective mass fluxes, in line with Assumption 2.
2.1. Kinetic Reactions
2.2. Hydrodynamic Relationship
3. State Observer Design
- Prediction Stage (green area): A process model, incorporating uncertainties, predicts the system’s future state based on its current state.
- Update Stage (yellow area): The predicted state and the measurement error are combined using the Kalman gain (). This updates the system’s estimated state (represented by ) and the error covariance matrix ().
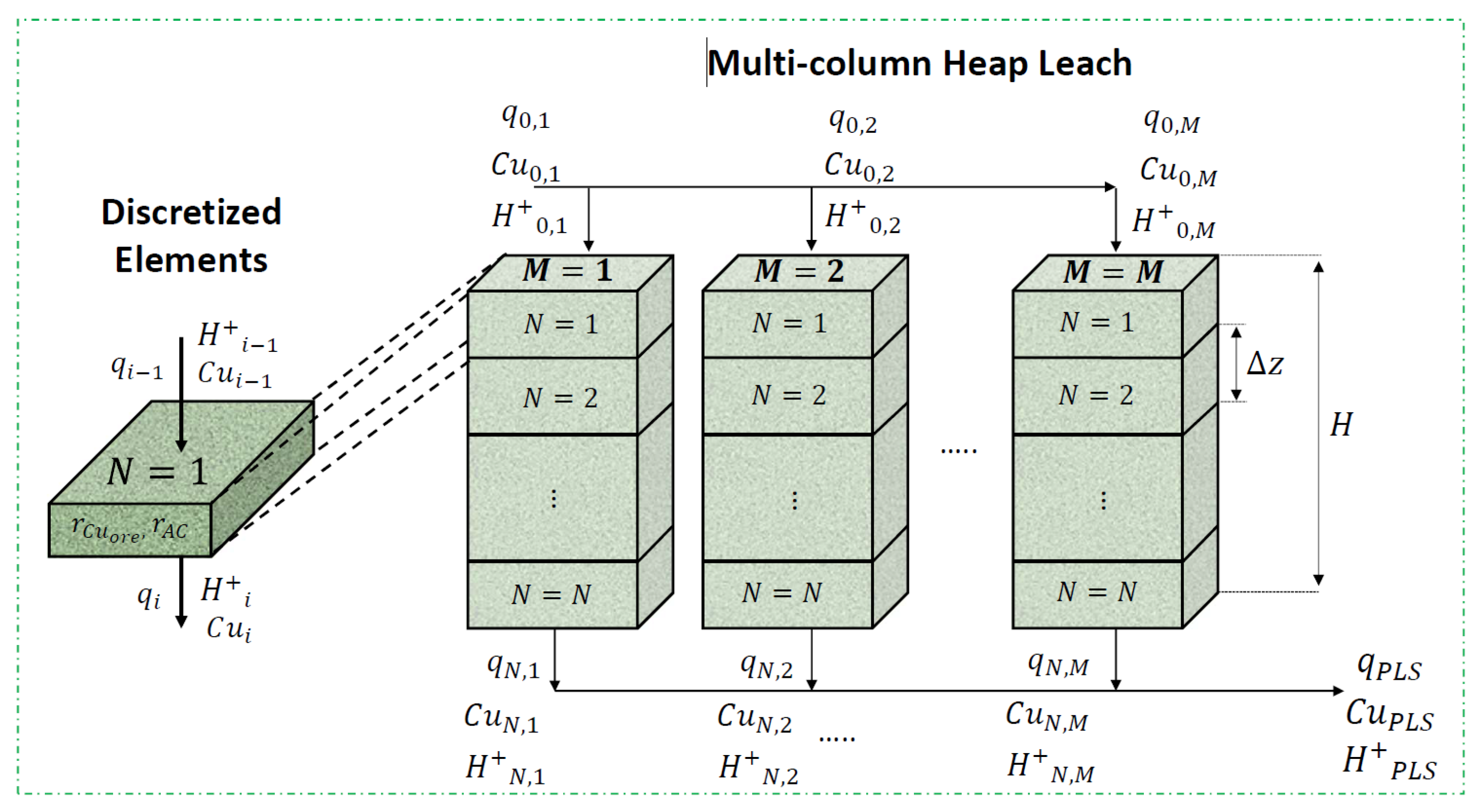
3.1. Measurements Multicolumn Model
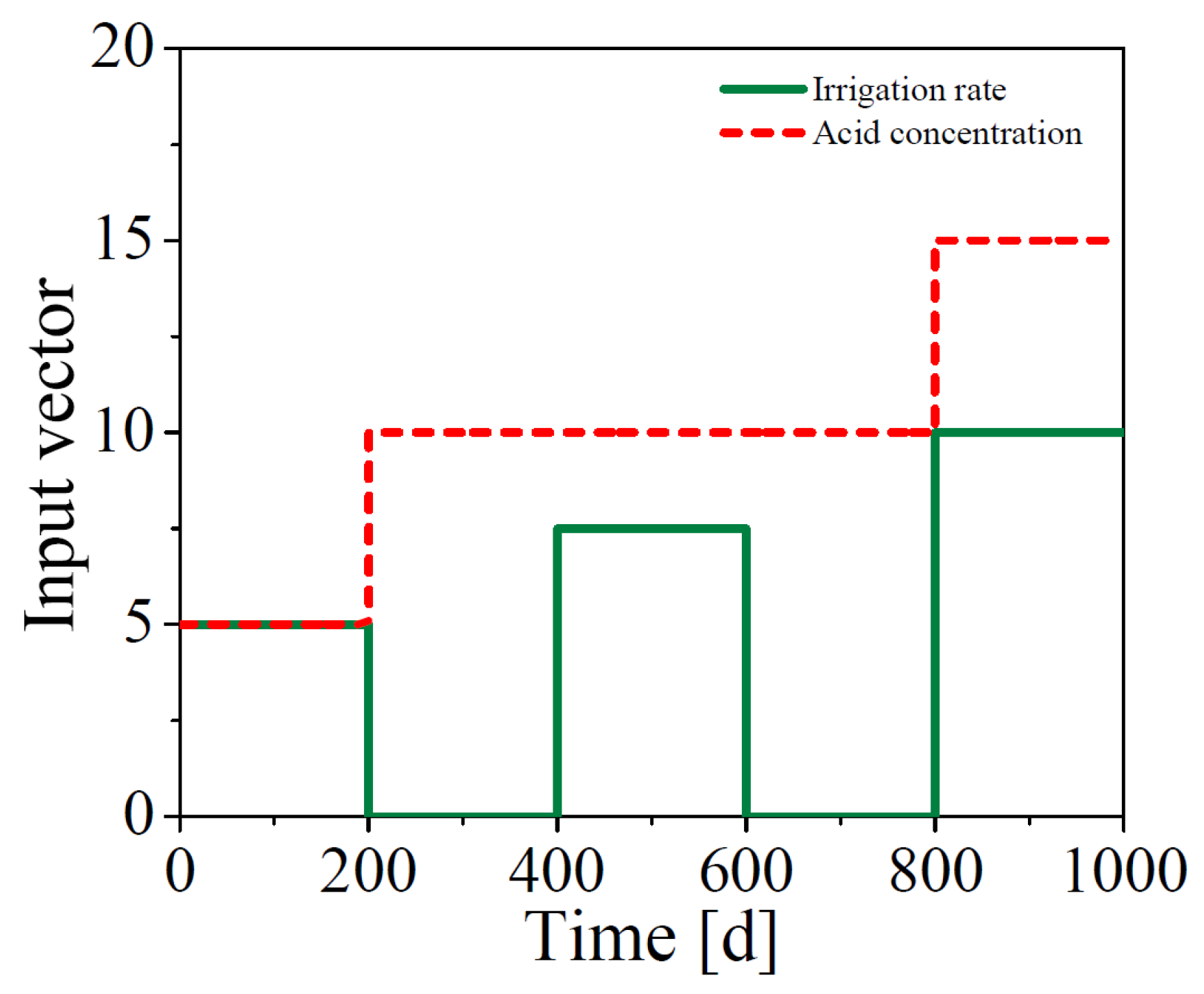
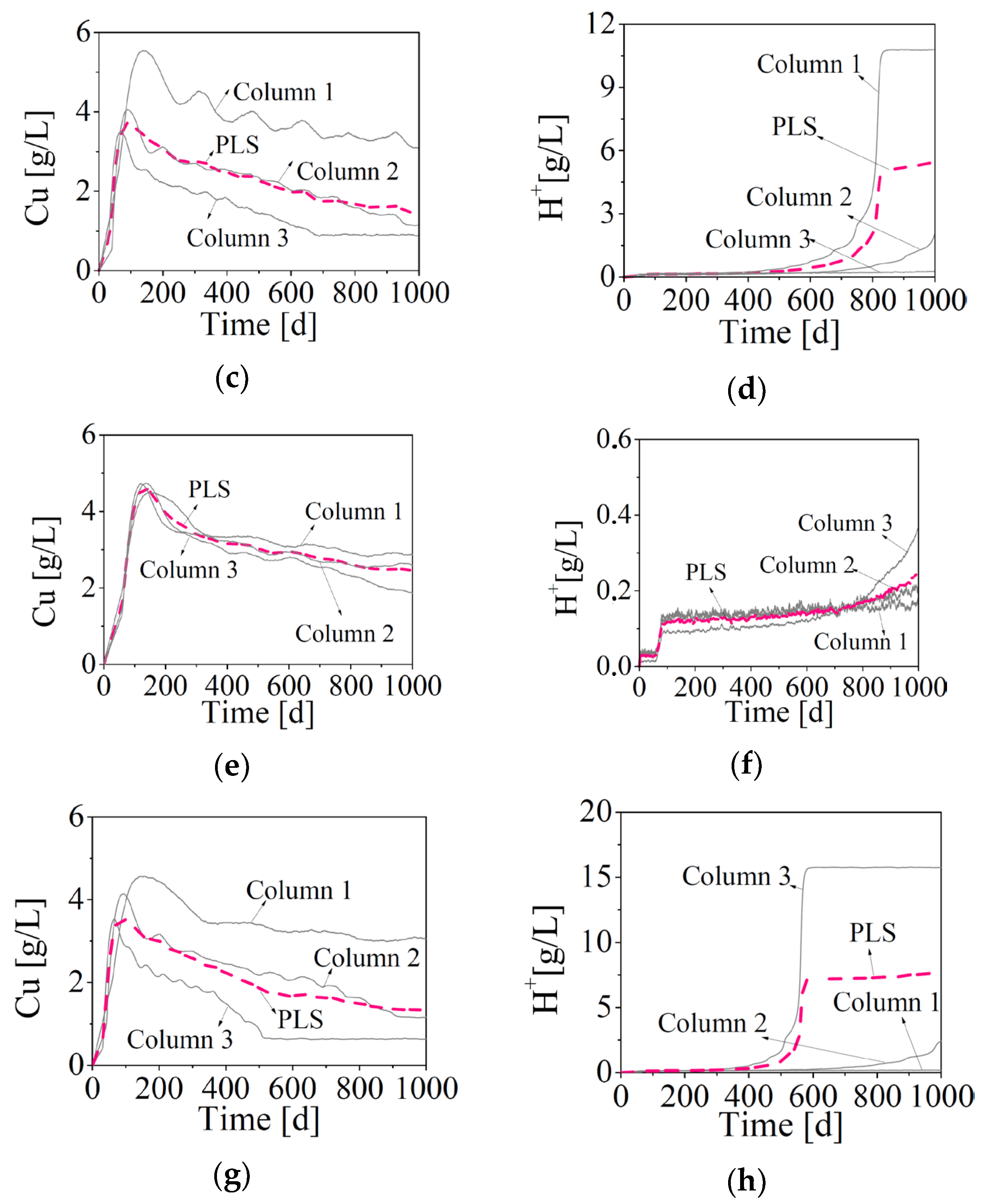
3.2. Simulation Cases
4. Results, Analysis, and Discussion
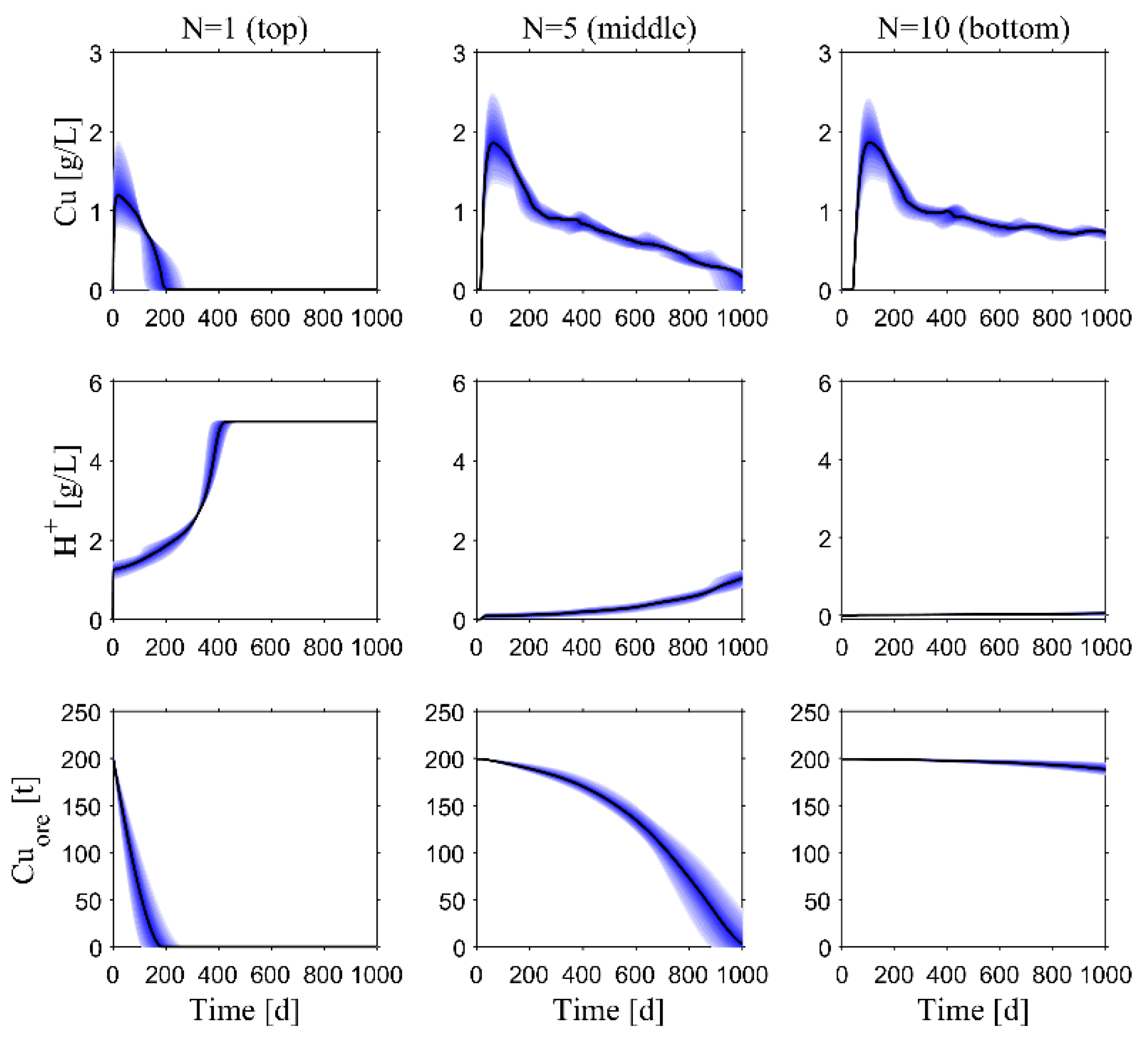
4.1. Preliminary Simulation of the Heap Leaching Model
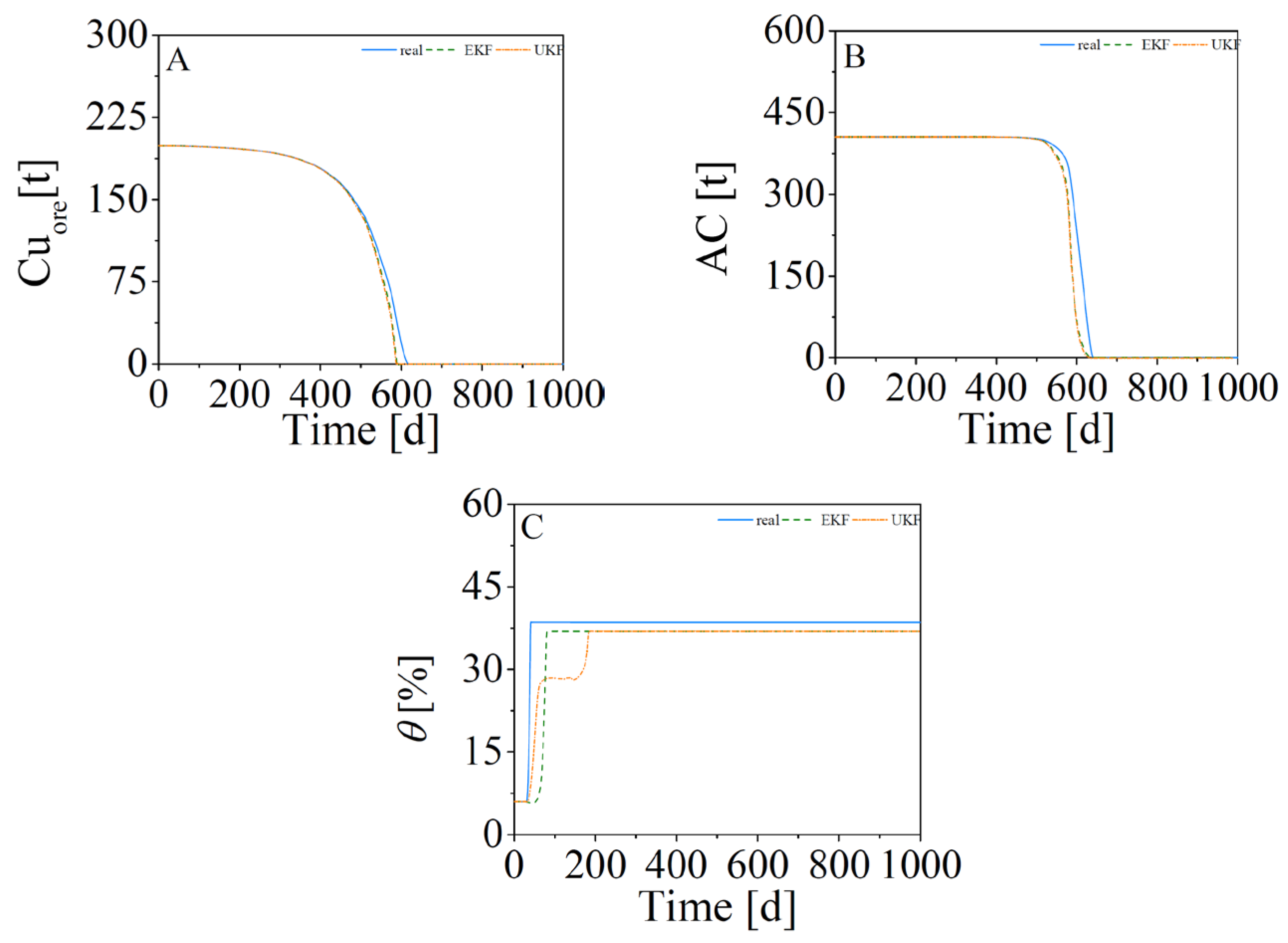
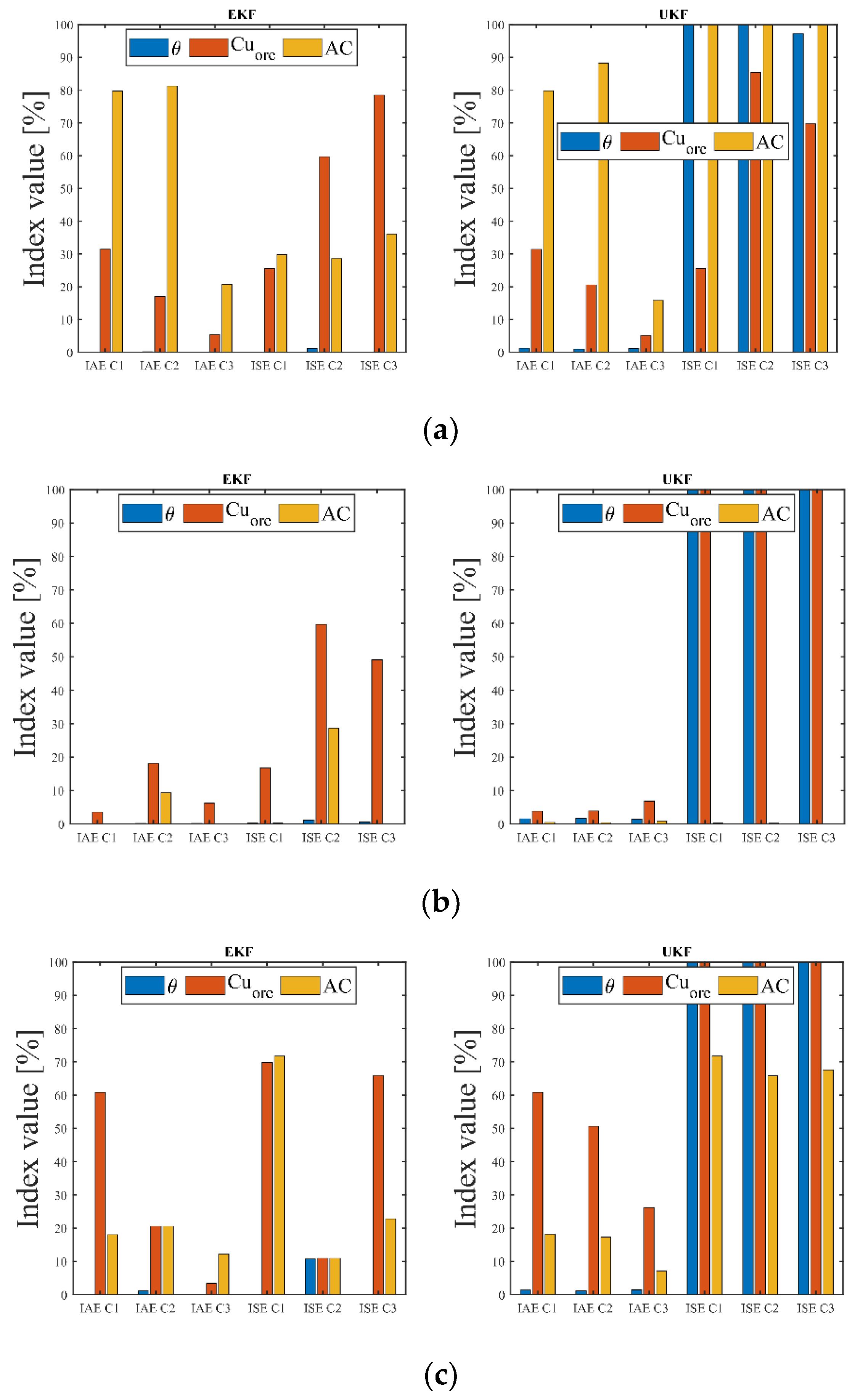
4.2. Observers’ Results
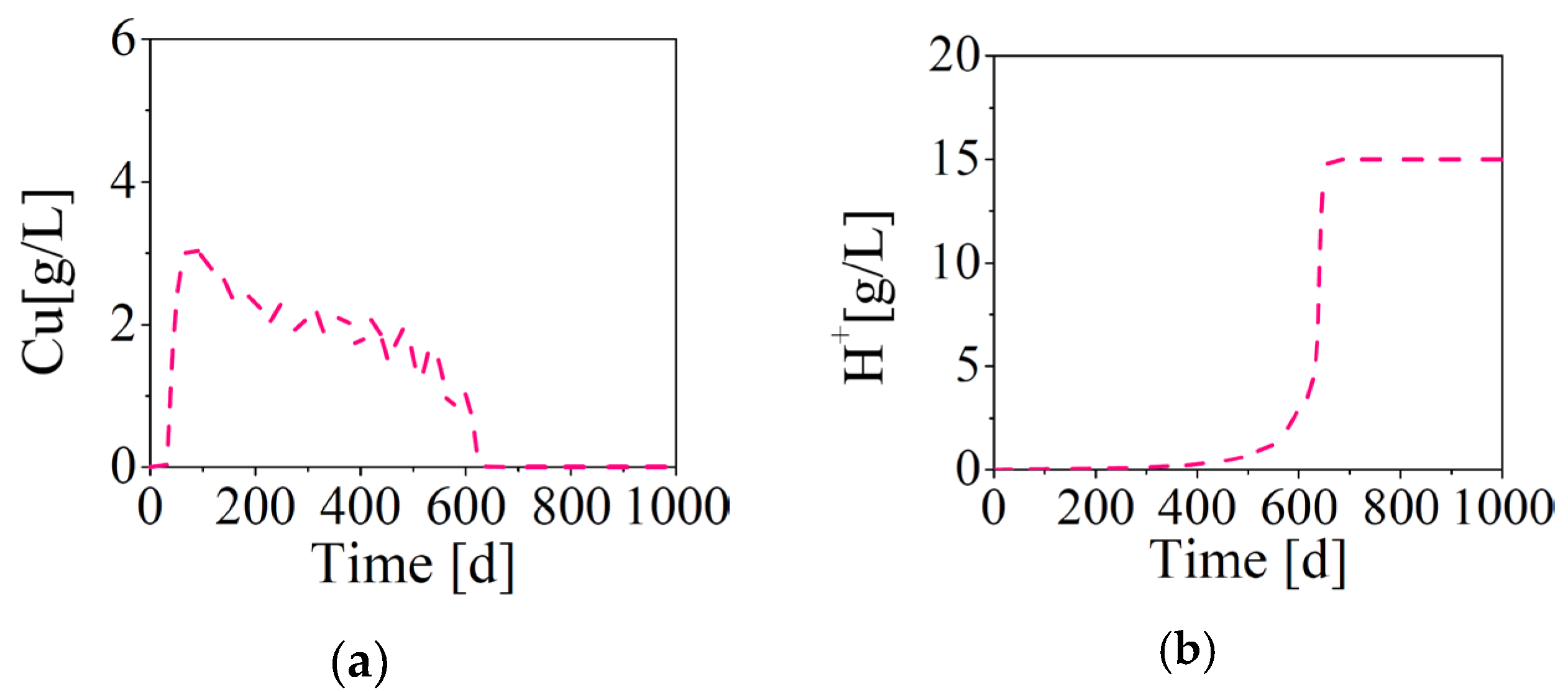
4.3. Simulation of One Module (Scenario 1)
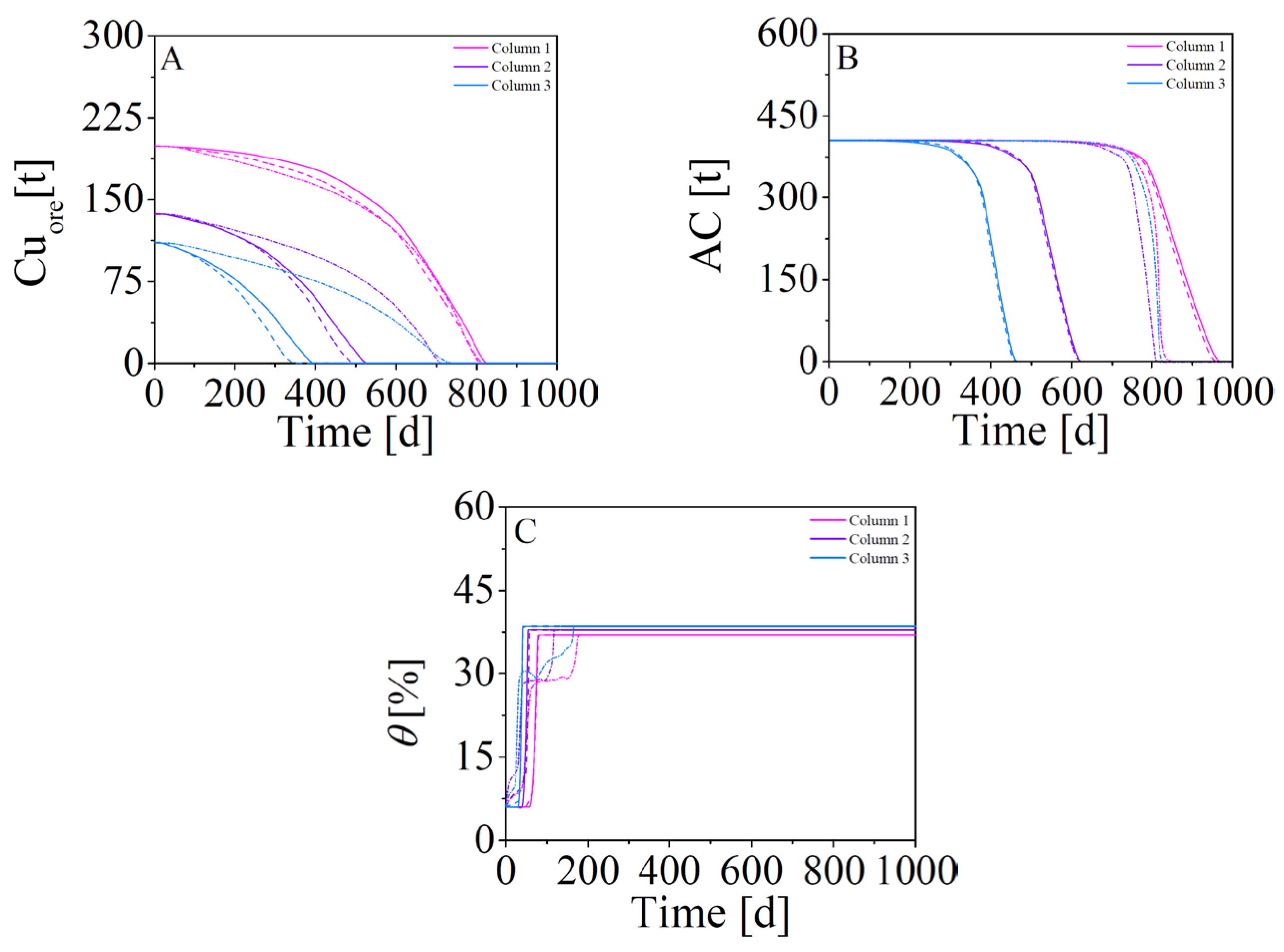
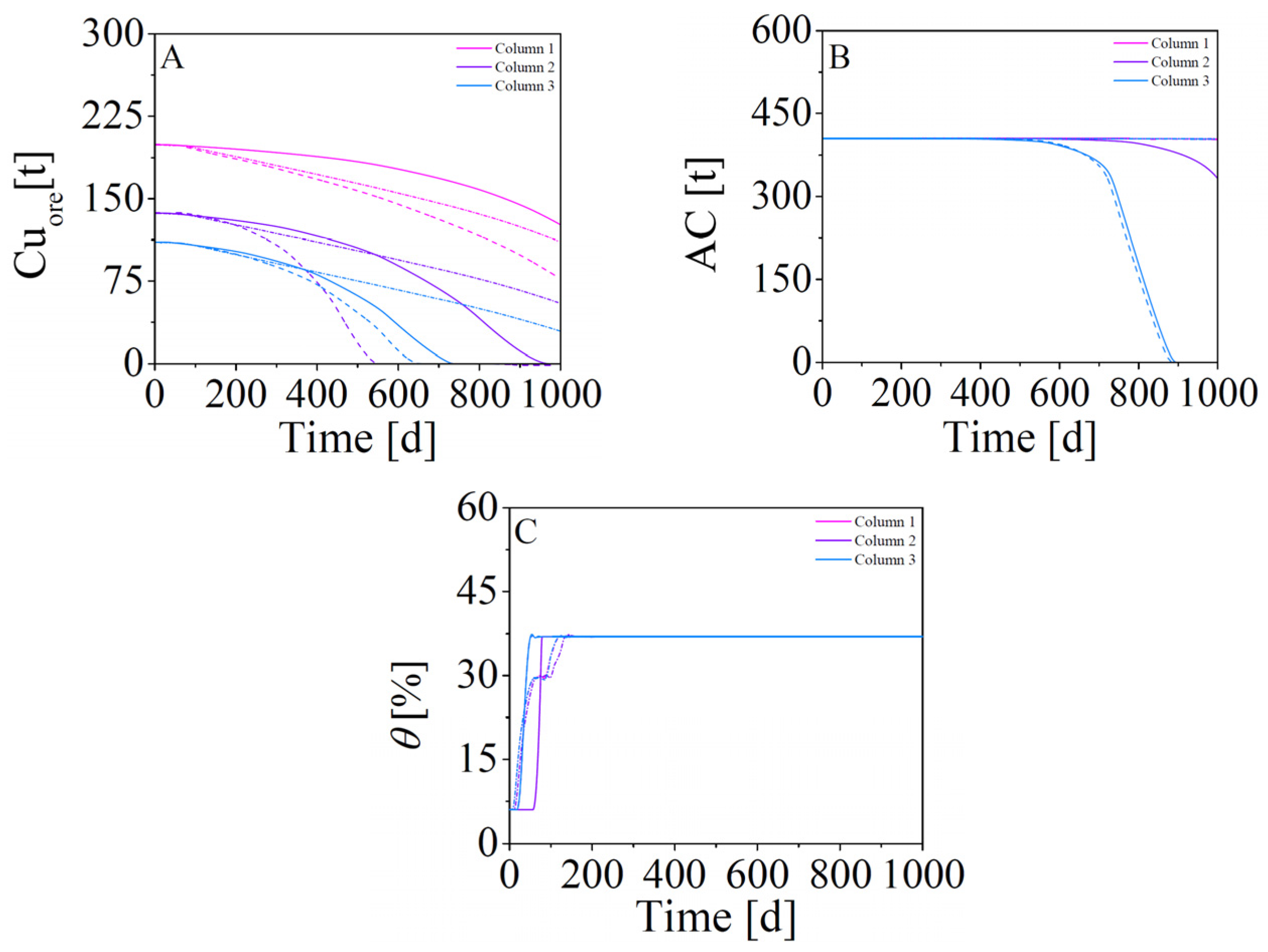
4.4. Simulation of Multiple Modules (Scenario 2–4)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Greek Letters | |
| Discrete element length | |
| Moisture content [%] | |
| Superscripts | |
| Estimated | |
| Variables | |
| Smooth Copper in the ore rate [kg/h] | |
| Smooth Acid reaction rate [kg/h] | |
| Acid consumption concentration [t] | |
| Aqueous copper concentration [g/L] | |
| Copper concentration in the ore [t] | |
| Extended Kalman Filter | |
| Heap Height [m] | |
| Acid concentration [g/L] | |
| Heap Length [m] | |
| Number of columns | |
| Mineral mass pile section [kg/m] | |
| Molecular weight of the mineral [kg/kmol] | |
| Number of elements | |
| Inlet flow [/h] | |
| Outlet flow [/h] | |
| Acid consumption rate [kg/h] | |
| Copper in the ore rate [kg/h] | |
| Copper reaction rate [kg/h] | |
| Acid reaction rate [kg/h] | |
| Irrigation rate [L/h-] | |
| Unscented Kalman Filter | |
| Heap Volume [] | |
| Heap Width [m] |
Appendix A. The Extended Kalman Filter (EKF)
Appendix B
References
- Petersen, J. Heap leaching as a key technology for recovery of values from low-grade ores—A brief overview. Hydrometallurgy 2016, 165, 206–212. [Google Scholar] [CrossRef]
- Ghorbani, Y.; Franzidis, J.-P.; Petersen, J. Heap leaching technology—Current state; innovations; future directions: A review. Miner. Process. Extr. Metall. Rev. 2016, 37, 73–119. [Google Scholar] [CrossRef]
- Estay, H.; Lois-Morales, P.; Montes-Atenas, G.; del Ruiz del Solar, J.R. On the Challenges of Applying Machine Learning in Mineral Processing and Extractive Metallurgy. Minerals 2023, 13, 788. [Google Scholar] [CrossRef]
- Daud, O.; Correa, M.; Estay, H.; del Solar, J.R.-D. Monitoring and Controlling Saturation Zones in Heap Leach Piles Using Thermal Analysis. Minerals 2021, 11, 115. [Google Scholar] [CrossRef]
- Tang, M.; Esmaeili, K. Heap Leach Pad Surface Moisture Monitoring Using Drone-Based Aerial Images and Convolutional Neural Networks: A Case Study at the El Gallo Mine, Mexico. Remote Sens. 2021, 13, 1420. [Google Scholar] [CrossRef]
- He, J.; DuPlessis, L.; Barton, I. Heap leach pad mapping with drone-based hyperspectral remote sensing at the safford copper mine, arizona. Hydrometallurgy 2022, 211, 105872. [Google Scholar] [CrossRef]
- Herrera, L.; Jun, K.J.; Baker, J.; Agrawal, B.N. Deep Learning Based Object Attitude Estimation for a Laser Beam Control Research Testbed. Appl. Artif. Intell. 2023, 37, 2151191. [Google Scholar] [CrossRef]
- Herrera, N.; Sinche Gonzalez, M.; Okkonen, J.; Canales, R.M. Predicting Flowability at Disposal of Spent Heap Leach by Applying Artificial Neural Networks Based on Operational Variables. Minerals 2023, 14, 40. [Google Scholar] [CrossRef]
- Thenepalli, T.; Chilakala, R.; Habte, L.; Tuan, L.Q.; Kim, C.S. A brief note on the heap leaching technologies for the recovery of valuable metals. Sustainability 2019, 11, 3347. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. FAST-LIO2: Fast Direct LiDAR-Inertial Odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, X.; Gu, B.; Gao, F. Power Scheduling Optimization Method of Wind-Hydrogen Integrated Energy System Based on the Improved AUKF Algorithm. Mathematics 2022, 10, 4207. [Google Scholar] [CrossRef]
- Bucci, A.; Franchi, M.; Ridolfi, A.; Secciani, N.; Allotta, B. Evaluation of UKF-Based Fusion Strategies for Autonomous Underwater Vehicles Multisensor Navigation. IEEE J. Ocean. Eng. 2023, 48, 1–26. [Google Scholar] [CrossRef]
- Garcia, R.; Pardal, P.; Kuga, H.; Zanardi, M. Nonlinear filtering for sequential spacecraft attitude estimation with real data: Cubature Kalman Filter, Unscented Kalman Filter and Extended Kalman Filter. Adv. Space Res. 2019, 63, 1038–1050. [Google Scholar] [CrossRef]
- Kaur, H.; Sahambi, J. Vehicle Tracking in Video using Fractional Feedback Kalman Filter. IEEE Trans. Comput. Imaging 2016, 4, 550–561. [Google Scholar] [CrossRef]
- Sotiropoulos, F.; Asada, H. Autonomous Excavation of Rocks Using a Gaussian Process Model and Unscented Kalman Filter. IEEE Robot. Autom. Lett. 2020, 5, 2491–2497. [Google Scholar] [CrossRef]
- Hashemzadeh, M.; Dixon, D.G.; Liu, W. Modelling the kinetics of chalcocite leaching in acidified cupric chloride media under fully controlled pH and potential. Hydrometallurgy 2019, 189, 105114. [Google Scholar] [CrossRef]
- Cariaga, E.; Martínez, R.; Sepúlveda, M. Estimation of hydraulic parameters under unsaturated flow conditions in heap leaching. Math. Comput. Simul. 2015, 109, 20–31. [Google Scholar] [CrossRef]
- McBride, D.; Gebhardt, J.E.; Croft, T.N.; Cross, M. Modeling the hydrodynamics of heap leaching in sub-zero temperatures. Miner. Eng. 2016, 90, 77–88. [Google Scholar] [CrossRef]
- Vargas, T.; Estay, H.; Arancibia, E.; Díaz-Quezada, S. In situ recovery of copper sulfide ores: Alternative process schemes for bioleaching application. Hydrometallurgy 2020, 196, 105442. [Google Scholar] [CrossRef]
- Saldaña, M.; Gálvez, E.; Robles, P.; Castillo, J.; Toro, N. Copper Mineral Leaching Mathematical Models—A Review. Materials 2022, 15, 1757. [Google Scholar] [CrossRef]
- Ghasemzadeh, H.; Sanaye Pasand, M.; Mollanouri Shamsi, M. Experimental study of sulfuric acid effects on hydro-mechanical properties of oxide copper heap soils. Miner. Eng. 2018, 117, 100–107. [Google Scholar] [CrossRef]
- Estay, H.; Díaz-Quezada, S. Deconstructing the Leaching Ratio. Min. Metall. Explor. 2020, 37, 1329–1337. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2022; Volume 19. [Google Scholar]
- Wadsworth, M.; Yong Sohn, H. Rate Processes of Extractive Metallurgy; Springer: Boston, MA, USA, 1979. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Robertson, S.; Basson, P.; van Staden, P.; Petersen, J. Properties governing flow of solution and air through crushed ore for heap leaching: Part ii unsaturated dual-phase flow. Hydrometallurgy 2023, 215, 105990. [Google Scholar] [CrossRef]
- Canales, C.; Díaz-Quezada, S.; Leiva, F.; Estay, H.; del Solar, J.R. Control of heap leach piles using deep reinforcement learning. Miner. Eng. 2024, 212, 108707. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A. Hydraulic Properties of Porous Media; Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Dingman, S.L. Physical Hydrology; Waveland Press: Long Grove, IL, USA, 2015. [Google Scholar]
- Bárzaga-Martell, L.; Duarte-Mermoud, M.A.; Ibáñez-Espinel, F.; Gamboa-Labbe, B.; Saa, P.A.; Pérez-Correa, J.R. A robust hybrid observer for monitoring high-cell density cultures exhibiting overflow metabolism. J. Process Control 2021, 104, 112–125. [Google Scholar] [CrossRef]
- Bogaerts, P.; Wouwer, A. Parameter identification for state estimation—Application to bioprocess software sensors. Chem. Eng. Sci. 2004, 59, 2465–2476. [Google Scholar] [CrossRef]
- Herrar, U. Influencia de las Concentraciones de Ácido Sobre la Cinética de Lixiviación de un Mineral Oxidado de Cobre. Bachelor’s Thesis, Universidad de Chile, Santiago, Chile, 2001. [Google Scholar]
- Kahlert, H.; Meyer, G.; Albrecht, A. Colour maps of acid–base titrations with colour indicators: How to choose the appropriate indicator and how to estimate the systematic titration errors. ChemTexts 2016, 2, 7. [Google Scholar] [CrossRef]
- Spectroscopy Editors. Copper Quantification in Geological Samples by Flame AAS. Spectroscopy. November 2023. Available online: https://www.spectroscopyonline.com/view/copper-quantification-geological-samples-flame-aas (accessed on 22 April 2025).


| Scenario | Column Index “j” | Copper Grade | Irrigation Rates | Acid. Conc. |
|---|---|---|---|---|
| 1 | 1 | 0.5110 | [5;7.5;10] | [5;10;15] |
| 2 | 1 | 0.5110 | 5 | 10 |
| 2 | 0.3508 | 7.5 | 10 | |
| 3 | 0.2833 | 10 | 10 | |
| 3 | 1 | 0.5110 | 5 | 5 |
| 2 | 0.3508 | 5 | 7.5 | |
| 3 | 0.2833 | 5 | 10 | |
| 4 | 1 | 0.5110 | [5;7.5;10] | [5;10;15] |
| 2 | 0.3508 | [5;7.5;10] | [5;10;15] | |
| 3 | 0.2833 | [5;7.5;10] | [5;10;15] |
| Parameter | Description | Value | Units | Ref. |
|---|---|---|---|---|
| Granulometry | 1 | [This work] | ||
| Stoichiometric coefficient of acid to copper | 1.54 | [35] | ||
| Bulk density ore | 1.8 | [35] | ||
| Heap Module Width | 50 | [This work] | ||
| Heap Module Length | 50 | [This work] | ||
| Heap Module Height | 50 | [This work] | ||
| Solution density | 1 | [35] | ||
| Initial moisture content | 6 | [This work] | ||
| Maximum acid consumption ineach module volume | 30 | [35] | ||
| Copper kinetic constant 1 | 502.5110 | [35] | ||
| Copper kinetic constant 2 | 87.7702 | [35] | ||
| Acid consumption kinetic constant | 1.15 × 103 | [35] | ||
| Copper topological exponent | 0.4492 | -- | [This work] | |
| Acid consumption topological ex-ponent | 0.9983 | -- | [This work] | |
| Copper reaction order | 1.2722 | -- | [This work] | |
| Copper reaction order | 1.5238 | -- | [This work] | |
| Acid consumption reaction order | 3.2658 | -- | [This work] | |
| Acid consumption reaction order | 0.5171 | -- | [This work] | |
| Residual saturation of the liquid | 0.115 | [32] | ||
| Residual saturation of the gas | 0.148 | [32] | ||
| Permeability of the medium | 7.34 × 1013 | [32] | ||
| Porosity | 0.485 | [32] | ||
| Characteristic parameter of the medium | 7710 | [32] | ||
| Characteristic parameter of the medium | 0.19 | -- | [28] |
| Var. | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 1 | |||||
|---|---|---|---|---|---|---|---|---|---|
| EKF | UKF | EKF | UKF | EKF | UKF | EKF | UKF | ||
| IAE C1 | 0.041 | 1.250 | 0.089 | 1.570 | 0.044 | 1.340 | 2.690 | 3.070 | |
| 31.44 | 31.40 | 3.574 | 3.480 | 60.82 | 60.80 | 1.590 | 1.960 | ||
| 79.70 | 79.80 | 0.050 | 49.40 | 18.04 | 18.10 | 7.520 | 8.340 | ||
| IAE C2 | 0.191 | 1.000 | 0.192 | 1.570 | 1.203 | 1.120 | -- | -- | |
| 17.09 | 20.60 | 18.09 | 3.860 | 20.57 | 20.60 | -- | -- | ||
| 81.28 | 88.30 | 90.30 | 40.90 | 20.57 | 17.30 | -- | -- | ||
| IAE C3 | 0.017 | 1.100 | 0.200 | 1.450 | 0.050 | 1.470 | -- | -- | |
| 5.341 | 5.060 | 6.208 | 6.890 | 3.413 | 2.260 | -- | -- | ||
| 20.78 | 15.80 | 0.079 | 945.0 | 12.07 | 7.130 | -- | -- | ||
| ISE C1 | 0.069 | 12.60 | 35.60 | 15.80 | 0.059 | 13.50 | 36.10 | 25.30 | |
| 25.29 | 25.50 | 16.70 | 19.30 | 69.77 | 69.70 | 29.40 | 39.30 | ||
| 29.84 | 29.90 | 35.70 | 339.0 | 71.74 | 71.80 | 87.70 | 96.20 | ||
| ISE C2 | 1.203 | 10.70 | 1.200 | 18.20 | 10.74 | 12.10 | -- | -- | |
| 59.74 | 85.40 | 59.70 | 18.20 | 10.94 | 10.90 | -- | -- | ||
| 28.66 | 31.10 | 28.70 | 242.0 | 10.94 | 65.80 | -- | -- | ||
| ISE C3 | 0.009 | 9.720 | 60.70 | 15.10 | 0.080 | 16.60 | -- | -- | |
| 78.47 | 69.70 | 49.10 | 59.70 | 65.90 | 40.30 | -- | -- | ||
| 36.14 | 21.10 | 104.2 | 129.0 | 22.95 | 67.60 | -- | -- | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bárzaga-Martell, L.; Diaz-Quezada, S.; Estay, H.; Ruiz-del-Solar, J. Estimation of Copper Grade, Acid Consumption, and Moisture Content in Heap Leaching Using Extended and Unscented Kalman Filters. Minerals 2025, 15, 521. https://doi.org/10.3390/min15050521
Bárzaga-Martell L, Diaz-Quezada S, Estay H, Ruiz-del-Solar J. Estimation of Copper Grade, Acid Consumption, and Moisture Content in Heap Leaching Using Extended and Unscented Kalman Filters. Minerals. 2025; 15(5):521. https://doi.org/10.3390/min15050521
Chicago/Turabian StyleBárzaga-Martell, Lisbel, Simón Diaz-Quezada, Humberto Estay, and Javier Ruiz-del-Solar. 2025. "Estimation of Copper Grade, Acid Consumption, and Moisture Content in Heap Leaching Using Extended and Unscented Kalman Filters" Minerals 15, no. 5: 521. https://doi.org/10.3390/min15050521
APA StyleBárzaga-Martell, L., Diaz-Quezada, S., Estay, H., & Ruiz-del-Solar, J. (2025). Estimation of Copper Grade, Acid Consumption, and Moisture Content in Heap Leaching Using Extended and Unscented Kalman Filters. Minerals, 15(5), 521. https://doi.org/10.3390/min15050521







