Metal Fingerprints of Eocene Rhyolite Magmas Coincident with Carlin-Type Gold Deposition in Nevada USA
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Microanalysis
2.2. Assessment of Post-Entrapment Modifications
2.3. Compositional Data (CoDa) Approach
2.4. Fluid/Melt Partitioning Model
3. Results
3.1. Pre-Eruptive Metal Budgets of Magmas
3.2. Metal Fingerprints of Pre-Eruptive Magmas
3.2.1. Metal Ratios
3.2.2. A Multivariate View: Compositional Data Principal Component Analysis (CoDa-PCA)
3.3. Modeled Magmatic Fluids
4. Discussion
4.1. Relationships Between Principal Components and Geologic Processes
4.2. Metals on the Move: Magmatic Fluid Exsolution
4.3. Magma Volume Estimates
4.4. Future Research Directions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hofstra, A.H. Critical minerals in Carlin-type systems of the United States. In U.S.Geological Survey Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, accepted.
- Muntean, J.L. Diversity in Carlin-Style Gold Deposits. Rev. Econ. Geol. 2018, 20, 1–363. [Google Scholar]
- Emsbo, P.; Groves, D.I.; Hofstra, A.H.; Bierlein, F.P. The giant Carlin gold province: A protracted interplay of orogenic, basinal, and hydrothermal processes above a lithospheric boundary. Miner. Depos. 2006, 41, 517–525. [Google Scholar] [CrossRef]
- Large, R.R.; Bull, S.W.; Maslennikov, V.V. A carbonaceous sedimentary source-rock model for Carlin-type and orogenic gold deposits. Econ. Geol. 2011, 106, 331–358. [Google Scholar] [CrossRef]
- Muntean, J.L.; Cline, J.S.; Simon, A.C.; Longo, A.A. Magmatic–hydrothermal origin of Nevada’s Carlin-type gold deposits. Nat. Geosci. 2011, 4, 122–127. [Google Scholar] [CrossRef]
- Large, S.J.E.; Bakker, E.Y.N.; Weis, P.; Wälle, M.; Ressel, M.; Heinrich, C.A. Trace elements in fluid inclusions of sediment-hosted gold deposits indicate a magmatic-hydrothermal origin of the Carlin ore trend. Geology 2016, 44, 1015–1018. [Google Scholar] [CrossRef]
- Ressel, M.W.; Henry, C.D. Igneous geology of the Carlin trend, Nevada: Development of the Eocene plutonic complex and significance for Carlin-type gold deposits. Econ. Geol. 2006, 101, 347–383. [Google Scholar] [CrossRef]
- Kesler, S.E.; Riciputi, L.C.; Ye, Z. Evidence for a magmatic origin for Carlin-type gold deposits: Isotopic composition of sulfur in the Betze-Post-Screamer Deposit, Nevada, USA. Miner. Depos. 2005, 40, 127–136. [Google Scholar] [CrossRef]
- Henry, C.D.; John, D.A.; Leonardson, R.W.; McIntosh, W.C.; Heizler, M.T.; Colgan, J.P.; Watts, K.E. Timing of Rhyolite Intrusion and Carlin-Type Gold Mineralization at the Cortez Hills Carlin-Type Deposit, Nevada, USA. Econ. Geol. 2023, 118, 57–91. [Google Scholar] [CrossRef]
- Mercer, C.N. Eocene magma plumbing system beneath Cortez Hills Carlin-type gold deposit, Nevada: Is there a deep-seated pluton? Econ. Geol. 2021, 116, 501–513. [Google Scholar] [CrossRef]
- Richards, J.P. Postsubduction porphyry Cu-Au and epithermal Au deposits: Products of remelting of subduction-modified lithosphere. Geology 2009, 37, 247–250. [Google Scholar] [CrossRef]
- Audétat, A.; Simon, A.C. Magmatic controls on porphyry copper deposits. In Geology and Genesis of Major Copper Deposits and Distracts of the World: A Tribute to Richard H. Sillitoe; Hedenquist, J.W., Harris, M., Camus, F., Eds.; Society of Economic Geologists: Littleton, CO, USA, 2012; Volume 16, pp. 553–572. [Google Scholar]
- Li, Y.; Audétat, A. Gold solubility and partitioning between sulfide liquid, monosulfide solid solution and hydrous mantle melts: Implications for the formation of Au-rich magmas and crust–mantle differentiation. Geochim. Cosmochim. Acta 2013, 118, 247–262. [Google Scholar] [CrossRef]
- Li, Y.; Audétat, A. Effects of temperature, silicate melt composition, and oxygen fugacity on the partitioning of V, Mn, Co, Ni, Cu, Zn, As, Mo, Ag, Sn, Sb, W, Au, Pb, and Bi between sulfide phases and silicate melt. Geochim. Cosmochim. Acta 2015, 162, 25–45. [Google Scholar] [CrossRef]
- Johnson, C.L.; Ressel, M.W.; Ruprecht, P. Toward a global Carlin-type exploration model: The relationship between Eocene magmatism and diverse gold-rich deposits in the Great Basin, USA. In Vision for Discovery, Geology and Ore Deposits of the Basin and Range, Proceedings of the Geological Society of Nevada; Koutz, F.R., Pennel, W.M., Eds.; Geological Society of Nevada: Reno, NV, USA, 2020; Volume 1, pp. 355–382. [Google Scholar]
- Simon, A.C.; Pettke, T.; Candela, P.A.; Piccoli, P.M.; Heinrich, C.A. Experimental determination of Au solubility in rhyolite melt and magnetite: Constraints on magmatic Au budgets. Am. Mineral. 2003, 88, 1644–1651. [Google Scholar] [CrossRef]
- Henry, C.D.; John, D.A.; Heizler, M.T.; Leonardson, R.W.; Colgan, J.; Watts, K.E.; Ressel, M.W.; Cousens, B.L. Why did Great Basin Eocene magmatism generate Carlin-type gold deposits when extensive Jurassic to Middle Miocene magmatism did not? Lessons from the Cortez region, northern Nevada, USA. In Vision for Discovery, Geology and Ore Deposits of the Basin and Range, Proceedings of the Geological Society of Nevada; Koutz, F.R., Pennel, W.M., Eds.; Geological Society of Nevada: Reno, NV, USA, 2020; Volume 1, pp. 339–353. [Google Scholar]
- Muntean, J.L.; Bonner, W.; Hill, T. Carlin-style gold-silver mineralization at the Cove deposit in Nevada, USA: Possible missing link between Carlin-type gold deposits and magmatic-hydrothermal systems. In Mineral Resources to Discover, Proceedings of the 14th biennial meeting of the Society for Geology Applied to Mineral Deposits, Quebec, QC, Canada, 20–23 August 2017; Mercier-Langevin, P., Ed.; Society for Geology Applied to Mineral Deposits: Genéve, Suisse, 2017; pp. 71–74. [Google Scholar]
- Johnson, C.L.; Dilles, J.H.; Kent, A.J.; Farmer, L.P.; Henry, C.D.; Ressel, M.W. Petrology and geochemistry of the Emigrant Pass volcanics, Nevada: Implications for a magmatic-hydrothermal origin of the Carlin gold deposits. In New Concepts and Discoveries, Proceedings of the Geological Society of Nevada; Pennell, W.M., Garside, L.G., Eds.; Geological Society of Nevada: Reno, NV, USA, 2015; Volume 1, pp. 391–408. [Google Scholar]
- Mercer, C.N.; Roberge, J.; Khoury, R.M.; Hofstra, A.H. Pre-eruptive characteristics of “suspect” silicic magmas in Carlin-type Au-forming systems. Am. Mineral. 2025. [Google Scholar]
- Hofstra, A.H.; Kreiner, D.C. Systems-Deposits-Commodities-Critical Minerals Table for the Earth Mapping Resources Initiative. In U.S. Geological Survey Open-File Report 2020–1042; United States Geological Survey: Reston, VA, USA, 2020; pp. 1–24. [Google Scholar]
- Brooks, W.E.; Thorman, C.H.; Snee, L.W. The 40Ar/39Ar ages and tectonic setting of the middle Eocene northeast Nevada volcanic field. J. Geophys. Res. Solid Earth 1995, 100, 10403–10416. [Google Scholar] [CrossRef]
- Ressel, M.W.; Noble, D.C.; Henry, C.D.; Trudel, W.S. Dike-Hosted Ores of the Beast Deposit and the Importance of Eocene Magmatism in Gold Mineralization of the Carlin Trend, Nevada. Econ. Geol. 2000, 95, 1417–1444. [Google Scholar] [CrossRef]
- Bond, R. Personal communication about informal names of dikes in the Cortez Hills pit used by Barrick Gold, 2013.
- Colgan, J.P.; Egger, A.E.; John, D.A.; Cousens, B.; Fleck, R.J.; Henry, C.D. Oligocene and Miocene arc volcanism in northeastern California: Evidence for post-Eocene segmentation of the subducting Farallon plate. Geosphere 2011, 7, 733–755. [Google Scholar] [CrossRef]
- Hastings, M.H. Relationship of Base-Metal Skarn Mineralization to Carlin-Type Gold Mineralization at the Archimedes Gold Deposit, Eureka, Nevada. Master’s Thesis, University of Nevada, Reno, NV, USA, 2008; p. 109. [Google Scholar]
- Nutt, C.J.; Hofstra, A.H. Alligator Ridge district, east-central Nevada: Carlin-type gold mineralization at shallow depths. Econ. Geol. 2003, 98, 1225–1241. [Google Scholar] [CrossRef]
- Farmer, M. An intrusive study of the Bluestar subdistrict: Carlin, Nevada. In Newmont Gold Company, Internal Report; Newmont: Vancouver, BC, Canada, 1996; p. 33. [Google Scholar]
- John, D.A.; Henry, C.D.; Colgan, J.P. Magmatic and tectonic evolution of the Caetano caldera, north-central Nevada: A tilted, mid-Tertiary eruptive center and source of the Caetano Tuff. Geosphere 2008, 4, 75–106. [Google Scholar] [CrossRef]
- Watts, K.E.; John, D.A.; Colgan, J.P.; Henry, C.D.; Bindeman, I.N.; Schmitt, A.K. Probing the volcanic–plutonic connection and the genesis of crystal-rich rhyolite in a deeply dissected supervolcano in the Nevada Great Basin: Source of the late Eocene Caetano Tuff. J. Petrol. 2016, 57, 1599–1644. [Google Scholar] [CrossRef]
- Mortensen, J.K.; Thompson, J.P.H.; Tosdal, R.M. U-Pb age constraints on magmatism and mineralization in the northern Great basin. In Geology and Ore Deposits 2000: The Great Basin and Beyond, Proceedings of the Geological Society of Nevada; Cluer, J.K., Price, J.G., Struhsacker, E.M., Hardyman, R.F., Morris, C.L., Eds.; Geological Society of Nevada: Reno, NV, USA, 2000; pp. 61–65. [Google Scholar]
- Dilles, P.A.; Wright, W.A.; Monteleone, S.E.; Russel, K.D.; Marlowe, K.E.; Wood, R.A.; Margolis, J. The geology of the West Archimedes deposit: A new gold discovery in the Eureka mining district, Eureka County, Nevada. In Geology and Ore Deposits of the American Cordillera, Proceedings of the Geological Society of Nevada Symposium, Reno, NV, USA, 10–13 April 1995; Coyner, A.R., Fahey, P.L., Eds.; Geological Society of Nevada: Reno, NV, USA, 1996; pp. 159–171. [Google Scholar]
- Nutt, C.J. Geologic map of the Alligator Ridge area, including the Buck Mountain East and Mooney Basin Summit quadrangles and parts of the Sunshine Well NE and Long Valley Slough quadrangles, White Pine County, Nevada. In U.S. Geological Survey Geologic Investigations Series Map I-2691, Scale 1:24,000; United States Geological Survey: Reston, VA, USA, 2000. [Google Scholar]
- Smith, M.T.; Rhys, D.; Ross, K.; Lee, C.; Gray, J.N. The Long Canyon deposit: Anatomy of a new off-trend sedimentary rock-hosted gold discovery in northeastern Nevada. Econ. Geol. 2013, 108, 1119–1145. [Google Scholar] [CrossRef]
- Chakurian, A.M.; Arehart, G.B.; Donelick, R.A.; Zhang, X.; Reiners, P.W. Timing constraints of gold mineralization along the Carlin trend utilizing apatite fission-track, 40Ar/39Ar, and apatite (U-Th)/He methods. Econ. Geol. 2003, 98, 1159–1171. [Google Scholar] [CrossRef]
- Tretbar, D.R.; Arehart, G.B.; Christensen, J.N. Dating gold deposition in a Carlin-type gold deposit using Rb/Sr methods on the mineral galkhaite. Geology 2000, 28, 947–950. [Google Scholar] [CrossRef]
- Esposito, R. Chapter 7: A protocol and review of methods to select, analyze and interpret melt inclusions to determine pre-eruptive volatile contents of magmas. In Fluid and Melt Inclusions: Applications to Geologic Processes; Lecumberri-Sanchez, P., Steele-MacInnis, M., Kontak, D., Eds.; Mineralogical Association of Canada: Quebec, QC, Canada, 2020; Volume 49, pp. 163–194. [Google Scholar]
- Rose-Koga, E.F.; Bouvier, A.S.; Gaetani, G.A.; Wallace, P.J.; Allison, C.M.; Andrys, J.A.; Angeles de la Torre, C.A.; Barth, A.; Bodnar, R.J.; Gartner, A.B.; et al. Silicate melt inclusions in the new millennium: A review of recommended practices for preparation, analysis, and data presentation. Chem. Geol. 2021, 570, 120145. [Google Scholar] [CrossRef]
- Mercer, C.N.; Hofstra, A.H.; Todorov, T.I.; Roberge, J.; Burgisser, A.; Adams, D.T.; Cosca, M. Pre-eruptive conditions of the Hideaway Park topaz rhyolite: Insights into metal source and evolution of magma parental to the Henderson porphyry molybdenum deposit, Colorado. J. Petrol. 2015, 56, 645–679. [Google Scholar] [CrossRef]
- Sisson, T.W.; Grove, T.L. Experimental investigations of the role of H2O in calc-alkaline differentiation and subduction zone magmatism. Contrib. Mineral. Petrol. 1993, 113, 143–166. [Google Scholar] [CrossRef]
- Kamenetsky, V.S.; Danyushevsky, L. Metals in quartz-hosted melt inclusions: Natural facts and experimental artifacts. Am. Mineral. 2005, 90, 1674–1678. [Google Scholar] [CrossRef]
- Zajacz, Z.; Hanley, J.J.; Heinrich, C.A.; Halter, W.E.; Guillong, M. Diffusive reequilibration of quartz-hosted silicate melt and fluid inclusions: Are all metal concentrations unmodified? Geochim. Cosmochim. Acta 2009, 73, 3013–3027. [Google Scholar] [CrossRef]
- Rottier, B.; Rezeau, H.; Casanova, V.; Kouzmanov, K.; Moritz, R.; Schlögova, K.; Wälle, M.; Fontboté, L. Trace element diffusion and incorporation in quartz during heating experiments. Contrib. Mineral. Petrol. 2017, 172, 1–20. [Google Scholar] [CrossRef]
- Ellis, B.S.; Szymanowski, D.; Magna, T.; Neukampf, J.; Dohmen, R.; Bachmann, O.; Ulmer, P.; Guillong, M. Post-eruptive mobility of lithium in volcanic rocks. Nat. Commun. 2018, 9, 3228. [Google Scholar] [CrossRef]
- Neukampf, J.; Ellis, B.S.; Magna, T.; Laurent, O.; Bachmann, O. Partitioning and isotopic fractionation of lithium in mineral phases of hot, dry rhyolites: The case of the Mesa Falls Tuff, Yellowstone. Chem. Geol. 2019, 506, 175–186. [Google Scholar] [CrossRef]
- Esposito, R.; Redi, D.; Danyushevsky, L.V.; Gurenko, A.; De Vivo, B.; Manning, C.E.; Bodnar, R.J.; Steele-MacInnis, M.; Frezzotti, M.L. Constraining the volatile evolution of mafic melts at Mt. Somma–Vesuvius, Italy, based on the composition of reheated melt inclusions and their olivine hosts. Eur. J. Mineral. 2023, 35, 921–948. [Google Scholar] [CrossRef]
- Lowenstern, J.B. Bursting the bubble of melt inclusions. Am. Mineral. 2015, 100, 672–673. [Google Scholar] [CrossRef]
- Moore, L.R.; Gazel, E.; Tuohy, R.; Lloyd, A.S.; Esposito, R. Bubbles matter: An assessment of the contribution of vapor bubbles to melt inclusion volatile budgets. Am. Mineral. 2015, 100, 806–823. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Gozzi, C.; Buccianti, A.; Pawlowsky-Glahn, V. Exploring geochemical data using compositional techniques: A practical guide. J. Geochem. Explor. 2024, 258, 107385. [Google Scholar] [CrossRef]
- Aitchison, J. Principal component analysis of compositional data. Biometrika 1983, 70, 57–65. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data. Monographs on Statistics and Applied Probability; Chapman & Hall Ltd.: London, UK, 1986; p. 416, Reprinted in 2003 with additional material by The Blackburn Press, London, UK. [Google Scholar]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data. Statistics in Practice; John Wiley & Sons: Chichester, UK, 2015; p. 272. [Google Scholar]
- Filzmoser, P.; Hron, K.; Templ, M. Applied Compositional Data Analysis. With Worked Examples in R; Springer Nature: Cham, Switzerland, 2018; p. 280. [Google Scholar]
- Greenacre, M. Compositional Data Analysis in Practice; Chapman and Hall/CRC: New York, NY, USA, 2018; p. 120. [Google Scholar]
- Greenacre, M. Compositional data analysis. Annu. Rev. Stat. Its Appl. 2021, 8, 271–299. [Google Scholar] [CrossRef]
- Le Moine Bauer, S.; Lu, G.S.; Goulaouic, S.; Puzenat, V.; Schouw, A.; Barreyre, T.; Pawlowsky-Glahn, V.; Egozcue, J.J.; Martelat, J.E.; Escartin, J.; et al. Structure and metabolic potential of the prokaryotic communities from the hydrothermal system of Paleochori Bay, Milos, Greece. Front. Microbiol. 2023, 13, 1060168. [Google Scholar] [CrossRef]
- Webster, J.D. The exsolution of magmatic hydrosaline chloride liquids. Chem. Geol. 2004, 210, 33–48. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Zajacz, Z.; Ulmer, P.; Heinrich, C.A. Chlorine partitioning between granitic melt and H2O-CO2-NaCl fluids in the Earth’s upper crust and implications for magmatic-hydrothermal ore genesis. Geochim. Cosmochim. Acta 2019, 261, 171–190. [Google Scholar] [CrossRef]
- Driesner, T.; Heinrich, C.A. The system H2O–NaCl. Part I: Correlation formulae for phase relations in temperature–pressure–composition space from 0 to 1000 C, 0 to 5000 bar, and 0 to 1 XNaCl. Geochim. Cosmochim. Acta 2007, 71, 4880–4901. [Google Scholar] [CrossRef]
- Alex, A.; Zajacz, Z. The solubility of Cu, Ag and Au in magmatic sulfur–bearing fluids as a function of oxygen fugacity. Geochim. Cosmochim. Acta 2022, 330, 93–115. [Google Scholar] [CrossRef]
- Tattitch, B.C.; Blundy, J.D. Cu-Mo partitioning between felsic melts and saline-aqueous fluids as a function of X NaCleq, fO2, and fS2. Am. Mineral. 2017, 102, 1987–2006. [Google Scholar] [CrossRef]
- Zajacz, Z.; Candela, P.A.; Piccoli, P.M. The partitioning of Cu, Au and Mo between liquid and vapor at magmatic temperatures and its implications for the genesis of magmatic-hydrothermal ore deposits. Geochim. Cosmochim. Acta 2017, 207, 81–101. [Google Scholar] [CrossRef]
- Zajacz, Z.; Halter, W.E.; Pettke, T.; Guillong, M. Determination of fluid/melt partition coefficients by LA-ICPMS analysis of co-existing fluid and silicate melt inclusions: Controls on element partitioning. Geochim. Cosmochim. Acta 2008, 72, 2169–2197. [Google Scholar] [CrossRef]
- Simon, A.C.; Frank, M.R.; Pettke, T.; Candela, P.A.; Piccoli, P.M.; Heinrich, C.A. Gold partitioning in melt-vapor-brine systems. Geochim. Cosmochim. Acta 2005, 69, 3321–3335. [Google Scholar] [CrossRef]
- Rudnick, R.L.; Gao, S. Composition of the continental crust. In Treatise on Geochemistry, 2nd ed.; Turekian, K.K., Holland, H.D., Eds.; Elsevier: Toronto, Canada, 2014; pp. 1–51. [Google Scholar]
- Robb, L. Introduction to Ore-Forming Processes, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2020; p. 439. [Google Scholar]
- Zhang, D.; Audétat, A. What Caused the Formation of the Giant Bingham Canyon Porphyry Cu-Mo-Au Deposit? Insights from Melt Inclusions and Magmatic Sulfides. Econ. Geol. 2017, 112, 221–244. [Google Scholar] [CrossRef]
- Audétat, A.; Li, W. The genesis of Climax-type porphyry Mo deposits: Insights from fluid inclusions and melt inclusions. Ore Geol. Rev. 2017, 88, 436–460. [Google Scholar] [CrossRef]
- Emsbo, P.; Hofstra, A.H.; Lauha, E.A.; Griffin, G.L.; Hutchinson, R.W. Origin of High-Grade Gold Ore, Source of Ore Fluid Components, and Genesis of the Meikle and Neighboring Carlin-Type Deposits, Northern Carlin Trend, Nevada. Econ. Geol. 2003, 98, 1069–1105. [Google Scholar] [CrossRef]
- Hofstra, A.H.; Snee, L.W.; Rye, R.O.; Folger, H.W.; Phinisey, J.D.; Loranger, R.J.; Dahl, A.R.; Naeser, C.W.; Stein, H.J.; Lewchuk, M.T. Age constraints on Jerritt Canyon and other Carlin-type gold deposits in the Western United States; relationship to mid-Tertiary extension and magmatism. Econ. Geol. 1999, 94, 769–802. [Google Scholar] [CrossRef]
- Audétat, A. The metal content of magmatic-hydrothermal fluids and its relationship to mineralization potential. Econ. Geol. 2019, 114, 1033–1056. [Google Scholar] [CrossRef]
- Chelle-Michou, C.; Rottier, B.; Caricchi, L.; Simpson, G. Tempo of magma degassing and the genesis of porphyry copper deposits. Sci. Rep. 2017, 7, 40566. [Google Scholar] [CrossRef]
- Chiaradia, M.; Caricchi, L. Supergiant porphyry copper deposits are failed large eruptions. Commun. Earth Environ. 2022, 3, 107. [Google Scholar] [CrossRef]
- Chiaradia, M. Distinct magma evolution processes control the formation of porphyry Cu–Au deposits in thin and thick arcs. Earth Planet. Sci. Lett. 2022, 599, 117864. [Google Scholar] [CrossRef]
- Hofstra, A.; Lisitsin, V.; Corriveau, L.; Paradis, S.; Peter, J.; Lauzière, K.; Lawley, C.; Gadd, M.; Pilote, J.; Honsberger, I.; et al. Deposit classification scheme for the Critical Minerals Mapping Initiative Global Geochemical Database. In U.S. Geological Survey Open-File Report 2021–1049; United States Geological Survey: Reston, VA, USA, 2021; pp. 1–60. [Google Scholar]
- Murakami, H.; Seo, J.H.; Heinrich, C.A. The relation between Cu/Au ratio and formation depth of porphyry-style Cu–Au ± Mo deposits. Miner. Depos. 2009, 45, 11–21. [Google Scholar] [CrossRef]
- Halter, W.E.; Heinrich, C.A.; Pettke, T. Magma evolution and the formation of porphyry Cu-Au ore fluids: Evidence from silicate and sulfide melt inclusions. Miner. Depos. 2005, 39, 845–863. [Google Scholar] [CrossRef]
- Fithian, M.T. Geology, Geochemistry, and Geochronology of the Marigold Mine, Battle Mountain-Eureka Trend, Nevada. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2015; p. 115. [Google Scholar]
- du Bray, E.A. Time, space, and composition relations among northern Nevada intrusive rocks and their metallogenic implications. Geosphere 2007, 3, 381–405. [Google Scholar] [CrossRef]
- Grondahl, C.; Zajacz, Z. Magmatic controls on the genesis of porphyry Cu–Mo–Au deposits: The Bingham Canyon example. Earth Planet. Sci. Lett. 2017, 480, 53–65. [Google Scholar] [CrossRef]
- Norling, B.; Rowe, M.C.; Chambefort, I.; Tepley III, F.J.; Morrow, S. Volatile behavior and trace metal transport in the magmatic–geothermal system at Pūtauaki (Mt. Edgecumbe), New Zealand. J. Volcanol. Geotherm. Res. 2016, 318, 27–44. [Google Scholar] [CrossRef]
- Johnson, E.R.; Kamenetsky, V.S.; McPhie, J. The Behavior of Metals (Pb, Zn, As, Mo, Cu) During Crystallization and Degassing of Rhyolites from the Okataina Volcanic Center, Taupo Volcanic Zone, New Zealand. J. Petrol. 2013, 54, 1641–1659. [Google Scholar] [CrossRef]
- Saunders, K.E.; Baker, J.A.; Wysoczanski, R.J. Microanalysis of large volume silicic magma in continental and oceanic arcs: Melt inclusions in Taupo Volcanic Zone and Kermadec Arc rocks, South West Pacific. J. Volcanol. Geotherm. Res. 2010, 190, 203–218. [Google Scholar] [CrossRef]
- Audétat, A.; Günther, D.; Heinrich, C.A. Magmatic-hydrothermal evolution in a fractionating granite: A microchemical study of the Sn-W-F-mineralized Mole Granite (Australia). Geochim. Cosmochim. Acta 2000, 64, 3373–3393. [Google Scholar] [CrossRef]
- Stefanova, E.; Driesner, T.; Zajacz, Z.; Heinrich, C.A.; Petrov, P.; Vasilev, Z. Melt and Fluid Inclusions in Hydrothermal Veins: The Magmatic to Hydrothermal Evolution of the Elatsite Porphyry Cu-Au Deposit, Bulgaria. Econ. Geol. 2014, 109, 1359–1381. [Google Scholar] [CrossRef]
- Stavast, W.J.; Keith, J.D.; Christiansen, E.H.; Dorais, M.J.; Tingey, D.; Larocque, A.C.L.; Evans, N. The fate of magmatic sulfides during intrusion or eruption, Bingham and Tintic districts, Utah. Econ. Geol. 2006, 101, 329–345. [Google Scholar] [CrossRef]
- Watts, K.E.; John, D.A.; Coble, M.A.; Colgan, J.P.; Henry, C.D. Ion microprobe study of Au and trace metals in sulfide melt inclusions from a rhyolite porphyry intrusion in the Caetano caldera, Nevada. In Geological Society of America Abstracts with Programs; Geological Society of America: Boulder, CO, USA, 2014; Volume 46, p. 447. [Google Scholar]
- Halter, W.E.; Pettke, T.; Heinrich, C.A. The origin of Cu/Au ratios in porphyry-type ore deposits. Science 2002, 296, 1844–1846. [Google Scholar] [CrossRef]
- Seedorff, E.; Einaudi, M.T. Henderson porphyry molybdenum system, Colorado: II. Decoupling of introduction and deposition of metals during geochemical evolution of hydrothermal fluids. Econ. Geol. 2004, 99, 39–72. [Google Scholar] [CrossRef]
- Ueki, K.; Iwamori, H. Geochemical differentiation processes for arc magma of the Sengan volcanic cluster, Northeastern Japan, constrained from principal component analysis. Lithos 2017, 290, 60–75. [Google Scholar] [CrossRef]
- Grunsky, E.C.; Caritat, P.D. State-of-the-art analysis of geochemical data for mineral exploration. Geochem. Explor. Environ. Anal. 2020, 20, 217–232. [Google Scholar] [CrossRef]
- Darabi-Golestan, F.; Hezarkhanı, A. Multivariate analysis of log-ratio transformed data and its priority in mining science: Porphyry and polymetallic vein deposits case studies. Bull. Miner. Res. Explor. 2019, 159, 185–200. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Daviran, M.; Yilmaz, H. Incorporation of principal component analysis, geostatistical interpolation approaches and frequency-space-based models for portraying the Cu-Au geochemical prospects in the Feizabad district, NW Iran. Geochemistry 2019, 79, 323–336. [Google Scholar] [CrossRef]
- Zhao, Z.; Qiao, K.; Liu, Y.; Chen, J.; Li, C. Geochemical data mining by integrated multivariate component data analysis: The Heilongjiang Duobaoshan area (China) case study. Minerals 2022, 12, 1035. [Google Scholar] [CrossRef]
- Su, Q.; Yu, H.; Xu, X.; Chen, B.; Yang, L.; Fu, T.; Liu, W.; Chen, G. Using Principal Component Analysis (PCA) Combined with Multivariate Change-Point Analysis to Identify Brine Layers Based on the Geochemistry of the Core Sediment. Water 2023, 15, 1926. [Google Scholar] [CrossRef]
- Hron, K.; Coenders, G.; Filzmoser, P.; Palarea-Albaladejo, J.; Faměra, M.; Matys Grygar, T. Analysing pairwise logratios revisited. Math. Geosci. 2021, 53, 1643–1666. [Google Scholar] [CrossRef]
- Salem, L.C.; Edmonds, M.; Corsaro, R.A.; Maclennan, J. Carbon dioxide in geochemically heterogeneous melt inclusions from Mount Etna, Italy. Geochem. Geophys. Geosystems 2019, 20, 3150–3169. [Google Scholar] [CrossRef]
- Vermeesch, P. Statistics for Geoscientists; University College London: London, UK, 2024; p. 224. [Google Scholar]
- Richards, J.P. High Sr/Y arc magmas and porphyry Cu±Mo±Au deposits: Just add water. Econ. Geol. 2011, 106, 1075–1081. [Google Scholar] [CrossRef]
- Chiaradia, M.; Ulianov, A.; Kouzmanov, K.; Beate, B. Why large porphyry Cu deposits like high Sr/Y magmas? Sci. Rep. 2012, 2, 685. [Google Scholar] [CrossRef]
- Chiaradia, M. Crustal thickness control on Sr/Y signatures of recent arc magmas: An Earth scale perspective. Sci. Rep. 2015, 5, 8115. [Google Scholar] [CrossRef]
- Xue, Q.; Zhang, L.; Chen, S.; Guo, K.; Li, T.; Han, Z.; Sun, W. Tracing black shales in the source of a porphyry Mo deposit using molybdenum isotopes. Geology 2023, 51, 688–692. [Google Scholar] [CrossRef]
- Simon, A.C.; Pettke, T.; Candela, P.A.; Piccoli, P.M. The partitioning behavior of silver in a vapor–brine–rhyolite melt assemblage. Geochim. Et Cosmochim. Acta 2008, 72, 1638–1659. [Google Scholar] [CrossRef]
- Zajacz, Z.; Seo, J.H.; Candela, P.A.; Piccoli, P.M.; Heinrich, C.A.; Guillong, M. Alkali metals control the release of gold from volatile–rich magmas. Earth Planet. Sci. Lett. 2010, 297, 50–56. [Google Scholar] [CrossRef]
- Heinrich, C.A.; Gunther, D.; Audétat, A.; Ulrich, T.; Frischknecht, R. Metal fractionation between magmatic brine and vapor, determined by microanalysis of fluid inclusions. Geology 1999, 27, 755–758. [Google Scholar] [CrossRef]
- Heinrich, C.A. How fast does gold trickle out of volcanoes? Science 2006, 314, 263–264. [Google Scholar] [CrossRef]
- Loucks, R.R.; Mavrogenes, J.A. Gold solubility in supercritical hydrothermal brines measured in synthetic fluid inclusions. Science 1999, 284, 2159–2163. [Google Scholar] [CrossRef] [PubMed]
- Frank, M.R.; Candela, P.A.; Piccoli, P.M.; Glascock, M.D. Gold solubility, speciation, and partitioning as a function of HCl in the brine-silicate melt-metallic gold system at 800 C and 100 MPa. Geochim. Cosmochim. Acta 2002, 66, 3719–3732. [Google Scholar] [CrossRef]
- Hanley, J.J.; Pettke, T.; Mungall, J.E.; Spooner, E.T. The solubility of platinum and gold in NaCl brines at 1.5 kbar, 600 to 800 C: A laser ablation ICP-MS pilot study of synthetic fluid inclusions. Geochim. Cosmochim. Acta 2005, 69, 2593–2611. [Google Scholar] [CrossRef]
- Simon, A.C.; Frank, M.R.; Pettke, T.; Candela, P.A.; Piccoli, P.M.; Heinrich, C.A.; Glascock, M. An evaluation of synthetic fluid inclusions for the purpose of trapping equilibrated, coexisting, immiscible fluid phases at magmatic conditions. Am. Mineral. 2007, 92, 124–138. [Google Scholar] [CrossRef]
- Arbonies, D.G.; Creel, K.D.; Jackson, M.L. Cortez Hills lower zone discovery and geologic update. In Proceedings of the Great Basin Evolution and Metallogeny; Steininger, R., Pennell, B., Eds.; Geological Society of Nevada: Reno/Sparks, NV, USA, 2011; pp. 447–462. [Google Scholar]
- Chelle-Michou, C.; Rottier, B. Transcrustal magmatic controls on the size of porphyry Cu systems: State of knowledge and open questions. SEG Special Publications, Soc. Econ. Geol. 2021, 24, 87–100. [Google Scholar]
- John, D.A.; Ayuso, R.A.; Barton, M.D.; Blakely, R.J.; Bodnar, R.J.; Dilles, J.H.; Gray, F.; Graybeal, F.T.; Mars, J.C.; McPhee, D.K.; et al. Porphyry copper deposit model, chap. B of Mineral deposit models for resource assessment. In U.S. Geological Survey Scientific Investigations Report 2010–5070–B; USGS: Reston, VA, USA, 2010; p. 169. [Google Scholar]
- Cox, D.P.; Singer, D.A. Gold—Distribution of gold in porphyry copper deposits. Contrib. Commod. Geol. Res. 1992, 1877, C1–C14. [Google Scholar]
- Mercer, C.N.; Hofstra, A.H. Melt inclusion and mineral geochemical analyses supporting the evaluation of petrogenesis, degassing, and metallogenic potential of mid-Cenozoic rhyolite magmas in northern Nevada, USA. In U.S. Geological Survey Data Release (Version 2.0, March 2025); USGS: Reston, VA, USA, 2020. [Google Scholar] [CrossRef]
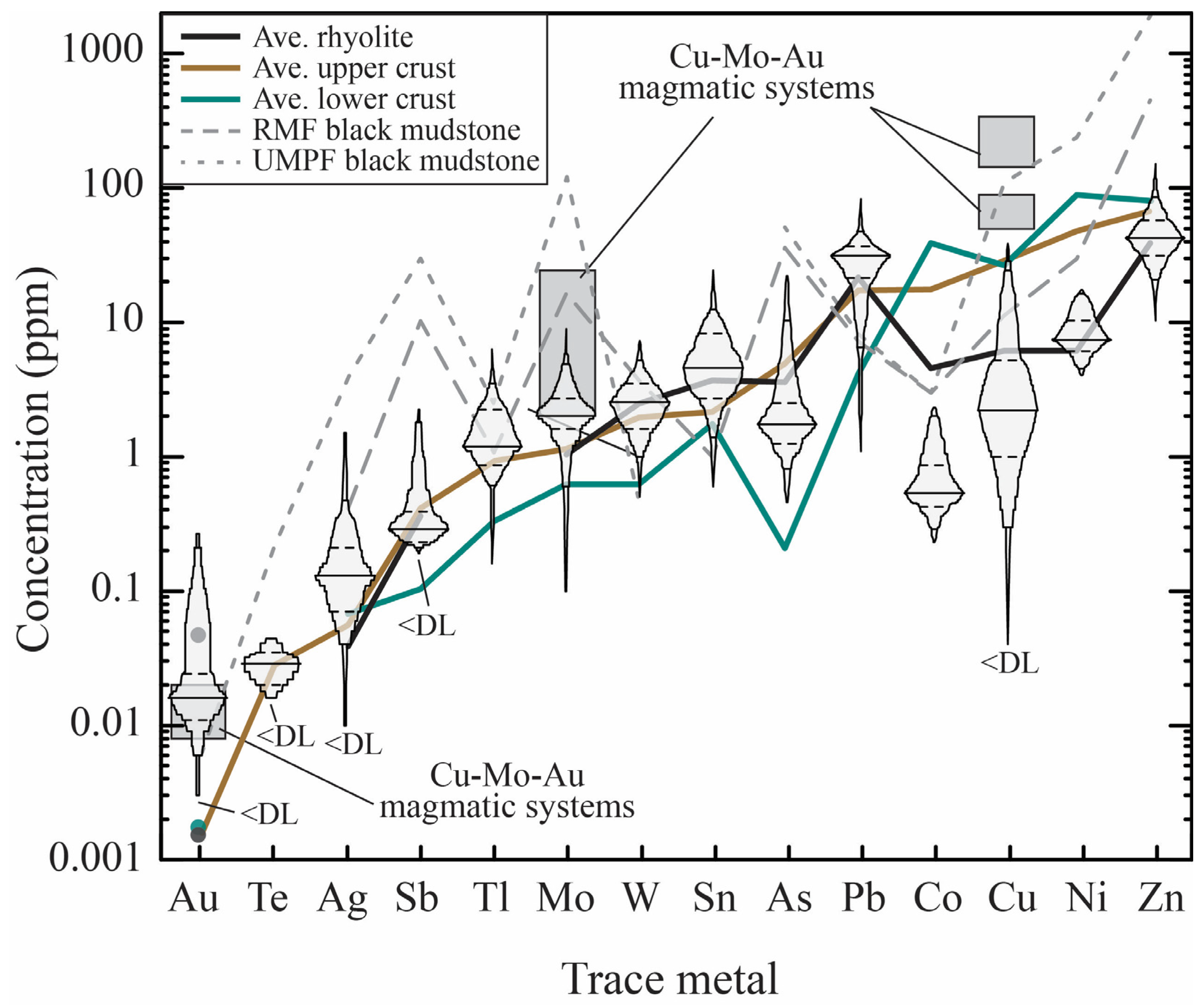
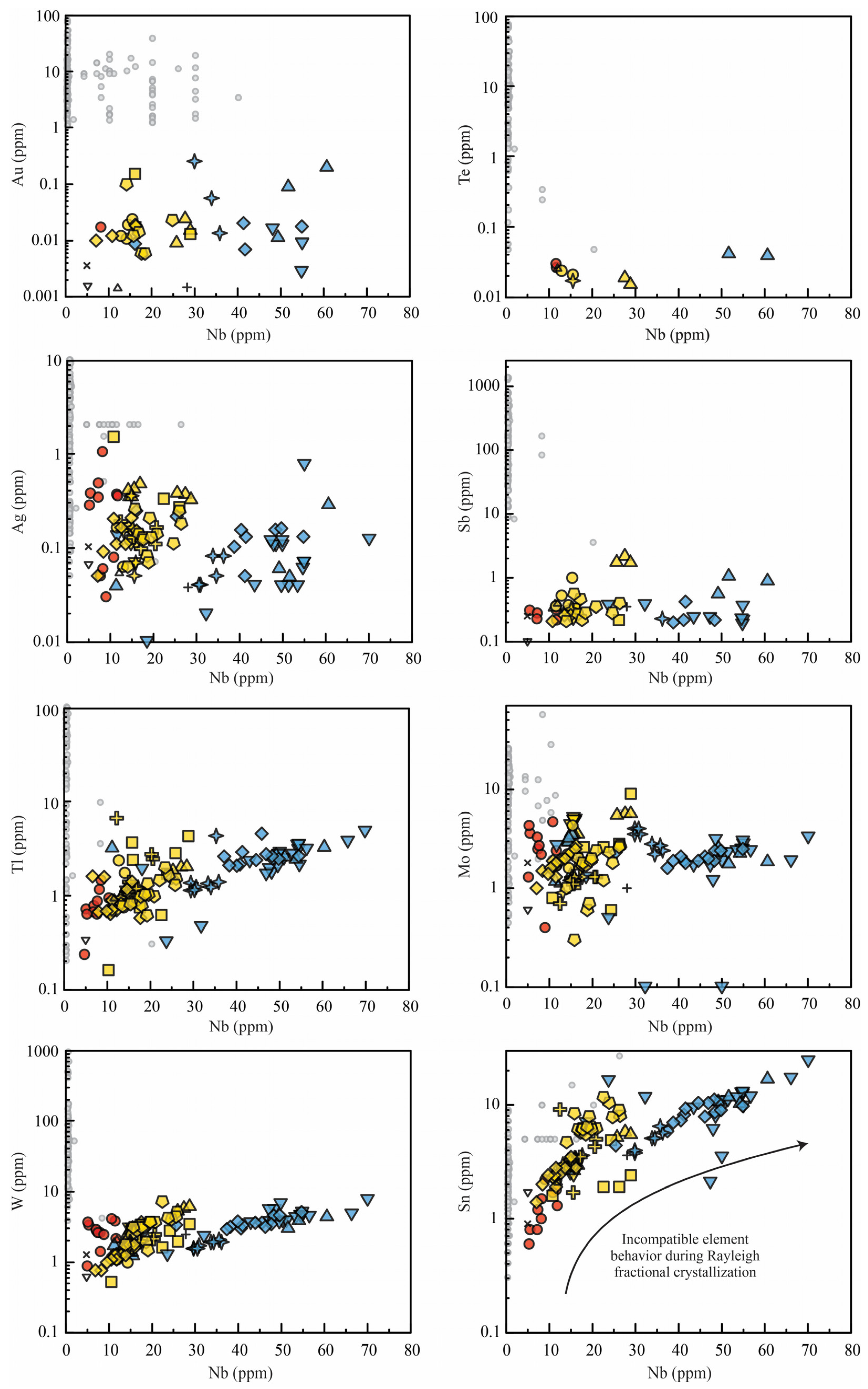
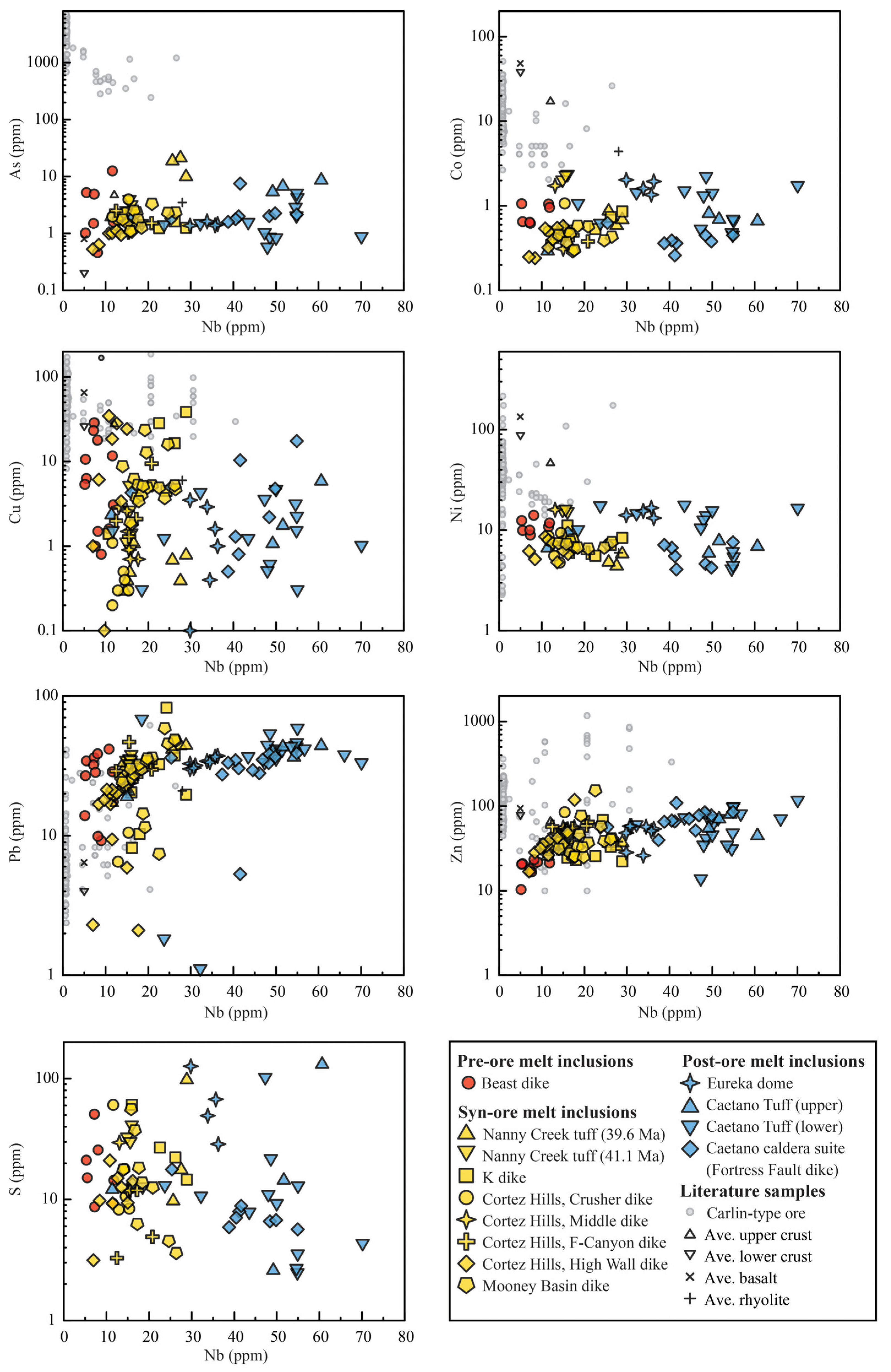
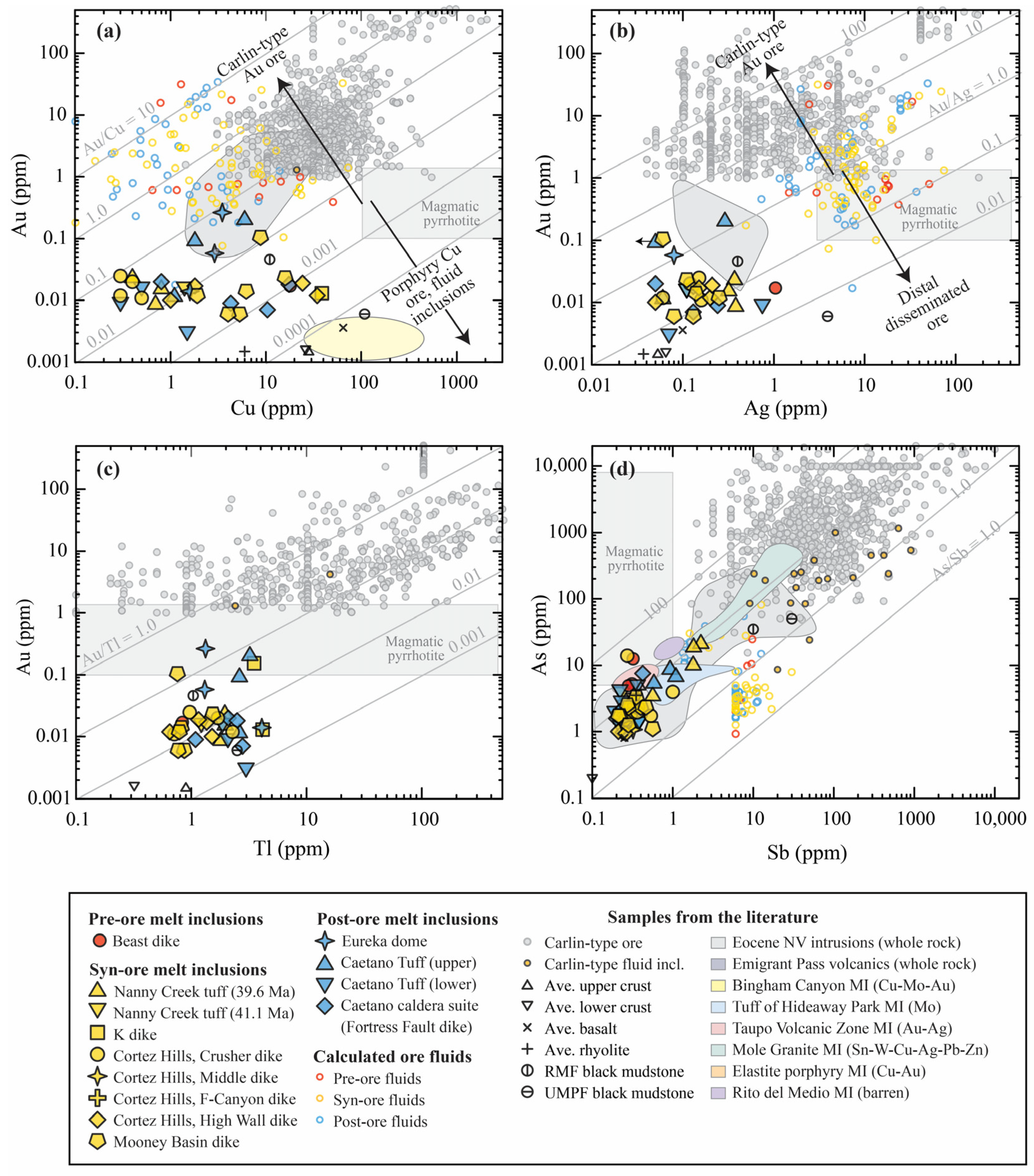
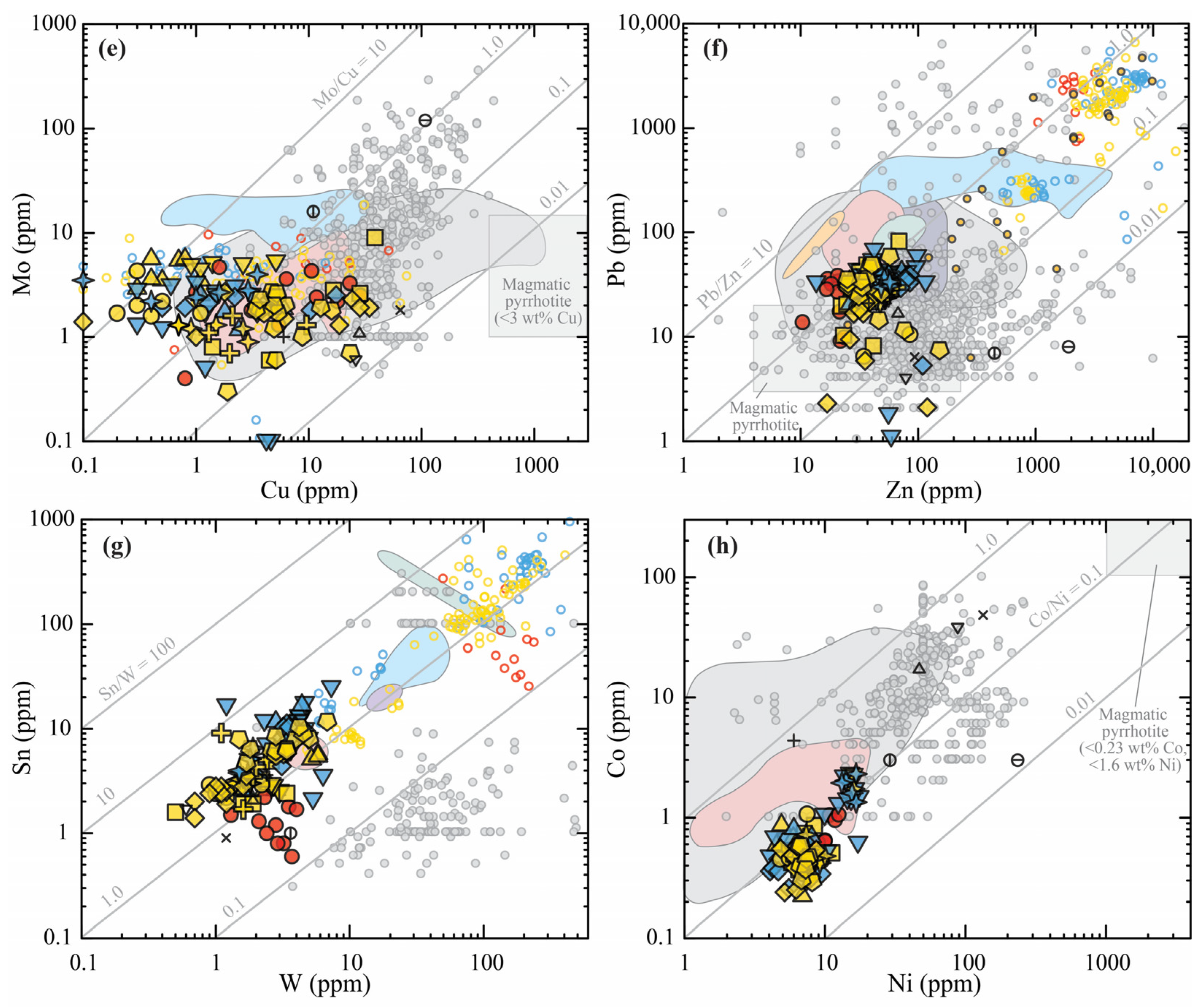
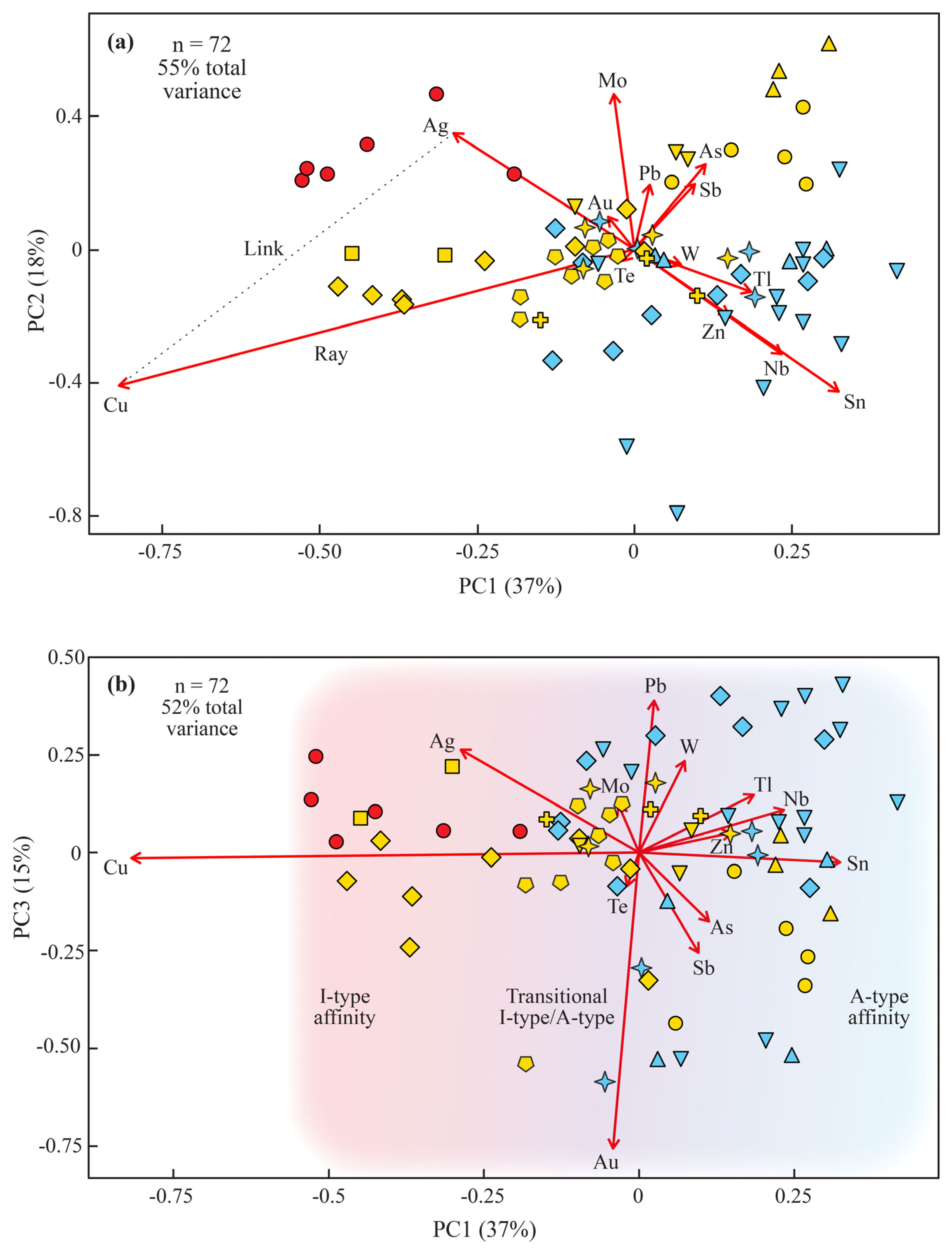
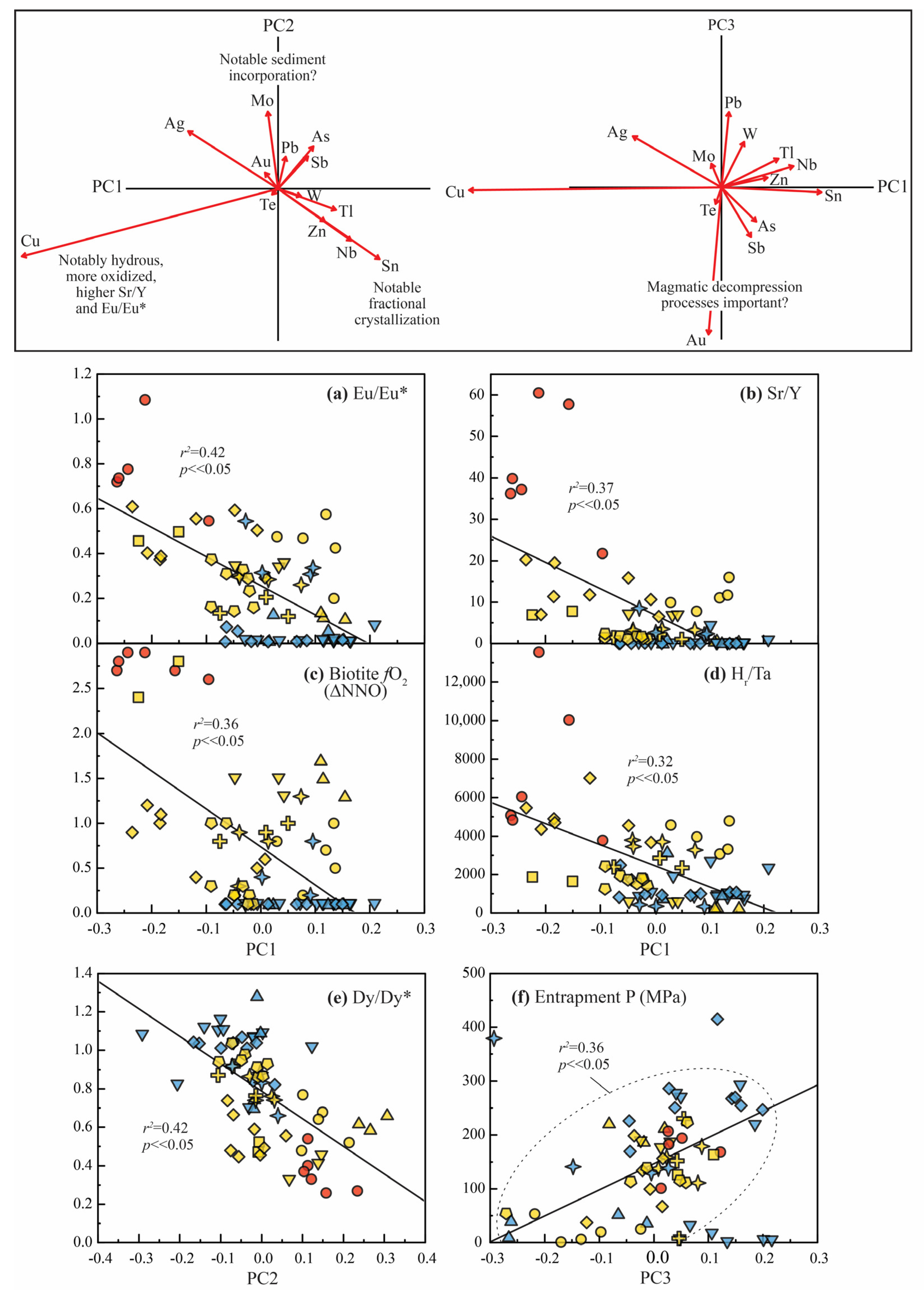
| Carlin Trend | Sample Name | Rock Type | Igneous Age (Ma) | Carlin-Type Au Deposit Nearby | Carlin-Type Au Deposit Age (Ma) | Interpreted Timing 1 | Interpreted Petrogenetic Affinity 2 |
|---|---|---|---|---|---|---|---|
| Long Canyon | Nanny Creek tuff | Rhyolite tuffs | 39.61–41.08 | Long Canyon | 39–41 | Syn-ore | Transitional I-type/A-type |
| Carlin | Beast dike | Porphyritic dike | 37.55 | Beast | <37.3 | Pre-ore | I-type endmember |
| K dike | Porphyritic dike | 40.3 | Genesis | <40.3 | Pre-/syn-ore | I-type | |
| Battle Mountain–Eureka | Caetano caldera suite | Intra-caldera tuff, ring fracture porphyry dike | 35.7 | Cortez Hills complex | 33.90–34.0 | Post-ore | A-type endmember |
| Cortez Hills dikes | Porphyritic dike | 35.7 | Cortez Hills complex | 35.71 | Syn-/post-ore | Transitional I-type/A-type | |
| Eureka dome | Rhyolite dome | 35.4 | Archimedes/Ruby Hill | >36 | Post-ore | A-type | |
| Alligator Ridge | Mooney Basin dike | Porphyritic dike | 35.9 | Galaxy, Horseshoe, Saga | <45, >34 | Syn-/post-ore | A-type |
| Principal Component | PC 1 | PC 2 | PC 3 | PC 4 | PC 5 | PC 6 | PC 7 | PC 8 | PC 9 | PC 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Nb | 0.23 | −0.32 | 0.11 | −0.07 | 0.05 | −0.09 | 0.27 | −0.14 | −0.31 | 0.13 |
| Cu | −0.82 | −0.41 | −0.01 | 0.03 | −0.27 | 0.03 | −0.05 | 0.01 | 0.01 | −0.03 |
| Zn | 0.15 | −0.20 | 0.05 | 0.11 | 0.24 | 0.40 | −0.04 | 0.24 | 0.48 | 0.50 |
| As | 0.11 | 0.26 | −0.18 | 0.44 | −0.47 | −0.22 | −0.17 | 0.40 | −0.06 | 0.25 |
| Mo | −0.03 | 0.47 | 0.12 | −0.23 | −0.35 | 0.63 | 0.27 | −0.10 | −0.15 | −0.04 |
| Ag | −0.29 | 0.35 | 0.26 | 0.27 | 0.62 | −0.09 | 0.16 | 0.28 | −0.25 | −0.13 |
| Sn | 0.32 | −0.43 | −0.03 | 0.06 | −0.10 | 0.05 | 0.33 | 0.34 | −0.01 | −0.52 |
| Sb | 0.10 | 0.20 | −0.26 | 0.38 | −0.02 | −0.08 | −0.11 | −0.41 | 0.23 | −0.40 |
| Te | −0.02 | −0.04 | −0.09 | 0.02 | 0.23 | 0.15 | −0.15 | −0.35 | 0.35 | −0.11 |
| W | 0.07 | −0.05 | 0.23 | 0.11 | −0.09 | −0.34 | 0.25 | −0.49 | −0.11 | 0.39 |
| Au | −0.04 | 0.10 | −0.76 | −0.45 | 0.20 | −0.15 | 0.10 | 0.08 | −0.13 | 0.15 |
| Tl | 0.19 | −0.13 | 0.15 | −0.14 | 0.07 | 0.15 | −0.75 | −0.03 | −0.45 | −0.06 |
| Pb | 0.02 | 0.19 | 0.39 | −0.53 | −0.12 | −0.43 | −0.10 | 0.17 | 0.42 | −0.14 |
| % variance | 37 | 18 | 15 | 9 | 5 | 5 | 3 | 2 | 2 | 1 |
| Cumulative % variance | 37 | 55 | 71 | 80 | 85 | 90 | 93 | 95 | 97 | 99 |
| Compositional Characteristic | Geological Process Interpretation |
|---|---|
| Nb | Highly incompatible element used to model Rayleigh fractional crystallization and as a proxy for melt evolution; higher values are more evolved melts |
| Ta | Highly incompatible element used to model Rayleigh fractional crystallization and as a proxy for melt evolution; higher values are more evolved melts |
| Hr | Restored water content; calculated dissolved H concentration in melt before post-entrapment diffusive loss |
| Hr/Nb, Hr/Ta | Restored water contents normalized to the extent of melt evolution |
| ASI | Aluminum saturation index; variable used to classify feldspathic igneous rocks, separating metaluminous from peraluminous compositions |
| MALI | Modified alkali–lime index; variable used to classify feldspathic igneous rocks, a measure of calcic to alkalic affinity |
| Peralk | Peralkalinity index; variable used in feldspathic igneous rock classification, discriminating peralkaline rocks from metaluminous and peraluminous rocks |
| Y+Nb | Incompatible elements used to discriminate I-type from A-type felsic compositions |
| Sr/Y | Indicator of melts that equilibrated with arc-metasomatized subcontinental lithospheric mantle and/or deep crust containing garnet and/or amphibole; typically high in porphyry Cu systems |
| Eu/Eu* | Indicator of melt evolution by plagioclase fractionation; value close to 1 indicates small anomaly and little plagioclase fractionation; value close to 0 indicates large negative anomaly and abundant plagioclase fractionation |
| Biotite IV(F/Cl) | Indicator of halogen activity in the magma, corrected for Mg/Fe ratio in the biotite, with lower values associated with higher degrees of F enrichment |
| Biotite fO2 (ΔNNO) | Estimate of magma redox relative to the nickel–nickel oxide buffer; for reference, ΔNNO+1 to +2 is relatively oxidized (on par with subduction zone processes) |
| La/Yb | Measure of the enrichment of LREE over HREE in melts that equilibrated with arc-metasomatized subcontinental lithospheric mantle and/or deep crust containing garnet and/or amphibole |
| Dy/Dy* | Measure of the curvature of REE patterns, highlighting melt contributions controlled by mid- to deep-crustal phases; low values may indicate interaction with amphibole/clinopyroxene and garnet, sediment-enriched source, or LREE enriched source, whereas high values indicate LREE-depleted source |
| P (MPa) | Pressure at which individual melt inclusions were trapped |
| T (°C) | Temperature at which individual melt inclusions were trapped |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercer, C.N.; Babel, H.R.; Mercer, C.M.; Hofstra, A.H. Metal Fingerprints of Eocene Rhyolite Magmas Coincident with Carlin-Type Gold Deposition in Nevada USA. Minerals 2025, 15, 479. https://doi.org/10.3390/min15050479
Mercer CN, Babel HR, Mercer CM, Hofstra AH. Metal Fingerprints of Eocene Rhyolite Magmas Coincident with Carlin-Type Gold Deposition in Nevada USA. Minerals. 2025; 15(5):479. https://doi.org/10.3390/min15050479
Chicago/Turabian StyleMercer, Celestine N., Hannah R. Babel, Cameron M. Mercer, and Albert H. Hofstra. 2025. "Metal Fingerprints of Eocene Rhyolite Magmas Coincident with Carlin-Type Gold Deposition in Nevada USA" Minerals 15, no. 5: 479. https://doi.org/10.3390/min15050479
APA StyleMercer, C. N., Babel, H. R., Mercer, C. M., & Hofstra, A. H. (2025). Metal Fingerprints of Eocene Rhyolite Magmas Coincident with Carlin-Type Gold Deposition in Nevada USA. Minerals, 15(5), 479. https://doi.org/10.3390/min15050479











