Abstract
This paper addresses the problem of infill drill hole placement for mineral resource estimation and classification. The placement is considered optimal when it maximizes an objective function that accounts for ore grades, mineral resource classes, extraction priorities, and block volumes, where the grade and resource classes are defined on the basis of a set of geostatistical simulations. To expedite the identification of the optimal solution within a condensed timeframe, modifications to the random search (RS) algorithm are introduced, including a partition of the region targeted for drilling and the definition of a maximum distance to existing drill holes. The modified RS divides the study area into smaller areas and examines all these areas to find the optimal solution, in order to reduce the search time and to reach the best possible solution. This approach, furthermore, eliminates the impact of different random starting points and the risk of getting trapped in certain areas of the solution space. Also, the incorporation of a geometallurgical parameter (recovered metal) instead of the ore grade represents an innovation that signifies the consideration of mineral processing perspectives to optimize the drill hole placement. The proposed modified RS algorithm is applied to a dataset from an Iranian iron deposit consisting of 240 exploration drill holes, and resulted in 11% to 21% of the indicated resources being converted into measured resources after locating nine infill drill holes accounting for the iron grade and the recovered metal, respectively. The modified RS also compares favorably to other traditional optimization techniques.
1. Introduction
1.1. Context and Problem Statement
In the fields of earth sciences and natural resources engineering, georeferenced data—information indexed by coordinates—often exhibit spatial continuity. This feature enables the estimation of quantitative variables at locations that have not been directly sampled, while also providing a quantifiable level of uncertainty that is influenced by the amount, quality, and spatial distribution of the data [1,2,3]. In the mining sector, high levels of uncertainty can result in inaccurate models of mineral resources and mineral reserves, as well as misclassifications of ore and waste, which in turn can cause deficient planning of the extraction, the non-fulfillment of production targets, and financial losses. The acceptable level of uncertainty varies depending on the type of deposit, its mineralization, and the project’s phase—whether it be exploration, scoping, prefeasibility, feasibility studies, or production [4,5]. A comprehensive data collection is therefore essential, regardless of the deposit type, mineralization, or project stage [6]. Drill hole data are the primary source for modeling in the mining industry for exploration and engineering studies. As acquiring accurate and precise data involves substantial expense, it is crucial to leverage all available information to formulate an effective drilling strategy.
Typically, the mining exploration stage comprises three phases: regional reconnaissance, mapping, and drilling. The initial stage of drilling, often performed in a systematic grid pattern, focuses on the highest-priority targets identified during detailed mapping [7]. The objective is to identify undisclosed ore deposits, and to provide a rough outline of the spatial distribution of mineralization. This stage is critical, as it yields comprehensive data regarding geological influences, ore varieties, and the spatial diversity of ore constituents [8]. All these data are then used in prefeasibility and feasibility studies aimed at assessing the economics of mine development. When the mineral deposits exhibit strong financial potential, advanced drilling and infill drilling initiatives will be formulated to delineate minable (proven/probable) reserves, providing the foundation for mine planning [9]. Subsequently, based on the desired level of uncertainty, the decision to cease additional drilling can be made to avoid incurring further costs [10].
Mining projects and mining operations encounter the need to make decisions about additional drilling multiple times throughout their existence. These decisions invariably revolve around two fundamental questions: whether further drilling is necessary and, if so, the optimal locations for the additional drill holes [11]. Therefore, the optimization of infill drill hole placement constitutes a principal challenge that the mining industry faces. A widely recognized concept addressing this challenge across various sectors is known as the “value of information” [2,10,12]. Numerous studies in this field highlight the significant value of forward-looking data. However, the high costs involved in obtaining such data can negatively impact the overall outcomes. Consequently, it is imperative to find a trade-off between the quantity of drill holes and the expenses linked to their drilling.
Infill drilling stands as a primary and dependable approach for acquiring subsurface data, offering insights for a more accurate and realistic modeling of mineral resources and mineral reserves. Nevertheless, the substantial expenses associated with drilling serve as a constraint on the utilization of this valuable information source [13]. Considering the limited number of infill drill holes, reducing drilling costs is often prioritized. Hence, in this study, we endeavor to employ novel techniques for the placement of infill drill holes to enhance estimation efficiency, ultimately leading to reduced future drilling costs.
1.2. State of the Art
In the mining industry, designing an effective infill drill hole pattern is a complex task, due to the array of considerations involved, which encompass geological, financial, and extraction-related factors [14]. During mining operations, there are constraints on possible locations for infill drill holes. For example, placing drill holes at the final positions of the toe and crest, or along access roads, is often impractical [15]. Additionally, the drilling process and the quality of core samples are significantly influenced by geological characteristics, such as rock quality, weathering, and moisture content. These factors are critical and should be evaluated using various infill drilling techniques. The optimal strategy for designing infill drill hole plans involves taking into account several project parameters to boost the mining project’s efficiency and flexibility [16].
Initially, infill drilling was proposed as a tool for planning and managing exploration activities. It was later utilized as a method to minimize expenses and handle budget constraints [17]. Once the number of infill drill holes and the selection criteria have been determined, the potential locations become limited. Consequently, this scenario evolves into an optimization challenge.
The first approach employed was a semi-systematic method involving the expert-guided placement of points. The application of geostatistics and mathematical and optimization techniques then came into play to reduce subjectivity and to increase efficiency in the drill hole placement [18]. At first, the primary aim was to minimize the kriging error variance [16,19,20,21,22,23], which depends on the data spatial correlation and their geometric configuration, and can be calculated before drilling commenced. However, such an approach often overlooks significant effects stemming from local geological and grade variability [24]. For example, although it is generally assumed that additional drilling will reduce grade uncertainty, Goria et al. [25] and Dimitrakopoulos and Jewbali [26] observed instances where gathering further data can, paradoxically, increase uncertainty. These findings advocate for a comprehensive evaluation of how infill drilling impacts the long-term mine strategy.
Over the years, a plethora of objective functions have been suggested as alternatives to the kriging error minimization. Unlike the kriging error variance, these objective functions can take into consideration multiple factors, such as local ore grade variability, metal contents, mineral resource categories, costs, profits, geological boundaries, and geological uncertainty [11,12,18,27,28,29,30], and are suitable for diverse purposes, encompassing grade assessment, mineralogical structure identification, delineation of ore zones or mineralization boundaries, ore-waste classification, reduction of long-term or short-term plan uncertainties, and cost–benefit analyses, among others [31,32,33].
Importantly, geostatistical simulation has emerged as an essential tool for optimizing infill drilling decisions in replacement of kriging models. For instance, Boucher et al. [34] employed geostatistical simulations to evaluate the impact of drilling on projected profits across different stockpiling strategies. By simulating a theoretical realization of future drill data and re-simulating with a denser pattern, they identified an optimized configuration by analyzing block classifications and economic outcomes. Kumral and Ozer [27] proposed optimizing the drilling setup with a genetic algorithm to minimize the maximum interpolation variance, utilizing simulated future drill hole data along with existing exploration information. Dirkx and Dimitrakopoulos [11] applied a multi-armed bandit approach to select infill drilling patterns in a stockpile based on how they alter material classification, aiming to lower the risk of misclassification. In assessing the benefits of infill drilling, additional data from stochastic simulations of prospective drilling outcomes are used to refine orebody simulations. Verly and Parker [35] used geostatistical simulations and confidence intervals to classify mineral resources as measured or indicated, offering an additional criterion for infill drill hole planning. A noted limitation of these simulation-based methods is their insufficient consideration of the relationship between the collected drilling information and its potential influence on long-term mine planning and production schedules, which may unlock further value. Recent research has yielded advancements in this direction, such as employing intelligent methods and machine learning, as evidenced by Levinson and Dimitrakopoulos [36].
1.3. Our Contributions
This study differs from the above works by the incorporation of geo-metallurgical parameters in the placement of infill drill holes. When developing a mineral resource model, economic criteria typically include parameters, such as ore grade, tonnage, and tonnage above a cutoff grade. Geo-metallurgy complements this by creating a spatial prediction model for mineral processing workflows, integrating both geological and metallurgical data [37]. This burgeoning field aims to combine a variety of parameters, including attributes such as hardness, crushability, recovery, mineral texture, degree of liberation, and elemental grade [38]. This approach involves a quantitative and comprehensive evaluation of the ore, accounting for processing characteristics such as crushing, milling, liberation, recovery, product quality, and environmental responsibility [37].
In addition to the ore grade and the recovered metal, which accounts for both the ore grade and the recovery, we furthermore consider probabilistic classification criteria when determining the locations for these drill holes, with a primary focus on evaluating the continuity of production resource categories. Indeed, mining ore from the highest confidence category (measured resources) is among the factors that hold special significance when going into production. Therefore, in this study, efforts have been made to take an effective step by implementing modifications to the optimization algorithm, so that upgraded blocks in terms of resource classification are aligned with and extend along the previous blocks. Additionally, by prioritizing blocks that have not been classified as measured in the block model, new infill drill holes are placed in these blocks, which enhances the classification while maintaining the spatial continuity of the block categories.
Concerning the methodology, the random search algorithm used in this study has also been modified to provide optimal solutions in a shorter period of time. To elucidate the rationale for selecting this modified algorithm, two commonly used algorithms in the field of drill hole layout optimization—particle swarm optimization (PSO) and the genetic algorithm (GA)—have also been evaluated, and their characteristics, strengths, and weaknesses have been outlined. Subsequently, a comparison of the convergence speed has been conducted between these two algorithms and the one used in this research. To complete the discussion, a portion of the block model has been selected, and the placement of supplementary drill holes has been performed using both the traditional random search and the modified random search algorithms (as utilized in this study). The results demonstrate that the modified random search algorithm delivers superior outputs.
1.4. Optimization Strategy: Global or Sequential?
In the field of mining engineering, effective sampling strategies are crucial for accurate resource estimation and efficient extraction processes. Despite their importance, the literature on systematic and optimized sampling strategies—particularly for infill drilling—remains relatively limited [39]. Traditional sampling methods often rely on heuristic or expert-driven approaches, which, while practical, may not provide the most statistically or economically efficient outcomes. In recent years, the research has incorporated more formal optimization and machine learning techniques into geological sampling, and applications specifically targeting infill drilling are still emerging [13,36,40,41]. Moreover, sampling strategies in geosciences are inherently multidisciplinary, drawing insights from geostatistics, spatial data science, and operations research. These strategies involve the systematic collection and analysis of geological data as a precursor to decision-making in resource management. Within this context, two prominent optimization frameworks have gained traction for determining the placement of infill drill holes: global optimization (simultaneous) and sequential optimization.
Global optimization involves assessing all potential drill hole placements simultaneously to identify an optimal set based on a defined objective function. Popular global optimization algorithms, such as the genetic algorithm, particle swarm optimization, and simulated annealing [42,43], aim to find the best configuration by exploring a wide solution space within the imposed constraints. While these algorithms can generate globally optimal drill plans [8,10,16,28,29], they operate under static assumptions, and do not incorporate the possibility of learning from intermediate outcomes. In real-world exploration settings, this can be a significant limitation. Geological environments are inherently uncertain and can vary significantly between sampling intervals. As a result, strategies that commit to a full set of drill holes from the outset may miss emerging trends or anomalies that become evident only after initial drilling. Furthermore, global algorithms can be computationally expensive, especially when working with high-resolution models or large search spaces, and their application becomes less practical in complex geological settings.
By contrast, sequential optimization adopts a step-by-step framework that mirrors the practical and operational reality of drilling programs. This approach updates the geological model after each iteration, enabling engineers and geologists to incorporate the most recent data into their decision-making processes. Infill drilling is fundamentally a sequential process, where the placement of each new drill hole should ideally be informed by the insights gained from previous drill holes. Sequential methods leverage this logic by dynamically adjusting the drill plan in response to real-time data, making them more robust in the face of geological uncertainty [44]. Moreover, this adaptability allows for better resource allocation, as decision-makers can halt or redirect drilling efforts based on the outcomes of earlier stages, thereby reducing unnecessary drilling and associated costs [2]. Given these advantages, sequential optimization not only aligns more closely with how drilling is conducted in practice but enhances decision-making under uncertainty—an essential consideration in mineral resource evaluation.
The real strength of sequential optimization lies in its ability to respond dynamically to the complexities and inherent uncertainties of subsurface environments. Unlike global optimization, which offers a static, one-time solution based on an initial model, sequential optimization enables continuous refinement of drilling strategies as new geological data become available. This flexibility is particularly crucial in mineral exploration, where the geological understanding evolves with each additional data point, often revealing spatial patterns or anomalies that were not evident in the initial model. Infill drilling is not only capital-intensive but carries a high level of geological risk; thus, a responsive strategy that can adapt to new information is essential for minimizing uncertainty and maximizing data utility [45].
Our understanding of the Earth’s structure is inherently limited due to spatial heterogeneity, data sparsity, and the stochastic nature of mineralization processes. As such, the geological model at any given time is an approximation that must be constantly revised in light of new observations. The sequential placement of drill holes facilitates this continuous learning process [9,11,12,18,30]. Each new drill hole not only adds data to the block model but potentially reshapes the estimation of grade distribution and geological continuity in adjacent areas. This iterative update mechanism allows for the development of what can be termed a semi-dynamic model—a representation that evolves with each decision. Although the most effective reduction in uncertainty is achieved through physical sampling, even simulated drill hole placements can contribute significantly to improved model accuracy if implemented within a sequential optimization framework [46]. Furthermore, the location and number of samples selected during this process have a direct and measurable impact on resource classification and confidence levels, underscoring the importance of smart, data-driven infill strategies [47].
It is important to recognize that both the global and sequential optimization strategies come with inherent challenges and trade-offs. Global optimization, while theoretically capable of identifying the optimal configuration of drill hole placements in a single step, relies on a static view of the geological model. This lack of flexibility can lead to suboptimal outcomes if the actual subsurface conditions deviate from the initial assumptions. On the other hand, sequential optimization, despite its adaptability and ability to incorporate new data in real time, is susceptible to path dependency—early-stage decisions may disproportionately affect subsequent steps, especially if based on uncertain or incomplete information. Additionally, the need for continuous model updates at each step introduces computational overhead, particularly in high-resolution or large-scale models. Nonetheless, sequential optimization remains more consistent with the dynamic, uncertain nature of real-world mineral exploration and offers a more practical framework for decision-making in such contexts.
In light of these considerations, the present research adopts a hybrid approach to the placement of infill drill holes, mixing global and sequential strategies. At each stage of the latter strategy, an optimal subset of new infill drill holes is identified using a tailored optimization algorithm designed to maximize information gain or minimize geological uncertainty. Once selected, the simulated data from these new drill holes are incorporated into the existing dataset, updating the block model, and informing subsequent drilling decisions. This iterative process continues until the model reaches a predefined number of infill drill holes. Details of this process are provided in Section 2.7.
Such a hybrid approach not only improves the efficiency of resource estimation but mirrors how infill drilling is conducted in practice—incrementally, with the flexibility to adapt plans as new data emerge. It addresses a gap in many previous studies, which often treat drill planning as a static, one-time optimization problem, and overlook the feedback loop between data acquisition and model evolution. By contrast, the methodology that will be employed herein treats the model as a living system, adapting to the changes introduced by new drill holes. This reflects operational realities in the field, where even predetermined drill plans are frequently revised based on early drilling results, unforeseen geological features, or logistical constraints [36]. Moreover, this research contributes a novel framework that blends the practical wisdom of adaptive drilling with formalized optimization theory—something that has received limited attention in the existing geostatistical and mining optimization literature. Therefore, the proposed hybrid optimization strategy not only reinforces the scientific rigor of infill planning but enhances its alignment with the dynamic, uncertain nature of mineral exploration projects.
2. Methodology
In order to position infill drill holes, an objective function has been defined, which includes various parameters, such as ore grade, classification components, and extraction priorities. The goal is to maximize the extractable resources while maintaining the spatial continuity of resource categories and enhancing the mean grade of the simulated block model. The objective function related to classification components is among the most practical, aiming both to reduce simulation uncertainty and to maximize the resource by improving the classification rankings through the placement of new infill drill holes in non-measured areas. This method employs geostatistical simulation and probability criteria for block classification, with a moving window approach to finalize classification results.
To maintain continuity, a technique has been used, where a neighborhood radius for previous drill holes is defined based on the drilling grid and the surrounding classification ranks. New infill drill holes are positioned at the boundary of this neighborhood radius or at a reasonable distance from existing holes. This ensures that the new classification is not only enhanced, but is continuous, preventing the creation of spatially isolated resource classes.
Ultimately, the infill drill hole placement is determined using ore grades or recovered metal obtained from various realizations. Objective functions and conditional simulation offer a range of possible solutions for infill drilling, necessitating the use of optimization algorithms to obtain the solution. In this research, the random search (RS) algorithm, as a practical example of these algorithms, has been employed. The subsequent sections elucidate the concept of classification and its associated methods, culminating in the introduction of the employed optimization method.
2.1. Mineral Resource Classification
Mineral resource classification holds a pivotal position in the economic assessment of mining projects. Geometric methods are most often employed for such a classification [48,49]. While it is preferable to classify the mineral resources on a fine scale, artifacts in the delimitation of the measured, indicated, and inferred categories tend to emerge near the drill hole locations, such as small, isolated volumes of measured resources [50]. A common approach to address this issue is to classify the resources on broader scales, such as monthly, quarterly, or yearly production volumes [35].
Applying probabilistic criteria can offer quantitative control over the confidence levels used to define the resource categories [51]. For instance, the classification procedure for the selective mine unit (SMU) blocks, outlined by Silva [14], involves the following steps:
- Allocate a panel volume at the center of the SMU for classification;
- Assess the ore grades of the blocks within the panel through simulation;
- Compute the mean panel grade and subsequently establish lower and upper thresholds for each classification, aligning them with the desired level of accuracy;
- Count the number of blocks falling within the thresholds for each classification;
- Determine the classification based on the requisite confidence interval for each class.
The outcomes of the classification process are contingent not only on the spatial coordinates of the data but on the ore grade values. As the grade level rises, the associated accuracy interval for the mean grade often widens [4]. The spectrum of probabilistic criteria typically spans accuracy rates ranging from 10% to 30%, and confidence intervals from 95% to 80% [2].
2.2. Particle Swarm Optimization
Particle swarm optimization (PSO) is a population-based optimization technique inspired by the social behavior of birds and fish [52]. It involves a group of particles (potential solutions) that “fly” through the solution space seeking the best solutions based on their own experiences and those of their neighbors. Each particle adjusts its position based on a velocity vector, influenced by its personal best position and the global best position found by the swarm. PSO is widely used in various optimization problems due to its simplicity, ease of implementation, and ability to efficiently explore large search spaces.
2.3. Genetic Algorithms
Genetic algorithms (GAs) are a class of optimization and search algorithms inspired by the principles of natural selection and genetics, and are designed to solve optimization problems by evolving solutions over successive generations. In the GA, a population of candidate solutions, known as chromosomes, undergoes processes analogous to biological evolution, such as selection, crossover (recombination), and mutation. The fitness of each solution is evaluated, and the fittest individuals are selected to create the next generation, potentially leading to better solutions over time. Genetic algorithms are particularly useful for problems with complex search spaces and have been applied in numerous fields, including engineering, economics, and artificial intelligence [53].
2.4. Random Search
In the field of optimization, various algorithms have been employed to locate optimal drilling positions in mining operations. Among these, the random search (RS) algorithm has emerged as a competitive alternative when compared to the genetic algorithm (GA), particle swarm optimization (PSO), and simulated annealing (SA). The main strengths of the RS include the following:
- Solution optimality. Unlike the GA and PSO, which rely heavily on population dynamics and historical solutions, the RS samples solutions randomly throughout the search space, and is able to explore diverse regions without bias, enhancing its capability of escaping local optima—a common challenge faced by the GA and PSO due to their reliance on previously selected solutions [52,53]. In mineral deposits with a complex geology and spatial distribution of key technical variables, this advantage may significantly increase the likelihood of identifying optimal drilling locations [54].
- Robustness to noise. Geological and mining data often present a considerable amount of noise arising from geological variability and measurement errors. Previous studies have shown the robustness of the RS in such noisy environments, since it does not depend on gradient information or population interactions prone to erratic behavior. In scenarios characterized by uncertainty—where mineral deposits may shift unexpectedly based on real-time data—the RS proves to be effective due to its stochastic nature allowing for steadier performance amidst variability [55].
- Efficacy in high dimensional problems. The efficacy of optimization algorithms typically decreases when increasing the problem dimensionality—a phenomenon known as the “curse of dimensionality”. Research indicates that, while the GA and PSO may struggle with maintaining diversity among candidate solutions as dimensions rise, the RS maintains efficiency through its independent sampling strategy. In high-dimensional search spaces representative of complex mining datasets that incorporate multiple geological features, this scalability allows the RS not only quick evaluations, but greater adaptability during optimizations [56].
- Ease of implementation. The RS offers substantial advantages with respect to implementation simplicity, compared with more sophisticated algorithms like the GA or PSO, which require extensive parameter tuning, including crossover rates or swarm sizes, to achieve desired results. The straightforward nature of the RS makes it particularly appealing for dynamic applications where conditions change frequently, allowing practitioners immediate adaptability without undergoing lengthy pre-processing stages required by other techniques [57].
Random search optimization techniques select answer locations in a random manner, where new answer locations are accepted if they improve the objective function to be maximized. These techniques encompass three categories: blind, localized, and modified random search. The blind random search is the simplest one, earning its name due to its approach of disregarding previous results in each iteration, not factoring them into the calculations. Expanding the scope of work, which involves increasing the number of required drill holes while considering their azimuths and dips, can rapidly reduce the efficiency of this method, which may reach a point where it fails to produce meaningful outputs or identify suitable solutions [58]. The localized random search differs from the blind random search by introducing, in each iteration, a predetermined solution radius to the current best answer before reevaluating the objective function, as opposed to generating entirely independent variables from the previous set of variables. Localized random search has demonstrated its effectiveness when dealing with a substantial number of drill holes [59]. In the modified random search algorithm, instead of altering all the variables in each iteration, only one variable or a subset of variables is modified, with a subsequent recalculation of the objective function.
2.5. Proposed Objective Function
Objective functions are employed to address the complexity and diversity of variables involved in the placement of infill drill holes. A multitude of such functions can be selected to tackle the problem, resulting in a wide range of potential solutions, and optimization methods can be utilized to achieve a unique solution. The objective function considered in this work is as follows:
where:
- N is the number of blocks (selective mining units) discretizing the resource model;
- Gi is the expected ore grade of block i (average of the realizations);
- Pi is the extraction priority of block i (0 ≤ Pi ≤ 1);
- Ci is the resource classification ranking of block i (0 for measured and 1 for indicated);
- Vi is the unit block volume (1 for a block, a fraction between 0 and 1 for a sub-block);
- w1,i, w2,i, w3,i, and w4,i are the weights associated with each parameter, reflecting their relative importance in the objective function (0 ≤ w ≤ 1).
To reflect the extraction efficiency, blocks within the final pit are assigned a priority value Pi of 1, with weights w2,i increasing as the distance from the pit boundaries increases; whereas blocks outside the final pit have a priority value Pi of 0.
In light of the dense and systematically arranged network of existing drill holes, the classification of the blocks has been delineated into only two categories: measured and indicated (see the discussion in Section 3). To favor infill drilling in areas with an indicated classification, which have the potential for upgrading to the measured classification, w3,i is set to 1 if the block is close to a drill hole (either original or infill), and decreases to 0 for blocks far from all the drill holes. This way, placing a drill hole in the middle of a cluster of indicated blocks (for which Ci = 1) leads to a significant increase in the objective function; whereas, placing it in an area dominated by measured blocks (for which Ci = 0) does not significantly affect the objective function. The same strategy is adopted for the weight w1,i to favor infill drilling in high-grade areas: w1,i is set to 1 when the block is close to an original or infill drill hole, and decreases to 0 when the block is far from all the drill holes. The relative values of w1,i and w3,i depend on the infill strategy—whether the focus is more on improving resource classification or on targeting high-grade areas.
Finally, due to their smaller volumes, sub-blocks are assigned lesser importance to the aggregate effect in the objective function. The approach to implement this involves the use of a normalization factor and an adjustment of the weight w4,i to prioritize larger, more impactful blocks.
2.6. Proposed Optimization Algorithm
The algorithm chosen here is a hybrid of modified and localized random search and incorporates two key features. The first feature involves employing potential weights to determine the initial starting point for the algorithm, while the second feature entails the utilization of a restricted search radius for refining local solutions. In the modified random search algorithm, a drill hole is chosen, and optimization adjustments are simultaneously implemented. However, the selection of the drill hole is contingent on probabilistic factors [60], in such a way that a drill hole is more likely to be relocated as it has a low impact on the objective function. The likelihood of relocating a drill hole is linked to the cumulative enhancement of the target function and its rate of increase. After each recalculation of the target function, the accrued improvement is recorded, and this value is utilized to compute the probability of repositioning each drill hole in the subsequent iteration [61].
To elaborate, when a drill hole is placed in space, it affects multiple neighboring blocks. The contribution to the objective function is computed for each of these blocks and summed over the blocks. Subsequently, the maximum and minimum values of this cumulative contribution to the objective function (CCOF) among the drill holes are determined, and the probability for selecting a drill hole is calculated using the following formula [14]:
where n is the number of drill holes being optimized, pi is the probability of selecting the i-th drill hole, and CCOFi is the cumulated contribution to the objective function of the i-th drill hole.
When a drill hole is randomly chosen based on the previous probabilities, and its attributes (collar, azimuth, dip) are altered for optimization, the drill hole relocates to different coordinates. This relocation can encompass any point within the domain. In such scenarios, an exploration of all potential solutions is pursued. However, given the vast expanse of the available space, arriving at the precise answer becomes challenging and, at times, unattainable. Gradient-based methods were initially attempted for local fine-tuning within random search algorithms. However, these methods proved unsuccessful even at the local level, primarily due to the characteristics of the defined objective function [62]. Consequently, random approaches are employed for local refinement, and a constrained search method is introduced for this purpose. This method involves defining the range of variation for drill hole parameters in each iteration. The initial search magnitude corresponds to the complete spectrum of values attributed to each variable. The optimal spacing, as determined by the average separation between pre-existing drill holes, serves as an effective parameter for the intermediate stage of collar parameter adjustment [15]. Introducing a delay between collar scheduling and angle configuration (azimuth and dip) is advisable to facilitate finer local adjustments to angles subsequent to the selection of a suitable collar location [33].
In this research, some adjustments were made to accommodate the large volume of data and drill targets, and to find optimal solutions in a shorter period of time. In the proposal by Silva [14], all the drill targets were initially dispersed randomly across the environment. Subsequently, to optimize the drill holes within a search radius, their locations were altered, which was a time-consuming process. There was also the possibility of drill holes being confined to specific areas.
Therefore, in designing our new random search algorithm, to maximally cover all possible areas for placement in the shortest possible time, the targeted region was first partitioned into smaller areas. Then, one infill drill hole was randomly placed in each partition area. Subsequently, the optimization algorithm was applied by selecting a drill hole (Equation (2)) and randomly changing its location within its partition area, until the best possible solution for the whole set of infill drill holes was found. In the next stage, a comparison was made between the drill holes so obtained, and the best three drill holes were selected and added to the initial database, after which the placement operation was repeated.
Additionally, to maintain continuity in the resource classification, while upgrading indicated blocks to the measured class, a search radius from the existing drill holes is defined. This ensures that the new drill targets are positioned not too far from the existing holes and that the mineral resource classification resulting from the newly positioned drill holes will extend the previous classification without artifacts (isolated measured blocks surrounded by indicated blocks).
2.7. Proposed Methodology
Building on the previous elements, a novel methodology is proposed to enhance the mineral resource classification, expand the measured class, and ensure that newly identified resources seamlessly align and extend in continuity with the existing resources. This methodology builds on probabilistic criteria for block classification, which are derived from a set of realizations obtained from geostatistical simulation based on the well-known multi-Gaussian model [1].
First, the entire block model (with ore grade and recovered metal) is simulated, leading to a total of 100 realizations of the mineral deposit. The next step involves classifying the blocks using probabilistic criteria. An initial classification is carried out, while the final classification is executed through a moving window method, considering the classification of neighboring blocks around the target block. This moving window method is employed to refine the classification outcomes and to minimize artifacts (the “spotted dog” effect). In the following step, the value of each block is calculated, based on a predefined objective function (Equation (1)). Blocks with an indicated classification and with high grades will be prioritized. This approach aims both to reduce uncertainty and to increase the average grade of the produced resources.
A procedure utilizing the modified random search, as described above, is employed to ascertain the optimal locations for infill drill hole placement. The following steps outline the optimization process:
- Data preparation in a suitable format.
- Divide the block model into smaller, more defined zones for a comprehensive and precise analysis of potential drill hole placements.
- Place an infill drill hole randomly within each restricted zone, ensuring compliance with the defined maximum distance to the initial drill holes or to the other drill holes undergoing optimization. Care must be taken to maintain reasonable distances both in relation to the existing drill holes and among the new set of drill holes themselves.
- Randomly select one infill drill hole (Equation (2)) and shift its position within its restricted zone subject to the above distance restrictions.
- Evaluate the objective function to accept or reject the shift proposed in Step 4.
- Go back to Step 3 and loop until the objective function does not increase any more, or a maximum number of iterations (3000) is reached. The resulting configuration of infill drill holes (one per restricted zone) is the optimal one, or close to the optimal one.
- Evaluate the cumulated contribution to the objective function of each infill drill hole and select the best three drill holes.
- Update the database by adding the three new drill holes to the existing ones, and update the realizations of the block model, by re-rerunning the simulation of the ore grade and recovered metal conditioned to the information of the updated database.
- Continue the placement process using the updated database, repeating Steps 3 to 7 until the desired number of optimal infill drill holes is achieved.
While Steps 3 to 7 pertain to a global optimization strategy, where all the infill drill holes are jointly assessed to identify an optimal subset of them, the repetition of the placement and optimization process at Step 9 pertains to a sequential strategy. Hence, our approach can be qualified as a hybrid one. The methodology has been implemented using the Python 3.10 programming language and is summarized in Figure 1 for clarity.
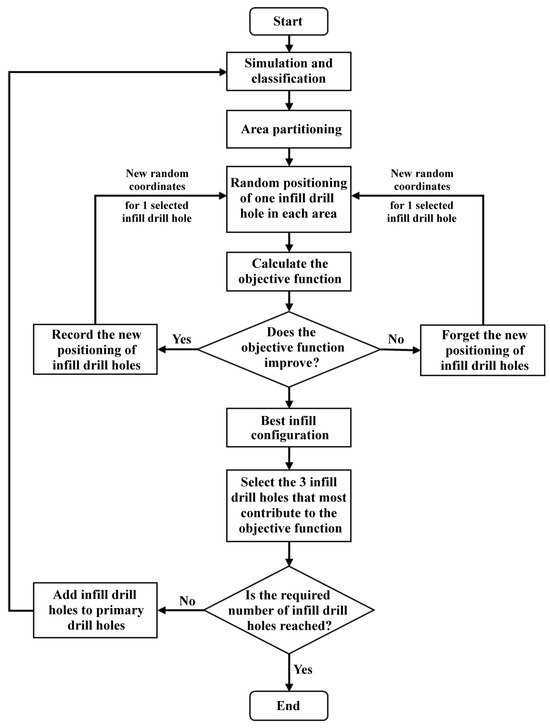
Figure 1.
Steps of the proposed methodology.
3. Case Study
3.1. Deposit and Data
The Gol Gohar deposit, renowned as one of the largest Kiruna-type iron ore deposits in Iran, is situated in the southern region of Iran in the province of Kerman (Figure 2). This complex lies in the southeastern part of the Sanandaj–Sirjan zone, as depicted on the 1:100,000 geological map (Figure 3). Within this region, a total of 12 mineralized anomalies have been documented, boasting combined potential resources of 1135 million tons.
Figure 2.
Geographical location and ways of access to Gol Gohar iron ore deposit.
Figure 3.
Location of Gol Gohar mine on a 1:100,000 geological map.
Among these twelve anomalies, the initial anomaly is currently undergoing exploration and exploitation. It appears as an elongated lens with an east–west orientation, holding confirmed resources of 185 million tons and potential resources of 780 million tons. The geological formations in the Gol Gohar area encompass mica schist, quartzite, marble, amphibole schist, graphite schist, and amphibole.
Anomaly No. 1 within the Gol Gohar deposit has been subject to sampling through both vertical and inclined drill holes at various exploration stages. For the purposes of this work, we will use a dataset consisting of 240 exploratory drill holes, situated in an area spanning 1750 m in length, 650 m in width, and 400 m in depth, featuring an average inter-hole distance of 70 m and an average drill hole length of 250 m. A composite length of three meters was considered for the drill hole samples, with records of essential parameters that include the percentages of iron-oxide, sulfur, and phosphorus. Additionally, the recovered metal (mass of recovered iron per metric ton of feed ore, expressed in %) was computed and applied as a significant geo-metallurgical parameter in this dataset, as presented in Figure 4 and Figure 5, and in Table 1.
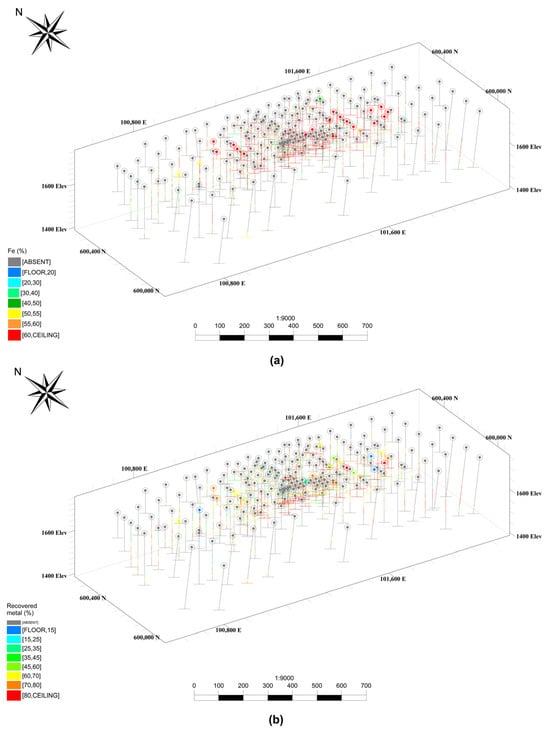
Figure 4.
3D views of available drill hole data: (a) Fe grade (%); (b) recovered metal (%).
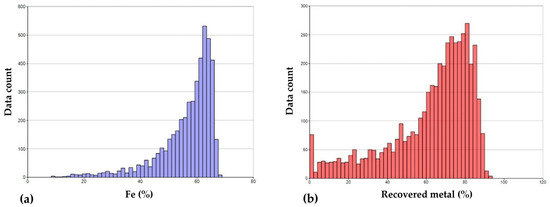
Figure 5.
Histograms of drill hole data: (a) Fe grade (%); (b) recovered metal (%).

Table 1.
Statistical information of drill hole data.
Given the high geological continuity of the deposit, with variogram ranges of about 100 m, low relative nugget effect (less than 0.1), and low coefficients of variation for both the iron grade (0.17) and the recovered metal (0.35) (Table 1), the inter-hole distance ensures that almost all the blocks in the block model are classified as measured or indicated, i.e., the inferred resources are practically inexistent. The context of the work is therefore that of a feasibility study, in which one objective (as part of the objective function in Equation (1)) is to convert indicated resources into measured resources as much as possible, in order to move on to the production stage. To this end, we assume that a rolling budget is available for nine infill drill holes. If the methodology is successful, the drilling budget can be updated and the methodology can be applied again to incrementally convert indicated into measured resources.
3.2. Application of the Proposed Methodology
Following the statistical analysis of the data, sequential Gaussian simulation (SGS) was conducted separately for the iron grade and the recovered metal. SGS is a geostatistical technique employed to generate multiple equally probable realizations of a spatially distributed variable, and is widespread in natural resource modeling and environmental assessment, where understanding spatial variability and uncertainty is crucial. SGS begins with transforming the data into a standard normal distribution. A fine grid covering the study area is then defined to discretize the block model. The simulation proceeds sequentially, generating point-support values at each grid node using conditional Gaussian distributions informed by the observed data and the previously simulated nodes. Simple kriging is used to determine the means and variances of these conditional Gaussian distributions. At each node, a random value is drawn from the corresponding distribution and assigned accordingly. This sequential approach results in a single realization of the variable at the same support as the input data. By repeating the process multiple times, various realizations are obtained. While each realization depicts a potential spatial distribution of the variable, the set of realizations illuminate the inherent uncertainty in the study area. The statistical results related to the simulation of the iron grade and the recovered metal (Figure 6) show that the realizations reproduce the trends of the drill hole data.
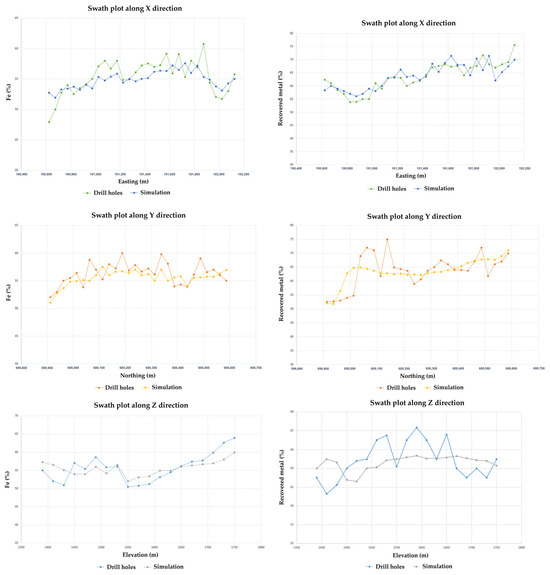
Figure 6.
Swath plots of drill hole data vs average of realizations: left: Fe grade (%); right: recovered metal (%).
SGS allows for assigning the values of the iron grade or of the recovered metal to any potential infill drill hole, as well as average values to any block or sub-block in the block model. In the present study, the number of sub-blocks is less than 5% of the total number of blocks, the latter being approximately 72,000. The dimensions of the block are 25 m (x direction) by 25 m (y direction) by 10 m (z direction) and have been defined on account of the data grade distribution and of the block-support variance for different scenarios. Considering smaller blocks would not be helpful for the purposes of infill drill hole placement, because the blocks only intervene in the calculation of the objective function (Equation (1)), the components of which (Gi, Pi, Ci, Vi, and the weights w1,i, w2,i, w3,i, and w4,i) vary smoothly in space. For the same reason, the modified random search algorithm is scalable, with a numerical complexity and a memory footprint of the order of the number N of blocks; high-performance computing can be used to calculate the objective function should N be very large.
The blocks were classified into measured or indicated resources based on their simulated values and on probabilistic criteria. Following these steps, nine infill drill hole locations were determined in accordance with the methodology described in Section 2.7. The first application of the methodology considered only the iron grade as the variable of interest. In a second step, the iron grade was replaced by the recovered metal to facilitate a comparison of the changes resulting from the inclusion of the geo-metallurgical component. The next sections provide details on the improvements observed following the locations of these two sets of nine infill drill holes.
4. Results and Discussions
4.1. Simulation and Resource Classification
To conduct simulation, the initial step involved transforming the data into normal scores, followed by a variogram analysis in various directions [1]. The normal score method [2] has been employed to transform and back-transform data to and from the standard normal scale. One hundred realizations were constructed and back-transformed to the original scale (iron grade Fe (%) and recovered metal (%)) for further processing.
Subsequently, based on the simulated grade for each block and the average grade from the 100 realizations, an initial resource classification was carried out. Blocks in which more than 95% of the simulated grades fell within ±15% of the average grade were categorized as measured, while the other blocks received an indicated classification. One challenge associated with the use of this classification method, and the application of probabilistic criteria at a small scale, is the considerable variability it introduces into the classifications. To address this issue, and to achieve the ultimate classification of blocks, a moving window method was employed. Through the application of this method, the final classification for each block was established, taking into account the classifications of the neighboring blocks. A 3 × 3 × 3 block window was delineated, with the target block situated at the center of this grid and classified based on the neighboring blocks. This window systematically traversed the entire block model to establish the ultimate classification (Figure 7a). The same procedure was applied with the recovered metal instead of the iron grade (Figure 7b).
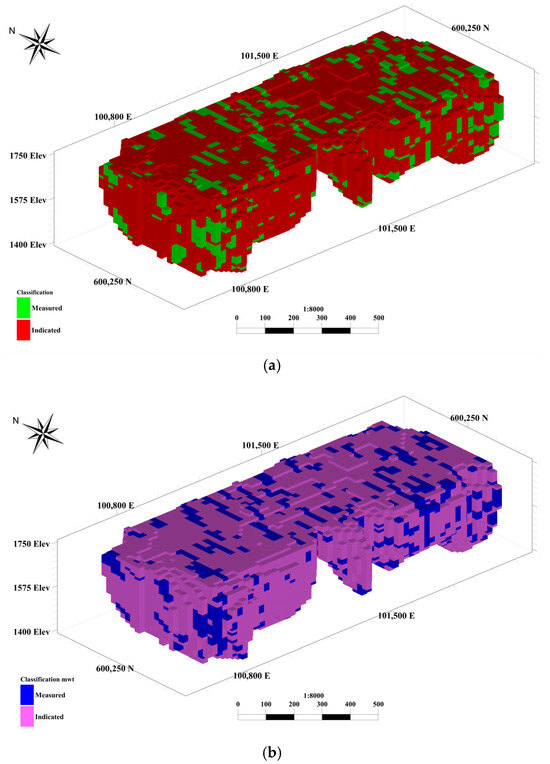
Figure 7.
Results of classifications based on (a) Fe grade (%); (b) recovered metal (%).
4.2. Infill Sampling Based on Iron Grade Data
Once the block classification and the corresponding simulated grade have been ascertained, this dataset is input into the optimization algorithm to pinpoint the drill hole locations. Notably, blocks classified as measured receive a reduced coefficient compared to the indicated blocks. This distinction is essential because, to improve classification, it is imperative to position the infill drill holes in regions characterized by an indicated classification. Each block value is ascertained according to its grade and classification. Consequently, in the process of locating infill drill holes, both the classification and the grade value play pivotal roles.
Near the initial drill holes, additional drill holes have been positioned to address the limitations posed by the relatively shallow depth of the initial ones. Following the placement of these infill drill holes and their integration with the initial set, a comparative analysis was conducted between the first scenario (lacking infill drill holes) and the second scenario (involving infill drill holes) (Table 2). In the second scenario, new measured resources have been generated adjacent to the original measured resources, thus avoiding artifacts and preserving continuity of the resource categories (Figure 8 and Figure 9).

Table 2.
Results of locating nine infill drill holes based on the iron grade data.
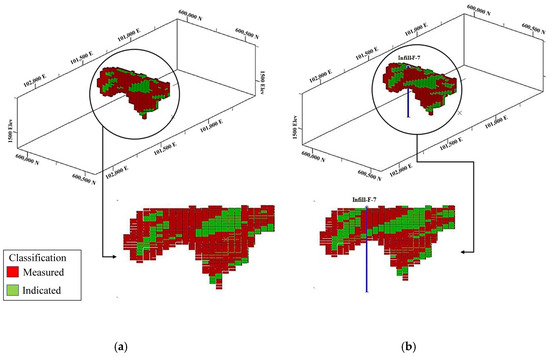
Figure 8.
Improvement of resource classification near infill drill holes. Red blocks are indicated resources and green blocks are measured resources: (a) first scenario; (b) second scenario.
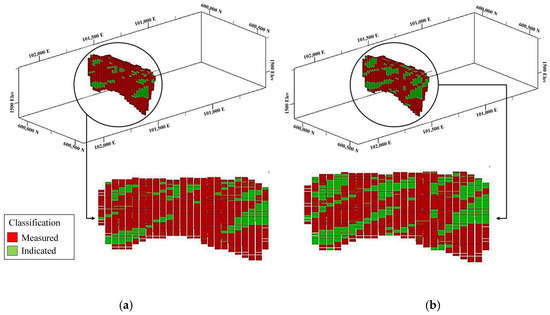
Figure 9.
Improvement of resource classification far from infill drill holes. Red blocks are indicated resources and green blocks are measured resources: (a) first scenario; (b) second scenario.
4.3. Infill Sampling Based on Recovered Metal Data
The aforementioned steps were replicated in a similar fashion for the recovered metal. In order to address the limited depth information from the initial drill holes, additional drill holes were initially positioned near the original ones. The outcomes of this process are presented in Table 3 and Figure 10 and Figure 11. Again, in the second scenario, new measured resources (blue blocks) are adjacent to the original measured resources, avoiding artifacts and preserving continuity of the resource categories.

Table 3.
Results of locating nine infill drill holes based on the recovered metal data.
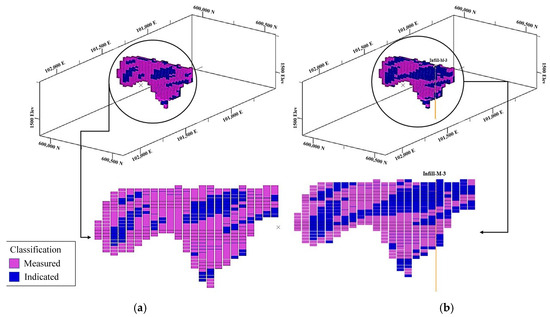
Figure 10.
Improvement of resource classification near infill drill holes. Purple blocks are indicated resources and blue blocks are measured resources: (a) first scenario; (b) second scenario.
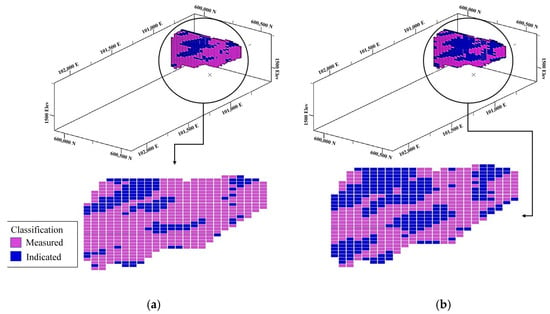
Figure 11.
Improvement of resource classification far from infill drill holes. Purple blocks are indicated resources and blue blocks are measured resources: (a) first scenario; (b) second scenario.
4.4. Comparison of Results
As per the defined block valuation parameters, the drill holes have been positioned in a manner that ensures consistency while also enhancing the block classification. Figure 12 compares the drill hole locations based on the iron grade and recovered metal data. The absence of common points between the infill drill holes for grade and recovered metal underscores the pivotal role of geo-metallurgical parameters in drill hole placement. This can be explained because the recovered metal essentially accounts not only for the grade, but for the recovery, the rock type, and the presence of deleterious elements, therefore its correlation coefficient with the iron grade is moderate (0.57) and the optimized drill hole layout changes significantly. As indicated in Table 4, the recovered metal also leads to a more substantial improvement compared to the iron grade in terms of classification. Therefore, by incorporating geo-metallurgical parameters alongside grades, it becomes possible to create an optimal drilling pattern that increases resources with reduced uncertainty by factoring in the recovered metal rate.
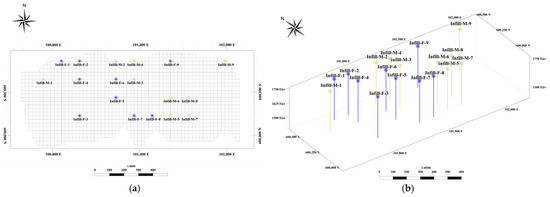
Figure 12.
Comparison between the locations of proposed infill drill holes. Blue: infill based on iron grade data. Orange: infill based on recovered metal data: (a) plan view; (b) 3D view.

Table 4.
Comparison between mineral resource classifications based on the iron grade and the recovered metal data.
4.5. Comparison of Optimization Algorithms
To facilitate a comparative evaluation with commonly used optimization methods for determining the placement of supplementary drill holes, a representative sub-model of the block model within the study area was selected. This test region incorporated both simulated drill holes and corresponding block data, enabling a controlled yet realistic environment for analysis. Three algorithms were implemented for comparison: the modified random search (MRS) algorithm, particle swarm optimization (PSO), and the genetic algorithm (GA). The PSO implementation was based on the PySwarms library, and the GA was constructed using the DEAP framework—both widely adopted in the optimization community and offering robust customization features.
While the aim was not to conduct an exhaustive hyperparameter tuning exercise for each algorithm, care was taken to select reasonable, literature-informed parameters that reflect standard practices. For PSO, parameters included a population of 30 particles, inertia weight of 0.7, cognitive and social coefficients of 1.5, and a maximum velocity of 0.2. The GA was initialized with 50 individuals, a crossover rate of 0.8, a mutation rate of 0.01, tournament selection of size 3, and elitism preserving the top 2 individuals. These configurations align with typical values used in mining optimization and spatial search problems.
Over 1000 iterations, the performance was evaluated based on convergence speed and solution quality in reaching high objective function values. As shown in Figure 13, the MRS algorithm demonstrated faster convergence and superior solution quality in this particular use case. PSO and the GA exhibited slower progress in objective function improvements, which can be attributed in part to their population dynamics and sensitivity to initialization, especially in high-dimensional or rugged search spaces.
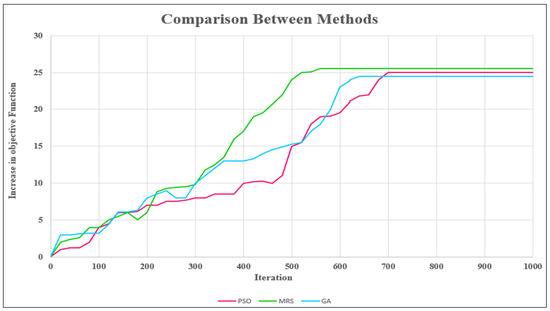
Figure 13.
Comparison between three common optimization algorithms.
However, it must be acknowledged that performance outcomes for population-based algorithms can vary significantly with different parameter choices, hybridization strategies, or problem structures and dimensionality. Therefore, the results presented here—where the modified random search (MRS) algorithm outperformed PSO and the GA in terms of convergence speed and solution quality—should not be interpreted as evidence of the general inferiority of these population-based methods. Instead, they highlight the suitability of the MRS for the specific characteristics of the problem addressed in this study, including the spatial continuity of the deposit, the limited number of infill drill holes, and the nature of the optimization objective. Further research should involve deeper tuning, hybrid strategies, or problem-specific adaptations of PSO and the GA to enhance their performance.
Following the identification of the most suitable algorithm for our use case, we compared the modified random search algorithm with its unmodified counterpart. As detailed in earlier sections, the standard RS may tend to over-exploit specific regions of the search space and is prone to premature convergence. Our modifications aimed to improve the global search capabilities and to ensure a more uniform spatial distribution of drill hole placements. This is especially important for infill drilling, where spatial redundancy and over-sampling of high-grade clusters can lead to misleading classifications.
The comparison (Figure 14 and Figure 15) illustrates that the unmodified RS algorithm heavily favored one corner of the study area, with high uncertainty and proximal high-grade drill holes, resulting in clustered placements. By contrast, the modified version sampled across broader regions, placed drill holes with more spatial dispersion, and led to improved classification upgrades across the deposit. These results further support the utility of the MRS for dynamic, spatially aware drill hole planning.
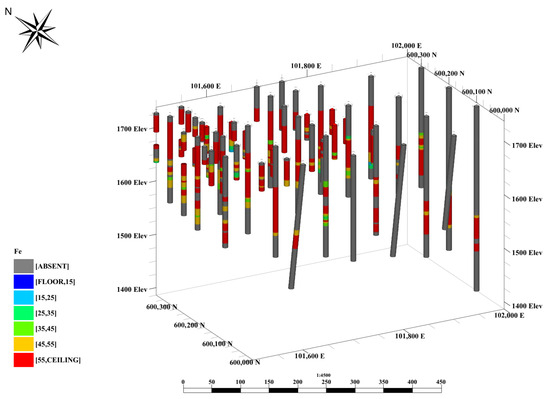
Figure 14.
3D views of selected drill hole data.
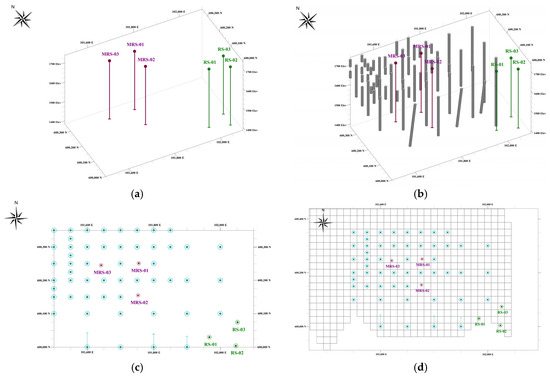
Figure 15.
3D representations (a,b) of drill holes positioned using the RS (green) and the MRS (purple). Position of the drill holes relative to the previous drill holes (c) and to the block model (d).
4.6. Validation
For validation, 25 drill holes were planned and incorporated in a regular 5 × 5 grid configuration, as depicted in Figure 16. Next, a random selection process was employed to remove five drill holes, while the remaining drill holes were used as an input for the proposed algorithm, as illustrated in Figure 17.
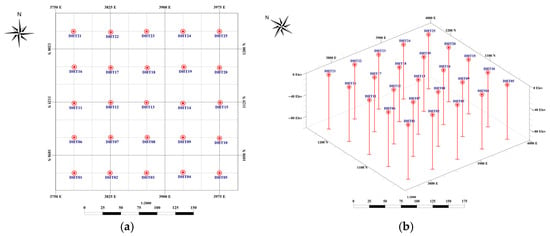
Figure 16.
Synthetic drill holes for validation: (a) plan view; (b) 3D view.
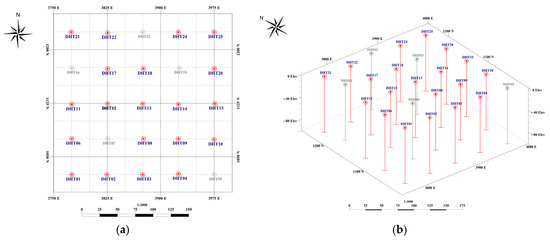
Figure 17.
Selection of five drill holes (gray) to be removed from the database: (a) plan view; (b) 3D view.
It was anticipated that the omission of drill holes in specific areas would lead to a deterioration in the classification and the discontinuity of the resource classes in those regions. As a result, the algorithm was expected to recommend new drill hole locations around the omitted ones. After the algorithm positioned the drill holes, it was observed (as depicted in Figure 18) that the recommended drill holes were accurately situated in the vicinity of the excluded drill holes, confirming the algorithm’s effectiveness.
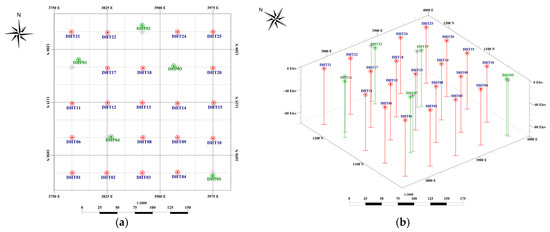
Figure 18.
Location of new drill holes (green) by the proposed algorithm: (a) plan view; (b) 3D view.
5. Conclusions
The findings outlined in this paper demonstrate that the developed algorithm is successful in the placement of infill drill holes. Despite the limited number of drill holes taken into account, the enhancement achieved in mineral resource classification is substantial. This model is consistent with the established objective of attaining optimal outcomes with a minimal number of drill holes. Moreover, the enhancement in the mineral resource classification coincides with the preservation of the spatial continuity of the resource categories, which has been achieved by introducing a control component into the objective function.
The traditional random search algorithm offers the advantage of simplicity in execution while delivering the desired outcomes. However, owing to its stochastic nature and the abundance of potential solutions, it often entails prolonged processing times. Modifications to the algorithm were introduced with the objective of expediting the identification of optimal solutions within a condensed timeframe, encompassing all potential scenarios. The utilization of Python 3.10 code for optimization has significantly contributed to this time reduction.
Furthermore, the incorporation of a geo-metallurgical parameter (recovered metal) as a supplementary variable alongside a primary variable (iron grade) represents an innovative approach, signifying the consideration of mineral processing perspectives in drill hole placement.
To further enhance this method, it is recommended to leverage an extensive database encompassing additional geo-metallurgical and geological variables. The objective function can be enriched to include all these variables and geostatistical co-simulation can be used to construct realizations that reproduce not only the spatial structure of each variable, but also their cross-correlations.
Author Contributions
Conceptualization, M.H.A., O.A., and X.E.; methodology, M.H.A., O.A., and X.E.; formal analysis, M.H.A.; investigation, M.H.A.; writing—original draft preparation, M.H.A.; writing—review and editing, X.E.; supervision, O.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Agency for Research and Development of Chile, grant number ANID PIA AFB230001.
Data Availability Statement
The data that support this study are not publicly available due to limitations imposed by the source of the data. We were unable to obtain permission to share the data from the data owner.
Acknowledgments
The authors acknowledge two anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Abzalov, M. Applied Mining Geology; Springer: New York, NY, USA, 2016. [Google Scholar]
- Rossi, M.E. Uncertainty and risk models for decision-making processes. In Proceedings of the 28th Symposium on Application of Computers and Operations Research to the Minerals Industry, Perth, WA, Australia, 2–4 December 2019; Dagdelen, K., Ed.; Colorado School of Mines: Golden, CO, USA, 1999; pp. 185–195. [Google Scholar]
- White, M.E.; Harrington, I. Feasibility studies–Scope and accuracy. In Mineral Resource and Ore Reserve Estimation: The AusIMM Guide to Good Practice; Australasian Institute of Mining and Metallurgy: Melbourne, Australia, 2014; pp. 507–518. [Google Scholar]
- Minnitt, R.C.A. Sampling: The impact on costs and decision making. J. S. Afr.Inst. Min. Metall. 2007, 107, 451–462. [Google Scholar]
- Dailami, K.; Nasriani, H.R.; Sajjadi, S.A.; Rafiee, M.R.; Whitty, J.; Francis, J. Optimizing the ultimate recovery by infill drilling using streamline simulation. Acta Sci.–Technol. 2020, 42, 1–9. [Google Scholar] [CrossRef]
- Soltani-Mohammadi, S.; Safa, M.; Sohrabian, B.J. Reducing uncertainty in mineralization boundary by optimally locating additional drill holes through particle swarm optimization. Nat. Resour. Res. 2021, 30, 2067–2083. [Google Scholar] [CrossRef]
- Fatehi, M.; Asadi, H.H.; Hossein Morshedy, A. 3D Design of optimum complementary boreholes by integrated analysis of various exploratory data using a sequential-MADM approach. Nat. Resour. Res. 2020, 29, 1041–1061. [Google Scholar] [CrossRef]
- Soltani-Mohammadi, S.; Hezarkhani, A. Optimum locating of additional drillholes to optimize the statistical value of information. J. Min. Metall. 2013, 49A, 21–29. [Google Scholar]
- Dirkx, R.; Dimitrakopoulos, R. Optimizing infill drilling decisions using multi-armed bandits: Application in a long-term, multi-element stockpile. Math. Geosci. 2018, 50, 35–52. [Google Scholar] [CrossRef]
- Caers, J.; Scheidt, C.; Yin, Z.; Wang, L.; Mukerji, T.; House, K. Efficacy of information in mineral exploration drilling. Nat. Resour. Res. 2022, 31, 1157–1173. [Google Scholar] [CrossRef]
- Hossein-Morshedy, A.; Khorram, F.; Emery, X. A multi-objective approach for optimizing the layout of additional boreholes in mineral exploration. Minerals 2023, 13, 1252. [Google Scholar] [CrossRef]
- Silva, D.S.F. Mineral Resource Classification and Drill Hole Optimization Using Novel Geostatistical Algorithms with A Comparison to Traditional Techniques. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2015. [Google Scholar]
- Cuba, M.A.; Boisvert, J.B.; Deutsch, C.V. Evaluation of infill drilling in the SLM framework. In CCG Annual Report 14; University of Alberta: Edmonton, AB, Canada, 2012. [Google Scholar]
- Soltani, S.; Safa, M. Optimally locating additional drill holes to increase the accuracy of ore/waste classification. Trans. Inst. Min. Metall. Sect. A: Min. Technol. 2015, 124, 213–221. [Google Scholar] [CrossRef]
- Sabourin, R.L. Application of a geostatistical method to quantitatively define various categories of resources. In Geostatistics for Natural Resources Characterization; Verly, G., David, M., Journel, A.G., Maréchal, A., Eds.; Springer: Dordrecht, The Netherlands, 1984; pp. 201–215. [Google Scholar]
- Dutaut, R.; Marcotte, D. A new semi-greedy approach to enhance drillhole planning. Nat. Resour. Res. 2020, 29, 3599–3612. [Google Scholar] [CrossRef]
- Diehl, P.; David, M. Classification of ore reserves/resources based on geostatistical methods. C. Bull. 1982, 75, 838. [Google Scholar]
- Scheck, D.E.; Chou, D.R. Optimum locations for exploratory drill holes. Int. J. Min. Eng. 1983, 29, 343–355. [Google Scholar] [CrossRef]
- Gershon, M.; Allen, L.E.; Manley, G. Application of a new approach for drillholes location optimization. Int. J. Surf. Min. Reclam. Environ. 1988, 2, 27–31. [Google Scholar] [CrossRef]
- Barnes, R.J. Sample design for geologic site characterization. In Geostatistics; Armstrong, M., Ed.; Springer: Dordrecht, The Netherlands, 1989; pp. 809–822. [Google Scholar]
- Hossein Morshedy, A.; Memarian, H. A novel algorithm for designing the layout of additional boreholes. Ore Geol. Rev. 2015, 67, 34–42. [Google Scholar] [CrossRef]
- Delmelle, E.M.; Goovaerts, P. Second-phase sampling designs for non-stationary spatial variables. Geoderma 2009, 153, 205–216. [Google Scholar] [CrossRef]
- Goria, S.; Armstrong, M.; Galli, A. Quantifying the impact of additional drilling on an open-pit gold project. In Proceedings of the Annual Conference of the International Association for Mathematical Geology, IAMG2001, Cancun, Mexico, 6–12 September 2001. [Google Scholar]
- Dimitrakopoulos, R.; Jewbali, A. Joint stochastic optimisation of short and long term mine production planning: Method and application in a large operating gold mine. Min. Technol. 2013, 122, 110–123. [Google Scholar] [CrossRef]
- Kumral, M.; Ozer, U. Planning additional drilling campaign using two-space genetic algorithm: A game theoretical approach. Comput. Geosci. 2013, 52, 117–125. [Google Scholar] [CrossRef]
- Soltani-Mohammadi, S.; Safa, M.; Mokhtari, H. Comparison of particle swarm optimization and simulated annealing for locating additional boreholes considering combined variance minimization. Comput. Geosci. 2016, 95, 146–155. [Google Scholar] [CrossRef]
- Fatehi, M.; Asadi Haroni, H.; Hossein Morshedy, A. Designing infill directional drilling in mineral exploration by using particle swarm optimization algorithm. Arab. J. Geosci. 2017, 10, 487. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N. Optimal location of additional exploratory drillholes using a fuzzy-artificial bee colony algorithm. Arab. J. Geosci. 2017, 10, 213. [Google Scholar] [CrossRef]
- Aspie, D.; Barnes, R.J. Infill-sampling design and the cost of classification errors. Math. Geol. 1990, 22, 915–932. [Google Scholar] [CrossRef]
- Pilger, G.G.; Costa, J.F.C.L.; Koppe, J.C. Additional samples: Where they should be located. Nat. Resour. Res. 2001, 10, 197–207. [Google Scholar] [CrossRef]
- Hossein Morshedy, A.; Torabi, S.A.; Memarian, H. A new method for 3D designing of complementary exploration drilling layout based on ore value and objective functions. Arab. J. Geosci. 2015, 8, 8175–8195. [Google Scholar] [CrossRef]
- Boucher, A.; Dimitrakopoulos, R.; Vargas-Guzmán, J. Joint simulations, optimal drillhole spacing and the role of the stockpile. In Geostatistics Banff 2004; Leuangthong, O., Deutsch, C.V., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 35–44. [Google Scholar]
- Verly, G.; Parker, H.M. Conditional simulation for mineral resource classification and mining dilution assessment from the early 1990s to now. Math. Geosci. 2021, 53, 279–300. [Google Scholar] [CrossRef]
- Levinson, Z.; Dimitrakopoulos, R. A reinforcement learning approach for selecting infill drilling locations considering long-term production planning in mining complexes with supply uncertainty. Min. Technol. 2024, 133, 176–187. [Google Scholar] [CrossRef]
- Williams, S.R.; Richardson, J.M. Geometallurgical mapping: A new approach that reduces technical risk geometallurgical mapping. In Proceedings of the 34th Annual Canadian Mineral Processors Meeting; Canadian Institute of Mining, Metallurgy and Petroleum: Ottawa, ON, Canada, 2004; pp. 1–13. [Google Scholar]
- Keeney, L. The Development of a Novel Method for Integrating Geometallurgical Mapping and Orebody Modelling. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2010. [Google Scholar]
- Ramos, G.Z. Hybrid Objective Function Applied to Optimize Infill Sampling Location. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2022. [Google Scholar]
- Su, S.; Schulze-Riegert, R.; Mustapha, H.; Lang, P.; Kada Kloucha, C. Artificial intelligence for infill well placement and design optimization in multi-layered/stacked reservoirs under subsurface uncertainty. In Abu Dhabi International Petroleum Exhibition and Conference; Society of Petroleum Engineers: Houston, TX, USA, 2021; p. D021S027R003. [Google Scholar]
- Tang, E.; Zhang, J.; Xia, A.; Jin, Y.; Li, L.; Chen, J.; Sun, X. Infill well placement optimization for polymer flooding in offshore oil reservoirs via an improved Archimedes optimization algorithm with a Halton sequence. Energies 2024, 17, 5552. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithm in Search, Optimization and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Morosov, A.L.; Bratvold, R.B. Drilling-campaign optimization using sequential information and policy analytics. SPE J. 2021, 26, 3609–3625. [Google Scholar] [CrossRef]
- Hall, T.; Scheidt, C.; Wang, L.; Yin, Z.; Mukerji, T.; Caers, J. Sequential value of information for subsurface exploration drilling. Nat. Resour. Res. 2022, 31, 2413–2434. [Google Scholar] [CrossRef]
- Caers, J. Modeling Uncertainty in the Earth Sciences; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Meinert, L.D.; Robinson, G.R., Jr.; Nassar, N.T. Mineral resources: Reserves, peak production and the future. Resources 2016, 5, 14. [Google Scholar] [CrossRef]
- Silva, D.S.F.; Boisvert, J.B. Mineral resource classification: A comparison of new and existing techniques. J. S. Afr. Inst. Min. Metall. 2014, 114, 265–273. [Google Scholar]
- Owusu, S.K.A.; Dagdelen, K. Critical review of mineral resource classification techniques in the gold mining industry. In Mining Goes Digital; Mueller, C., Assibey-Bonsu, W., Baafi, E., Dauber, C., Doran, C., Jaszczuk, M.J., Nagovitsyn, O., Eds.; CRC Press: Boca Raton, FL, USA, 2019; pp. 201–209. [Google Scholar]
- Stephenson, P.R.; Allman, A.; Carville, D.P.; Stoker, P.T.; Mokos, P.; Tyrrell, J.; Burrows, T. Mineral resource classification—It’s time to shoot the spotted dog! In Proceedings of the Sixth International Mining Geology Conference; The Australasian Institute of Mining and Metallurgy: Melbourne, Australia, 2006; pp. 91–96. [Google Scholar]
- Mery, N.; Maleki, M.; País, G.; Molina, A.; Cáceres, A.; Emery, X. Fuzzy classification of mineral resources: Moving towards overlapping categories to account for geological, economic, metallurgical, environmental, and operational criteria. Nat. Resour. Res. 2025, 34, 1271–1299. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; pp. 1942–1948. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the First International Conference on Genetic Algorithms; Grefenstette, J.J., Ed.; Taylor & Francis: Boca Raton, FL, USA, 1985; pp. 93–100. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- De Jong, K.A. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Stützle, T. Automatic algorithm configuration based on local search. In Association for the Advancement of Artificial Intelligence; AAAI: Washington, DC, USA, 2007; pp. 1152–1157. [Google Scholar]
- Spall, J.C. Stochastic optimization. In Handbook of Computational Statistics: Concepts and Methods; Gentle, J., Härdle, W., Mori, Y., Eds.; Springer: Heidelberg, Germany, 2012; pp. 173–201. [Google Scholar]
- Masri, S.F.; Bekey, G.A.; Safford, F.B. A global optimization algorithm using adaptive random search. Appl. Math. Comput. 1980, 7, 353–375. [Google Scholar] [CrossRef]
- Zagré, G.E.; Marcotte, D.; Gamache, M.; Guibault, F. New tabu algorithm for positioning mining drillholes with blocks uncertainty. Nat. Resour. Res. 2019, 28, 609–629. [Google Scholar] [CrossRef]
- Nayak, S. Fundamentals of Optimization Techniques with Algorithms; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Blackwell, G.H.; Anderson, M.; Ronson, K. Simulated grades and open pit mine planning–Resolving opposed positions. In Proceedings of the 28th Symposium on Application of Computers and Operations Research to the Minerals Industry, Perth, WA, Australia, 2–4 December 2019; Dagdelen, K., Ed.; Colorado School of Mines: Golden, CO, USA, 1999; pp. 205–215. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).