Abstract
Metallic minerals and some nonmetallic deposits (such as gas hydrate and natural gas) exhibit significant resistivity contrast with their surrounding rocks. Therefore, magnetotelluric (MT) sounding, which is highly sensitive to low-resistivity anomalies, offers a unique advantage in identifying these mineral resources. For metallogenic systems in sedimentary environments with approximately layered structures, we propose the Dynamic Error Bat Algorithm (DEBA), which integrates the cooling strategy, the dynamized fit error function, and the Bat Algorithm. DEBA enhances the breadth of global exploration in the early iteration stages while focusing on the depth of local exploitation in the later stages, yielding a more effective fitting outcome and better identification of electrical interfaces. Validity and noise immunity tests on typical synthetic models prove the robustness of DEBA. For broadband MT stations from the central Songliao Basin, we observed that the model derived from three-dimensional inversion did not provide an ideal layering effect for the shallow structure. Notably, the apparent resistivity and phase curves of these MT stations are similar, suggesting that the shallow structure in the study area has approximately one-dimensional (1-D) features, a conclusion that was further supported by phase tensor analysis. To gain a clearer understanding of the shallow structure, we applied DEBA to perform an averaged 1-D inversion. The subsequent results reveal a low-resistivity layer, which may be attributed to metallic sulfides or saline fluids.
1. Introduction
Over the past few years, the relationship between metallogenic systems and the multi-scale electrical structures revealed through magnetotelluric (MT) sounding in the lithosphere has become a key focus and a frontier in academic research. Beyond metallic mineral deposits, MT has also proven valuable in the exploration of nonmetallic resources, such as gas hydrates and natural gas [1,2,3,4,5]. Correspondingly, the inversion theories of MT, encompassing one-dimensional (1-D), two-dimensional (2-D), and three-dimensional (3-D) approaches, have undergone substantial development [6,7,8,9,10].
The geological background of Songliao Basin (SLB), northeast China, is closely related to magmatic activity and a hydrothermal system, which provides favorable conditions for the formation of metal minerals, oil, and gas, as well as hydrothermal fluids [11,12]. These resources typically exhibit significant electrical contrasts with the surrounding strata, making them theoretically detectable via MT [13,14,15]. Interestingly, during our investigation, we found that data from five adjacent broadband magnetotelluric (BBMT) stations in the central SLB exhibited high similarity. Phase tensor analysis further indicated that the shallow subsurface structure in this region is approximately 1-D. Due to the strong 1-D characteristics of the sedimentary layers and basement in the central SLB, our 3-D inversion result did not produce an optimal stratification resolution in the upper crust, potentially leading to significant depth estimation errors for anomalies. Therefore, in regions with relatively simple lateral structures, such as when identifying mineral layer interfaces and evaluating sediment thickness, a fast, high-resolution 1-D inversion approach is essential to obtain a clearer resistivity structure.
However, in the process of selecting and testing 1-D inversion methods, we encounter the following challenges. (1) Traditional linear inversion methods, while advantageous in terms of efficiency and smoothness, tend to hinge excessively on initial model selection, leading to the risk of falling into local minima, with results that may be overly smooth and fail to clearly resolve resistivity interfaces [16]. (2) The application of deep learning to inversion offers faster computation and lower dependence on prior knowledge, but it requires large amounts of high-quality data for training. Without sufficient training data, generalization ability may be limited, and performance may be poor under geological conditions not covered by the training data [17,18]. (3) Global optimization algorithms, such as Simulated Annealing (SA) and the Bat Algorithm (BA), have been applied to inversion tasks [19,20,21,22,23]. These algorithms avoid the constraints of the initial model and Jacobi partial derivative matrix calculations. Nevertheless, they often require careful tuning of multiple parameters to achieve optimal performance [24].
To address these issues, based on BA and SA, the Dynamic Error Bat Algorithm (DEBA) is presented for MT 1-D inversion in this study, which aims to improve the ability to find the global optimal solution by effectively balancing global exploration and local exploitation. Additionally, DEBA incorporates the dynamic fit error function to further enhance the fitness and to improve the accuracy of electrical mutation interface recognition. Moreover, the cooling search mechanism reduces the number of parameters that require tuning, thereby lowering the complexity of practical applications. DEBA is effective, exhibits low noise sensitivity, and can identify electrical mutation interfaces, as demonstrated by the numerical experiments.
Finally, BBMT data from SLB, which shows 1-D features, were successfully inverted using DEBA. We reveal the characteristics of the low-resistivity anomaly in the upper crust of the central SLB and, combined with the petrophysical analysis, put forward the hypothesis that it may be related to metal sulfide deposits or saline fluids. These results, along with DEBA, may provide valuable geophysical support and insights for mineral exploration, sediment thickness evaluation, and oil and gas assessment.
2. Materials and Methods
2.1. Magnetotelluric Sounding Method
Using the natural alternating electromagnetic field (with a frequency range of – Hz), MT is a passive source geophysical method for investigating the electrical structure of the subsurface [25,26]. Due to the skin depth effect, electromagnetic fields of different frequencies penetrate to varying depths in subsurface media. Consequently, the frequency response of the magnetotelluric field observed at the surface reflects the resistivity distribution of the underlying medium. In magnetotelluric sounding work, the observable data on the surface are an orthogonal electric field (, ) and a magnetic field (, ) [27]. The electromagnetic field is connected to the Earth’s interior electrical structure, demonstrated through Equation (1):
Entries and , represent the diagonal and off-diagonal impedance elements, respectively, which provide information regarding resistivity in the deep Earth.
The method we use to estimate the averaged 1-D model is similar to Berdichevsky averaging but redefined with another rotational invariant, which is the sum of the squared elements of the impedance tensor [28].
where is the impedance used for 1-D inversion of the measured data in this study, which proves to be advantageous in terms of distortion resistance and smoothness [29,30].
In the case of the 1-D n-layered model, the ground impedance can be calculated through Equation (3):
where is the impedance and is the characteristic impedance of the m-th layer (). is the magnetic reflection coefficient at the bottom interface of the m-th layer. The term represents the complex wave number, where is the electrical resistivity of the m-th layer. is the thickness of the m-th layer, is the imaginary unit, is the angular frequency, and is the magnetic permeability of free space.
The apparent resistivity is determined by the impedance magnitude, which encapsulates the electrical properties of the subsurface within the penetration depth of the electromagnetic field at a given frequency. It is calculated using the following formula:
The impedance phase represents the phase difference between the horizontal electric field and the perpendicular horizontal magnetic field at the surface. It provides insights into the electrical properties of the subsurface. The formula for calculating the impedance phase is
herein, and represent the imaginary and real parts of .
Utilizing the apparent resistivity and phase, a reasonable geoelectric model that is consistent with the measured data can be obtained through MT inversion [31].
2.2. BA Principle
Bats use echolocation to detect prey, with each bat flying randomly at velocity and position [19]. The position (global exploration solution) and velocity of the bat in the t-th generation are modeled through
where represents the velocity increment of bat and as well as are constants. is a random number, and is the current global best position.
The local exploitation solution is generated around :
where is a random number, while is the average loudness of all of the bats in the -th generation.
Because the search space narrows as the bat approaches its prey, it will progressively drop the acoustic loudness while raising the acoustic rate to comprehend the orientation of the target prey swiftly and dynamically. With the change in position, according to conventional BA theory [19], the acoustic loudness and rate for the bat are updated though the following equations:
where is the loudness attenuation coefficient, is the rate enhancement coefficient, and represents the initial rate of bat .
2.3. Improved DEBA Inversion
Global exploration and local exploitation are influenced by loudness. More global exploration is performed in the early stages of the optimization process when loudness is high, while more local exploitation occurs in the later stages as loudness gradually decreases. However, the means of updating the loudness in Equation (10) tends to cause convergence that is too fast in the early stage and fall into local minima. DEBA uses Equation (12) to iterate the loudness to ensure that a balance is achieved between global exploration and local exploitation, thus finding the global optimal solution.
By incorporating the cooling search mechanism of SA into the optimization process, DEBA aims to address the scenario in which classic BA is prone to premature convergence. We obtain the function (Figure 1) using four control points through piecewise cubic Hermite interpolation as an iterative formula for loudness . The function is monotonically decreasing and can be divided into four segments: The first segment, where the dependent variable exceeds 1, represents that DEBA exclusively performs global exploration. The second segment, ranging from 1 to 0.5, indicates that the global exploration probability surpasses local exploitation. The third segment, falling between 0.5 and 0.1, signifies that the global exploration probability is less than local exploitation. The fourth segment, when the dependent variable is less than 0.1, primarily focuses on local exploitation. This makes it possible for the bat population to undergo more mutation and exploration in the early generations, increasing the capacity to escape local minima, while, in the later generations, the algorithm concentrates more on local exploitation and convergence [32].
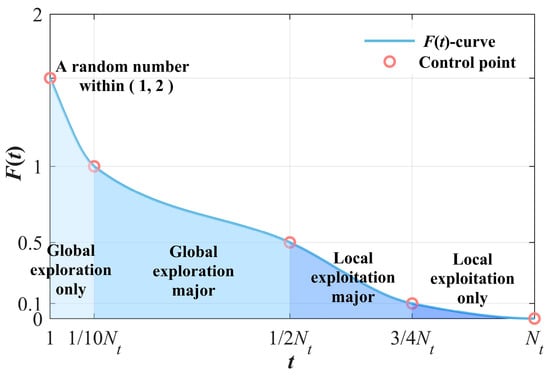
Figure 1.
The cooling function , here the generation number .
Rate controls the velocity of convergence to the optimal solution; the slower the algorithm searches and the more fully, the faster and the more likely it is to fall into local minima. We want to be slow in the early stages to search extensively and fast in the later stages to develop quickly, so we make take a random value within and after the test.
Essentially, the objective of MT inversion is to minimize the objective function, which in this study is the fit error function . Nevertheless, due to the skin effect of electromagnetic waves, the apparent resistivity and phase at different frequencies exhibit varying sensitivities to the parameters of each stratigraphic layer. Extensive inversion results indicate that fitting the low-frequency components of the apparent resistivity and phase curves poses a greater challenge than fitting their high-frequency counterparts. To address this issue, our inversion approach integrates a dynamic fit error function (Equation (13)). This function consists of sub-errors corresponding to different frequencies, with their weights dynamically adjusted by a factor based on the ratio of each sub-error to the total error. This adaptive weighting enhances the inversion’s sensitivity to low-frequency components, ensuring a more accurate and robust fitting process. In DEBA, the relative position (the fit error function) of the t-th generation of bats to the prey is defined as
where is the number of electromagnetic field periods , is the apparent resistivity, is the phase, and and are determined by
where is calculated by plugging and into Equation (13).
Because DEBA takes the dynamical fit error function, to facilitate visual comparison of data fits during the DEBA and BA inversion processes, we employed a uniform formula for calculating Uniform Fit Error (UFE) used in the figures:
where and denote data obtained through inversion calculation and and denote synthetic or measured data. In short, is used in the inversion process, while UFE is used in the interpretation of the figures.
Assuming an -layered geoelectric model, there are inversion parameters to be inverted ( resistivities and thicknesses of each layer), denoted as and , respectively. These parameters are recorded in terms of the position . With a bat population size of , the bat colony will make moves, generating a total of sets of inversion parameters. The inversion process is shown in Figure 2.
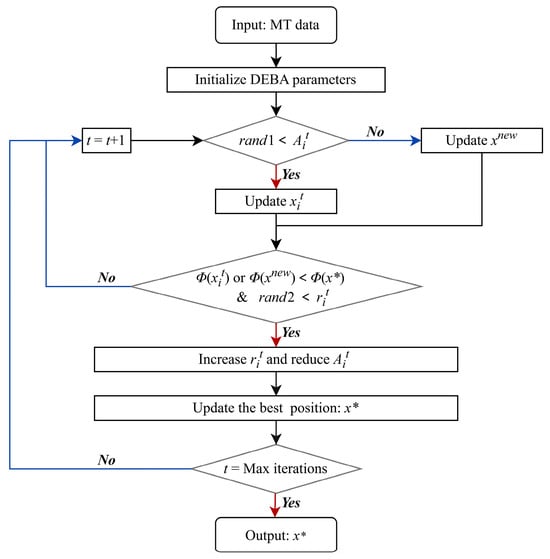
Figure 2.
Flowchart of MT 1-D inversion based on DEBA. MT data include period, apparent resistivity, and phase. and are random numbers within [0, 1]. is the current global best solution and is the local exploitation solution. The parameters of DEBA include bat population size , iteration number , fit error function , bat position , velocity , acoustic frequency , loudness and rate mentioned above.
3. Model Test
3.1. Numerical Test
This study rigorously evaluated the performance and effectiveness of DEBA by testing it against three representative geoelectric models. A systematic comparison was conducted between DEBA, conventional BA, and OCCAM inversion methods. In the synthetic model calculations, the period ranging from 320 Hz to 1000 s was divided into 19 intervals with equal logarithmic spacing. The apparent resistivity and phase data were obtained through 1-D MT forward modeling, with 5% Gaussian noise added to simulate field data. During DEBA and BA inversions, the search space was constrained within ±50% of the synthetic model parameters. For OCCAM inversion, the number of layers and their thicknesses in the initial model were set to be identical to those of the synthetic model, with an assumed resistivity of 100 Ω·m.
The six-layered geoelectric model named Model 1 was designed, with parameters illustrated in Figure 3c. It incorporates four fundamental electrical variations (descending –ascending, ascending–ascending, ascending–descending, and descending–descending). MT 1-D inversion for Model 1 was performed using DEBA, BA, and OCCAM, and the results (Figure 3) are analyzed as follows. First of all, as shown by the apparent resistivity–period curves (Figure 3a) and the phase–period curves (Figure 3b), even with the addition of 5% Gaussian noise, the three methods still fit the theoretical data, with smooth curves and minimal errors. Among them, DEBA exhibits the smallest error compared to BA and OCCAM. Secondly, a comparison of the inverted and theoretical models (Figure 3c) shows that while OCCAM and BA capture the correct electrical changes, these two methods fail to achieve sufficient accuracy in resistivity estimation. In contrast, DEBA closely matches the theoretical model, with only minor discrepancies in resistivity and depth. Although all three approaches provide reasonable fits to the apparent resistivity–phase curves, DEBA is closer to the global minimum. Consequently, DEBA outperforms BA and OCCAM in terms of both fitting accuracy and inversion quality. Thirdly, as indicated by the UFE curve (Figure 3d), DEBA effectively balances global exploration and local exploitation, as defined by Equation (16). During the first 10% of iterations, DEBA primarily focuses on global exploration, followed by a gradual reduction in the proportion of global search, with the final 25% dedicated to local refinement. In contrast, BA converges prematurely in the early iteration stages, leading to entrapment in local minima. Last but not least, in terms of computational effort, each iteration requires forward modeling calculations for all bat positions. Consequently, a full DEBA inversion process involves forward computations, where is the bat population size and is the number of iterations. The total number of forward modeling calculations typically ranges from to . Even on a standard personal computer, the total computation time generally falls within 0.1 to 100 s. For instance, in a typical three-layered geoelectric model with a standard configuration of 100 bats and 100 iterations, a single DEBA inversion run takes approximately one second. For the three complex models investigated in this study, the computation time ranges from several seconds to tens of seconds depending on model complexity (scaling with the number of bats and iterations from hundreds to thousands).
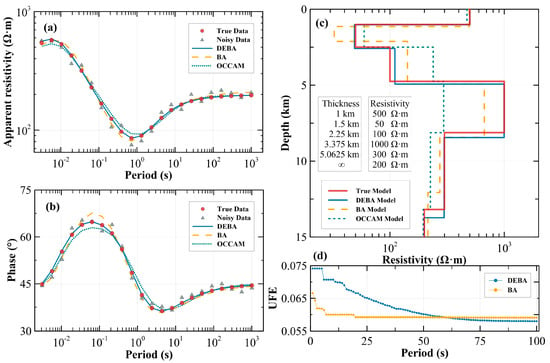
Figure 3.
Validity test of the DEBA using Model 1. The inversion results and their forward response using DEBA, OCCAM, and BA methods are compared. (a) Apparent resistivity–period curve; (b) phase–period curve; (c) true and inversion models; (d) UFE curve.
Because the presence of double low-resistivity layers poses a significant challenge in MT inversion, Model 2 was designed as a five-layered structure, with the second and fourth layers exhibiting low-resistivity characteristics. This model was specifically developed to evaluate DEBA’s capability in resolving low-resistivity anomalies. The model parameters are illustrated in Figure 4c. The inversion results for Model 2 demonstrate that all three methods achieve good fit to the apparent resistivity and phase curves (Figure 4a,b), and they successfully identify the two low-resistivity anomalies. However, BA and OCCAM exhibit better reconstruction of the first low-resistivity layer, while their resolution of the second low-resistivity layer is suboptimal, with discrepancies in both depth and resistivity values. In contrast, DEBA achieves the highest accuracy in recovering both depth and resistivity, indicating its superior performance in detecting double low-resistivity anomalies (Figure 4c).
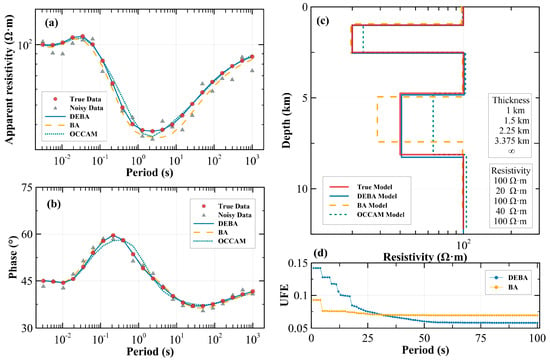
Figure 4.
Validity test of the DEBA using Model 2. The inversion results and their forward response using DEBA, OCCAM, and BA methods are compared. (a) Apparent resistivity–period curve; (b) phase–period curve; (c) true and inversion models; (d) UFE curve.
MT is generally more sensitive to low-resistivity structures, whereas resolving high-resistivity anomalies remains a challenge, particularly when multiple high-resistivity layers are present. To address this, Model 3 was constructed with a five-layered structure, where the second and fourth layers are high-resistivity zones. This model was used to assess DEBA’s ability to distinguish between double high-resistivity layers, with model parameters shown in Figure 5c. A comparative analysis of the inversion results for Model 3 (Figure 5) reveals strong agreement between the predicted and theoretical apparent resistivity and phase curves. Although BA successfully captures the general trend of electrical variations, its predicted resistivity and depth values deviate from those of the synthetic model. OCCAM accurately identifies the two high-resistivity layers, but its resistivity values remain imprecise. Specifically, for the first high-resistivity layer, the resistivity values obtained from both BA and OCCAM are slightly underestimated. For the second high-resistivity layer, BA overestimates the resistivity, while OCCAM underestimates it. In contrast, DEBA accurately reconstructs the synthetic model, demonstrating its superior capability in resolving double high-resistivity anomalies compared to BA and OCCAM.
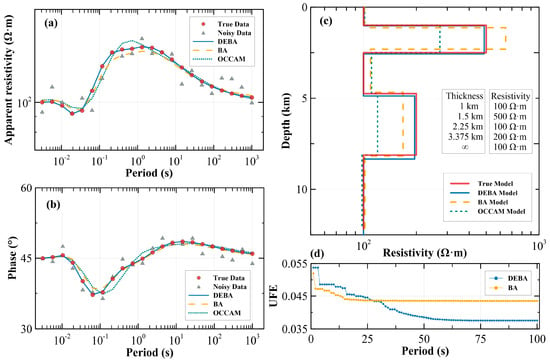
Figure 5.
Validity test of the DEBA using Model 3. The inversion results and their forward responses using DEBA, OCCAM, and BA methods are compared. (a) Apparent resistivity–period curve; (b) phase–period curve; (c) true and inversion models; (d) UFE curve.
3.2. Noise Sensitivity Test
The measured data inherently contain noise, which significantly impacts inversion accuracy. To assess the noise sensitivity of DEBA, after obtaining stable inversion results using data with 5% Gaussian noise, additional inversion tests were conducted on the synthetic data of Model 1 with progressively increased noise levels of 10%, 20%, and 30%. As illustrated in Figure 6, the fitting performance under varying noise levels is demonstrated, yielding final UFE values of 0.0602, 0.1388, and 0.2252, respectively. This suggests that increased noise adversely impacts the fitting accuracy, with larger noise levels resulting in poorer fits. Comparing the inversion results, the data with 5% noise (Figure 3c) and 10% noise (Figure 6a) exhibit satisfactory fitting to the synthetic model. However, the data affected by 20% noise (Figure 6b) can only invert the general trend of electrical changes in the model but failed to derive the correct resistivity and layer thickness. The inversion becomes notably more challenging with the addition of 30% Gaussian noise (Figure 6c), resulting in significant discrepancies from the synthetic model. In short, qualified inversion results can be obtained with noise below 10%, indicating that DEBA can be used for inversion of measured data.
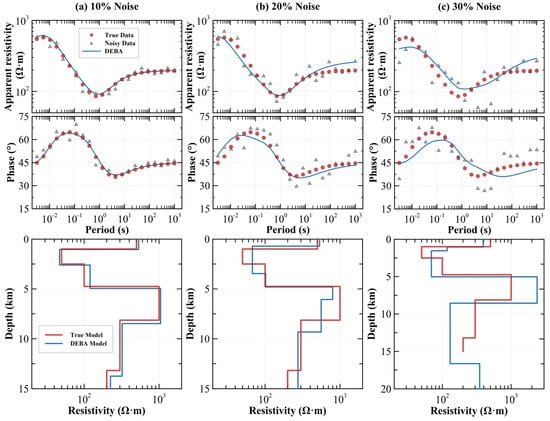
Figure 6.
Effects of different levels of Gaussian noise on DEBA. (a) 10% Gaussian noise test; (b) 20% Gaussian noise test; (c) 30% Gaussian noise test.
Overall, DEBA exhibited independence from the initial model and provided a more direct approach to achieving a globally optimal solution (validation of the forward code is given in Figure S1 of the Supplementary Material). The effectiveness and superiority of DEBA have been validated through synthetic model experiments and noise immunity tests. These results demonstrate that DEBA serves as a reliable and efficient method for high-precision identification of deep-seated geoelectric anomalies.
4. Evidence of Upper Crust Low-Resistivity Layers Beneath SLB
4.1. MT Data and Dimensionality Analysis
The study area is in the central depression of SLB (Figure 7), a major oil- and gas-producing region in northeast China with a typical composite structure of faults and depressions. SLB is a large intra-land rift basin that has developed since the Late Mesozoic period [33,34]. The BBMT data in the study area were collected in 2017 for more than 20 hours at each site.
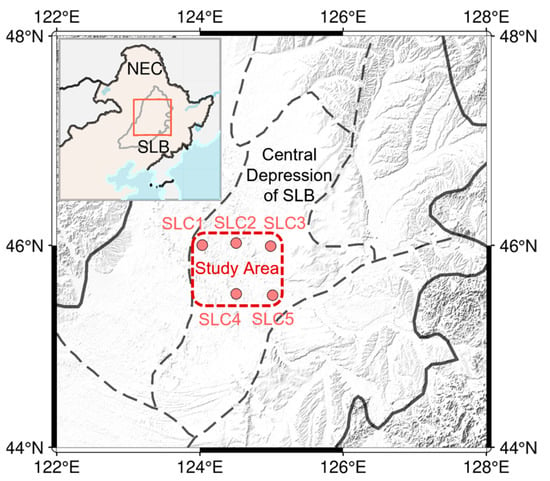
Figure 7.
Distribution of the BBMT stations in the central depression of SLB. BBMT stations (SLC1, SLC2, SLC3, SLC4, SLC5) are marked with light-red-filled circles. NEC: northeast China. SLB: Songliao Basin. The black solid lines represent the boundary of the SLB, while the black dashed lines denote the first-order structural boundaries within the basin [11].
An MT impedance phase tensor can qualitatively reflect the dimensionality of the geologic structure and the direction of the electrical main axes in the study area [35,36]. Figure 8 shows the results of the phase tensor analysis of the measurement stations at T = 0.01 s, 0.1 s, 1 s, 10 s, 100 s, and 1000 s, and the different colors represent the different 2-D deviation. For T < 10 s, the 2-D deviations of the measurement stations are very small, and the long and short axes of the ellipses are the same, which indicates that the subsurface medium is strongly one-dimensional and similar to the layer structure, the two-dimensionality of the measurement stations increases after T ≥ 10 s, and the three-dimensionality is more obvious after T ≥ 100 s. In general, the shallow part of the study area shows obvious one-dimensionality, whereas the deep medium has inhomogeneity, so MT 1-D inversion is suitable for imaging the upper crustal structure of the study area.
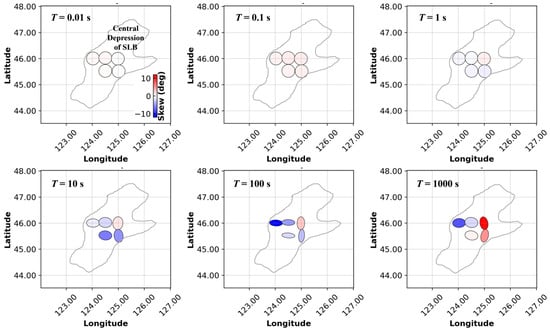
Figure 8.
Phase tensor analysis results for different periods. The long axis of the ellipse represents the direction of the electrical major axis; the color represents the degree of 2-D deviation. The gray outline represents the central depression of the SLB boundary [11].
Valid impedance ranging from 320 Hz to 1000 s was acquired after processing the raw data [37,38]. The high quality of the processed measured data is demonstrated by the smooth and continuous apparent resistivity and phase curves (see Figure 9). Our analysis of the processed data revealed that the apparent resistivity and phase curves from five BBMT stations within the study area exhibit similar trends. This consistency further supports the feasibility of performing an averaged 1-D inversion. Therefore, based on these observations, we proceeded with an averaged MT 1-D inversion to characterize the subsurface structure of the study area.
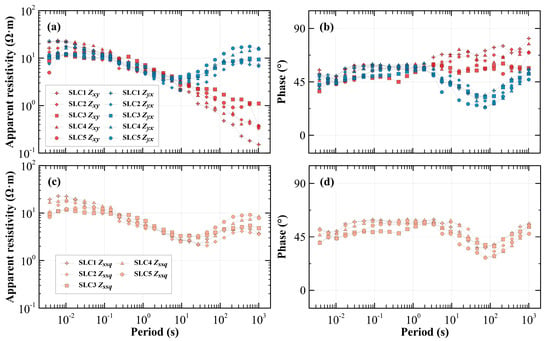
Figure 9.
Apparent resistivity and phase curves of five BBMT measurement stations. (a) Apparent resistivity–period curve calculated from and ; (b) Phase–period curve calculated from and ; (c) Apparent resistivity–period curve calculated from ; (d) Phase–period curve calculated from . The locations of the stations are shown in Figure 7.
4.2. Results
In the DEBA inversion, the stratigraphy was set to 19 layers, with the first layer having a thickness of 500 m. The thickness of subsequent layers increases progressively by a factor of 1.1. The search range for layer thickness was set to ±50%, while the resistivity search range was set to 0.1–1000 Ω·m. After obtaining reasonable results from preliminary tests, the search space was further refined, leading to the final inversion results. In the OCCAM inversion, the number of initial model layers was 14, the thickness of the first and second layers was 100 and 200 m, the third layer thickness was 500 m, the fourth to fourteenth layer thicknesses were sequentially increased by a factor of 1.1, and the initial resistivity was set to 100 Ω·m. The geometric mean of from all BBMT stations represents the 1-D average impedance of the study area [8,39]. The averaged apparent resistivity and phase are derived in terms of , while the apparent resistivity and phase of the measured data are derived in terms of each (see Figure 10a,b). The averaged 1-D resistivity model was generated using DEBA-based MT 1-D inversion applied to the averaged apparent resistivity and phase (Figure 10d). After the previous tensor analysis (see Figure 8), we find that the shallow part of the study area shows strong one-dimensionality, and the averaged resistivity is estimated to be 30 Ω·m. According to the calculation of skinning depth, the approximate bathymetry depth is 10–20 km when the period is less than 100 s. Therefore, for the 1-D inversion results, this paper discusses the upper crustal scales that are as shallow as 10 km only.
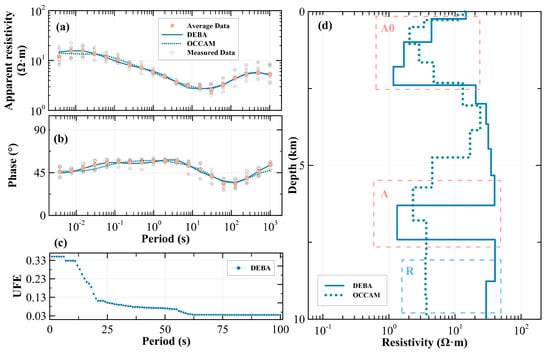
Figure 10.
Averaged 1-D inversion results of BBMT data in the study area. Measured data denote data from a single MT station, and average data denote the apparent resistivity and phase from . (a) Apparent resistivity–period curve; (b) Phase–period curve; (c) UFE curve of DEBA; (d) Average inversion models. A0, A, and R indicate three resistivity anomalies.
The inversion results for the study area are presented in Figure 10. Figure 10a,b display the apparent resistivity–period and phase–period curves for both the measured and inverted data. The averaged apparent resistivity and phase curves (Average Data) closely resemble those of the five individual BBMT measurement stations (measured data). With a small UFE, DEBA inversion data exhibit a strong fit to the average data. Figure 10d illustrates the averaged 1-D inversion models obtained using DEBA and OCCAM. Both models yield resistivity values ranging from 0.1 to 100 Ω·m, and their electrical structures exhibit a high degree of overlap, following a low–high–low resistivity distribution pattern. The DEBA model identifies two low-resistivity anomalies: one at a shallow depth of ~2.5 km (A0) and another at approximately 7 km (A). To verify these findings, we include the OCCAM model, as both inversion techniques identify comparable low-resistivity layers. The near-surface low-resistivity anomaly A0 (at depths shallower than 2.5 km) corresponds to a low shear-wave velocity zone [40], which we interpret as the sedimentary overburden of SLB [11]. The identification of resistivity of R is different between the two models, which may be because OCCAM, as a linear inversion method, effectively captures the overall resistivity trend but struggles to accurately resolve deep resistivity values. Additionally, the robustness of the single anomaly described above is demonstrated by the results of model perturbation analysis (Figure 11).
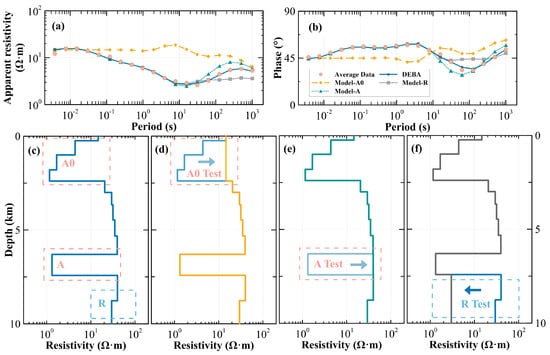
Figure 11.
Validation of resistivity anomalies in averaged 1-D DEBA inversion model. (a) Apparent resistivity–period curve; (b) Phase–period curve; (c) DEBA model; (d–f) indicate that model-A0, model-A, and model-R from the DEBA model are used to verify the reliability of resistivity anomalies A0, A, and R, respectively.
To verify the reliability of anomalies, we modified the DEBA model (Figure 11c) to create three new models for testing and analysis. Firstly, we constructed model-A0 (Figure 11d) by adjusting the resistivity of anomaly A0 in the DEBA model to 14.66 Ω·m. Subsequently, we conducted forward modeling of model-A0 to obtain corresponding apparent resistivity and phase curves. Through detailed comparison with the forward response of the original DEBA model, we observed significant differences in the curves, strongly confirming the reliability of anomaly A0. Next, we constructed model-A (Figure 11e) by uniformly adjusting the resistivity of anomaly A in the DEBA model to 40 Ω·m. Comparing forward response of Model-A with the DEBA model revealed significant differences at the tail of the curves, supporting the reliability of anomaly A. Furthermore, although both OCCAM and DEBA methods revealed electrical differences between anomalies A and R during inversion, there were discrepancies in the resistivity values obtained for R. To investigate this issue, we uniformly adjusted the resistivity of anomaly R in the DEBA model to 3 Ω·m, creating model-R (Figure 11f). Comparing the forward response of model-R with the DEBA model, we observed significant differences at the tail of the curves. This result not only confirmed the reliability of anomaly R but also indicated limitations on the thickness of anomaly A. Forward calculations for model-A0, model-A, and model-R show a significant deterioration in the apparent resistivity versus phase curve fit (Figure 11a,b), indicating that the low resistivity at two depths and the relatively high resistivity below 7.5 km are required by our observations at the same time. Through testing and analyzing the results, we verified the anomalies reliability from multiple perspectives (see Figures S2–S4 in the Supplementary Material for more validations).
4.3. The Potential Causes of Low-Resistivity Anomaly A
The low-resistivity anomalies in the crust can possibly be attributed to (1) metal sulfide deposits, (2) grain-boundary graphite films, (3) partial melting, and (4) saline fluids [2,41,42,43,44,45]. We analyzed the potential origin of the low-resistivity anomaly A based on the current geophysical and geochemical data in SLB. (1) The geological background of SLB is closely related to magmatic activity and hydrothermal systems, providing favorable conditions for the formation of metal sulfides. The basin has undergone complex tectonic evolution, including multiple phases of magmatic activity. These activities not only supplied heat for the formation of metal sulfides but also contributed to the necessary material sources. In addition, the extensive development of hydrothermal systems within the basin created an environment conducive to the precipitation of metal sulfides. The presence of faults provided pathways and space for the migration and concentration of metallogenic fluids, further promoting the local enrichment and mineralization of metal sulfides [11,12]. (2) Considering the multiple phases of magmatism and volcanism that have occurred in the study area [33,46], it seems improbable that the formation of A can be attributed to grain-boundary graphite films [47,48,49]. (3) Because electrical resistivity obtained from MT data of rocks is particularly sensitive to the presence of interconnected low-resistivity phases in rock volumes, these phases include aqueous fluids and partial melts [13]. If the rock is in a partially melting state with a high content of melt and substantial connectivity, the bulk resistivity of the rock will experience a significant reduction. Based on geothermal heat flow data calculations in the study area [50], the temperature corresponding to a depth of 7 km ranges from about 260 to 310 °C. However, it is crucial to note that the minimum temperature at which crustal materials can produce melt in the presence of water is approximately 700 °C [51]. Consequently, it can be reasonably inferred that the observed anomaly A cannot be attributable to partial melting. (4) Given that the upper crust operates within the brittle regime and typically experiences temperatures too low for metamorphic reactions to consume fluids, free fluids can persist in available pore spaces [48]. The presence of saline fluids is identified as the probable cause for the observed low resistivities in the upper crust [52,53]. We employed the modified Archie’s law to calculate resistivity values for crustal materials containing varying amounts of saline fluid [54]. In the modified Archie’s law, the resistivity of the rock is dependent on these factors: the resistivity of the rock matrix, the resistivity of the saline fluid, the Archie constant C, the Archie cementation exponent m, and the volume fraction of saline fluid in the rock. The bulk resistivity of A ranges from 1.326 to 2.5 Ω·m, and the temperature at its occurrence depth is about 310 °C. In this instance (Figure 12), 1.9 to 4.3 vol.% of fluids with a salinity of 5–7 wt.% is required [55].
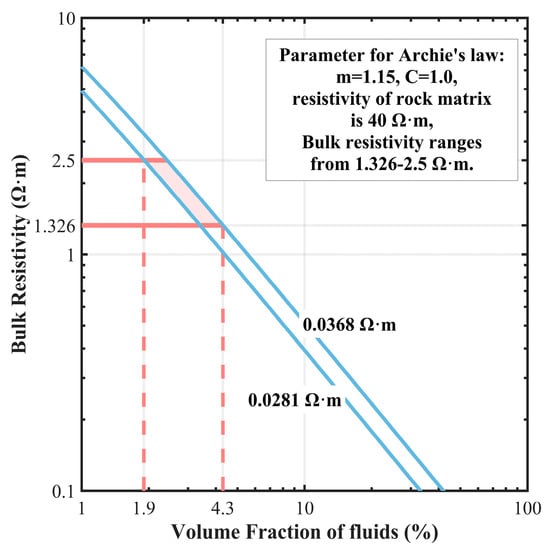
Figure 12.
Rock physics interpretation of anomaly A. Bulk resistivity of a two-phase system as a function of the conducting phase volume fraction using the modified Archie’s law [54]. Blue lines represent the resistivities of the conductive saline fluids with a salinity of 5–7 wt.% at 310 °C [56].
5. Conclusions
Through a series of MT 1-D inversion experiments on various synthetic geoelectric models, this study demonstrated that DEBA significantly outperforms conventional approaches in inversion accuracy and robustness. DEBA offers the following advantages. (1) The inversion results exhibit high reliability and strong global convergence, effectively reducing dependence on the initial model and mitigating the risk of local minima entrapment. This advantage is especially pronounced when resolving abrupt electrical discontinuities. DEBA demonstrates superior capability in approximating the global optimal solution, particularly in delineating complex geoelectric interfaces. (2) By integrating the dynamic fit error function (Equation (13)) and the cooling search mechanism (Equation (12)), DEBA achieves improved inversion stability and optimizes the selection of some parameters, such as loudness.
Despite these advantages, certain aspects of DEBA still require further refinement when addressing highly nonlinear and non-uniqueness challenges in practical inversion scenarios. (1) In general, the computational efficiency of global optimization algorithms is not superior to that of well-trained deep learning inversion methods or conventional linear inversion techniques. Because each bat within the same generation operates independently, future implementations can integrate multi-core parallel computing to significantly improve computational efficiency. (2) The performance of DEBA is dependent on the proper tuning of key algorithmic parameters, such as population size and number of iterations. Systematic experimental calibration is necessary to determine the optimal parameter configuration for different inversion scenarios. Future research should further investigate adaptive optimization strategies for key parameters, such as bat population size and iteration count, to achieve an optimal balance between computational efficiency and inversion accuracy.
Nevertheless, with optimized parameter selection, DEBA consistently outperforms both BA and SA in inversion accuracy. Unlike deep-learning-based methods, DEBA does not require large-scale training datasets, making it a more adaptable approach for geophysical applications in different geological settings. Furthermore, compared to traditional linear inversion, DEBA exhibits superior capability in resolving abrupt geoelectric discontinuities. These attributes establish DEBA as a robust and effective tool for the refined interpretation of deep geophysical data.
Following the averaged 1-D inversion of the study area in the central SLB, the low-resistivity anomaly in the upper crust was identified. Upon analysis, it may correspond to metal sulfide deposits or saline fluids. Hydrothermal fluids are not only associated with mineralization processes but may also lubricate faults, potentially triggering earthquakes. Therefore, in subsequent studies, we plan to acquire additional MT data and utilize the results of this study as an initial model for 3-D inversion. This approach will enable a more detailed investigation of the structure and origin of the identified anomaly and assess whether anomaly A has a deeper root as a potential source. These efforts will provide deeper insights into its formation mechanisms and its implications for mineralization.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/min15040359/s1. Figure S1. Comparison of forward responses for Model 1 using ModEM and DEBA [57]; Figures S2–S4. Reliability assessment of the resistivity for each layer in the DEBA model.
Author Contributions
S.Q.: conceptualization, methodology, visualization, writing—original draft, writing—review and editing. Y.Y.: investigation, methodology. Z.Z.: investigation, methodology. S.L.: investigation, supervision. C.L.: supervision, validation. X.L.: supervision, validation. X.W.: conceptualization, supervision, validation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (Grant No. 2023YFF0804100) and the National Natural Science Foundation of China (Grant 42074080 to Aihua Weng and Grant 42130302 to Aihua Weng and Wenliang Xu).
Data Availability Statement
Data will be made available upon request.
Acknowledgments
We are very grateful to the computational resources provided by Jilin Kingti Geoexploration Tech. Thanks to Junhao Guo, Ci Gao, and Weijie Guan for some suggestions. We acknowledge Xianfu Meng and Yaxin Sun for their efforts in field data acquisition. Additionally, MTPy code and the GMT software package are used for some figures. We sincerely thank the two anonymous reviewers for their insightful comments, which have greatly improved this paper.
Conflicts of Interest
The authors have no conflicts of interest related to any of the materials presented.
Abbreviations
The following abbreviations are used in this manuscript:
| MT | Magnetotelluric |
| BBMT | Broadband magnetotelluric |
| SLB | Songliao Basin |
| DEBA | Dynamic Error Bat Algorithm |
| BA | Bat Algorithm |
| SA | Simulated Annealing |
| UFE | Uniform Fit Error |
| 1-D | One-dimensional |
| 2-D | Two-dimensional |
| 3-D | Three-dimensional |
References
- Jin, S.; Sheng, Y.; Liu, C.; Wei, W.; Ye, G.; Jing, J.; Zhang, L.; Dong, H.; Yin, Y.; Xie, C. A Review of Relationship between the Metallogenic System of Metallic Mineral Deposits and Lithospheric Electrical Structure: Insight from Magnetotelluric Imaging. Minerals 2024, 14, 541. [Google Scholar] [CrossRef]
- Li, Y.; Weng, A.; Xu, W.; Zou, Z.; Tang, Y.; Zhou, Z.; Li, S.; Zhang, Y.; Ventura, G. Translithospheric Magma Plumbing System of Intraplate Volcanoes as Revealed by Electrical Resistivity Imaging. Geology 2021, 49, 1337–1342. [Google Scholar] [CrossRef]
- Ma, C.; Li, B.; Li, J.; Wang, P.; Dong, J.; Cui, Z.; Yang, S. Characteristics and Deep Mineralization Prediction of the Langmuri Copper–Nickel Sulfide Deposit in the Eastern Kunlun Orogenic Belt, China. Minerals 2024, 14, 786. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Tang, B.; Yan, G.; Ye, G.; Dong, J.; Liu, B.; Zhang, Y. Three-Dimensional Electrical Structure and Metallogenic Background of the Southeastern Hubei Ore Concentration Area. Minerals 2024, 14, 558. [Google Scholar] [CrossRef]
- Ye, G.; Unsworth, M.; Wei, W.; Jin, S.; Liu, Z. The Lithospheric Structure of the Solonker Suture Zone and Adjacent Areas: Crustal Anisotropy Revealed by a High-Resolution Magnetotelluric Study. J. Geophys. Res. Solid Earth 2019, 124, 1142–1163. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational Recipes for Electromagnetic Inverse Problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef]
- Key, K. Marine Electromagnetic Studies of Seafloor Resources and Tectonics. Surv. Geophys. 2012, 33, 135–167. [Google Scholar] [CrossRef]
- Comeau, M.J.; Käufl, J.S.; Becken, M.; Kuvshinov, A.; Grayver, A.V.; Kamm, J.; Demberel, S.; Sukhbaatar, U.; Batmagnai, E. Evidence for Fluid and Melt Generation in Response to an Asthenospheric Upwelling beneath the Hangai Dome, Mongolia. Earth Planet. Sci. Lett. 2018, 487, 201–209. [Google Scholar] [CrossRef]
- Heagy, L.J.; Cockett, R.; Kang, S.; Rosenkjaer, G.K.; Oldenburg, D.W. A Framework for Simulation and Inversion in Electromagnetics. Comput. Geosci. 2017, 107, 1–19. [Google Scholar] [CrossRef]
- Castillo-Reyes, O.; de la Puente, J.; García-Castillo, L.E.; Cela, J.M. Parallel 3-D Marine Controlled-Source Electromagnetic Modelling Using High-Order Tetrahedral Nédélec Elements. Geophys. J. Int. 2019, 219, 39–65. [Google Scholar] [CrossRef]
- Zhi-qiang, F.; Cheng-zao, J.; Xi-nong, X.; Shun, Z.; Zi-hui, F.; Cross, T.A. Tectonostratigraphic Units and Stratigraphic Sequences of the Nonmarine Songliao Basin, Northeast China. Basin Res. 2010, 22, 79–95. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, S.; Feng, Z. Discovery of “Enveloping surface of oil and gas overpressure migration” in the Songliao Basin and its bearings on hydrocarbon migration and accumulation mechanisms. Sci. China Earth Sci. 2012, 55, 2005–2017. [Google Scholar] [CrossRef]
- Comeau, M.J.; Becken, M.; Kuvshinov, A.V. Imaging the Whole-Lithosphere Architecture of a Mineral System—Geophysical Signatures of the Sources and Pathways of Ore-Forming Fluids. Geochem. Geophys. Geosyst. 2022, 23, e2022GC010379. [Google Scholar] [CrossRef]
- Cai, H.; Zhdanov, M.S. Joint Inversion of Gravity and Magnetotelluric Data for the Depth-to-Basement Estimation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1228–1232. [Google Scholar] [CrossRef]
- Xie, C.; Jin, S.; Wei, W.; Ye, G.; Jing, J.; Zhang, L.; Dong, H.; Yin, Y.; Wang, G.; Xia, R. Crustal Electrical Structures and Deep Processes of the Eastern Lhasa Terrane in the South Tibetan Plateau as Revealed by Magnetotelluric Data. Tectonophysics 2016, 675, 168–180. [Google Scholar] [CrossRef]
- Smith, J.T.; Booker, J.R. Rapid Inversion of Two- and Three-Dimensional Magnetotelluric Data. J. Geophys. Res. Solid Earth 1991, 96, 3905–3922. [Google Scholar] [CrossRef]
- Gao, C.; Li, Y.; Wang, X. AUTL: An Attention U-Net Transfer Learning Inversion Framework for Magnetotelluric Data. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3004505. [Google Scholar] [CrossRef]
- Jia, Z.; Li, Y.; Wang, Y.; Li, Y.; Jin, S.; Li, Y.; Lu, W. Deep Learning for 3-D Magnetic Inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5905410. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm; González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. [Google Scholar]
- Wang, R.; Yin, C.; Wang, M.; Wang, G. Simulated Annealing for Controlled-Source Audio-Frequency Magnetotelluric Data Inversion. Geophysics 2012, 77, E127–E133. [Google Scholar] [CrossRef]
- Abdelazeem, M.; Emary, E.; Hassanien, A.E. A Hybrid Bat-Regularized Kaczmarz Algorithm to Solve Ill-Posed Geomagnetic Inverse Problem. In Proceedings of the 1st International Conference on Advanced Intelligent System and Informatics (AISI2015), Beni Suef, Egypt, 28–30 November 2015; Gaber, T., Hassanien, A.E., El-Bendary, N., Dey, N., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 263–272. [Google Scholar]
- Poormirzaee, R.; Sarmady, S.; Sharghi, Y. A New Inversion Method Using a Modified Bat Algorithm for Analysis of Seismic Refraction Data in Dam Site Investigation. J. Environ. Eng. Geophys. 2019, 24, 201–214. [Google Scholar] [CrossRef]
- Essa, K.S.; Diab, Z.E. Magnetic Data Interpretation for 2D Dikes by the Metaheuristic Bat Algorithm: Sustainable Development Cases. Sci. Rep. 2022, 12, 14206. [Google Scholar] [CrossRef]
- Yang, X.-S. Bat Algorithm: Literature Review and Applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef]
- Cagniard, L. Basic Theory of the Magneto-telluric Method of Geophysical Prospecting. Geophysics 1953, 18, 605–635. [Google Scholar] [CrossRef]
- Tikhonov, T.A. On Determining Electrical Characteristics of the Deep Layers of the Earth’s Crust. Dokl. Akad. Nauk. SSSR 1950, 73, 295–297. [Google Scholar]
- Simpson, F.; Bahr, K. Practical Magnetotellurics; Cambridge University Press: Cambridge, UK, 2005; ISBN 978-0-521-81727-1. [Google Scholar]
- Rung-Arunwan, T.; Siripunvaraporn, W.; Utada, H. On the Berdichevsky Average. Phys. Earth Planet. Inter. 2016, 253, 1–4. [Google Scholar] [CrossRef]
- Gómez-Treviño, E.; Esparza Hernández, F.J.; Romo Jones, J.M. Effect of Galvanic Distortions on the Series and Parallel Magnetotelluric Impedances and Comparison with Other Responses. Geofís. Int. 2013, 52, 135–152. [Google Scholar] [CrossRef]
- Rung-Arunwan, T.; Siripunvaraporn, W.; Utada, H. Use of Ssq Rotational Invariant of Magnetotelluric Impedances for Estimating Informative Properties for Galvanic Distortion. Earth Planets Space 2017, 69, 80. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Three-Dimensional Magnetotelluric Inversion Using Non-Linear Conjugate Gradients. Geophys. J. Int. 2000, 140, 410–424. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. In Readings in Computer Vision; Fischler, M.A., Firschein, O., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1987; pp. 606–615. ISBN 978-0-08-051581-6. [Google Scholar]
- Ren, J.; Tamaki, K.; Li, S.; Junxia, Z. Late Mesozoic and Cenozoic Rifting and Its Dynamic Setting in Eastern China and Adjacent Areas. Tectonophysics 2002, 344, 175–205. [Google Scholar] [CrossRef]
- Wang, T.; Ma, G.; Comeau, M.J.; Becken, M.; Zhou, Z.; Liu, W.; Kang, J.; Han, J. Evidence for the Superposition of Tectonic Systems in the Northern Songliao Block, NE China, Revealed by a 3-D Electrical Resistivity Model. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022827. [Google Scholar] [CrossRef]
- Booker, J.R. The Magnetotelluric Phase Tensor: A Critical Review. Surv. Geophys. 2014, 35, 7–40. [Google Scholar] [CrossRef]
- Caldwell, T.G.; Bibby, H.M.; Brown, C. The Magnetotelluric Phase Tensor. Geophys. J. Int. 2004, 158, 457–469. [Google Scholar] [CrossRef]
- Jones, A.G.; Chave, A.D.; Egbert, G.; Auld, D.; Bahr, K. A Comparison of Techniques for Magnetotelluric Response Function Estimation. J. Geophys. Res. Solid Earth 1989, 94, 14201–14213. [Google Scholar] [CrossRef]
- Yadav, K.; Shah, M.; Sircar, A. Application of Magnetotelluric (MT) Study for the Identification of Shallow and Deep Aquifers in Dholera Geothermal Region. Groundw. Sustain. Dev. 2020, 11, 100472. [Google Scholar] [CrossRef]
- Chave, A.D.; Jones, A.G. (Eds.) The Magnetotelluric Method: Theory and Practice; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Zhan, W.; Pan, L.; Chen, X. A Widespread Mid-Crustal Low-Velocity Layer beneath Northeast China Revealed by the Multimodal Inversion of Rayleigh Waves from Ambient Seismic Noise. J. Asian Earth Sci. 2020, 196, 104372. [Google Scholar] [CrossRef]
- Bai, D.; Unsworth, M.J.; Meju, M.A.; Ma, X.; Teng, J.; Kong, X.; Sun, Y.; Sun, J.; Wang, L.; Jiang, C.; et al. Crustal Deformation of the Eastern Tibetan Plateau Revealed by Magnetotelluric Imaging. Nat. Geosci. 2010, 3, 358–362. [Google Scholar] [CrossRef]
- Becken, M.; Ritter, O.; Bedrosian, P.A.; Weckmann, U. Correlation between Deep Fluids, Tremor and Creep along the Central San Andreas Fault. Nature 2011, 480, 87–90. [Google Scholar] [CrossRef]
- Li, S.; Weng, A.; Li, J.; Shan, X.; Han, J.; Tang, Y.; Zhang, Y.; Wang, X. Deep Origin of Cenozoic Volcanoes in Northeast China Revealed by 3-D Electrical Structure. Sci. China Earth Sci. 2020, 63, 533–547. [Google Scholar] [CrossRef]
- Tang, Y.; Weng, A.; Yang, Y.; Li, S.; Niu, J.; Zhang, Y.; Li, Y.; Li, J. Connection between Earthquakes and Deep Fluids Revealed by Magnetotelluric Imaging in Songyuan, China. Sci. China Earth Sci. 2021, 64, 161–176. [Google Scholar] [CrossRef]
- Wannamaker, P.E.; Caldwell, T.G.; Jiracek, G.R.; Maris, V.; Hill, G.J.; Ogawa, Y.; Bibby, H.M.; Bennie, S.L.; Heise, W. Fluid and Deformation Regime of an Advancing Subduction System at Marlborough, New Zealand. Nature 2009, 460, 733–736. [Google Scholar] [CrossRef]
- Watson, M.P.; Hayward, A.B.; Parkinson, D.N.; Zhang, Z.M. Plate Tectonic History, Basin Development and Petroleum Source Rock Deposition Onshore China. Mar. Pet. Geol. 1987, 4, 205–225. [Google Scholar] [CrossRef]
- Hyndman, R.D.; Vanyan, L.L.; Marquis, G.; Law, L.K. The Origin of Electrically Conductive Lower Continental Crust: Saline Water or Graphite? Phys. Earth Planet. Inter. 1993, 81, 325–345. [Google Scholar] [CrossRef]
- Selway, K. On the Causes of Electrical Conductivity Anomalies in Tectonically Stable Lithosphere. Surv. Geophys. 2014, 35, 219–257. [Google Scholar] [CrossRef]
- Yoshino, T.; Noritake, F. Unstable Graphite Films on Grain Boundaries in Crustal Rocks. Earth Planet. Sci. Lett. 2011, 306, 186–192. [Google Scholar] [CrossRef]
- Jiang, G.-Z.; Gao, P.; Rao, S.; Zhang, L.-Y. Compilation of heat flow data in the continental area of China (4th edition). Chin. J. Geophys. 2016, 59, 2892–2910. (In Chinese) [Google Scholar] [CrossRef]
- Sawyer, E.W.; Cesare, B.; Brown, M. When the Continental Crust Melts. Elements 2011, 7, 229–234. [Google Scholar] [CrossRef]
- Nover, G. Electrical Properties of Crustal and Mantle Rocks—A Review of Laboratory Measurements and Their Explanation. Surv. Geophys. 2005, 26, 593–651. [Google Scholar] [CrossRef]
- Sun, X.; Zhan, Y.; Zhao, L.; Xu, J.; Zhao, Y.; Zhao, B.; Yang, W. Does a Shallow Magma Reservoir Exist in the Wudalianchi Volcanic Field? Constraints From Magnetotelluric Imaging. Geophys. Res. Lett. 2023, 50, e2023GL104318. [Google Scholar] [CrossRef]
- Glover, P.W.J.; Hole, M.J.; Pous, J. A Modified Archie’s Law for Two Conducting Phases. Earth Planet. Sci. Lett. 2000, 180, 369–383. [Google Scholar] [CrossRef]
- Li, Y.; Weng, A.; Zhou, Z.; Guo, J.; Li, S.; Ventura, G.; Xu, W. Crustal Root Shapes the Plumbing System of a Monogenetic Volcanic Field as Revealed by Magnetotelluric Data. Earth Planet. Sci. Lett. 2024, 626, 118523. [Google Scholar] [CrossRef]
- Sinmyo, R.; Keppler, H. Electrical Conductivity of NaCl-Bearing Aqueous Fluids to 600 °C and 1 GPa. Contrib. Miner. Pet. 2017, 172, 4. [Google Scholar] [CrossRef]
- Kelbert, A.; Meqbel, N.; Egbert, G.D.; Tandon, K. ModEM: A Modular System for Inversion of Electromagnetic Geophysical Data. Comput. Geosci. 2014, 66, 40–53. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).